Что такое луч в математике
Не секрет, что знания, которые вы получили в школьные годы не всегда остаются с вами впоследствии Иногда бывает полезно изучить новое или освежить в памяти то, что вы давно забыли. Сегодня вы вспомните такое понятие как луч.
Луч — геометрическое понятие
Луч — это такая прямая линия, один из концов которой ограничен точкой, а другой продолжается до бесконечности. Таким образом, фигура тянется вперёд без ограничений. но только с одной стороны. Вторая сторона не может тянуться дальше точки, которая является началом фигуры.
На картинке вы можете посмотреть, что такое луч и как он выглядит:
Луч отмечается посредством строчной латинской буквы или двух таких точек, которые обозначены заглавными буквами латинского алфавита.
Если вы увидите отрезок с двумя точками и продолжите его в одну из сторон, как показано на рисунке, то получится луч.
Отличия луча от прямой и от отрезка
В геометрии есть три схожих понятия, которые подразумевают под собой черту — это луч, отрезок, прямая. Эти фигуры всегда изображаются без изгибов и имеют ряд особенностей.
В рамках курса математики луч — это полупрямая. Дело в том, что с одного конца он обладает признаком бесконечности, который присущ прямой линии.
В начальной точке луч имеет сходство с отрезком, так как он так же ограничен точкой.
Обратите внимание — быстро отличить фигуры друг от друга вы можете по наличию у них начала и конца:
- отрезок имеет начальную и конечную точки;
- луч — только начало;
- прямая — не располагает начальной и конечной точками.
Взаимное расположение лучей
Если на прямой линии вы поставите точку, то на ней сформируются два таких луча, начало которых находится в одной точке.
На рисунке начало для лучей — общая точка A.
По взаимному расположению лучи делятся на пересекающиеся и непересекающиеся.
Параллельный луч — это фигура, у которой любая точка находится на одинаковом расстоянии от соответствующей точки другого луча. Параллельные лучи не могут пересекаться.
Дополнительные лучи — это фигуры, которые обладают такими признаками, как:
- имеют совпадающее начало в одной точке;
- располагаются на одной прямой линии;
- направляются в разные стороны, то есть угол между ними составляет 180 градусов.
Можно ли сравнить два луча?
Луч — это такая фигура, которую нельзя измерить. Он продолжается без ограничений, поэтому не обладает характеристикой длины.
Так как невозможно измерить несколько лучей, сравнить их вы тоже не сможете.
Луч — альтернативные значения слова
Русский язык достаточно сложен и необычайно многообразен, поэтому многие слова имеют несколько разных значений, а разнообразные сочетания способны радикально менять смысл слов, которые являются их составными частями.
Сможете ли вы сходу ответить на вопрос: «Что такое луч света?». Это словосочетание употребляется нами с детства, но не так легко выразить, что оно означает.
Такая фраза описывает прямую линию, по которой направляется световая энергия. Эта энергия исходит от разных источников:
В быту вы можете услышать словосочетание «луч света в тёмном царстве». Такие слова означают — среди негативных явлений присутствует что-то хорошее. Короткое слово всегда ассоциируется с чем-то светлым, добрым и положительным.
Фраза «луч надежды» указывает, что среди множества нежелательных последствий существует не высокая вероятность благополучного исхода.
Плоскость, прямая линия, луч
Плоскость в математике можно сравнить с другими плоскостями, которые окружают нас в повседневной жизни: школьная доска, лист бумаги, экран планшета или смартфона и т.д. На них мы можем легко обозначить точки и линии, которые мы изучали на предыдущем уроке. На школьной доске мы это делаем мелом или фломастером, на листе бумаги можем нарисовать их ручкой, карандашом, фломастером; когда мы прокручиваем окно сайта или приложения на смартфоне, мы проводим на экране пальцем линию, когда переходим по ссылкам – ставим на его плоскости точку.
Но эти примеры плоскостей из жизни имеют свои размеры и границы, они конечные, их можно измерять.
Плоскость – это воображаемая абсолютно ровная и неизменяемая поверхность, которая не имеет толщины, но обладает бесконечными длиной и шириной.
Плоскость нельзя измерять, потому что она бесконечная.
Плоскость нельзя согнуть, в каком бы положении она ни находилась.
Все объекты и фигуры, которые изучаются в курсе математики 5 класса, находятся на плоскости.
Прямая линия
Прямая линия – абсолютно ровная линия, которая длится бесконечно в обе стороны, и на всем ее протяжении не изгибается и не преломляется.
Даже когда мы рисуем на листе бумаги небольшой кусок прямой линии, то мы предполагаем , что этот лист бумаги – это бесконечная плоскость, и мы можем мысленно раздвинуть видимые границы бумаги и продлить прямую бесконечно долго.
Обозначение прямой
В основном прямую, как и любую другую линию, обозначают при помощи строчной (маленькой) буквы латинского алфавита .
Иногда обозначение прямой линии происходит при помощи двух точек , которые принадлежат (часто говорят просто – лежат на) этой прямой. В этом случае ее обозначают названием этих двух точек.
Например, на рисунке 1 обозначены такие прямые:
Рис. 1 Обозначение прямой линии
Если на одной прямой лежат три и более известных нам точек, то обозначить эту линию можно любой из комбинаций имен любых двух точек .
Рис. 2 Обозначение прямой с несколькими точками
На рисунке 2 видно, что на одной прямой b лежат четыре точки: D , G , H , O . Поэтому данную прямую мы можем назвать любым из этих семи имен: b , DG , DH , DO , GH , GO или HO .
Некоторые свойства прямой
Две точки, лежащие на одной прямой, создают отрезок этой прямой.
Через две любые точки на плоскости можно провести единственную прямую.
Рис. 3 Отрезок на прямой
Две разные прямые могут пересекаться или не пересекаться.
Две прямые пересекаются в том случае, если у них есть общая точка.
И наоборот, если у двух разных прямых нет общей точки, тогда эти прямые не пересекаются .
Рис. 5 Пересечение прямых
На рисунке 5 можно видеть, что прямые l и q пересекаются в точке O , а прямые q и g не пересекаются.
Обозначение пересечения письменно записывается при помощи символа ∩: l ∩ q — прямая l пересекается с прямой q .
Как вам уже известно из этого урока, на рисунках мы можем отображать только часть прямых (поскольку они бесконечные), и что их можно мысленно увеличивать, делать более протяженными. Поэтому, если мысленно продлить прямые l и g , то станет понятно, что они тоже пересекаются.
Взаимное расположение точек и прямой , а также их обозначение, точно такое же, как и у всех линий вообще.
Более подробно об этих и других свойствах прямой написано в уроке геометрии 7 класса.
Луч – это часть прямой, которая начинается в определенной точке и длится бесконечно в одну сторону.
Рис. 6 Деление прямой линии точкой
На рисунке 1 точка O делит прямую a на две части, то есть, на два луча. Один из них, как вы видите, длится бесконечно вправо, а другой – бесконечно влево. Оба они начинаются в одной и той же точке O , которую называют началом луча.
У луча есть начало, но нет конца. От прямой луч отличается тем, что луч бесконечно продолжается только в одну сторону.
Свое название этот математический объект получил по аналогии с лучом света, который имеет начало (источник света), но определенного конца у него нет.
Обозначение луча
Луч, как и прямую, обозначают двумя способами.
Рис. 7 Обозначение луча
На рисунке 2 приведены примеры обозначения луча:
- a – строчной (маленькая) буква латинского алфавита;
- OF – точками, расположенными на луче. При этом на первом месте всегда пишут точку начала луча, а на втором – любую точку, которая принадлежит лучу.
Луч имеет второе название – полупрямая.
Два луча, которые лежат на одной прямой, начинаются в одной точке и направлены в разные стороны, называются дополнительными друг другу лучами , поскольку в соединенном виде они формируют одну прямую линию в точке их начала.
Если лучи лежат на одной прямой, начинаются в одной точке и направлены в одну сторону, их называют совпадающие , или говорят, что эти лучи совпадают .
Рис. 8 Дополнительные друг другу и совпадающие лучи
На рисунке 8 видно, что:
- CB и CH – дополнительные друг другу лучи,
- BC и BH – совпадающие лучи,
- HC и HB – совпадающие лучи.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.7 / 5. Количество оценок: 23
Луч математика в треугольнике
Луч — это часть прямой линии, расположенная по одну сторону от любой точки, лежащей на этой прямой. Луч также называется полупрямой.
Любой луч имеет начало и направление. Начало луча, начальная точка или вершина луча — это точка, из которой исходит луч. Таким образом, у луча есть начало, но нет конца.
Рассмотрим три луча с общим началом:
Все 3 луча имеют общую начальную точку O, но разные направления. Про каждый из них можно сказать: луч исходит из точки O или луч исходящий из точки O .
Дополнительные лучи
Любая точка, лежащая на прямой линии, делит эту прямую на две полупрямые, то есть на две части. Каждая из этих частей будет называться дополнительным лучом относительно второго луча:
Дополнительные лучи — это лучи, имеющие общее начало, противоположные направления и лежащие на одной прямой. Также можно сказать, что дополнительными называются лучи, дополняющие друг друга до прямой линии.
Обозначение лучей
Луч обозначают одной строчной латинской буквой:
Также луч можно обозначить двумя точками, лежащими на нём:
При обозначении луча двумя точками, на первом месте ставится буква, обозначающая начало луча, а на втором — буква, обозначающая какую-либо другую его точку: луч BC.
Посмотрим на следующий пример:
Луч с началом в точке A можно обозначить как AB или AC.
http://izamorfix.ru/matematika/planimetriya/luch.html
Треугольник – это геометрическая фигура, состоящая из трех точек на плоскости, которые не лежат на одной прямой, и трех последовательно соединяющих их отрезков.
Точки называют вершинами треугольника, а отрезки – сторонами. Вершины треугольника обозначают заглавными латинскими буквами.
Виды треугольников по углам
Треугольники классифицируются по углам: остроугольные; тупоугольные; прямоугольные.
Виды треугольников по сторонам
Треугольники классифицируются по сторонам: разносторонний; равнобедренный; равносторонний.
Медиана, биссектриса, высота, средняя линия треугольника
Медиана
Определение
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
В любом треугольнике можно провести три медианы, так как сторон – три. На рисунке показаны медианы треугольника АВС: AF, EC, BD.
По данному рисунку также видно, что медианы треугольника пересекаются в одной точке – точке О. Это справедливо для любого треугольника.
Биссектриса
Определение
Биссектрисой треугольника называется луч, исходящий из вершины угла треугольника и делящий его пополам.
В любом треугольнике можно провести три биссектрисы, так как углов – три. На рисунке показаны биссектрисы треугольника ЕDC: DD1, EE1 и CC1.
По рисунку также видно, что биссектрисы имеют одну точку пересечения. Это справедливо для любого треугольника.
Высота
Определение
Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к противоположной стороне.
На рисунке показаны высоты треугольника АВС: АН1, ВН2 и СН3.
По рисунку видно, что высоты треугольника пересекаются в одной точке. Это также справедливо для любого треугольника.
Средняя линия
Определение
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке показаны три средние линии треугольника АВС: MN, KN и MK.
Средняя линия обладает следующими свойствами: она параллельна противоположной стороне; она равна половине противоположной стороны. Так, на данном рисунке MN параллельна АС, KN параллельна АВ, MK параллельна ВС. Также MN=0,5АС, KN=0,5АВ и MK=0,5ВС. Например, если известно, что сторона АС=20 см, то средняя линия МN равна половине АС, то есть МN=10 см. Или, например, если средняя линия МК=12 см, то сторона ВС будет в два раза больше, то есть ВС=24 см.
Задание 25OM21R
В треугольнике АВС известны длины сторон АВ=36, АС=54, точка О – центр окружности, описанной около треугольника АВС. Прямая ВD, перпендикулярная прямой АО, пересекает сторону АС в точке D. Найдите СD.
Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.
При построении прямой АО образовалась точка пересечения этой прямой с окружностью, обозначим её буквой Е и соединим с точкой В и с точкой С. Получим вписанные углы АВЕ и АСЕ, опирающиеся на диаметр АЕ, следовательно угол АВЕ и АСЕ равны по 900.
Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.
Составим отношение сторон:
AEAB=ABAF откуда по свойству пропорции АВ2=АЕ∙АF
Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.
Составим отношение сторон:
AEAD=ACAF ; откуда выразим AD=AE∙AFАC=AE∙AFAC
Теперь рассмотрим наши два полученных равенства: АВ2=АЕ∙АF и AD=AE∙AFAC
Видим, что 362=АЕ∙АF (подставили вместо АВ значение 36), также у нас известно, что АС=54. Найдем из второго равенства AD=AE∙AFAC=36254=24
Теперь найдем CD=AC-AD=54-24=30
Ответ: 30
pазбирался: Даниил Романович | обсудить разбор
Задание 18OM21R
На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.
Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.
Ответ: 4
pазбирался: Даниил Романович | обсудить разбор
Задание 15OM21R
В треугольнике АВС известно, что угол ВАС равен 840, АD – биссектриса. Найдите угол ВАD. Ответ дайте в градусах.
Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 840:2=420
Ответ: 42
pазбирался: Даниил Романович | обсудить разбор
Даниил Романович | Просмотров: 7.8k
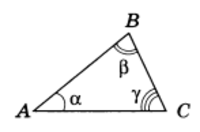
Рис.1
Пусть А, В, С — три произвольные точки, не лежащие на одной прямой. Фигура, состоящая из трех отрезков АВ, ВС, АС (рис.1), называется треугольником
ABC (обозначается: Л ABC). Треугольником также называют часть плоскости, ограниченную отрезками АВ, ВС, АС (плоский треугольник).
Точки А, В, С — вершины, отрезки АВ, ВС, АС — стороны треугольника. Сумма длин трех сторон треугольника называется его периметром.
Углом (или внутренним углом) треугольника ABC при вершине А называется угол, образованный лучами АВ и АС. Так же определяются углы треугольника при вершинах В и С.
Углы CAB, ABC у ВСА треугольника ABC часто обозначают одной буквой (А, В, С соответственно) или греческими буквами α, β, γ (при этом внутри углов рисуют дуги, см. рис. 1). Говорят, что угол А противолежит стороне ВС или сторона ВС противолежит углу А; так же угол В и сторона АС, угол С и сторона АВ противолежат (друг другу).
Рис.2
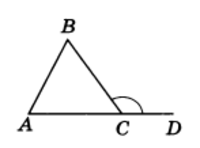
Угол, смежный с каким-нибудь углом треугольника, называется внешним углом этого треугольника. Таков, например, угол BCD (рис.2). При каждом угле треугольника можно построить по два внешних угла (продолжив одну или другую сторону угла). Эти два угла равны как углы вертикальные.
Рис.3
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противолежащей стороны, называется биссектрисой треугольника (рис.3).
Любой треугольник имеет три биссектрисы.
Рис.4
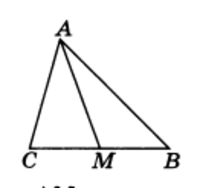
Отрезок, соединяющий вершину треугольника с серединой противолежащей стороны, называется медианой треугольника (рис.4).
Любой треугольник имеет три медианы.
Рис.5
Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противолежащую сторону, называется высотой треугольника (рис. 5).
Любой треугольник имеет три высоты.
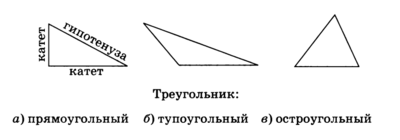
Рис.6
Если один из углов треугольника прямой, то треугольник прямоугольный (рис.6, а); если один из углов тупой — тупоугольный (рис.6, б); если все три угла острые — остроугольный (рис.6, в).
В прямоугольном треугольнике сторона, лежащая против прямого угла, называется гипотенузой, две другие стороны — катетами.
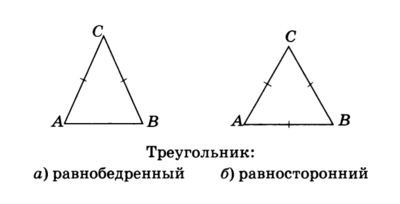
Рис.7
Треугольник, две стороны которого равны, называется равнобедренным (АС = ВС на рис.7, а). Третья сторона — основание, равные стороны — боковые стороны.
Треугольник, три стороны которого равны (АС = ВС = АВ на рис.7, б), называется равносторонним.
Пример 1. Периметр равнобедренного треугольника равен 50 м, боковая сторона — 15 м. Найти основание.
Решение. Обозначим основание через х. Тогда периметр треугольника составит x + 15 + 15. По условию эта сумма равна 50 м, т. е. х + 30 = 50, откуда х = 20. Итак, основание равно 20 м.
Пример 2. Периметр равнобедренного треугольника равен 70 м. Боковая сторона больше основания на 5 м. Найти стороны треугольника.
Решение. Воспользуемся рисунком 7, а. Обозначим АВ через х, тогда ВС = АС через х + 5.

Рис.7
Тогда периметр треугольника составит (х + 5) + (х + 5) + х.
По условию эта сумма равна 70, т. е. Зх + 10 = 70, или х = 20.
Следовательно, стороны треугольника 20 см, 25 см и 25 см.
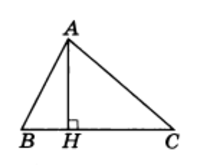
Пример 3. Треугольник, периметр которого равен 24 см, делится высотой на два треугольника, периметры которых равны 12 см и 20 см. Найти высоту треугольника.
Решение. Пусть условию задачи отвечает рисунок 5.
АН — высота треугольника ABC
Рис.5
Обозначим периметры треугольников АВС, АВН и АСН соответственно через Р, Р1 и Р2. Из рисунка 5 видно, что Р1 + Р2 = Р + 2АН, или 12 + 20 = 24 + 2AH, откуда АН = 4.
Пример 4. Укажите номера верных утверждений.
-
Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
-
Треугольник со сторонами 1, 2, 4 существует.
-
Если в ромбе один из углов равен 90°, то такой ромб — квадрат.
Видео-решение.
Укажите номера верных утверждений
Луч и угол

Обновлено 04.08.2020
Луч
Луч — это часть прямой, у которой есть
начало, но нет конца.
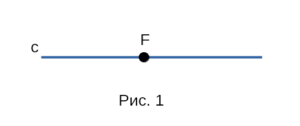
Проведём прямую с и отметим на ней точку F. Точка F разделяет прямую c на две части.
Каждая из этих частей называется лучом, исходящим из точки F. Пример двух лучей,
исходящих из точки F на рисунке 1.
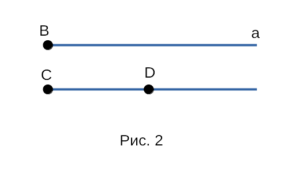
Точка F — начало каждого из лучей. Луч обычно обозначают малой латинской буквой,
либо двумя большими латинскими буквами (первая буква обозначает начало луча,
а вторая буква обозначает какую-нибудь точку на луче). Примеры лучей на рисунке 2.
Угол
Угол — геометрическая фигура, состоящая из точки и
двух лучей, исходящих из этой точки.
Лучами называются стороны угла, а точка называется вершиной угла.
Угол обозначают математическим символом ∠.
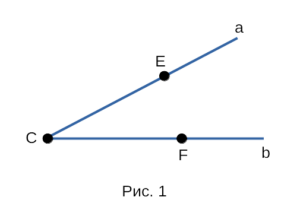
На рисунке 1 изображен угол с вершиной С и сторонами a и b. На сторонах отмечены
точки E и F. Угол в данном случае обозначают вот так: ∠ab, или ∠ECF, или еще проще ∠О.
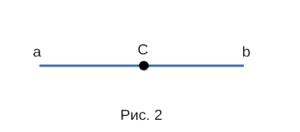
Если обе стороны угла лежат на одной прямой, то угол развернутый, иначе угол неразвернутый.
На рисунке 2 изображен развернутый угол с вершиной С и сторонами a и b.
Любой угол разделяет плоскость на две части. Существует внешняя
и внутренняя область угла рисунок 3.
Если плоскость разделяет развернутый угол, то каждую из двух частей
можно считать внутренней областью угла. Фигуру также называют углом,
если она состоит из угла и его внутренней области. Если луч исходящий из
вершины неразвернутого угла и проходящий внутри угла, делит угол на два угла.
Перпендикуляр от точки к прямой
Отрезок (AC) называется перпендикуляром, проведённым из точки (A) прямой (a), если прямые (AC) и (a) перпендикулярны.
Точка (C) называется основанием перпендикуляра.
От точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

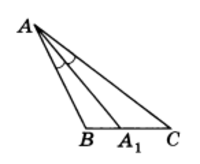
Докажем, что от точки (A), не лежащей на прямой (BC), можно провести перпендикуляр к этой прямой.
Допустим, что дан угол
∠ABC
.
Отложим от луча (BC) угол, равный данному, и совместим эти углы накладыванием (представим, что сложим лист бумаги с равными углами по стороне (BC)).
Сторона (BA) совместится со стороной
BA1
.
При этом точка (A) наложится на некоторую точку
A1
.
Следовательно, совмещается угол
∠ACB
с
∠A1CB
.
Но углы
∠ACB
и
∠A1CB
— смежные, значит, каждый из них прямой.
Прямая
AA1
перпендикулярна прямой (BC), а отрезок (AC) является перпендикуляром от точки (A) к прямой (BC).
Если допустить, что через точку (A) можно провести ещё один перпендикуляр к прямой (BC), то он бы находился на прямой, пересекающейся с
AA1
. Но две к одной и той же прямой перпендикулярные прямые должны быть параллельны и не могут пересекаться.
Это противоречие, что означает: через данную точку к прямой можно провести только один перпендикуляр.
Медианы, биссектрисы и высоты треугольника
Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
Поэтому для построения медианы необходимо выполнить следующие действия:
1) найти середину стороны;
2) соединить точку, являющуюся серединой стороны треугольника, с противолежащей вершиной отрезком — это и будет медиана.
У треугольника три стороны, следовательно, можно построить три медианы.
Все медианы пересекаются в одной точке.
Биссектриса треугольника — это отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противоположной стороне.
Поэтому для построения биссектрисы необходимо выполнить следующие действия:
1) построить биссектрису какого-либо угла треугольника (биссектриса угла — это луч, выходящий из вершины угла и делящий его на две равные части);
2) найти точку пересечения биссектрисы угла треугольника с противоположной стороной;
3) соединить вершину треугольника с точкой пересечения на противоположной стороне отрезком — это и будет биссектриса треугольника.
У треугольника три угла и три биссектрисы.
Все биссектрисы пересекаются в одной точке.
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противоположную сторону.
Поэтому для построения высоты необходимо выполнить следующие действия:
1) провести прямую, содержащую одну из сторон треугольника (в случае, если проводится высота из вершины острого угла в тупоугольном треугольнике);
2) из вершины, лежащей напротив проведённой прямой, опустить перпендикуляр к ней (перпендикуляр — это отрезок, проведённый из точки к прямой, составляющей с ней угол 90°) — это и будет высота.
Так же как медианы и биссектрисы, треугольник имеет три высоты.
Высоты треугольника пересекаются в одной точке.
Но, как выше упомянуто, для некоторых видов треугольников построение высот и точки их пересечения отличаются.
Если треугольник с прямым углом, то стороны, образующие прямой угол, можно назвать высотами, так как они перпендикулярны одна к другой. Точкой пересечения высот является общая вершина перпендикулярных сторон.
Если треугольник с тупым углом, то высоты, опущенные с вершин острых углов, выходят вне треугольника к продолжениям сторон. Прямые, на которых расположены высоты, пересекаются вне треугольника.
Обрати внимание!
Если из одной и той же вершины провести медиану, биссектрису и высоту, то медиана окажется самым длинным отрезком, а высота — самым коротким отрезком.
Равнобедренный треугольник
Если у треугольника две стороны равны, то такой треугольник называют равнобедренным.
Равные стороны называют боковыми, а третью сторону — основанием.
(AB = BC) — боковые стороны , (AC) — основание.
Если у треугольника все три стороны равны, то такой треугольник является равносторонним.
Равнобедренный треугольник имеет некоторые свойства, которые не имеют треугольники с разными сторонами.
1. В равнобедренном треугольнике углы при основании равны.
2. В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
3. В равнобедренном треугольнике медиана, проведённая к основанию, является биссектрисой и высотой.
4. В равнобедренном треугольнике высота, проведённая к основанию, является биссектрисой и медианой.
Первое и второе свойство можно доказать, если докажем равенство двух треугольников, которые образуются, если из угла напротив основания провести биссектрису (BD).
Рассмотрим равнобедренный треугольник (ABC) с основанием (AC) и докажем, что
ΔABD=ΔCBD
.
Пусть (BD) — биссектриса треугольника (ABC).
ΔABD=ΔCBD
по первому признаку равенства треугольников ((AB = BC) по условию, (BD) — общая сторона,
∠ABD=∠CBD
, так как (BD) — биссектриса).
У равных треугольников равны все соответствующие элементы:
1.
∠A=∠C
— доказано, что прилежащие основанию углы равны.
2. (AD = DC) — доказано, что биссектриса является медианой.
3.
∠ADB=∠CDB
— так как смежные углы, сумма которых
180°
, равны, то каждый из них равен
90°
, то есть медиана является высотой.
Можно очень легко самостоятельно доказать и третье, и четвёртое свойства.