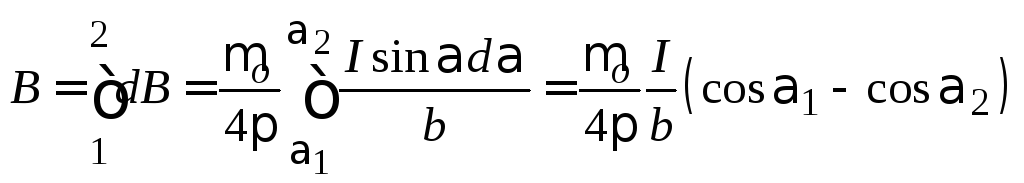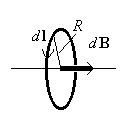Как найти магнитную индукцию в центре квадрата

Решение.
Для решения задачи необходимы: μ₀ = 4∙π⋅10^-7 Гн/м − магнитная постоянная. 
Рассмотрим четыре участка, АВ, ВС, СД, ДА.
Направление вектора магнитной индукции на каждом участке определим по правилу буравчика. В точке О результирующий вектор магнитной индукции направлен от нас. Применим принцип суперпозиции.

[ begin{align}
  & vec{B}={{{vec{B}}}_{AB}}+{{{vec{B}}}_{BC}}+{{{vec{B}}}_{CD}}+{{{vec{B}}}_{DA}},  \
 & Ox: B={{B}_{AB}}+{{B}_{BC}}+{{B}_{CD}}+{{B}_{DA}} (1). \
end{align}
 ]

Определим модуль вектора магнитной индукции на участке АВ.
Индукция магнитного поля в произвольной точке О, созданного отрезком проводника с током конечной длины, определим используя закон Био —  Савара —  Лапласа.

[ begin{align}
  & dB=frac{{{mu }_{0}}cdot I}{4cdot pi cdot R}cdot sin alpha dalpha , B=frac{{{mu }_{0}}cdot I}{4cdot pi cdot R}cdot intlimits_{{{alpha }_{1}}}^{{{alpha }_{2}}}{sin alpha dalpha ,} \
 & B=frac{{{mu }_{0}}cdot I}{4cdot pi cdot R}cdot (cos {{alpha }_{1}}-cos {{alpha }_{2}}) (3). \
end{align} ]

Где: R — расстояние от т. О до проводника; – α₁ и α₂ углы, образованные радиус-вектором, проведенном в т. О соответственно из начала и конца проводника, с направлением тока.
Определим модуль вектора магнитной индукции на каждом участке.
α₂ = 3∙π/4, α₁ =  π/ 4.

[ begin{align}
  & B=frac{{{mu }_{0}}cdot I}{4cdot pi cdot R}cdot (cos frac{pi }{4}-cos frac{3cdot pi }{4}) , B=frac{{{mu }_{0}}cdot I}{4cdot pi cdot R}cdot (frac{sqrt{2}}{2}+frac{sqrt{2}}{2}) , \
 & {{B}_{BC}}={{B}_{DA}}={{B}_{CD}}={{B}_{AB}}=frac{sqrt{2}cdot {{mu }_{0}}cdot I}{4cdot pi cdot R} (5),R=frac{d}{2} (6), \
 & B=4cdot frac{sqrt{2}cdot {{mu }_{0}}cdot I}{2cdot pi cdot d}, B=2cdot frac{sqrt{2}cdot {{mu }_{0}}cdot I}{pi cdot d} (7). \
 & B=frac{2cdot sqrt{2}cdot 4cdot pi cdot {{10}^{-7}}cdot 5}{pi cdot 0,15}=37,6cdot {{10}^{-6}}. \
end{align}
 ]

Ответ 9,43 мкТ получается если бы квадрат был изготовлен из проволоки длиной 15 см.
Ответ: В = 37,6∙10^-6 Тл.

где
v
– скорость направленного движения
свободных носителей заряда. Умножив В
на количество свободных носителей
заряда в элементе проводника dl,
получим индукцию магнитного поля,
созданную этим элементом проводника с
током,

поскольку
env
= j*,

;

поскольку
dl^.j
= dl^.j
(dl
и j совпадают
по направлению),

.

Таким
образом, индукция магнитного поля,
созданного элементом dl
проводника с током I
на расстоянии r
от элемента проводника, определяется
выражением

.

Это выражение и
представляет собой закон Био–Савара–Лапласа.

Из
закона видно, что вектор магнитной
индукции dB
всегда перпендикулярен плоскости, в
ко-торой лежат векторы dl
и r.
Его направление определяется по правилу
правого винта.

Модуль
вектора dB
определяется из выражения

,

где

– угол между векторами dl
и r.

______________________

*
Здесь j
– вектор плотности тока.

Необходимо
учесть, что полученное выражение
позволяет рассчитать индукцию магнитного
поля, созданную одним бесконечно малым
элементом проводника dl
с током I.

Для
того чтобы найти магнитную индукцию,
созданную всем
проводником,
необходимо использовать принцип
суперпозиции, т. е. просуммировать
векторы dB,
созданные каждым элементом проводника
в интересующей нас точке.

3.4.1. Индукция магнитного поля отрезка прямолинейного проводника с током

Для всех бесконечно
малых элементов dl
отрезка векторы dl
и r
лежат в плоскости листа.
Поэтому векторы dB,
созданные в выбранной нами точке
различными элементами проводника
направлены одинаково – перпендикулярно
плоскости листа. Следовательно, сложение
векторов dB
можно заменить сложением их модулей
dB.

И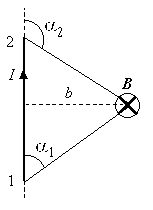з
рисунка видно, чтоr
= b/sin

(b
– расстояние от проводника до инте-ресующей
нас точки), и

.

Тогда
индукция, созданная элементом проводника
dl,
равна

.

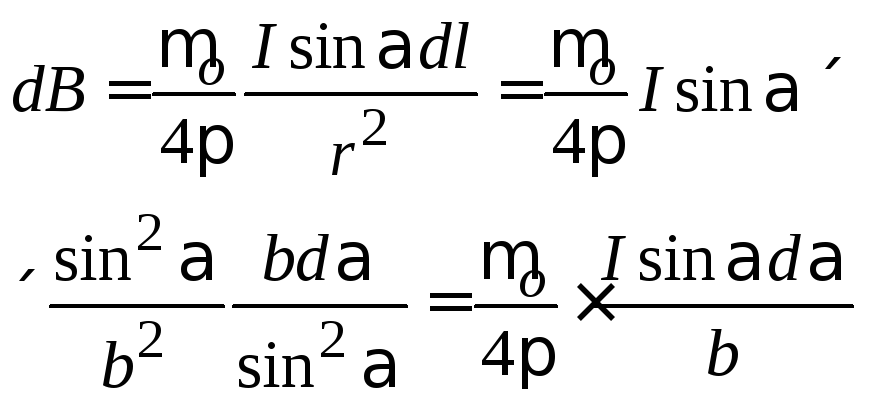
Индукция
магнитного поля, созданного всем
проводником, может быть найдена как
интеграл от dB
в пределах от  ₁
до + ₂:

Иногда
удобнее воспользоваться другим
выражением:

(обратите
внимание на рисунок, показывающий углы
₁
и ₂).

О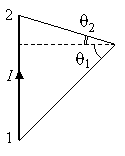братите
также внимание на то, что если точка
расположена так, как показано на следующем
рисунке, то₂
меняет знак и формула для расчёта
магнитного поля прямолинейного отрезка
записывается следующим образом:

.

3.4.2. Индукция магнитного поля бесконечно длинного прямолинейного проводника с током

Если
длина прямого проводника бесконечно
велика, то ₁
= 0, а ₂
= .

В
этом случае индукция магнитного поля,
созданного проводником, будет равна

.

Т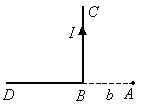аким
образом, индукция магнитного поля,
созданного бесконечно длинным проводником
прямо пропорциональна току в проводнике
и обратно пропорциональна расстоянию
от проводника до интересующей нас точки.

Дополнительно
рассмотрим магнитное поле, созданное
бесконечным проводником, который изогнут
под прямым углом.

Ограничимся
получением расчётной формулы для точки
А,
расположенной на продолжении одной из
половин проводника.

Участок
DB
в точке А
не создаёт магнитного поля, так как для
него ₁
и ₂
равны 0.

Для
участка ВС
₁
= 90⁰,
₂
= -180⁰.
Поэтому индукция, созданная этим
участком, равна

.

Таким
образом, индукция магнитного поля в
точке А
равна половине индукции, созданной
прямым бесконечно длинным проводником
с таким же током.

3.4.3. Индукция магнитного поля в центре квадрата

Рассмотрим
квадрат со стороной а, в котором течёт
токI.

Все
стороны квадрата создают в его центре
одинаковое магнитное поле. Поэтому если
индукция, созданная одной стороной,
равна В,
то магнитная индукция, созданная всеми
сторонами, равна 4В.

В
рассматриваемом случае ₁
= 45⁰,
а ₂
= 135⁰
(см. рисунок).

Индукция магнитного
поля, созданного одной стороной, равна:

.

Соответственно
индукция магнитного поля, созданного
всеми сторонами, равна

.

В показанном на
рисунке случае индукция магнитного
поля направлена перпендикулярно
плоскости квадрата на нас.

3.4.4. Расчёт магнитного поля замкнутого кругового тока (витка с током).

Пусть
радиус витка равен R,
а ток в нём – I.

Вначале рассмотрим расчёт
поля в центре витка.

Каждый
элемент тока будет создавать индукцию,
направленную вдоль оси витка. Поэтому,
как и в предыдущем случае, сложение dB
алгебраическое и

,

(в
каждой точке 
= 90⁰)

.

Поле
на оси витка на расстоянии bот центра
витка рассчитывается несколько сложнее.Вэтом случае векторыdBне параллельны друг другу.

При суммировании
составляющие векторов dB,
перпендикулярные оси, уничтожаются, а
параллельные оси – складываются.

Из рисунка видно,
что

;

.

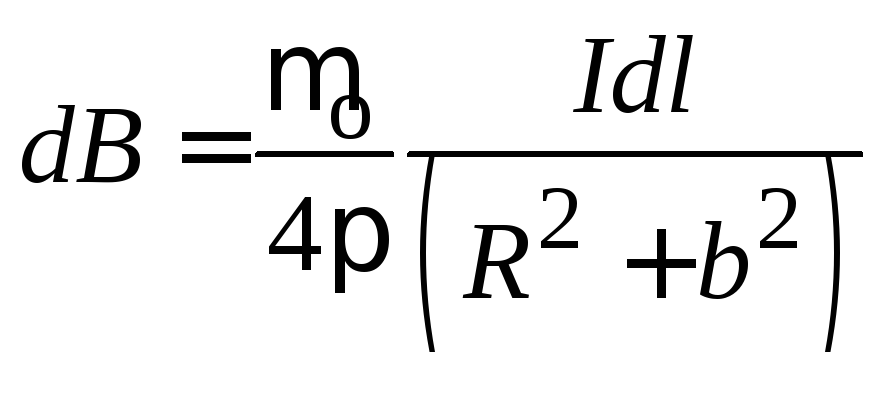
Проинтегрировав
это выражение по всему контуру, получаем

.

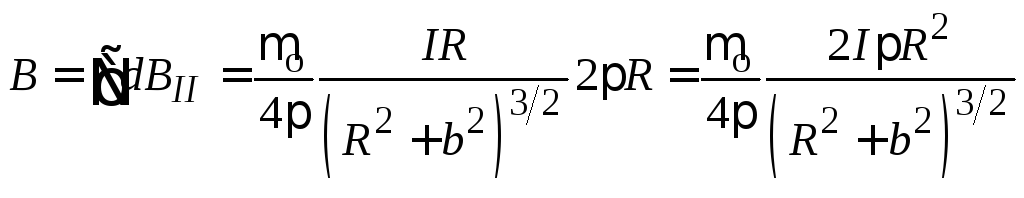
Таким
образом, индукция магнитного поля на
оси кругового витка с током убывает
обратно пропорционально третьей степени
расстояния от центра витка до точки на
оси. Вектор магнитной индукции на оси
витка параллелен оси. Его направление
можно определить с помощью правого
винта: если направить правый винт
параллельно оси витка и вращать его по
направлению тока в витке, то направление
поступательного движения винта покажет
направление вектора магнитной индукции.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

«Из
всех гипотез выбирайте ту,

которая
не пресекает дальнейшего

мышления
об исследуемых вещах».

Джеймс
Максвелл

Данная
тема будет посвящена решению задач на взаимодействие токов и определение модуля
вектора магнитной индукции.

Задача
1.
По контуру протекает ток, равный 5 А. Этот ток создаёт магнитное поле с
индукцией 3 мТл. Найдите радиус контура.

ДАНО:	СИ	РЕШЕНИЕ Запишем формулу по которой вычисляется магнитное поле кругового тока Из этой формулы выразим радиус контура

Ответ:
1 см.

Задача
2.
Магнитное поле внутри соленоида равно 80 мкТл. Найдите ток, протекающий по
виткам соленоида, если на каждый сантиметр соленоида приходится 10 витков.

ДАНО:	СИ	РЕШЕНИЕ Применим формулу, по которой рассчитывается магнитное поле внутри соленоида Из этой формулы выразим силу тока Т.к. все величины входящие в формулу известны, то

Ответ:
157 мА.

Задача
3. К проводнику с сопротивлением 5 Ом приложено напряжение 100 В. Известно, что
модуль вектора магнитной индукции поля, создаваемого током в проводнике, равен
2 мТл на расстоянии 2 см от проводника. Найдите магнитную проницаемость среды,
в которой находится проводник.

ДАНО:	СИ	РЕШЕНИЕ Запишем формулу для магнитного поля прямого тока Закон Ома для участка цепи Тогда формула для магнитного поля прямого тока с учётом закона Ома будет иметь вид Из этой формулы выразим магнитную проницаемость среды

Ответ:
10.

Задача
4.
По двум параллельным тонким проводникам, находящимся на расстоянии 0,1 м друг
от друга, протекают токи 3 А и 2 А в противоположных направлениях. Найдите модуль
вектора магнитной индукции в точке, находящейся посередине между проводниками.

ДАНО:	РЕШЕНИЕ Запишем принцип суперпозиции полей Магнитное поле прямого тока определяется по формуле Так как векторы B1 и B2 направлены в противоположные стороны, ясно, что модуль результирующего вектора будет равен разности модулей этих векторов

Ответ:
4 мкТл.

Задача
5.
По четырём длинным тонким проводникам, проходящим через вершины квадрата со
стороной 5 см перпендикулярно его плоскости, текут токи I₁,
I₂
по 15 А и I₃,
I₄
– по 20 А. По проводникам, проходящим через противолежащие вершины, текут
токи в одном направлении, а по проводникам, проходящим через соседние вершины —
в противоположных направлениях. Найдите модуль вектора магнитной индукции в
центре квадрата.

ДАНО:	СИ	РЕШЕНИЕ Чтобы найти модуль вектора магнитной индукции в центре квадрата, необходимо использовать принцип суперпозиции полей Магнитное поле прямого тока определяется по формуле Длину диагонали квадрата определим из теоремы Пифагора Расстояние от центра квадрата до проводника с током будет равно половине длины диагонали Теперь используем принцип суперпозиции: поскольку векторы B3 и B1 направлены в противоположные стороны, можно просто вычислить разность их модулей, чтобы найти магнитное поле в центре квадрата, создаваемое проводниками 1 и 3 Аналогично для проводников 2 и 4: поскольку векторы B4 и B2 направлены в противоположные стороны, можно просто вычислить разность их модулей, чтобы найти магнитное поле в центре квадрата, создаваемое проводниками 2 и 4 Исходя из условия, разность между токами I1 и I3 равна разности между токами I2 и I4. Поэтому, можем заключить, что модули векторов B1,3 и B2,4 равны Из принципа суперпозиции полей получаем

Ответ:
40 мкТл.

 Готовое решение: Заказ №8367

 Тип работы: Задача

Статус:  Выполнен (Зачтена преподавателем ВУЗа)

 Предмет: Физика

 Дата выполнения: 18.08.2020

 Цена: 227 руб.

Чтобы получить решение, напишите мне в WhatsApp, оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным, не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу, я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

Определить магнитную индукцию в центре проволочной квадратной рамки со стороной a = 15 см, если по рамке течёт ток I = 5 А.

Решение.

Для нахождения магнитной индукции , создаваемой в центре рамки одной стороной, воспользуемся формулой для индукции от проводника конечных размеров: , где Гн/м – магнитная постоянная; − сила тока в проводнике; − расстояние от точки, для которой определяется магнитная индукция, до проводника;

2018-05-14   

Найти индукцию магнитного поля в центре контура, имеющего вид прямоугольника, если его диагональ $d = 16 см$, угол между диагоналями $phi = 30^{ circ}$ и ток в контуре $I = 5,0 А$.

Решение:

Мы знаем, что магнитная индукция, связанная с проводником постоянного тока в любой точке, на перпендикулярном расстоянии от него дается:

$B = frac{ mu_{0} }{4 pi} frac{i}{r} ( sin theta_{1} + sin theta_{2})$,

где $r$ — перпендикулярное расстояние от провода до рассматриваемой точки, а $theta_{1}$ — угол между линией, соединяющий верхнюю точку прямого провода с рассматриваемой точкой и перпендикуляр, опущенный на провод, а $theta_{2}$, из нижней точки провода.

Здесь $B_{1} = B_{3} = frac{ mu_{0} }{4 pi} frac{i}{(d/2) sin frac{ phi}{2} } left ( cos frac{ phi}{2} + cos frac{ phi}{2} right )$

и $B_{2} = B_{4} = frac{ mu_{0} }{4 pi} frac{i}{(d/2) cos frac{ phi}{2} } left ( sin frac{ phi}{2} + sin frac{ phi}{2} right )$

Следовательно, величина полной магнитной индукции в O,

$B_{0} = B_{1} + B_{2} + B_{3} + B_{4} = frac{ mu_{0} }{4 pi} frac{4i}{d/2} left [ frac{ cos frac{ phi}{2} }{ sin frac{ phi}{2} } + frac{ sin frac{ phi}{2} }{ cos frac{ phi}{2} } right ] = frac{4 mu_{0}i }{ pi d sin phi} = 0,10 мТ $