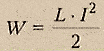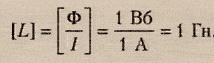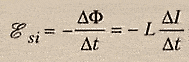Условие задачи:
Найти максимальный магнитный поток через прямоугольную рамку, вращающуюся в однородном магнитном поле с частотой 10 об/с, если амплитуда индуцируемой в рамке ЭДС 3 В.
Задача №8.3.4 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(nu=10) об/с, (rm E_{imax}=3) В, (Phi_{max}-?)
Решение задачи:
[{rm E_i} = – Phi ^prime left( t right);;;;(1)]
Магнитный поток через некоторую площадку, помещённую в однородном магнитном поле, можно определить по такой формуле:
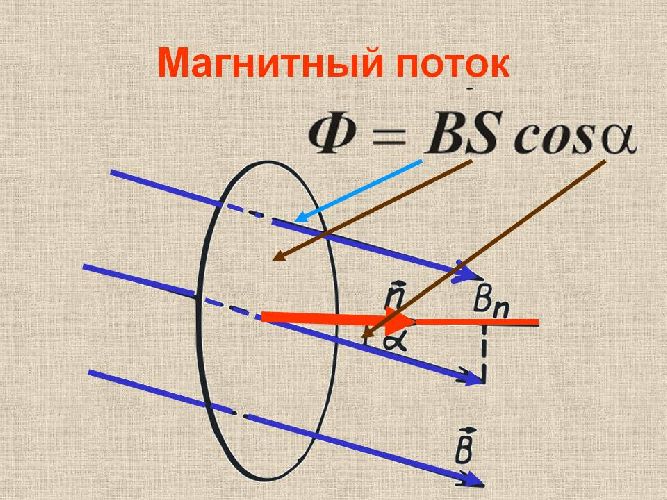
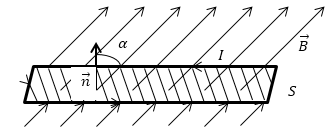
[Phi = BScos alpha ;;;;(2)]
В этой формуле (B) – индукция магнитного поля, (S) – площадь поверхности, через которую определяется магнитный поток, (alpha) – угол между нормалью к площадке и вектором магнитной индукции.
Учитывая, что произведение индукции магнитного поля (B) на площадь поверхности (S) дают максимальный магнитный поток (Phi_{max}), то формулу (2) можно записать в следующем виде:
[Phi = {Phi _{max }}cos alpha ;;;;(3)]
Прямоугольная рамка вращается в магнитном поле, то есть угол (alpha) меняется со временем. Чтобы формула (3) стала выглядеть как функция изменения магнитного потока от времени, нужно представить угол (alpha) в следующем виде:
[alpha = omega t + {alpha _0}]
Здесь (alpha_0) – некоторый начальный угол (также называют начальной фазой), а (omega) – угловая скорость вращения рамки, которую можно определить через известную частоту (nu) по формуле:
[omega = 2pi nu ]
Учитывая всё написанное, формула (3) примет вид:
[Phi = {Phi _{max }}cos left( {2pi nu t + {alpha _0}} right)]
Это выражение подставим в формулу (1):
[{rm E_i} = – {left( {{Phi _{max }}cos left( {2pi nu t + {alpha _0}} right)} right)^prime }]
Теперь нужно взять производную, тогда мы получим:
[{rm E_i} = {Phi _{max }} cdot 2pi nu cdot sin left( {2pi nu t + {alpha _0}} right)]
Очевидно, что ЭДС индукции достигнет своего максимального значения, когда синус будет равен единице, поэтому:
[{{rm E}_{imax}} = {Phi _{max }} cdot 2pi nu ]
Откуда искомый максимальный магнитный поток (Phi_{max}) равен:
[{Phi _{max }} = frac{{{{rm E}_{imax} }}}{{2pi nu }}]
Задача решена в общем виде, посчитаем численный ответ (об/с и Гц – это одно и то же):
[{Phi _{max }} = frac{3}{{2 cdot 3,14 cdot 10}} = 0,0478;Вб = 47,8;мВб]
Ответ: 47,8 мВб.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
8.3.3 Определить силу тока, протекающего по плоскому контуру площадью 5 см2, находящемуся
8.3.5 Определить индуктивность катушки, в которой возникает поток 0,12 Вб при силе тока
8.3.6 Полоску площадью 200 см2, расположенную под углом 60 к направлению однородного
Магнитный поток
Автор:
Субботин Б.П.
На
картинке показано однородное магнитное
поле. Однородное означает одинаковое
во всех точках в данном объеме. В поле
помещена поверхность с площадью S. Линии
поля пересекают поверхность.
Определение
магнитного потока:
Магнитным
потоком Ф через поверхность S называют
количество линий вектора магнитной
индукции B, проходящих через поверхность
S.
Формула
магнитного потока:
Ф
= BS cos α
здесь
α — угол между направлением вектора
магнитной индукции B и нормалью к
поверхности S.
Из
формулы магнитного потока видно, что
максимальным магнитный поток будет при
cos α = 1, а это случится, когда вектор B
параллелен нормали к поверхности S.
Минимальным магнитный поток будет при
cos α = 0, это будет, когда вектор B
перпендикулярен нормали к поверхности
S, ведь в этом случае линии вектора B
будут скользить по поверхности S, не
пересекая её.
А
по определению магнитного потока
учитываются только те линии вектора
магнитной индукции, которые пересекают
данную поверхность.
Измеряется
магнитный поток в веберах (вольт-секундах):
1 вб = 1 в * с. Кроме того, для измерения
магнитного потока применяют максвелл:
1 вб = 108 мкс.
Соответственно 1 мкс = 10-8 вб.
Магнитный
поток является скалярной величиной.
ЭНЕРГИЯ
МАГНИТНОГО ПОЛЯ ТОКА
Вокруг
проводника с током существует магнитное
поле, которое обладает энергией.
Откуда
она берется? Источник тока, включенный
в эл.цепь, обладает запасом энергии.
В
момент замыкания эл.цепи источник тока
расходует часть своей энергии на
преодоление действия возникающей ЭДС
самоиндукции. Эта часть энергии,
называемая собственной энергией тока,
и идет на образование магнитного
поля.
Энергия магнитного поля
равна собственной
энергии тока.
Собственная
энергия тока численно равна работе,
которую должен совершить источник тока
для преодоления ЭДС самоиндукции, чтобы
создать ток в цепи.
Энергия
магнитного поля, созданного током, прямо
пропорциональна квадрату силы тока.
Куда
пропадает энергия магнитного поля после
прекращения тока? — выделяется ( при
размыкании цепи с достаточно большой
силой тока возможно возникновение искры
или дуги)
4.1. Закон электромагнитной индукции. Самоиндукция. Индуктивность
Основные
формулы
· Закон
электромагнитной индукции (закон
Фарадея):
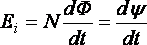
(39)
где – эдс индукции;
–
полный магнитный поток (потокосцепление).
· Магнитный
поток, создаваемый током в контуре,
,
(40)
где –
индуктивность контура;–
сила тока.
· Закон
Фарадея применительно к самоиндукции
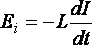
(41)
· Эдс индукции, возникающая при
вращении рамки с током в магнитном поле,
,
(42)
где –
индукция магнитного поля;–
площадь рамки;–
угловая скорость вращения.
· Индуктивность
соленоида
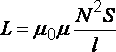
(43)
где –
магнитная постоянная;–
магнитная проницаемость вещества;–
число витков соленоида;–
площадь сечения витка;–
длина соленоида.
· Сила
тока при размыкании цепи
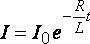
(44)
где –
установившаяся в цепи сила тока;–
индуктивность контура,–
сопротивление контура;–
время размыкания.
· Сила
тока при замыкании цепи
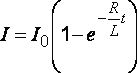
(45)
· Время
релаксации
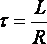
(46)
Примеры
решения задач
Пример
1.
Магнитное
поле изменяется по закону ,
где=
15 мТл,. В
магнитное поле помещен круговой
проводящий виток радиусом = 20
см под угломк
направлению поля (в начальный момент
времени). Найти эдс индукции, возникающую в
витке в момент времени=
5 с.
Решение
По
закону электромагнитной индукции возникающая в
витке эдс индукции 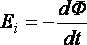
где–
магнитный поток, сцепленный в витке.
,
где –
площадь витка,;
– угол
между направлением вектора магнитной
индукциии
нормалью к контуру:.
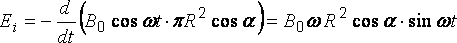
Подставим
числовые значения: =
15 мТл,,
= 20
см = = 0,2 м,.
Вычисления
дают .
|
Пример В Решение При |
|
По
закону Фарадея ,
где,
тогда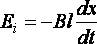
но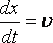
поэтому.
Так, .
Знак
«–» показывает, что эдс индукции
и индукционный ток направлены против
часовой стрелки.
САМОИНДУКЦИЯ
Каждый
проводник, по которому протекает эл.ток,
находится в собственном магнитном поле.
При
изменении силы тока в проводнике меняется
м.поле, т.е. изменяется магнитный поток,
создаваемый этим током. Изменение
магнитного потока ведет в возникновению
вихревого эл.поля и в цепи появляется
ЭДС индукции.
Это
явление называется самоиндукцией.Самоиндукция —
явление возникновения ЭДС индукции в
эл.цепи в результате изменения силы
тока.
Возникающая при этом ЭДС
называется ЭДС
самоиндукции
Проявление
явления самоиндукции
Замыкание
цепи
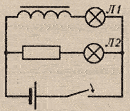
замыкании в эл.цепи нарастает ток, что
вызывает в катушке увеличение магнитного
потока, возникает вихревое эл.поле,
направленное против тока, т.е. в катушке
возникает ЭДС самоиндукции, препятствующая
нарастанию тока в цепи ( вихревое поле
тормозит электроны).
В результатеЛ1
загорается позже, чем
Л2.
Размыкание
цепи
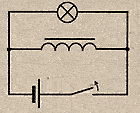
размыкании эл.цепи ток убывает, возникает
уменьшение м.потока в катушке, возникает
вихревое эл.поле, направленное как ток
( стремящееся сохранить прежнюю силу
тока) , т.е. в катушке возникает ЭДС
самоиндукции, поддерживающая ток в
цепи.
В результате Л при выключении ярко
вспыхивает.
Вывод
в
электротехнике явление самоиндукции
проявляется при замыкании цепи (эл.ток
нарастает постепенно) и при размыкании
цепи (эл.ток пропадает не сразу).
ИНДУКТИВНОСТЬ
От
чего зависит ЭДС самоиндукции?
Эл.ток
создает собственное магнитное поле .
Магнитный поток через контур пропорционален
индукции магнитного поля (Ф ~ B), индукция
пропорциональна силе тока в проводнике
(B
~ I), следовательно магнитный поток
пропорционален силе тока (Ф ~ I).
ЭДС
самоиндукции зависит от скорости
изменения силы тока в эл.цепи, от свойств
проводника
(размеров и формы) и от
относительной магнитной проницаемости
среды, в которой находится
проводник.
Физическая величина,
показывающая зависимость ЭДС самоиндукции
от размеров и формы проводника и от
среды, в которой находится проводник,
называется коэффициентом самоиндукции
или индуктивностью.
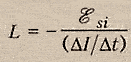
физ. величина, численно равная ЭДС
самоиндукции, возникающей в контуре
при изменении силы тока на 1Ампер за 1
секунду.
Также индуктивность можно
рассчитать по формуле:
где
Ф — магнитный поток через контур, I — сила
тока в контуре.
Единицы
измерения индуктивности в
системе СИ:
Индуктивность
катушки зависит от:
числа витков,
размеров и формы катушки и от относительной
магнитной проницаемости среды
(
возможен сердечник).
ЭДС
САМОИНДУКЦИИ
ЭДС
самоиндукции препятствует нарастанию
силы тока при включении цепи и убыванию
силы тока при размыкании цепи.
Для
характеристики намагниченности вещества
в магнитном поле используетсямагнитный
момент (Рм). Он
численно равен механическому моменту,
испытываемому веществом в магнитном
поле с индукцией в 1 Тл.
Магнитный
момент единицы объема вещества
характеризует его намагниченность
— I,
определяется по формуле:
I= Рм /V,
(2.4)
где V —
объем вещества.
Намагниченность
в системе СИ измеряется, как и напряженность,
в А/м,
величина векторная.
Магнитные
свойства веществ характеризуются объемной
магнитной восприимчивостью — cо , величина
безразмерная.
Если
какое-либо тело поместить в магнитное
поле с индукцией В0,
то происходит его намагничивание.
Вследствие этого тело создает свое
собственное магнитное поле с индукцией В‘,
которое взаимодействует с намагничивающим
полем.
В
этом случае вектор индукции в среде (В)будет
слагаться из векторов:
В
= В0 +
В‘(знак
вектора опущен), (2.5)
где В‘ —индукция
собственного магнитного поля
намагнитившегося вещества.
Индукция
собственного поля определяется магнитными
свойствами вещества, которые характеризуются
объемной магнитной восприимчивостью
— cо ,
справедливо выражение:В‘ = cо В0 (2.6)
Разделим
на m0 выражение
(2.6):
В‘/
mо= cо В0 /m0
Получим: Н‘ = cо Н0 , (2.7)
но Н‘ определяет
намагниченность вещества I,
т.е. Н‘ = I,
тогда из (2.7):
I
= cо Н0.
(2.8)
Таким
образом, если вещество находится во
внешнем магнитном поле с напряженностьюН0,
то внутри него индукция определяется
выражением:
В=В0 +
В‘ =
m0Н0 +m0Н‘ =
m0 (Н0 +
I) (2.9)
Последнее
выражение строго справедливо, когда
сердечник (вещество) находится полностью
во внешнем однородном магнитном поле
(замкнутый тор, бесконечно длинный
соленоид и т.д.).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Магнитный поток

3.9
Средняя оценка: 3.9
Всего получено оценок: 124.
3.9
Средняя оценка: 3.9
Всего получено оценок: 124.
Для количественного описания явления электромагнитной индукции необходимо введение понятия магнитного потока. Рассмотрим эту тему подробнее.
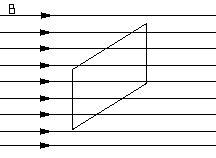
Проводящая рамка в магнитном поле
Явление электромагнитной индукции состоит в том, что при изменении поля, пронизывающего проводящую рамку или катушку, в ней возникает электродвижущая сила (ЭДС):
Энергия используемого в этом опыте магнитного поля характеризуется магнитной индукцией. Однако, при попытке описать наблюдаемое явление выяснилось, что одной этой величины мало.
Если выписать в таблицу значения ЭДС, наводимые магнитным полем, имеющим одну и ту же плотность магнитных линий, в разных условиях, то окажется, что ЭДС, возникающая в квадратной рамке, имеет гораздо большее значение, чем ЭДС в длинной узкой рамке (при одном периметре).
А наибольшая ЭДС возникает в круглом витке.
Причиной этого оказался разный «охват поля» рамкой. Площадь длинной узкой рамки невелика, она «охватывает» малое «количество поля», и ЭДС в ней также мала. У квадратной рамки площадь при одинаковом периметре больше, а у круглого витка – она наибольшая, в результате рамка «охватывает» большее «количество поля», и ЭДС в такой рамке тоже получается больше.
Не менее важной оказалась ориентация рамки по отношению к направлению магнитного поля. Наибольшая ЭДС возникает, если проводящая рамка перпендикулярна линиям магнитной индукции. Если плоскость рамки параллельна этим линиям – то независимо от ее площади и силы магнитного поля ЭДС в рамке не возникнет.
Понятие магнитного потока
Таким образом, для описания явления электромагнитной индукции было введено понятие «магнитный поток», характеризующее «охват поля» рамкой. В этом понятии объединяются все величины, от которых зависит наведенная в рамке ЭДС – индукция поля, площадь и ориентация рамки. Для обозначения используется большая греческая буква Ф (фи):
$$Ф=BScosalpha$$
Таким образом, магнитный поток – это величина, равная произведению индукции магнитного поля, площади проводящего контура, и косинуса угла между нормалью к контуру и направлением линий индукции.
Из приведенной формулы магнитного потока можно вывести определение его единицы – вебер(Вб):
$$1Вб=1Тл×1м^2×cosalpha$$,
то есть, магнитный поток 1 Вебер – это магнитный поток, проходящий через рамку площадью 1 квадратный метр, которая ориентирована перпендикулярно линиям однородного магнитного поля с индукцией 1Тесла.
Для понимания термина «магнитный поток» можно представить аналогию с обычным водяным потоком. Водяной поток, как правило, зависит от напора воды (аналог индукции) и площади сечения трубы (аналог площади рамки), а поскольку вода, в отличие от магнитного поля, всегда заключена внутрь трубы, то водяной поток всегда ориентирован поперек сечения трубы, и значение косинуса в формуле всегда равно единице.
Что мы узнали?
Для описания явления электромагнитной индукции в проводящем контуре необходимо учесть индукцию магнитного поля, «охват» поля контуром и ориентацию контура. Все эти факторы объединяются в понятии «магнитный поток». Изменение магнитного потока приводит к возникновению ЭДС в контуре. Постоянный магнитный поток ЭДС не вызывает.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
3.9
Средняя оценка: 3.9
Всего получено оценок: 124.
А какая ваша оценка?
Поток вектора магнитной индукции (магнитный поток)
Роман Алексеевич Лалетин
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Определение
Определение
Потоком вектора магнитной индукции (магнитным потоком) (Ф) через площадку S называют скалярную величину равную:
[Ф=BScosalpha ={ B}_nS=overrightarrow{B}overrightarrow{S}left(1right),]
где $alpha $ угол между $overrightarrow{n}$ и $overrightarrow{B}$, $overrightarrow{n}$ — нормаль к площадке S.
Ф равен количеству линий магнитной индукции, которые пересекают площадку S (рис.1). Поток магнитной индукции может быть положительным и отрицательным. Знак потока зависит от выбора положительного направлении нормали к площадке S. Обычно, положительное направление нормали связывают с направлением обхода контура током. За положительное направление нормали принимают поступательное перемещение правого винта, при вращении его по току.
Рис. 1
В том случае, если магнитное поле неоднородно, S не является плоской, то поверхность можно разбить на элементарные площадки dS, которые рассматриваются как плоские, а поле на этой площадке можно считать однородным. В таком случае магнитный поток (dФ) можно через такую поверхность определить как:
[dФ=BdScosalpha =overrightarrow{B}doverrightarrow{S}left(2right).]
Тогда полный поток через поверхность S находится как:
[Ф=intlimits_S{BdScosalpha =intlimits_S{overrightarrow{B}doverrightarrow{S}}left(3right).}]
Основная единица измерения магнитного потока в системе СИ — вебер (Вб). $1 Вб=frac{1Тл}{1м^2}$.
Связь магнитного потока и работы сил магнитного поля
Элементарную работу ($delta A$), которую совершают силы магнитного поля можно выразить через элементарное изменение потока вектора магнитной индукции (dФ):
[delta A=IdФ left(4right).]
В том случае, когда проводник с током совершил конечное перемещение, а сила тока постоянна, то работа сил поля равна:
[A=Ileft(Ф_2-Ф_1right)left(5right),]
где $Ф_1$ — поток через контур в начале перемещения, $Ф_2$ — поток через контур в конце перемещения.
Теорема Гаусса для магнитного поля
Суммарный магнитный поток через замкнутую поверхность S равен нулю:
[oint{overrightarrow{B}doverrightarrow{S}}=0 (6) .]
Уравнение (6) справедливо для любых магнитных полей. Это уравнение аналог теоремы Остроградского — Гаусса в электростатике (в вакууме):
[oint{overrightarrow{E}doverrightarrow{S}}=frac{q}{{varepsilon }_0}left(7right).]
Уравнение (6) означает, что источником магнитного поля являются не магнитные заряды (их в природе не существует), а электрические токи. Данную теорему мы подробно рассматривали в разделе «Отсутствие в природе магнитных зарядов».
Пример 1
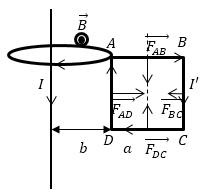
Задание: Недалеко от бесконечно длинного прямого проводника с током I находится квадратная рамка, по которой течет ток с силой $I’$. Сторона рамки равна $а$. Рамка лежит в плоскости с проводом (рис.2). Расстояние от ближайшей стороны рамки до проводника равно b. Найдите работу магнитной силы при удалении рамки из поля. Считать токи постоянными.
Рис. 2
Индукция магнитного поля длинного проводника с током в части, где расположена квадратная рамка, направлена на нас.
Решение:
При решении этой задачи необходимо помнить, что рамка с током находится в неоднородном поле, магнитная индукция убывает при удалении от провода.
В качестве основы для решения задачи используем формулу связи потока и работы:
[A=I’left(Ф_2-Ф_1right)left(1.1right),]
$I’$- сила тока в рамке, $Ф_1$- поток через квадратную рамку, когда расстояние от ее стороны, ближайшей к проводу равна $b$. $Ф_2=0$, так как в конечном положении рамка вне магнитного поля по условию. Следовательно, формула (1.1) запишется как:
[A=-I’Ф_1left(1.2right).]
Выберем направление нормали ($overrightarrow{n}$) к квадратному контуру от нас (по правилу правого винта). Тогда для всех элементов поверхности, которая ограничена контуром квадратной рамки угол между нормалью $overrightarrow{n}$ и вектором $overrightarrow{B}$ равен $pi $. Тогда формула для потока через поверхность рамки на расстоянии x от провода имеет вид:
[dФ=-BdS=-Bcdot acdot dх=-frac{{mu }_0}{2pi }Ilfrac{dх}{х} left(1.3right),]
где индукция магнитного поля бесконечно длинного проводника с током силы I равна:
[B=frac{mu_0}{2pi х}Illeft(1.4right).]
Следовательно, весь поток из (1.3) найдем как:
[Ф_1=intlimits_S{-frac{{mu }_0}{2pi }Ilfrac{dх}{х}}=-frac{{mu }_0}{2pi }Ilintlimits^{b+a}_b{frac{dх}{х}}=-frac{{mu }_0}{2pi }Ilcdot lnfrac{b+a}{b}left(1.5right).]
Подставим формулу (1.5) в выражение (1.2) найдем искомую работу:
[A=I’frac{{mu }_0}{2pi }Ilcdot lnfrac{b+a}{b}.]
Ответ: $A=frac{{mu }_0}{2pi }II’lcdot lnfrac{b+a}{b}.$
«Поток вектора магнитной индукции (магнитный поток)» 👇
Пример 2
Задание: Найдите силу, которая действует на рамку в предыдущем примере.
Решение:
Для того чтобы найти силу, которая действует на квадратную рамку с током в поле длинного провода положим, что под действием магнитной силы рамка сместилась на малое расстояние dx. В таком случае сила совершает работу равную:
[delta A=Fdx (2.1)]
Элементарную работу $delta A$ с другой стороны выразим как:
[delta A=I’dФ left(2.2right).]
Выразим силу, используя (2.1) и (2.2), получим:
[Fdx=I’dФ to F=I’frac{dФ}{dx}left(2.3right).]
Используя формулу, полученную в примере 1:
[dФ=-frac{{mu }_0}{2pi }Ilfrac{dх}{х} to frac{dФ}{dx}=-frac{{mu }_0}{2pi }frac{Il}{х} left(2.4right).]
Подставим $frac{dФ}{dx}$ в выражении для модуля силы (2.3), получим:
[F=I’frac{{mu }_0}{2pi }frac{Il}{х}left(2.5right).]
На каждый элемент контура квадратной рамки действует сила (сила Ампера), всего на рамку действует четыре составляющих силы, однако, очевидно, что силы, которые действуют на стороны AB и DC равны по модулю и противоположны по направлению:
[overrightarrow{F_{AB}}+overrightarrow{F_{DC}}=0 (2.6)]
их сумма равна нулю, в таком случае, результирующая сила, приложенная к контуру будет:
[overrightarrow{F}=overrightarrow{F_{AD}}+overrightarrow{F_{BC}}left(2.6right).]
Эти силы, в соответствии с правилом левой руки, направлены вдоль одной прямой в противоположные стороны, то есть:
[F=F_{AD}-F_{BC} left(2.7right).]
Найдем силу $F_{AD,}$ используя формулу (2.5), где $x=b$, получим:
[F_{AD}=I’frac{м_0}{2pi}frac{Il}{b}left(2.8right).]
Тогда $F_{BC}$ равна:
[F_{BC}=I’frac{{mu }_0}{2pi }frac{Il}{b+a}left(2.9right).]
Искомая сила получается равной:
[F=I’frac{{mu }_0}{2pi }frac{Il}{b}-I’frac{{mu }_0}{2pi }frac{Il}{b+a}={II}’frac{{mu }_0l}{2pi }left(frac{1}{b}-frac{1}{b+a}right).]
Ответ: $F={II}’frac{{mu }_0l}{2pi }left(frac{1}{b}-frac{1}{b+a}right). $Магнитные силы выталкивают рамку стоком, пока она сохраняет первоначальную ориентацию относительно поля провода.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 10.02.2023
В этой статье приведены хорошие стартовые задачи по теме «магнитный поток». Задачи несложные, вполне можно начинать изучать эту тему с их использованием.
Задача 1.
За с магнитный поток, пронизывающий проволочную рамку, равномерно уменьшается от некоторого значения
до нуля. При этом в рамке генерируется ЭДС, равная 4 В. Чему равен начальный магнитный поток
через рамку?
ЭДС равна
Так как поток уменьшился до нуля, то его изменение . Следовательно,
Ответ: 8 Вб
Задача 2.
Рамка площадью см
с числом витков
и сопротивлением
Ом находится в однородном магнитном поле, вектор индукции
которого перпендикулярен плоскости рамки. Какой заряд пройдет по рамке при ее повороте на 90°?
мТл.
Поток через один виток равен , а через
витков –
При повороте рамки поток изменится до нуля, следовательно, . Тогда ЭДС
Но ток равен
Тогда
Ответ: 2,5 мКл
Задача 3.
За какое время магнитный поток сквозь один виток катушки, содержащей 50 витков, изменился с 5 до 1 мВб, если в результате этого изменения по катушке сопротивлением 100 Ом прошел индукционный ток силой 0,1 А?
По закону Ома
Откуда
Ответ: 0,02 с
Задача 4.
Рамка, имеющая 100 витков площадью см
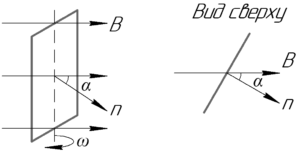
каждый, вращается вокруг вертикальной оси, принадлежащей плоскости рамки, в горизонтальном постоянном однородном магнитном поле с индукцией В = 2 мТл. Средняя ЭДС индукции, возникающая на зажимах рамки за четверть периода, равна 8 мВ. Сколько оборотов делает рамка за 10 с?
За четверть периода поток изменяется от максимального до нулевого, так как рамка повернется на 90 градусов за это время. Поэтому
Итак, рамка повернется на 90 градусов за с, следовательно, на 360 градусов она повернется за 0,5 с, ну а за 10 с – успеет повернуться 20 раз.
Ответ: 20 оборотов.
Задача 5.
Проволочную рамку поместили в однородное периодически изменяющееся магнитное поле перпендикулярно линиям магнитной индукции. Выберите два верных утверждения.
1) Сила тока будет изменяться обратно пропорционально величине индукции.
2) Сила тока будет периодически изменяться по величине.
3) Сила тока будет равна нулю.
4) Сила тока будет изменяться по направлению.
Так как поле изменяется, то будет меняться поток чрез рамку. Следовательно, в рамке будет наводиться ЭДС, которая тоже будет переменной. И ток вследствие этого будет переменным. Так как поле меняется периодически, то будут периоды, когда индукция нарастает, и будут периоды убывания. Значит, ЭДС будет менять знак, а следовательно, ток тоже будет менять направление.
Ответ: 24
Задача 6.
В проволочное кольцо вставили магнит, при этом по кольцу прошел заряд Кл. Определите магнитный поток, пересекающий кольцо, если сопротивление кольца 30 Ом.
Ток равен
Тогда
Ответ: 600 мкВб
Задача 7.
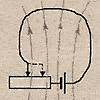
Длинную изолированную проволоку А) наматывают на катушку, а концы проволоки присоединяют к гальванометру, Б) складывают вдвое и наматывают на катушку, концы проволоки присоединяют к гальванометру (см. рис.).
К задаче 7
Появится ли индукционный ток в катушке при введении в нее полосового магнита?
1) да, появится ток
2) нет, тока в катушке не будет
3) да, но ток будет появляться только в случае, если сложенный провод намотан по часовой стрелке, а магнит вдвигают северным полюсом
4) да, но ток будет появляться только в случае, если сложенный провод намотан против часовой стрелки, а магнит вдвигают северным полюсом .
В случае А появится, в случае B – нет. В случае A поток изменяется, следовательно, наводится ЭДС, и возникает ток. Катушка, намотанная так, как показано на рисунке, называется бифиллярной. Магнитное поле, созданное одной обмоткой равно и направлено противоположно созданному другой, приводя к взаимонейтрализации магнитных полей. Так что во втором случае в половине провода наводится ЭДС одного знака, а во второй половине провода – ЭДС другого знака, которые компенсируют друг друга.
Ответ: 12
Задача 8.
Виток, замкнутый на гальванометр, поместили в пространство между полюсами электромагнита, магнитное поле в котором изменяется по некоторому закону. При этом изменение тока в контуре от времени описывает зависимость на рисунке.
К задаче 8 — рисунок 1
Какой график может соответствовать изменению значения индукции магнитном поле от времени?
К задаче 8 — рисунок 2
Чтобы решить эту задачу, нужно смотреть не на числа, а на фазы изменения тока и индукции в контуре. Ток в первый момент максимален, следовательно, ЭДС максимальна, ведь по фазе они совпадают друг с другом. Поток же всегда опережает ЭДС на 90 градусов, то есть на четверть периода. Остается найти график, сдвинутый на четверть периода от заданного: первый и третий отпадают, из оставшихся подойдет №2. Индукция на этом графике опережает ток как раз на 90 градусов.
Ответ: 2
Задача 9.
Координата перемычки, движущейся вдоль оси Х по параллельным металлическим стержням (см. рис.), изменяется по законам:
К задаче 9
А) ;
Б) .
Какой из графиков соответствует зависимости индукционного тока от времени в каждом случае в первые 0,5 с? Вся система находится в поcтоянном однородном магнитном поле, перпендикулярном плоскости, в которой лежат перемычка и стержни.
Графики зависимостей тока от времени
Определим, как меняется скорость. Для этого возьмем производную координаты по времени:
A)
Б)
В момент времени 0,5 с скорость в случае А) будет равна (-1), а в случае Б) — (+2). То есть в первом случае площадь рамки увеличивается, и индукционный ток будет таким, чтобы уменьшить поток, то есть будет направлен против часовой стрелки, а в случае Б) наоборот, по часовой, так как будет стремиться восстановить уменьшающийся поток. Скорость в обоих случаях непостоянна, но меняетсн по линейному закону, значит, ток будет меняться линейно. Графики 1 и 3 – отбрасываем. В первом случае начальная скорость есть, значит, какой-то ток на начало отсчета уже присутствовал, а во втором – нет, поэтому для второго случая выберем график 2, а для первого – 4.
Ответ: 42
Задача 10.
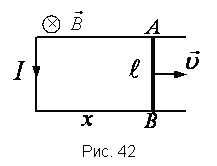
В однородном магнитном поле с индукцией В = 5 мТл движется металлический стержень длиной см перпендикулярно вектору магнитной индукции со скоростью 2 м/с (см. рис.). Какова разность потенциалов, возникающая между концами стержня?
К задаче 10
Так как стержень движется перпендикулярно, то угол между линиями индукции и скоростью равен , а синус этого угла – 1, поэтому
Ответ: 5 мВ