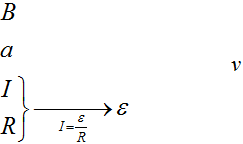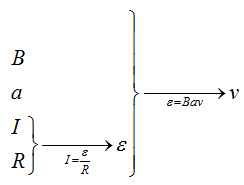Как найти магнитный поток в кольце

0 Пользователей и 1 Гость просматривают эту тему.

---

---

 Циркуляция вектора магнитной индукции
В вдоль замкну­того контура

где
B_i
— проекция
вектора магнитной индукции на направление
элементарного перемещения dl
вдоль контура L.
Циркуляция век­тора напряженности Н
вдоль замкнутого контура

,

 Закон полного тока (для магнитного
поля в вакууме)

где ₀
— магнитная постоянная;

— алгебраическая сумма токов,
охватываемых контуром; п — число
токов.

Закон полного тока (для произвольной
среды)

 Магнитный
поток Ф через плоский контур площадью
S:

а) в случае однородного поля

Ф=BS cos
; или Ф = B_nS,

где  — угол между
вектором нормали n к
плоскости контура и век­тором магнитной
индукции В; В_n
— проекция вектора В на нормаль
n (B_n=B
cos );

б) в случае неоднородного поля

где интегрирование ведется во всей
поверхности S.

 Потокосцепление,
т.е. полный магнитный поток, сцепленный
со всеми витками соленоида или тороида,

где Ф — магнитный поток через один
виток; N — число витков со­леноида
или тороида.


Магнитное поле тороида, сердечник
которого составлен из двух частей,
изготовлен­ных из веществ с раз­личными
магнитными проницаемостями:

а) магнитная индук­ция на осевой линии
тороида

где I — сила тока в
об­мотке тороида; N — чис­ло ее
витков; l₁ и l₂ -­
длины первой и второй частей сердечника
торо­ида; ₁ и
₂
—магнитные проницаемости ве­ществ
первой и второй частей сердечника
торо­ида; ₀
—магнитная постоянная

б) напряженность магнитного поля на
осе­вой линии тороида в первой и второй
частях сердечника

H₁=B
/(₁
₂);
H₁=B
/(₂
₀
);

в) магнитный поток в сердечнике тороида

или по аналогии с законом Ома (формула
Гопкинсона)

Ф_m=F_m/R_m,

где F_m
— магнитодвижущая сила; R_m
— полное магнитное сопро­тивление
цепи;

г) магнитное
сопротивление участка цепи

R_m=l/(μμ₀S).

• Магнитная проницаемость μ,
ферромагнетика связана с маг­нитной
индукцией В поля в нем и напряженностью
Н намагничи­вающего поля соотношением

μ=B/(μ₀H).

• Связь между магнитной индукцией В
поля в ферромагнетике и напряженностью
Н намагничивающего поля выражается
графи­чески (рис. 24.1).

Примеры решения задач

Пример 1. В одной плоскости с бесконечно
длинным прямым проводом, по которому
течет ток I=50 А,
расположена прямоуголь­ная рамка
так, что две большие стороны ее длиной
l=65 см парал­лельны
проводу, а расстояние от провода до
ближайшей из этих сторон равно ее ширине.
Каков магнитный поток Ф, пронизываю­щий
рамку?

Решение.
Магнитный поток Ф через поверхность
площадью S определяется
выражением

В нашем случае вектор магнитной индукции
В перпендикулярен плоскости рамки.
Поэтому для всех точек рамки В_n=В.
Магнитная индукция В, создаваемая
бесконечно длинным прямым проводником
с током, определяется формулой

,

где x— расстояние
от провода до точки, в которой определяется
В.

Для вычисления магнитного потока
заметим, что так как В зависит от х
и элементарный поток Ф будет также
за­висеть от х, то

dф=B(x)dS.

Разобьем площадь рамки на узкие
элементарные площадки длиной l,
шири­ной dx и площадью
dS=ldx
(рис. 24.2). В пределах этой площадки
магнитную индукцию можно считать
постоянной, так как все части площад­ки
равноудалены (на расстояние х) от
провода. С учетом сделанных замечаний
элементарный магнитный поток можно
записать в виде

dФ=

Проинтегрировав полученное выражение
в пределах от x₁=a
до х₂=2а, найдем

|_^2.

Подставив пределы, получим

Убедимся в том, что правая часть
полученного равенства дает единицу
магнитного потока (Вб): [₀]
[I] [l]=
Гн/м 1 А 1
м=1 Вб. Произведя вычисления по формуле
(1), найдем Ф=4,5 мкВб.

Пример 2. Определить индукцию В
и напряженность Н магнит­ного
поля на оси тороида без сердечника, по
обмотке которого, со­держащей N=200
витков, идет ток I=5 А. Внешний диаметр
d₁ тороида
равен 30 см, внутренний d₂=
20 см.

Решение. Для определения напряженности
магнитного поля внутри тороида вычислим
циркуляцию вектора Н вдоль линии
маг­нитной индукции поля:

Из условия симметрии следует, что линии
магнитной индукции тороида представляют
собой окружности и что во всех точках
этой линии напряженности одинаковы.
Поэтому в выражении циркуля­ции
напряженность Н можно вынести за
знак интеграла, а интегри­рование
проводить в пределах от нуля до 2 r,
где r — радиус
ок­ружности, совпадающей с линией
индукции, вдоль которой вычис­ляется
циркуляция, т. e.

(1)

С другой стороны, в соответствии с
законом полного тока цир­куляция
вектора напряженности магнитного поля
равна сумме то­ков, охватываемых
контуром, вдоль которого вычисляется
цирку­ляция:

(2)

Приравняв
правые части равенств (1) и (2), получим

(2)

Линия, проходящая вдоль тороида,
охватывает число токов, равное числу
витков тороида. Сила тока во всех витках
одинакова. Поэтому формула (3) примет
вид 2rH=-NI,
откуда

(4)

Для средней линии тороида
r=1/2(R₁R₂)=1/4(d₁+d₂).
Подставив это выражение r в формулу
(4), найдем

(5)

Магнитная индукция В₀ в
вакууме связана с напряженностью поля
соотношением B₀=₀H.
Следовательно,

(6)

Подставив значения величин в выражения
(5) и (6), получим:

H=1,37 кА/м, B₀=1,6
мТл.

Пример. 3. Чугунное кольцо имеет
воздушный зазор длиной lо=5 мм. Длина
l средней линии кольца равна 1 м.
Сколько витков N содержит обмотка
на кольце, если при силе тока I=4 А
индукция В магнитного поля в воздушном
зазоре равна 0,5 Тл? Рассеянием маг­нитного
потока в воздушном зазоре можно
пренебречь. Явление гистерезиса не
учитывать.

Решение. Пренебрегая рассеянием
магнитного потока, мы можем принять,
что индукция поля в воздушном зазоре
равна ин­дукции поля в чугуне. На
основании закона полного тока запишем

IN=Hl+H₀I₀.

По графику (см. рис. 24.1) находим, что при
В=0,5 Тл напря­женность Н
магнитного поля в чугуне равна 1,2 кА/м.
Так как для воздуха =1,
то напряженность поля в воздушном
зазоре

H₀=B₀=0,4
MA/м.

Искомое число витков

N=(Hl+H₀
l_o)/I==800.

Магнитный поток, проходящий через площадь S равен:

Ф = BScosα;

где:

Ф ― величина магнитного потока [Вб],

S ― площадь контура [м2],

B ― индукция магнитного поля [Тл],

α ― угол между нормалью $overrightarrow{n}$ к площади контура и вектором индукции магнитного поля $overrightarrow{B}$.

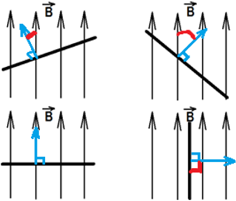
Если вектор индукции магнитного поля $overrightarrow{B}$ перпендикулярен площади контура, то магнитный поток равен:

Ф = BScos90° = BS;

Максимальное значение потока будет тогда, когда косинус будет максимальным (cosα = 1), то есть угол между вектором $overrightarrow{B}$ и вектором нормали к пластинке равен 0°, чему соответствует картинка 3. Наименьшее же значение потока будет тогда, когда косинус будет равен нулю (cosα = 0), то есть угол между нормалью к пластинке и вектором индукции равен 90°, чему соответствует картинка 4.

Электромагнитная индукция ― явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через контур. Если контур разомкнут, то на его концах наблюдается разносность потенциалов, равная ЭДС индукции.

ЭДС электромагнитной индукции возникает только тогда, когда изменяется магнитный поток.

Закон Фарадея об электромагнитной индукции и гласит, что индуцируемая ЭДС прямо пропорциональна скорости изменения магнитного потока:

$varepsilon_i = -frac{Delta text{Ф}}{Delta t}$

где:

$varepsilon_i $ ― ЭДС электромагнитной индукции [B],

$frac{Delta text{Ф}}{Delta t}$ ― скорость изменения магнитного потока [Вб/с],

∆Ф ― изменение магнитного потока [Вб],

∆t ― время, за которое происходит это изменение [c].

Кроме того, ЭДС индукции равна производной магнитного потока по времени:

$varepsilon_i = -text{Ф}_t’$

где:

• ― ЭДС электромагнитной индукции [B],
• ― производная магнитного потока по времени [Вб/с].

Задача 1

Замкнутый контур площадью S из тонкой проволоки помещён в магнитное поле. Плоскость контура перпендикулярна вектору магнитной индукции поля. В контуре возникают колебания тока с амплитудой iм = 35 мА, если магнитная индукция поля меняется с течением времени в соответствии с формулой B = acos (bt), где a = 6 · 10-3Тл, b = 3500 c-1. Электрическое сопротивление контура R = 1,2 Ом. Чему равна площадь контура?

Решение:

Обратите внимание на величины, данные в условии. Они здесь совсем не такие, к которым вы привыкли, потому что не дано значение магнитного поля, а дана зависимость магнитного поля от времени. Посмотрим, как это скажется на решении задачи.

Поскольку магнитное поле, а вместе с ним и поток меняются, то будет возникать ЭДС индукции, именно это ЭДС и вызовет электрический ток, поэтому запишем закон электромагнитной индукции.

По закону электромагнитной индукции $varepsilon_i = -frac{Delta text{Ф}}{Delta t}$

ЭДС — это изменение магнитного потока за время. Ничего в определении ЭДС не сказано про это самое время. Дело в том, что изменение какой-то величины за небольшой промежуток времени называется производной по времени. То есть наше ЭДС, которое является изменением магнитного потока за небольшой промежуток времени, это просто производная магнитного потока по времени $varepsilon_i = -text{Ф}_t’$

И это очень важный момент, без которого мы не сможем решить такого рода задачу.

Теперь посчитаем ЭДС индукции.

Напишем, чему равен магнитный поток Ф = BS = acos (bt) · S.

ЭДС индукции — это производная магнитного потока по времени. Теперь придётся вспомнить немного математики. Множители “a” и “S” перед косинусом не зависят от времени, поэтому производная их не трогает, а вот у косинуса в скобках стоит зависимость от времени, поэтому именно от косинуса производную и нужно взять.

Обратите внимание на полученную формулу магнитного потока. В ней стоит просто множитель aS перед сложной функцией косинуса

$text{Ф} underset{text{множитель}}{underbrace{aS}} ;; cdot ;; underset{text{сложная функция}}{underbrace{cos(bt)}}$.

Взяв производную от этой функции, получаем Ф´ = –abS · sin (bt). А теперь, раз мы знаем производную магнитного потока, значит, знаем и ЭДС индукции, потому что $varepsilon_i = -text{Ф}_t’$

Подставив сюда значение производной, получим $varepsilon_i = -text{Ф}_t’$ = abS · sin (bt).

Мы получили значение ЭДС. Кроме этого, мы знаем сопротивление и максимальную силу тока, поэтому запишем закон Ома.

По закону Ома $I = frac{varepsilon}{R}$ , подставив сюда значение ЭДС, получаем $I = frac{abScdot sin(bt)}{R}$.

Мы получили зависимость силы тока от времени.

Из-за синуса, который стоит в этой формуле, ток постоянно меняет свое значение, то он становится больше, то меньше, поскольку синус меняет своё значение от -1 до 1.

В условии дано максимальное значение силы тока, которое протекает по контуру. Когда эта величина будет максимальной? В тот момент, когда синус будет максимальным, то есть равный единице. Поэтому запишем sin (bt) = 1.

Максимальное значение тока будет в тот момент, когда будет максимальным значение ЭДС индукции, то есть когда, $I_{max} = frac{abS}{R}$.

Отсюда можно легко выразить площадь контура $S = frac{I_{max}R}{ab}$, подставив сюда все значения, получим $S = frac{I_{max}R}{ab} = frac{35cdot 10^{-3} Acdot 1,2text{Ом}}{6cdot 10^{-3}text{Тл} cdot 35000c^{-1}} = 0,002text{м}^2$

Ответ: 0,002

Как видно из формулы магнитного потока Ф = BScosα, изменение магнитного потока может быть вызвано разными факторами:

• увеличением или уменьшением модуля индукции магнитного поля (т. е. величины $frac{Delta B}{Delta t}$);
• изменением направления вектора магнитного поля (т. е. изменением угла α);
• деформацией контура, причем такой деформацией, при которой изменяется площадь контура (т. е. изменением величины $frac{Delta S}{Delta t}$ );
• изменением нескольких из этих величин одновременно.

Таким образом, изменение модуля или направление вектора магнитной индукции или площади контура неизбежно приводят к тому, что в контуре возникает электродвижущая сила.

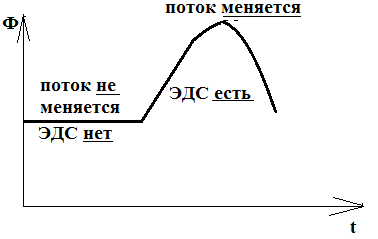
Если нарисовать график зависимости магнитного потока, то он может выглядеть либо так: тогда поток не будет менятьсяи ЭДС не возникает.

Либо так, тогда будет меняться поток и возникать ЭДС:

Знак «минус» перед скоростью изменения магнитного потока в формуле отражает правило Ленца: индуцированный ток всегда направлен так, чтобы магнитное поле, которое он создает, препятствовало изменению магнитного потока.

Если магнитный поток, проходящий через площадь контура, уменьшается, то магнитное поле индуцированных токов будет стремиться его увеличить.

Если поток увеличивается ― магнитное поле индуцированных токов будет стремиться его уменьшить.

Задача 2

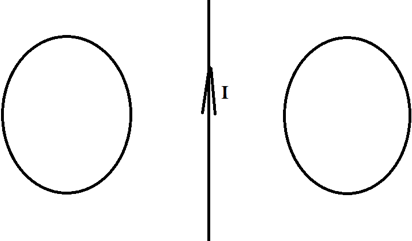
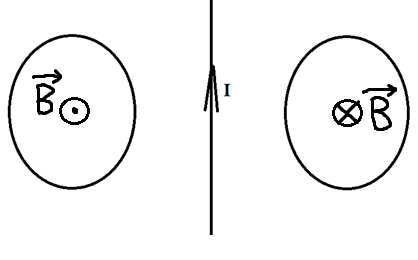
Два проводящих кольца расположены относительно проводника с током в одной плоскости, как это показано на рисунке. В каком направлении будет индуцироваться ток в этих кольцах, если начать двигать их в направлении проводника?

Решение:

Первым делом необходимо понять, как вообще может возникать индуцированный ток, если даже магнитного поля нет?

Его направление мы можем определить по правилу правого винта. Отметим это на рисунке.

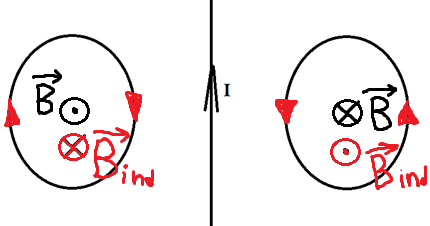
Теперь эти два проводника начинают двигать. Разве от этого меняется поток? Ведь площадь остаётся та же самая, угол между нормалью и вектором тоже не меняется. Однако, чем ближе к проводнику с током, тем сильней поле, а чем дальше от него, тем слабее! Поэтому, когда мы двигаем кольца к проводнику, мы увеличиваем поток, ведь ближе поле сильнее. Значит, будет появляться ток, а его направление можно определить по правилу Ленца. Что нам говорит правило Ленца?

Раз поток увеличивается, то по правилу Ленца ток будет индуцироваться так, чтобы уменьшить поток, то есть магнитное поле в левом кольце будет направлено от нас, а в правом ─ на нас. А значит, по правилу правого винта мы можем определить, что ток будет течь по часовой стрелке слева и против часовой стрелки справа.

Движение проводников

Если к концам проводника, движущегося в магнитном поле, подключить вольтметр, то прибор покажет наличие разности потенциалов на концах проводника. Таким образом, когда проводник перемещается в области с магнитным полем, в нем возникает электромагнитная движущая сила (ЭДС).

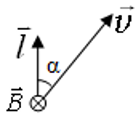
Согласно закону Лоренца, в проводнике, движущемся в магнитном поле, создается ЭДС $|varepsilon_i| = Blvsinalpha$;

где:

$varepsilon_i$― ЭДС электромагнитной индукции [B],

B ― индукция магнитного поля [Тл],

l ― длина проводника [м],

v ― скорость движения проводника [м/с],

α ― угол между направлением вектора скорости $overrightarrow{v}$ и длиной проводника $overrightarrow{l}$ , если вектор индукции магнитного поля $overrightarrow{B}$перпендикулярен проводнику и вектору скорости его движения: $overrightarrow{B} perp overrightarrow{v}, overrightarrow{B} perp overrightarrow{l}$

Используя силу Лоренца, можно получить это определение ЭДС. Сила Лоренца ― это проявленное действие магнитного поля на заряженную частицу.

В проводнике присутствует большое количество свободных зарядов (именно это отличает проводники от диэлектриков), и на каждый из зарядов действует сила Лоренца, перемещая их по проводнику так, что в одной его части скапливается отрицательный заряд, а в другой, соответственно, положительный. Это распределение зарядов и является физической основой для возникновения электродвижущей силы.

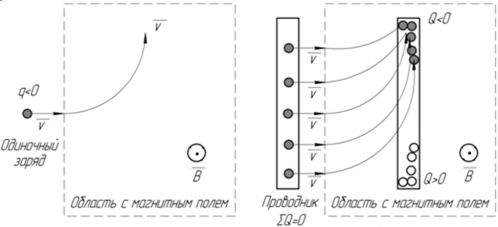
На рисунке показано как сила Лоренца, действующая на каждый из зарядов проводника, создаёт ЭДС в проводнике. Если одиночный отрицательный заряд попадает в магнитное поле, направленное от нас, то, согласно правилу левой руки, направление его движения изменяется так, как показано на рисунке. Если в область с таким же магнитным полем входит проводник, суммарный заряд которого равен нулю, но внутри которого находятся электроны, способные свободно перемещаться в проводнике, то электроны стекаются в один конец проводника. Так как электроны переместились в один конец проводника, то этот конец приобретает отрицательный заряд, а противоположный ему ― положительный. Таким образом, в проводнике возникает разность потенциалов и электродвижущая сила.

В некоторых случаях удобно решать задачи, используя определение ЭДС через закон Лоренца (обычно это задачи о движении прямолинейного проводника в поле), в других ― через закон Фарадея.

В проводнике, движущемся в магнитном поле, образуется разность потенциалов U = lvBsinα;

где:

U — разность потенциалов [В],

l — длина проводника [м],

v — скорость движения проводника $big[ frac{text{м}}{c} big]$

B — индукция магнитного поля [Тл],

α — угол между направлением скорости и длиной проводника.

В случае, если есть какой-то замкнутый контур, то ЭДС в нем возникает только тогда, когда меняется магнитный потокчерез этот контур. В случае же тонкого стержня, для которого нельзя применить понятия магнитного потока, потому что у него просто нет площади, ЭДС возникает при движении в постоянном магнитном поле.

В случае, если в задаче дана проводящая рамка или контур, для определения ЭДС (напряжения) используем формулу $varepsilon_i = — frac{Delta text{Ф}}{Delta t}$

В случае, если в задачи дан проводник, движущейся в поле, для определения ЭДС (напряжения) используем формулу $varepsilon$ =U= lvBsinα.

Задача 3

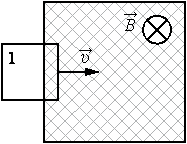
В заштрихованной области на рисунке действует однородное магнитное поле, перпендикулярное плоскости рисунка с индукцией В = 0,1 Тл. Квадратную проволочную рамку, сопротивление которой 10 Ом и длина стороны 10 см, перемещают в этом поле в плоскости рисунка поступательно равномерно с некоторой скоростью υ. При попадании рамки в магнитное поле в положении 1 в ней возникает индукционный ток, равный 1 мА. Какова скорость движения рамки?

Решение:

Составим цепочку.

Зная силу тока и сопротивление, что можно найти? Мы сможем найти напряжение, то есть ЭДС, а ЭДС, уже можно легко связать со скоростью движения рамки.

Составим цепочку. Мы знаем магнитное поле (В), длину стороны (a), сопротивление (R) и силу тока (I), а найти нужно скорость(v).

Зная ток и сопротивление, что сразу можно найти? Напряжение, то есть ЭДС, которое мы сможем найти по закону Ома.

А связать ЭДС с индукцией поля, стороной рамки и скоростью движения очень легко, воспользовавшись той формулой, которую мы получили в прошлой задаче.

Пройдёмся вдоль этой цепочки.

Запишем закон Ома $I = frac{varepsilon}{R}$, подставив сюда формулу для ЭДС, которую мы получили в прошлой задаче, отбросив знак «минус» получим $I = frac{varepsilon}{R} = frac{Bav}{R}$отсюда выразим скорость, и, подставив все величины, получим $v = frac{IR}{Ba} = frac{1cdot 10^{-3} Acdot 10text{Ом}}{0,1 text{Тл} cdot 0,1 text{м}} = 1 frac{text{м}}{c}$

Ответ: 1

Содержание книги

Предыдующая страница

§12. Постоянное магнитное поле

12.11 Магнитный поток, теорема о магнитном потоке.

Ранее мы убедились насколько полезно и удобно понятие потока векторного поля. Не является исключением и описание магнитного поля – для него также определяется поток, и формулируется теорема об этом потоке.

Поток вектора магнитной индукции (который также называется магнитным потоком) определяется традиционно ^[1]. Пусть в некоторой малой области пространства существует магнитное поле, которое можно считать однородным, то есть в этой области вектор магнитной индукции постоянен, как по величине, так и по направлению.

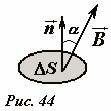
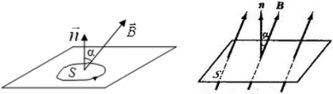
Выделим малую площадку площадью ΔS, ориентация которой задается единичным вектором нормали (~vec n) (Рис. 44). Магнитный поток через эту площадку ΔФ_m определяется как произведение площади площадки на нормальную составляющую вектора индукции магнитного поля

(~Delta Phi_m = B cos alpha Delta S = (vec B cdot vec n) Delta S = B_n Delta S) . (1)

где (~(vec B cdot vec n) = B cos alpha) — скалярное произведение векторов (~vec B) и (~vec n); B_n — нормальная к площадке компонента вектора магнитной индукции.

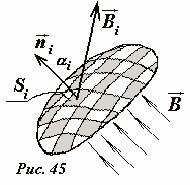
В произвольном магнитном поле магнитный поток через произвольную поверхность, определяется следующим образом (Рис. 45):

— поверхность разбивается на малые площадки ΔS_i (которые можно считать плоскими);

— определяется вектор индукции (~vec B_i) на этой площадке (который в пределах площадки можно считать постоянным);

— вычисляется сумма потоков через все площадки, на которые разбита поверхность

(~Phi = Delta Phi_1 + Delta Phi_2 + Delta Phi_3 + ldots = sum_i Delta Phi_i = sum_i B_i cos alpha_i Delta S_i) . (2)

Эта сумма называется потоком вектора индукции магнитного поля через заданную поверхность (или магнитным потоком).

Обратите внимание, что при вычислении потока суммирование проводится по точкам наблюдения поля, а не по источникам, как при использовании принципа суперпозиции. Поэтому магнитный поток является интегральной характеристикой поля, описывающей его усредненные свойства на всей рассматриваемой поверхности.

Трудно найти физический смысл магнитного потока, как и для иных полей это полезная вспомогательная физическая величина. Но в отличие от других потоков, магнитный поток настолько часто встречается в приложениях, что в системе СИ удостоился «персональной» единицы измерения — Вебер: 1 Вебер – магнитный поток однородного магнитного поля индукции 1 Тл через площадку площадью 1 м² ориентированную перпендикулярно вектору магнитной индукции.

Теперь докажем простую, но чрезвычайно важную теорему о магнитном потоке через замкнутую поверхность.

Ранее мы установили, что силовые любого магнитного поля являются замкнутыми, уже из этого следует, что магнитный поток, через любую замкнутую поверхность равен нулю.

Тем не менее, приведем более формальное доказательство этой теоремы.

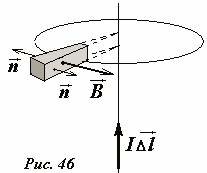
Прежде всего, отметим, что для магнитного потока справедлив принцип суперпозиции: если магнитное поле создано несколькими источниками, то для любой поверхности поток поля, созданного системой элементов тока, равен сумме потоков полей, созданных каждым элементом тока в отдельности. Это утверждение следует непосредственно из принципа суперпозиции для вектора индукции и прямо пропорциональной связью между магнитным потоком и вектором магнитной индукции. Следовательно достаточно доказать теорему для поля, созданного элементом тока, индукция которого определяется по закону Био-Саварра-Лапласа. Здесь для нас важна структура поля, обладающего осевой круговой симметрией, значение модуля вектора индукции несущественно. Выберем в качестве замкнутой поверхности поверхность бруска, вырезанного, как показано на рис. 46. Магнитный поток отличен от нуля только через его две боковые грани, но эти потоки имеют противоположные знаки. Вспомним, что для замкнутой поверхности выбираю внешнюю нормаль, поэтому на одной из указанных граней (передней) поток положительный, а на задней отрицательный. Причем модули этих потоков равны, так как распределение вектора индукции поля на этих гранях одинаково. Данный результат не зависит от положения рассмотренного бруска. Произвольное тело можно разбить на бесконечно малые части, каждая из которых подобна рассмотренному бруску.

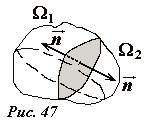
Наконец, сформулируем еще одно важное свойство потока любого векторного поля. Пусть произвольная замкнутая поверхность ограничивает некоторое тело (Рис. 47). Разобьем это тело на две части, ограниченные частями исходной поверхности Ω₁ и Ω₂, и замкнем их общей границей раздела тела. Сумма потоков через эти две замкнутые поверхности равна потоку через исходную поверхность! Действительно сумма потоков через границу (один раз для одного тела, другой раз для другого) равна нулю, так как в каждом случае надо брать разные, противоположные нормали (каждый раз внешнюю). Аналогично можно доказать утверждение для произвольного разбиения тела: если тело разбито на произвольное число частей, то поток через поверхность тела равен сумме потоков через поверхности всех частей разбиения тела. Это утверждение очевидно для потока жидкости.

Фактически мы доказали, что если поток векторного поля равен нулю через некоторую поверхность ограничивающее малый объем, то этот поток равен нулю через любую замкнутую поверхность.

Итак, для любого магнитного поля справедлива теорема о магнитном потоке: магнитный поток через любую замкнутую поверхность равен нулю Ф_m = 0.

Ранее мы рассматривали теоремы о потоке для поля скоростей жидкости и электростатического поля. В этих случаях поток через замкнутую поверхность полностью определялся точечными источниками поля (истоками и стоками жидкости, точечными зарядами). В общем случае наличие ненулевого потока через замкнутую поверхность свидетельствует о наличии точечных источников поля. Следовательно, физическим содержанием теоремы о магнитном потоке является утверждение об отсутствии магнитных зарядов.

Если вы хорошо разобрались в данном вопросе и сумеете объяснить и отстоять свою точку зрения, то можете формулировать теорему о магнитном потоке и так: «Еще никто не нашел монополя Дирака».

Следует особо подчеркнуть, что, говоря об отсутствии источников поля, мы имеем виду именно точечных источников, подобных электрическим зарядам. Если провести аналогию с полем движущейся жидкости, электрические заряды подобны точкам, из которых вытекает (или втекает) жидкость, увеличивая или уменьшая ее количество. Возникновение магнитного поля, благодаря движению электрических зарядов подобно движению тела в жидкости, которое приводит к появлению вихрей, не изменяющих общего количества жидкости.

Векторные поля, для которых поток через любую замкнутую поверхность равен нулю получили красивое, экзотическое название – соленоидальные. Соленоидом называется проволочная катушка, по которой можно пропускать электрический ток. Такая катушка может создавать сильные магнитные поля, поэтому термин соленоидальный означает «подобный полю соленоида», хотя можно было назвать такие поля попроще – «магнитоподобные». Наконец такие поля еще называют вихревыми, подобно полю скоростей жидкости, образующей в своем движении всевозможные турбулентные завихрения.

Теорема о магнитном потоке имеет большое значение, она часто используется при доказательстве различных свойств магнитных взаимодействий, с ней мы будем встречаться неоднократно. Так, например, теорема о магнитном потоке доказывает, что вектор индукции магнитного поля, создаваемого элементом, не может иметь радиальной составляющей (Рис. 23.а), иначе поток через цилиндрическую поверхность коаксиальную с элементом тока был бы отличен от нуля.

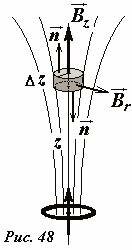
Теперь проиллюстрируем применение теоремы о магнитном потоке для расчета индукции магнитного поля. Пусть магнитное поле создается кольцом с током, которое характеризуется магнитным моментом p_m. Рассмотрим поле вблизи оси кольца на расстоянии z от центра, значительно большем радиуса кольца (Рис. 48). Ранее мы получили формулу для индукции магнитного поля на оси для больших расстояний от центра кольца

(~B_z = frac{mu_0 p_m}{2 pi z^3}) . (3)

Мы не допустим большой ошибки, если будем считать, что такое же значение имеет вертикальная (пусть ось кольца вертикальна) компонента поля в пределах небольшого кольца радиуса r, плоскость которого перпендикулярна оси кольца. Так как вертикальная компонента поля изменяется с изменением расстояния, то неизбежно должны присутствовать радиальные компоненты поля, иначе не будет выполняться теорема о магнитном потоке! Оказывается этой теоремы и формулы (3) достаточно, чтобы найти эту радиальную компоненту. Выделим тонкий цилиндр толщиной Δz и радиуса r, нижнее основание которого находится на расстоянии z от центра кольца, соосный с кольцом и применим теорему о магнитном потоке к поверхности этого цилиндра. Магнитный поток через нижнее основание равен (учтите, что вектора индукции и нормали здесь противоположны)

(~Phi_1 = -B_z(z) pi r^2) ,

где B_z(z) — значение вертикальной компоненты вектора индукции на высоте z; поток через верхнее основание равен

(~Phi_2 = B_z(z + Delta z) pi r^2) ,

где B_z(z + Δz) — значение вертикальной компоненты вектора индукции на высоте z + Δz;

поток через боковую поверхность (из осевой симметрии следует, что модуль радиальной составляющей вектора индукции B_r на этой поверхности постоянен):

(~Phi_3 = B_r 2 pi r Delta z) .

По доказанной теореме сумма этих потоков равна нулю, поэтому справедливо уравнение

(~Phi_1 + Phi_2 + Phi_3 = -B_z(z) pi r^2 + B_z(z + Delta z) pi r^2 + B_r 2 pi r Delta z) ,

из которого определим искомую величину

(~B_r = — frac{r}{2} cdot frac{B_z(z + Delta z) — B_z(z)}{Delta z}) . (4)

Осталось использовать формулу (3) для вертикальной составляющей поля и провести необходимые вычисления ^[2]

(~B_r = — frac{r}{2} cdot frac{mu_0 p_m}{2 pi Delta z} left( frac{1}{(z + Delta z)^3} — frac{1}{z^3} right ) = -r frac{mu_0 p_m}{4 pi z^3 Delta z} left( left( 1 + frac{Delta z}{z} right )^{-3} — 1 right ) approx -r frac{mu_0 p_m}{4 pi z^3 Delta z} left( left( 1 — 3 frac{Delta z}{z} right ) — 1 right ) = frac{3 mu_0 p_m}{4 pi z^4} r) . (5)

Действительно, убывание вертикальной компоненты поля приводит к появлению горизонтальных компонент: уменьшение вытекания через основания приводит к «течи» через боковую поверхность.

Таким образом, мы доказали «криминальную теорему»: если через один конец трубы вытекает меньше, чем вливают в нее с другого конца, то где-то воруют через боковую поверхность.

Примечания

1. ↑ Достаточно взять текст с определением потока вектора напряженности электрического поля и изменить обозначения (что здесь и сделано).
2. ↑ Самые грамотные могут увидеть в последней дроби производную функции (3) и элементарно ее вычислить, нам же придется очередной раз воспользоваться приближенной формулой (~(1 + x)^beta approx 1 + beta x)

Следующая страница

Скачать материал

Скачать материал

Описание презентации по отдельным слайдам:

• 

• 

  2 слайд

  вектор магнитной индукции

  Там, где силовые линии гуще, индукция магнитного поля больше.

  Там, где силовые линии реже, индукция магнитного поля меньше
  В
  В
  В
  В

• 

  3 слайд

  Отличие магнитной индукции от магнитного потока
  Вектор магнитной индукции В характеризует магнитное поле в каждой точке пространства, а магнитный поток – определенную область пространства

• 

  4 слайд

  Определение магнитного потока
  Произведение индукции магнитного поля, пронизывающей поперечное сечение контура, на площадь этого контура называется магнитным потоком
  В
  S

• 

  5 слайд

  Обозначение и формула магнитного потока
  Ф — символ магнитного потока
  Ф — скалярная величина.

  Формула для расчета магнитного потока
  Ф=В·S·cosα

  В
  f
  α
  n
  s

• 

  6 слайд

  Величины, входящие в формулу
  Ф=В·S·cosα

  n

  В – магнитная индукция,
  S – площадь контура,
  ограничивающего площадку,
  α – угол между направлением вектора индукции В и нормалью n
  (перпендикуляром) к площадке

  S
  В
  α

• 

  7 слайд

  Единица измерения магнитного потока
  Вб
  1 Вб — магнитный поток, созданный магнитным полем с индукцией 1 Тл через поверхность площадью 1м2 , расположенную перпендикулярно вектору магнитной индукции.
  S=1м2

  В=1 Тл

• 

  8 слайд

  Способы изменения магнитного потока Δ Ф

  1) Путем изменения площади
  контура Δ S

  2) Путем изменения величины магнитного поля Δ В

  3) Путем изменения угла Δ α

• 

  9 слайд

  S

  Зависимость ΔФ от площади ΔS
  При одинаковой магнитной индукции В, чем больше
  площадь контура S ,
  тем больше
  изменение магнитного потока Δ Ф,
  пронизывающего данный контур:

  S

  В
  В
  ΔФ=В·ΔS·cosα

• 

  10 слайд

  Зависимость ΔФ от магнитной индукции ΔВ
  При одинаковой площади S,чем сильнее поле, тем гуще линии магнитной индукции, соответственно увеличивается В, а значит и больше изменение магнитного потока:

  ΔФ=ΔВ·S·cosα

  В
  В
  s
  s

• 

  11 слайд

  Зависимость ΔФ от угла Δα
  Если угол α = 0º
  В этом случае линии В и нормали n к площадке параллельны.
  Но В и площадка S перпендикулярны друг другу !!!
  Тогда cos 0º =1 , изменение магнитного потока принимает свое максимальное значение:
  Δ Ф = B · S

  n
  B
  n
  n
  s

• 

  12 слайд

  Зависимость ΔФ от угла Δα
  2) Если угол α= 90 º
  В этом случае линии В и нормали n к площадке перпендикулярны
  Но В и площадка S параллельны друг другу!!!
  cos 90º =0 и изменение магнитного потока будет минимальным:
  ΔФ=0

  n
  В
  s

• 

  13 слайд

  Зависимость ΔФ от угла Δα
  При вращении рамки определенной площади S в постоянном магнитном поле В ,угол между В и S постоянно меняется от α1 до α2

  Тогда изменение магнитного потока находится по формуле:

  В
  ΔФ = В · S · (cosα1 – cosα2 )

  S

• 

  14 слайд

  Решение задач
  Задача №1
  Контур с площадью
  100 см2 находится в однородном магнитном поле с индукцией 2 Тл. Чему равен магнитный поток, пронизывающий контур, если плоскость контура и вектор индукции перпендикулярны ?
  S=100 см2 0,01м2
  В=2 Тл
  α=0º
  Ф — ?

  Ф=В·S·cosα
  Ф=0,02 Вб

• 

  15 слайд

  Решение задач
  Задача №2
  Контур площадью 1 м2 находится в однородном магнитном поле с индукцией 0,5Тл, угол между вектором индукции и нормалью к поверхности контура 60º. Каков магнитный поток через контур?

   S=1 м2
  В=0,5 Тл
  α=60º
  Ф — ?

  Ф=В·S·cosα
  Ф=0,25 Вб

• 

  16 слайд

  Решение задач
  Задача 3
  Проволочное кольцо радиусом 1 м ,
  поворачивается на 1800 относительно вертикальной оси. Индукция магнитного поля равна 5 Тл и сразу перпендикулярна кольцу. Найдите изменение магнитного потока через кольцо в результате поворота
  R=1 м2
  В=5 Тл
  α1 =0º
  α2 =180º S=2R
  ΔФ — ?

  ΔФ=В·S·(cosα1- cosα2)
  ΔФ=62,8 Вб

• 

  17 слайд

  Домашнее задание

  § 2 или 1.4.2

  4.7, 4.8

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 268 655 материалов в базе

• Выберите категорию:

• Выберите учебник и тему

• Выберите класс:

• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

Вам будут интересны эти курсы:

• Курс повышения квалификации «Информационные технологии в деятельности учителя физики»

• Курс профессиональной переподготовки «Маркетинг: теория и методика обучения в образовательной организации»

• Курс повышения квалификации «Основы местного самоуправления и муниципальной службы»

• Курс повышения квалификации «Формирование компетенций межкультурной коммуникации в условиях реализации ФГОС»

• Курс повышения квалификации «История и философия науки в условиях реализации ФГОС ВО»

• Курс повышения квалификации «Основы построения коммуникаций в организации»

• Курс профессиональной переподготовки «Организация деятельности по подбору и оценке персонала (рекрутинг)»

• Курс повышения квалификации «Экономика: инструменты контроллинга»

• Курс повышения квалификации «Организация маркетинга в туризме»

• Курс повышения квалификации «ЕГЭ по физике: методика решения задач»

• Курс повышения квалификации «Финансовые инструменты»