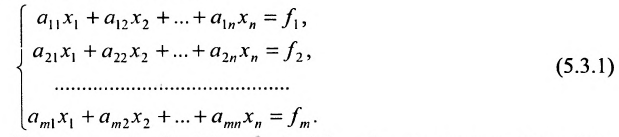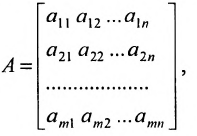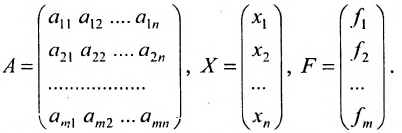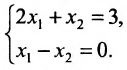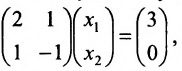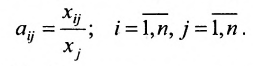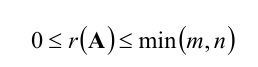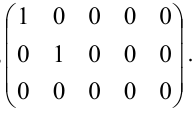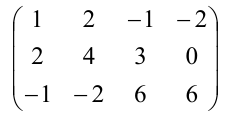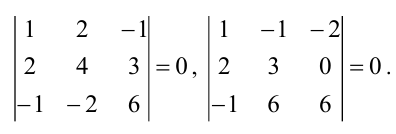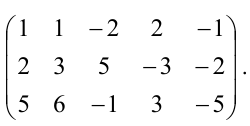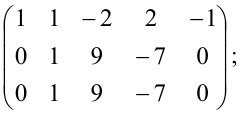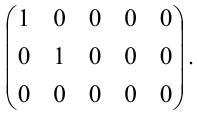Понятие ранга матрицы тесно связано с
понятием линейной зависимости и линейной
независимости строк (столбцов) матрицы.
В матрице

Обозначим строки
;
;
…;.
Определение 1.16 Строка
называется линейной комбинацией
строк,
если ее можно представить в виде
,
где—
числовые коэффициенты;
,
В этом случае, говорят, что строка
линейно выражается через строки
.
Определение 1.17 Система, состоящая
из строк матрицы,
называетсялинейно зависимой,
если хотя бы одна из этих строк является
линейной комбинацией других строк этой
системы, например,
.
В противном случае, если ни одна из строк
не может быть представлена в виде
линейной комбинации других строк этой
системы, строкиназываютсялинейно независимыми.
Замечание. Следует отметить,
что определение 1.17 не является строгим.
Строгое определение линейно зависимой
и линейно независимой системы будет
дано ниже.
Примеры.
-
Рассмотрим строки
и
.
Нетрудно, заметить, чтот.
е. строкалинейно выражается через строку
,
следовательно, строки—
линейно зависимы.
Две пропорциональные строки –
линейно зависимы.
Соответственно, две непропорциональные
строки – линейно независимы.
-
Рассмотрим три строки
,
,
Нетрудно заметить, что строка
может быть представлена в виде суммы
строки
,
т.е..
Следовательно, строки— линейно зависимые.
Если отбросить строку
,
то строкии
—
линейно независимые, так как
непропорциональные. Следовательно,
максимальное число линейно независимых
строк в данной системе равно двум.
Теорема о ранге матрицы
Ранг матрицы равен максимальному
числу линейно независимых строк
(столбцов) матрицы, через которые линейно
выражаются все остальные строки матрицы.
Пример.
Найти максимальное число линейно
независимых строк матрицы

Решение.
Задача сводится к отысканию ранга
матрицы
.
Найдем ранг матрицы, приведя ее к
ступенчатому виду с помощью элементарных
преобразований.

̴

В ступенчатой матрице две ненулевые
строки, следовательно,
,
а значит, максимальное число линейно
независимых строк матрицы равно 2.
Первая и вторая строки матрицы – линейно
независимые.
Теорема о ранге матрицы имеет принципиальное
значение при изучении систем линейных
алгебраических уравнений.
Соседние файлы в папке Теория ЛА (первый семестр)
- #
25.03.2016583.68 Кб5~WRL3348.tmp
- #
- #
- #
- #
- #
Ранг системы столбцов (строк) матрицы
Пусть дана система столбцов размеров
. Рангом системы столбцов называется максимальное число линейно независимых столбцов этой системы и обозначается
. Максимальной линейно независимой подсистемой столбцов (или базой системы столбцов) называется линейно независимая подсистема, состоящая из
столбцов. Максимальность здесь понимается в том смысле, что любое большее количество столбцов данной системы образует линейно зависимую подсистему.
Для нахождения максимальной линейно независимой подсистемы столбцов надо выполнить следующие действия.
1. Составить из данных столбцов матрицу размеров
.
2. Найти базисный минор этой матрицы.
3. Столбцы, в которых расположен базисный минор, образуют искомую подсистему (т.е. базу данной системы столбцов).
Замечания 3.6.
1. Ранг системы столбцов равен рангу матрицы, составленной из этих столбцов:
2. У системы столбцов может быть несколько максимальных линейно независимых подсистем, но все они состоят из одинакового количества столбцов.
3. Столбцы, в которых расположен базисный минор матрицы , можно найти методом Гаусса. Для этого приводим матрицу
к ступенчатому виду, используя только преобразования ее строк. В матрице ступенчатого вида выбираем базисный минор. Столбцы, в которых расположен базисный ми нор матрицы
, совпадают (по номерам) со столбцами, в которых расположен базисный минор матрицы ступенчатого вида (см. следствие 2 теоремы 3.4 о ранге матрицы).
4. Пусть дана система строк размеров
. Рангом системы строк называется максимальное число линейно независимых строк этой системы. Для нахождения максимальной линейно независимой подсистемы строк нужно составить из этих строк матрицу и найти ее базисный минор (например, используя только элементарные преобразования ее столбцов). Строки, в которых расположен базисный минор, образуют искомую подсистему. Другим путем решения задачи является ее сведение к нахождению максимальной линейно независимой системы столбцов
(см. следствие 1 теоремы 3.4 о ранге матрицы).
Пример 3.9. Дана система столбцов
Найти ранг системы и максимальную линейно независимую подсистему столбцов.
Решение. 1. Составляем из данных столбцов матрицу
2. Находим базисный минор этой матрицы. Для этого приводим ее к ступенчатому виду, преобразовывая только строки:
Следовательно, — базисный минор этой матрицы (один из них) и
. Второй и четвертый столбцы преобразованной матрицы линейно независимы. Так как преобразования выполнялись только над строками, то второй и четвертый столбцы исходной матрицы
также линейно независимы (см. следствие 2 теоремы 3.4). Поэтому ранг системы столбцов равен 2. Следовательно,
— максимальная линейно независимая подсистема системы столбцов
. В примере 3-3 были найдены и другие максимальные линейно независимые подсистемы, каждая из которых состоит из двух столбцов.
Пример 3.10. Дана система строк
Найти ранг и максимальную линейно независимую подсистему строк.
Решение. 1. Составляем из данных строк матрицу
2. Преобразуем матрицу, используя элементарные преобразования ее столбцов:
Хотя это не ступенчатый вид, нетрудно заметить, что минор — базисный (один из них) и
. Поэтому ранг данной системы строк равен 3. Первые три строки преобразованной матрицы линейно независимы. Так как преобразовывались только столбцы матрицы, делаем вывод, что первые три строки исходной матрицы также линейно независимы. Поэтому
— максимальная линейно независимая подсистема строк данной системы.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Содержание:
Элементарные преобразования матриц:
Рассмотрим прямоугольную матрицу:
состоящую из m строк и n столбцов. В п.3.2 отмсчалось, что каждую строку матрицы можно рассматривать как n-мсрный вектор, а каждый столбец — как m-мерный вектор. Тогда матрицу А можно записать в виде:
и, следовательно, данную матрицу можно рассматривать как систему вектор строк или вектор столбцов. Б указанных системах вектор-строк и вектор-столбцов можно выделять линейно независимые (зависимые) векторы. Тогда будем говорить, что строки (столбцы) матрицы линейно независимы (зависимы), если соответствующие им векторы независимы (зависимы).
Определения
Определение: Рангом системы строк (соответственно столбцов) матрицы А называется наибольшее число линейно независимых среди них.
Поскольку легко доказать, что ранг системы строк матрицы равен рангу системы её столбцов, то справедливо следующее
Определение: Рангом матрицы, обозначаемым r(А), называется максимальное число линейно независимых строк (столбцов) матрицы.
При транспонировании матрицы ранг её не изменяется.
Другой метод определения ранга матрицы связан с понятием определителя.
Выделим в матрице А любые k строк и k столбцов. Элементы, стоящие на их пересечении, образуют квадратную матрицу, определитель которой называется минором k-го порядка матрицы А. Ясно, что величина к должна удовлетворять двум условиям: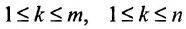
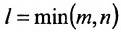
Определение: Рангом матрицы, обозначаемым r(А), называется порядок самого старшего минора этой матрицы, не равного нулю.
Из определения следует, что если ранг матрицы А равен l, то среди всех её миноров существует хотя бы один минор l-го порядка, отличный от нуля, но все миноры (l+1)-го порядков либо равны нулю, либо не могут быть составлены.
Вычисление ранга матрицы путём перебора всех её миноров весьма трудоёмко. Существует, однако, более простой способ вычисления ранга матрицы, основанный на упрощении структуры матрицы с помощью элементарных преобразований. Элементариыми преобразованиями матрицы называют следующие преобразования:
- обмен местами двух строк или двух столбцов матрицы;
- умножение всех элементов строки или столбца матрицы на произвольное число
, не равное нулю;
- прибавление ко всем элементам строки (столбца) матрицы соответствующих элементов другой строки (столбца), предварительно умноженных на одно и то же число;
- исключение из матрицы строки или столбца, состоящего из нулей.
Матрицы называются эквивалентными, если от одной из них к другой можно перейти путём конечного числа элементарных преобразований.
Ступенчатой матрицей называется матрица, удовлетворяющая тому свойству, что если в какой-либо из сё строк первый отличный от нуля элемент стоит на l-м месте, то во всех следующих строках на первых l местах стоят нули:
где элементы 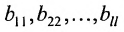
Для вычисления ранга матрицы приводят её с помощью цепочки элементарных преобразований к ступенчатому виду. Тогда ранг матрицы совпадает с числом её ненулевых диагональных элементов.
Теоремы о ранге матриц. Свойства ранга матриц
Относительно ранга матриц можно сформулировать следующие теоремы:
Теорема: Если матрица имеет минор порядка r, отличный от нуля, для которого все содержащие его миноры порядка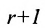
Вычисление ранга матрицы при помощи метода окаймления нужно вести от низших порядков к высшим. Сначала ищем минор первого порядка (т.е. элемент матрицы) или сразу второго порядка, отличный от нуля. Затем вычисляем окаймляющие его миноры следующего порядка, пока не найдём среди них отличного от нуля и т.д., пока не найдем минор порядка l, отличный от нуля, для которого либо все окаймляющие его миноры порядка l+1 равны нулю, либо такие миноры не могут быть составлены.
Теорема: Элементарные преобразования не меняют ранга матрицы.
Доказательство теоремы следует из определения ранга матрицы и свойств определителей.
Пример:
Найти ранг матрицы:
Решение:
Минор первого порядка в левом верхнем углу равен 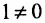
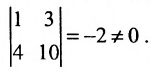
Значит ранг матрицы равен 2.
Пример:
Найти ранг матрицы:
Решение:
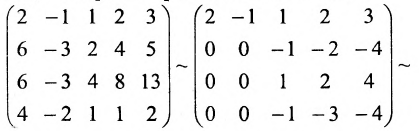
При помощи элементарных преобразований приведём данную матрицу к ступенчатому виду. На первом шаге умножим последовательно первую строку на 3, 3, 2 и вычтем из второй, третьей, четвёртой строк соответственно:
В эквивалентной матрице прибавим к третьей строке вторую и вычтем вторую из четвёртой строки:
(поменяем местами третью и четвертую строки)
(поменяем местами третий, четвёртый и пятый столбцы со вторым и опустим строки, состоящие из нулей) 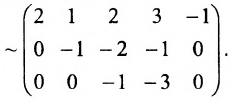
Отмстим некоторые свойства ранга матриц.
- Ранг суммы двух (или нескольких) матриц не больше суммы их рангов.
- Любую матрицу ранга r можно представить в виде суммы r матриц ранга 1, но нельзя представить в виде суммы менее чем r таких матриц.
- Любую матрицу С ранга r можно представить в виде произведения
, где А состоит из r линейно независимых столбцов, г B -из r линейно независимых строк.
- Ранг произведения матриц порядка n удовлетворяет неравенству
.
Определение системы m линейных уравнений с n неизвестными
Системой m линейных уравнений с n неизвестными 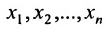
Числа 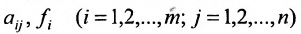
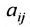
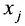
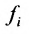
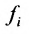
С помощью знака суммирования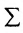
Матрица
составленная из коэффициентов системы 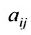
системы. Если к этой матрице добавить столбец свободных членов, то получим расширенную матрицу системы: 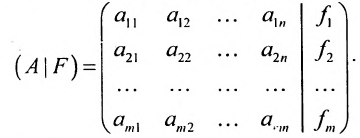
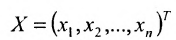
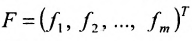

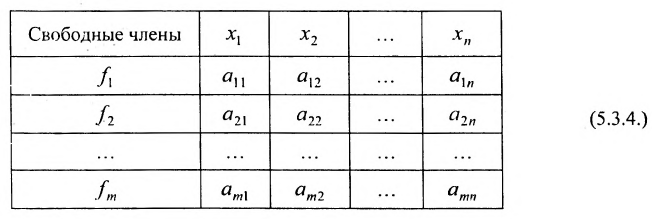
Используется также табличная форма записи системы (5.3.1):
Отметим, что (5.3.1), (5.3.2), (5.3.3), (5.3.4)- различные виды записи одной и той же системы линейных уравнений.
Решением системы (5.3.1) называется любой упорядоченный набор действительных чисел 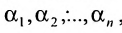
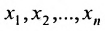
Система уравнений (5.3.1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений. Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Две системы уравнений с одинаковыми наборами неизвестных 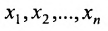
Отмстим, что для любой системы (5.3.1) возможны только три случая:
- система (5.3.1) имеет единственное решение;
- система (5.3.1) имеет бесчисленное множество решений;
- система (5.3.1) несовместна.
Множество всех решений системы (5.3.1) называется ее общим решением.
Решить систему (5.3.1) — значит найти ее общее решение.
Пример:
Пусть задана система
Тогда эту систему можно записать в матричном виде:
или в виде таблицы:
Система определенная, так как она имеет единственное решение 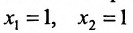
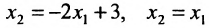
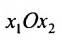
Экономические задачи, приводящие к системе линейных уравнений
Предположим, что производственные мощности для изготовления n различных видов продукции установлены в т цехах. Пусть 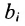
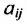
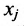
Широкий круг задач экономики приводит к составлению системы уравнений. Так в примере 4.3.2 составлялась система линейных уравнений (4.3.1) балансовой модели для трёх отраслей. В общем случае под балансовой моделью понимается система уравнений, каэ/сдое из которых выражает требование баланса между производимым количеством продукции и совокупной потребностью в этой продукции.
При построении балансовых моделей используется понятие чистой (или технологической) отрасли, т.е. условной отрасли, объединяющей всё производство данного продукта независимо от ведомственной (административной) подчинённости и форм собственности предприятий и фирм. Всё народное хозяйство представляется в виде совокупности п отраслей, каждая из которых рассматривается как производящая и как потребляющая.
Если обозначить через:
то систему уравнений баланса можно записать в виде:
или в матричной форме:
где Х- вектор-столбец валовой продукции; Y- вектор-столбец конечной продукции; А — матрица коэффициентов прямых затрат.
Основу экономико-математической модели межотраслевого баланса составляет технологическая матрица А, содержащая коэффициенты прямых затрат на производство единицы продукции:
Коэффициент!,! прямых затрат являются довольно стабильной величиной во времени.
Переписав матричное уравнение (5.4.2) в виде EX-AX = Y или (E-A)X = Y, (5.4.3) получим стандартную форму записи системы уравнений.
Определение ранга матрицы
Рассмотрим прямоугольную матрицу (4.1). Если в этой матрице выделить произвольно 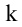
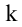
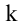
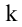
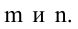
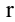
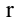
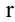
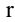
Очевидно, что выполняется соотношение
Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D 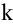
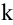
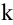
Элементарными называются следующие преобразования матрицы:
- перестановка двух любых строк (или столбцов),
- умножение строки (или столбца) на отличное от нуля число,
- прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.
Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.
Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: А ~ В.
Канонической матрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы
равны нулю, например,
При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической. Ранг канонической матрицы равен числу единиц на ее главной диагонали.
- Заказать решение задач по высшей математике
Пример:
Найти методом окаймления миноров ранг матрицы
Решение:
Начинаем с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор (элемент) 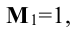
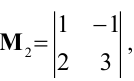
Переходим теперь к минорам 3-го порядка, окаймляющим 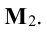
Таким образом, асе окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум.
Пример:
Найти ранг матрицы 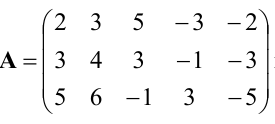
Решение:
Из второй строки вычтем первую и переставим эти строки:
Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 2 и 5:
из третьей строки вычтем первую; получим матрицу 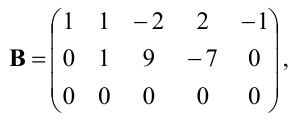
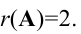
Вычисление ранга матрицы
Для исследования разрешимости систем линейных уравнений важную роль играет понятие ранга матрицы. Рассмотрим прямоугольную матрицу А
Выделим k произвольных строк и k произвольных столбцов этой матрицы. Определитель k-го порядка, составленный из элементов матрицы А, расположенных на пересечении выделенных строк и столбцов, называется минором k-го порядка матрицы А.
Рангом матрицы А называется наибольший порядок ее миноров, отличных от нуля. Обозначение: rank А,
Базисным минором матрицы называется всякий отличный от нуля ее минор, порядок которого равен рангу матрицы.
Рассмотрим некоторые методы вычисления ранга матрицы.
Метод окаймляющих миноров
Минор порядка k+1, содержащий в себе минор порядка k, называется окаймляющим минором.
Вычисляя ранг матрицы, удобнее переходить от миноров меньших порядков к минорам больших порядков. Если найден минор k-го порядка, отличный от нуля, а все окаймляющие его миноры порядка k+1 равны нулю, то ранг матрицы равен k.
- Определители второго и третьего порядков и их свойства
- Метод Гаусса — определение и вычисление
- Прямая линия на плоскости и в пространстве
- Плоскость в трехмерном пространстве
- Кратный интеграл
- Ряды в математике
- Дифференциальные уравнения с примерами
- Обратная матрица — определение и нахождение
Here’s the specific question:
For the matrix $$begin{bmatrix}1&2 & 0 & 3\ 1 & 2& 3 & 3 \ 1 & 0 &
1 & 1 \1 & 1 & 1 & 2 end{bmatrix}$$ determine the maximum number of
linearly independent rows and the maximum number of linearly
independent columns.
I know that we say that rows/columns $mathbf{x_1},mathbf{x_2},ldotsmathbf{x_p}$ are called linearly independent if the only scalars $lambda_1, ldots,lambda_p$ which are such that $$lambda_1mathbf{x_1}+lambda_2mathbf{x_2}+ldots+lambda_nmathbf{x_p}=mathbf{0}$$ are $lambda_1=lambda_2=ldots=lambda_p=0$.
Okay, but that leaves me 11 possible sets of columns and rows to consider. First let us consider the columns $mathbf{x_1},mathbf{x_2},mathbf{x_3}, mathbf{x_4}$. Suppose that we have $lambda_1mathbf{x_1}+lambda_2mathbf{x_2}+lambda_3mathbf{x_3}+lambda_4mathbf{x_4}=mathbf{0}$ for some scalars $lambda_1,lambda_2,lambda_3,lambda_4$. Then
$$lambda_1begin{bmatrix}1\1\1\1end{bmatrix} + lambda_2begin{bmatrix}2\2\0\3end{bmatrix} + lambda_3begin{bmatrix}0\3\1\1end{bmatrix} + lambda_4begin{bmatrix}3\3\1\2end{bmatrix} = begin{bmatrix}0\0\0\0end{bmatrix}$$
and consequently
$$begin{eqnarray}
lambda_1 + 2lambda_2 + 3lambda_4 &=& 0 \
lambda_1 + 2lambda_2 + 3lambda_3 + 3lambda_4 &=& 0 \
lambda_1 + lambda_3 + lambda_4 &=& 0 \
lambda_1 + lambda_2 + lambda_3 + 2lambda_4 &=& 0
end{eqnarray}$$
and clearly $lambda_1 = 1 , lambda_2 = 1 , lambda_3 = 0 , lambda_4 =-1$ is a solution. Thus, columns $mathbf{x_1},mathbf{x_2},mathbf{x_3}, mathbf{x_4}$ are not linearly independent.
Do I need to repeat this for every possible group of columns and rows? But then if we consider $3$ columns, we’ll get a homogeneous system of $4$ equations with $3$ unknowns. How do I tackle this problem?
This is a question from Basic Linear Algebra — Blyth, Robertson. The authors have defined row reduced matrices and hermite matrices in the quest of a systematic method of tackling system of linear equations. Rank of matrices, Vector Spaces, Linear Mappings, Determinants are yet to be discussed.
Максимальное число — линейно независимая строка
Cтраница 1
Максимальное число линейно независимых строк ( или, что то же, столбцов) матрицы А называется ее рангом и обозначается через rang А.
[1]
Максимальное число линейно независимых строк матрицы совпадает с максимальным числом линейно независимых столбцов.
[2]
Пусть г обозначает максимальное число линейно независимых строк матрицы A, s — максимальное число линейно независимых столбцов. Оставим эти строки, уберем остальные, и применим к оставшейся матрице метод Гаусса. Выше он был описан для квадратной матрицы, но в прямоугольном случае почти ничего не меняется.
[3]
Из линейной алгебры известно, что максимальное число линейно независимых строк в матрице равно ее рангу. Если в матрице выбрать s строк и s столбцов, то минором порядка s матрицы называется детерминант матрицы порядка s, образованный элементами, расположенными на пересечении выбранных строк и столбцов.
[4]
Максимальное число линейно независимых столбцов матрицы равно максимальному числу линейно независимых строк, так как при транспонировании матрицы ее строки становятся столбцами, а ранг матрицы не меняется.
[5]
Из линейной алгебры известно, чт о максимальное число линейно независимых строк в матрице равно ее рангу. Если в матрице выбрать S строк и s столбцов, то минором порядка s матрицы называется детерминант матрицы порядка s, образованный элементами, расположенными на пересечении выбранных строк и столбцов.
[6]
Другими словами, р ( Л) есть максимальное число линейно независимых строк матрицы А.
[7]
В данном определении заложена теорема, поскольку совпадение максимального числа линейно независимых строк и столбцов сразу неочевидно, но это так.
[8]
Точно так же доказывается, что ранг матрицы равен максимальному числу линейно независимых строк, Отсюда вытекает интересное следствие.
[9]
Точно так же доказывается, что ранг матрицы равен максимальному числу линейно независимых строк. Отсюда вытекает интересное следствие.
[10]
Действительно, величина, стоящая в левой части, есть максимальное число линейно независимых строк матрицы А, в правой же части стоит максимальное число линейно независимых строк матрицы А; но это число, очевидно, совпадает с максимальным числом линейно независимых столбцов матрицы А.
[11]
В этом пункте мы убедимся, что ранг произвольной матрицы А равен максимальному числу линейно независимых строк ( или столбцов) этой матрицы.
[12]
Пусть матрица А имеет ранг г. Как доказано в предшествующем параграфе, г равно максимальному числу линейно независимых строк матрицы А. Пусть, для определенности, первые г строк матрицы А линейно независимы, а каждая из остальных будет их линейной комбинацией. Тогда первые г строк матрицы А также будут линейно независимыми: всякая линейная зависимость между ними была бы линейной зависимостью и между первыми г строками матрицы А ( вспомнить определение сложения векторов.
[13]
В частности, отсюда будет следовать весьма нетривиальная теорема о том, что у любой матрицы максимальное число линейно независимых строк совпадает с максимальным числом линейно независимых столбцов.
[14]
О В частности, отсюда будет следовать весьма нетривиальная теорема о том, что у любой матрицы максимальное число линейно независимых строк совпадает с максимальным числом линейно независимых столбцов.
[15]
Страницы:
1
2












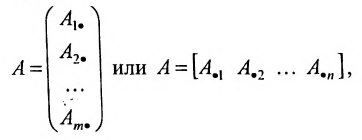
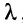 , не равное нулю;
, не равное нулю;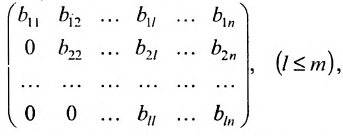
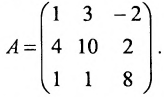
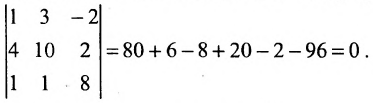



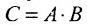 , где А состоит из r линейно независимых столбцов, г B -из r линейно независимых строк.
, где А состоит из r линейно независимых столбцов, г B -из r линейно независимых строк.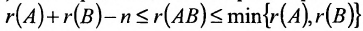 .
.