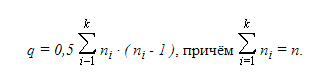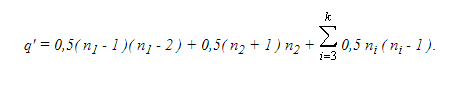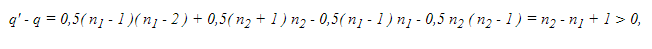Как найти максимальное количество ребер в графе - Исправление недочетов и поиск решений вместе с Examum.ru

Теорема. Пусть G – обыкновенный неориентированный граф с n вершинами и k компонентами связности. Тогда максимальное число ребер в графе G равно

q = 0,5( n — k )( n — k + 1 ).

Доказательство. Граф G имеет максимальное число ребер, если каждая компонента связности Gi , i = 1, 2, … , k имеет максимальное число ребер. Компонента связности Gi, имеющая максимальное число ребер, является полным графом. Число ребер полного графа с ni вершинами равно 0,5 · ni · ( ni — 1 ). Таким образом, максимальное число ребер графа G, компоненты связности Gi которого имеют по ni вершин, равно

Полученное число зависит от того, как распределены вершины графа G по его компонентам связности. Предположим, что существует связные компоненты G1 и G2 графа G, имеющие более чем по одной вершине, т.е. n1 > 1 и n2 > 1. Пусть n1 ≤ n2. Рассмотрим граф Go, получаемый из графа G заменой компонент G1 и G2 на полные графы с ( n1 — 1 ) и ( n2 + 1 ) вершинами соответственно. Граф Go имеет n вершин и k компонент связности, а число его ребер равно

Тогда

поэтому q’ > q. Итак, граф Go имеет больше ребер, чем граф G. Если и далее перестраивать граф указанным образом, то в результате получим граф, состоящий из k — 1 изолированной вершины и одной полной компоненты связности с n — k + 1 вершиной. Этот граф имеет максимальное число ребер, равное 0,5( n — k )( n — k + 1 ). Теорема доказана.

Следствие. Если обыкновенный неориентированный граф G с n вершинами имеет больше, чем 0,5( n — 1 )( n — 2 ) ребер, то он связен.

Источник

Если граф двудольный, то у любого цикла должна быть четная длина. Чтобы убедиться в этом, начнем с предположения, что два двусоставных множества называются

. Выберем любой цикл в графе и пометим вершины

Предположим, мы начинаем трассировку с вершины

. Тогда вторая, четвертая, шестая и следующие четные вершины находятся в

, а остальные — в

. Когда мы вернемся в начальную вершину, пройдем четное количество шагов. Это значит, что у цикла четная длина:

Предположим, что у нас есть граф, в котором нет нечетных циклов. Выберем любую компоненту графа и любую вершину в ней. Пусть

— все вершины компоненты на четном расстоянии от

, а

— все вершины компоненты на нечетном расстоянии от

Мы утверждаем, что это образует двудольное разбиение компоненты. Для этого покажем, что нет ребер ни внутри

, ни внутри

Предположим, что существует такое ребро между вершинами

, которые находятся в

или в

. Значит,

находятся либо на четном расстоянии от

, либо на нечетном.

Напомним, что расстояние между вершинами — это длина кратчайшего пути между ними. Рассмотрим кратчайшие пути из

и из

. Пусть

— последняя общая вершина этих путей. Путь

, за которым следует ребро

, а затем путь

образует цикл.

Его длина — это сумма слагаемых:

Расстояние от

до
Расстояние от

до

При этом сумма этих слагаемых будет четной. Внутри

и внутри

не может быть ни одного ребра. Таким образом,

образуют двудольное разбиение компонента. Мы можем проделать тот же процесс для каждой компоненты, чтобы получить двудольное разбиение всего графа.

Пример нечетного цикла, который создали во второй части доказательства:

Теперь нужно выбрать вершину и разбить граф на две группы:

Вершины, которые находятся на четном расстоянии от выбранной вершины
Вершины, которые находятся на нечетном расстоянии от выбранной вершины

Это основная идея доказательства. Во многих теоремах в теории графов есть одна большая идея, вокруг которой вращается доказательство.

Источник

Существуют различные типы графиков в зависимости от количества вершин, количества ребер, взаимосвязанности и их общей структуры. Мы обсудим только несколько важных типов графиков в этой главе.

Нулевой график

Граф, не имеющий ребер , называется нулевым графом .

пример

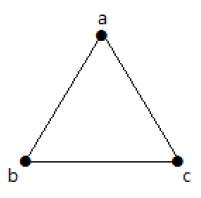
На приведенном выше графике есть три вершины с именами «a», «b» и «c», но среди них нет ребер. Следовательно, это нулевой граф.

Тривиальный график

Граф с единственной вершиной называется тривиальным графом .

пример

На приведенном выше графике есть только одна вершина «а» без других ребер. Следовательно, это тривиальный граф.

Ненаправленный граф

Ненаправленный граф содержит ребра, но ребра не являются ориентированными.

пример

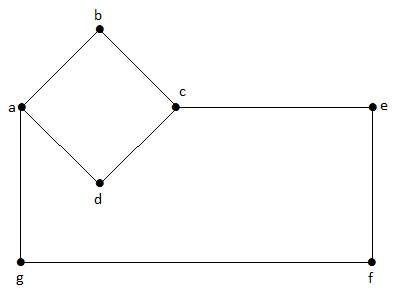
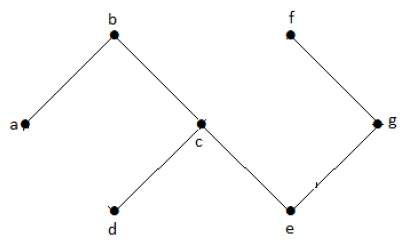
В этом графе «a», «b», «c», «d», «e», «f», «g» – вершины, а «ab», «bc», «cd», «da». ‘,’ ag ‘,’ gf ‘,’ ef ‘- ребра графа. Поскольку это ненаправленный граф, ребра «ab» и «ba» совпадают. Точно так же другие ребра также рассматриваются аналогичным образом.

Направленный граф

В ориентированном графе каждое ребро имеет направление.

пример

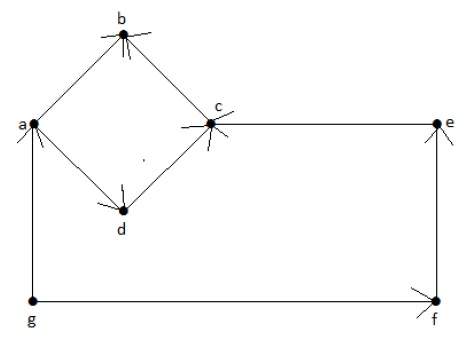
На приведенном выше графике у нас есть семь вершин «a», «b», «c», «d», «e», «f» и «g», и восемь ребер «ab», «cb», « dc ‘,’ ad ‘,’ ec ‘,’ fe ‘,’ gf ‘и’ ga ‘. Поскольку это ориентированный граф, на каждом ребре есть метка стрелки, показывающая его направление. Обратите внимание, что в ориентированном графе «ab» отличается от «ba».

Простой график

Граф без петель и параллельных ребер называется простым графом.

Максимально возможное число ребер в одном графе с n вершинами равно ⁿ C _2, где ⁿ C ₂ = n (n – 1) / 2.
Число простых графов возможно с n вершинами = 2 ^{ⁿ c ₂} = 2 ^{n (n-1) / 2} .

Максимально возможное число ребер в одном графе с n вершинами равно ⁿ C _2, где ⁿ C ₂ = n (n – 1) / 2.

Число простых графов возможно с n вершинами = 2 ^{ⁿ c ₂} = 2 ^{n (n-1) / 2} .

пример

На следующем графике есть 3 вершины с 3 ребрами, которые являются максимальными, исключая параллельные ребра и петли. Это можно доказать с помощью приведенных выше формул.

Максимальное количество ребер с n = 3 вершинами –

ⁿ C ₂ = n(n–1)/2
   = 3(3–1)/2
   = 6/2
   = 3 edges

Максимальное количество простых графов с n = 3 вершинами –

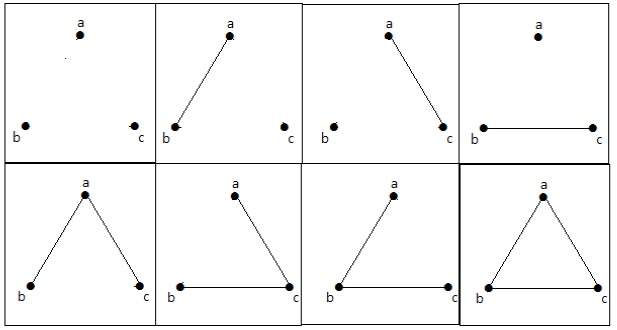
2 ^{ⁿ C ₂} = 2 ^n(n-1)/2
   = 2 ^3(3-1)/2
   = 2 ³
   = 8

Эти 8 графиков, как показано ниже –

Связанный график

Граф G называется связным, если между каждой парой вершин существует путь . Для каждой вершины графа должно быть хотя бы одно ребро. Так что мы можем сказать, что он связан с какой-то другой вершиной на другой стороне ребра.

пример

На следующем графике каждая вершина имеет свое ребро, соединенное с другим ребром. Следовательно, это связный граф.

Отключенный график

Граф G несвязен, если он не содержит хотя бы двух связанных вершин.

Пример 1

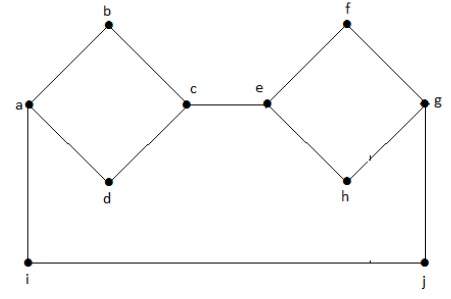
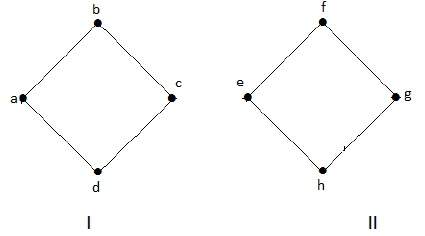
Следующий график является примером отключенного графа, где есть два компонента, один с вершинами «a», «b», «c», «d», а другой с «e», «f», «g», ‘h’ вершины.

Два компонента независимы и не связаны друг с другом. Следовательно, он называется несвязным графом.

Пример 2

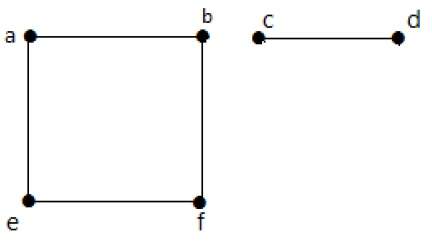
В этом примере есть два независимых компонента, abfe и cd, которые не связаны друг с другом. Следовательно, это несвязный граф.

Обычный график

Граф G называется регулярным, если все его вершины имеют одинаковую степень . В графе, если степень каждой вершины равна «k», то этот граф называется «k-регулярным графом».

пример

На следующих графиках все вершины имеют одинаковую степень. Поэтому эти графы называются регулярными графами.

В обоих графах все вершины имеют степень 2. Они называются 2-регулярными графами.

Полный график

Простой граф с «n» взаимными вершинами называется полным графом и обозначается «K _n » . В графе вершина должна иметь ребра со всеми остальными вершинами, тогда она называется полным графом.

Другими словами, если вершина связана со всеми остальными вершинами графа, то она называется полным графом.

пример

В следующих графах каждая вершина графа связана со всеми остальными вершинами графа, кроме самой себя.

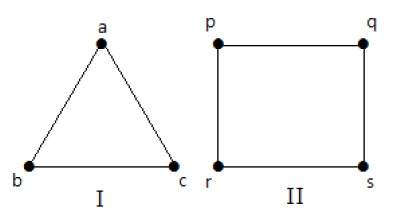
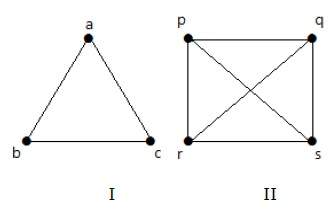
На графике я

		б	с
	Нет соединения	Связано	Связано
б	Связано	Нет соединения	Связано
с	Связано	Связано	Нет соединения

На графике II

	п	Q	р	s
п	Нет соединения	Связано	Связано	Связано
Q	Связано	Нет соединения	Связано	Связано
р	Связано	Связано	Нет соединения	Связано
s	Связано	Связано	Связано	Нет соединения

Цикл графика

Простой граф с n вершинами (n> = 3) и ребрами n называется графом циклов, если все его ребра образуют цикл длины n.

Если степень каждой вершины в графе равна двум, то она называется циклическим графом .

Обозначение – C _n

пример

Посмотрите на следующие графики –

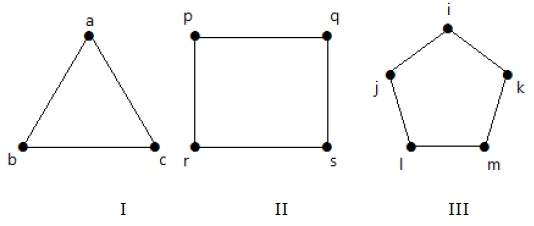
Граф I имеет 3 вершины с 3 ребрами, которые образуют цикл ‘ab-bc-ca’.
Граф II имеет 4 вершины с 4 ребрами, которые образуют цикл ‘pq-qs-sr-rp’.
Граф III имеет 5 вершин с 5 ребрами, которые образуют цикл ‘ik-km-ml-lj-ji’.

Граф I имеет 3 вершины с 3 ребрами, которые образуют цикл ‘ab-bc-ca’.

Граф II имеет 4 вершины с 4 ребрами, которые образуют цикл ‘pq-qs-sr-rp’.

Граф III имеет 5 вершин с 5 ребрами, которые образуют цикл ‘ik-km-ml-lj-ji’.

Следовательно, все данные графы являются графами циклов.

Колесо График

Граф колеса получается из графа циклов C _n-1 путем добавления новой вершины. Эта новая вершина называется Hub, которая связана со всеми вершинами C _n .

Обозначение – W _n

No. of edges in W _n = No. of edges from hub to all other vertices +
                     No. of edges from all other nodes in cycle graph without a hub.
                     = (n–1) + (n–1)
                     = 2(n–1)

пример

Посмотрите на следующие графики. Они все колесные графики.

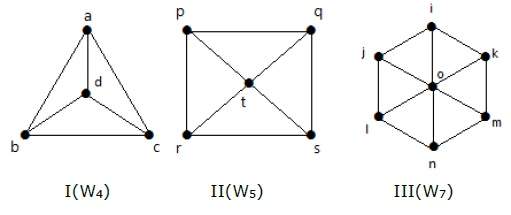
На графике I он получен из C ₃ путем добавления вершины в середине, названной ‘d’. Обозначается как W ₄ .

Number of edges in W ₄ = 2(n-1) = 2(3) = 6

На графике II он получен из C ₄ путем добавления вершины в середине, названной ‘t’. Обозначается как W ₅ .

Number of edges in W ₅ = 2(n-1) = 2(4) = 8

На графике III он получен из C ₆ путем добавления вершины в середине, названной ‘o’. Обозначается как W ₇ .

Number of edges in W ₄ = 2(n-1) = 2(6) = 12

Циклический график

Граф с хотя бы одним циклом называется циклическим графом.

пример

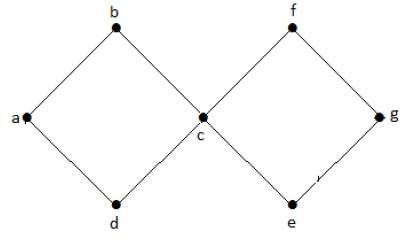
В приведенном выше примере графа у нас есть два цикла abcda и cfgec. Следовательно, он называется циклическим графом.

Ациклический Граф

Граф без циклов называется ациклическим графом.

пример

В приведенном выше примере графа у нас нет циклов. Следовательно, это нециклический граф.

Двудольный график

Простой граф G = (V, E) с разбиением вершин V = {V ₁ , V ₂ } называется двудольным графом, если каждое ребро E соединяет вершину в V ₁ с вершиной в V ₂ .

В общем случае бипертитовый граф имеет два набора вершин, скажем, V ₁ и V ₂ , и если ребро нарисовано, он должен соединить любую вершину в наборе V ₁ с любой вершиной в наборе V ₂ .

пример

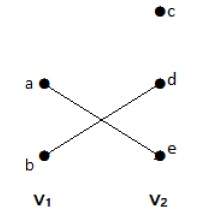
На этом графике вы можете наблюдать два набора вершин – V ₁ и V ₂ . Здесь два ребра с именами «ae» и «bd» соединяют вершины двух множеств V ₁ и V _2.

Полный двудольный график

Двудольный граф ‘G’, G = (V, E) с разбиением V = {V ₁ , V ₂ } называется полным двудольным графом, если каждая вершина в V ₁ соединена с каждой вершиной V ₂ .

В общем, полный двудольный граф соединяет каждую вершину из множества V ₁ с каждой вершиной из множества V ₂ .

пример

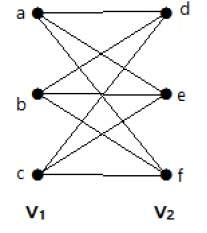
Следующий граф является полным двудольным графом, потому что у него есть ребра, соединяющие каждую вершину из множества V ₁ с каждой вершиной из множества V ₂ .

Если | V ₁ | = m и | V ₂ | = n, то полный двудольный граф обозначается через K _{m, n} .

K _{m, n} имеет (m + n) вершин и (mn) ребер.
K _{m, n} регулярный граф, если m = n.

K _{m, n} имеет (m + n) вершин и (mn) ребер.

K _{m, n} регулярный граф, если m = n.

В общем случае полный двудольный граф не является полным графом .

K _{m, n} полный граф, если m = n = 1.

Максимальное число ребер в двудольном графе с n вершинами

Если n = 10, k5, 5 = ⌊ n 2/4 ⌋ = ⌊ 10 2/4 ⌋ = 25

Аналогично К6, 4 = 24

К7, 3 = 21

К8, 2 = 16

К9, 1 = 9

Если n = 9, k5, 4 = ⌊ n 2/4 ⌋ = ⌊ 9 2/4 ⌋ = 20

Аналогично К6, 3 = 18

К7, 2 = 14

К8, 1 = 8

«G» является двудольным графом, если в «G» нет циклов нечетной длины. Частным случаем двудольного графа является звездный граф .

Звездный График

Полный двудольный граф вида K _{1, n-1} является графом звезд с n-вершинами. Звездный граф является полным двудольным графом, если одна вершина принадлежит одному набору, а все остальные вершины принадлежат другому набору.

пример

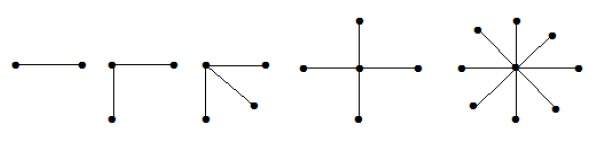
На приведенных выше графиках из n вершин все n – 1 вершины связаны с одной вершиной. Следовательно, оно имеет вид K _{1, n-1,} которые являются графами звезд.

Дополнение графика

Пусть ‘ G – ‘ – простой граф с некоторыми вершинами, такими как у G, и ребро {U, V} присутствует в ‘ G – ‘ , если ребро отсутствует в G. Это означает, что две вершины смежны в « G – », если две вершины не смежны в G.

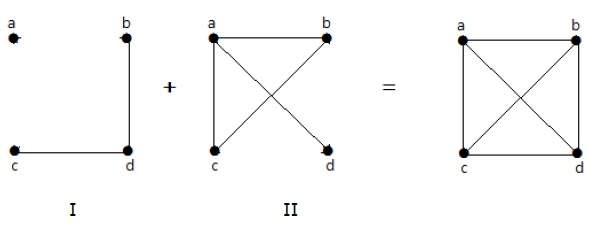
Если ребра, которые существуют в графе I, отсутствуют в другом графе II, и если граф I и граф II объединены вместе, чтобы сформировать полный граф, то граф I и граф II называются дополнениями друг друга.

пример

В следующем примере graph-I имеет два ребра: «cd» и «bd». Его граф дополнения II имеет четыре ребра.

Обратите внимание, что ребра в графе-I отсутствуют в графе-II и наоборот. Следовательно, комбинация обоих графов дает полный граф из n вершин.

Примечание . Сочетание двух дополнительных графов дает полный граф.

Если «G» – простой граф, то

| E (G) | + | E ( ‘ G – ‘ ) | = | E (K _n ) |, где n = количество вершин в графе.

пример

Пусть ‘G’ – простой граф с девятью вершинами и двенадцатью ребрами, найдите число ребер в ‘ G – ‘ .

У вас есть, | E (G) | + | E ( ‘ G – ‘ ) | = | E (K _n ) |

12 + | E ( ‘ G – ‘ ) | знак равно

9 (9-1) / 2 = ⁹ C ₂

12 + | E ( ‘ G – ‘ ) | = 36

| E ( ‘ G – ‘ ) | = 24

«G» – простой граф с 40 ребрами, а его дополнение « G – » имеет 38 ребер. Найдите количество вершин в графе G или ‘ G – ‘ .

Пусть количество вершин в графе равно n.

Имеем, | E (G) | + | E ( ‘ G – ‘ ) | = | E (K _n ) |

40 + 38 = n (n-1) / 2

156 = n (n-1)

13 (12) = n (n-1)

n = 13

Источник

Каково максимальное количество ребер в ориентированном графе с n узлами? Есть ли верхняя граница?

Ответ 1

Если у вас есть N узлы, есть N - 1 направленные ребра, которые могут привести к нему (переход к любому другому node). Поэтому максимальное число ребер N * (N - 1).

Ответ 2

В неориентированном графе (за исключением мультиграфов) ответ n * (n-1)/2. В ориентированном графе ребро может встречаться в обоих направлениях между двумя узлами, тогда ответ будет n * (n-1).

Ответ 3

Направленный график:

Вопрос. Какое максимальное количество ребер в ориентированном графе с n вершинами?

Предположим, что нет автопилот.
Предположим, что существует не более одного ребра из заданной начальной вершины в заданную конечную вершину.

Каждый ребро задается начальной вершиной и конечной вершиной. Нет выбор для начальной вершины. Поскольку нет самообучений, есть n-1 для конечной вершины. Умножение их вместе учитывает все возможные варианты.

Ответ: n(n−1)

Неадресный график

Вопрос. Какое максимальное количество ребер в неориентированном графе с n вершинами?

Предположим, что нет автопилот.
Предположим, что существует не более одного ребра из заданной начальной вершины в заданную конечную вершину.

В неориентированном графе каждое ребро задается двумя его конечными точками и порядок не имеет значения. Следовательно, число ребер является числом подмножеств размера 2, выбранных из множества вершин. Поскольку множество вершины имеют размер n, число таких подмножеств задается формулой биномиальный коэффициент C (n, 2) (также известный как «n выбрать 2» ). Используя формула для биномиальных коэффициентов, C (n, 2) = n (n-1)/2.

Ответ: (n*(n-1))/2

Ответ 4

В дополнение к интуитивному объяснению, предоставленному Крисом Смитом, мы можем рассмотреть, почему это имеет место с другой точки зрения: рассмотрение неориентированных графов.

Чтобы понять, почему в столбце DIRECTED ответ равен n*(n-1), рассмотрите неориентированный граф (что просто означает, что если есть связь между двумя узлами (A и B), тогда вы можете пойти в обоих направлениях: от A до B и от B до A). Максимальное количество ребер в неориентированном графе n(n-1)/2 и, очевидно, в ориентированном графе в два раза больше.

Хорошо, спросите вы, но почему существует максимум n(n-1)/2 ребер в неориентированном графике?
Для этого рассмотрим n точек (узлов) и спросим, сколько ребер можно сделать из первой точки. Очевидно, n-1 ребра. Теперь, сколько ребер можно извлечь из второй точки, учитывая, что вы подключили первую точку? Поскольку первая и вторая точки связаны с уже, существует n-2 ребра, которые можно выполнить. И так далее. Таким образом, сумма всех ребер равна:

Sum = (n-1)+(n-2)+(n-3)+...+3+2+1

Так как в сумме есть члены (n-1), а средний суммы в таком ряду — ((n-1)+1)/2 {(последний + первый)/2}, Sum = n(n-1)/2

Ответ 5

Если граф не является мультиграфом, то, очевидно, n * (n — 1), так как каждый node может иметь не все ребра для всех остальных node. Если это мультиграф, то максимальный предел отсутствует.

Ответ 6

Другими словами:

Полный граф — это неориентированный граф, где каждая отдельная пара вершин имеет единственное ребро, соединяющее их. Это интуитивно понятно в том смысле, что вы в основном выбираете 2 вершины из набора из n вершин.

nC2 = n!/(n-2)!*2! = n(n-1)/2

Это максимальное количество ребер, которое может иметь неориентированный граф. Теперь для ориентированного графа каждое ребро преобразуется в два направленных ребра. Поэтому просто умножьте предыдущий результат на два. Это дает вам результат: n (n-1)

Ответ 7

В ориентированном графе, имеющем N вершин, каждая вершина может подключаться к N-1 другим вершинам в графе (предположим, ни одна петля). Следовательно, общее число ребер может быть N (N-1).

Ответ 8

Правильный ответ: n * (n-1)/2. Каждый ребро подсчитывается дважды, следовательно, деление на 2. Полный граф имеет максимальное количество ребер, которое задается п, выбирает 2 = n * (n-1)/2.

Ответ 9

В графе может быть не более n(n-1)/2 ребер, если не разрешено многократное ребро.

И это достижимо, если мы помечаем вершины 1,2,...,n и там ребро от i до j iff i>j.

Смотрите здесь.

Ответ 10

Несправлено N ^ 2. Простой — каждый node имеет N опций ребер (включая себя), всего N узлов, таким образом, N * N

Ответ 11

В графе с циклом self

max edges= n*n

например, у нас есть 4 узла (вершина)

4 nodes = 16 edges= 4*4

Ответ 12

Что такое турнир?

Простой полный ориентированный граф — турнир.

Вы можете найти его в интернете…

Турнир имеет N * (N-1)/2 ребра… Таким образом, правильный ответ должен быть N * (N-1)/2.

Ответ 13

Можно также рассматривать как количество способов выбора пар узлов n выбрать 2 = n (n-1)/2. Истина, если только любая пара может иметь только одно ребро. Умножьте на 2 иначе

Источник

КАКОЕ НАИБОЛЬШЕЕ ЧИСЛО РЕБЕР МОЖЕТ СОДЕРЖАТЬ ГРАФ,

ИМЕЮЩИЙ N ВЕРШИН?

Выполнили: Воробьева Элиза Александровна, Тищенко Алина Витальевна ученицы 10 класса, руководитель: Славянская Лариса Владимировна. Волгоград 2013

Введение.

Тема «Графы» в школьном курсе информатики изучается в седьмом классе в теме «Математические модели», в 10 классе базовый уровень «Информационные модели», в 10 классе профильный уровень «Дискретные приближения непрерывных моделей.

Постановка проблемы.

В учебнике 1 «Информатика и ИКТ» мы прочитали задачу: Какое наибольшее число ребер может содержать граф, имеющий n вершин?

Цель исследования: Выявить, обосновать и экспериментально проверить одно из свойств графов.

Задача исследования:

Разработать принцип построение модели графов
Выявить и обосновать методику подсчета ребер
При построение модели графов учесть наглядность данного свойства

Объект исследования: изучение свойств графов.

Предмет исследования: установление зависимость количество ребер графа от количества его вершин.

Понятие графа. Простейшие свойства

Граф — это конечная совокупность вершин, некоторые из которых соединены ребрами. Мы будем рассматривать только такие графы, у которых две вершины могут быть соединены только одним ребром. Если ребро соединяет вершину саму с собой, то такое ребро называют петлей.

Мы будем рассматривать только такие графы, у которых две вершины могут быть соединены только одним ребром. Конфигурации, когда пара вершин соединена несколькими ребрами, — в этом случае говорят, что задан мультиграф, а ребра, соединяющие одну и ту же пару вершин, называют кратными. Если ребро соединяет вершину саму с собой, то такое ребро называют петлей.

Если две различные вершины графа соединены ребром, то такие вершины называются смежными. Количество ребер, выходящих из одной вершины, называется степенью этой вершины. Для петли будем считать, что это ребро выходит из вершины дважды. Степень вершины а будем обозначать v(а).

Свойство, относящееся к любым графам.

Теорема 1. Сумма степеней всех вершин графа равна удвоенному числу его ребер.

Лемма о рукопожатиях. Теорема 2. Количество вершин нечетной степени любого графа всегда четно.

Маршрутом на графе называется последовательность ребер е1, е2, …, еk, в которой конец одного ребра служит началом следующего. Если при этом конец последнего ребра последовательности совпал с началом первого ребра, то маршрут называется циклическим. Для графа, изображенного на рис. 2, последовательности е1, е2, е4, е5, е2, е3 и е2, е4, е5 являются маршрутами, причем второй из них — циклический. А последовательность е1, е2, е5 маршрутом не является. Рис. 2

Если вершина является концом какого-либо ребра, принадлежащего маршруту, то будем говорить, что данный маршрут проходит через эту вершину.

В таблице показаны результаты исследования для графов, имеющих петли, и для графов не имеющих петли.

Количество вершин N	Наибольшее число ребер графа, имеющего n вершин	Наибольшее число ребер графа , имеющего n вершин с петлей
3
	R=3=n (3*2/2)	R=6=2n (3+3*2/2)
4
	R=6=n+n/2 (4*3/2)	R=10=2n+n/2 (4+4*3/2)
5
	R=10=2n (5*4/2)	R=15=3n (5+ 5*4/2)
6
	R=15=2n+n/2 (6*5/2)	R=21=3n+n/2 (6+6*5/2)
7
	R=3n=21 2 (7*6/2)	R=4n=28 (7+7*6/2)
8
	R=3n+n/2=28 (8*7/2)	R=4n+n/2=36 (8+8*7/2)
9
	R=4n=36 2 (9*8/2)	R=5n=45 (9+9*8/2)
10
	R=4n+n/2=45 (10*9/2)	R=5n+n/2=55 (10+10*9/2)

При решении задачи мы увидели закономерность, которая подтвердилась при анализ большого количества примеров. На сайте http://rain.ifmo.ru/cat/view.php/theory/graph-general/random-2005 факультета «Информационных технологий и программирования», кафедра компьютерных технологий в разделе «Дискретная математика: алгоритмы» в теме «Модель Эрдёша-Реньи» упоминается формула максимального количество ребер, что совпадает с первым столбцом нашего исследования. О решении задачи информация нам не попалась, было просмотрено около 10 сайтов по данной теме. На просмотренных сайтах мы не нашли решение данной задачи:

При построении схем графов участвовали все учащиеся класса. Сложность построения заключается в том, чтобы не пропустить ребер, правильно их посчитать. Для построения использовался векторный графический редактор, встроенный в текстовый редактор «Word».

Вывод теоретический . Рассмотренная задача решена практическим методом построения последовательности графов. Для графов с вершинами без петель зависимость количество ребер графа от количества его вершин выражается формулой R=N*(N-1)/2. Для графов с вершинами с петлями зависимость количество ребер графа от количества его вершин выражается формулой R= N +N *(N-1)/2.

Вывод практический, мотивация учеников. Решение данной задачи позволит учащимся понять практический смысл графа и с большим интересом изучать сложный материал дискретной математики в школьном курсе информатики.

Литература

Информатика и ИКТ, А.Г. Гейн, А.И. Сенокосов, Москва, «Просвещение» 2009.

Электронные ресурсы

http://inf.1september.ru/article.php?ID=200702001
http://elar.urfu.ru/bitstream/10995/1659/5/1334886_schoolbook.pdf
http://rain.ifmo.ru/cat/view.php/theory/graph-general/random-2005

Источник