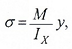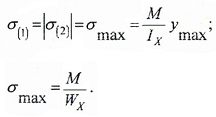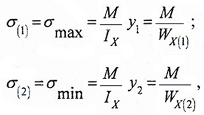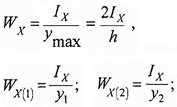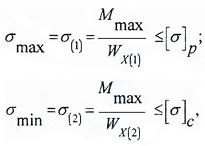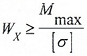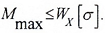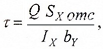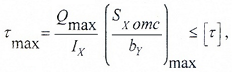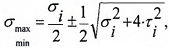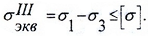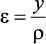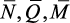Как найти максимальное напряжение изгиба

Из формулы видно,
что в разных точках с разными
напряжениеразное. При расчете на прочность
необходимо знать(максимальное сжимающее напряжение) и(максимальное
растягивающее напряжение).

Рассуждаем от
противного. Найдем сначала линию, на
которой напряжение минимально, то есть
.

Подставим
=0
в (19.1):

. (19.2)

В данном сечении
— это постоянные, поэтому уравнение
(19.2) – это уравнение прямой в плоскостих,у
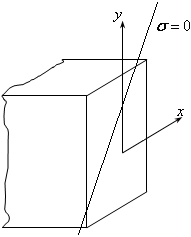
(см.рис.19.6).

Рис.19.6

Напомним определение:
прямая, на которой
,
называетсянейтральной.

Ясно, что вблизи
нейтральной линии напряжение не нуль,
но очень мало. И чем дальше от этой линии,
тем напряжение больше, следовательно,
,возникают в точках, наиболее удаленных
от этой нейтральной линии.

Определение:
точки, в которых
илиназываютсяопасными
точками.

Примечание. Из
(19.1) видно, что в разных сечениях
комбинация
может давать разные комбинациии,
то есть в одном сечении максимальным
будет,
а в другом.
Более того, нельзя заранее знать, в каком
сеченииилибудут наибольшими.

Поэтому при
растяжении с изгибом опасными являются
все те сечения, в которых или, илиэкстремальны.

19.4 Косой изгиб

Это случай сложной
деформации, при котором есть только
изгиб в двух плоскостях.

В этом случае в
формуле (19.1), полагаем
.

Тогда: .

Уравнение нейтральной
линии получает вид:

.

Видно, что нейтральная
линия проходит через центр тяжести.

Особенностью
косого изгиба и растяжения с изгибом в
общем случае является то, что нейтральная
линия (штриховая прямая на рис.19.7) не
перпендикулярна равнодействующей F
поперечных сил F_х
, F_у
.

Рис.19.7

19.5. Проверка прочности круглых стержней при кручении с изгибом

Будем рассматривать
только круглые стержни.

рис.19.8

Пусть стоит задача:
проверки прочности в опасном сечении.
Исследуем малый элемент в опасном
сечении (см.рис.19.8)

рис.19.9

Особенность
ситуации в том, что на элемент действуют
два вида напряжений одновременно,
поэтому условие прочности вида
,,
не обеспечивают прочность, поскольку
они справедливы только при простом
растяжении и при простом сдвиге. Так
какидействуют одновременно, то в зависимости
от материала, нужно применять различные
теории прочности.

Для стали, в запас
прочности, можно использовать III
теорию:

(19.3)

Здесь
вычисляется как обычно:

Для полого вала
имеет вид:

(19.4)

Для отыскания
для круглых стержней не обязательно
находить опасную точку. Действительно,
если найдена нейтральная линия, то мы
можем принять её за ось.

рис.19.10

В
этом случае опасной будет точка с
координатами х
= 0, у
= R
(рис.19.10). Изгибающий момент тогда
вычисляется как геометрическая сумма
и:

(19.5)

Поэтому по формуле
Навье найдем:

,

.

Если кроме кручения
и изгиба имеется растяжение, то
максимальное значение напряжения
вычисляется по формуле:

(19.6)

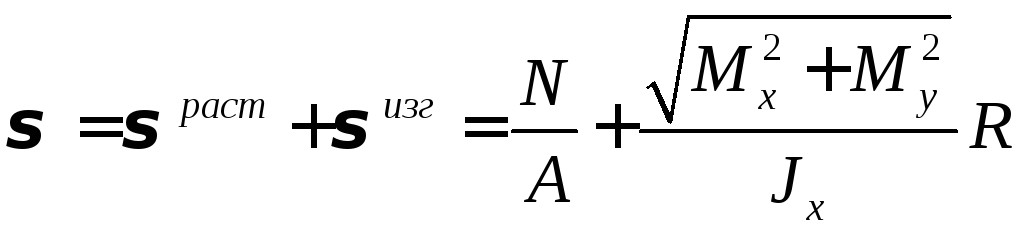
19.6 Внецентренное сжатие. Ядро сечения

Рассмотрим три
варианта нагружения колонны (рис.19.11).

1. сжатие
   силой по центру

2. сжатие
   силой, чуть сдвинутой от центра

3. сжатие
   по краю

В
сечении получим распределения напряжений,
приведенные на рис 19.11.

рис.19.11

Большинство
строительных материалов плохо работают
на растяжение (бетон, кирпич, камень,
стекло) поэтому наличие зон растяжения
требуется максимально уменьшить, а еще
лучше — исключить.

Как видно из рисунка
для этого силу нужно располагать как
можно ближе к центру.

Определение
1:

Внецентренным
сжатием или растяжением называется
такая деформация стержня, которая
происходит под действием продольной
силы, приложенной не в центре тяжести
сечения.

Определение
2:

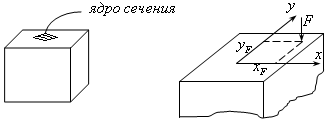
Ядро сечения
— это область, расположенная вокруг
центра тяжести (рис.19.12), причем, такая,
что если приложить продольную сжимающую
силу в этой области, то нигде в стержне
напряжение растяжения не возникнет,
будет только сжатие.

рис.19.12 рис.19.13

Исследуем
внецентренное сжатие (рис.19.13). Здесь
-координаты
точки приложения силы
F.
Тогда сила сжатия
.

Из рисунка видно,
что F
создает моменты относительно осей x
и y
(причем,
независимо от того на какой высоте
находится сечения):

Тогда получим:

. (19.7)

Рассмотрим уравнение
нейтральной линии, т.е. линии, где
:

Деля на F,
получим:

(19.8)

Таким образом, из
(19.8) следует, что положение
нейтральной линии, которое определяет
растянутые и сжатые зоны, не зависит от
величины силы F,
а зависит только от точек её приложения,
то есть от
.

Важнейшим критерием оценки прочности балок при изгибе являются напряжения.

Рассмотрим способы расчета напряжений при плоском поперечном изгибе балки

Расчет напряжений

Возникающий в поперечных сечениях при чистом прямом изгибе изгибающий момент M_x

представляет собой равнодействующий момент внутренних нормальных сил, распределенных по сечению и вызывающих нормальные напряжения в точках сечения.

Закон распределения нормальных напряжений по высоте сечения выражается формулой:

где:
M — изгибающий момент, действующий в рассматриваемом сечении относительно его нейтральной линии X;
I_x — осевой момент инерции поперечного сечения балки относительно нейтральной оси;
y – расстояние от нейтральной оси до точки, в которой определяется напряжение.

Нейтральная ось при изгибе проходит через центр тяжести поперечного сечения.

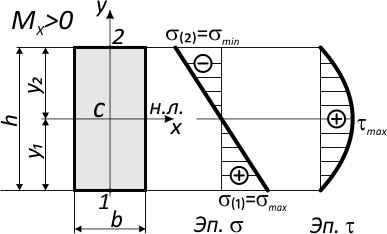
По вышеуказанной формуле, нормальные напряжения по высоте сечения изменяются по линейному закону.

Наибольшие значения имеют напряжения у верхнего и нижнего краев сечения.

Например, для симметричного относительно нейтральной оси сечения, где y₁=y₂=h/2:

Напряжения в крайних точках по вертикали (точки 1 и 2) равны по величине, но противоположны по знаку.

Для несимметричного сечения

напряжения определяются отдельно для нижней точки 1 и верхней точки 2:

где:

W_X — осевой момент сопротивления симметричного сечения;
W_X(1) и W_X(2) — осевые моменты сопротивления несимметричного сечения для нижних и верхних слоев балки.

Знаки нормальных напряжений при их расчете, рекомендуется определять по физическому смыслу в зависимости от того, растянуты или сжаты рассматриваемые слои балки.

Условия прочности при изгибе

Прочность по нормальным напряжениям

Условие прочности по нормальным напряжениям для балок из пластичного материала записывается в одной крайней точке.

В случае балки из хрупких материалов, которые, как известно, по-разному сопротивляются растяжению и сжатию – в двух крайних точках сечения.

Здесь:
M_max — максимальное значение изгибающего момента, определяемого по эпюре M_x;
[σ], [σ]_р, [σ]_с — допустимые значения напряжений для материала балки (для хрупких материалов – на растяжение (р) и сжатие (с)).

Для балки из хрупкого материала обычно применяют сечения, несимметричные относительно нейтральной оси. При этом сечения располагают таким образом, чтобы наиболее удаленная точка сечения размещалась в зоне сжатия, так как [σ]_с>[σ]_р.

В таких случаях, проверку прочности следует обязательно проводить в двух сечениях: с наибольшим положительным изгибающим моментом и с наибольшим по абсолютной величине (модулю) отрицательным значением изгибающего момента.

При расчете элементов конструкций, работающих на изгиб, с использованием вышеуказанных условий прочности решаются три типа задач:

1. Проверка прочности
   
2. Подбор сечений
   
3. Определение максимально допустимой нагрузки
   

Прочность по касательным напряжениям

В случае прямого поперечного изгиба в сечениях балки, кроме нормальных напряжений σ от изгибающего момента, возникают касательные напряжения τ от поперечной силы Q.

Закон распределения касательных напряжений по высоте сечения выражается формулой Д.И. Журавского

где
S_{x отс} — статический момент относительно нейтральной оси отсеченной части площади поперечного сечения балки, расположенной выше или ниже точки, в которой определяются касательные напряжения;
b_y — ширина поперечного сечения балки на уровне рассматриваемой точки, в которой рассчитывается величина касательных напряжений τ.

Другие видео

Условие прочности по касательным напряжениям записывается для сечения с максимальным значением поперечной силы Q_max:

где [τ] – допустимое значение касательных напряжений для материала балки.

Полная проверка прочности

Полную проверку прочности балки производят в следующей последовательности:

1. По максимальным нормальным напряжениям для сечения, в котором возникает наибольший по абсолютному значению изгибающий момент M.
2. По максимальным касательным напряжениям для сечения, в котором возникает наибольшая по абсолютному значению поперечная сила Q.
3. По главным напряжениям для сечения, в котором изгибающий момент и поперечная сила одновременно достигают значительных величин (или когда M_max и Q_max действуют в одном и том же сечении балки).

При анализе плоского напряженного состояния главные напряжения при изгибе, примут вид:

так как нормальные напряжения в поперечном направлении к оси балки принимаются равными нулю.

Другие видео

Проверка прочности осуществляется с помощью соответствующих гипотез прочности, например, гипотезы наибольших касательных напряжений:

Деформации при изгибе >
Угловые и линейные перемещения в балках >
Примеры решения задач >
Лекции по сопромату >

Лекция 9. НАПРЯЖЕНИЯ И ПЕРЕМЕЩЕНИЯ ПРИ ИЗГИБЕ

Гипотезы при изгибе. Нейтральный слой, радиус кривизны, кривизна,
распределение деформаций и нормальных напряжении по высоте поперечного
сечения стержня. Касательные напряжения при плоском поперечном изгибе
стержней. Расчет балок на прочность при изгибе. Перемещения при изгибе.
 

Нормальные напряжения при чистом прямом изгибе. Так как нормальные
напряжения зависят только от изгибающих моментов, то вывод формулы для
вычисления можно производить применительно к чистому изгибу. Отметим,
что методами теории упругости можно получить точную зависимость для
нормальных напряжений при чистом изгибе, если же решать эту задачу
методами сопротивления материалов, необходимо ввести некоторые
допущения.

Таких гипотез при изгибе три:

1) гипотеза плоских сечений (гипотеза Бернулли) – сечения плоские
до деформации остаются плоскими и после деформации, а лишь
поворачиваются относительно некоторой линии, которая называется
нейтральной осью сечения балки. При этом волокна балки, лежащие с одной
стороны от нейтральной оси будут растягиваться, а с другой – сжиматься;
волокна, лежащие на нейтральной оси своей длины не изменяют;

2) гипотеза о постоянстве нормальных напряжений – напряжения,
действующие на одинаковом расстоянии у от нейтральной оси, постоянны по
ширине бруса;

3) гипотеза об отсутствии боковых давлений – соседние продольные волокна не давят друг на друга.

 

Рис. 28. Гипотеза Бернулли

Статическая задача о плоском изгибе. Изгибающий момент в сечении
представляет собой сумму моментов всех элементарных внутренних
нормальных сил σ•dA, возникающих на элементарных площадках поперечного
сечения балки (рис. 29), относительно нейтральной оси: .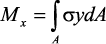

Данное выражение представляет собой статическую сторону задачи
о плоском изгибе. Но его нельзя использовать для определения нормальных
напряжений, так как неизвестен закон распределения напряжений по
сечению.

 

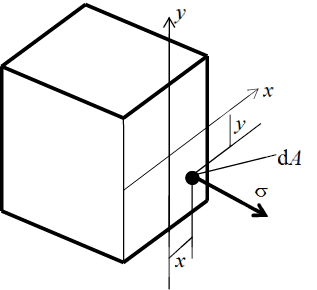
Рис. 29. Статическая сторона задачи

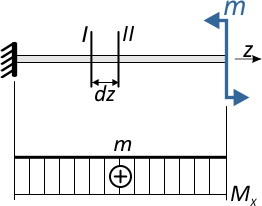
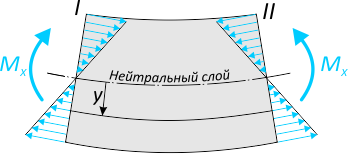
Геометрическая сторона задачи о плоском изгибе. Выделим двумя
поперечными сечениями элемент балки длиной dz. Под нагрузкой нейтральная
ось искривляется (радиус кривизны ρ), а сечения поворачиваются
относительно своих нейтральных линий на угол dθ. Длина отрезка волокон
нейтрального слоя при этом остается неизменной (рис. 30, б):

dz = ρ•dθ.

а                                б

 

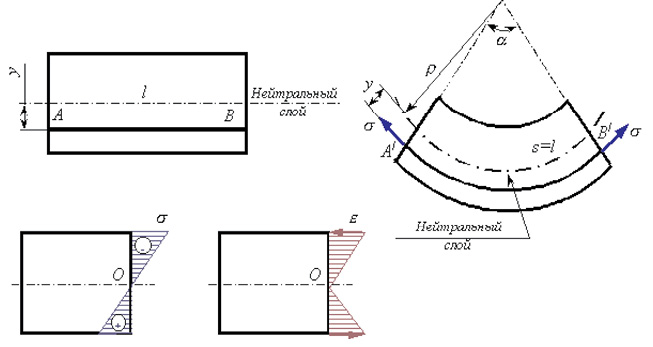
                                                     в                                      г

Рис. 30. Геометрическая сторона задачи:
а – элемент балки; б – искривление нейтральной оси; в – эпюра σ•dA; г – эпюра ε

Определим длину отрезка волокон, отстоящего от нейтрального слоя на расстоянии y

dz₁ = (ρ + y)dθ .

Относительное удлинение в этом случае будет

 

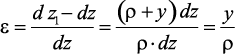
Зависимость
отражает геометрическую сторону задачи о плоском изгибе, из которой
видно, что деформации продольных волокон изменяются по высоте сечения по
линейному закону.

Совокупность волокон, не меняющих своей длины при изгибе балки, называется нейтральным слоем.

Линия, по которой поперечное сечение балки пересекается с нейтральным слоем балки, называется нейтральной линией сечения.

Физическая сторона задачи о плоском изгибе. Используя закон Гука при осевом растяжении, получаем

 

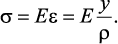
Подставив в выражение, отражающее статическую сторону задачи о плоском изгибе, значение σ, получаем

 

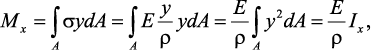
откуда

 

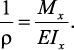
Подставив значение в исходную формулу, получаем

(13)

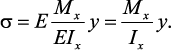
Данное выражение отражает физическую сторону задачи о плоском
изгибе, которое дает возможность рассчитать нормальные напряжения по
высоте сечения.

Хотя это выражение получено для случая чистого изгиба, но как
показывают теоретические и экспериментальные исследования, оно может
быть использовано и для плоского поперечного изгиба.

Нейтральная линия. Положение нейтральной линии определим из
условия равенства нулю нормальной силы в сечениях балки при чистом
изгибе

 

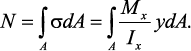
Так как M_x ≠ 0 и I_x ≠ 0, то необходимо, чтобы нулю был равен интеграл .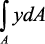
Данный интеграл представляет собой статический момент сечения
относительно нейтральной оси. Так как статический момент сечения равен
нулю только относительно центральной оси, следовательно, нейтральная
линия при плоском изгибе совпадает с главной центральной осью инерции
сечения.

Касательные напряжения. Касательные напряжения, которые возникают
в сечениях балки при плоском поперечном изгибе, определяются по
зависимости:

(14)

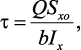
где Q – поперечная сила в рассматриваемом сечении балки; S_xo –
статический момент площади отсеченной части сечения относительно
нейтральной оси балки; b – ширина сечения в рассматриваемом слое;
Ix –момент инерции сечения относительно нейтральной оси.

Касательные напряжения равны нулю в крайних волокнах сечения и максимальны в волокнах нейтрального слоя.

Расчет балок на прочность при изгибе. Прочность балки будет обеспечена, если будут выполняться условия:

(15)

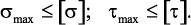
Максимальные нормальные напряжения при изгибе возникают
в сечениях, где действует максимальный изгибающий момент, в точках
сечения наиболее удаленных от нейтральной оси

 

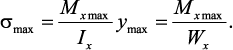
Максимальные касательные напряжения возникают в сечениях балки, где действует максимальная поперечная сила

 

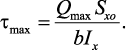
Касательные напряжения τmax обычно малы по сравнению с σmax
и в расчетах, как правило, не учитываются. Проверка по касательным
напряжениям производится только для коротких балок.

Перемещения при изгибе. Под расчетом на жесткость понимают оценку
упругой податливости балки под действием приложенных нагрузок и подбор
таких размеров поперечного сечения, при которых перемещения не будут
превышать установленных нормами пределов.

Условие жесткости при изгибе

 

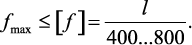
Перемещение центра тяжести сечения по направлению
перпендикулярному к оси балки, называется прогибом. Прогиб обозначается
буквой W.

Наибольший прогиб в пролете или на консоли балки, называется стрелой прогиба и обозначается буквой ƒ.

Угол q, на который каждое сечение поворачивается по отношению к своему первоначальному положению и есть угол поворота.

Угол поворота считается положительным, при повороте сечения против хода часовой стрелки

Угол поворота сечения равен значению производной от прогиба по координате Z в этом же сечении, то есть:

 

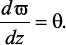
Уравнение упругой линии балки

(16)

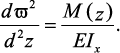
Существуют три метода решения дифференциального уравнения упругой
линии балки. Это метод непосредственного интегрирования, метод Клебша
и метод начальных параметров.

Метод непосредственного интегрирования. Проинтегрировав уравнение
упругой линии балки первый раз, получают выражение для определения углов
поворота:

 

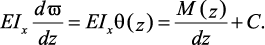
Интегрируя второй раз, находят выражения для определения прогибов:

 

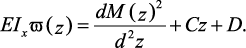
Значения постоянных интегрирования С и D определяют из начальных условий на опорах балки

Метод Клебша. Для составления уравнений необходимовыполнить следующие основные условия:

• начало координат, для всех участков, необходимо расположить в крайнем левом конце балки;
• интегрирование дифференциального уравнения упругой линии балки проводить, не раскрывая скобок;
• при включении в уравнение внешнего сосредоточенного момента М его необходимо помножить на (Z – a), где а – координата сечения, в котором приложен момент;
• в случае обрыва распределенной нагрузки ее продлевают до конца
  балки, а для восстановления действительных условий нагружения вводят
  «компенсирующую» нагрузку обратного направления

Метод начальных параметров

Для углов поворота

(17)

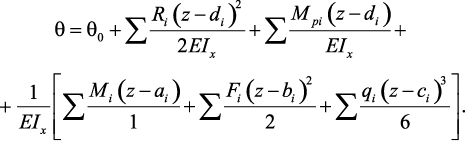
Для прогибов:

(18)

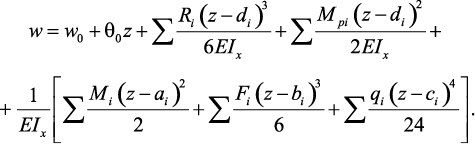
где θ – угол поворота сечения; w – прогиб; θo – угол поворота
в начале координат; w0 – прогиб в начале координат; dі – расстояние от
начало координат до i-й опоры балки; ai – расстояние от начало координат
до точки приложения сосредоточенного момента Mi; bi – расстояние от
начало координат до точки приложения сосредоточенной силы Fi; сi –
расстояние от начало координат до начала участка распределенной нагрузки
qi; Ri и Мрi – реакция и реактивный момент в опорах балки.

Определение стрелы прогибов для простых случаев

 

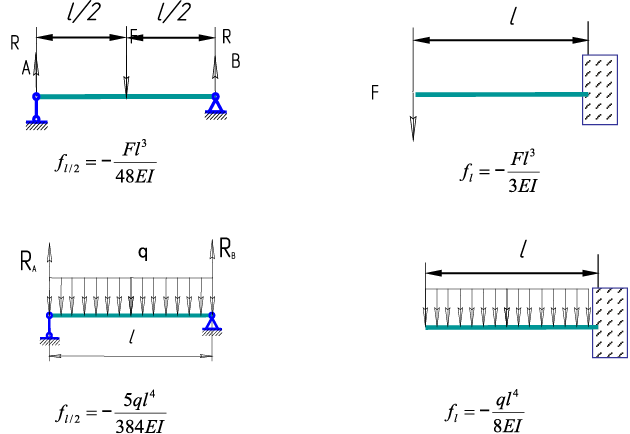
Рис. 31. Примеры нагрузок балок

Вычисление перемещений методом Мора

Если не требуется знание уравнения изогнутой линии бруса,
а необходимо определить только линейные или угловые перемещения
отдельного сечения, удобнее всего воспользоваться методом Мора.Для балок
и плоских рам интеграл Мора имеет вид:

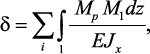
где δ – искомое перемещение (линейное или угловое); М_p, М_i –
аналитические выражения изгибающих моментов соответственно от заданной
и единичной cилы; EJ_x – жесткость сечения балки в плоскости изгиба. При
определении перемещений нужно рассматривать два состояния системы: 1 –
действительное состояние, с приложенной внешней нагрузкой; 2 –
вспомогательное состояние, в котором балка освобождается от внешней
нагрузки, а к сечению, перемещение которого определяется, прикладывается
единичная сила, если определяется линейное перемещение, или единичный
момент, если определяется угловое перемещение (рис. 32).

 

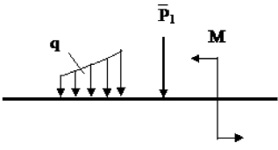
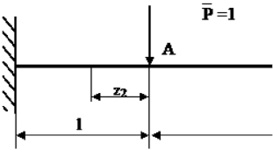
а                                   б

 

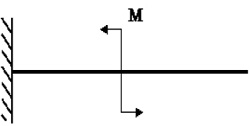
в

Рис. 32. Определение перемещений:
а – действительное состояние; б, в – вспомогательные состояния

Формулу Мора можно получить, например. используя принцип возможных перемещений.
 

 

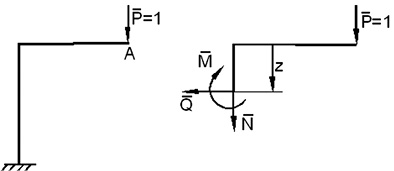
а                                                                                б

Рис. 33. Схема рамы:
а – под воздействием силы; б – внутренние усилия

Рассмотрим схему (рис. 33а), когда в точке А в направлении искомого перемещения ΔA приложена единичная сила 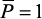, вызывающая в поперечном сечении системы внутренние силовые факторы
(рис. 33, б). В соответствии с принципом возможных перемещений работа
этих внутренних силовых факторов на любых возможных перемещениях должна
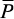
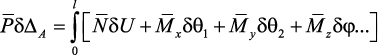
равняться работе единичной силы на возможном перемещении δΔA:

 

Выбираем возможные перемещения пропорциональными действительным:

 

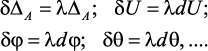
И после подстановки получим:

 

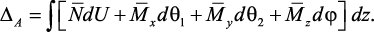
При учете, что

 

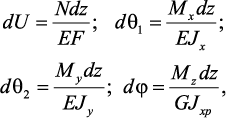
приходим к формуле Мора

(19)

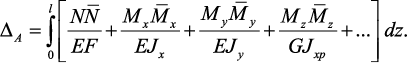
которая служит для определения любых обобщённых перемещений в стержневых системах.

В случае, когда брус работает только на изгиб (Mx ≠ 0, Nz = Mz = My = Qx = Qy = 0), выражение (1) принимает вид:

(20)

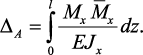
Правило Верещагина позволяет заменить непосредственное
интегрирование в формулах Мора так называемым перемножением эпюр. Способ
вычисления интеграла Мора путем замены непосредственного интегрирования
перемножением соответствующих эпюр называется способом (или правилом)
Верещагина, заключающемся в следующем: чтобы перемножить две эпюры, из
которых хотя бы одна является прямолинейной, нужно площадь одной эпюры
умножить на ординату другой эпюры, расположенную под центром тяжести
первой (ординаты используются только с прямолинейных эпюр). Эпюры
сложного очертания могут быть разбиты на ряд простейших: прямоугольник,
треугольник, квадратичную параболу и т.п. (рис. 34).

 

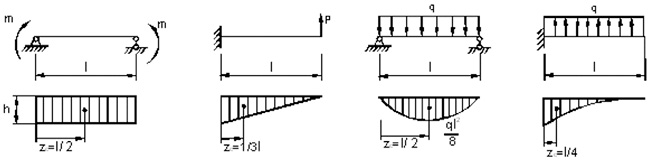
Рис. 34. Простейшие эпюры

Справедливость правила Верещагина.

 

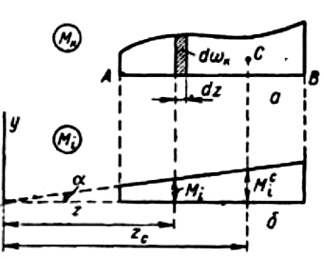
Рис. 35. Схема перемножения эпюр:
а – произвольная эпюра; б – прямолинейная

Приведены две эпюры изгибающих моментов, из которых одна Мk имеет
произвольное очертание, а другая Мi прямолинейна (рис. 35). Сечение
стержня считаем постоянным. В этом случае

 

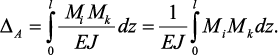
Величина Mkdz представляет собой элементарную площадь dω эпюры Мk (заштрихована). Получаем

 

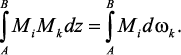
Но Mi = ztg α, поэтому,

 

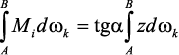
Выражение 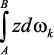 представляет
собой статический момент площади эпюры Мk относительно оси у,
проходящей через точку О, равный ωkΖc, где ωk – площадь эпюры моментов;
Ζс – расстояние от оси у до центра тяжести эпюры М_k. Из рисунка
очевидно:

Ζ_c = М_i/tg α,

где Мi – ордината эпюры Mi, расположенная под центром тяжести эпюры Мk (под точкой С).

(21)

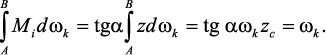
Формула (21) представляет правило вычисления интеграла Мора:
интеграл равен произведению площади криволинейной эпюры на ординату,
взятую с прямолинейной эпюры и расположенную под центром тяжести
криволинейной эпюры.

Встречающиеся на практике криволинейные эпюры могут быть разбиты
на ряд простейших: прямоугольник, треугольник, симметричную квадратичную
параболу и т.п.

При помощи разбивания эпюр на части можно добиться того, что при перемножении все эпюры были бы простой структуры.

Пример вычисления перемещений. Требуется определить прогиб
в середине пролета и угол поворота левого опорного сечения балки,
нагруженной равномерно распределенной нагрузкой (рис. 36, а), способом
Мора-Верещагина.

Рассмотрим 3 состояния балки: грузовое состояние ( при действии
распределенной нагрузки q;) ему соответствует эпюра Mq (рис. 36, б),
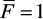
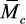
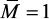
и два единичных: при действии силы , приложенной в точке С (эпюра , рис. 36, в), и момента , приложенного в точке В (эпюра , рис. 36, г).

Прогиб балки в середине пролета:

 

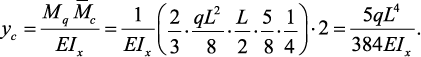
Обратим внимание, что перемножение эпюр выполняется для половины
балки, а затем из-за симметрии) полученный результат удваивается. При
вычислении угла поворота сечения в точке В площадь эпюры Mq умножается
на расположенную под ее центром тяжести ординату эпюры (1/2, рис. 9, г), т.к. эпюра изменяется по прямой линии:

 
 

 

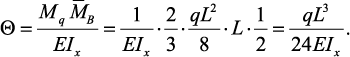
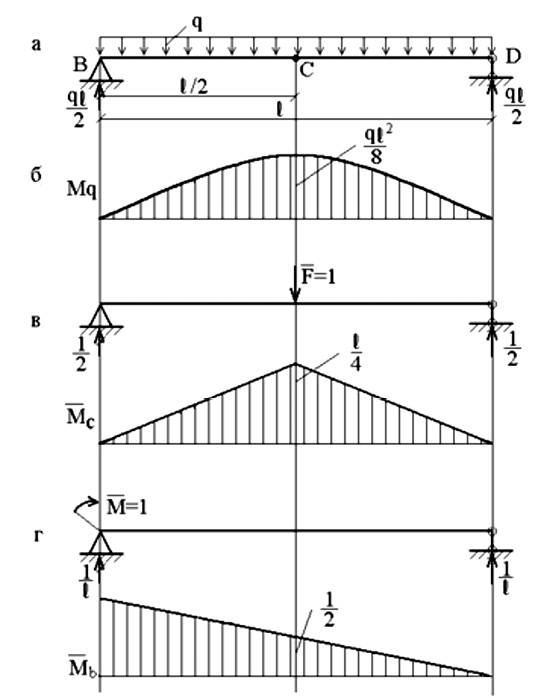
Рис. 36. Пример расчета:
а – заданная схема балки; б – грузовая эпюра моментов;
в – единичная эпюра от единичной силы; г – от единичного момента

Сопротивление материалов

Напряжения при изгибе



Нормальные напряжения при чистом изгибе

Как было установлено ранее, в поперечных сечениях балки при чистом изгибе возникают только нормальные напряжения растяжения и сжатия. Вопрос о распределении этих напряжений по поперечному сечению решается путем рассмотрения деформаций волокон балки.

Рассмотрим участок балки, подверженный деформации чистого изгиба. Двумя поперечными сечениями АВ и СD выделим элемент балки бесконечно малой длины ds (рис 1). Радиус кривизны нейтрального слоя балки обозначим ρ.

Рассмотрим слой волокон mn, находящийся на расстоянии y от нейтрального слоя NN. Это волокно в результате деформации изгиба удлинилось на величину nn₁. Ввиду малости расстояния ds заштрихованные треугольники будем считать прямолинейными; эти треугольники подобны (n₁F || mE):

Δ OEF ~ Δ Fnn₁.

Из подобия треугольников запишем равенство:

nn₁ / ds = y / ρ.

Так как левая часть этого равенства есть относительное удлинение, т. е. nn₁ / ds = ε, то y / ρ = ε.

Применив закон Гука при растяжении и сжатии σ = Еε, получим:

σ = Еy / ρ.

Из этой формулы видно, что нормальные напряжения при изгибе распределены по высоте сечения неравномерно: максимальные напряжения возникают в волокнах, наиболее удаленных от нейтральной оси. По ширине сечения нормальные напряжения не меняются.
Распределение нормальных напряжений изображено на рис. 2.

Полученная формула для определения нормальных напряжений неудобна, так как в нее входит радиус кривизны нейтрального слоя.
Для вывода формулы, связывающей нормальные напряжения с изгибающим моментом, применим метод сечений и рассмотрим равновесие части балки, изображенной на рис. 3.
В плоскости поперечного сечения выделим бесконечно малую площадку dA, в пределах которой будем считать нормальные напряжения σ постоянными; тогда нормальная сила dN, действующая на площадку dA, будет равна:

dN = σdA.

Составим уравнения равновесия:

1.    Σ Z = 0;    ∫dN = 0,     или:     ∫σ dA = ∫Еy / ρ dA = Е / ρ ∫y dA = 0.

(ρ для данного сечения, а также модуль упругости Е – величины постоянные, поэтому вынесены за знак интеграла). Поскольку ρ и Е не равны нулю, значит, ∫y dA = 0.
Этот интеграл представляет собой статический момент площади сечения относительно оси x, т. е. нейтральной оси бруса (балки). Равенство нулю статического момента инерции означает, что при изгибе нейтральная ось проходит через центр тяжести площади поперечного сечения;

2.    Σ М_и = 0; — m + ∫y dN = 0.

Так как при чистом изгибе изгибающий момент равен внешнему моменту М_и = m, то

М_и = ∫y dN = ∫y dA = ∫y Еy / ρ dA = Е / ρ ∫y² dA,

откуда:

М_и = Е I / ρ,

где: I = ∫y² dA – момент инерции поперечного сечения относительно нейтральной оси; ЕI – жесткость сечения при изгибе.

Так как при чистом изгибе балки постоянного сечения М_и = const, то:

ρ = EI / М_и = const.

Следовательно, изогнутая ось такой балки представляет собой дугу окружности. Выражение радиуса кривизны подставим в формулу для определения нормальных напряжений; тогда:

σ = Еy / ρ = Ey / EI / М_и = М_и y / I.

Максимальное значение нормальные напряжения будут иметь у волокон, наиболее удаленных от нейтральной оси:

σ_max = М_и y_max / I = М_и / I / y_max = М_и / W,

где W = I / y_max – момент сопротивления изгибу (или осевой момент сопротивления).
Момент сопротивления изгибу есть отношение осевого момента инерции поперечного сечения относительно нейтральной оси к расстоянию от этой оси до наиболее удаленного волокна.
Единица момента сопротивления сечения изгибу [W] = м³.

Итак, наибольшие нормальные напряжения при чистом изгибе вычисляются по формуле

σ_max = М_и / W.

Нетрудно заметить, что эта формула по своей структуре аналогична формулам для определения напряжений при растяжении, сжатии, сдвиге и кручении.

***



Касательные напряжения при изгибе

Очевидно, что при поперечном изгибе, вызванном приложением к балке поперечной силы, в сечениях балки должны возникнуть касательные напряжения.
Определением зависимости между внешними нагрузками, геометрическими и физическими параметрами балок и касательными напряжениями, возникающими в них, занимался русский мостостроитель Д. И. Журавский, который в 1855 году предложил следующую формулу:

τ = QS / (I d).

Эта формула называется формулой Журавского и читается так:
касательные напряжения в поперечном сечении балки равны произведению поперечной силы Q на статический момент S относительно центральной оси части сечения, лежащей выше рассматриваемого слоя волокон, деленному на момент инерции I всего сечения относительно нейтральной оси и на ширину b рассматриваемого слоя волокон.

По формуле Журавского можно вывести зависимости для определения касательных напряжений в балках, имеющих разную форму поперечного сечения (прямоугольную, круглую и т. п.).
Например, для балки круглого сечения формула Журавского в результате преобразований выглядит так:

τ_max = 4Q / (3A) = 4τ_сред / 3,

***

Расчеты на прочность при изгибе

Условие на прочность при изгибе заключается в том, что максимальное нормальное напряжение в опасном сечении не должно превышать допускаемое.
Полагая, что гипотеза о не надавливании волокон справедлива не только при чистом, но и при поперечном изгибе, мы можем нормальные напряжения при поперечном изгибе определять по такой же формуле, что и при чистом изгибе, при этом расчетная формула выглядит так:

σ_max = Ми_max / W ≤ [σ]

и читается так: нормальное напряжение в опасном сечении, определенное по формуле σ_max = Ми_max / W ≤ [σ] не должно превышать допускаемое.
Допускаемое нормальное напряжение при изгибе выбирают таким же, как при растяжении и сжатии.
Максимальный изгибающий момент определяют по эпюре изгибающих моментов или расчетом.
Так как момент сопротивления изгибу W в расчетной формуле стоит в знаменателе, то чем больше W, тем меньшие напряжения возникают в сечении бруса.

Ниже приведены моменты сопротивления изгибу для наиболее часто встречающихся сечений:

1. Прямоугольное сечение размером b x h:    W_пр = bh² / 6.

2. Круглое сечение диаметром d:    W_круг = π d³ / 32 ≈ 0,1d³

3. Кольцо размером D x d:    W_кольца = ≈ 0,1 (D⁴ – d⁴) / D; (момент сопротивления кольцевого сечения нельзя определять, как разность моментов сопротивления большого и малого кругов).

***

Материалы раздела «Изгиб»:

• Понятие деформации изгиба.
• Дифференциальные зависимости при изгибе. Теорема Журавского.

Деформации растяжения и сжатия