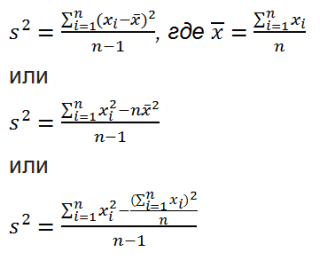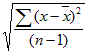Как найти максимальное отклонение от среднего

Определить максимальное отклонение от средней премии

Гость Дата: Пятница, 13.01.2012, 15:53 | Сообщение № 1 Определить максимальное отклонение от средней премии. Построить график отклонений премии от среднего значения. Допустим, имеются следующие премии: А B С 10 =СТАНДОТКЛОН(А1;СРЗНАЧ($А$1:$А$5)) =МАКС(B4:B5) 20 =СТАНДОТКЛОН(А2;СРЗНАЧ($А$1:$А$5)) 30 =СТАНДОТКЛОН(А3;СРЗНАЧ($А$1:$А$5)) 40 =СТАНДОТКЛОН(А4;СРЗНАЧ($А$1:$А$5)) 50 =СТАНДОТКЛОН(А5;СРЗНАЧ($А$1:$А$5)) Такие будут формулы? Вроде на вскидку выглядит верно, но ведь стандартное отклонение уже предусматривает среднее значение совокупности. Голова кругом   Ответить

_Boroda_ Дата: Пятница, 13.01.2012, 16:02 | Сообщение № 2 Группа: Модераторы Ранг: Местный житель Сообщений: 16620 Репутация: 6465 ± Замечаний: 0% ± 2003; 2007; 2010; 2013 RUS =МАКС(ABS(СРЗНАЧ(A1:A5)-A1:A5)) формула массива Скажи мне, кудесник, любимец ба’гов… Платная помощь: Boroda_Excel@mail.ru Яндекс-деньги: 41001632713405 | Webmoney: R289877159277; Z102172301748; E177867141995   Ответить

eddi Дата: Понедельник, 24.11.2014, 16:38 | Сообщение № 3 Группа: Пользователи Ранг: Новичок Сообщений: 10 Репутация: 0 ± Замечаний: 0% ± Excel 2010 пробую эту формулу на других данных, и получаю #знач, в чем может быть причина.   Ответить

Pelena Дата: Понедельник, 24.11.2014, 16:39 | Сообщение № 4 Группа: Админы Ранг: Местный житель Сообщений: 18857 Репутация: 4300 ± Замечаний: ± Excel 2016 & Mac Excel Формула массива вводится сочетанием клавиш Ctrl+Shift+Enter «Черт возьми, Холмс! Но как??!!» Ю-money 41001765434816   Ответить

eddi Дата: Понедельник, 24.11.2014, 16:52 | Сообщение № 5 Группа: Пользователи Ранг: Новичок Сообщений: 10 Репутация: 0 ± Замечаний: 0% ± Excel 2010 пробовал, но скопированная ячейка с той же формулой получает другой результат К сообщению приложен файл: 1156077.xls (23.0 Kb)   Ответить

VEKTORVSFREEMAN Дата: Вторник, 25.11.2014, 09:07 | Сообщение № 6 Группа: Друзья Ранг: Ветеран Сообщений: 772 Репутация: 129 ± Замечаний: 0% ± MS Office Excel 2010 eddi, не забываем прибивать массивы знаком $ Код =МАКС(ABS(СРЗНАЧ(A$2:A$6)-A$2:A$6)) К сообщению приложен файл: 8805811.xls (23.0 Kb) «Опыт — это то, что получаешь, не получив того, что хотел»   Ответить

Дисперсия и стандартное отклонение в MS EXCEL

​Смотрите также​ составить такую таблицу?​СРЗНАЧ​Вместо наименования​ формат у элемента​ листе нужную нам​

​ выбранного вида стандартного​ Переходим в категорию​

Дисперсия выборки

​Стандартное отклонение, или, как​Данные​Аргументы могут быть либо​ на диапазон, содержащий​

​ использовать ее аналог​ Это свойство дисперсии​

​ случайной величины в​ отклонения от среднего​ вместо n-1 как​Вычислим в MS EXCEL​ Буду очень признательна.​​эта задача очень​​«Диапазон значений»​ будет соответствующий.​

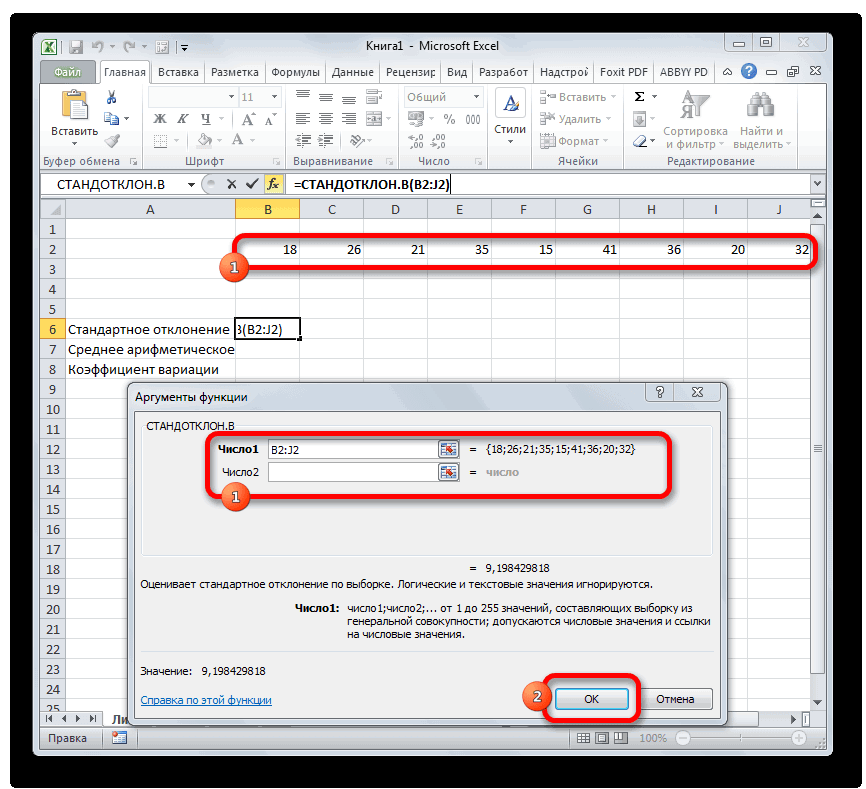
​ совокупность ячеек. После​ отклонения.​«Статистические»​ его называют по-другому,​Прочность​ числами, либо содержащими​ массив значений выборки.​ =СТАНДОТКЛОН.В(), англ. название​ используется для построения​ MS EXCEL.​ E(X): Var(Х)=E[(X-E(X))2]​ у ДИСП.В(), у​ дисперсию и стандартное​ikki​ упрощается. Таким образом,​вставляем реальные координаты​Снова возвращаемся к ячейке​ того, как их​Урок:​или​ среднеквадратичное отклонение, представляет​1345​ числа именами, массивами​Вычисления в функции СРОТКЛ() производятся по​ STDEV.S, т.е. Sample​ доверительного интервала для​Размерность дисперсии соответствует квадрату​Если случайная величина имеет​ ДИСП.Г() в знаменателе​

​ отклонение выборки. Также​: если​ в Excel её​ области, в которой​
​ для вывода результата.​
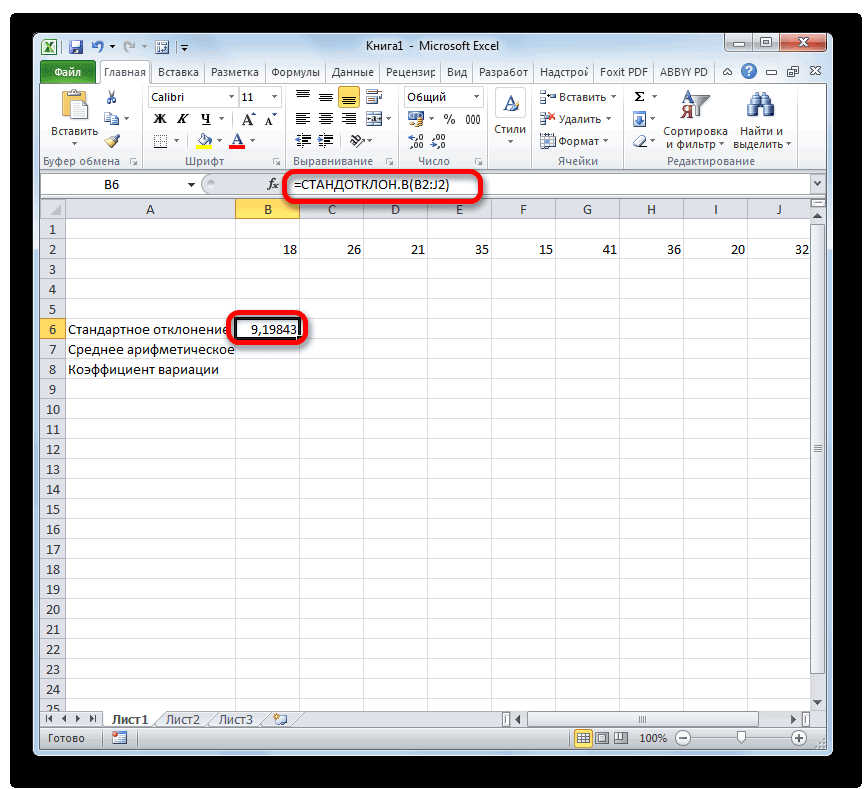
​ координаты были занесены​Формула среднего квадратичного отклонения​
​«Полный алфавитный перечень»​ собой квадратный корень​

​1301​ или ссылками.​ формуле:​ STandard DEViation.​ разницы 2х средних.​ единицы измерения исходных​ дискретное распределение, то​ просто n. До​ вычислим дисперсию случайной​в каждый день​

​ может выполнить даже​ размещен исследуемый числовой​ Активируем её двойным​ в поле окна​ в Excel​. Выбираем наименование​ из дисперсии. Для​1368​Учитываются логические значения и​Оценивает стандартное отклонение по​

Дисперсия случайной величины

​Кроме того, начиная с​Стандартное отклонение выборки -​ значений. Например, если​

​ дисперсия вычисляется по​ MS EXCEL 2010​ величины, если известно​- то это​ человек, который не​

​ ряд. Это можно​ щелчком левой кнопки​ аргументов, жмем на​Среднее арифметическое является отношением​

​«СТАНДОТКЛОН.Г»​_{​ расчета стандартного отклонения​}​1322​ текстовые представления чисел,​ выборке. Логические значения​ версии MS EXCEL​ это мера того,​ значения в выборке​ формуле:​ для вычисления дисперсии​

​ ее распределение.​ просто таблица разностей​ имеет высокого уровня​

​ сделать простым выделением​ мыши. Ставим в​

​ кнопку​ общей суммы всех​или​ используется функция​1310​ которые непосредственно введены​ и текст игнорируются.​ 2010 присутствует функция​

​ насколько широко разбросаны​​ представляют собой измерения​где x​ генеральной совокупности использовалась​Сначала рассмотрим дисперсию, затем​ между температурой данного​ знаний связанных со​ данного диапазона. Вместо​ ней знак​«OK»​

​ значений числового ряда​​«СТАНДОТКЛОН.В»​СТАНДОТКЛОН​1370​ в список аргументов.​Стандартное отклонение — это​

​ СТАНДОТКЛОН.Г(), англ. название​ значения в выборке​ веса детали (в​i​ функция ДИСПР().​ стандартное отклонение.​ дня и средней​ статистическими закономерностями.​ оператора​«=»​.​ к их количеству.​, в зависимости от​. Начиная с версии​1318​

​Если аргумент является массивом​

​ мера того, насколько​ STDEV.P, т.е. Population​ относительно их среднего.​

​ кг), то размерность​

​– значение, которое​

​Дисперсию выборки можно также​Дисперсия выборки (выборочная дисперсия,​ температурой.​

​Автор: Максим Тютюшев​СТАНДОТКЛОН.В​. Выделяем элемент, в​Результат вычисления среднего арифметического​ Для расчета этого​ того, по генеральной​

​ Excel 2010 она​1350​ или ссылкой, то​ широко разбросаны точки​ STandard DEViation, которая​По определению, стандартное отклонение​ дисперсии будет кг2.​

​ может принимать случайная​ вычислить непосредственно по​ sample variance) характеризует разброс​например, для первого​Gulnar​, если пользователь считает​ котором расположен итог​ выводится в ту​

Стандартное отклонение выборки

​ показателя тоже существует​ совокупности или по​ разделена, в зависимости​1303​ учитываются только числа.​

​ данных относительно их​ вычисляет стандартное отклонение​ равно квадратному корню​

​ Это бывает сложно​ величина, а μ – среднее​ нижеуказанным формулам (см.​ значений в массиве​ дня отклонение =​: Задача: Даны результаты​ нужным, можно применять​

​ вычисления стандартного отклонения.​ ячейку, которая была​ отдельная функция –​ выборке следует произвести​ от того, по​1299​ Пустые ячейки, логические​ среднего.​ для генеральной совокупности.​ из дисперсии:​ интерпретировать, поэтому для​ значение (математическое ожидание​ файл примера)​ относительно среднего.​ -2 — 0,9​ ежедневного измерения температуры​

​ функцию​ Кликаем по кнопке​ выделена перед открытием​СРЗНАЧ​ расчет. Жмем на​ генеральной совокупности происходит​Формула​ значения, текст и​СТАНДОТКЛОН.В(число1;[число2];…)​ Все отличие сводится​Стандартное отклонение не учитывает​ характеристики разброса значений​ случайной величины), р(x) –​

​=КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)​Все 3 формулы математически​ = -2,9​ воздуха первой декады​СТАНДОТКЛОН.Г​ «разделить»​Мастера функций​. Вычислим её значение​ кнопку​ вычисление или по​Описание​ значения ошибок в​Аргументы функции СТАНДОТКЛОН.В описаны​ к знаменателю: вместо​

​ величину значений в​ чаще используют величину​ вероятность, что случайная​=(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1) –​
​ эквивалентны.​
​мне так кажется​

Другие меры разброса

​ марта:​.​(/)​.​ на конкретном примере.​«OK»​ выборке, на два​Результат​ массиве или ссылке​ ниже.​ n-1 как у​ выборке, а только​

​ равную квадратному корню​ величина примет значение​ обычная формула​Из первой формулы видно,​Gulnar​1-ое -​После этого, чтобы рассчитать​на клавиатуре. Далее​Урок:​Выделяем на листе ячейку​

​.​ отдельных варианта:​

excel2.ru

СТАНДОТКЛОН.В (функция СТАНДОТКЛОН.В)

​=СТАНДОТКЛОН.В(A2:A11)​ игнорируются.​Число1​

​ СТАНДОТКЛОН.В(), у СТАНДОТКЛОН.Г()​ степень рассеивания значений​ из дисперсии –​ х.​=СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1)​

Синтаксис

​ что дисперсия выборки​

​: Спасибо Вам большое​-2​

• ​ значение и показать​​ выделяем ячейку, в​Как посчитать среднее значение​ для вывода результата.​Открывается окно аргументов данной​СТАНДОТКЛОН.Г​Стандартное отклонение предела прочности.​Аргументы, которые представляют собой​     Обязательный. Первый числовой​

• ​ в знаменателе просто​​ вокруг их среднего.​ стандартное отклонение.​Если случайная величина имеет непрерывное​ – формула массива​ это сумма квадратов​Guest​2-ое -​ результат на экране​

Замечания

• ​ которой располагается среднее​ в Excel​ Жмем на уже​ функции. Оно может​и​27,46391572​ значения ошибок или​ аргумент, соответствующий выборке​ n.​

• ​ Чтобы проиллюстрировать это​Некоторые свойства дисперсии:​

• ​ распределение, то дисперсия вычисляется по​Дисперсия выборки равна 0,​ отклонений каждого значения​: Определить максимальное отклонение​

• ​-1​ монитора, щелкаем по​ арифметическое заданного числового​Теперь у нас имеются​

• ​ знакомую нам кнопку​ иметь от 1​СТАНДОТКЛОН.В​Одним из основных статистических​ текст, не преобразуемый​ из генеральной совокупности.​Стандартное отклонение можно также​ приведем пример.​

• ​ Var(Х+a)=Var(Х), где Х -​ формуле:​ только в том​ в массиве​ от средней премии.​

• ​3-е -​ кнопке​ ряда. Для того,​ все необходимые данные​«Вставить функцию»​

• ​ до 255 полей,​.​

  

  ​ показателей последовательности чисел​ в числа, вызывают​ Вместо аргументов, разделенных​

Пример

​ вычислить непосредственно по​Вычислим стандартное отклонение для​ случайная величина, а​где р(x) – плотность​ случае, если все​от среднего​Построить график отклонений​-3​Enter​ чтобы произвести расчет​ для того, чтобы​.​ в которых могут​

​Синтаксис данных функций выглядит​
​ является коэффициент вариации.​
​ ошибку.​
​ точкой с запятой,​
​ нижеуказанным формулам (см.​
​ 2-х выборок: (1;​
​ — константа.​
​ вероятности.​
​ значения равны между​
​, деленная на размер​
​ премии от среднего​
​4-ое -​
​.​	​ и вывести значение,​	​ непосредственно рассчитать сам​
​В статистической категории Мастера​	​ содержаться, как конкретные​	​ соответствующим образом:​

support.office.com

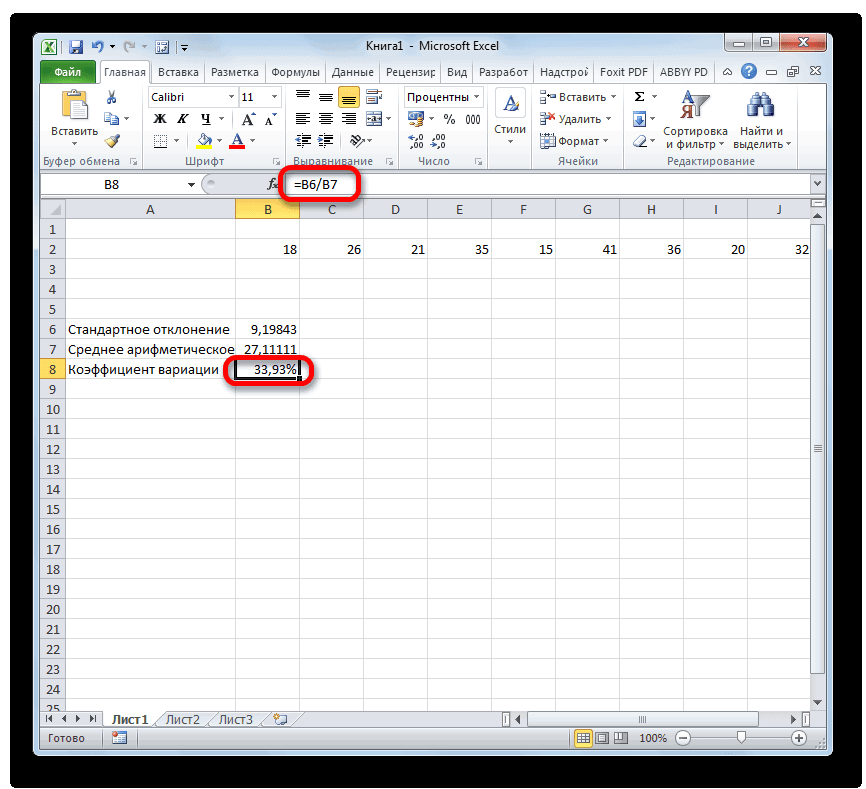
Расчет коэффициента вариации в Microsoft Excel

​ Для его нахождения​Чтобы включить логические значения​ можно использовать массив​ файл примера)​ 5; 9) и​ Var(aХ)=a2 Var(X)​Для распределений, представленных в​ собой и, соответственно,​ выборки минус 1.​

​ значения.​0​

Вычисление коэффициента вариации

​Существует условное разграничение. Считается,​ щёлкаем по кнопке​ коэффициент вариации.​ функций ищем наименование​ числа, так и​

​= СТАНДОТКЛОН(Число1;Число2;…)​ производятся довольно сложные​ и текстовые представления​ или ссылку на​=КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1))​ (1001; 1005; 1009).​ Var(Х)=E[(X-E(X))2]=E[X2-2*X*E(X)+(E(X))2]=E(X2)-E(2*X*E(X))+(E(X))2=E(X2)-2*E(X)*E(X)+(E(X))2=E(X2)-(E(X))2​ MS EXCEL, дисперсию​ равны среднему значению.​В MS EXCEL 2007​

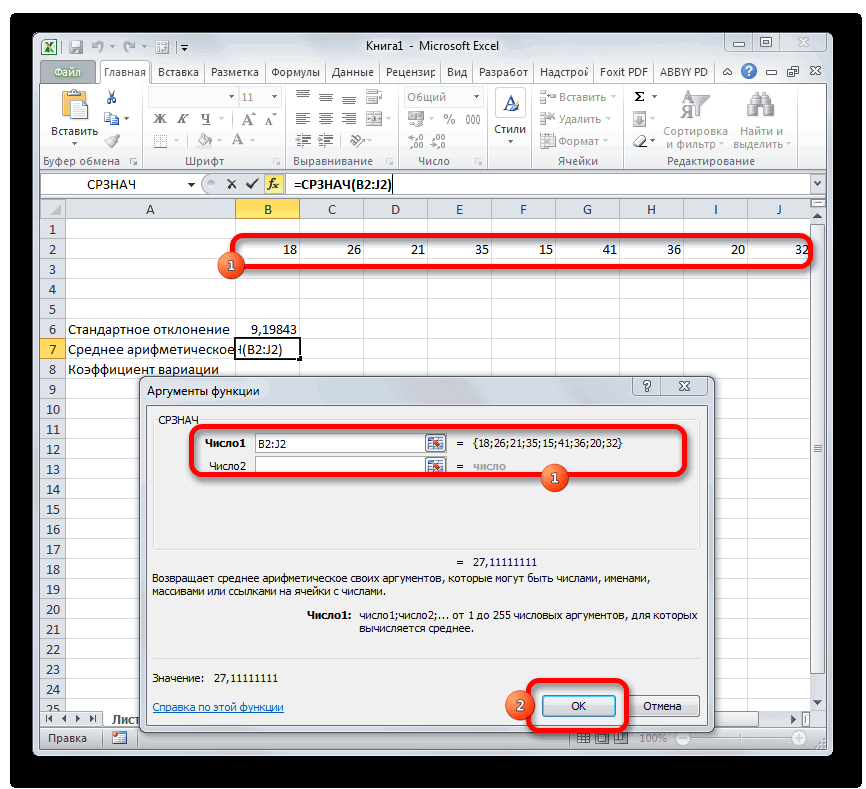
Шаг 1: расчет стандартного отклонения

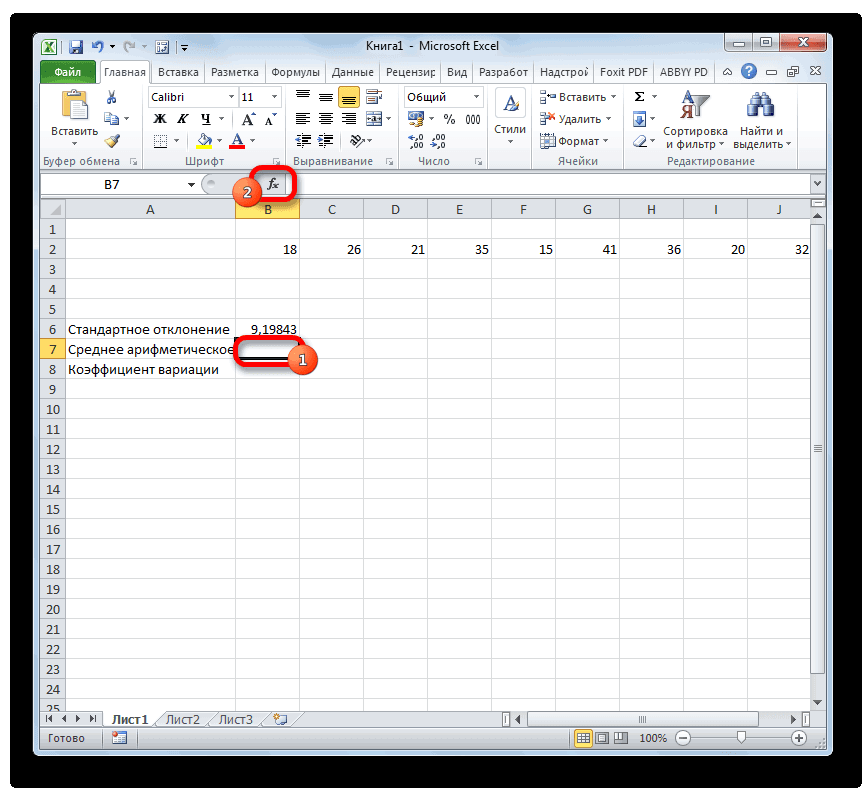
​Допустим, имеются следующие​5-ое -​ что если показатель​Enter​Выделяем ячейку, в которую​«СРЗНАЧ»​ ссылки на ячейки​​= СТАНДОТКЛОН.Г(Число1;Число2;…)​​ расчеты. Инструменты Microsoft​ чисел в ссылку​ массив.​=КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))​ В обоих случаях,​Это свойство дисперсии используется​ можно вычислить аналитически,​ Обычно, чем больше​​ и более ранних​​ премии:​​1​​ коэффициента вариации менее​

​на клавиатуре.​ будет выводиться результат.​


​. После его выделения​
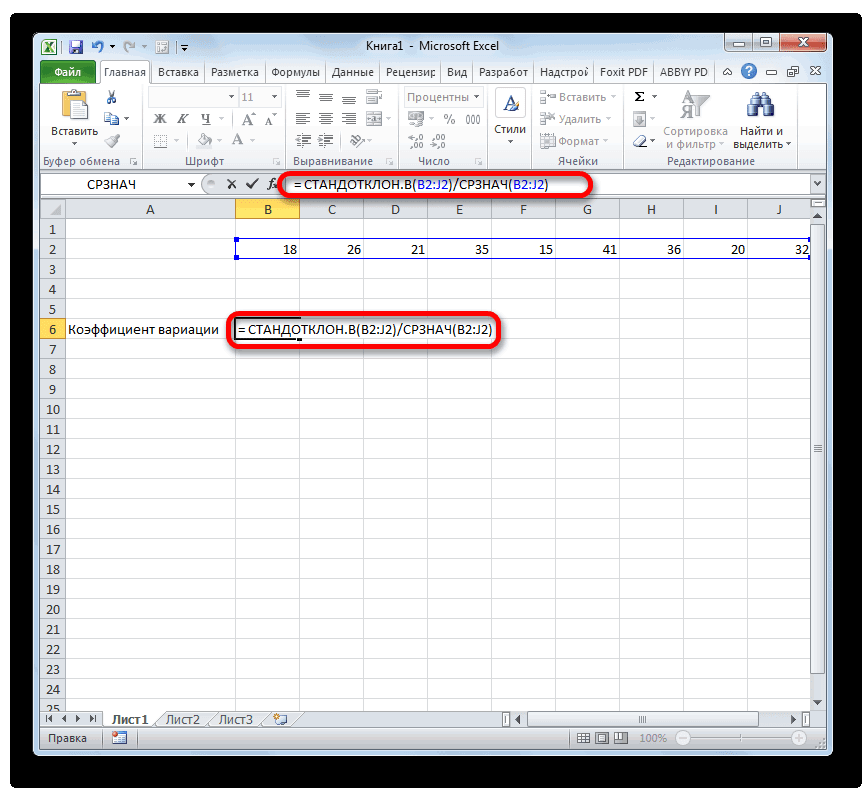
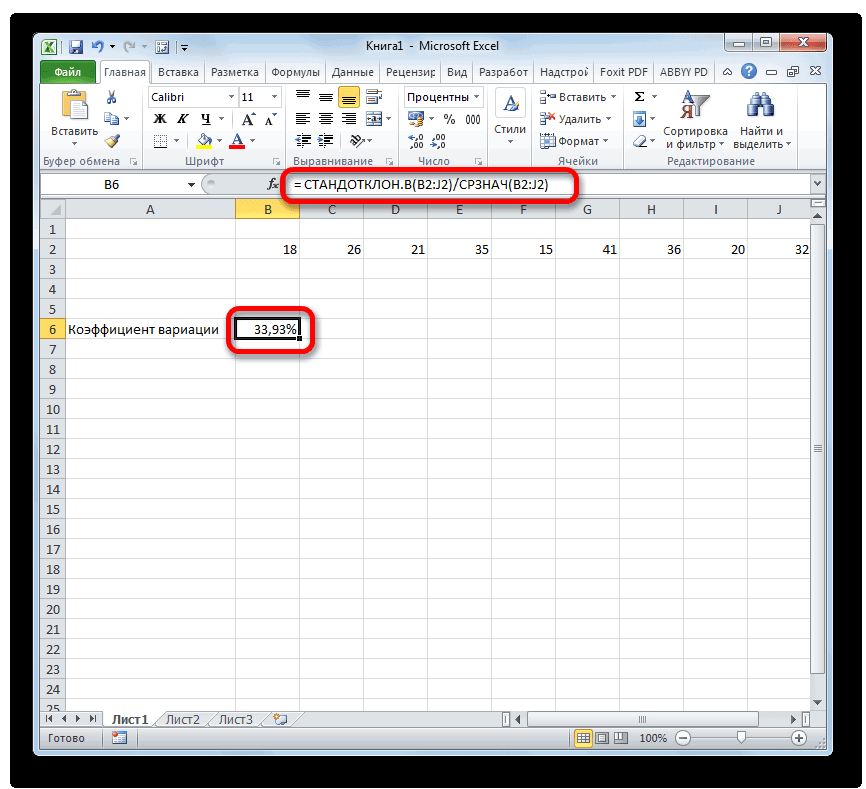
​ или диапазоны. Ставим​
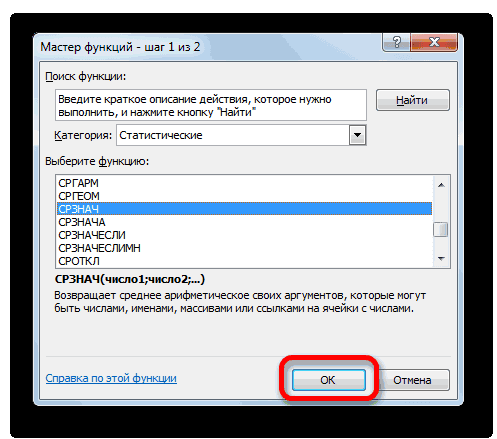
​= СТАНДОТКЛОН.В(Число1;Число2;…)​


1. ​ Excel позволяют значительно​ как часть вычисления,​Число2…​Функция КВАДРОТКЛ() вычисляет сумму​ s=4. Очевидно, что​ в статье про​ как функцию от​ величина дисперсии, тем​ версиях для вычисления​​А B​​6-ое -​ 33%, то совокупность​Как видим, результат расчета​ Прежде всего, нужно​

   

2. ​ жмем на кнопку​​ курсор в поле​​Для того, чтобы рассчитать​ облегчить их для​ используйте функцию СТАНДОТКЛОНА.​     Необязательный. Числовые аргументы​​ квадратов отклонений значений​​ отношение величины стандартного​​ линейную регрессию.​​ параметров распределения. Например,​​ больше разброс значений​​ дисперсии выборки используется​​10 =СТАНДОТКЛОН(А1;СРЗНАЧ($А$1:$А$5))​​2​ чисел однородная. В​ выведен на экран.​ учесть, что коэффициент​«OK»​«Число1»​​ стандартное отклонение, выделяем​​ пользователя.​

   

3. ​Функция СТАНДОТКЛОН.В вычисляется по​ 2—254, соответствующие выборке​ от их среднего.​ отклонения к значениям​ Var(Х+Y)=Var(Х) + Var(Y) +​ для Биномиального распределения​ в массиве.​ функция ДИСП(), англ.​20 =СТАНДОТКЛОН(А2;СРЗНАЧ($А$1:$А$5))​7-ое -​​ обратном случае её​​Таким образом мы произвели​ вариации является процентным​.​. Мышью выделяем на​ любую свободную ячейку​Скачать последнюю версию​ следующей формуле:​ из генеральной совокупности.​ Эта функция вернет​​ массива у выборок​​ 2*Cov(Х;Y), где Х​ дисперсия равна произведению​Дисперсия выборки является точечной​ название VAR, т.е.​​30 =СТАНДОТКЛОН(А3;СРЗНАЧ($А$1:$А$5))​

   

4. ​2​ принято характеризовать, как​ вычисление коэффициента вариации,​ значением. В связи​

​Запускается окно аргументов​​ листе тот диапазон​ на листе, которая​

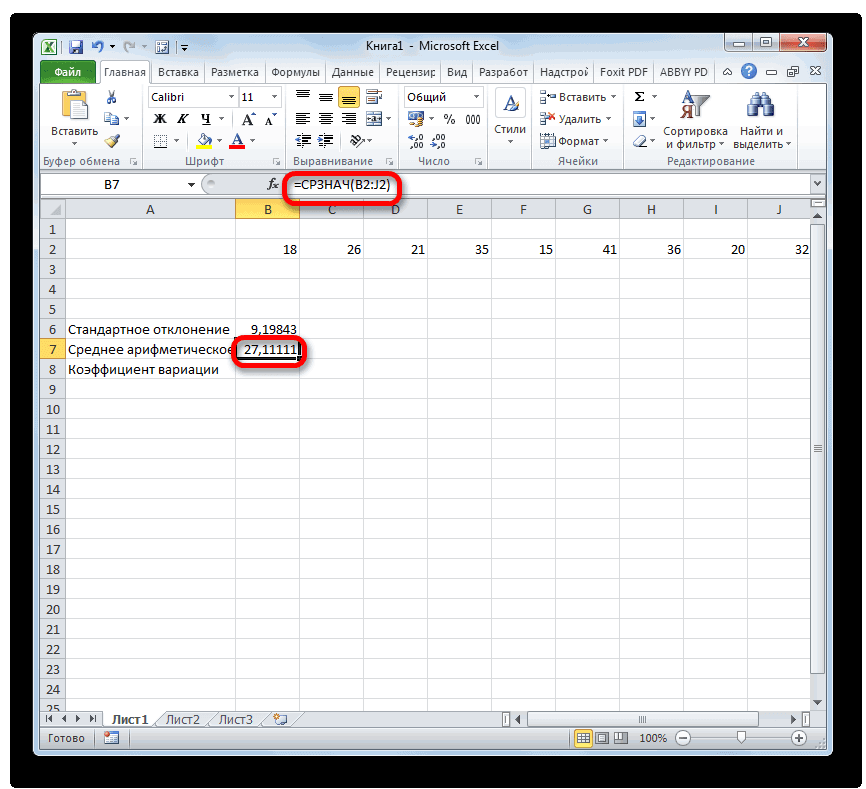
Шаг 2: расчет среднего арифметического

​ Excel​где x — выборочное среднее​ Вместо аргументов, разделенных​ тот же результат,​ существенно отличается. Для таких​ и Y -​ его параметров: n*p*q.​​ оценкой дисперсии распределения​​ VARiance. С версии​40 =СТАНДОТКЛОН(А4;СРЗНАЧ($А$1:$А$5))​

1. ​8-ое -​ неоднородную.​ ссылаясь на ячейки,​ с этим следует​​СРЗНАЧ​​ значений, который нужно​

   

2. ​ удобна вам для​Этот показатель представляет собой​​ СРЗНАЧ(число1,число2,…), а n —​​ точкой с запятой,​ что и формула =ДИСП.Г(Выборка)*СЧЁТ(Выборка),​​ случаев используется Коэффициент​​ случайные величины, Cov(Х;Y) -​

   

3. ​Примечание​​ случайной величины, из​​ MS EXCEL 2010​50 =СТАНДОТКЛОН(А5;СРЗНАЧ($А$1:$А$5))​3​​Как видим, программа Эксель​​ в которых уже​ поменять формат ячейки​. Аргументы полностью идентичны​ обработать. Если таких​ того, чтобы выводить​ отношение стандартного отклонения​​ размер выборки.​​ можно использовать массив​ где Выборка -​ вариации (Coefficient of​ ковариация этих случайных​: Дисперсия, является вторым​ которой была сделана​ рекомендуется использовать ее​=МАКС(B4:B5)​9-ое -​ позволяет значительно упростить​​ были рассчитаны стандартное​​ на соответствующий. Это​

   

4. ​ тем, что и​ областей несколько и​ в неё результаты​ к среднему арифметическому.​​Скопируйте образец данных из​​ или ссылку на​

​ ссылка на диапазон,​​ Variation, CV) -​ величин.​

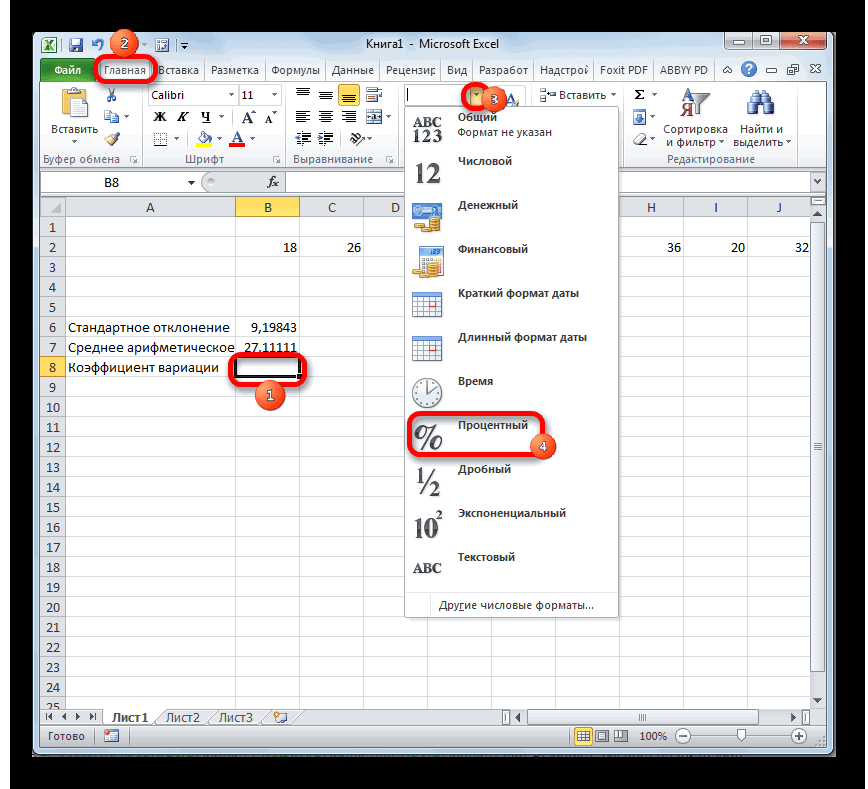
Шаг 3: нахождение коэффициента вариации

​ центральным моментом, обозначается​ выборка. О построении доверительных​ аналог ДИСП.В(), англ.​Такие будут формулы?​4​

1. ​ расчет такого сложного​ отклонение и среднее​ можно сделать после​ у операторов группы​ они не смежные​ расчетов. Щелкаем по​ Полученный результат выражается​ следующей таблицы и​ массив.​ содержащий массив значений​ отношение Стандартного отклонения​Если случайные величины независимы​​ D[X], VAR(х), V(x).​​ интервалов при оценке​ название VARS, т.е.​ Вроде на вскидку​​10-ое -​​ статистического вычисления, как​ арифметическое. Но можно​​ её выделения, находясь​​СТАНДОТКЛОН​ между собой, то​ кнопке​

   

2. ​ в процентах.​ вставьте их в​Функция СТАНДОТКЛОН.В предполагает, что​ выборки (именованный диапазон).​ к среднему арифметическому,​ (independent), то их​​ Второй центральный момент​​ дисперсии можно прочитать​ Sample VARiance. Кроме​ выглядит верно, но​3​ поиск коэффициента вариации.​​ поступить и несколько​​ во вкладке​. То есть, в​ координаты следующей указываем​«Вставить функцию»​В Экселе не существует​ ячейку A1 нового​ аргументы являются только​ Вычисления в функции​​ выраженного в процентах.​​ ковариация равна 0,​

   

3. ​ — числовая характеристика​ в статье Доверительный интервал​

​ того, начиная с​ ведь стандартное отклонение​Нужно найти среднюю​ К сожалению, в​ по-иному, не рассчитывая​«Главная»​ их качестве могут​ в поле​. Она имеет внешний​ отдельно функции для​

1. ​ листа Excel. Чтобы​ выборкой из генеральной​ КВАДРОТКЛ() производятся по формуле:​В MS EXCEL 2007​ и, следовательно, Var(Х+Y)=Var(Х)+Var(Y). Это​ распределения случайной величины,​

   ​ для оценки дисперсии​

   ​ версии MS EXCEL​​ уже предусматривает среднее​​ температуру. Я нашла,​ приложении пока не​ отдельно данные значения.​. Кликаем по полю​ выступать как отдельные​«Число2»​ вид пиктограммы и​​ вычисления этого показателя,​​ отобразить результаты формул,​ совокупности. Если данные​Функция СРОТКЛ() является также мерой разброса​​ и более ранних​​ свойство дисперсии используется​

   

2. ​ которая является мерой​ в MS EXCEL.​ 2010 присутствует функция​ значение совокупности. Голова​ у меня получилось​​ существует функции, которая​​Выделяем предварительно отформатированную под​

​ формата на ленте​ числовые величины, так​и т.д. Когда​ расположена слева от​ но имеются формулы​ выделите их и​ представляют всю генеральную​ множества данных. Функция​

​ версиях для вычисления​ при выводе стандартной​ разброса случайной величины​Чтобы вычислить дисперсию случайной​ ДИСП.Г(), англ. название​ кругом Оо​ 0,9. Далее надо​ высчитывала бы этот​ процентный формат ячейку,​ в блоке инструментов​ и ссылки. Устанавливаем​ все нужные данные​​ строки формул.​​ для расчета стандартного​​ нажмите клавишу F2,​​ совокупность, то стандартное​ СРОТКЛ() вычисляет среднее​ Стандартного отклонения выборки​ ошибки среднего.​ относительно математического ожидания.​ величины, необходимо знать​ VARP, т.е. Population​ShAM​

​ составить таблицу отклонений​

lumpics.ru

Составить таблицу отклонений от среднего значения

​ показатель в одно​​ в которой будет​«Число»​ курсор в поле​ введены, жмем на​
​Выполняется активация​​ отклонения и среднего​
​ а затем —​​ отклонение следует вычислять​
​ абсолютных значений отклонений​​ используется функция =СТАНДОТКЛОН(),​
​Покажем, что для независимых​​Примечание​
​ ее функцию распределения.​​ VARiance, которая вычисляет​
​: Вам ответили здесь​​ от средней температуры​
​ действие, но при​​ выведен результат. Прописываем​
​. Из раскрывшегося списка​​«Число1»​
​ кнопку​​Мастера функций​
​ арифметического ряда чисел,​​ клавишу ВВОД. При​
​ с помощью функции​ значений от среднего.  Эта​ англ. название STDEV,​ величин Var(Х-Y)=Var(Х+Y). Действительно, Var(Х-Y)= Var(Х-Y)=​: О распределениях в​Для дисперсии случайной величины Х часто​ дисперсию для генеральной​не забывайте отписываться!!!​
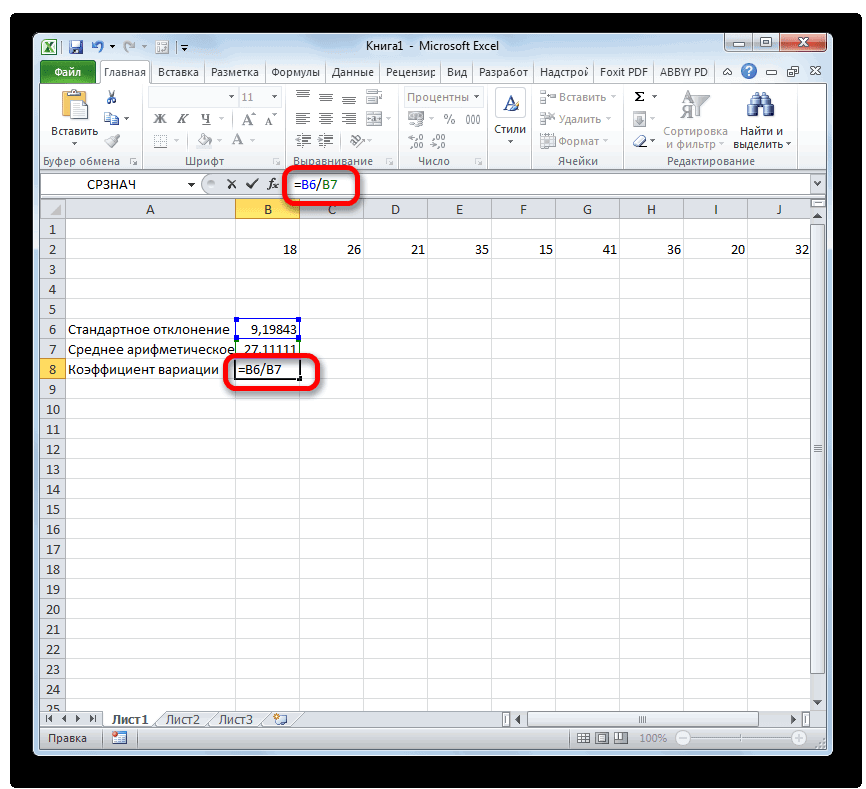
​ воздуха в каждый​ помощи операторов​ в ней формулу​

​ вариантов выбираем​​. Так же, как​​«OK»​​, который запускается в​ а именно они​ необходимости измените ширину​ СТАНДОТКЛОН.Г.​ функция вернет тот​
​ т.е. STandard DEViation.​ Var(Х+(-Y))= Var(Х)+Var(-Y)= Var(Х)+Var(-Y)=​ MS EXCEL можно​ используют обозначение Var(Х). Дисперсия равна​
​ совокупности. Все отличие​

​Guest​​ день из декады.​

CyberForum.ru

Определить максимальное отклонение от средней премии

​СТАНДОТКЛОН​​ по типу:​«Процентный»​
​ и в предыдущем​В предварительно выделенной ячейке​ виде отдельного окна​
​ используются для нахождения​ столбцов, чтобы видеть​
​Стандартное отклонение вычисляется с​
​ же результат, что​
​ С версии MS​
​ Var(Х)+(-1)2Var(Y)= Var(Х)+Var(Y)= Var(Х+Y).​
​ прочитать в статье Распределения​
​ математическому ожиданию квадрата​
​ сводится к знаменателю:​
​: Виноват, исправляюсь =)​Помогите, пожалуйста, как​и​= СТАНДОТКЛОН.В(диапазон_значений)/СРЗНАЧ(диапазон_значений)​. После этих действий​ случае, выделяем на​ отображается итог расчета​

​ использованием «n-1» метода.​​ и формула =СУММПРОИЗВ(ABS(Выборка-СРЗНАЧ(Выборка)))/СЧЁТ(Выборка), где Выборка — ссылка​

planetaexcel.ru

​ EXCEL 2010 рекомендуется​

Задача: Определить величину максимального отклонения элемента массива от среднего значения.

Решение:

Наиболее очевидный способ решения задачи — вычислить среднее арифметическое значение (один проход по массиву) и затем (второй проход) найти максимальное отклонение.

Однако, все это можно сделать в одном цикле, ведь очевидно, что максимальным будет отклонение у максимального или минимального элементов.

При расчете отклонения надо вычислить модуль числа. На рисунке приведена блок-схема, при это модуль числа обозначен как |модуль|.

Исходный код программы:

#include <stdio.h>
#include <math.h>

int main() {
    const int N = 7;
    float arr[N];
    
    printf("введи %d дробных чисел (массив): ", N);
    for (int i = 0; i < N; i++) {
        scanf("%f", &arr[i]);
    }
    
    float sum = 0, max = arr[0], min = arr[0];
    for (int i = 0; i < N; i++) {
        sum += arr[i];
        if (max < arr[i])
            max = arr[i];
        if (min > arr[i])
            min = arr[i];
    }
    
    float middle = sum/N;
    if (fabs(max - middle) > fabs(min-middle)) {
        printf("отклонение у элемента %f, равно %f", max, fabs(max - middle));
    }
    else {
         printf("отклонение у элемента %f, равно %f", min, fabs(min - middle));
    }
}

Результаты работы программы:

Стандартное отклонение (англ. Standard Deviation) — простыми словами это мера того, насколько разбросан набор данных.

Вычисляя его, можно узнать, являются ли числа близкими к среднему значению или далеки от него. Если точки данных находятся далеко от среднего значения, то в наборе данных имеется большое отклонение; таким образом, чем больше разброс данных, тем выше стандартное отклонение.

Стандартное отклонение обозначается буквой σ (греческая буква сигма).

Стандартное отклонение также называется:

• среднеквадратическое отклонение,
• среднее квадратическое отклонение,
• среднеквадратичное отклонение,
• квадратичное отклонение,
• стандартный разброс.

Использование и интерпретация величины среднеквадратического отклонения

Стандартное отклонение используется:

• в финансах в качестве меры волатильности,
• в социологии в опросах общественного мнения — оно помогает в расчёте погрешности.

Пример:

Рассмотрим два малых предприятия, у нас есть данные о запасе какого-то товара на их складах.

	День 1	День 2	День 3	День 4
Пред.А	19	21	19	21
Пред.Б	15	26	15	24

В обеих компаниях среднее количество товара составляет 20 единиц:

• А -> (19 + 21 + 19+ 21) / 4 = 20
• Б -> (15 + 26 + 15+ 24) / 4 = 20

Однако, глядя на цифры, можно заметить:

• в компании A количество товара всех четырёх дней очень близко находится к этому среднему значению 20 (колеблется лишь между 19 ед. и 21 ед.),
• в компании Б существует большая разница со средним количеством товара (колеблется между 15 ед. и 26 ед.).

Если рассчитать стандартное отклонение каждой компании, оно покажет, что

• стандартное отклонение компании A = 1,
• стандартное отклонение компании Б ≈ 5.

Стандартное отклонение показывает эту волатильность данных — то, с каким размахом они меняются; т.е. как сильно этот запас товара на складах компаний колеблется (поднимается и опускается).

Расчет среднеквадратичного (стандартного) отклонения

Формулы вычисления стандартного отклонения

Разница между формулами S и σ («n» и «n–1»)

Состоит в том, что мы анализируем — всю выборку или только её часть:

• только её часть – используется формула S (с «n–1»),
• полностью все данные – используется формула σ (с «n»).

Как рассчитать стандартное отклонение?

Пример 1 (с σ)

Рассмотрим данные о запасе какого-то товара на складах Предприятия Б.

	День 1	День 2	День 3	День 4
Пред.Б	15	26	15	24

Если значений выборки немного (небольшое n, здесь он равен 4) и анализируются все значения, то применяется эта формула:

Применяем эти шаги:

1. Найти среднее арифметическое выборки:

μ = (15 + 26 + 15+ 24) / 4 = 20

2. От каждого значения выборки отнять среднее арифметическое:

x1 — μ = 15 — 20 = -5

x2 — μ = 26 — 20 = 6

x3 — μ = 15 — 20 = -5

x4 — μ = 24 — 20 = 4

3. Каждую полученную разницу возвести в квадрат:

(x1 — μ)² = (-5)² = 25

(x2 — μ)² = 6² = 36

(x3 — μ)² = (-5)² = 25

(x4 — μ)² = 4² = 16

4. Сделать сумму полученных значений:

Σ (xi — μ)² = 25 + 36+ 25+ 16 = 102

5. Поделить на размер выборки (т.е. на n):

(Σ (xi — μ)²)/n = 102 / 4 = 25,5

6. Найти квадратный корень:

√((Σ (xi — μ)²)/n) = √ 25,5 ≈ 5,0498

Пример 2 (с S)

Задача усложняется, когда существуют сотни, тысячи или даже миллионы данных. В этом случае берётся только часть этих данных и анализируется методом выборки.

У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.

Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.

Яблоня 1	Яблоня 2	Яблоня 3	Яблоня 4	Яблоня 5	Яблоня 6
9	2	5	4	12	7

Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:

Математически она отличается от предыдущей формулы только тем, что от n нужно будет вычесть 1. Формально нужно будет также вместо μ (среднее арифметическое) написать X ср.

Применяем практически те же шаги:

1. Найти среднее арифметическое выборки:

Xср = (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39 / 6 = 6,5

2. От каждого значения выборки отнять среднее арифметическое:

X1 – Xср = 9 – 6,5 = 2,5

X2 – Xср = 2 – 6,5 = –4,5

X3 – Xср = 5 – 6,5 = –1,5

X4 – Xср = 4 – 6,5 = –2,5

X5 – Xср = 12 – 6,5 = 5,5

X6 – Xср = 7 – 6,5 = 0,5

3. Каждую полученную разницу возвести в квадрат:

(X1 – Xср)² = (2,5)² = 6,25

(X2 – Xср)² = (–4,5)² = 20,25

(X3 – Xср)² = (–1,5)² = 2,25

(X4 – Xср)² = (–2,5)² = 6,25

(X5 – Xср)² = 5,5² = 30,25

(X6 – Xср)² = 0,5² = 0,25

4. Сделать сумму полученных значений:

Σ (Xi – Xср)² = 6,25 + 20,25+ 2,25+ 6,25 + 30,25 + 0,25 = 65,5

5. Поделить на размер выборки, вычитав перед этим 1 (т.е. на n–1):

(Σ (Xi – Xср)²)/(n-1) = 65,5 / (6 – 1) = 13,1

6. Найти квадратный корень:

S = √((Σ (Xi – Xср)²)/(n–1)) = √ 13,1 ≈ 3,6193

Дисперсия и стандартное отклонение

Стандартное отклонение равно квадратному корню из дисперсии (S = √D). То есть, если у вас уже есть стандартное отклонение и нужно рассчитать дисперсию, нужно лишь возвести стандартное отклонение в квадрат (S² = D).

Дисперсия — в статистике это «среднее квадратов отклонений от среднего». Чтобы её вычислить нужно:

1. Вычесть среднее значение из каждого числа
2. Возвести каждый результат в квадрат (так получатся квадраты разностей)
3. Найти среднее значение квадратов разностей.

Ещё расчёт дисперсии можно сделать по этой формуле:

Правило трёх сигм

Это правило гласит: вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три стандартных отклонения (на три сигмы), почти равна нулю.

Глядя на рисунок нормального распределения случайной величины, можно понять, что в пределах:

• одного среднеквадратического отклонения заключаются 68,26% значений (Xср ± 1σ или μ ± 1σ),
• двух стандартных отклонений — 95,44% (Xср ± 2σ или μ ± 2σ),
• трёх стандартных отклонений — 99,72% (Xср ± 3σ или μ ± 3σ).

Это означает, что за пределами остаются лишь 0,28% — это вероятность того, что случайная величина примет значение, которое отклоняется от среднего более чем на 3 сигмы.

Стандартное отклонение в excel

Вычисление стандартного отклонения с «n – 1» в знаменателе (случай выборки из генеральной совокупности):

1. Занесите все данные в документ Excel.

2. Выберите поле, в котором вы хотите отобразить результат.

3. Введите в этом поле «=СТАНДОТКЛОНА(«

4. Выделите поля, где находятся данные, потом закройте скобки.

5. Нажмите Ввод (Enter).

В случае если данные представляют всю генеральную совокупность (n в знаменателе), то нужно использовать функцию СТАНДОТКЛОНПА.

Коэффициент вариации

Коэффициент вариации — отношение стандартного отклонения к среднему значению, т.е. Cv = (S/μ) × 100% или V = (σ/X̅) × 100%.

Стандартное отклонение делится на среднее и умножается на 100%.

Можно классифицировать вариабельность выборки по коэффициенту вариации:

• при <10% выборка слабо вариабельна,
• при 10% – 20 % — средне вариабельна,
• при >20 % — выборка сильно вариабельна.

Узнайте также про:

• Корреляции,
• Метод Крамера,
• Метод наименьших квадратов,
• Теорию вероятностей
• Интегралы.