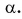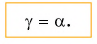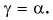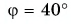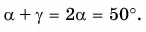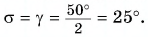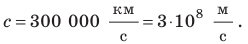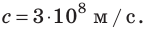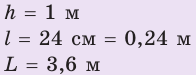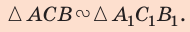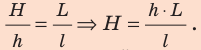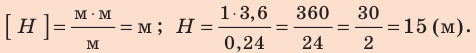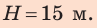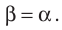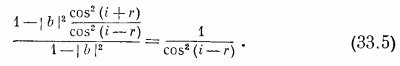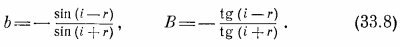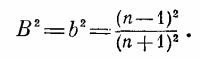Как найти максимальное отражение света

Примеры решения задач

Задача 1. В опыте Ллойда (рис. 1.2.1) световая
волна, исходящая непосредственно из
источника
(узкой щели), интерферирует с волной,
отраженной от зеркала.
В результате на экранеобразуется система интерференционных
полос. Расстояние от источника до экрана.
При некотором положении источника
ширина интерференционной полосы на
экране,
а после того как источник отодвинули
от плоскости зеркала на,
ширина полос уменьшилась враза. Найти длину волны света.

Решение

Решение данной задачи можно свести к
решению задачи о двух источниках, заменяя
зеркало изображением
источника в нем. Будем отсчитывать
положение точки наблюдения на экране
от линии пересечения зеркала и экрана.

Рис. 1.2.1

Определим геометрические длины путей,
которые прошли волны, взаимодействующие
в точке
,
от источника и его изображения. Обозначая
начальное расстояние от источника до
плоскости зеркала через,
по теореме Пифагора находим

,,

откуда следует

.
(1.2.1)

Поскольку первая скобка в (1.2.1) равна
оптической разности хода волн
(так как показатель преломления воздуха
принимаем равным единице), а вторую с
учетом условияможно приближенно принять равной,
получаем

.
(1.2.2)

Применяя условие минимумов интенсивности
света при интерференции, находим линейные
координаты минимумов освещенности

,

и ширину интерференционной полосы

.
(1.2.3)

Рассуждая аналогично, находим ширину
интерференционной полосы после
передвижения источника

.
(1.2.4)

Так как, согласно условию
,
из (1.2.3), (1.2.4) следует

.

Задача 2. На вершине сферической
поверхности плоско-выпуклой стеклянной
линзы имеется сошлифованный плоский
участок радиуса
,
которым она соприкасается со стеклянной
пластинкой. Радиус кривизны выпуклой
поверхности линзы.
Найти радиус шестого светлого кольца
при наблюдении в отраженном свете с
длиной волны.

Решение

Определим высоту сферического сегмента
,
удаленного при шлифовании линзы. По
теореме Пифагора

.
(1.2.5)

откуда при условии
приближенно следует

.
(1.2.6)

Обозначая через
толщину воздушной прослойки в том месте,
где наблюдается-е
светлое кольцо, при помощи теоремы
Пифагора аналогично получаем

,

откуда при условии
приближенно находим

.
(1.2.7)

Из (1.2.6), (1.2.7) находим толщину воздушной
прослойки между линзой и пластинкой

.
(1.2.8)

Оптическая разность хода волн, отразившихся
от выпуклой поверхности линзы и от
пластинки, равна

,
(1.2.9)

где учтено, что при отражении света от
оптически более плотной среды фаза
волны изменяется на
.
Применяя условие максимумов интенсивности
света при интерференциис учетом (1.2.9) получаем

,

что позволяет при помощи (1.2.8) получить

.
(1.2.10)

Подстановка в (1.2.10) числовых значений
дает

.

Задача 3. Найти минимальную толщину
пленки с показателем преломления
,
при которой свет с длиной волныиспытывает максимальное отражение, а
свет с длиной волныне отражается совсем. Угол падения света.

Решение

Запишем условия максимумов и минимумов
интенсивности света, отраженного от
тонкой пленки для первой и второй волны
соответственно

(1.2.11)

,
(1.2.12)

где
и— числа натурального ряда,— толщина пленки. Так как левые части
уравнений (1.2.11), (1.2.12) одинаковы, можно
приравнять их правые части, что после
подстановки значений длин волн позволяет
получить уравнение, связывающееи

.
(1.2.13)

Левая часть уравнения (1.2.13) кратна 8, а
наименьшее натуральное значение
,
при котором это условие будет выполняться
для правой части, равно 4, следовательно,
условиям задачи отвечает такое решение
этого уравнения:.
Подстановка любого из этих значений в
формулы (1.2.11), (1.2.12) позволяет найти
минимальную толщину пленки, например,

.

Задача 4. Между точечным источником
света и экраном поместили диафрагму с
круглым отверстием, радиус которого
можно менять в процессе опыта. Расстояния
от диафрагмы до источника и экрана равны
соответственнои.
Определить длину волны света, если
максимум освещенности в центре
дифракционной картины на экране
наблюдается прии следующий максимум при.

Решение

Поскольку в центре дифракционной картины
наблюдаются максимумы освещенности,
то для данного положения экрана отверстие
в диафрагме открывает в обоих случаях
нечетное число зон Френеля. Предположим,
что в первом случае открыто
зон Френеля, тогда во втором случае
открытыми окажутсязоны. Запишем формулу радиуса зон Френеля
для сферической волны (источник света
– точечный) для этих двух случаев:

,.
(1.2.14)

Вычитая первое уравнение (1.2.14) из второго
и решая полученное уравнение относительно
длины волны, находим

.

Задача 5. Определить длину волны
монохроматического света, падающего
нормально на дифракционную решетку с
периодом
,
если угол между направлениями на
дифракционные максимумы первого и
второго порядка составляет.

Решение

Традиционное в подобных задачах
приближение малых углов дифракции с
учетом значения угла в условии использовать
неправомерно, поэтому будем решать
задачу без помощи этого приближения.
Запишем условия дифракционных максимумов
первого и второго порядка при дифракции
на решетке

,.
(1.2.15)

Решая уравнения (1.2.15) относительно углов
и находя разность углов дифракции,
получаем

,

откуда при помощи тождества

следует

.
(1.2.16)

Таким образом, для определения длины
волны необходимо решить уравнение

.
(1.2.17)

Обозначим выражение в скобках в (1.2.17)
через
,
возведем его в квадрат и применим формулы
(1.2.15) и основное тригонометрическое
тождество. В результате получим

.
(1.2.18)

С учетом соотношения
преобразуем (1.2.18) к виду

.

Таким образом,
и решение задачи записывается в виде

.

Задача 6. Узкий пучок рентгеновских
лучей падает под углом скольжения
на
естественную грань монокристалла,
плотность которого.
При зеркальном отражении от этой грани
образуется максимум второго порядка.
Определить длину волны излучения.

Решение

Воспользуемся условием Вульфа – Брэггов,
которое определяет дифракционные
максимумы при отражении рентгеновского
излучения от кристаллографических
плоскостей

.
(1.2.19)

Для определения расстояния между
плоскостями кристалла учтем, что кристалл
поваренной соли имеет ионную структура
с кубической элементарной ячейкой. В
такой ячейке каждый ион принадлежит
восьми соседним ячейка, следовательно,
одной ячейке принадлежит половина иона
натрия и половина иона хлора, то есть
половина молекулы поваренной соли. Так
как масса молекулы поваренной соли
может быть найдена по формуле

,

где
— молярная масса поваренной соли, то для
плотности кристалла получаем выражение

,

откуда находим длину ребра элементарной
ячейки (расстояние между кристаллографическими
плоскостями)

.
(1.2.20)

Подстановка (1.2.20) в (1.2.19) приводит к
расчетной формуле длины волны излучения

.

Задача 7. На пути частично поляризованного
пучка поместили николь. При повороте
николя на угол
из положения, соответствующего максимуму
пропускания света, интенсивность
прошедшего света уменьшилась враза. Найти степень поляризации падающего
света.

Решение

Падающий на николь свет можно представить
в виде смеси естественного и
плоскополяризованного. При любом
положении николя интенсивность прошедшего
через него естественного света будет
уменьшаться в два раза, а интенсивность
поляризованной составляющей буде
подчиняться закону Малюса. Тогда для
начального положения николя получаем

,

а для конечного

.

Используя условие
,
получаем для отношения интенсивностей
естественной и поляризованной составляющей
формулу

.
(1.2.21)

Очевидно, что максимальная интенсивность
света, прошедшего через николь

,
(1.2.22)

а минимальная

.
(1.2.23)

Подставляя (1.2.22), (1.2.23) в формулу степени
поляризации, получаем

,

откуда с учетом (1.2.21) следует

.

Задача 8. Свет проходит через систему
из двух скрещенных николей, между
которыми расположена кварцевая пластинка,
вырезанная перпендикулярно к оптической
оси. Определить минимальную толщину
пластинки, при которой свет с длиной
волны
будет полностью задерживаться этой
системой, а свет с длиной волны— пропускаться наполовину. Удельное
вращение для этих длин волн равно
соответственнои.

Решение

Будем предполагать николи идеальными
и пренебрежем поглощением света в
пластинке. Согласно условию плоскости
пропускания николей образуют друг с
другом прямой угол, поэтому для первой
длины волны толщина пластинки должна
быть такой, чтобы повернуть плоскость
поляризации света, прошедшего через
первый николь, на угол

,
(1.2.24)

так как в это случае плоскость колебаний
светового вектора будет перпендикулярна
плоскости пропускания второго николя.
Для второй длины волны поворот плоскости
поляризации должен быть на
меньше, так как в этом случае плоскость
поляризации волны, прошедшей через
первый николь, совпадет с плоскостью
пропускания второго николя, и она
полностью пройдет через него, то есть

(1.2.25)

(число
в формулах (1.2.24), (1.2.25) является натуральным).

Применяя формулу угла поворота плоскости
поляризации для двух данных волн,
получаем

,

откуда следует

.

Задача 9. Монохроматический пучок света
падает нормально на поверхность
плоскопараллельной пластины толщины
.
Показатель поглощения вещества пластины
линейно изменяется вдоль нормали к ее
поверхности от значениядо.
Коэффициент отражения от каждой
поверхности пластины равен.
Пренебрегая вторичными отражениями,
определить коэффициент пропускания
такой пластины.

Решение

Обозначим интенсивность света, падающего
на пластину через
,
тогда интенсивность света после отражения
от передней поверхности пластины
составит

.
(1.2.26)

Рассмотрим теперь распространение
света внутри пластины. Согласно условию
изменение интенсивности света, прошедшего
расстояние
внутри пластины составит

.
(1.2.27)

Так как закон изменения
— линейный, то с учетом данных условия
можно получить

.
(1.2.28)

Таким образом, для решения задачи о
распространении волны внутри вещества
необходимо решить уравнение

.
(1.2.29)

с начальным условием

.
(1.2.30)

Уравнение (1.2.29) легко интегрируется при
помощи разделения переменных, что дает

.
(1.2.31)

Подстановка в (1.2.31) начального условия
(1.2.30) позволяет найти
,
а подстановкадает интенсивность света перед отражением
на задней поверхности пластины

.
(1.2.32)

Учитывая отражение на задней поверхности
пластины, получаем

.
(1.2.33)

Объединяя формулы (1.2.26), (1.2.32), (1.2.33),
находим коэффициент пропускания пластины

.

Задача 10. По некоторой прямой движутся
в одном направлении наблюдатель со
скоростью
и впереди него источник монохроматического
света со скоростью.
Источник излучает свет на частоте.
Найти частоту света, которую зафиксирует
наблюдатель.

Решение

Определим относительную скорость
удаления источника от наблюдателя,
воспользовавшись соотношением специальной
теории относительности

.
(1.2.34)

В данном случае скорость объекта
(источника) в неподвижной системе отсчета
равна,
скорость подвижной системы(наблюдателя) относительно неподвижной
равна,
тогда скорость источника относительно
наблюдателя будет равна

.

Тогда
и подстановка этого значения в формулу
эффекта Доплера с учетомдает

.

Задача 11. Определить минимальную
кинетическую энергию, которой должен
обладать электрон, чтобы в среде с
показателем преломления
возникло черенковское излучение.

Решение

Воспользуемся условием излучения
Вавилова – Черенкова
,
из которого следует

.
(1.2.35)

Подставляя выражение (1.2.35) в формулу
кинетической энергии специальной теории
относительности, получаем

.
(1.2.36)

Подстановка в (1.2.36) числовых значений
дает

.

32

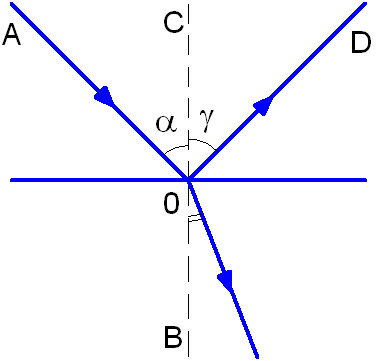
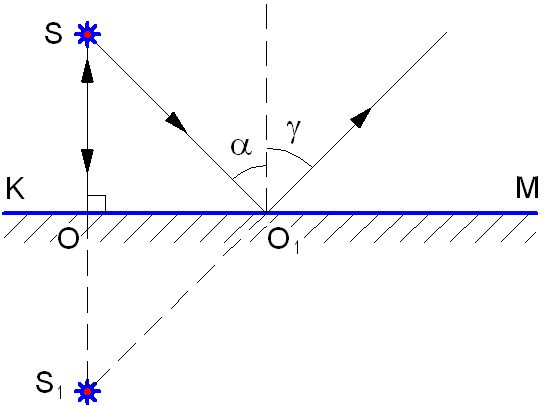
На границе раздела двух различных сред, если эта граница раздела значительно превышает длину волны, происходит изменение направления распространения света: часть световой энергии возвращается в первую среду, то есть отражается, а часть проникает во вторую среду и при этом преломляется. Луч АО носит название падающий луч, а луч OD – отраженный луч (см. рис. 1.3). Взаимное расположение этих лучей определяют законы отражения и преломления света.

Рис. 1.3. Отражение и преломление света.

Угол α между падающим лучом и перпендикуляром к границе раздела, восстановленным к поверхности в точке падения луча, носит название угол падения.

Угол γ между отражённым лучом и тем же перпендикуляром, носит название угол отражения.

Каждая среда в определённой степени (то есть по своему) отражает и поглощает световое излучение. Величина, которая характеризует отражательную способность поверхности вещества, называется коэффициент отражения. Коэффициент отражения показывает, какую часть принесённой излучением на поверхность тела энергии составляет энергия, унесённая от этой поверхности отражённым излучением. Этот коэффициент зависит от многих причин, например, от состава излучения и от угла падения. Свет полностью отражается от тонкой плёнки серебра или жидкой ртути, нанесённой на лист стекла.

Законы отражения света

1	Падающий луч, отражающий луч и перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости.
2	Угол отражения γ равен углу падения α: γ = α

Законы отражения света были найдены экспериментально ещё в 3 веке до нашей эры древнегреческим учёным Евклидом. Также эти законы могут быть получены как следствие принципа Гюйгенса, согласно которому каждая точка среды, до которой дошло возмущение, является источником вторичных волн. Волновая поверхность (фронт волны) в следующий момент представляет собой касательную поверхность ко всем вторичным волнам. Принцип Гюйгенса является чисто геометрическим.

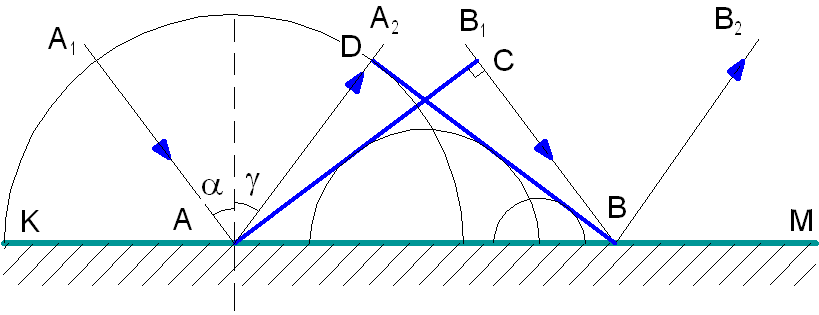
На гладкую отражательную поверхность КМ (рис. 1.4) падает плоская волна, то есть волна, волновые поверхности которой представляют собой полоски.

Рис. 1.4. Построение Гюйгенса.

А₁А и В₁В – лучи падающей волны, АС – волновая поверхность этой волны (или фронт волны).

Пока фронт волны из точки С переместится за время t в точку В, из точки А распространится вторичная волна по полусфере на расстояние AD = CB, так как AD = vt и CB = vt, где v – скорость распространения волны.

Волновая поверхность отражённой волны – это прямая BD, касательная к полусферам. Дальше волновая поверхность будет двигаться параллельно самой себе по направлению отражённых лучей АА₂ и ВВ₂.

Прямоугольные треугольники ΔАСВ и ΔADB имеют общую гипотенузу АВ и равные катеты AD = CB. Следовательно, они равны.

Углы САВ = = α и DBA = = γ равны, потому что это углы со взаимно перпендикулярными сторонами. А из равенства треугольников следует, что α = γ.

Из построения Гюйгенса также следует, что падающий и отражённый лучи лежат в одной плоскости с перпендикуляром к поверхности, восстановленным в точке падения луча.

Законы отражения справедливы при обратном направлении хода световых лучей. В следствие обратимости хода световых лучей имеем, что луч, распространяющийся по пути отражённого, отражается по пути падающего.

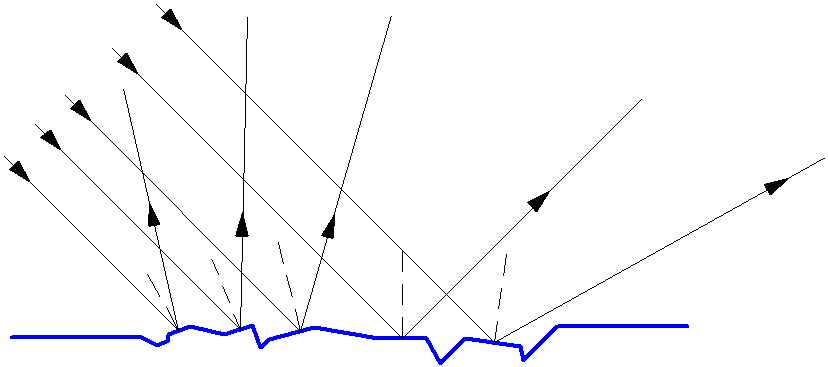
Большинство тел лишь отражают падающее на них излучение, не являясь при этом источником света. Освещённые предметы видны со всех сторон, так как от их поверхности свет отражается в разных направлениях, рассеиваясь. Это явление называется диффузное отражение или рассеянное отражение. Диффузное отражение света (рис. 1.5) происходит от всех шероховатых поверхностей. Для определения хода отражённого луча такой поверхности в точке падения луча проводится плоскость, касательная к поверхности, и по отношению к этой плоскости строятся углы падения и отражения.

Рис. 1.5. Диффузное отражение света.

Например, 85% белого света отражается от поверхности снега, 75% — от белой бумаги, 0,5% — от чёрного бархата. Диффузное отражение света не вызывает неприятных ощущений в глазу человека, в отличие от зеркального.

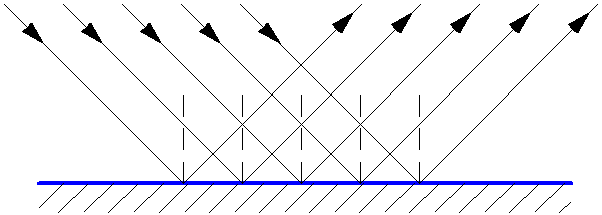
Зеркальное отражение света – это когда падающие на гладкую поверхность под определённым углом лучи света отражаются преимущественно в одном направлении (рис. 1.6). Отражающая поверхность в этом случае называется зеркало (или зеркальная поверхность). Зеркальные поверхности можно считать оптически гладкими, если размеры неровностей и неоднородностей на них не превышают длины световой волны (меньше 1 мкм). Для таких поверхностей выполняется закон отражения света.

Рис. 1.6. Зеркальное отражение света.

Плоское зеркало – это зеркало, отражающая поверхность которого представляет собой плоскость. Плоское зеркало даёт возможность видеть предметы, находящиеся перед ним, причём эти предметы кажутся расположенными за зеркальной плоскостью. В геометрической оптике каждая точка источника света S считается центром расходящегося пучка лучей (рис. 1.7). Такой пучок лучей называется гомоцентрическим. Изображением точки S в оптическом устройстве называется центр S’ гомоцентрического отражённого и преломлённого пучка лучей в различных средах. Если свет, рассеянный поверхностями различных тел, попадает на плоское зеркало, а затем, отражаясь от него, падает в глаз наблюдателя, то в зеркале видны изображения этих тел.

Рис. 1.7. Изображение, возникающее с помощью плоского зеркала.

Изображение S’ называется действительным, если в точке S’ пересекаются сами отражённые (преломлённые) лучи пучка. Изображение S’ называется мнимым, если в ней пересекаются не сами отражённые (преломлённые) лучи, а их продолжения. Световая энергия в эту точку не поступает. На рис. 1.7 представлено изображение светящейся точки S, возникающее с помощью плоского зеркала.

Луч SO падает на зеркало КМ под углом 0°, следовательно, угол отражения равен 0°, и данный луч после отражения идёт по пути OS. Из всего множества попадающих из точки S лучей на плоское зеркало выделим луч SO₁.

Луч SO₁ падает на зеркало под углом α и отражается под углом γ (α = γ). Если продолжить отражённые лучи за зеркало, то они сойдутся в точке S₁, которая является мнимым изображением точки S в плоском зеркале. Таким образом, человеку кажется, что лучи выходят из точки S₁, хотя на самом деле лучей, выходящих их этой точки и попадающих в глаз, не существует. Изображение точки S₁расположено симметрично самой светящейся точке S относительно зеркала КМ. Докажем это.

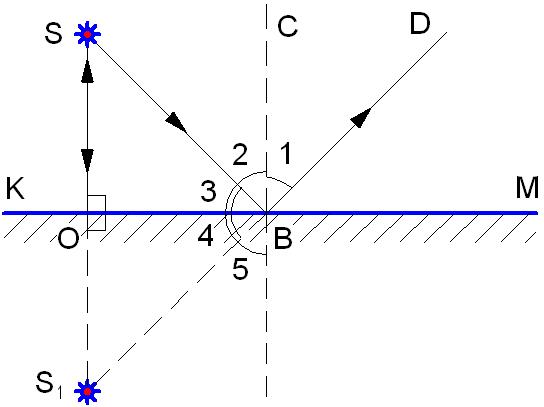
Луч SB, падающий на зеркало под углом 2 (рис. 1.8), согласно закону отражения света отражается под углом 1 = 2.

Рис. 1.8. Отражение от плоского зеркала.

Из рис. 1.8 видно, что углы 1 и 5 равны – как вертикальные. Суммы углов 2 + 3 = 5 + 4 = 90°. Следовательно, углы 3 = 4 и 2 = 5.

Прямоугольные треугольники ΔSOB и ΔS₁OB имеют общий катет ОВ и равные острые углы 3 и 4, следовательно, эти треугольники равны по стороне и двум прилежащим к катету углам. Это означает, что SO = OS₁, то есть точка S₁ расположена симметрично точке S относительно зеркала.

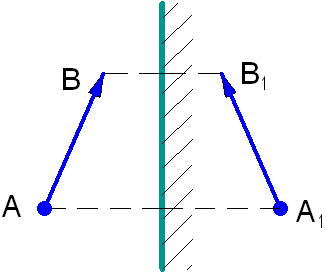
Для того чтобы найти изображение предмета АВ в плоском зеркале, достаточно опустить перпендикуляры из крайних точек предмета на зеркало и, продолжив их за пределы зеркала, отложить за ним расстояние, равное расстоянию от зеркала до крайней точки предмета (рис. 1.9). Это изображение будет мнимым и в натуральную величину. Размеры и взаимное расположение предметов сохраняются, но при этом в зеркале левая и правая стороны у изображения меняются местами по сравнению с самим предметом. Параллельность падающих на плоское зеркало световых лучей после отражения также не нарушается.

Рис. 1.9. Изображение предмета в плоском зеркале.

В технике часто применяют зеркала со сложной кривой отражающей поверхностью, например, сферические зеркала. Сферическое зеркало – это поверхность тела, имеющая форму сферического сегмента и зеркально отражающая свет. Параллельность лучей при отражении от таких поверхностей нарушается. Зеркало называют вогнутым, если лучи отражаются от внутренней поверхности сферического сегмента. Параллельные световые лучи после отражения от такой поверхности собираются в одну точку, поэтому вогнутое зеркало называют собирающим. Если лучи отражаются от наружной поверхности зеркала, то оно будет выпуклым. Параллельные световые лучи рассеиваются в разные стороны, поэтому выпуклое зеркало называют рассеивающим.

Содержание:

Отражение света:

Можем ли мы увидеть друг друга темной ночью? А если мы приблизимся к светящемуся фонарю? Именно благодаря отраженному свету мы видим предметы, различаем цвет одежды, любуемся картиной художника. Известно, что свет отражается от самых разных предметов. Например, и от белой стенки, и от зеркала. Но почему только в зеркале мы видим свое изображение? И почему мы при этом почти не видим самого зеркала и в магазине можем ошибочно протянуть руку не к яблоку, а к его изображению в зеркальной витрине?

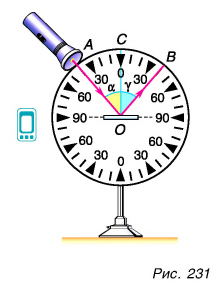
Каким бывает отражение света? Какими законами оно описывается? Проведем опыт. На оптическом диске (рис. 231), представляющем собой круг с делениями, укрепим зеркало. Направим из осветителя (лампочка в футляре с отверстием) на зеркало пучок света (луч АО).

От зеркала (гладкая отполированная поверхность) световой луч АО практически полностью отразится (луч ОВ). Опустим в точку падения луча АО перпендикуляр СО к поверхности зеркала. Угол между падающим лучом и перпендикуляром, проведенным в точку падения, называется углом падения. Обозначим этот угол буквой

Угол, образованный отраженным лучом и тем же перпендикуляром, называется углом отражения. Обозначим его буквой 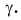А теперь сравним эти углы. Из опыта видно, что углы отражения и падения равны:

Увеличим угол падения а, повернув осветитель влево. Угол отражения 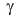 тоже увеличится (рис. 232, а). Ио по-прежнему

То, что мы на оптическом диске видим не только падающий луч, но и отраженный, говорит о том, что они оба лежат в одной плоскости — плоскости диска.

На основании результатов опыта можно сформулировать законы отражения света.

1.  Луч падающий, луч отраженный и перпендикуляр к отражающей поверхности, проведенный в точку падения, лежат в одной плоскости.
2. Угол отражения равен углу падения.

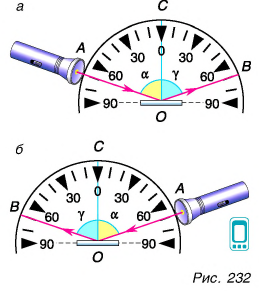
А теперь по направлению отраженного луча (см. рис. 232, а) пустим луч света от осветителя (см. рис. 232, б). Он отразится от зеркала и пойдет но направлению, по которому в предыдущем опыте шел падающий луч. Лучи и углы поменялись местами. Это свойство отраженного и падающего лучей называют обратимостью (или взаимностью) световых лучей.

Одинаково ли отражают свет различные поверхности

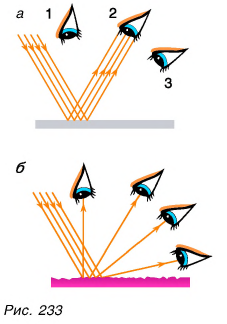
Пусть на поверхность зеркала падают направленные лучи света. После отражения от него свет попадает в глаз только тогда, когда глаз находится в положении 2 (рис. 233, а). Если он будет находиться в положениях 1 или 3, то отраженные лучи в глаз не попадут. В этом особенность зеркал. Зеркально отражает свет поверхность воды (рис. 234).

А если поверхность шероховатая? Направленные лучи света отражаются в различных направлениях (рис. 233, б). Такое отражение называется диффузным (иногда говорят: рассеянное отражение).

В случае диффузного отражения поверхность видна при любом положении глаза, так как в него попадают отраженные лучи. Шероховатыми поверхностями, отражающими свет диффузно, являются поверхности стен, потолков, тканей, ваты, снега (рис. 235), кожи лица, рук и т. д. Только благодаря диффузному отражению мы видим предметы, которые сами не излучают свет.

Диффузно отражающие поверхности называют матовыми, зеркально отражающие — блестящими.

Приведите сами примеры блестящих и матовых поверхностей. Чем больше света отражает поверхность (чем меньше поглощает),

тем она кажется светлее. Белый лист бумаги отражает света больше, чем серый картон, но этот же картон отражает света больше, чем черный бархат.

Главные выводы:

1. Отраженный луч лежит в той же плоскости, что и падающий луч, и перпендикуляр к поверхности, проведенный в точку падения.
2. Угол отражения светового луча равен углу падения.
3. Световые лучи обладают свойством обратимости.
4. Зеркальные поверхности отражают свет направленно, шероховатые (матовые) — диффузно, т. е. по всем направлениям.

Пример решения задачи:

Солнечные лучи образуют с горизонтом угол 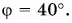Как надо расположить плоское зеркало, чтобы отраженные лучи пошли вертикально вверх?
Дано:

Решение:

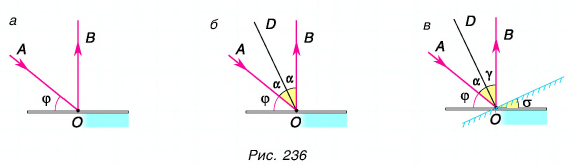
Проведем отраженный луч ОВ (рис. 236, а). Угол АОВ, равный 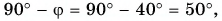— это сумма двух равных углов (падения и отражения от зеркала):

Проведя биссектрису OD этого угла, мы получим положение перпендикуляра к зеркалу (рис. 236, б). Изобразим и само зеркало (рис. 236, в). Из чертежа видно, что искомый угол

Ответ: 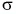 = 25°.

Световые явления и скорость распространения света

Из пяти органов чувств больше всего информации об окружающем мире дает нам зрение. Но видеть мир вокруг мы можем только потому, что нам в глаза попадает свет. Итак, начинаем изучение световых, или оптических (греч. optikos — зрительный), явлений, то есть явлений, связанных со светом.

Со световыми явлениями мы сталкиваемся каждый день, ведь они являются частью природной среды, в которой мы живем.

Некоторые оптические явления кажутся нам настоящим чудом, например миражи в пустыне, полярные сияния. Но согласитесь, что и более привычные световые явления: блеск капельки росы в солнечном луче, лунная дорожка на воде, семицветный мост радуги после летнего дождя, молния в грозовых облаках, мерцание звезд в ночном небе — тоже удивительны, ведь они делают мир вокруг нас прекрасным, полным волшебной красоты и гармонии.

Что такое источники света

Источники света — это физические тела, частицы (атомы, молекулы, ионы) которых излучают свет.

Посмотрите вокруг, обратитесь к своему опыту — и вы, без сомнения, назовете много источников света: звезда, вспышка молнии, пламя свечи, лампа, монитор компьютера и т. д. (см., например, рис. 9.1). Свет могут излучать и организмы: светлячки — яркие точки света, которые можно увидеть теплыми летними ночами в лесной траве, некоторые морские животные, радиолярии и др.

В ясную лунную ночь можно достаточно хорошо видеть предметы, освещенные лунным светом. Однако Луну нельзя считать источником света, ведь она не излучает, а только отражает свет, идущий от Солнца.

Рис. 9.1. Некоторые источники света

Различаем источники света:

В зависимости от происхождения различают естественные и искусственные (созданные человеком) источники света.

К естественным источникам света относятся Солнце и звезды, раскаленная лава и полярное сияние, некоторые живые организмы (глубоководная каракатица, светящиеся бактерии, светлячки) и т. д.

Еще в древности люди начали создавать искусственные источники света. Сначала это были костры, лучины, позже — факелы, свечи, масляные и керосиновые лампы; в конце XIX в. была изобретена электрическая лампа. Сегодня разные виды электрических ламп используются повсюду (рис. 9.2, 9.3).

Рис. 9.2. Мощные источники искусственного света — галогенные лампы в фарах современного автомобиля

Рис. 9.3. Сигналы современных светофоров хорошо заметны даже при ярком солнце. В таких светофорах лампы накаливания заменены светодиодными

Различают также тепловые и люминесцентные источники света.

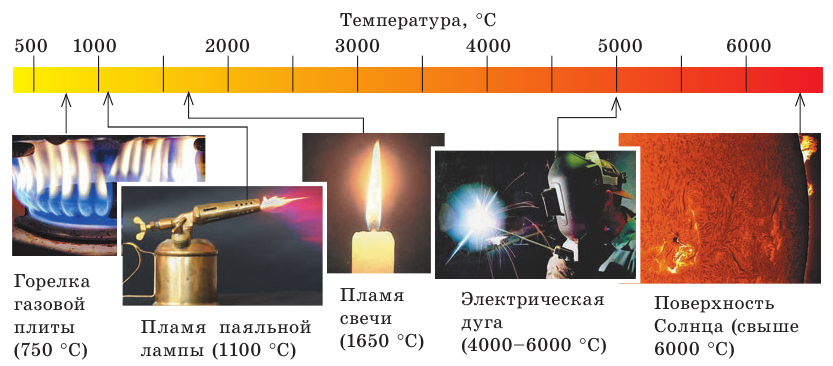
Тепловые источники излучают свет благодаря тому, что имеют высокую температуру (рис. 9.4).

Для свечения люминесцентных источников света не нужна высокая температура: световое излучение может быть достаточно интенсивным, а источник при этом остается относительно холодным. Примерами люминесцентных источников света могут быть полярное сияние и морской планктон, экран телефона, лампа дневного света, покрытый люминесцентной краской дорожный знак и т. д.

Рис. 9.4. Некоторые тепловые источники света

Точечные и протяженные источники света

Источник света, который излучает свет одинаково во всех направлениях и размерами которого, учитывая расстояние до места наблюдения, можно пренебречь, называют точечным источником света.

Наглядный пример точечных источников света — звезды: мы наблюдаем их с Земли, то есть с расстояния, которое в миллионы раз превышает размеры самих звезд.

Источники света, которые не являются точечными, называют протяженными источниками света. В большинстве случаев мы имеем дело именно с протяженными источниками света. Это и лампа дневного света, и экран мобильного телефона, и пламя свечи, и огонь костра.

В зависимости от условий один и тот же источник света может считаться как протяженным, так и точечным.

Характеризуем приемники света

Приемники света — это устройства, которые изменяют свои свойства под действием света и с помощью которых можно выявить световое излучение.

Приемники света бывают искусственные и естественные. В любом приемнике света энергия светового излучения преобразуется в другие виды энергии — тепловую, которая проявляется в нагревании тел, поглощающих свет, электрическую, химическую и даже механическую. В результате таких преобразований приемники определенным образом реагируют на свет или его изменение.

Например, некоторые системы охраны работают на фотоэлектрических приемниках света — фотоэлементах. Пучки света, пронизывающие пространство вокруг охраняемого объекта, направлены на фотоэлементы (рис. 9.6). Если перекрыть один из таких пучков, фотоэлемент не получит световую энергию и сразу об этом «сообщит».

Рис. 9.6. В современных системах охраны используют чувствительные фотоэлементы

В солнечных батареях фотоэлементы преобразуют энергию света в электрическую энергию. Многие современные солнечные электростанции — это большие «энергетические поля» из солнечных батарей.

Долгое время для получения фотографий применяли только фотохимические приемники света (фотопленку, фотобумагу), в которых в результате действия света происходят определенные химические реакции (рис. 9.7).

Рис. 9.7. Фотопленка и фотобумага — фотохимические приемники света

В современных цифровых фотоаппаратах вместо фотопленки используют матрицу, состоящую из большого количества фотоэлементов. Каждый из таких элементов принимает «свою» часть светового потока, преобразует ее в электрический сигнал и передает этот сигнал в определенное место экрана.

Естественными приемниками света являются глаза живых существ (рис. 9.8). Под воздействием света в сетчатке глаза происходят определенные химические реакции, возникают нервные импульсы, вследствие чего мозг формирует представление об окружающем мире.

Рис. 9.8. Глаза живых существ — это естественные приемники света

Скорость распространения света

Когда вы смотрите на звездное небо, то вряд ли догадываетесь, что некоторые звезды уже погасли. Более того, несколько поколений наших предков любовались этими же звездами, а эти звезды не существовали уже тогда! Как может быть так, что свет от звезды есть, а самой звезды нет?

Дело в том, что свет распространяется в пространстве с конечной скоростью. Скорость с распространения света огромна, и в вакууме она составляет около трехсот тысяч километров в секунду:

Свет преодолевает многокилометровые расстояния за тысячные доли секунды. Именно поэтому, если расстояние от источника света до приемника невелико, кажется, что свет распространяется мгновенно. А вот от далеких звезд свет идет к нам тысячи и миллионы лет.

При решении задач мы будем использовать приблизительное значение скорости распространения света в вакууме:

От ближайшей к нам звезды Альфа Центавра свет идет к Земле почти 4 года. Значит, когда мы смотрим на эту звезду, на самом деле видим, какой она была 4 года назад. А ведь существуют галактики, удаленные от нас на миллионы световых лет (то есть свет идет к ним миллионы лет!). Представьте себе, что в такой галактике существует высокотехнологичная цивилизация. Тогда получается, что они видят нашу планету такой, какой она была во времена динозавров!

Подводим итоги:

Физические тела, атомы и молекулы которых излучают свет, называют источниками света. Источники света бывают тепловые и люминесцентные; естественные и искусственные; точечные и протяженные. Например, полярное сияние — естественный протяженный люминесцентный источник света.

Устройства, которые изменяют свои параметры в результате действия света и с помощью которых можно выявить световое излучение, называют приемниками света. В приемниках света энергия светового излучения преобразуется в другие виды энергии. Органы зрения живых существ — естественные приемники света.

Свет распространяется в пространстве с конечной скоростью. Скорость распространения света в вакууме составляет примерно:

Световой луч и световой пучок. Закон прямолинейного распространения света. Солнечное и лунное затмения

Оказывается, когда вы играете в прятки или пускаете «солнечных зайчиков», то пользуетесь законом прямолинейного распространения света. Выясним, в чем заключается этот закон и какие явления он объясняет.

Для наблюдения световых пучков нам не нужно никакого специального оборудования (рис. 10.1). Достаточно, например, или открыть дверь в темный коридор из освещенной комнаты, или включить в темноте фонарик, или в ясный солнечный день неплотно сдвинуть в комнате шторы. Пучки света в первом случае падают на пол через дверной проем; во втором случае свет направляется рефлектором фонарика; в последнем случае пучки света попадают в комнату через щель между шторами.

Рис. 10.1. Пучки солнечного света, пробивающиеся сквозь тучи

В реальной жизни мы имеем дело только с пучками света. При этом для нас привычно, когда говорят: луч солнца, луч прожектора, зеленый луч и т. п. На самом деле, с точки зрения геометрической оптики, которую вы будете изучать в этом учебном году, правильно было бы говорить: пучок солнечных лучей, пучок зеленых лучей и т. д. А вот для схематического изображения световых пучков используют световые лучи (см. рис. 10.2).

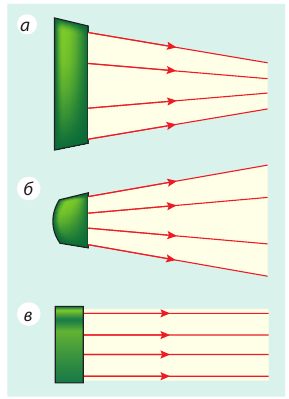
Рис. 10.2. Световой пучок — это совокупность световых лучей. Световые пучки: а — сходящийся; б — расходящийся; в — параллельный

Световой луч — это линия, указывающая направление распространения энергии света.

Таким образом, если далее в тексте будут встречаться фразы, словосочетания типа «луч света падает», «преломление луча» и т. п., следует иметь в виду, что речь идет о пучке света, направление которого задано данным лучом.

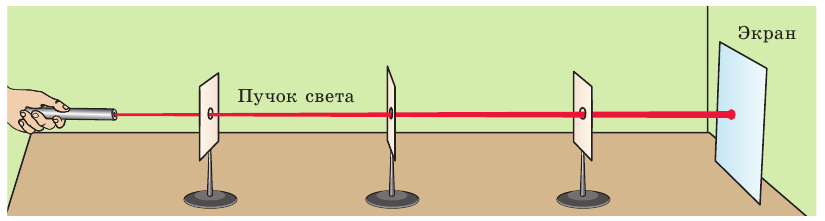
Рис. 10.3. Опыт, демонстрирующий прямолинейное распространение света

Прямолинейность распространения света

Проведем простой опыт. Расположим источник света, несколько листов картона с отверстиями (диаметром примерно 5 мм) и экран так, чтобы на экране появилось пятно света (рис. 10.3). Если теперь взять, например, спицу, она легко пройдет сквозь все отверстия, то есть окажется, что отверстия расположены на одной прямой.

Данный опыт демонстрирует закон прямолинейного распространения света

B прозрачной однородной среде свет распространяется прямолинейно.

Об этом законе еще более 2500 лет назад писал древнегреческий ученый Евклид. В геометрии понятия луча и прямой линии возникли на основе представления о световых лучах.

Полная тень и полутень

Прямолинейностью распространения света можно объяснить тот факт, что любое непрозрачное тело, освещенное источником света, отбрасывает тень.

Если источник света точечный, тень от предмета будет четкой. В данном случае образуется только полная тень (рис. 10.4).

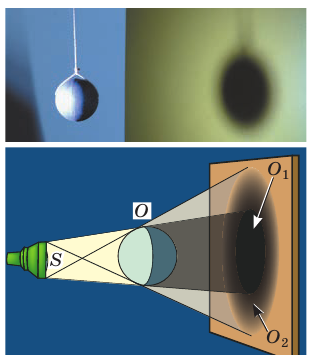
Рис. 10.5. Образование полной тени O₁ и полутени O2 от предмета О, освещенного протяженным источником света S

Полная тень — это область пространства, в которую не попадает свет от источника.

Если тело освещено протяженным источником света, образуется тень с нечеткими контурами, то есть образуется не только полная тень, а еще и полутень (рис. 10.5).

Полутень — это область пространства, освещенная некоторыми из имеющихся точечных источников света или частью протяженного источника.

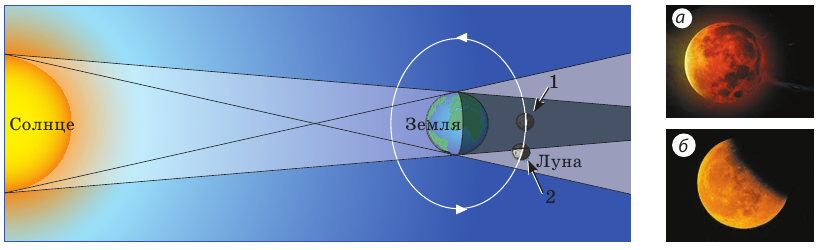
Образование полной тени и полутени в космических масштабах мы наблюдаем во время солнечных и лунных затмений.

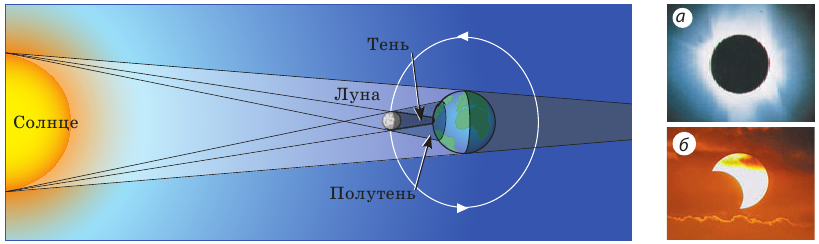
Дело в том, что из-за вращения Луны вокруг Земли бывает так, что Луна, Солнце и Земля оказываются на одной прямой. Если при этом Луна расположена между Солнцем и Землей, то тень от Луны падает на Землю, — на Земле наблюдается солнечное затмение (рис. 10.7). В тех местах Земли, на которые упала полная тень Луны, наблюдается полное солнечное затмение, а в местах полутени — частичное солнечное затмение. За год на Земле наблюдается 2-5 солнечных затмений.

Когда Луна, вращаясь вокруг Земли, попадает в зону тени, которую отбрасывает Земля, наступает лунное затмение (рис. 10.8). За год на Земле наблюдается 2-4 лунных затмения.

Рис. 10.7. Солнечное затмение: а — полное (в области полной тени), б — частичное (в области полутени)

Рис. 10.8. Лунное затмение: а — полное (Луна в положении 1); б— частичное (Луна в положении 2).

• Заказать решение задач по физике

Пример №1

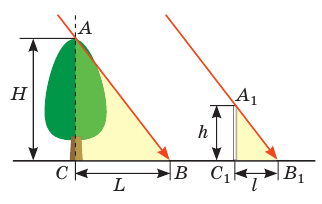
В солнечный день длина тени от вертикально поставленной метровой линейки равна 24 см, а длина тени от дерева — 3,6 м. Определите высоту дерева.

Анализ физической проблемы. Для решения задачи воспользуемся законом прямолинейного распространения света. Выполним пояснительный рисунок; отметим, что пучок света, идущий от Солнца, является параллельным.

Дано:

Найти:

Поиск математической модели, решение

Из рисунка видим, что

Из подобия треугольников имеем:

Проверим единицу, найдем значение искомой величины:

Ответ:

Подводим итоги:

В прозрачной однородной среде свет распространяется прямолинейно. Линию, указывающую направление распространения энергии света, называют световым лучом.

Из-за того что свет распространяется прямолинейно, непрозрачные тела отбрасывают тень (полную тень, полутень).

Полная тень — область пространства, в которую не попадает свет от источника (источников) света. Полутень — область пространства, освещенная некоторыми из имеющихся точечных источников света или частью протяженного источника.

Во время солнечных и лунных затмений наблюдается образование тени и полутени в космических масштабах.

Первыми приборами для измерения времени были солнечные часы. Действие солнечных часов основано на том, что длина и расположение тени от освещаемого солнцем предмета изменяются в течение дня.

Любые солнечные часы состоят из кадрана (плоская поверхность с нанесенным на нее циферблатом) и гномона (небольшой стержень из металла, пластика или дерева, закрепленный на кадране).

Отражение света

Большинство окружающих вас объектов: дома, деревья, ваши одноклассники и т. д. — не являются источниками света. Но вы их видите. Ответ на вопрос «Почему так?» вы найдете в этом параграфе.

Почему мы видим тела, не являющиеся источниками света

Вы уже знаете, что в однородной прозрачной среде свет распространяется прямолинейно. А что происходит, если на пути пучка света находится какое-то тело? Часть света может пройти сквозь тело, если оно прозрачное, часть поглотится, а часть обязательно отразится от тела. Некоторые отраженные лучи попадут нам в глаза, и мы увидим это тело (рис. 11.1).

Рис. 11.1. При отсутствии источника света невозможно ничего увидеть. Если есть источник света, мы видим не только сам источник, но и предметы, которые отражают свет, идущий от источника

Законы отражения света

Чтобы установить законы отражения света, воспользуемся специальным прибором — оптической шайбой*. В центре шайбы закрепим зеркало и направим на него узкий пучок света так, чтобы он давал на поверхности шайбы светлую полосу. Видим, что пучок света, отраженный от зеркала, тоже дает светлую полосу на поверхности шайбы (см. рис. 11.2).

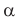
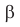
Рис. 11.2. Установление законов отражения света с помощью оптической шайбы: — угол падения; — угол отражения

Направление падающего пучка света зададим лучом СО (рис. 11.2). Этот луч называют падающим лучом. Направление отраженного пучка света зададим лучом ОК. Этот луч называют отраженным лучом.

Из точки О падения луча проведем перпендикуляр ОВ к поверхности зеркала. Обратим внимание на то, что падающий луч, отраженный луч и перпендикуляр лежат в одной плоскости, — в плоскости поверхности шайбы.

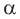
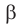
Угол между падающим лучом и перпендикуляром, проведенным из точки падения, называют углом падения; угол между отраженным лучом и данным перпендикуляром называют углом отражения.

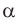
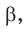
Измерив углы и можно убедиться, что они равны.

* Оптическая шайба — белый диск с нанесенными делениями; на краю диска установлен осветитель. отражения

Рис. 11.3. С изменением угла падения света изменяется и угол отражения. Угол отражения всегда равен углу падения

Если перемещать источник света по краю диска, угол падения светового пучка будет изменяться и соответственно будет изменяться угол отражения, причем каждый раз угол падения и угол отражения света будут равны (рис. 11.3). Итак, мы установили законы отражения света:

1. Луч падающий, луч отраженный и перпендикуляр к поверхности отражения,проведенный из точки падения луча, лежат в одной плоскости.
2. Угол отражения равен углу падения:

Законы отражения света установил древнегреческий ученый Евклид еще в III в. до н. э.

С помощью зеркала на оптической шайбе можно продемонстрировать также обратимость световых лучей: если падающий луч направить по пути отраженного, то отраженный луч пойдет по пути падающего (рис. 11.5).

Рис. 11.5. Демонстрация обратимости световых лучей: отраженный луч идет по пути падающего луча

Изображение в плоском зеркале:

Рассмотрим, как создается изображение в плоском зеркале (рис. 11.6).

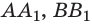
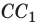
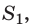
Пусть из точечного источника света S на поверхность плоского зеркала падает расходящийся пучок света. Из этого пучка выделим лучи SA, SB и SC. Используя законы отражения света, построим отраженные лучи и (рис. 11.7, а). Эти лучи пойдут расходящимся пучком. Если продлить их в противоположном направлении (за зеркало), все они пересекутся в одной точке — расположенной за зеркалом.

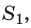
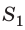
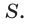
Если часть отраженных от зеркала лучей попадет в ваш глаз, вам будет казаться, что отраженные лучи выходят из точки хотя в действительности никакого источника света в точке нет. Поэтому точку называют мнимым изображением точки Плоское зеркало всегда дает мнимое изображение.

Выясним, как расположены предмет и его изображение относительно зеркала. Для этого обратимся к геометрии. Рассмотрим, например, луч SC, который падает на зеркало и отражается от него (рис. 11.7, б).

Рис. 11.7. Получение изображения точечного источника света в плоском зеркале: S — источник света; 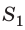— мнимое изображение источника света

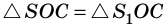
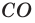
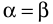
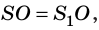
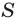
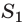
Из рисунка видим, что — прямоугольные треугольники, имеющие общую сторону и равные острые углы (так как по закону отражения света ). Из равенства треугольников имеем, что то есть точка и ее изображение симметричны относительно поверхности плоского зеркала.

То же можно сказать и об изображении протяженного предмета: предмет и его изображение симметричны относительно поверхности плоского зеркала.

Итак, нами установлены общие характеристики изображений в плоских зеркалах.

1. Плоское зеркало дает мнимое изображение предмета.

2. Изображение предмета в плоском зеркале и собственно предмет симметричны относительно поверхности зеркала, и это означает:

• изображение предмета равно по размеру самому предмету;
• изображение предмета расположено на том же расстоянии от поверхности зеркала, что и сам предмет;
• отрезок, соединяющий точку на предмете и соответствующую ей точку на изображении, перпендикулярен поверхности зеркала.

Зеркальное и рассеянное отражение света

Вечером, когда в комнате горит свет, мы можем видеть свое изображение в оконном стекле. Но изображение исчезает, если задернуть шторы: на ткани мы своего изображения не увидим. А почему? Ответ на этот вопрос связан по меньшей мере с двумя физическими явлениями.

Первое такое физическое явление — отражение света. Чтобы появилось изображение, свет должен отразиться от поверхности зеркально: после зеркального отражения света, идущего от точечного источника S, продолжения отраженных лучей пересекутся в одной точке S₁, которая и будет изображением точки S (рис. 11.8, а). Такое отражение возможно только от очень гладких поверхностей. Их так и называют — зеркальные поверхности. Кроме обычного зеркала примерами зеркальных поверхностей являются стекло, полированная мебель, спокойная гладь воды и т. п. (рис. 11.8, б, в).

Если свет отражается от шероховатой поверхности, такое отражение называют рассеянным (диффузным) (рис. 11.9). В этом случае отраженные лучи распространяются в разных направлениях (именно поэтому мы видим освещенный предмет с любой стороны). Понятно, что поверхностей, рассеивающих свет, намного больше, чем зеркальных.

Рис. 11.8. Зеркальное отражение света — это отражение света от гладкой поверхности

Рис. 11.9. Рассеянное (диффузное) отражение света — это отражение света от шероховатой поверхности

Второе физическое явление, влияющее на возможность видеть изображение, — это поглощение света. Ведь свет не только отражается от физических тел, но и поглощается ими. Лучшие отражатели света — зеркала: они могут отражать до 95 % падающего света. Хорошими отражателями света являются тела белого цвета, а вот черная поверхность поглощает практически весь свет, падающий на нее.

Пример №2

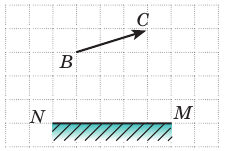
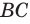
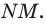
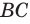
На рис. 1 схематически изображены предмет и зеркало Найдите графически участок, из которого изображение предмета видно полностью.

Анализ физической проблемы. Чтобы видеть изображение некоторой точки предмета в зеркале, необходимо, чтобы в глаз наблюдателя отразилась хотя бы часть лучей, падающих из этой точки на зеркало. Понятно, что если в глаз отразятся лучи, исходящие из крайних точек предмета, то в глаз отразятся и лучи, исходящие из всех точек предмета.

Рис. 1

Решение, анализ результатов

1. Построим точку B₁ — изображение точки B в плоском зеркале (рис. 2, а). Область, ограниченная поверхностью зеркала и лучами, отраженными от крайних точек зеркала, и будет той областью, из которой видно изображение B₁ точки B в зеркале.

2. Аналогично построив изображение C₁ точки C, определим область ее видения в зеркале (рис. 2, б).

3. Видеть изображение всего предмета наблюдатель может только в том случае, если в его глаз попадают лучи, которые дают оба изображения — B₁ и C₁ (рис. 2, в). Значит, участок, выделенный на рис. 2, в оранжевым, и есть тот участок, из которого изображение предмета видно полностью.

Подводим итоги:

Все видимые тела отражают свет. При отражении света выполняются два закона отражения света: 1) луч падающий, луч отраженный и перпендикуляр к поверхности отражения, проведенный из точки падения луча, лежат в одной плоскости; 2) угол отражения равен углу падения.

Изображение предмета в плоском зеркале мнимое, равное по размеру самому предмету и расположено на том же расстоянии от зеркала, что и сам предмет.

* Различают зеркальное и рассеянное отражения света. В случае зеркального отражения мы можем видеть мнимое изображение предмета в отражающей поверхности; в случае рассеянного отражения изображение не возникает.

Главная >> Фейнмановские лекции по физике >> Том 3 >> Глава 33. Поляризация

Интенсивность отраженного света

Рассмотрим здесь количественную зависимость коэффициента отражения от угла падения. На фиг. 33.6, а показан пучок света, падающий на поверхность стеклянной пластинки, от которой он частично отражается, а остальная его часть преломляется и уходит в глубь стекла. Пусть падающий луч имеет единичную амплитуду и линейно поляризован перпендикулярно плоскости рисунка. Обозначим амплитуду отраженной волны буквой b, а амплитуду преломленной —буквой а. Отраженная и преломленная волны будут, разумеется, линейно поляризованы, а направления электрического поля в падающей, отраженной и преломленной волнах параллельны друг другу. На фиг. 33.6, б показана подобная же ситуация, но в предположении, что падающий луч поляризован в плоскости рисунка. Здесь через В и А обозначены соответственно амплитуды отраженной и преломленной волн.

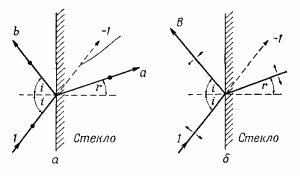
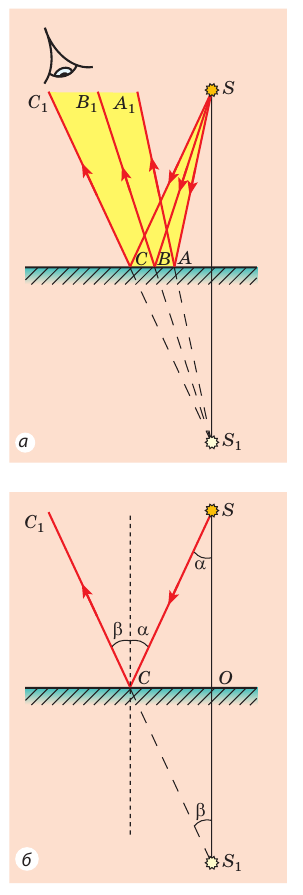
Мы хотим вычислить интенсивности отраженного луча в обоих случаях, приведенных на фиг. 33.6. Как мы уже знаем, в случае, показанном на фиг. 33.6,б, отраженной волны не возникает, если угол между отраженным и преломленным лучами прямой, но нам хотелось бы получить количественный результат — точную формулу для амплитуд В и b как функций угла падения i. Полезно усвоить следующий принцип. Индуцированные в стекле токи генерируют две волны. Прежде всего они создают волну отражения. Далее, если бы в стекле токов не было, падающая волна прошла бы его насквозь, не меняя направления. Вспомним, что все заряды во Вселенной создают некое результирующее поле. Источник, создавший падающий пучок, дает поле единичной амплитуды, которое само по себе должно было бы проходить внутрь стекла по пунктирной линии (см. фиг. 33.6). Но это поле внутри стекла не наблюдается, а, следовательно, токи, возбуждаемые в стекле, должны излучать поле с амплитудой —1 вдоль той же пунктирной линии. ЭТО позволяет вычислить амплитуды преломленных волн а и А.

Из фиг. 33.6, а видно, что поле с амплитудой b создается движением зарядов стекла, а внутри стекла это же движение дает поле с амплитудой а; следовательно, амплитуда b пропорциональна амплитуде а. Далее, если отвлечься от направления поляризации, можно было бы предположить, что отношение В/А равно отношению b/а, так как обе схемы на фиг. 33.6 можно считать одинаковыми. На самом деле это не совсем правильно, потому что на фиг. 33.6, б в отличие от ситуации, изображенной на фиг. 33.6, а, направления поляризаций не параллельны друг другу. В создании амплитуды В эффективно участвует только компонента А, параллельная В, т. е. Acos(i+r). Правильное соотношение пропорциональности выглядит поэтому так:

 

Теперь немного схитрим. Как мы знаем, на обоих рисунках фиг. 33.6 электрическое поле в стекле вызывает движение зарядов, которое генерирует поле с амплитудой, равной —1, поляризованное точно так же, как и в падающем луче, и распространяющееся вдоль пунктирной линии. Но из фиг. 33.6, б видно, что только перпендикулярная пунктирной линии компонента А дает полю необходимую поляризацию, тогда как на фиг. 33.6,а в создании поля на пунктирной линии эффективно участвует вся амплитуда а, поскольку ее поляризация параллельна поляризации поля с амплитудой —1. Следовательно, справедливо соотношение

 

 

Проверим правильность этого результата на уже известном нам факте. Положив (i+r) =90°, из (33.3) получим B=0, что и было найдено в свое время Брюстером; таким образом, наш результат по крайней мере не содержит очевидной ошибки.

По предположению падающая волна имеет единичную амплитуду; тогда |В|²/1² есть коэффициент отражения лучей, поляризованных в плоскости падения, а |b|²/1² — коэффициент отражения лучей, поляризованных перпендикулярно плоскости падения. Отношение этих двух коэффициентов определяется с помощью формулы (33.3).

А теперь сотворим чудо и вычислим не только отношение, но и каждый коэффициент |В|² и |b|² в отдельности! Из закона сохранения энергии вытекает, что энергия преломленной волны должна быть равна энергии падающей волны минус энергия отраженной волны, т. е. 1– |В|² в одном случае и 1–|b|² — в другом. Более того, энергия света, прошедшего внутрь стекла в случае, показанном на фиг. 33.6, а, и такая же энергия в случае фиг. 33.6, б относятся как квадраты амплитуд преломленных волн: |A|²/|а|². Возникает вопрос, возможно ли вычислить энергию волны в стекле, если кроме энергии электрического поля, вообще говоря, имеется и энергия движения атомов. Однако ясно, что любой вклад в полную энергию должен быть пропорционален квадрату амплитуды электрического поля. Следовательно,

 

Подставим сюда соотношение (33.2) и исключим A/a в написанном выражении, а величину В выразим через b с помощью формулы (33.3):

 

Здесь неизвестной величиной остается только b. Разрешая уравнение относительно |b|² , получаем

 

и, воспользовавшись (33.3), находим

 

Таким образом, мы нашли коэффициент отражения |b|² для падающей волны, поляризованной перпендикулярно плоскости падения, и коэффициент отражения |В|² для волны, поляризованной в плоскости падения!

Используя подобные приемы доказательства, можно пойти дальше и вывести, что b действительно. Для доказательства рассмотрим случай, когда свет приходит одновременно с обеих сторон поверхности стекла (ситуация, трудно осуществимая на опыте, но забавная в теоретическом отношении). Анализируя этот общий случай, можно убедиться в действительности величины b, откуда следует, что b = ±sin(i—r)/sin(i+r). Если взять очень тонкий слой, в котором отражение происходит от обеих поверхностей, и вычислить интенсивность отраженного света, то можно установить даже знак b. Доля света, отраженного тонким слоем, нам известна, поскольку мы знаем ток, генерируемый в таком слое, и даже получили формулу для поля, создаваемого током. Эти аргументы приводят к соотношениям

 

Формулы (33.8) для коэффициентов отражения как функций углов падения и преломления называются формулами Френеля.

В пределе, когда углы i и r стремятся к нулю, т. е. в случае падения по нормали, мы получаем В² ≈ b² ≈ (i—r)²/(i+ r)² для обеих поляризаций, поскольку и синусы, и тангенсы в этих условиях практически равны углам. Но, как мы уже знаем, sin i/sin r = n, а для малых углов i/r ≈ n. Отсюда совсем просто вывести, что коэффициент отражения в случае падения по нормали равен

 

Интересно вычислить, например, коэффициент отражения для воды. В этом случае n = ⁴/₃ и коэффициент отражения равен (¹/₇)² ≈ 2%. При падении лучей по нормали к поверхности от воды отражается только 2% всей энергии.

СМОТРИТЕ ТАКЖЕ:

Социальные комментарии Cackle