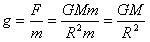Как найти максимальное перемещение - Исправление недочетов и поиск решений вместе с Examum.ru

Транскрипция к видео

Я хотел бы продолжить тему последнего видеоурока, где мы подбрасывали мячи в воздух и смотрели, как долго они оставались там. Мы использовали это, чтобы вычислить, насколько быстро мы изначально бросили мяч,
и насколько высоко он поднимался в воздух.
В последнем видео-уроке
мы делали это с определёнными числами. В этом уроке я просто хочу посмотреть, сможем ли мы получить
некоторые формулы так, чтобы мы могли быстро сделать
расчёты в уме, пока мы занимаемся этим делом где-то вдали от дома, и у нас необязательно есть бумага под рукой.
Допустим, что мяч находится в воздухе в течение дельта T. Дельта T равна времени нахождения в воздухе.
Время в воздухе.
Кроме того, нам известно,
что время подъёма будет равно его половине, оно равно времени падения вниз. Время подъёма будет равно дельта Т…
мы будем использовать то же цвет…,
будет равно времени в воздухе, делённому на два. Итак, какова была начальная скорость?
Теперь нам нужно вспомнить, что изменение скорости —
это то же самое, что конечная скорость
минус начальная скорость. Итак, конечная скорость… помните что мы говорим о половине траектории этого мяча.
В момент, когда он отпускается, он движется так, что вначале его скорость максимальна, затем он движется всё медленнее и медленнее, пока он не остановится на мгновение, а затем начнёт двигаться вниз. Помните, что ускорение постоянно и направлено вниз
всё это время. Чему равна конечная скорость, если мы рассматриваем половину этого времени?
Итак, это будет ноль минус начальная скорость, минус начальная скорость,
которая была, когда он был отпущен. Это наше изменение скорости.
Наше изменение скорости, оно будет равно ускорению силы тяжести. Равно ускорению силы тяжести. -9,8 м/с2… или ускорению под действием силы тяжести, когда тело находится в свободном падении,
точнее говоря, умноженное,
на время подъёма. Итак, умноженное на дельта Т, которая равна…
Я даже не буду писать дельта T подъёма,
это то же, что наше полное время в воздухе,
делённое на два, и таким образом мы получаем минус начальная скорость равно вот этому, делённому на два, что в свою очередь равно 4,9 м/с2 у нас всё ещё стоит минус впереди,
умноженное на дельта Т умноженное на дельта Т, и помните, что это полное время в воздухе, и не только время подъёма, это полное время в воздухе. Затем мы умножим обе части на минус один и получим, что начальная скорость будет равна четырём целым и девяти десятым, 4,9 м/с2 умноженным на полное время, которое мы находились в воздухе. Или можно сказать так — это будет 9,8 м/с, умноженных на половину
времени нахождения в воздухе. Оба этих выражения дадут один и тот же результат. Давайте найдём полный путь или путь, который мы проходим вверх, это даст нам путь до верхней точки. Вспомним, что путь
или здесь я должен сказать перемещение, равно средней скорости, умноженной на изменение времени. Изменение времени, о котором мы говорим, — это время подъёма, так что это дельта Т, делённое на два,
наше полное время делённое на два. Это наше время подъёма. Время подъёма. Какова наша средняя скорость? Средняя скорость,
если мы будем считать ускорение постоянным, равна начальная скорость плюс конечная скорость,
делённое на два.
Фактически это средняя из двух величин. Мы знаем начальную скорость. Это вот эта величина, вот она. Конечная скорость… напомню, что мы говорим о первой половине того времени, когда мяч находится в воздухе. Итак, конечная скорость равна нулю. Мы говорили, что это так в верхней точке вот здесь.
Это было два урока назад, эта верхняя точка. Средняя скорость будет равна вот этому, делённому на два. Итак, она будет равна 4,9 м/с2, умноженным на дельта T… умноженным на дельта T, делённому на два. Вот здесь справа наша средняя скорость.
Средняя скорость.
Теперь давайте вернёмся вот к этому выражению. Наше максимальное перемещение,
наше максимальное перемещение будет равно
нашей средней скорости, это будет 4,9 м/с2, умноженных на дельта T, и всё это делённое на два.
Затем мы умножим это снова на время подъёма. Умножим на дельта T, снова делённое на два, и это те же самые величины. И затем мы можем упростить это. Наше максимальное перемещение равно
4,9 м/с2, умноженным на дельта T2, всё это делённое на 4,
и далее мы можем просто разделить на 4,9, делённое на 4, 4,9, делённое на 4, — это одна целая,
1,2, 1,225, как мне кажется. Я достану свой калькулятор. Добравшись до этой стадии, я не хочу выполнять вычисления в уме, чтобы не сделать ошибку.
4,9, делённое на 4, равно 1,225.
Максимальное перемещение будет равно 1,225,
умноженным на полное время в воздухе в квадрате, что довольно
легко, это просто вычислить. Итак, это наше максимальное перемещение,
то, как далеко, как высоко мы переместимся до той точки, в которой мяч замирает, в которой результирующая скорость равна 0
всего на мгновение, и затем мяч ускоряется вниз. Итак, мы можем использовать это. Если мяч находится в воздухе в течение 5 с… Мы можем проверить правильность расчётов Максимальное перемещение равно 1,225, умноженным на 5 в квадрате, что равно 25. В результате получается 30,625, что мы получили в последнем видео-уроке.
Если мяч находится в воздухе 2,3 секунды, то это 1,225,
умноженных на 2,3 в квадрате, это означает, что он прошёл 6,48 м в воздухе.
В любом случае я хотел дать вам простое выражение, которое позволяет найти максимальное перемещение от земли,
предполагая, что сопротивлением воздуха
можно пренебречь. Не знаю, как вы, a я нахожу это очень интересным и увлекательным занятием!!! Subtitles by the Amara.org community

Источник

Исходные
данные: υ_D3, υ_D6= 0; ω₃=
ω₆= 0;а_D3=а_D6=
0.

Определить:
υ_D5,а_D5.

Решение.Построение плана скоростей. Также
как и вЗадаче 4, в точкеDсоединяются четыре звена. Поэтому будут
четыре точки:D₃,
D₄, D₅,
D₆(рисунок
2.11). После расчета масштабного коэффициента
скорости по формуле (2.30) записываются
векторные уравнения-формулы (2.54).
Построение плана скоростей ведется
аналогичноЗадаче 4. Угловые скорости
звеньев4и5равны нулю, т.к. они
движутся поступательно (ω₄=
ω₅= 0). Рассчитывается
скорость точкиD₅по формуле (2.54). Строится план ускорений.
Высчитывается масштабный коэффициент
плана ускорений по формуле (2.56). Затем
записываются векторные уравнения –
формулы (2.57). В данном случае кориолисово
ускорениеа^к_D₃_D₄= 0, т.к.ω₄= 0.

Построение
плана ускорений ведется аналогично
Задаче4. В конце рассчитывается
ускорение точкиD₅по формуле (2.59).

а) б) в)

у 6
5 уυ_D5
а_D5

P_υ

d₅
d₅
P_a

D(D₃,D₄,D₅,D₆) 4
υ_D3
υ_D5D3 а_D5D3а_D3

3
υ_D₃
d₃
d₃

a_D₃

а
– структурная группа; б
— план скоростей; в
— план ускорений

Рисунок
2.11 — К кинематическому расчету структурной
группы II
класса 5 вида

Итак,
мы рассмотрели определение скоростей
и ускорений методом планов для всех
видов структурных групп. Пример
кинематического расчета шестизвенного
механизма будет приведен в главе 3, п.
3.1.8. А теперь подведем некоторые итоги
по правилам построения планов.

Свойства
планов скоростей, ускорений

Векторы всех полных
(абсолютных) скоростей (ускорений) имеют
своим началом точку полюса, а векторы
относительных скоростей (ускорений)
соединяют собой концы векторов полных
скоростей (ускорений).
Векторы полных
скоростей (ускорений) всегда направлены
от полюса. Векторы относительных
скоростей (ускорений) направлены так,
чтобы удовлетворялись векторным
уравнениям (т.е. к той точке, которую
строим).
Скорости (ускорения)
точек подобных фигур (жестких треугольников
или отрезков) находятся по правилу
подобия (см. Задачи 1 и 2).
Точки, скорости и
ускорения которых равны нулю, находятся
в полюсе.
При плоскопараллельном
движении векторы относительных ускорений
образуют со звеном угол μ, тангенс
которого равен tgμ=ξ /ω².

2.4.3 Определение перемещений, скоростей и ускорений методом построения кинематических диаграмм

При
кинематическом исследовании механизма
необходимо определять скорости и
ускорения за полный цикл движения
механизма. Для этого исследование
проводится для ряда положений механизма,
достаточно близко отстоящих друг от
друга. По полученным значениям строятся
графики, носящие названия кинематических
диаграмм.

Кинематические
диаграммы — графики зависимости
перемещенияS, скорости
Vи ускоренияa
от времениtили от
угла поворота φ, а именно

S
= f(t);
υ =f(t);
a= f(t).

В
зависимости от характера движения
исследуемых звеньев или отдельных точек
механизма могут быть построены и
различные кинематические диаграммы.
Например, если известен ход поршня
(ползуна), то можно построить диаграмму
перемещения, а по ней методом
графического
дифференцирования
строятся графики скорости и ускорения.
Если же задается диаграмма ускорения
ведомого звена, то методом
графического
интегрирования
строятся графики скорости и перемещения.

Задача
1. Метод графического дифференцирования

Графическое
дифференцирование можно проводить
методом касательных или методом хорд.
Метод касательных имеет более низкую
точность по сравнению с методом хорд.

Метод
хордпредполагает замену заданной
кривой ломаной линией, т.е. полученные
точки соединяют хордами. При этом
принимают следующее допущение: угол
наклона касательных в точках, расположенных
посередине каждого участка кривой,
равен углу наклона соответствующей
хорды. Это допущение вносит некоторую
погрешность, но она относится только к
данной точке. Эти погрешности не
суммируются, что обеспечивает большую
точность метода по сравнении с методом
касательных.

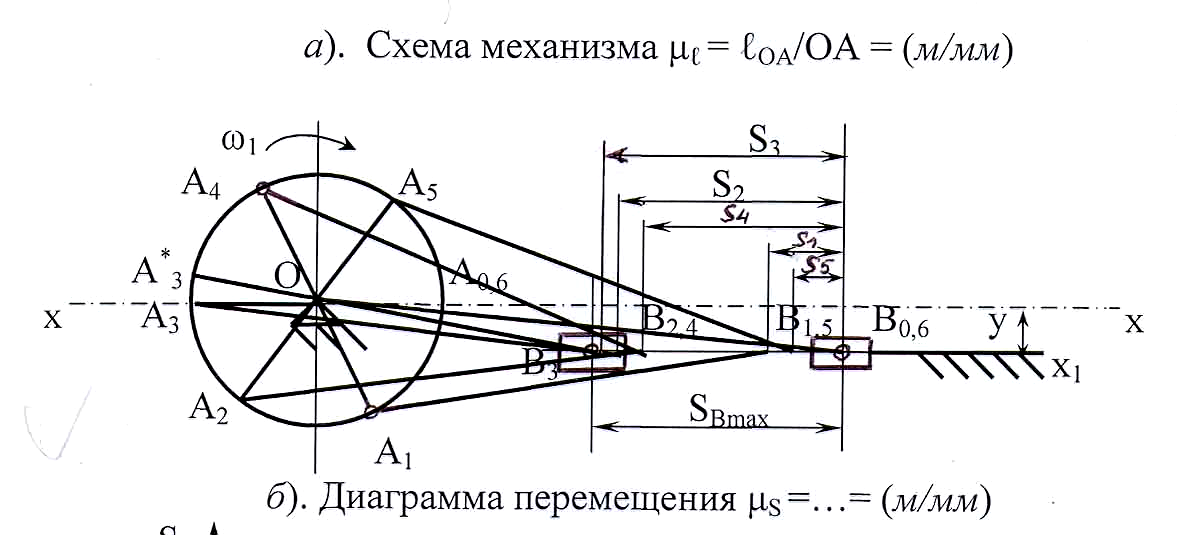
Рассмотрим
на примере кривошипно-ползунного
механизма (рисунок 2.1). Изобразим
кривошипно-ползунный механизм в 6-и
положениях, начиная с крайних (см. гл.
2. §2.2). Затем делим траекторию движения
точки А(окружность радиусом ОА) от
точкиА₀на 6 частей в
сторону вращения (рисунок 2.12). Получаем
точкиА₁, А₂,
А₃и т.д. Из полученных точек
радиусомАВделаем засечки на
траектории движения точкиВ. Получаем
точкиВ₁, В₂,
В₃и т.д. Второе крайнее
положение не совпало с разбивкой, поэтому
его нужно достроить. Переходим к
построению диаграммы перемещения.

Построение
диаграммы перемещения. Строим оси
координатS—t.
Ось абсцисс (времениt)
делим на 6 равных частей. Диаграмму
перемещения можно строить в масштабе
μ_S= μ_ℓ.
Для этого замеряем расстояния от точкиВ₀до точекВ₁,
В₂и т.д. Получаем расстоянияS₁= h₁,S₂= h₂и т.д.,
которые откладываем по вертикали.

Расстояние
S_maxдолжно равнятьсяh_max.
Если же получается слишком низкий или
очень высокий график, то масштабный
коэффициент считают заново:

μ_S=S_maxμ_ℓ/h_max,
(2.60)

где
h_maxвыбирают нужной величины. Затем считают
высотыh₁=
S₁μ_ℓ/μ_S=(мм),h₂и т.д.

Mаксимум
на графике перемещения должен
соответствовать второму крайнему
положению. Поэтому, находим на осиtточку 3*. Для этого определим отрезок3-3*из пропорции:

и от
полученной точки (3*) откладываем вверх
высоту h_max.

Приступаем
к построению диаграмм скоростей и
ускорений методом графического
дифференцирования.

Для
построения диаграммы скоростипродолжаем осьОSвниз. Горизонтально проводим осьt
и делим ее на те же равные 6 частей.
Влево от точкиОпроизвольно
откладываем полюсное расстояние Н₁=ОР₁(чем большеполюс, тем выше будет
диаграмма скоростей). Параллельно
хордам 0-1, 1-2, 2-3 и т.д. из полюсаР₁проводим лучи и на серединах каждого
участка отмечаем точки 1,
2, 3и т.д. Соединяем все точки плавной линией.
Заметим:максимальному значению
ординатыдиаграммы перемещения
соответствует нулевое
значение ординаты диаграммы скорости.

Имея
диаграмму скоростей аналогично можно
построить диаграмму ускорений,
дифференцируя первую. Нужно отметить,
что первая и последняя точки получатся
на ¼ первого и последнего участков,
остальные же точки должны получится на
делительных отрезках.

Схема механизма μ_ℓ= ℓ_ОА/ОА
= (м/мм)

SДиаграмма
перемещения μ_S=…= (м/мм)

3 max

2 h₃
4

h_max

h₂

1
h₄5

h₁h₅

0
1 2 3 3* 4 5 6
t

Диаграмма
скорости μ_V=…=
(^м/с/_мм)

2^΄

3^΄

1^΄
h’₁
h’₂

Р₁

0
1 2 3 *4
h’₄
h’₅
5 6t

4^΄6^΄

Н₁
5^΄

Диаграмма
ускоренияμ_а=…=
(^м/с2/_мм)

h»₀
h»₁
h»₅
h»₆

Р₂0
1/4
1 2 3 4 5 1/4
6 t

h»₂
μ_t=…=
(^с/_мм)

h»₃

Н₂

Рисунок
2.12 — Построение диаграмм методом
графического

дифференцирования
с помощью хорд

Также
нужно учесть, что возрастающим
координатамдиаграммы скорости
соответствуют положительные значения
ординат диаграммы ускорения, а убывающим
ординатам – отрицательные. Хорды
ускорений вписываются по средним
значениям скоростей.

После
построения диаграмм высчитываются
масштабные коэффициенты:

t_дейст= 2π/ω₁= (с);

μ_t= t_дейст/[0-6] = (с/мм);

μ_υ=
μ_S/H₁μ_t=(^м/с/_мм);(2.61)

μ_а=
μ_υ/H₂μ_t=(^м/с2/_мм),

где: Н₁,
Н₂– полюсные отрезки, взятые
с чертежа вмм.

Для
того чтобы посчитать действительные
значения перемещений, скоростей и
ускорений, необходимо замерить ординаты
в ммна делительных отрезках и
умножить на соответствующий масштабный
коэффициент.

Задача 2.
Метод графического интегрирования

Метод
графического интегрирования— метод,
обратный графическому дифференцированию.
Позаданной диаграмме ускорениястроятся диаграммы скорости и перемещения.
Если смотреть на графики снизу вверх
(см. рисунок 2.12), то получатся нужные нам
диаграммы. Рассмотрим на примере.

Пример.По заданной диаграмме ускорения
определить максимальную скорость и
максимальное перемещение методом
графического интегрирования.

Задано:
диаграмма ускорения,
максимальное ускорениеа_max(м/с²), времяt(c).

Определить:
максимальную скоростьυ_max(м/с), максимальное перемещениеS_max(м).

Решение.Перечерчиваем заданную диаграмму
ускорения в произвольном масштабе
(рисунок 2.13), при этом высотуhвыбираем произвольно. Высчитываем
масштабные коэффициенты ускорения и
времени

μ_а= а_max/
h= ();.

μ_t= t/
[0÷6]= (),

где [0÷6]– отрезок
оси времени вмм.

Строим
диаграмму скорости методом графического
интегрирования. Для этого слева от оси
ординат выбираем произвольно полюсное
расстояние Н₁(чем больше Н₁тем положе и ниже будет график скорости).

исунок 2.13 — Построение диаграмм
методом графического интегрирования

Делим
участки [0÷1], [1÷2] [2÷3] и т.д. пополам,
проводим вверх до пересечения с графиком
и соединяем с полюсом Р₁. Полученные
линии параллельно переносим на
соответствующие участки диаграммы
скорости. Аналогично строим диаграмму
перемещения.

Масштабные
коэффициенты диаграмм будут рассчитываться
по следующим формулам:

μ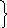_V= μ_aμ_tH₁= (^м/с/_мм);
(2.62)

μ_S=
μ_Vμ_tH₂= (м/мм),

где
H₁,H₂– полюсные расстояния, замеренные с
диаграмм вмм.

Определяем
максимальные действительные значения
скорости и перемещения

υ_max
= h·μ_V=(м/с);S_max
= h·μ_S=(м).

Более
подробно построение диаграмм этим
методом будет рассказано в главе 4, §1,
п. 1.4.

Итак,
мы рассмотрели кинематическое исследование
плоских рычажных механизмов
графоаналитическими методами. Это
позволяет представить движение отдельных
точек звеньев механизма более наглядно.
Теперь приступим к изучению работы
механизма под действием заданных сил.

Вопросы для
самопроверки

Постройте
в крайних положениях выходного звена
кривошипно-ползунный механизм, шарнирный
четырехзвенный и кулисный механизмы.
Расскажите
о преимуществах и недостатках определения
скоростей и ускорений методом планов.
Укажите
порядок построения планов скоростей
и ускорений в многозвенном механизме.
Расскажите,
как, пользуясь планом скоростей,
определить величину и направление
угловой скорости звена?
Как,
пользуясь планом ускорений, определить
величину и направление углового
ускорения?
Объясните
правило подобия для определения скорости
(ускорения) какой-либо точки звена.
При
каких движениях звена возникает
кориолисово ускорение? Как определить
его величину и направление?
Расскажите
о преимуществах и недостатках определения
скоростей и ускорений методом построения
кинематических диаграмм.
Какие
характерные точки позволяют проверить
правильность построения диаграмм?

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Все вы в своей жизни наблюдали за тем, что тела, не имеющие опоры или подвеса, падают вниз. В чем причина такого падения? Конечно же в том, что на все тела у поверхности Земли действует сила тяжести.

Свободным падением тела называется движение тела только под действием силы тяжести.

Проведем мысленный эксперимент. Представьте, что одновременно начинают падение мяч, камень, лист дерева и перо птицы. В какой очередности упадут эти тела?

Первым упадут камень и мяч, затем перо и лист.

Почему? На перо и лист оказывает заметное влияние сила сопротивления воздуха, направленная против силы тяжести.

Падение тела не может считаться свободным, если сила сопротивления воздуха сравнима с силой тяжести.

Еще в конце XVI века знаменитый итальянский ученый Г. Галилей предположил, что все тела падают с одинаковым ускорением и опытным путем доказал, что это предположение верно.

Согласно биографии Галилео Галилея, написанной его учеником Винченцо Вивиани, в 1589 году Галилей провёл эксперимент, сбросив два шара различной массы (ядро и мушкетную пулю) со знаменитой падающей башни в Пизе, чтобы продемонстрировать, что время падения не зависит от массы шара. С помощью этого эксперимента Галилей якобы обнаружил, что тела упали практически одновременно, тем самым доказав, что в отсутствии сопротивления воздуха все тела падают на Землю равноускоренно и что в данной точке Земли ускорение всех тел при падении одно и то же.

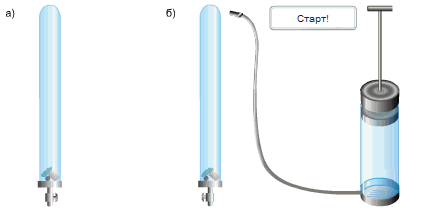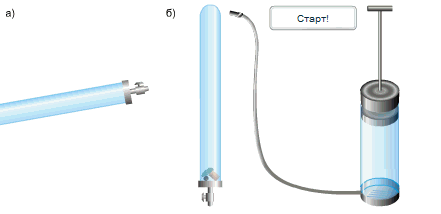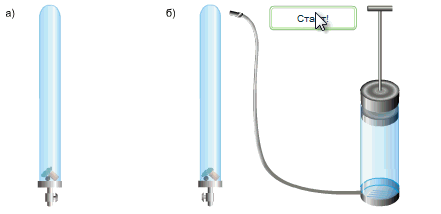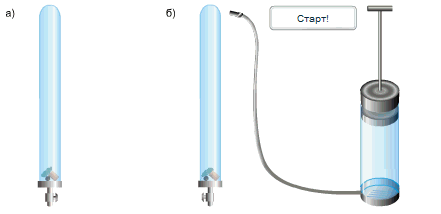
Исаак Ньютон доказал справедливость выводов Галилео простым опытом.

В стеклянную трубку он поместил дробинку, пробку и перышко. Если резко перевернуть расположенную вертикально трубку, то быстрее всего упадет дробинка, за ней кусочек пробки и потом плавно опустится перышко. Если же из трубки откачать воздух и опять резко перевернуть её,то все три тела опустятся на дно одновременно.

Какие выводы можно сделать из опыта Ньютона?

1. Тела падают с одинаковым ускорением.

2. Существует сила сопротивления воздуха

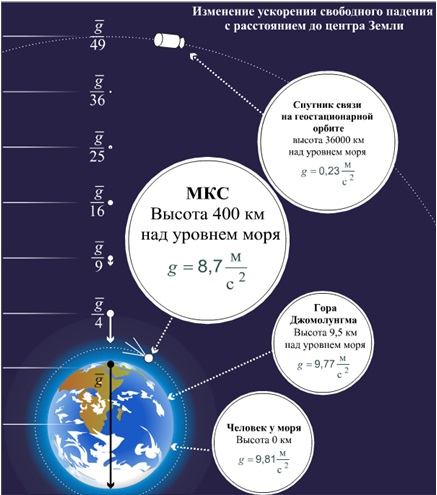
Ускорение, с которым тела падают на Землю, называется ускорением свободного падения.

Ускорение свободного падения — ускорение, сообщаемое телу, поднятому над Землей, силой тяжести.

Вектор ускорения свободного падения обозначается символом g.

g=9,8 м/с²≈10м/с²

Из закона всемирного тяготения:

Ускорение свободного падения:

1) Всегда направлено по вертикали вниз

2) Не зависит от массы падающего тела

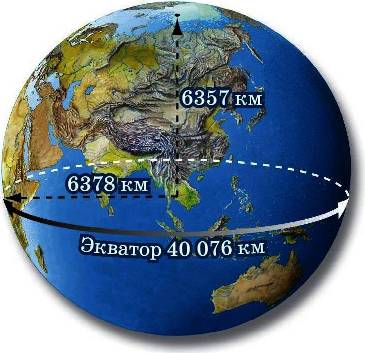
3) Зависит от географической широты. Так как Земля не шар, а эллипсоид вращения, т.е. радиус Земли на полюсе меньше, чем радиус Земли на экваторе.

Поэтому сила тяжести и вызвемое ей ускорение больше на полюсе, чем на экваторе. g изменяется примерно от 9,83 м/с² на полюсах до 9,78 м/с² на экваторе. На широте Москвы g = 9,81523 м/с². Обычно, если в расчетах не требуется высокая точность, то числовое значение g у поверхности Земли принимают равным 9,8 м/с² или даже 10 м/с².

4) Зависит от высоты над уровнем моря

Рассмотрим несколько примеров движения тел под действием силы тяжести. При решении подобных задач очень важно правильно выполнить чертеж, на котором указать направление осей и всех векторных величин.

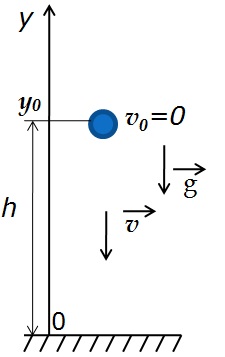
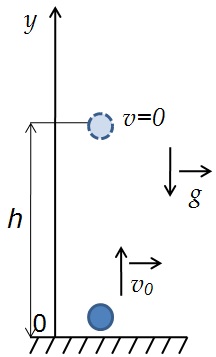
Простым примером свободного падения является падение тела с некоторой высоты h без начальной скорости.

Анализируем рисунок.

Свободное падение является прямолинейным движением с постоянным ускорением a=g, значит, к нему применимы все формулы для равноускоренного движения.

Так как тело движется вертикально, то будем рассматривать его движение вдоль оси y, которую направим вертикально вверх.

Тогда проекция ускорения на ось y отрицательна g_y=-g

Перемещение тела равно по модулю высоте, с которой тело падало s=h, а проекция перемещения на ось y отрицательна: s_y=-h

Начальная скорость движения равна нулю v₀=0

Проекция конечной скорости на ось y отрицательна v_у =-v

Начальная координата тела y₀=h

Теперь работаем с формулами.

Проекция скорости на ось y при равноускоренном движении находится по формуле

v_у=v₀_у+a_yt

учитывая, что тело движется с ускорением свободного падения и g_y=-g, а также то, что v₀=0 и v_у=-v, получаем -v=0-gt

Упростив выражение, получим формулу для нахождения скорости свободно падающено тела в любой момент времени:

v=gt

Проекция перемещения на ось y при равноускоренном движении находится по формуле

s_у=v₀_уt+a_yt²/2

учитывая, что тело движется с ускорением свободного падения и g_y=-g, а также то, что v₀=0 и s_у=-h, получаем -h=0-gt²/2

Упростив выражение, получим формулу для нахождения перемещения тела при свободном падении в любой момент времени:

h=gt²/2

Уравнение координаты при равноускоренном движении находится по формуле

y=y₀+v₀_уt+a_yt²/2

учитывая, что тело движется с ускорением свободного падения и g_y=-g, а также то, что v₀=0 и y₀=h, получаем y=h-gt²/2

То есть, формула для нахождения координаты тела при свободном падении в любой момент времени:

y=h-gt²/2

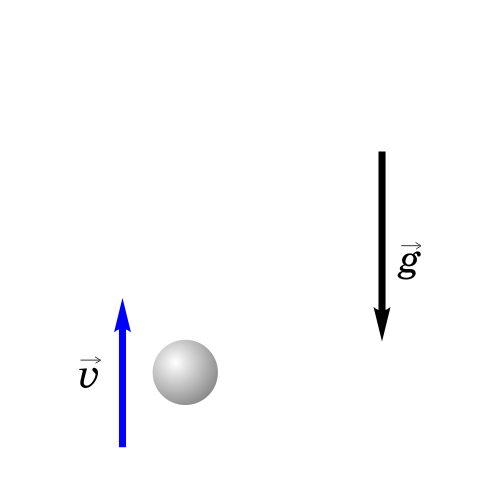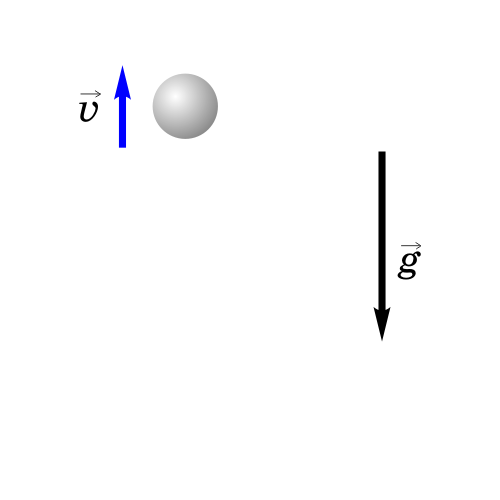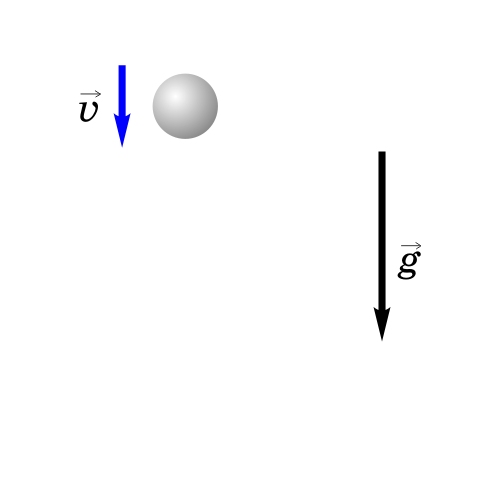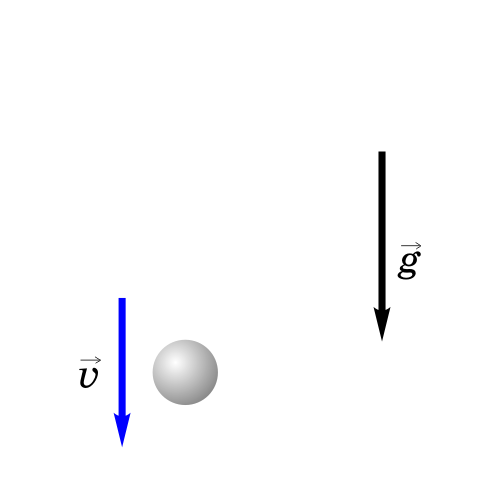
2. Тело брошено вертикально вверх.

Как будет двигаться тело, брошенное вертикально вверх?

Если бросить тело вертикально вверх, то некоторое время оно будет двигаться вверх. Действующая на него сила тяжести направлена вниз и сообщает ему ускорение g, тоже направленное вниз. Поэтому скорость тела будет уменьшаться со временем и в некоторый момент она станет равной нулю, после чего тело начнет падать вниз с увеличивающейся скоростью.

Анализируем рисунок.

Движение тела, брошенного вертикально вверх тоже является прямолинейным движением с постоянным ускорением a=g, значит, к нему применимы все формулы для равноускоренного движения.

Тогда проекция ускорения на ось y отрицательна g_y=-g

Перемещение тела равно по модулю высоте, на которую тело поднимется s=h, а проекция перемещения на ось y полжительна: s_y=h

Проекция начальной скорости движения на ось y положительна v_0y=v₀

Конечная скорость в верхней точке равна нулю v =0

Начальная координата тела равна нулю y₀=0, а конечная координата равна высоте, на которую тело поднимется y=h

Теперь работаем с формулами.

Проекция скорости на ось y при равноускоренном движении находится по формуле

v_у=v₀_у+a_yt

учитывая, что тело движется с ускорением свободного падения и g_y=-g, а также то, что v_0y=v₀ и v_у=v, получаем, что скорость тела, брошенного вертикально в любой момент времени:

v=v₀-gt

Если учесть, что в верхней точке v =0, получим 0=v₀-gt

Упростив выражение, получим формулу для нахождения начальной скорости тела, брошенного вертикально:

v₀=gt

Проекция перемещения на ось y при равноускоренном движении находится по формуле

s_у=v₀_уt+a_yt²/2

учитывая, что тело движется с ускорением свободного падения и g_y=-g, а также то, что v_0y=v₀ и s_у=h, получим формулу для нахождения перемещения тела, брошенного вертикально, в любой момент времени:

h=v₀t-gt²/2

Уравнение координаты при равноускоренном движении находится по формуле

y=y₀+v₀_уt+a_yt²/2

учитывая, что тело движется с ускорением свободного падения и g_y=-g, а также то, что v_0y=v₀ , y₀=0 и y=h, получаем формулу для нахождения координаты тела, брошенного вертикально, в любой момент времени:

y=v₀t-gt²/2

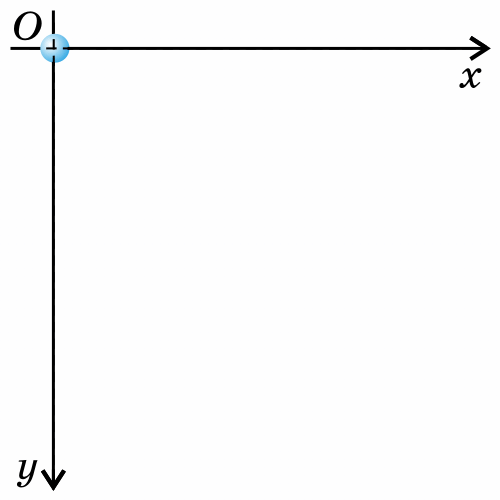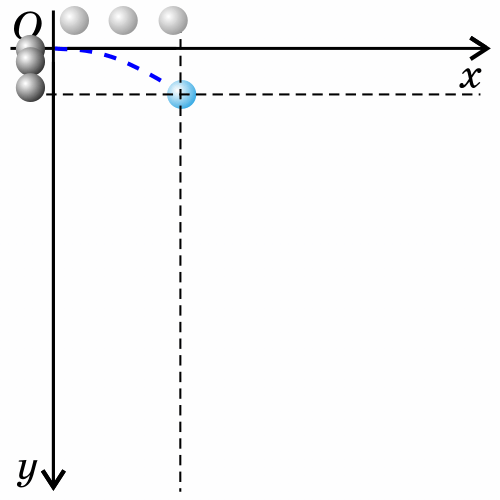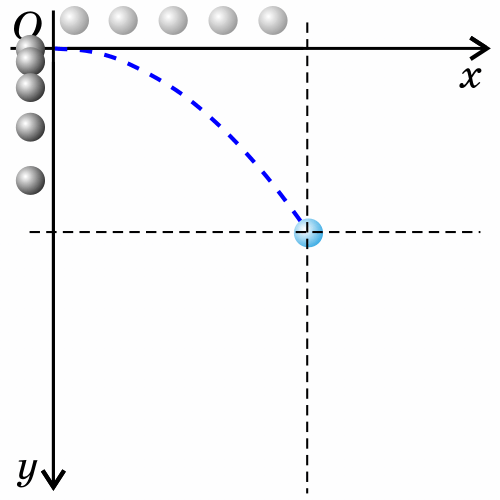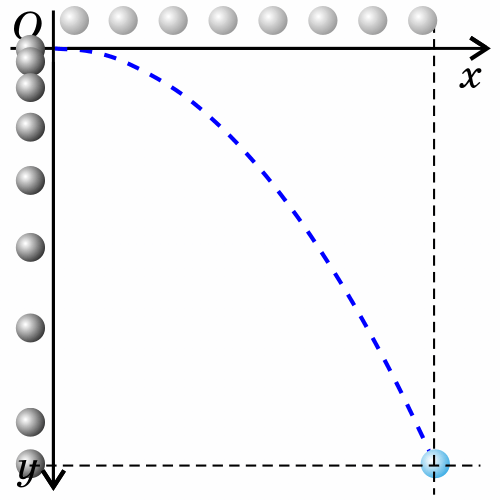
3. Тело брошено горизонтально.

Как будет двигаться тело, брошенное горизонтально?

Если тело бросить горизонтально, оно будет двигаться криволинейно — по параболе, хотя на тело все время действует сила тяжести, направленная вертикально вниз.

Такое движение тела рассматривают как два движения: по горизонтали — вдоль оси х, и по вертикали — вдоль оси y.

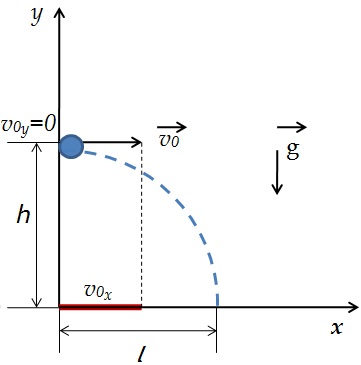
Анализируем рисунок.

Ось y направим вертикально вверх. Проекция ускорения на ось y отрицательна g_y=-g

Перемещение тела равно по модулю высоте, с которой тело бросили s=h, а проекция перемещения на ось y отрицательна: s_y=-h

Начальные координаты тела х₀=0 y₀=h

Проекция начальной скорости на ось х равна v_0х=v₀

Проекция начальной скорости на ось y равна v_0y=0

Перемещение тела вдоль оси х это дальность полета s_х=l=х-х₀

Теперь работаем с формулами.

По горизонтали, т.е. вдоль оси х тело движется равномерно (т.к. нет ускорения) с постоянной скоростью, равной проекции начальной скорости на ось х. Поэтому при рассмотрении движения вдоль оси х нужно пользоваться формулами, полученными для равномерного движения.

Уравнение скорости: v_0x=v₀=const

Уравнение перемещения (дальность полета): l=v_0х·t= v₀·t

Уравнение координаты: x= x₀ + v₀·t

По вертикали, т.е. вдоль оси y тело свободно падает с высоты h. Поэтому при рассмотрении движения вдоль оси y применимы формулы для свободного падения.

Уравнение скорости: v=g·t

Уравнение перемещения: h=g·t²/2

Уравнение координаты: y= y₀-g·t²/2

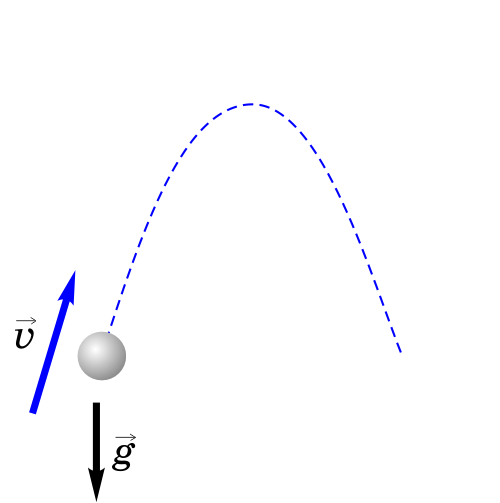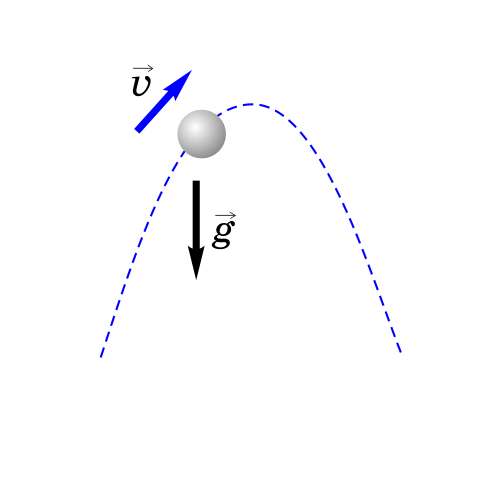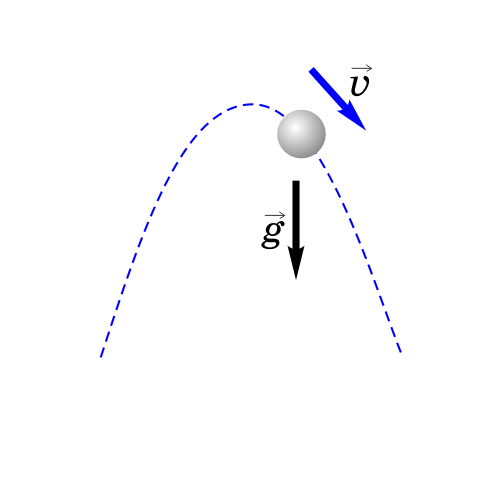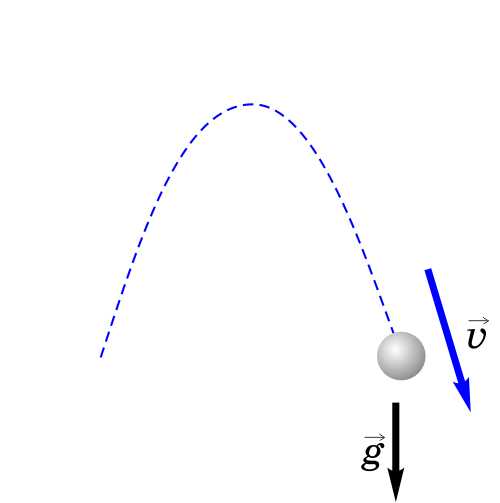
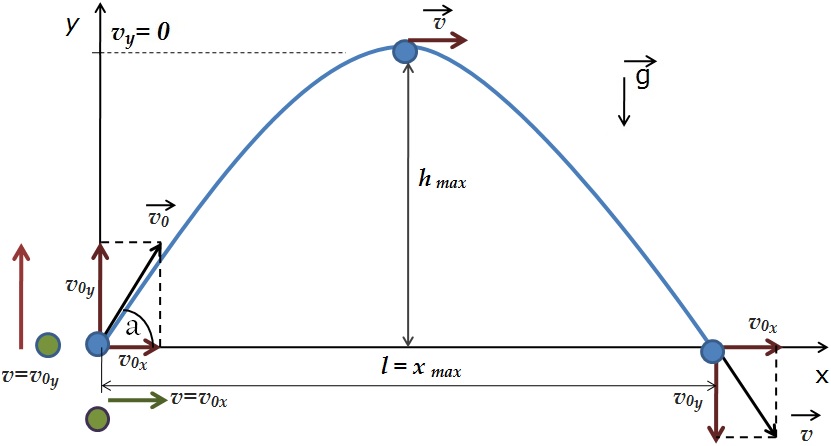
4. Тело брошено под углом к горизонту.

Как будет двигаться тело, брошенное под углом к горизонту?

Если тело бросить под углом к горизонту, оно будет двигаться криволинейно — по параболе, хотя на тело все время действует сила тяжести, направленная вертикально вниз.

Анализируем рисунок.

Ось y направим вертикально вверх. Проекция ускорения на ось y отрицательна g_y=-g

Начальные координаты тела равны нулю х₀=0 y₀=0

Проекция начальной скорости на ось х равна v_0х=v₀·cosa

Проекция начальной скорости на ось y равна v_0y=v₀·sina

h — максимальная высота, на которую тело поднимется. На этой высоте проекция скорости на ось y равна 0.

Перемещение тела вдоль оси х это дальность полета s_х=l=х-х₀

Теперь работаем с формулами.

По горизонтали, т.е. вдоль оси х тело движется равномерно (т.к. нет ускорения) с постоянной скоростью, равной проекции начальной скорости на ось х. Поэтому при рассмотрении движения вдоль оси ОХ нужно пользоваться формулами, полученными для равномерного движения.

Уравнение скорости: v_0x=v₀·cosa=const

Уравнение перемещения (дальность полета): l=v_xt= v₀·cosa·t

Уравнение координаты: x= x₀ + v₀·cosa·t

По вертикали, т.е. вдоль оси y тело движется сначало равнозамедленно, подобно телу, брошенному вертикально вверх со скоростью, равной проекции начальной скорости на ось y, а затем равноускоренно (свободно падая).

Проекция ускорения на ось y g_y= -g , проекция начальной скорости на ось y v_0у=v₀·sina, начальная координата y₀=0

Таким образом, применимы формулы, которые мы использовали ранее для равноускоренного движения по вертикали.

Уравнение скорости: v_y=v₀·sina-g·t

Уравнение перемещения (максимальная высота полета): h=v₀·sina·t-g·t²/2

Уравнение координаты: y= v₀·sina·t-g·t²/2

Время полета в 2 раза больше времени подъема тела на максимальную высоту

t= 2·t_max = 2·v₀·sina/g

Скорость тела находится по теореме Пифагора:

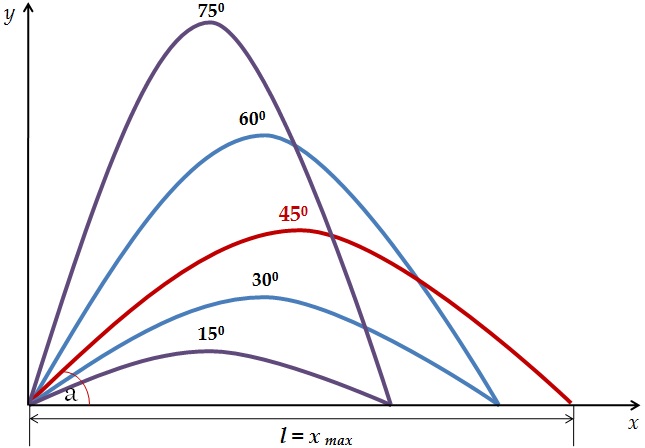
l = x _max= v₀²·sin2a /g

Дальность полета максимальна, когда максимален sin2a.
Максимальное значение синуса равно единице при угле 2a=90⁰, откуда a = 45⁰
Для углов, дополняющих друг друга до 90⁰ дальность полета одинакова.

Расширения для Joomla

Источник

Вычисление перемещения по графику проекции скорости

Из кодификатора по физике, 2020.
«1.1.3. Вычисление перемещения по графику зависимости υ(t).»

Теория

Пусть задан график зависимости проекции скорости ${ v }_{ x }$ от времени t (рис. 1).

Проекция перемещении тела ${ s }_{ x }$ за промежуток времени от ${ t }_{ 1 }$ до ${ t }_{ 2 }$ численно равна по величине площади фигуры, ограниченной графиком ${ v }_{ x }(t)$ , осью времени 0t и перпендикулярами к ${ t }_{ 1 }$ и ${ t }_{ 2 }$ (см. рис. 1, площадь выделена штриховкой).

Проекцию перемещения на ось 0Х будем считать:

— положительной, если проекция скорости на данную ось будет положительной (тело движется по направлению оси) (см. рис. 1);

— отрицательной, если проекция скорости на данную ось будет отрицательной (тело движется против оси) (рис. 2).

Путь s может быть только положительным:

Напоминаем формулы для расчета площадей фигур:

— прямоугольника –

— треугольника – $S=frac { acdot h }{ 2 }$

— трапеции – $S=frac { a+b }{ 2 } cdot h$

Задачи

Задача 1. По графику проекции скорости тела (рис. 3) определите проекцию его перемещения между 1 и 5 с.

Ответ: ____ м.

Решение. Проекция перемещения за промежуток времени Δt= ${ t }_{ 2 }$ – ${ t }_{ 1 }$ =5с–1с=4c численно равна площади фигуры, ограниченной графиком ${ v }_{ x }(t)$ , осью времени 0t и перпендикулярами к ${ t }_{ 1 }=1$ с и ${ t }_{ 2 }=5$ с (рис. 4, площадь выделена штриховкой). Фигура ABCD — это трапеция, ее площадь равна

$S=frac { a+b }{ 2 } cdot h=frac { AD+BC }{ 2 } cdot DC$

где DC = Δt = 4 c, AD = 3 м/c, BC = 5 м/c. Тогда S = 16 м.
Проекция перемещения ${ s }_{ x }>0$ , т.к. проекция скорости ${ v }_{ x }>0$ .
${ s }_{ x }=S=16$ м.

Ответ: 16.

Задача 2. Автомобиль движется по прямой улице вдоль оси X. На рисунке 5 представлен график зависимости проекции скорости автомобиля от времени. Определите путь, пройденный автомобилем в течение указанных интервалов времени.

Интервал времени	Путь
от 0 до 10 с	Ответ: м.
от 30 до 40 с	Ответ: м.

В бланк ответов перенесите только числа, не разделяя их пробелом или другим знаком.

Решение. Путь за промежуток времени Δt = ${ t }_{ 2 }$ – ${ t }_{ 1 }$ численно равна площади фигуры, ограниченной графиком ${ v }_{ x }(t),$ осью времени 0t и перпендикулярами к ${ t }_{ 1 }$ и ${ t }_{ 2 }$ .

На интервале [0 с, 10 с] ищем площадь треугольника (рис. 6).

${ S }_{ 1 }=frac { acdot h }{ 2 }$ ,

где a = 20 м/c, $h=triangle { t }_{ 1 }=10c-0c=10c$ . Тогда ${ S }_{ 1 }=100$ м.

Путь равен значению площади (путь всегда положительный, т.е. s > 0).

${ s }_{ 1 }={ S }_{ 1 }=100$ м.

На интервале [30 с, 40 с] ищем площадь трапеции (см. рис. 6).

${ S }_{ 2 }=frac { a+b }{ 2 } cdot h$ ,

где a = 10 м/c, b = 15 м/c, h = Δt = 40 c – 30 с = 10 с. Тогда ${ s }_{ 2 }={ S }_{ 2 }=125$ м.

Ответ: 100125.

Задача 3. Определите за первые 4 с (рис. 7):

а) проекцию перемещения тела;

б) пройденный путь.

Ответ: а) ____ м; б) ____ м.

Решение. Проекция перемещения за время $triangle t={ t }_{ 2 }-{ t }_{ 1 }=4c-0=4c$ (пер-вые 4 с) численно равна площади фигуры, ограниченной графиком ${ v }_{ x }(t)$ , осью времени 0t и перпендикулярами к ${ t }_{ 1 }=0$ с и ${ t }_{ 2 }=4$ с (рис. 8, площадь выделена штриховкой).

Так как при ${ t }_{ 0 }=3$ с проекция скорости поменяла знак, то получили две фигуры, два треугольника, площади которых равны:

${ S }_{ 1 }=frac { { a }_{ 1 }cdot { h }_{ 1 } }{ 2 } ,quad { S }_{ 2 }=frac { { a }_{ 2 }cdot { h }_{ 2 } }{ 2 }$ ,

где

${ a }_{ 1 }=30quad$ м/с, $quad { h }_{ 1 }=triangle { t }_{ 1 }=3c-0c=3c$

${ a }_{ 2 }$ =|-10 м/c|=10 м/c, $quad { h }_{ 2 }=triangle { t }_{ 2 }=4c-3c=1c$ .

Тогда ${ S }_{ 1 }=45$ м, $quad { S }_{ 2 }=5$ м.

а) Проекция перемещения ${ s }_{ 1x }>0$ , т.к. проекция скорости ${ v }_{ 1x }>0$ ; проекция перемещения ${ s }_{ 2x }<0$ , т.к. проекция скорости ${ v }_{ 2x }<0$ . В итоге получаем: ${ s }_{ x }={ s }_{ 1x }+{ s }_{ 2x }={ S }_{ 1 }-{ S }_{ 2 },quad { s }_{ 1x }=$ 45м — 5м = 40 м. б) Путь равен значению площади (путь всегда положительный, т.е. s>0).

$s={ S }_{ 1 }+{ S }_{ 2 }$ , s = 45 м + 5 м = 50 м.

Ответ: а) 40; б) 50.

Задача 4. График зависимости проекции скорости материальной точки, движущейся вдоль оси 0Х, от времени изображен на рисунке 9. Определите перемещение точки, которое она совершила за первые 6 с.

Ответ: ____ м.

Решение. Проекция перемещения за время $triangle t={ t }_{ 2 }-{ t }_{ 1 }=6c-0=6c$ (пер-вые 6 с) численно равна площади фигуры, ограниченной графиком ${ v }_{ x }(t)$ , осью времени 0t и перпендикулярами к ${ t }_{ 1 }=0 c$ и ${ t }_{ 2 }=6 c$ (рис. 10, площадь выделена штриховкой).

Так как при ${ t }_{ 01 }=2c$ и ${ t }_{ 02 }=4c$ проекция скорости меняет знак, то получили три фигуры, три треугольника, площади которых равны:

${ S }_{ 1 }=frac { { a }_{ 1 }cdot { h }_{ 1 } }{ 2 } ,quad { S }_{ 2 }=frac { { a }_{ 2 }cdot { h }_{ 2 } }{ 2 } ,quad { S }_{ 3 }=frac { { a }_{ 3 }cdot { h }_{ 3 } }{ 2 } ,$

где

${ a }_{ 1 }=3$ м/с, $h_{ 1 }=triangle { t }_{ 1 }=2c-0c=2c$

${ a }_{ 2 }=$ |-2 м/c| = 2 м/с, $h_{ 2 }=triangle { t }_{ 2 }=4c-2c=2c$

${ a }_{ 2 }=$ 3м/c, $h_{ 3 }=triangle { t }_{ 3 }=6c-4c=2c$ .

Тогда ${ S }_{ 1 }=3$ м, ${ S }_{ 2 }=2$ м, ${ S }_{ 3 }=3$ м.

Проекция перемещения ${ s }_{ 1x }>0$ , т.к. проекция скорости ${ v }_{ 1x }>0$ .

Проекция перемещения ${ s }_{ 2x }<0$ , т.к. проекция скорости ${ v }_{ 2x }<0$ . Проекция перемещения ${ s }_{ 3x }>0$ , т.к. проекция скорости ${ v }_{ 3x }>0$ . В итоге получаем:

${ s }_{ x }={ s }_{ 1x }+{ s }_{ 2x }+{ s }_{ 3x }={ S }_{ 1 }-{ S }_{ 2 }+{ S }_{ 3 },quad { s }_{ x }=$ 3 м – 2 м + 3 м = 4 м.

Ответ: 4.

Задача 5. На рисунке приведен график зависимости v_x скорости тела от времени .

Определите путь, пройденный телом в интервале времени от 0 до 5 с.

Ответ: ____ м.

Решение. Решение любых графических задач основывается на умении «читать» графики. В данной задаче рассматривается зависимость проекции скорости тела от времени. На интервале от 0 до 3с проекция скорости уменьшается от значения 15 м/с до 0. На интервале от 3 до 5с модуль проекции начинает возрастать от нулевого значения до 10 м/с. Причем важно «увидеть», что тело в этом временном интервале начинает движение в направлении, противоположном оси ОХ.

Пройденный путь будет определяться площадью геометрической фигуры, образованной под графиком проекции скорости.

Рис.1

Дальнейшее решение задачи сводится к нахождению площадей двух треугольников, заштрихованных на рис.1

$S_1=frac{15cdot 3}{2}=22,5$ (м).

$S_2=frac{10cdot 2}{2}=10$ (м).

Тогда, общий путь в интервале времени от 0 до 5с будет определяться суммой отдельных путей S_1 и S_2 .

(м).
Ответ: 32,5 м

По условию этой задачи можно поставить второй вопрос: найти проекцию перемещения в интервале времени от 0 до 5с.

В этом случае надо учесть, что проекция перемещения в интервале времени от 0 до 3 с положительная и её значение равно пройденному пути на этом интервале.

$S_{1x}=S_1=22,5$ (м).

В интервале времени от 3 с до 5 с проекция перемещения отрицательная, так как тело движется в направлении противоположном оси ОХ.

$S_{2x}=-10$ (м).

Проекция перемещения за весь интервал времени будет равна $S_{o.x}=S_{1x}+S_{2x}$
$S_{o.x}=22,5+(-10)=12,5$ (м).

Ответ: 12,5 м

Задача 6. На рисунке представлен график зависимости модуля скорости v прямолинейно движущегося тела от времени t. Определите по графику путь, пройденный телом в интервале времени от 1 до 5 с.

Ответ: ____ м.

Решение. Для нахождения пройденного пути в интервале времени от 1с до 5с необходимо рассчитать площадь геометрической фигуры под графиком модуля скорости.

Рис.1

Дальнейшее решение сводится к расчету площади трапеции, заштрихованной на графике (см. рис.1).

$S=frac{4+2}{2}cdot 10=30$ (м).

Особенностью подобной задачи является то, что при решении, необходимо внимательно отследить временной интервал, на котором требуется рассчитать пройденный путь.
Ответ: 30 м.

Задача 7. Из двух городов навстречу друг другу с постоянной скоростью двиижутся два автомобиля. На графике показана зависимость расстояния между автомобилями от времени. Скорость первого автомобиля равна 15 м/с. Какова скорость второго автомобиля?

Ответ: ____ м.

Решение. При движении навстречу друг к другу расстояние между двумя автомобилями уменьшается от значения 144 км до 0. На графике видно, что встреча автомобилей произошла в момент времени 60 минут, так как расстояние между автомобилями стало равным 0. Расчеты в этой задаче требуют обязательного применения системы «СИ».

144 км = 144000 м; 60 мин = 3600 с.
Используя эти данные, можно рассчитать скорость сближения автомобилей.

$v=frac{144000}{3600}=40$ м/с

Так как автомобили движутся навстречу друг другу, то отсюда скорость второго автомобиля можно выразить как

(м/с)

Ответ: 25 м/с.

Задача 8. На рисунке представлен график зависимости модуля скорости тела от времени. Найдите путь, пройденный телом за время от момента времени 0 с до момента времени 5 с. (Ответ дайте в метрах.)

Ответ: ____ м.

Решение. Для нахождения пройденного пути необходимо рассчитать площадь геометрической фигуры (трапеции) под графиком модуля скорости (см.рис.1). Это относится к интервалу времени от 0 до 3 с. От 3 с до 5 с скорость тела равна 0, следовательно, тело находилось в состоянии покоя и пройденный путь в этом интервале равен 0.

Рис.1

$S_1=frac{3+1}{2}cdot 10=20$ (м).
S_2=0
(м).

Сакович А.Л., 2020

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Вычисление перемещения по графику проекции скорости» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Задача. Для балки определить перемещения в т. А, В, С, D, подобрать сечение из двух швеллеров из условия прочности, проверить жесткость, показать изогнутую ось балки. Материал — сталь Ст3, допускаемое перемещение .

Определим опорные реакции.

Наносим значение опорных реакций на расчетную схему

2. Строим эпюру моментов от заданной нагрузки – грузовую эпюру М_F.

Т.к. под равномерно распределенной нагрузкой линия параболическая кривая, то для её проведения потребуется дополнительная точка – поставим т.К в середине нагрузки.

Строим эпюру М_F от заданной нагрузки.

3. Подберем сечение из двух швеллеров:

Подбираем 2 швеллера №33 см³.

Проверим прочность подобранного сечения.

Прочность обеспечена.

4. Определим перемещения в заданных точках. Снимаем с балки всю нагрузку. Для определения линейных перемещений (прогибов) прикладываем единичную силу (F=1), а для определения угловых перемещений — единичный момент .

Точки А и В – это опоры, и по граничным условиям в шарнирных опорах прогиб невозможен, а угловое перемещение присутствует. В точках С и D будут и линейные (прогибы), и угловые (углы поворота) перемещения.

Определим угловое перемещение в т.А. Прикладываем в А единичный момент (рис. б). Строим эп , определяем в ней необходимые ординаты. (рис. в).

Ординаты эп.М_F – все положительные, эп. – тоже.

Перемещения будем определять методом Мора по формуле Симпсона.

Определим момент инерции I_х для сечения.

Модуль продольной упругости Е для Ст3 Е = 2·10⁵МПа = 2·10⁸кПа. Тогда:

Угол поворота φ_А получился положительным, это значит, что угол поворота сечения совпадает с направлением единичного момента.

Определим угол поворота φ_В. (рис.г,д )

Теперь определим перемещения в т. С (линейное и угловое). Прикладываем единичную силу (рис. е), определяем опорные реакции и строим эп. от единичной силы (рис.ж).

Рассмотрим рис. е.

Строим эп. :

Определим прогиб в т. С.

Для определения угла поворота в т. С приложим единичный момент (рис. з), определим опорные реакции и построим эпюру единичных моментов (рис. и).

(знак «— « говорит о том, что реакция R_А направлена в обратную сторону. Показываем это на расчетной схеме – рис.з).

Строим эп. ,

Поскольку m=1 приложен в т. С пролета балки, то момент в т. С определим как от левых, так и от правых сил.

Определим прогиб в точке С.

(знак «-» говорит о том, что угол поворота направлен противоположно направлению единичного момента)

Аналогично определим линейное и угловое перемещения в т. D.

Определим у_D. (рис. к).

Строим эп. (рис.л) :

Определим φ_D (рис. м):

Строим эп. — (рис.н).

Определим угол поворота:

(угол поворота направлен в сторону, противоположную единичному моменту).

Теперь покажем изогнутую ось балки (упругую линию), которой стала прямолинейная ось под действием нагрузки. Для этого зарисуем первоначальное положение оси и в масштабе отложим вычисленные перемещения (рис.о).

Проверим жесткость балки , где f – максимальный прогиб.

Максимальный прогиб — жесткость не обеспечена.

Т.о. в данной задаче мы убедились в том, что не всегда сечения, подобранные из условия прочности (в данном случае – сечение из двух швеллеров) удовлетворяют условиям жесткости.

Для решения вопросов жесткости элементов требуется определять перемещения (линейные, угловые). Существуют несколько способов определения перемещений, одним из которых является определение перемещений по интегралу Мора.

Алгоритм вычисления перемещений по интегралу (формуле) Мора:

1. Составляем выражение изгибающего момента M_F от действующей нагрузки.

2. Снимаем с балки (рамы, фермы и т.д.) все нагрузки, и в точке, где необходимо определить перемещение, прикладываем единичную силу (если определяем линейное перемещение) либо единичный момент (если определяем угловое перемещение) по направлению искомого перемещения. Составляем выражение изгибающего момента от единичного фактора.

3. Подставляем выражения моментов в интеграл Мора:

где: Δ — перемещение в общем виде, знак Σ распространяется на все участки балки; EI – изгибная жесткость на участке.

Потенциальную энергию можно определять через работу внешних сил (см. — здесь).

В общем случае: , где Р₀ – любой силовой фактор (растягивающая сила, крутящий момент и тому подобное) называется обобщённой силой;

δ₀ – соответствующая этой силе деформация (удлинение, угол закручивания, угол поворота и тому подобное) называется обобщённым перемещением.

Под обобщённой силой Р₀ следует понимать не одну силу, а уравновешенную систему сил (включая сюда и реактивные усилия), которая производит деформацию.

Рассмотрим общий случай нагружения при изгибе.

За отдельные обобщенные силы здесь можно принимать:

1) Сосредоточенную силу Р с реакциями и

2) Два момента М₀ с соответствующими реакциями.

3) Равномерно распределённую нагрузку q с реакциями А и В.

Обобщённым перемещением δ₀ будем называть величину, характеризующую деформацию, на которую нужно умножить обобщённую силу, чтобы подсчитать произведённую ею работу.

Обобщённым перемещением будут:

1) Прогиб f под силой P,

2) Взаимный угол поворота сечений, где приложены моменты М₀:

θ=θ₁+θ₂, или углы поворота в отдельности θ₁и θ₂.

3) Площадь, заключённая между первоначальной и изогнутой осью балки в районе расположения распределённой нагрузки:

Следует отметить, что если действующая на конструкцию нагрузка представлена несколькими обобщёнными силами (Р₀₁, P₀₂, P₀₃,… и т. д.),то каждое из обобщённых перемещений (δ₀₁, δ₀₂, δ₀₃ и т. д.) является, вообще говоря, функцией всех обобщённых сил:

и так далее.

Так, прогиб под силой Р (см. рисунок) является результатом действия не только силы Р , но и моментов М₀ и распределённой нагрузки q.

Обобщённое перемещение будем считать положительным, если соответствующая обобщённая сила на этом перемещении совершает положительную работу.

Обобщённое перемещение, соответствующее определённой обобщённой силе, не изменится при изменении способа закрепления элемента конструкции.

Зависимости могут быть записаны так:

Здесь а₁₁, а₂₁ и т. д. – некоторые коэффициенты пропорциональности.

Первый индекс указывает порядковый номер перемещения, второй – порядковый номер обобщённой силы.

Потенциальная энергия деформации, создающаяся в упругой системе в результате действия нескольких обобщённых сил, равна половине суммы произведений обобщённых сил на соответствующие обобщённые перемещения, получающиеся от совместного действия всех обобщённых сил:

Потенциальная энергия деформации U равна работе внешних сил W (см. — здесь).

Рассмотрим отдельные виды деформаций.

Растяжение -сжатие

Кручение

Изгиб

При вычислении потенциальной энергии будем предполагать, что деформации не только материала, но и всей конструкции, следуя закону Гука, пропорциональны нагрузкам, т. е. линейно с ними связаны и растут постепенно вместе с ними. Множитель ½ появился здесь как следствие того, что нагружение является статическим и деформации упруги – работа внешних сил измеряется площадью заштрихованного треугольника.

Из полученных выражений следует, что потенциальная энергия деформации равна половине произведения силы или пары сил на перемещение по ее направлению в том сечении, где эта сила приложена.

Таким образом, в общем случае можно записать:

, где U — потенциальная энергия деформации, W — работа внешних сил, P₀ — любой силовой фактор (растягивающая сила, крутящий момент и тому подобное) называется обобщённой силой ; δ₀ — соответствующая этой силе деформация (удлинение, угол закручивания, угол поворота и тому подобное) называется обобщённым перемещением (или — обобщенная координата).

Под обобщённой силой Р₀ следует понимать не одну силу, а уравновешенную систему сил (включая сюда и реактивные усилия), которая производит деформацию.

Для определения перемещений при изгибе (прогибов и углов поворота сечений балок) существуют различные методы (способы). Это интеграл (формула) Мора, метод начальных параметров, метод (правило) Верещагина, формула Симпсона. Кроме них существует более общий метод, пригодный для определения деформаций любых упругих конструкций. Он основан на применении закона сохранения энергии.

Представим, что к стержню подвешен груз. При статическом растяжении упругого стержня происходит превращение потенциальной энергии из одного вида в другой; часть потенциальной энергии действующего на стержень груза (уменьшение) за счёт перемещения нижнего конца стержня полностью переходит в потенциальную энергию деформации стержня (увеличение).

Действительно, если мы будем нагружать стержень путем постепенного подвешивания к его нижнему концу очень малых грузов dP, то при добавлении каждого такого груза подвешенная уже часть нагрузки опустится, и ее потенциальная энергия уменьшится, а потенциальная энергия деформации стержня соответственно увеличится. Это явление имеет место при любом виде деформации всякой упругой конструкции при статической нагрузке; такую конструкцию можно рассматривать как своеобразную машину, преобразующую один вид потенциальной энергии в другой.

Статической называется такая нагрузка, которая возрастает постепенно и таким образом, что ускорениями элементов конструкции можно пренебречь; передача давлений (сил) от одной части конструкции на другую не меняет характера движения этих частей, т. е. их скорость остается постоянной и ускорение отсутствует. При этих условиях деформация конструкции не будет сопровождаться изменением кинетической энергии системы, и будет иметь место лишь преобразование потенциальной энергии из одного вида в другой.

При этом мы пренебрегаем магнитными, электрическими и тепловыми явлениями, сопровождающими упругие статические деформации тела лишь в очень слабой мере. Так как характер движения всех элементов конструкции с течением времени не меняется, то в каждый момент времени будет иметь место равновесие как для каждой части конструкции в целом под действием внешних сил и реакций, так и для каждого элемента этой части под действием внешних сил и напряжений, приложенных к этому элементу.

Деформации конструкции, напряжения в ее частях и реакции, передающиеся от одной части на другую, успевают следовать за ростом нагрузки.Таким образом, можно сказать, что полное преобразование одного вида потенциальной энергии в другой имеет место, если деформация происходит без нарушения равновесия системы.

Мерой энергии, превратившейся в другой вид, является величина работы, произведенной силами, действующими на конструкцию.

Обозначим величину накопленной потенциальной энергии деформации через U, а уменьшение потенциальной энергии внешних нагрузок U_F. Тогда величина U_Fизмеряется положительной работой этих нагрузок W_F, с другой стороны, накоплению потенциальной энергии деформации U соответствует отрицательная работа внутренних, междучастичных сил W, так как перемещения точек тела при деформации происходят в обратном по отношению к внутренним силам направлении.

Закон сохранения энергии при деформациях упругих систем принимает вид:

U_F= U

Заменяя в этой формуле величины U_Fи U численно равными им значениями работ W_Fи —W, получаем иную формулировку этого закона:

W_F= —W или W_F+ W = 0

Эта формулировка закона сохранения энергии совпадает с так называемым «началом» возможных перемещений в применении к упругим системам. Последнее равенство выражает, что при перемещениях без нарушения равновесия сумма работ всех сил, приложенных к точкам тела, равна нулю. Таким образом, начало возможных перемещений в применении к упругим системам является следствием закона сохранения энергии. А потенциальная энергия деформации U численно равна работе внешних сил W_F, проделанной ими этой деформации:

U = W_F

Для определения перемещения по формуле Симпсона необходимо:

Построить грузовую эпюру моментов (эпюру моментов от действия всех внешних нагрузок).
Построить единичную эпюру моментов. Для этого в сечении, где нужно определить линейное перемещение (прогиб) приложить единичную силу, а для определения углового перемещения — единичный момент, и от данного единичного фактора построить эпюру изгибающих моментов.
Перемножить эпюры (грузовую и единичную) по формуле, которая называется формулой Симпсона:

где l_i– длина участка;

EI_i– жесткость балки на участке;

– значения изгибающих моментов с грузовой эпюры, соответственно в начале, в середине и в конце участка;

– значения изгибающих моментов с единичной эпюры, соответственно в начале, в середине и в конце участка.

Если ординаты эпюр расположены с одной стороны от оси балки, то при перемножении учитывается знак «+», если с разных, то знак «-».

Если результат получился со знаком «-», значит искомое перемещение по направлению не совпадает с направлением соответствующего единичного силового фактора.

Во многих случаях интегрирования по Мору можно избежать и применить способ«перемножения» эпюр. Одним из таких способов является способ Симпсона, но также можно определить перемещения по способу (правилу) Верещагина. Этот способ А.К. Верещагин предложил в 1924 году, будучи студентом.

Рассмотрим последовательность действий по правилу Верещагина. Начальный этап такой же, как по формуле Мора и способу Симпсона, т.е. вначале строится грузовая эпюра от действующих нагрузок (действительное состояние), затем рассматриваем балку во вспомогательном состоянии. Вспомогательное состояние получается следующим образом: сначала всю заданную нагрузку нужно удалить, затем приложить «единичный силовой фактор» в том месте, где требуется определить перемещение, и по направлению этого искомого перемещения. Причем, когда определяем линейное перемещение (прогиб балки), то в качестве «единичного силового фактора» принимается сосредоточенная сила, равная единице , а если требуется найти угол поворота, то приложить следует сосредоточенную пару сил, момент, равный единице. Строится эпюра единичных моментов или эпюра от единичной нагрузки. Далее перемещение вычисляется по формуле:

, где в числителе — произведение площади грузовой эпюры на ординату единичной (обязательно прямолинейной), взятой под центром тяжести грузовой эпюры, а в знаменателе — жесткость сечения.

Этот способ становится понятным,если доказать, что результат перемножения двух эпюр ,одна и которых произвольна ,а другая линейна, равен произведению площади грузовой эпюры на ординату единичной, взятой под центром тяжести грузовой эпюры.

Следует иметь в виду, что способы «перемножения» эпюр применимы только при наличии двух условий:

Изгибная жесткость балки на рассматриваемом участке должна быть постоянной(EI=Const),
Одна из двух эпюр моментов на этом участке (грузовая или единичная) должна быть обязательно линейной. При этом обе эпюры не должны в пределах данного участка иметь перелома.

Пусть грузовая эпюра произвольна, а единичная линейна (так как единичной нагрузкой бывает обычно либо сосредоточенная сила, либо пара сил, то единичная эпюра М⁰оказывается ограниченной прямыми линиями). Пусть грузовая эпюра М(z) имеет криволинейное очертание, а эпюра М⁰ – прямолинейное (см. рисунок). Произведение можно рассматривать как элемент площади эпюры М, заштрихованной на рисунке.

Так как ордината М⁰равна то произведение , а весь интеграл , где

— статический момент площади эпюры М(z) относительно оси ординат

Но! Статический момент площади ,как известно, это произведение самой площади на координату центра тяжести. Тогда

, где — это

ордината в единичной эпюре, расположенной под центром тяжести грузовой эпюры. Окончательно, перемещение равно:

Таким образом, результат перемножения двух эпюр равен произведению площади грузовой эпюры на ординату другой (обязательно прямолинейной), взятой под центром тяжести грузовой эпюры.

Правило знаков: если обе «перемножаемые» ординаты в двух эпюрах расположены по одну сторону от оси эпюры (то есть они одного знака), то перед их произведением мы должны поставить знак «плюс», а если они по разные стороны от оси эпюры, то перед произведением ставим знак «минус».

Виды перемещений. Дифференциальное уравнение упругой линии балки

При плоском изгибе балки её упругая линия, лежащая в плоскости действия внешних сил, искривляется, точки этой линии получают некоторые перемещения.

Произвольно выбранная точка С перемещается как в направлении, перпендикулярном АВ, так и вдоль этой линии на величину . Наибольший практический интерес представляет перемещение , которое называется прогибом балки. Угол между направлениями 1-1 и 2-2 называется углом поворота сечения балки. Таким образом , перемещения бывают линейные и угловые.

Наряду с расчётом балки на прочность необходимо производить и расчёт на жёсткость, то есть определять прогибы и углы поворота балки. Существует несколько способов решения задачи о деформациях балок. Рассмотрим аналитический способ. Установим зависимость координаты – уравнение упругой линии.

Из рисунка видно ,что Но! В упругой стадии работы материала углы поворота настолько малы ,что можно считать угол равным его тангенсу. Вспомнив геометрический смысл производной, можно принять угол поворота равным первой производной прогиба по абсциссе сечения.

Правила знаков для перемещений, знаки перемещений

Угол считается положительным, если сечение поворачивается против хода часовой стрелки и наоборот. Прогиб считают положительным согласно принятому направлению осей координат. Если ось координат направлена вверх, то положительным будет прогиб вверх, а отрицательным — вниз.

Для нахождения зависимости y=f(z) используем известное соотношение между кривизной оси с изгибающим моментом и жесткостью сечения балки

При постоянных моменте, кривизне и жесткости балка изгибается по окружности.

Из математики известно, что кривизна кривой может быть выражена так:

Пренебрегая получим приближённое дифференциальное уравнение изогнутой оси балки:

Или

При приближённом дифференциальном уравнении изогнутой оси балки пользуются принципом малости перемещений, а если перемещения очень большие, то используют точное дифференциальное уравнение. В технике допускаемая величина прогиба , где — длина пролёта балки. Уравнение представляет собой линейное дифференциальное уравнение второго порядка с разделяющимися переменными и может быть проинтегрировано в общем виде:

где v- линейное перемещение (прогиб), θ – угловое перемещение, С₁ и С₂ – постоянные интегрирования.

С₁– угол поворота в начале координат, умноженной на величину ЕI;

С₂ – прогиб балки в начале координат, умноженный на EI.

Значения этих постоянных определяют из граничных условий ,т.е. условий опирания балки и условий на границах смежных участков. Вот эти условия:

— у свободно лежащей балки прогибы на обеих опорах равны нулю. При симметричном нагружении у такой балки угол поворота в середине пролета также равен нулю;

— у консольной балки в заделке и прогиб и угол поворота равны нулю;

— на границе смежных участков балки прогиб и угол поворота одинаковы как для левого, так и для правого участка.

Определение перемещений по методу начальных параметров (или по универсальным формулам прогибов и углов поворота сечений)

где у₀ и φ₀ – начальные параметры, то есть прогиб и угол поворота в начале координат, которые определяются из условий закрепления балки:

Порядок определения перемещений по универсальным формулам:

Определить все опорные реакции.
Поместить начало координат обязательно в крайнее сечение балки (левое или правое).
Ось у направить вверх, ось z — вдоль балки.
Найти начальные параметры из условий закрепления балки (возможные случаи показаны выше).
Зная начальные параметры у₀ и φ₀, по универсальным формулам определить интересующие нас перемещения.

При использовании универсальных формул необходимо выполнять следующие требования:

а) В универсальные формулы включать только те внешние силы, которые действуют между началом координат (т.0) и сечением, в котором определяются перемещения. Следует помнить, что опорные реакции – тоже внешние силы.

б) Каждая внешняя сила (Мi, Fi, qi) вводится со знаком изгибающего момента, который эта сила вызывает в сечении, где определяется перемещение.

Для определения любого перемещения (линейного или углового) в методе Мора балка рассматривается в двух состояниях: действительном и вспомогательном. Вспомогательное состояние получается следующим образом: сначала всю заданную нагрузку нужно удалить, затем приложить «единичный силовой фактор» в том месте, где требуется определить перемещение, и по направлению этого искомого перемещения. Причем, когда определяем линейное перемещение (прогиб балки), то в качестве «единичного силового фактора» принимается сосредоточенная сила , а если требуется найти угол поворота, то приложить следует сосредоточенную пару .

Далее в одном и том же произвольном сечении обоих состояний (то есть и действительного, и вспомогательного) составляются аналитические выражения изгибающего момента, которые подставляются в формулу, называемую «интегралом Мора»:

где: знак Σ распространяется на все участки балки,

а EI – изгибная жесткость на участке.

Во многих случаях интегрирования по Мору можно избежать и применить способ «перемножения» эпюр. Одним из таких способов является способ Симпсона, по которому значение интеграла Мора на участке длиной ℓ вычисляется по следующей формуле:

Здесь обозначено: a, b и с – соответственно крайние и средняя ординаты эпюры изгибающих моментов действительного состояния М,

— крайние и средняя ординаты эпюры изгибающих моментов, но только вспомогательного состояния .

Правило знаков: если обе «перемножаемые» ординаты в двух эпюрах расположены по одну сторону от оси эпюры (то есть они одного знака), то перед их произведением мы должны поставить знак «плюс: а если они по разные стороны от оси эпюры, то перед произведением ставим знак «минус».

Следует иметь в виду, что способы «перемножения» эпюр (кроме способа Симпсона известен еще способ Верещагина) применимы только при наличии двух условий:

Изгибная жесткость балки на рассматриваемом участке должна быть постоянной (EI=Const),
Одна из двух эпюр моментов на этом участке должна быть обязательно линейной. При этом обе эпюры не должны в пределах данного участка иметь перелома.

При наличии нескольких участков на балке, удовлетворяющих указанным двум условиям, формула для определения перемещений принимает вид:

Если результат вычисления получается положительным, то, следовательно, направление искомого перемещения совпадает с направлением «единичного силового фактора» ( ), а если результат отрицательный, значит искомое перемещение происходит в направлении, противоположном этому фактору.

Формула Симпсона, записанная через моменты, выглядит следующим образом: перемещения (прогиб или угол поворота) равны

где li – длина участка;

EIi – жесткость балки на участке;

M_F – значения изгибающих моментов с грузовой эпюры, соответственно в начале, в середине и в конце участка;

– значения изгибающих моментов с единичной эпюры, соответственно в начале, в середине и в конце участка.

При перемножении эпюр будет полезным для определения ординат эпюр изгибающих моментов:

, где

Задача

Определить угол поворота сечения на левой опоре φ_А

1) Находим опорные реакции действительного состояния .

2) Строим эпюру моментов действительного состояния М.

3) Выбираем вспомогательное состояние для определения угла поворота φ_А.

4) Находим опорные реакции вспомогательного состояния

«Реагируем» на знак «минус».

5) Строим эпюру моментов вспомогательного состояния:

6) «Перемножаем» эпюры

Поскольку одна из них (а именно ) линейна на всем пролете и не имеет перелома, а эпюра М тоже без перелома, то в формуле Симпсона будет всего один участок, и тогда

Знак «плюс» говорит о том, что сечение А поворачивается в сторону «единичного момента»

Метод начальных параметров (или по универсальным формулам прогибов и углов поворота сечений)

Порядок определения перемещений по универсальным формулам:

Определить все опорные реакции.
Поместить начало координат обязательно в крайнее сечение балки (левое или правое).
Ось у направить вверх, ось z — вдоль балки.
Найти начальные параметры из условий закрепления балки (возможные случаи показаны выше).
Зная начальные параметры у₀ и φ₀, по универсальным формулам определить интересующие нас перемещения.

При использовании универсальных формул необходимо выполнять следующие требования:

б) Каждая внешняя сила (М_i, F_i, q_i) вводится со знаком изгибающего момента, который эта сила вызывает в сечении, где определяется перемещение.

Задача

Найти прогиб конца консоли.

Решение

Задаемся направлениями опорной реакции А и реактивного момента в заделке М_А и составляем уравнения статики:

(1) ,

откуда А = q·2 + F = 10·2 + 20 = 40кН,

(2) ,

откуда

Помещаем начало координат в заделку (т.0).
Ось у направляем вверх, ось z – вдоль балки (вправо).
Формулируем условия закрепления балки при выбранном расположении начала координат:

при z = 0: у_А = 0 (1)

φ_А= 0 (2).

Реализуем эти условия с помощью универсальных формул:

(1): 0=ЕIу₀, откуда у₀=0,

(2): 0=ЕIφ₀, откуда φ₀=0.

Учитывая найденные значения у₀ и φ₀, с помощью формулы прогибов найдём прогиб конца консоли:

при z = 4м

Знак «плюс» результата говорит о том, что прогиб конца консоли происходит в положительном направлении оси у, то есть вверх.

Для получения численного значения прогиба результат следует разделить на изгибную жёсткость балки ЕI, то есть

Источник