Существуют различные
методы описания гармонических колебаний.
Приведём некоторые из них.
-
Аналитический
метод
Задаётся уравнение
колебаний гармонического осциллятора
х=Аsin(ωt+φ0)
по которому и
определяется смещение его от положения
равновесия в любой момент времени.
-
Графический
метод

график гармонического колебания
(рис.6.4) х=Аsin(ωt+φ0).
По оси абсцисс (ОХ) откладывается время
t
или фаза колебаний ωt+φ0,
по оси ординат (ОУ) – смещение х от
положения равновесия.
3. Метод векторной
диаграммы
Э
метод состоит в следующем. Гармоническое
колебание может быть задано с помощью
вектора, длина которого равна амплитуде
А колебания, а направление образует с
осью х угол, равный начальной фазе
колебания (рис. 6.5). Если привести этот
вектор во вращение с угловой скоростью
ω0,
то проекция конца вектора на ось х будет
перемещаться в пределах от +А до -А, а
колеблющаяся величина будет изменяться
со временем по закону
x
= Asin(ω0t+φ0),
совершая гармоническое колебание.
§ 6.1.6 Скорость и ускорение колеблющейся точки
Чтобы
найти скорость материальной точки при
гармоническом колебании, возьмем
производную от смещения колеблющейся
точки x
= Asin(ω0t+φ0)
по времени:
(6.18)
где
υmax
= Аω0
— максимальная скорость (амплитуда
скорости).
На
основании тригонометрических формул
преобразуем (4.18):
(6.19)
Сравнивая
выражения для смещения и скорости
замечаем, что фаза скорости
на больше фазы смещения, т.е. скорость
опережает по фазе смещение на
Продифференцировав (4.18), найдем
ускорение:
(6.20)
где
аmax
= А ω02
— максимальное ускорение (амплитуда
ускорения).
Вместо
(6.20) запишем
а
= аmax
соs
[π + (ω0t+φ0)] (6.21)
Из
сравнения (6.21) и (6.17) следует, что фазы
ускорения и смещения различаются на π,
т. е. эти величины изменяются в противофазе.
Это значит, что при положительном
максимальном смещении ускорение
максимально, но отрицательно. На рисунке
показаны графические зависимости
смещения, скорости и ускорения от времени
(рис.6.6, а) и их векторные диаграммы
(рис.6.6, б) .
§ 6.1.7 Кинетическая и потенциальная энергии колебательного движения
Гармонический
осциллятор обладает как кинетической,
так и потенциальной энергией, которые
последовательно переходят друг в друга
при колебаниях осциллятора. Полная
энергия осциллятора равна сумме
кинетической и потенциальной энергии:
Е
= Ек+Еп
(6.22)
Кинетическая
энергия осциллятора, колеблющегося по
гармоническому закону, вычисляют по
формуле:
(6.23)
с
учётом mω2
=
k
Потенциальную
энергию колебательного движения найдём,
исходя из формулы для потенциальной
энергии упругой деформации:
(6.24)
Складывая
кинетическую и потенциальную энергию,
получим полную механическую энергию
материальной точки, колеблющейся по
гармоническому закону:

Полученное
выражение показывает, что энергия
гармонического осциллятора от времени
не зависит, т.е. с течением времени
остаётся величиной постоянной, а зависит
только от квадрата амплитуды и частоты.
При
отсутствии сил трения полная механическая
энергия системы не изменяется:
(6.26)
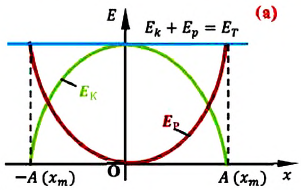
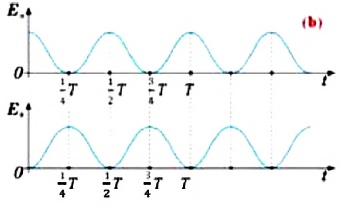
Графически
зависимости кинетической, потенциальной
и полной механической энергий колеблющейся
системы от времени показаны на рис. 4.7,
а.
Потенциальная
яма (ограниченная область пространства,
в которой потенциальная энергия меньше,
чем в не её), соответствующая гармоническому
колебанию, изображена на рис. 6.7, б. Она
определяется зависимостью
.
Отложив на оси ординат полную механическую
энергию Е, по графику определяют интервал
координат (-А, +А), за пределы которого
частица, обладающая такой энергией,
выйти не может.
Соседние файлы в папке Физика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Гармонические колебания:
Некоторые движения, встречающиеся в быту, за равные промежутки времени повторяются. Такое движение называется периодическим движением. Часто встречается движение, при котором тело перемещается то в одну, то в другую сторону относительно равновесного состояния. Такое движение тела называется колебательным движением или просто колебанием.
Колебания, совершаемые телом, которое выведено из равновесного состояния в результате действия внутренних сил, называются собственными (свободными) колебаниями. Величина удаления от равновесного состояния колеблющегося тела называется его смещением (
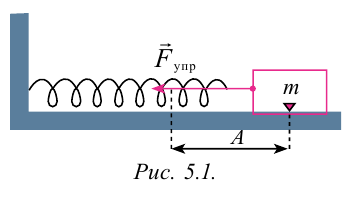
Для наблюдения механических колебаний ознакомимся с колебаниями груза, закрепленного на конце пружины (рис. 5.1). На этом рисунке груз, закрепленный на пружине, сможет двигаться без трения с горизонтальным стержнем, так как силу тяжести шарика приводит в равновесие реакционная сила стержня.
Коэффициент упругости пружины – 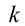
Если груз, который находится в равновесии, потянем вправо на расстояние 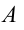
сторону равновесного состояния.
С течением времени смещение груза уменьшается относительно 
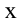
Для определения закономерности изменения в течение времени системы, которая периодически совершает колебания, заполним воронку песком, подвесим на веревке, подложим бумагу под систему и раскачаем воронку. В ходе колебания начинаем равномерно вытягивать бумагу из-под системы. В результате мы увидим, что следы песка на бумаге образуют синусоиду. Из этого можно сделать следующий вывод: смещение периодически колеблющегося тела по истечении времени изменяется по закону синусов и косинусов. При этом самое большое значение смещения равняется амплитуде (
здесь: 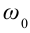
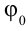
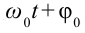
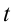
Из математики известно, что 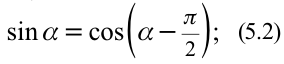
Колебания, в которых с течением времени параметры меняются по закону синуса или косинуса, называются гармоническими колебаниями.
Значит, пружинный маятник, вышедший из равновесного состояния, совершает гармоническое колебание. Для того чтобы система совершала гармоническое колебание: 1) при выходе тела из равновесного состояния, для возвращения его в равновесное состояние должна появиться внутренняя сила; 2) колеблющееся тело должно обладать инертностью и на него не должны оказывать воздействие силы трения и сопротивления. Эти условия называется условиями проявления колебательных движений.
Основные параметры гармонических колебаний
a) период колебания 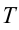

б) частота колебания 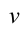
Единица
c) циклическая частота 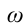
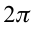
С учетом формул (5.5) и (5.6) уравнение гармонических колебаний (5.2) можно записать в следующей форме.
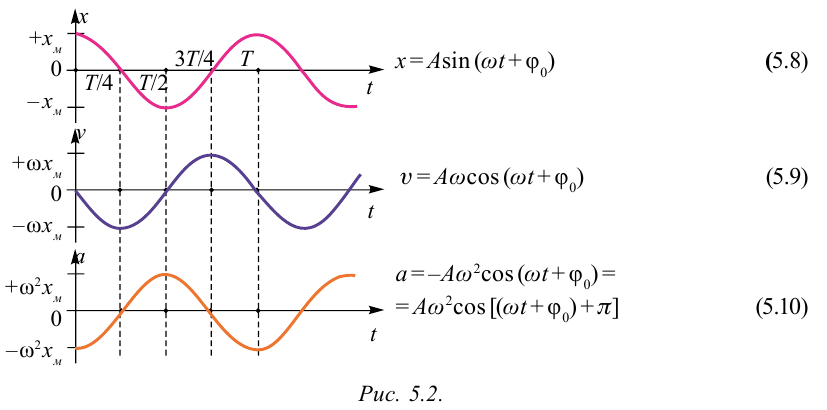
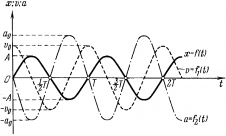
Большинство величин, количественно описывающих гармонические колебания, смещения которых с течением времени меняются по закону синусов или косинусов (скорость, ускорение, кинетическая и потенциальная энергия), тоже гармонически меняются.
Это подтверждается следующими графиками и уравнениями:
Пример решения задачи:
Точка совершает гармоническое колебательное движение. Максимальное смещение и скорость соответственно равны 0,05 м и 0,12 м/с. Найдите максимальное ускорение и скорость колебательного движения, а также ускорение точки в момент, когда смещение равно 0,03 м.
Дано:
Найти:
Формула и решение:
Гармонические колебания пружинного маятника
В 1985 году в городе Мехико произошла ужасная катастрофа, причина которой было землетрясение: 5526 человек погибли, 40 ООО человек ранены, 31000 человек остались без крова. Из проведенных затем исследований ученые выяснили, что главной причиной разрушений во время землетрясения является совпадение частоты свободных колебаний зданий с частотой вынужденных колебаний Земли. Поэтому при возведении новых зданий в сейсмически активной зоне необходимо, чтобы эти частоты не совпадали. Это даст возможность уменьшить последствия землетрясения. С этой целью важно знать, от чего зависят частота и период колебаний.
Одной из простейших колебательных систем, совершающих гармонические колебания, является пружинный маятник.
Пружинный маятник — это колебательная система, состоящая из пружины и закрепленного на ней тела. Колебания, возникающие в пружинном маятнике, являются гармоническими колебаниями:
Под гармоническими колебаниями подразумеваются колебания, возникающие под действием силы, прямо пропорциональной перемещению и направленной против направления перемещения.
Исследование колебаний пружинного маятника имеет большое практическое значение, например, при вычислении колебаний рессор автомобиля при езде; в исследовании воздействия колебаний на фундамент зданий и тяжелых станков, в определении эластичности ушных перепонок при диагностике лор-заболеваний. По этой причине изучение колебаний пружинного маятника является актуальной проблемой.
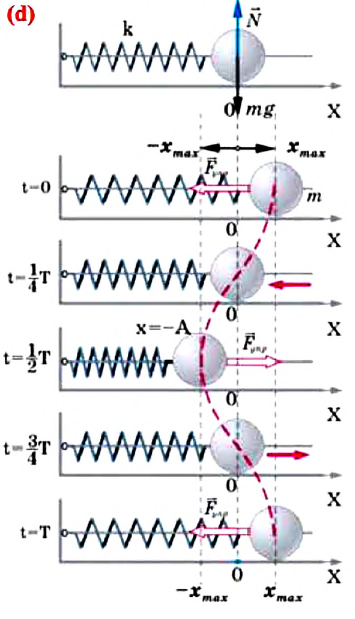
С целью уменьшения количества сил, действующих на колебательную систему, целесообразно использовать горизонтально расположенную колебательную систему пружина-шарик (d).
В этой системе действия силы тяжести и реакции опоры уравновешивают друг друга. При выведении шарика из состоянии равновесия, например, при растяжении пружины до положения 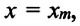
или
Формула (4.9) является уравнением свободных гармонических колебаний пружинного маятника.
Где 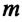
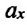
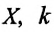
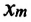
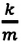
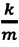
или
Таким образом, уравнение движения пружинного маятника можно записать и так:
Уравнение (4.12) показывает, что колебания пружинного маятника с циклической частотой 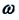
Так как тригонометрическая функция является гармонической функцией, то и колебания пружинного маятника являются гармоническими колебаниями.
Здесь 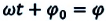
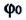
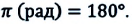
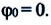

Из сравнения выражений (4.11) и (4.5) определяются величины, от которых зависят период и частота колебаний пружинного маятника:
Из выражений (4.14) и (4.15) видно, что период и частота пружинного маятника зависят от жесткости пружины и массы груза, подвешенного к нему.
Гармонические колебания математического маятника
До наших дней дошла такая историческая информация: однажды в 1583 году итальянский ученый Г. Галилей, находясь в храме города Пиза, обратил внимание на колебательное движение люстры, подвешенной на длинном тросе. Он, сравнивая колебания люстры со своим пульсом, определил, что, несмотря на уменьшение амплитуды колебания, время, затрачиваемое на одно полное колебание (период колебания) люстры, не изменяется. Затем Галилей в результате многочисленных проведенных исследований, изменяя длину нитевого маятника, массу подвешенного к нему груза, высоту расположения маятника (по сравнению с уровнем моря), определил, от чего зависят период и частота колебаний маятника.
Гармонические колебания возникают также под действием силы тяжести. Это можно наблюдать с помощью математического маятника.
Математический маятник — это идеализированная колебательная система, состоящая из материальной точки, подвешенной на невесомой и нерастяжимой нити.
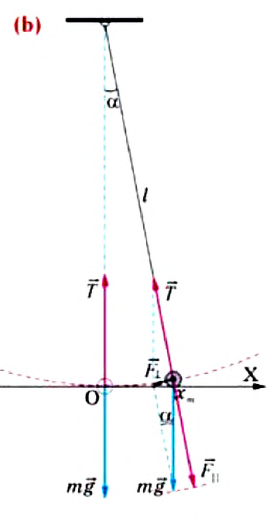
Для исследования колебаний математического маятника можно использовать систему, состоящую из тонкой длинной нити и шарика (b).
Сила тяжести 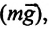
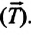
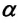
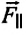
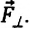
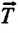
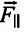
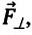
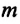
Приняв во внимание, что:
Для уравнения движения математического маятника получим:
Где 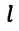
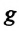
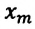
Для данной колебательной системы отношение 

или
Таким образом, уравнение движения математического маятника можно записать и так:
Уравнение (4.19) показывает, что колебания математического маятника являются гармоническими колебаниями с циклической частотой со. Из математики вы знаете, что решением этого уравнения является нижеприведенная функция:
Так как эта функция является гармонической, то и колебания математического маятника являются гармоническими колебаниями.
Отсюда определяются величины, от которых зависят период и частота колебаний математического маятника:
Таким образом, период и частота колебаний математического маятника зависят от длины маятника и напряженности гравитационного поля в данной точке.
Скорость и ускорение при гармонических колебаниях
Вы уже знакомы с основными тригонометрическими функциями и умеете строить графики тригонометрических уравнений, описывающих гармонические колебания.
При гармонических колебаниях маятника его смещение изменяется по гармоническому закону, поэтому не трудно доказать, что его скорость и ускорение также изменяются по гармоническому закону. Предположим, что смещение изменяется по закону косинуса и начальная фаза равна нулю
Так как скорость является первой производной смещения (координат) по времени, то:
или
Как видно из выражения (4.23), скорость, изменяющаяся по гармоническому закону, опережает колебания смещения по фазе на 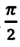
Максимальное (амплитудное) значение скорости зависит от амплитуды, частоты и периода колебаний:
Так как ускорение является первой производной скорости по времени, то получим:
или
Как видим, колебания ускорения, изменяющегося по гармоническому закону, опережают колебания скорости по фазе на 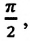
Превращения энергии при гармонических колебаниях
Теоретический материал
Потенциальная и кинетическая энергия свободных гармонических колебаний в замкнутой системе периодически превращаются друг в друга.
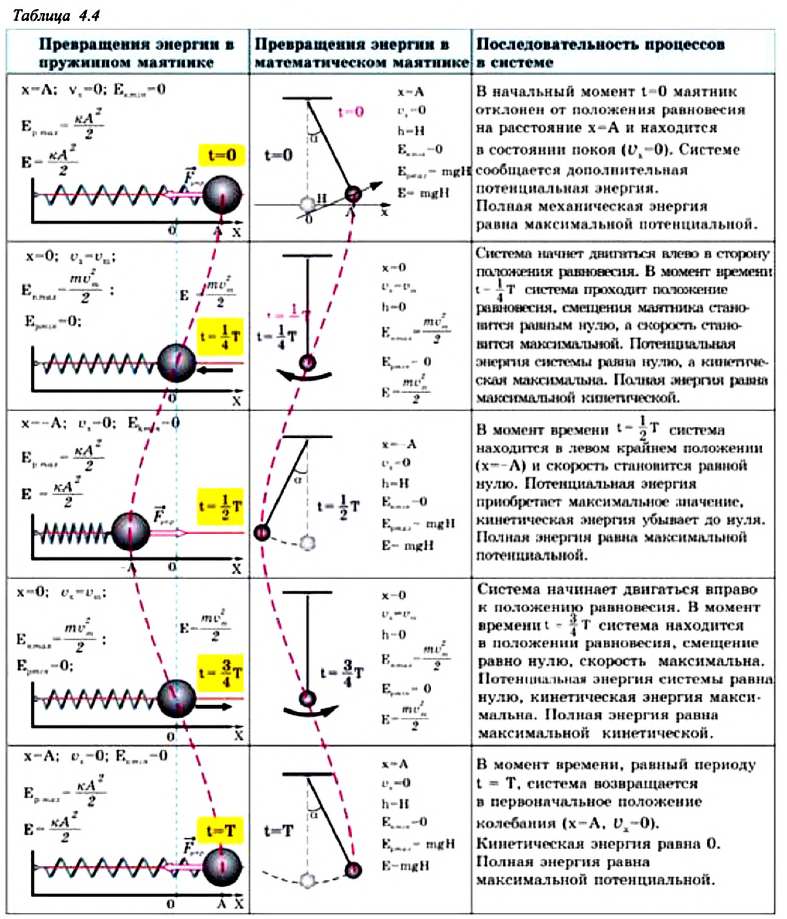
В таблице 4.4 дано сравнение превращений энергий в пружинном и математическом маятниках. Как видно из таблицы, потенциальная энергия колебательной системы в точке возвращения 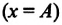
Если же маятник находится в точке равновесия, потенциальная энергия минимальна:
Кинетическая энергия системы, наоборот, в точке возвращения минимальна 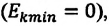
На рисунке (а) даны графики зависимости потенциальной и кинетической энергии при гармоническом колебательном движении от смещения.
Полная механическая энергия замкнутой колебательной системы в произвольный момент времени 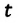
a) для пружинного маятника:
b) для математического маятника:
Если принять во внимание изменение смещения и скорости по гармоническому закону в формулах потенциальной и кинетической энергии колебательного движения, то станет очевидно, что при гармонических колебаниях эти энергии так же изменяются по гармоническому закону (b):
Как было отмечено выше, полная энергия системы не изменяется по гармоническому закону:
• Полная энергия гармонических колебаний прямо пропорциональна квадрату амплитуды колебаний.
Если же в системе существует сила трения, то его полная энергия не сохраняется — изменение полной механической энергии равно работе силы трения. В результате колебания затухают:
Превращения энергии при гармонических колебаниях
Механическая энергия системы равна сумме ее кинетической и потенциальной энергий. Кинетической энергией тело обладает вследствие своего движения, а потенциальная энергия определяется взаимодействием тела с другими телами или полями. Механическая энергия замкнутой системы, в которой не действуют силы трения (сопротивления), сохраняется.
Поскольку при колебаниях гармонического осциллятора силу трения не учитывают, то его механическая энергия сохраняется.
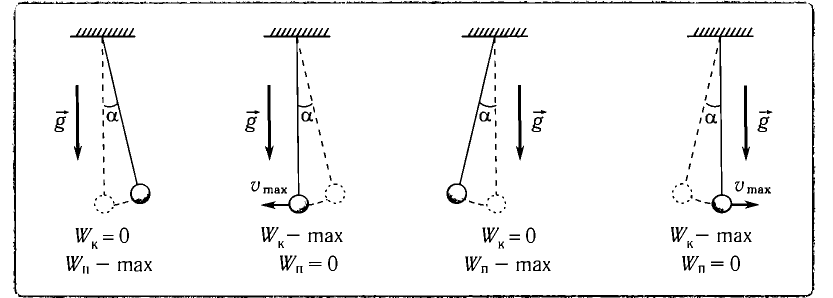
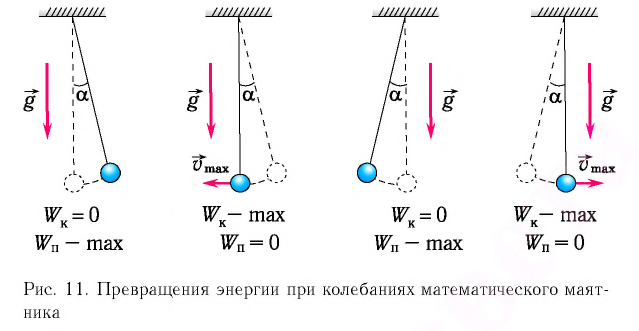
Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю.
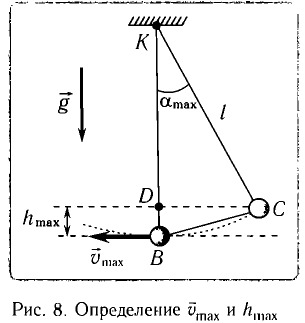
При отклонении маятника на угол а (рис. 7), соответствующий максимальному смещению от положения равновесия, потенциальная энергия максимальна, а кинетическая энергия равна нулю:
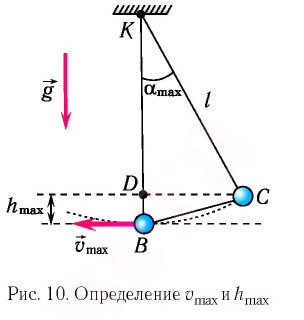
Рис. 7. Превращения энергии при колебаниях математического маятника
Поскольку при прохождении положения равновесия его потенциальная энергия равна нулю, то кинетическая энергия (а следовательно, и скорость) будет максимальна:
Из закона сохранения механической энергии следует (рис. 8), что
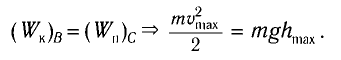
Отсюда найдем модуль максимальной скорости маятника:
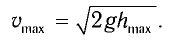
Высоту 
Если колебания малые, то 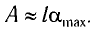
Отсюда
Подставив выражение для 
Подставляя выражения для 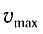

Таким образом, в положении равновесия потенциальная энергия полностью переходит в кинетическую, а в положениях максимального отклонения кинетическая энергия полностью переходит в потенциальную.
В любом промежуточном положении
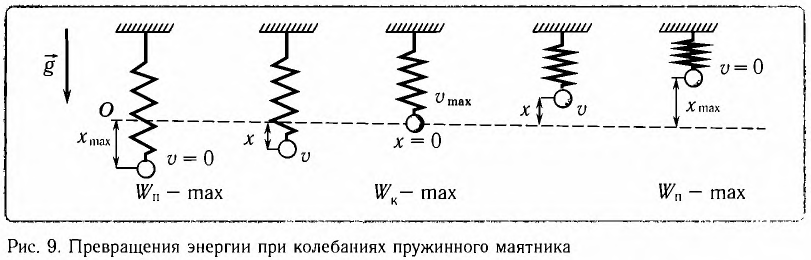
Покажем, что аналогичные превращения энергии имеют место и для пружинного маятника (рис. 9). В крайних точках, когда координата груза принимает значение 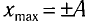
Таким образом, получаем, что механическая энергия гармонического осциллятора пропорциональна квадрату амплитуды колебаний.
В положении равновесия, когда x = 0, вся энергия осциллятора переходит в кинетическую энергию груза:
где 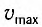
В промежуточных точках полная механическая энергия
Отсюда можно вывести выражение для модуля скорости 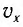
координатой х:
Так как
Энергия при гармонических колебаниях
Механическая энергия системы равна сумме ее кинетической и потенциальной энергии. Механическая энергия замкнутой системы, в которой не действуют силы трения (сопротивления), сохраняется.
Поскольку при колебаниях гармонического осциллятора силой трения пренебрегают, то его механическая энергия сохраняется. Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю.
При отклонении маятника на угол 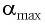
Поскольку при прохождении положения равновесия потенциальная энергия равна нулю 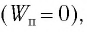
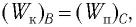
Запишем закон сохранения механической энергии, подставив в него выражения для потенциальной и кинетической энергии:
Отсюда найдем модуль максимальной скорости маятника:
Высоту 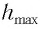
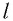
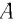
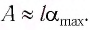
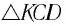
или
Подставив выражение (3) для 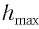
Подставляя выражения (3) для 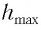
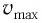
Таким образом, в положении равновесия потенциальная энергия полностью переходит в кинетическую, а в положениях максимального отклонения кинетическая энергия полностью переходит в потенциальную (рис. 11). В любом промежуточном положении
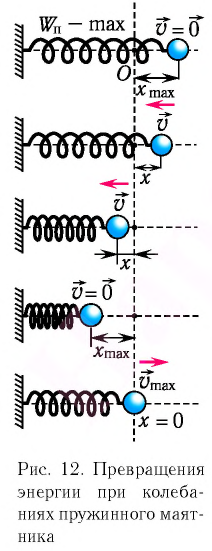
Покажем, что аналогичные превращения энергии имеют место и для пружинного маятника (рис. 12).
В крайних положениях, когда 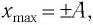
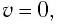
Таким образом, из соотношения (6) следует, что механическая энергия пружинного маятника пропорциональна квадрату амплитуды колебаний.
В положении равновесия, когда 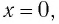
где 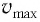
В положениях между крайними точками полная энергия
С учетом выражений для координаты 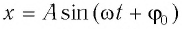
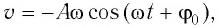
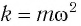
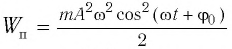
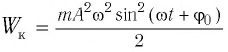
Тогда полная механическая энергия пружинного маятника в этот же. момент времени есть величина постоянная и равная:
Таким образом, начальное смещение 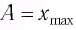
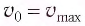
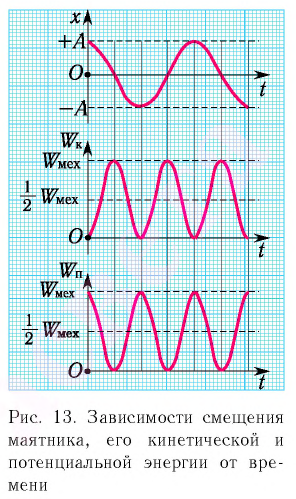
Заметим, что частота периодических изменений кинетической (потенциальной) энергии колеблющегося тела в два раза больше частоты колебаний маятника. Действительно, дважды за период механическая энергия тела будет полностью превращаться в потенциальную (в двух крайних положениях маятника) и дважды за период — в кинетическую (при его прохождении через положение равновесия) (рис. 13).
Пример №1
Математический маятник при колебаниях от одного крайнего положения до другого смещается на расстояние 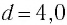
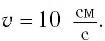
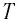
Дано:
Решение
По закону сохранения механической энергии
Отсюда:
Ответ:
Пример №2
Груз массой 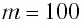
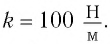
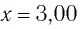
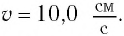
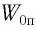
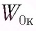
Дано:
Решение Потенциальная энергия груза:
Кинетическая энергия груза:
Начальное смещение груза не является амплитудой, так как вместе с начальным отклонением грузу сообщили и скорость. Однако полная энергия может быть выражена через амплитуду колебаний:
Отсюда
Циклическая частота:
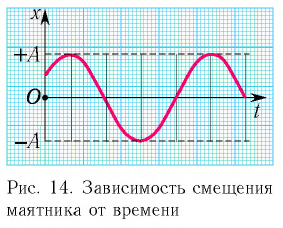
В начальный момент времени 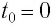
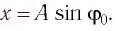
Тогда закон гармонических колебаний имеет вид (рис. 14):
Ответ:
- Вынужденные колебания в физике
- Электромагнитные колебания
- Свободные и вынужденные колебания в физике
- Вынужденные электромагнитные колебания
- Закон Архимеда
- Движение жидкостей
- Уравнение Бернулли
- Механические колебания и волны в физике
|
ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ |
|
|
Колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону), наз. гармоническими колебаниями. Например, в случае механических гармонических колебаний:. В этих формулах ω – частота колебания, xm – амплитуда колебания, φ0 и φ0’ – начальные фазы колебания. Приведенные формулы отличаются определением начальной фазы и при φ0’ = φ0 +π/2 полностью совпадают. |
|
|
Это простейший вид периодических колебаний. Конкретный вид функции (синус или косинус) зависит от способа выведения системы из положения равновесия. Если выведение происходит толчком (сообщается кинетическая энергия), то при t=0 смещение х=0, следовательно, удобнее пользоваться функцией sin, положив φ0’=0; при отклонении от положения равновесия (сообщается потенциальная энергия) при t=0 смещение х=хm, следовательно, удобнее пользоваться функцией cos и φ0=0. |
|
|
Выражение, стоящее под знаком cos или sin, наз. фазой колебания: Фаза колебания измеряется в радианах и определяет значение смещения (колеблющейся величины) в данный момент времени. |
|
|
Амплитуда колебания зависит только от начального отклонения (начальной энергии, сообщенной колебательной системе). |
|
|
Скорость и ускорение при гармонических колебаниях. |
|
|
Согласно определению скорости, скорость – это производная от координаты по времени |
|
|
Таким образом, мы видим, что скорость при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания скорости опережают колебания смещения по фазе на π/2. |
|
|
Величина |
|
|
Следовательно, для скорости при гармоническом колебании имеем: |
|
|
Согласно определению ускорения, ускорение – это производная от скорости по времени:
Ускорение при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания ускорения опережают колебания скорости на π/2 и колебания смещения на π (говорят, что колебания происходят в противофазе). |
|
|
Величина — максимальное ускорение (амплитуда колебаний ускорения). Следовательно, для ускорения имеем: |
|
|
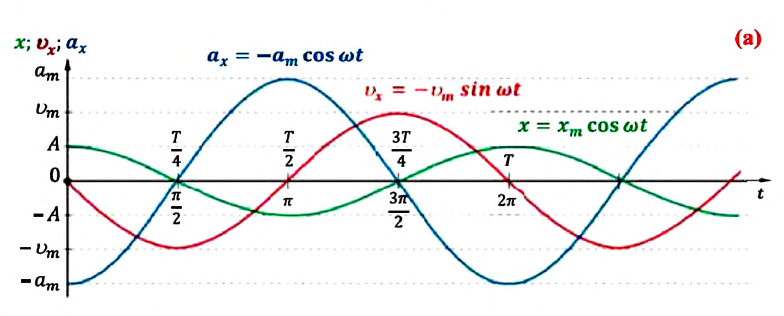
Из анализа процесса колебательного движения, графиков и соответствующих математических выражений видно, что при прохождении колеблющимся телом положения равновесия (смещение равно нулю) ускорение равно нулю, а скорость тела максимальна (тело проходит положение равновесия по инерции), а при достижении амплитудного значения смещения – скорость равна нулю, а ускорение максимально по модулю (тело меняет направление своего движения). |
|
|
Сравним выражения для смещения и ускорения при гармонических колебаниях:
|
|
|
Можно записать: т.е. вторая производная смещения прямо пропорциональна (с противоположным знаком) смещению. Такое уравнение наз. уравнением гармонического колебания. Эта зависимость выполняется для любого гармонического колебания, независимо от его природы. Поскольку мы нигде не использовали параметров конкретной колебательной системы, то от них может зависеть только циклическая частота. |
|
|
Часто бывает удобно записывать уравнения для колебаний в виде: где T – период колебания. Тогда, если время выражать в долях периода подсчеты будут упрощаться. Например, если надо найти смещение через 1/8 периода, получим: |
|
Содержание книги
Предыдующая страница
§17. Механические колебания
17.2 Кинематика колебательного движения.
В данном разделе мы рассмотрим простейшую кинематическую модель колебательного движения материальной точки, движущейся вдоль прямой. Условия, при которых эта модель адекватно описывает реальные колебания, могут быть получены только на основании физических законов, в частности, законов динамики.
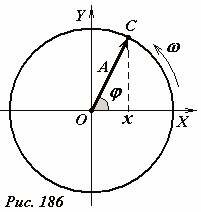
Для построения этой модели обратим внимание, что равномерное движение точки по окружности является периодическим процессом. Действительно, пусть материальная точка C движется с постоянной угловой скоростью ω по окружности радиуса A. При этом угловая координата точки будет изменяться по линейному закону
(~varphi = varphi_0 + omega t) , (1)
где φ0 — начальная координата точки. Не смотря на то, что угол поворота монотонно возрастает, через равные промежутки времени, равные периоду вращения (~T = frac{2 pi}{omega}) точка возвращается в исходное положение, в котором ее кинематические характеристики (скорость, ускорение) принимают исходные значения. Если радиус-вектор точки, векторы ее скорости и ускорения изменяются по периодическому закону, то и их проекции также изменяются по периодическим законам. Иными словами, движение проекции точки на любую из осей координат является колебательным движением вдоль прямой.
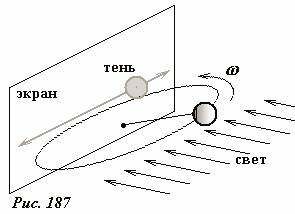
Отметим, что такое колебательное движение проекции можно наблюдать в реальном эксперименте. Для этого необходимо поместить вращающийся по окружности шарик перед плоским экраном и осветить его световым потоком, параллельным плоскости вращения (Рис. 187). В этом случае тень от шарика будет совершать колебания вдоль одной прямой.
Даже будучи не знакомы с тригонометрическими функциями, достаточно легко построить график закона движения тени шарика. Для этого необходимо изобразить окружность, отметить на ней равноотстоящие точки, а затем нанести на график временной зависимости их координаты через равноотстоящие интервалы времени. (Рис. 188).
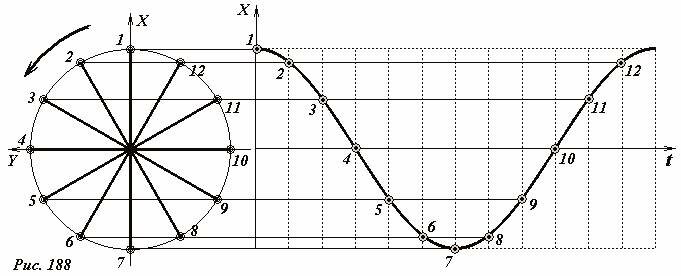
Не будем делать вид, что нам совсем незнакома ни тригонометрия, ни кинематические законы равномерного движения по окружности, и на их основании получим строгие выражения для кинематических характеристик рассматриваемой модели колебательного движения.
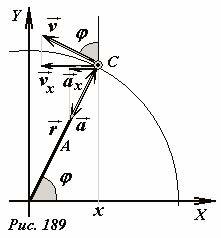
Еще раз изобразим часть окружности радиуса A, по которой движется материальная точка C (Рис. 189). Положение точки задается радиус-вектором (~vec r), направленным под переменным углом φ к оси Ox. Проекция этого вектора на ось Ox равна
(~x = A cos varphi) . (2)
Учитывая, что угол поворота изменяется в соответствии с формулой (1), получим закон изменения координаты точки от времени
(~x(t) = A cos (varphi_0 + omega t)) . (3)
Движение, при котором координата точки изменяется по закону косинуса (или синуса) называется гармоническим [1] колебанием. Таким образом, при равномерном движении точки по окружности ее проекция совершает гармонические колебания.
Как следует из вида функции (3), гармоническое колебание точки определяется тремя параметрами, каждый из которых имеет наглядный смысл[2]. Параметр A называется амплитудой колебаний, он равен максимальному отклонению точки от центрального положения. Эта величина имеет ту же размерность, что и координата x, то есть размерность длины. Изменяющаяся величина (varphi = varphi_0 + omega t) называется фазой колебания, а величина φ0 — начальной фазой.
Параметр ω называется круговой частотой колебаний. Так как период косинуса равен 2π, то при изменении аргумента косинуса на эту величину значения функции принимает прежнее значение. Это обстоятельство позволяет выразить круговую частоту через время одного колебания T (которое также называется периодом колебаний). Для этого следует учесть, что при изменении времени на период Δt = T фаза колебания изменяется на (Delta varphi = omega Delta t = 2 pi), то есть (omega T = 2 pi). Таким образом, круговая частота связана с периодом колебания соотношением
(~omega = frac{2 pi}{T}) . (4)
Более наглядной характеристикой колебаний является обычная частота ν — число колебаний в единицу времени. Если период – это время одного колебания, то величина обратная периоду равна числу колебаний в единицу времени, то есть частоте колебаний
(~nu = frac{1}{T}) . (5)
С помощью соотношений (4)-(5) легко связать круговую и обычную частоты колебаний
(~omega = 2 pi nu) . (5)
Очевидно, что круговая и обычные частоты являются размерными физическими величинами, их размерность обратная размерности времени [ω] = [ν] = [T]-1 = c-1. Для обычной частоты колебаний единица ее измерения называется Герц (сокращенно Гц): частота колебаний 1 Герц означает одно колебание в секунду.
На основании полученного соотношения (6) иногда говорят, что круговая частота колебаний равна числу колебаний за 2π секунд .Однако, по нашему мнению, такое определение является излишним, потому, что, во-первых, попробуйте точно отмерить указанное количество секунд, а, во-вторых, время не обязательно измерять в секундах. Поэтому к этой величине следует относиться как к удобной вспомогательной математической величине – если везде использовать только физически наглядную частоту колебаний ν, то во всех формулах придется дописывать множитель 2π, что приводит к необоснованному перерасходу чернил и бумаги. Также не следует искать особого наглядного смысла в фазе колебаний.
Отметим, что подобные замечания касательно угловой скорости вращения ω (аналогом которой является круговая частота) не обоснованы, так угловая скорость имеет явный физический смысл – угол поворота (измеренный в радианах) в единицу времени.
При движении по окружности вектор скорости точки направлен по касательной к окружности (см. Рис. 189), его модуль равен (upsilon = omega A) (напомним, здесь A — радиус окружности). Если проекция радиус-вектора (~vec r) есть координата точки x , то проекция вектора скорости (~vec upsilon) на ту же ось будет равна скорости движения проекции. Из рисунка не сложно определить, что проекция вектора скорости на ось Ox равна (upsilon_x = -upsilon sin varphi). Используя выражения для модуля скорости и выражение для угла поворота, определяем, что скорость точки при гармоническом колебании (3) зависит от времени по закону
(~upsilon(t) = — omega A sin (omega t + varphi_0)) . (7)
Величина (omega A = upsilon_0) равна максимальной скорости движения точки при гармонических колебаниях. Отметим также, что при гармонических колебаниях скорость точки также изменяется по гармоническому закону.
Аналогичным образом найдем ускорение точки, совершающей гармонические колебания. Так при равномерном движении по окружности ускорение точки является центростремительным, то есть вектор ускорения (~vec a) направлен к центру окружности, а его модуль равен (a = omega^2 A). Из рис. 189 следует, проекция вектора ускорения на выбранную ось Ox равна (a_x = -a cos varphi). Следовательно, зависимость ускорения от времени при гармонических колебаниях имеет вид
(~a(t) = — omega^2 A cos (omega t + varphi_0)) . (8)
Полученные функции зависимости скорости и ускорения точки от времени можно получить непосредственно из закона движения (3). Действительно, мгновенная скорость является первой производной координаты по времени, поэтому функция (7) является первой производной от функции (3).
(~upsilon(t) = (x(t))’ = — omega A sin (omega t + varphi_0)) . (7а)
Аналогично зависимость ускорения от времени (8) является первой производной от скорости (7) или второй производной координаты (3).
(~a(t) = (upsilon(t))’ = (x(t))» = — omega^2 A cos (omega t + varphi_0)) . (8а)
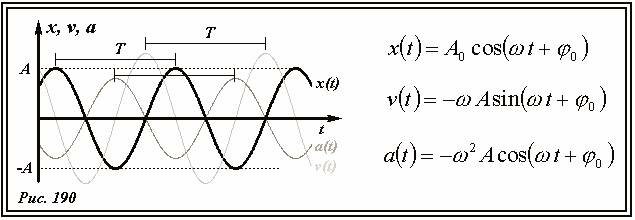
На рис. 190 показаны графики зависимостей координаты x(t), скорости υ(t) и ускорения a(t) точки, совершающей гармонические колебания. Все эти зависимости описываются гармоническими функциями одного периода (одинаковой частоты), сдвинутыми друг относительно друга на четверть периода, (которой соответствует сдвиг фазы на (~frac{pi}{2})). Между нулями и экстремумами этих функций существуют очевидные соответствия: координата движущейся точки достигает максимального и минимального значения, когда ее скорость обращается в нуль; модуль скорости максимален, когда точка проходит через нулевую координату; модуль ускорения максимален, когда скорость равна нулю, а отклонение точки максимально.
Теперь обратим внимание, на чрезвычайно интересное и важное соотношение между ускорением точки и ее координатой[3], которое следует из сравнения функций (8) и (3):
(~a(t) = — omega^2 x) . (9)
При гармонических колебаниях ускорение точки пропорционально его координате, с отрицательным коэффициентом пропорциональности.
При изучении механического движение мы неоднократно подчеркивали, что известная зависимость ускорения тела (~vec a(t, vec r, vec upsilon)) от времени, координат, скорости при известных начальных условиях позволяет однозначно найти закон движения – зависимость координат от времени (~vec r(t)), то есть решить основную задачу механики. Уравнение (9) является частным случаем этой задачи: ускорение зависит от координаты, причем элементарным образом, оно просто пропорционально ей. Следовательно, если на основании динамических законов нам удастся показать, что в некоторой реальной физической системе выполняется уравнение (9), то мы можем однозначно утверждать, что эта система может совершать гармонические колебания.
Мы получили это важнейшее уравнение исходя из рассмотрения закона движения (3). Теперь мы можем решить обратную задачу: если при движении материальной точки ее ускорение связано с координатой соотношением (9), то зависимость координаты от времени описывается функцией:
(~x(t) = A_0 cos (omega t + varphi_0)) . (10)
В этом выражении параметры A0 (амплитуда колебаний) и φ0 (начальная фаза) могут быть любыми – при любых значениях этих параметров, функция (10) удовлетворяет уравнению (9).
Заметим, что, не смотря на указанный произвол в решении уравнения (9), само уравнение уже немало говорит о возможных движениях системы: во-первых, оно указывает, что движение есть гармоническое колебание, во-вторых, однозначно указывает частоту колебаний. Коэффициент пропорциональности в этом уравнении есть квадрат круговой частоты, взятый с противоположным знаком.
Вспомним. Пусть все силы, действующие на тело постоянны, и по величине, и по направлению. В этом случае из законов динамики следует, что движение тела является равноускоренным, причем величина ускорения также определяется на основании этих же законов. Однако, для однозначного нахождения закона движение требуется задание начальных условий.
Чтобы однозначно определить закон движения при гармонических колебаниях необходимо произвольные параметры A0 и φ0 выразить через начальные условия. Итак, пусть заданы начальные условия:
при t = 0 (~left{begin{matrix} x = x_0 \ upsilon = upsilon_0 end{matrix}right.) . (11)
Используя тригонометрическую формулу для косинуса суммы, перепишем выражение (10) в виде
(~x(t) = A_0 cos (omega t + varphi_0) = A_0 (cos varphi_0 cdot cos omega t — sin varphi_0 cdot sin omega t) = A cos omega t + B sin omega t) , (12)
в котором вместо двух произвольных параметров A0 и φ0 введены два новых параметра:
(~begin{matrix} A = A_0 cos varphi_0 \ B = -A_0 sin varphi_0 end{matrix}) . (13)
Аналогичным образом можно преобразовать выражение[4] для скорости частицы (7)
(~upsilon(t) = — omega A_0 sin (omega t + varphi_0) = — omega A_0 (sin omega t cdot cos varphi_0 + cos omega t cdot sin varphi_0) = -omega A sin omega t + omega B cos omega t) . (14)
Подставим в функции (12) и (14) начальные условия (11) получим выражения
(~left{begin{matrix} x(0) = x_0 = A cos 0 + B sin 0 =A \ upsilon(0) = upsilon_0 = -omega A sin 0 + omega B cos 0 = omega B end{matrix}right.) ,
из которых следуют искомые формулы для параметров функции (12):
(~A = x_0 ; B = frac{upsilon_0}{omega}) .
Таким образом, решение уравнения (9) с начальными условиями (11) имеет вид
(~x(t) = x_0 cos omega t + frac{upsilon_0}{omega} sin omega t) . (15)
Не составляет труда представить эту же функцию в виде (10). Так амплитуда колебаний при заданных начальных условиях определяется выражением
(~A_0 = sqrt{A^2 + B^2} = sqrt{x^2_0 + left( frac{upsilon_0}{omega} right)^2}) . (16)
а начальная фаза удовлетворят условию
(~operatorname{tg} varphi_0 = frac{sin varphi_0}{cos varphi_0} = -frac{B}{A} = -frac{upsilon_0}{omega x_0}) . (17)
Подчеркнем еще одно важнейшее свойство гармонических колебаний, описываемых уравнением (9) – период и частота этих колебаний не зависят от их амплитуды. Если амплитуда колебаний определяется начальными условиями, то их частота полностью определяется коэффициентом пропорциональности между ускорением и координатой точки.
Отметим, что формально с математической точки уравнение (9) можно рассматривать в общем виде. Пусть некоторая функция X(t) удовлетворяет условию, что ее вторая производная пропорциональна самой функции (с отрицательным коэффициентом пропорциональности)
(~X» = -omega^2 X) . (18)
тогда эта функция изменяется по гармоническому закону (X(t) = A cos (omega t + varphi_0)), в котором параметры A и φ0 находят из начальных условий, а круговая частота определяется самим уравнением.
17.2.1 Фазовые траектории колебательного движения.
Рассмотрим еще один наглядный способ графического представления произвольных (не только гармонических) колебаний. Пусть закон колебательного движения описывается функцией x(t), которая обязательно является периодической. По известному закону движения можно определить зависимость скорости от времени, как производную от координаты υ(t) = (x(t))′. Введем на плоскости систему декартовую систему координат, вдоль одной из осей которой будем откладывать координату точки, а вдоль другой — ее скорость. Введенная таким образом система называется фазовой плоскостью. Две функции x(t) и υ(t) в любой момент времени определяют на этой плоскости некоторую точку, а геометрическое место этих точек образует некоторую непрерывную линию, которая называется фазовой траекторией.
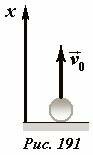
Приведем пример построения фазовой траектории. Пусть небольшой упругий шарик брошен вертикально вверх (Рис. 191) с начальной скоростью υ0. Если пренебречь сопротивлением воздуха, то скорость шарика будет изменяться со временем по закону
(~upsilon = upsilon_0 — gt) , (1)
где g — ускорение свободного падения. Изменение координаты шарика с течением времени описывается функцией
(~x = upsilon_0 t — frac{gt^2}{2}) . (2)
Поднявшись на максимальную высоту (~x_0 = frac{upsilon^2_0}{2g}), шарик упадет на горизонтальную поверхность и отразится от него. Если удар считать абсолютно упругим, то скорость шарика после удара примет первоначальное значение, после чего движение шарика будет повторяться. Графики зависимостей координаты и скорости шарика[5] от времени показаны на Рис. 192а, б.
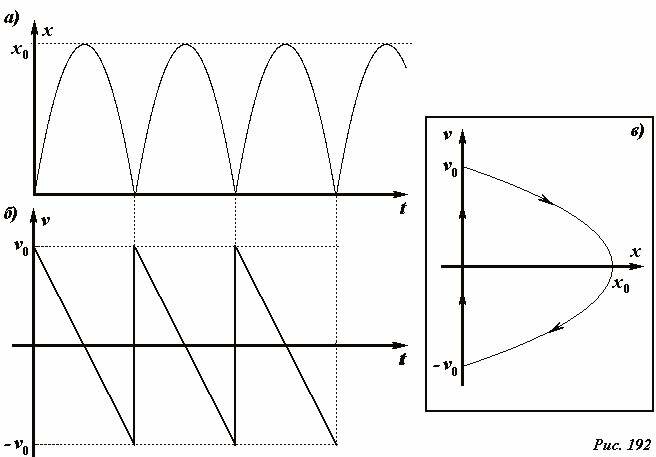
Эти же функции (1), (2) определяют в параметрической форме линию на фазовой плоскости – фазовую траекторию движения шарика. Эта линия показана на Рис. 192 в. Понятно, что при периодическом движении фазовая траектория является замкнутой. На фазовой траектории принято указывать направление движения: при положительной скорости координата возрастает, а при отрицательной скорости координат убывает.
Иногда говорят, что фазовая траектория указывает зависимость скорости от координаты, но такое высказывание не всегда корректно: так одной координате может соответствовать несколько значений скорости (как в рассмотренном примере). А функциональная зависимость требует однозначного соответствия – каждому значению координаты соответствует единственное значение скорости.
Особенно просто выглядит фазовая траектория гармонического колебания, при котором координата и скорость описываются функциями
(~left{begin{matrix} x = A cos (omega t + varphi_0) \ upsilon = -omega A sin (omega t + varphi_0) end{matrix}right.) . (3)
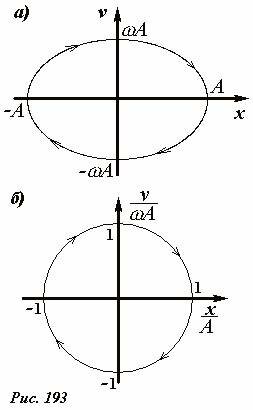
Из этих уравнений следует, что уравнение фазовой траектории можно записать в виде
(~left( frac{x}{A} right)^2 + left( frac{upsilon}{omega A} right)^2 = 1) , (4)
которое является уравнением эллипса[6] с полуосями A и ωA (Рис. 193 а). Еще более предпочтительным является построение фазовой траектории в относительных единицах: когда по одной оси откладывается отношение координаты к амплитуде колебаний (~left( frac{x}{A} right)) , а на другой отношение скорости к максимальной скорости движения (~left( frac{upsilon}{omega A} right)) . В этих координатах
фазовая траектория гармонического колебания является окружностью единичного радиуса (Рис. 193 б). С помощью фазовой диаграммы легко анализировать характер колебания – так отличить окружность от другой замкнутой кривой легко даже «на глаз».
17.2.2 Негармонические колебания. Разложение Фурье.
Сейчас мы покажем, что использование модели гармонических колебаний позволяет описывать и более сложные периодические движения. Еще в 1822 году французский физик и математик Жан Батист Жозеф Фурье в своей работе «Аналитическая теория теплоты» показал, что любая периодическая функция может быть представлена в виде суммы гармонических функций (то есть синусов и косинусов), при чем частоты этих функций являются кратными основной частоте. Так, если период некоторой функции x(t) равен T, то эта функция может быть представлена в виде суммы (разложения Фурье):
(~x(t) = A_0 + (A_1 cos omega t + B_1 sin omega t) + (A_2 cos 2omega t + B_2 sin 2omega t) + (A_3 cos 3omega t + B_3 sin 3omega t)+ ldots = A_0 + sum_k (A_k cos komega t + B_k sin komega t)) .
В общем случае эта сумма должна содержать бесконечно много слагаемых, однако в большинстве практически значимых случаев коэффициенты этого разложения достаточно быстро убывают с ростом номера k (и соответствующе ей частоты (~omega_k = k frac{2 pi}{T})), поэтому практически всегда с достаточной степенью точности можно ограничиться относительно небольшим числом слагаемых.
С разложением периодической функции хорошо знакомы музыканты, которые знают, что каждой ноте (основному тону), взятой на любом музыкальном инструменте соответствует целый набор кратных частот (обертонов). Набор этих колебаний с кратными частотами составляет тембр звука.
Существуют достаточно простые формулы, позволяющие находить коэффициенты разложения Фурье. Мы не собираемся в дальнейшем использовать разложение Фурье, поэтому ограничимся рядом простых примеров разложения периодических функций.
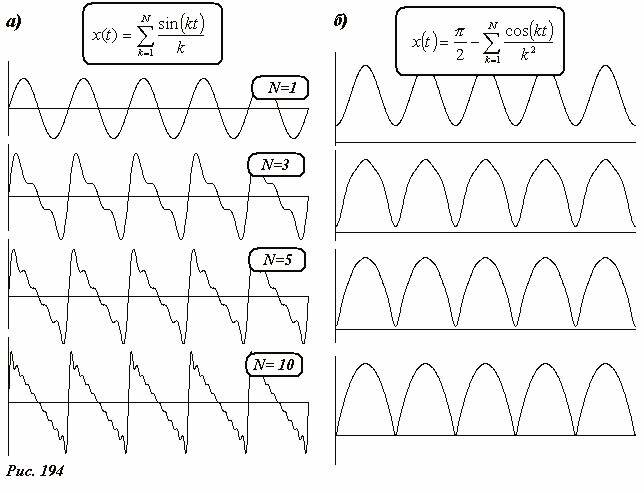
На Рис. 194 а. показаны графики функций (~x(t) = sum_{k=1}^N frac{sin (kt)}{k}) при различных значения числа слагаемых N. Не трудно догадаться, что при больших N эти функции стремятся к рассмотренной выше зависимости скорости от времени, изображенной на Рис. 192. Даже при относительно небольшом N = 5 сходство этих функций уже вполне узнаваемо. Можно найти и разложение Фурье для зависимости координаты от времени в этом же примере, являющейся набором парабол. Эта зависимость выражается суммой (~x(t) = frac{pi}{2} — sum_{k=1}^N frac{cos (kt)}{k^2}).
Графики этих функций для разного числа слагаемых изображены на Рис. 194 б.
Таким образом, с математической точки зрения прыгающий шарик вполне можно описать суммой десяти гармонических колебаний с кратными частотами.
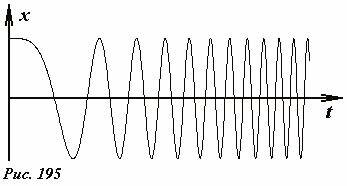
На этом мы заканчиваем рассмотрение кинематического описания колебательного движения, которое, во многом, построено на основании описания равномерного движения материальной точки по окружности. Подчеркнем, что многократное упоминание о равномерности движения не является излишним. Так как при неравномерном движении по окружности, движущаяся материальная точка, конечно, будет возвращаться в исходные положения, но не через равные промежутки времени – поэтому ее движение не будет периодическим, кроме того, скорость и ускорение также не будут изменяться периодически. Для примера, на Рис. 195 показан график зависимости координаты точки, движущейся по окружности равноускоренно. Эта функция описывается выражением (~x = A cos frac{beta t^2}{2}). Видно, что эта функция не периодическая.
Примечания
- ↑ Подчеркнем, что не все колебания являются гармоническими, однако рассматриваемый здесь вид колебаний является простейшей моделью колебательного движения, тем не менее, достаточно часто встречающегося в действительности. Название этого вида движения связано с тем, что функции синус и косинус называются гармоническими функциями, как наиболее совершенные и изящные (по мнению некоторых математиков).
- ↑ Все эти параметры имеют явные аналоги в характеристиках движения по окружности, однако в теории колебательного движения они получили «персональные имена».
- ↑ Это соотношение настолько важно для дальнейшего изложения теории колебаний, что мы его заключили в рамку.
- ↑ Конечно, можно просто взять производную от функции (12).
- ↑ Строго говоря, процесс движения шарика не будет строго периодическим, так как скорость шарика будет изменяться вследствие сопротивления воздуха и неупругости его ударов, но этими факторами мы пренебрежем. Кроме того, удар шарика и изменение его скорости происходит не мгновенно, а в течение некоторого промежутка времени, которой пренебрежимо мало по сравнением со временем его свободного движения.
- ↑ Можно дать следующее «определение» этой хорошо знакомой линии: эллипс – «это круг, который можно вписать в квадрат со сторонами 3×4».
Следующая страница
Колебания и волны: скорости и ускорения
В этой статье мы вспомним кинематику: то, что скорость — производная координаты, а ускорение — производная скорости или вторая производная координаты. Заодно потренируемся брать производные от сложных функций.
Задача 1.
Материальная точка совершает гармонические колебания по закону . Определить амплитуду, круговую частоту, период и начальную фазу колебаний. Найти амплитуды скорости и ускорения. Построить графики зависимости координаты. скорости и ускорения точки от времени.
Амплитуда равна , круговая частота (или циклическая, или угловая) равна
, начальная фаза равна
, период колебаний —
с.
Скорость – производная координаты. Возьмем производную:
Тогда м/с.
Ответ: амплитуда , круговая частота
, начальная фаза
, период колебаний —
с,
м/с,
м/с
Задача 2.
Материальная точка совершает гармонические колебания с частотой Гц. Амплитуда колебаний А =3 см. Определить скорость точки в момент времени, когда смещение
см.
Запишем закон колебаний. Так как не указано, по какому закону они совершаются, то выберем косинус.
Скорость – производная координаты. Возьмем производную:
Ответ: см/с.
Задача 3.
Написать закон гармонического колебания точки, если максимальное ускорение ее см/с2, период колебаний
с и смещение точки от положения равновесия в начальный момент времени
см. Колебания совершаются по закону синуса.
В момент времени смещение равно 2,5 см:
Выясним, какая у точки амплитуда колебаний. Для этого определим скорость (первую производную) и ускорение(вторую производную):
Максимальное ускорение – это амплитуда ускорения, то есть
Откуда :
Тогда в момент времени :
Определим начальную фазу:
Закон колебаний тогда будет таким:
Ответ: см.



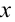


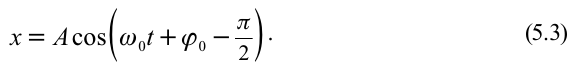

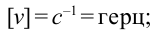

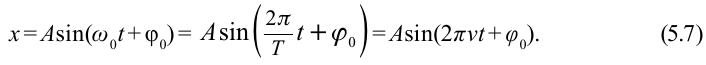
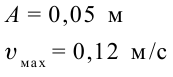
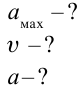
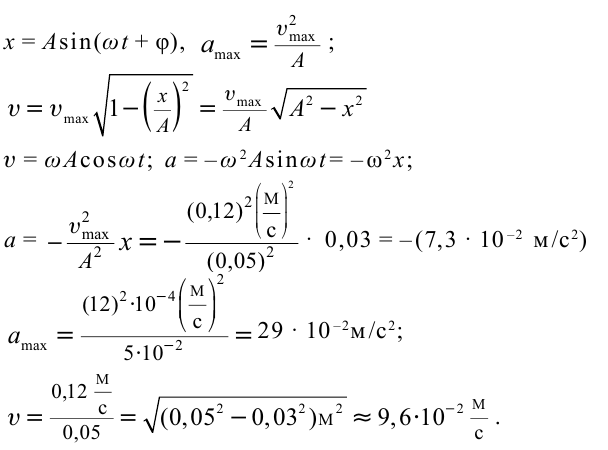
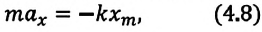
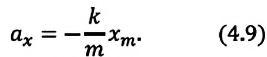
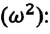
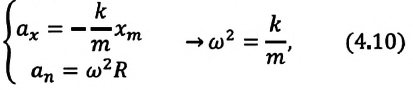
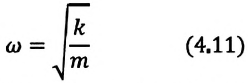
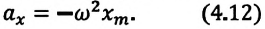
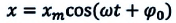
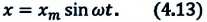
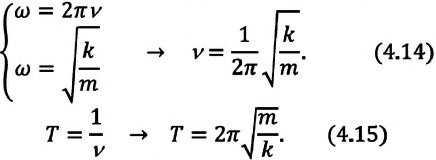
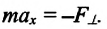
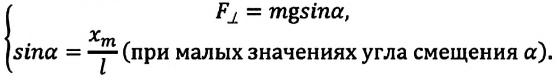
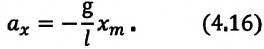


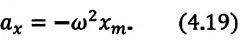
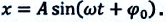
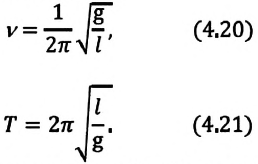
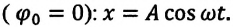
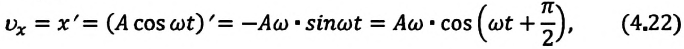
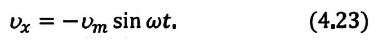
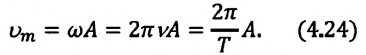
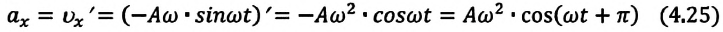

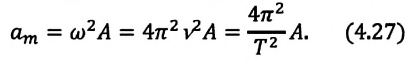
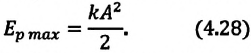
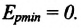
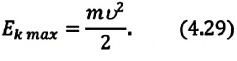
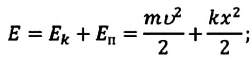
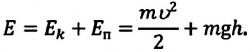
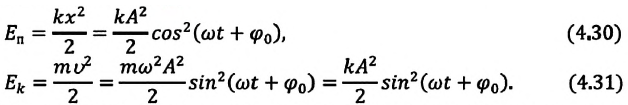
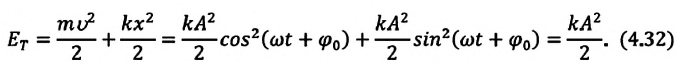
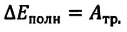
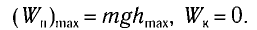
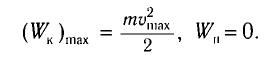
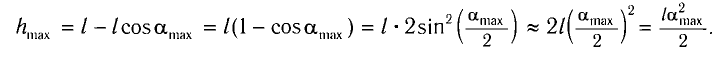
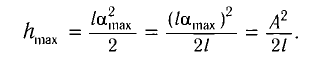
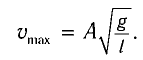
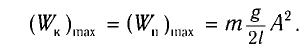
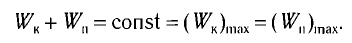
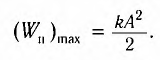
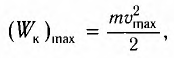
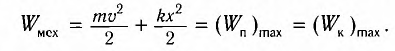
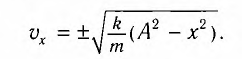
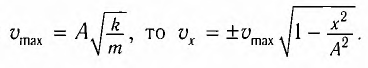
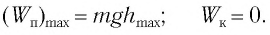
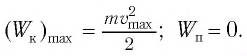
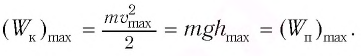
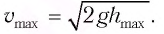
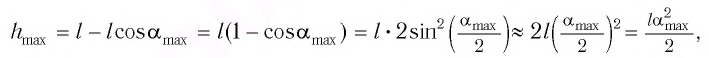
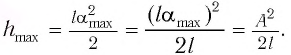
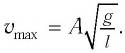
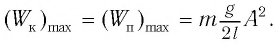
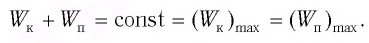
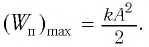
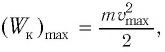
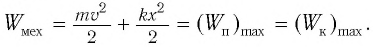
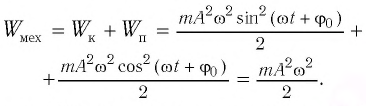
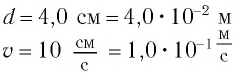
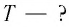
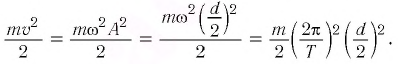
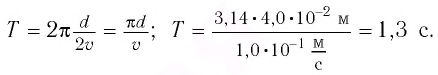
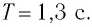

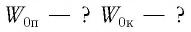
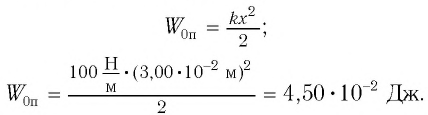
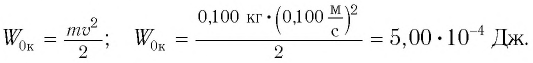
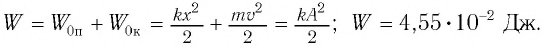
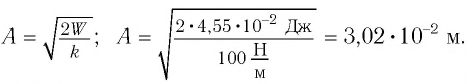
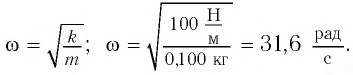
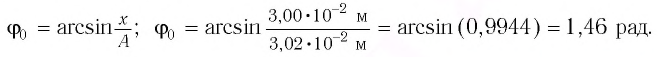
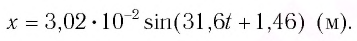
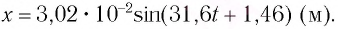
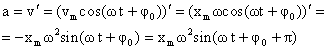 .
.