Как найти максимальное значение дроби

Значение дроби будет тем больше, чем меньше будет знаменатель и больше числитель. В приведенном примере в числителе стоит натуральное число 18, следовательно, изменить числитель нельзя.

В знаменателе 4Х^2+9+Y^2+4X*Y содержится 2 переменных. Рассмотрим варианты:

• х — отрицательная, у — отрицательная. Тогда оба отрицательных числа в квадрате + их произведение положительно.
• х — положительная, у — положительная, тогда оба положительных числа + их произведение тоже положительно
• х (или у) положительно, вторая переменная отрицательная.

В последнем случае требуется найти, возможно ли выражение (4Х^2+9+Y^2+4X*Y) принять отрицательное значение. Подобное невозможно, т.е. имеем минимальное значение функции при равных нулю переменных.

Получаем 18/(4*х^2+9+y^2+4*х*­y)= 18/(4*0+9+0+0)=18/9=­2

   azernot

03.09.12 — 16:25

Всего мнений: 8

   Волшебник

1 — 03.09.12 — 16:25

Дети пошли в школы. Родители взялись за дроби.

   Ненавижу 1С

2 — 03.09.12 — 16:26

18/(4x^2 + 9 + y^2 + 4xy) = 18/((2*x+y)^2+9)

   andrewks

3 — 03.09.12 — 16:26

с началом учебного года всех!

   azernot

4 — 03.09.12 — 16:27

Да уж, такой вот пресс прямо с первого дня..

   Axel2009

5 — 03.09.12 — 16:27

F'(x) = 0

F'(y) = 0

решай. находи точки экстремума и вперед =)

   shamannk

6 — 03.09.12 — 16:27

8 класс говоришь… Уже можно обосновать так: ..ля буду!

   SUA

7 — 03.09.12 — 16:27

   azernot

8 — 03.09.12 — 16:28

(2) Т.е. через такое выражение надо доказать, что знаменатель не может быть меньше 9-ки?

   Trier

9 — 03.09.12 — 16:29

   Axel2009

10 — 03.09.12 — 16:29

(8) ну как бы все что внутри квадрата не может быть меньше нуля. значит минимальное значение в знаменателе — 9. соответственно 2

   Trier

11 — 03.09.12 — 16:30

   nbIx

12 — 03.09.12 — 16:30

(0) Стыд одЫнэснегу который не может решить задачу 8 класса

Ответ 2 будет.

   andrewks

13 — 03.09.12 — 16:31

максимальное значение дроби при фиксированном числителе достигается при минимальном значении знаменателя

   azernot

14 — 03.09.12 — 16:31

(12) Решить-то могу, но вот обосновать в правильных терминах — увы нет

   Ненавижу 1С

15 — 03.09.12 — 16:32

(13) в общем случае неверно

   Ненавижу 1С

16 — 03.09.12 — 16:33

(14) интересно, а что такое тогда решить, если обосновать не можешь?

   andrewks

17 — 03.09.12 — 16:33

(15) согласен. это для положительных чисел

   Fish

18 — 03.09.12 — 16:33

(16) Это значит посмотреть в ответы в конце учебника :)))

   azernot

19 — 03.09.12 — 16:33

(16) Ну я же говорю, на интуитивном уровне.. брут-форсом

   AlexTim03

20 — 03.09.12 — 16:34

   CaptanG

21 — 03.09.12 — 16:34

   andrewks

22 — 03.09.12 — 16:35

   Axel2009

23 — 03.09.12 — 16:36

(17) или >= 1? =)

   andrewks

24 — 03.09.12 — 16:38

   Mucmuk

25 — 03.09.12 — 16:46

   БледноЗолотистый

26 — 03.09.12 — 16:48

(0) Нужно выразить у = …, взять производную, прировнять к 0, найти х, потом смотрим где производная меняет знак с — на +, берем этот х, потом находим у, подставляем в исходное. ЕМНИП.

   Axel2009

27 — 03.09.12 — 16:55

(24) сам туплю =)

   Волшебник

28 — 03.09.12 — 16:57

   Гобсек

29 — 05.09.12 — 04:16

(0) гы-гы-гы… Мы еще в августе с ребенком просмотрели все учебники на предмет изучаемых тем.

Try manipulating the first inequality to define $a$ in terms of $b$ (or vice versa)

$$ frac{ab+1}{a+b} < frac{3}{2} Rightarrow 2ab+2 < 3a+3b$$
$$ Rightarrow 2ab — 3a < 3b-2 $$
$$ Rightarrow a < frac{3b-2}{2b-3}$$

Notice that if $a=1$, then the second fraction involving $a$ and $b$ would become
$$ frac{(1)^3b^3+1}{(1)^3+b^3} = frac{b^3+1}{b^3+1} = 1$$

Similarly, if $b=1$, this second fraction would become
$$ frac{a^3(1)^3+1}{a^3+(1)^3} = frac{a^3+1}{a^3+1} = 1$$

Let’s exclude these possibilities for $a$ and $b$ because they don’t offer much useful information for finding a maximum bound. Then since $a$ and $b$ are both positive integers, we can setup a new inequailty for $a > 2$ using the value of $a$ we defined in terms of $b$

$$ frac{3b-2}{2b-3} > 2$$

Since we want $b > 1$, we can multiply both sides by $2b-3$ to simplify

begin{align*}
frac{3b-2}{2b-3}cdot (2b-3) &> 2cdot(2b-3)\
3b-2 &> 4b-6\
Rightarrow b < 4
end{align*}

Since you said «Hints only» I’ll leave the rest up to you. Let me know if you’d like further help!

Как найти наибольшую и наименьшую дробь

Не только простые числа можно сравнивать, но и дроби тоже. Ведь дробь — это такое же число как, к примеру, и натуральные числа. Нужно знать только правила, по которым сравнивают дроби.

Сравнение дробей с одинаковыми знаменателями.

Если у двух дробей одинаковые знаменатели, то такие дроби сравнить просто.

Чтобы сравнить дроби с одинаковыми знаменателями, нужно сравнить их числители. Та дробь больше у которой больше числитель.

Знаменатели у обоих дробей одинаковые равны 26, поэтому сравниваем числители. Число 13 больше 7. Получаем:

Если мы до решаем эти дроби, то получим числа (frac = 5) и (frac = 2). Получаем, что 5 > 2

В этом и заключается правило сравнения дробей с одинаковыми числителями.

Рассмотрим еще пример.

Сравните дроби с одинаковым числителем (frac ) и (frac ) .

Так как числители одинаковые, больше та дробь, где знаменатель меньше.

Пример №2:
Сравните правильную дробь с единицей?

Решение:
Любая правильная дробь всегда меньше 1.

Задача №1:
Сын с отцом играли в футбол. Сын из 10 подходов в ворота попал 5 раз. А папа из 5 подходов попал в ворота 3 раза. Чей результат лучше?

Решение:
Сын попал из 10 возможных подходов 5 раз. Запишем в виде дроби (frac ).
Папа попал из 5 возможных подходов 3 раз. Запишем в виде дроби (frac ).

Сравним дроби. У нас разные числители и знаменатели, приведем к одному знаменателю. Общий знаменатель будет равен 10.

Если у двух (или нескольких) дробей числитель одинаковый (то, что сверху черточки), то наименьшей дробью будет та, у которой знаменатель (то, что ниже черточки) наибольший, а наибольшей та, у которой знаменатель (то, что ниже черточки) наименьший.

В б наоборот – числители одинаковые, зато разные знаменатели. Представь себе пирог. Его разделили на столько частей, сколько написано внизу дроби. Из них взяли 31 часть. Чем на большее число частей поделили пирог, тем меньше часть (следовательно, находим где в знаменателе самое большое число – 53). Следовательно, пирог поделили на 53 части (маленькие) и из них взяли 31.

Ответы: 22/23 (самая большая в а)
31/53 (самая маленькая в б)

wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали авторы-волонтеры.

Количество источников, использованных в этой статье: 5. Вы найдете их список внизу страницы.

Сравнивают дроби обычно для того, чтобы узнать, какая больше, а какая меньше. Чтобы сравнить дроби, вам нужно привести их к одному знаменателю, тогда дробь с большим числителем большая, а с меньшим — меньшая. Самое сложное — это уяснить, как делать так, чтобы дроби имели одинаковые знаменатели, но все не так сложно, как кажется. Мы расскажем, как все это делать. Читайте дальше!

Источник

как определить наибольшую и наименьшую дробь?

Если у двух (или нескольких) дробей знаменатель одинаковый (то, что ниже черточки), то
наименьшей дробью будет та, у которой числитель (то, что сверху черточки) наименьший, а наибольшей та, у которой числитель (то, что сверху черточки) наибольший.

Если у двух (или нескольких) дробей числитель одинаковый (то, что сверху черточки), то наименьшей дробью будет та, у которой знаменатель (то, что ниже черточки) наибольший, а наибольшей та, у которой знаменатель (то, что ниже черточки) наименьший.

В а ты тупик) У них знаменатели (то, что внизу) одинаковые, а числители (то, что наверху) разные. Значит, чем больше числитель, тем больше дробь. Тут самая большая — предпоследняя (22/23). Представь пирог. Его поделили на 23 части. И взяли столько, сколько написано вверху

В б наоборот — числители одинаковые, зато разные знаменатели. Представь себе пирог. Его разделили на столько частей, сколько написано внизу дроби. Из них взяли 31 часть. Чем на большее число частей поделили пирог, тем меньше часть (следовательно, находим где в знаменателе самое большое число — 53). Следовательно, пирог поделили на 53 части (маленькие) и из них взяли 31.

Ответы: 22/23 (самая большая в а)
31/53 (самая маленькая в б)

В остальных случаях только приводить к общему знаменателю 🙂

Источник

Чему равно наибольшее значение дроби (см.)?

В знаменателе ( 2 * x + y ) ^ 2 + 9 — отрицательным быть не может по определению (квадрат числа плюс положительное число). Наибольшее значение дробь принимает при наименьшем знаменателе, а он (наименьший знаменатель) равен 9 при x = y = 0 или 2 * x = — y, итого, наибольшее значение 18 / 9 = 2

Дробь — это какая-то часть от целого. Дроби делятся на обыкновенные и десятичные. Обыкновенные дроби состоят из двух чисел: числителя и знаменателя, разделённых дробной чертой, причём нет никаких ограничений на их (числителя и знаменателя) величину. например: 23/598, 69/23 и т.п. В принципе, десятичные дроби ничем не отличаются от обычных, только знаменатель у них кратен 10, например 3/10, 248/1000, 23/100000, и т.п. Но, поскольку у нас принята десятичная система счисления, и при записи чисел один разряд отличается от другого в 10 раз, то для десятичных дробей возможна более удобная система записи, «в строчку», достаточно отделить дробную часть от целой специальным знаком (запятой, а иногда, во многих языках программирования, — точкой).

Таким образом число, равное (23 + 67/1000) («23 целых и 67 тысячных) удобно записать в виде 23,067.

Бывают правильные дроби, например 5/10=1/2, это когда чилситель меньше знаменателя.

Есть неправильные дроби, например 10/5 ; 5/5 это когда числитель равень или больше знаменателя.

Есть обыкновенные дроби, это 1/2 или 2/10

Есть десятинчные дроби, этьо 0.5 или 0.2

Обыкновенная (простая) дробь — это число, записанное в виде m/n, где горизонтальная (-), или наклонная (/) черта обозначает деление. При этом m называют числителем, а n — знаменателем.

Обыкновенная дробь называется правильной, если m n

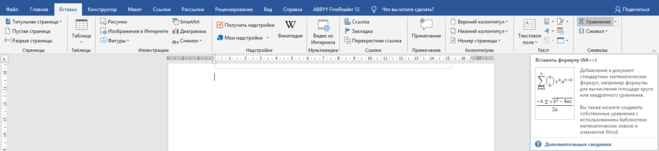
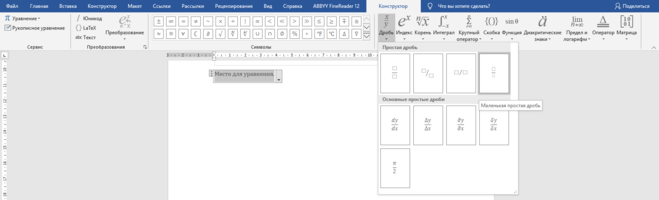
Есть несколько способов написать дробь в программе Ворд.

Ввод осуществляется только с клавиатуры. Знак дроби заменяется «/».

Переходим во вкладку Вставка. Выбираем команду Уравнение.

В открывшейся вкладке Конструктор находим кнопку дробь. Кликаем на понравившийся макет.

На месте пустых квадратов необходимо ввести числа числителя и знаменателя. Итог.

В старых версиях программы нет команды Уравнение (Формула). Ввод формул происходит через microsoft equation.

Активация microsoft equation. Во вкладке Вставка перейти в меню Текст. Нажать Объект. В открывшемся окне найти microsoft equation из списка и нажать ОК.

Источник

Решение уравнений с дробями

О чем эта статья:

5 класс, 6 класс, 7 класс

Понятие дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:

• обыкновенный вид — ½ или a/b,
• десятичный вид — 0,5.

Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.

Дроби бывают двух видов:

1. Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
2. Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.

Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.

Основные свойства дробей

Дробь не имеет значения, если делитель равен нулю.

Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.

Дроби a/b и c/d называют равными, если a × d = b × c.

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:

• Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
• Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Решить уравнение значит найти все его корни или убедиться, что корней нет.

Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.

Линейное уравнение выглядит так	ах + b = 0, где a и b — действительные числа. Что поможет в решении: если а не равно нулю, то у уравнения единственный корень: х = −b : а; если а равно нулю, а b не равно нулю — у уравнения нет корней; если а и b равны нулю, то корень уравнения — любое число.
Квадратное уравнение выглядит так:	ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Понятие дробного уравнения

Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:

Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.

Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:

На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.

Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.

Как решать уравнения с дробями

1. Метод пропорции

Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.

Итак, у нас есть линейное уравнение с дробями:

В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.

После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.

2. Метод избавления от дробей

Возьмем то же самое уравнение, но попробуем решить его по-другому.

В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:

• подобрать число, которое можно разделить на каждый из знаменателей без остатка;
• умножить на это число каждый член уравнения.

Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!

Вот так просто мы получили тот же ответ, что и в прошлый раз.

Что еще важно учитывать при решении

• если значение переменной обращает знаменатель в 0, значит это неверное значение;
• делить и умножать уравнение на 0 нельзя.

Универсальный алгоритм решения

Определить область допустимых значений.

Найти общий знаменатель.

Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.

Раскрыть скобки, если нужно и привести подобные слагаемые.

Решить полученное уравнение.

Сравнить полученные корни с областью допустимых значений.

Записать ответ, который прошел проверку.

Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.

Примеры решения дробных уравнений

Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.

Пример 1. Решить дробное уравнение: 1/x + 2 = 5.

1. Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
2. Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
3. Избавимся от знаменателя. Умножим каждый член уравнения на х.

Решим обычное уравнение.

Пример 2. Найти корень уравнения

1. Область допустимых значений: х ≠ −2.
2. Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
3. Избавимся от знаменателя. Умножим каждый член уравнения на х.

Переведем новый множитель в числитель..

Сократим левую часть на (х+2), а правую на 2.

Пример 3. Решить дробное уравнение:

Найти общий знаменатель:

Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:

Выполним возможные преобразования. Получилось квадратное уравнение:

Решим полученное квадратное уравнение:

Получили два возможных корня:

Если x = −3, то знаменатель равен нулю:

Если x = 3 — знаменатель тоже равен нулю.

Вывод: числа −3 и 3 не являются корнями уравнения, значит у данного уравнения нет решения.

Источник

Как найти наибольшую и наименьшую дробь

Не только простые числа можно сравнивать, но и дроби тоже. Ведь дробь — это такое же число как, к примеру, и натуральные числа. Нужно знать только правила, по которым сравнивают дроби.

Сравнение дробей с одинаковыми знаменателями.

Если у двух дробей одинаковые знаменатели, то такие дроби сравнить просто.

Чтобы сравнить дроби с одинаковыми знаменателями, нужно сравнить их числители. Та дробь больше у которой больше числитель.

Знаменатели у обоих дробей одинаковые равны 26, поэтому сравниваем числители. Число 13 больше 7. Получаем:

Если мы до решаем эти дроби, то получим числа (frac<20> <4>= 5) и (frac<20> <10>= 2). Получаем, что 5 > 2

В этом и заключается правило сравнения дробей с одинаковыми числителями.

Рассмотрим еще пример.

Сравните дроби с одинаковым числителем (frac<1><17>) и (frac<1><15>) .

Так как числители одинаковые, больше та дробь, где знаменатель меньше.

Пример №2:
Сравните правильную дробь с единицей?

Решение:
Любая правильная дробь всегда меньше 1.

Задача №1:
Сын с отцом играли в футбол. Сын из 10 подходов в ворота попал 5 раз. А папа из 5 подходов попал в ворота 3 раза. Чей результат лучше?

Решение:
Сын попал из 10 возможных подходов 5 раз. Запишем в виде дроби (frac<5> <10>).
Папа попал из 5 возможных подходов 3 раз. Запишем в виде дроби (frac<3> <5>).

Сравним дроби. У нас разные числители и знаменатели, приведем к одному знаменателю. Общий знаменатель будет равен 10.

Если у двух (или нескольких) дробей числитель одинаковый (то, что сверху черточки), то наименьшей дробью будет та, у которой знаменатель (то, что ниже черточки) наибольший, а наибольшей та, у которой знаменатель (то, что ниже черточки) наименьший.

В б наоборот — числители одинаковые, зато разные знаменатели. Представь себе пирог. Его разделили на столько частей, сколько написано внизу дроби. Из них взяли 31 часть. Чем на большее число частей поделили пирог, тем меньше часть (следовательно, находим где в знаменателе самое большое число — 53). Следовательно, пирог поделили на 53 части (маленькие) и из них взяли 31.

Ответы: 22/23 (самая большая в а)
31/53 (самая маленькая в б)

wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали авторы-волонтеры.

Количество источников, использованных в этой статье: 5. Вы найдете их список внизу страницы.

Сравнивают дроби обычно для того, чтобы узнать, какая больше, а какая меньше. Чтобы сравнить дроби, вам нужно привести их к одному знаменателю, тогда дробь с большим числителем большая, а с меньшим — меньшая. Самое сложное — это уяснить, как делать так, чтобы дроби имели одинаковые знаменатели, но все не так сложно, как кажется. Мы расскажем, как все это делать. Читайте дальше!