Виталий Викторович Карабут
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Кинетическая энергия
Определение 1
Кинетическая энергия — внутренняя энергия движущегося тела, обусловленная его инертностью (массой) и скоростью. Она равна энергии, которую нужно затратить, чтобы снизить скорость этого тела до нуля.
Например, движущийся автомобиль невозможно остановить мгновенно. Для остановки необходимо затратить энергию трения тормозных колодок о тормозные диски колес и шин об асфальт.
Замечание 1
Кинетическая и потенциальная энергия измеряются в джоулях ($1 Дж = Н cdot м$).
В некоторых физических системах происходят циклические преобразования потенциальной (запасенной) энергии в кинетическую и обратно. Такие системы называются маятниками. Например, для груза, подвешенного на нити, потенциальная энергия максимальна, когда он отклонен на максимальный угол от вертикали. Мгновенная скорость груза в этот момент равна нулю и, следовательно, нулю равна и кинетическая энергия. По мере движения вниз под действием силы тяжести, скорость груза нарастает и достигает максимума в нижней точке, после чего снова начинает запасаться по мере движения вверх.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Проще всего изучать переход кинетической и потенциальной энергий друг в друга на примере пружинного маятника, где действует, если пренебречь силой трения, лишь сила упругости. Когда пружину сжимают, энергия запасается. Когда отпускают — потенциальная энергия, сохраненная в кристаллической решетке материала, высвобождается и превращается в кинетическую, разгоняя груз. Когда скорость груза достигает максимума, он продолжает движение по инерции, растягивая пружину в противоположном направлении, вновь запасая энергию и снижая скорость. Характеристики такого колебательного движения зависят только от материала пружины, толщины проволоки, из которой она намотана, диаметра и количества витков. Все эти факторы описываются единым параметром — коэффициентом упругости.
Максимальная кинетическая энергия груза
Для простого пружинного маятника полную энергию груза в любой момент времени можно выразить как
$E = E_p + E_k = frac{m cdot v^2}{2} + frac{k cdot x^2}{2}$, где:
- $E_p$ — потенциальная энергия,
- $E_k$ — кинетическая энергия,
- $m$ — масса,
- $v$ — моментальная скорость,
- $k$ — коэффициент упругости,
- $x$ — приращение длины пружины в данный момент.
«Максимальная кинетическая энергия груза: формула» 👇
Максимальную кинетическую энергию можно вычислить как
$(E_k)_{max} = frac{m cdot v_{max}^2}{2}$,
где $v_{max}$ — максимальная скорость груза. Однако измерить ее на практике сложно. Проще, опираясь на постоянство суммы кинетической и потенциальной энергий, определить максимальную потенциальную (когда кинетическая равна нулю). Поскольку справедливо и обратное, можно записать:
$(E_k)_{max} = (E_p)_{max} = frac{k cdot x_{max}^2}{2}$,
где $x_{max}$ — максимальное приращение растяжения пружины. Его легко измерить, а коэффициент упругости посмотреть в справочнике.
Пример 1
Компактный груз, массой 0,5 кг прикреплен к движущейся горизонтально пружине. Ее коэффициент упругости равен 2000 $frac{Н}{м}$. Каково было начальное приращение длины пружины, если его максимальная скорость во время колебаний составляет 1 $frac{м}{с}$?
Из условий задачи можно найти максимальную кинетическую энергию груза:
$(E_k)_{max} = frac{0,5 cdot 1^2}{2} = 0,25 Дж$
Выразив максимальную потенциальную энергию через приращение длины пружины, составим равенство:
$0,25 = frac{2000 cdot x_{max}^2}{2} implies x_{max} = sqrt{frac{2 cdot 0,25}{2000}} approx 0,016 м$.
Ответ: $approx 1,6 мм$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Одним из важнейших понятий в физике является энергия, то есть способность тела совершать ту или иную работу. Механическая энергия подразделяется на кинетическую и потенциальную. Рассмотрим первый ее вид.
Кинетическая энергия – понятие и определение
Определение
Кинетическая энергия – это способность движущегося тела совершать определенную работу.
Например, движущийся автомобиль способен снести находящееся перед ним препятствие, а падающий камень – оставить вмятину на металлической пластинке.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Кинетическая энергия зависит от скорости движения и массы тела. Она описывается формулой:
(E_k=frac{mnu^2}2)
Единицей измерения кинетической энергии является Джоуль (Дж).
Проведя простые преобразования, легко вывести формулы для вычисления массы тела и скорости движения:
(m=frac{2E_k}{nu^2})
(nu=sqrt{frac{2E_k}m})
Из основной формулы видно: во сколько раз изменяется масса тела, во столько раз изменяется и величина кинетической энергии. Например, если масса будет уменьшена или увеличена в 5 раз, то и величина кинетической энергии станет соответственно меньше или больше в 5 раз.
При увеличении скорости кинетическая энергия увеличивается в квадратичной зависимости. Допустим, скорость движения тела стала в 6 раз больше. Соответственно его кинетическая энергия возросла в 36 раз.
Формула кинетической энергии тела справедлива только для скоростей значительно меньших, чем скорость света. Если же скорость движения приближается к 300 000 км/с, то тут начинает действовать теория относительности, созданная Альбертом Эйнштейном.
Кинетическая энергия зависит от особенностей рассмотрения системы. Если тело принимают как макроскопический объект, то оно будет обладать внутренней энергией. В этом случае кинетическая энергия возникнет только в момент его движения.
Это же тело можно рассматривать и с микроскопической точки зрения. Тепловое движение атомов и молекул обуславливает внутреннюю энергию тела. В то же время средняя кинетическая энергия этого движения пропорциональна абсолютной температуре тела. Коэффициент этой пропорциональной зависимости называется постоянной Больцмана.
Кинетическая энергия атомов и молекул при рассмотрении тела на микроскопическом уровне описывается формулой:
(E_k=frac32kT)
где (k) – это постоянная Больцмана.
Теорема об изменении кинетической энергии
Рассмотрим наиболее простой пример движения, при котором скорость движения и сила, действующая на тело имеют одинаковое направление. Тело совершает перемещение (S), так как сила (F) совершает работу (A). Также она изменяет и скорость движения, придавая телу некоторое ускорение. Это свидетельствует о наличии связи между работой силы и изменением скорости движения.
В данном случае работа силы будет описываться формулой:
A=FS
Запишем второй закон Ньютона в стандартном виде:
F=ma
При условии, что движение является равноускоренным (сила не зависит от координат и времени), работу можно записать так:
A=maS
Вспомним формулу из курса кинематики, связывающую перемещение, ускорение, начальную и конечную скорости движения тела:
(S=frac{nu^2-nu_0^2}{2a})
Подставляем ее в формулу работы:
(A=frac{ma(v^2-v_0^2)}{2a}=frac{mv^2}2-frac{mv_0^2}2)
Полученное равенство показывает, что разность между кинетической энергией в конечной и начальный момент времени равна работе силы. Это позволяет сформулировать теорему об изменении кинетической энергии.
Изменение кинетической энергии тела равна равнодействующей всех сил или работе силы:
(A=E_{k2}-E_{k1})
Таким образом, сила будет совершать отрицательную работу, если она направлена в сторону, противоположную движению тела. В этом случае начальная кинетическая энергия будет больше, чем конечная:
(frac{mv_0^2}2>frac{mv^2}2)
Так как сила имеет противоположное скорости направление, то модуль скорости будет уменьшаться, что и становится причиной уменьшения величины кинетической энергии.
Если же сила будет направлена в сторону движения, то кинетическая энергия будет возрастать:
(frac{mv_0^2}2<frac{mv^2}2)
Фактически теорему об изменении кинетической энергии можно рассматривать как иную формулировку второго закона Ньютона. Поэтому ее использование возможно в различных случаях, например, при рассмотрении действия силы трения, тяжести или упругости.
Примеры решения задач, как найти кинетическую энергию
Рассмотрим примеры решения задач на нахождение кинетической энергии.
Задача 1
Тело, имеющее массу 2 кг движется поступательно со скоростью 36 км/ч. Найдите, какой кинетической энергией оно обладает.
Решение
Прежде чем приступить к вычислению необходимо перевести скорость тела в единицы СИ:
36 км/ч = 10 м/с
Подставим известные значения в формулу кинетической энергии и выполним расчет:
(E_k=frac{2times10^2}2=100;Дж\)
Ответ: кинетическая энергия тела составляет 100 Джоулей.
Задача 2
Груз массой 0,2 кг прикреплен к пружине, которая закреплена горизонтально. Максимальная скорость колебания 3 м/с. Вычислить максимальную кинетическую энергию тела.
Решение
Воспользуемся выражением определения кинетической энергии:
(E_{k_{max}}=frac{mv^2}2)
Выполним вычисление:
(E_{k_{max}}=frac{0.2times3^2}2=0.9;Дж)
Ответ: максимальная кинетическая энергия пружины и груза составляет 0,9 Дж.
Задача 3
Найдите среднюю кинетическую энергию поступательного движения молекулы водорода при температуре Т = 280 К.
Решение
Для решения задачи воспользуемся уравнением, связывающим температуру и энергию:
(E_k=frac32kT)
где k – это постоянная Больцмана
Проведем вычисление:
(E_k=frac{3times1,38times10^{-23}times280}2=579,6times10^{-23};Дж)
Ответ: средняя кинетическая скорость молекулы водорода составляет (579,6times10^{-23};Дж.)
Введём энергию колебания.
Колебательная система движется со скоростью , тогда его кинетическая энергия должна быть равна:
(1)
- где
Вспомним зависимость скорости от времени при гармоническом колебании:
(2)
- где
Подставим (2) в (1) при условии (для упрощения):
=
(3)
Тогда максимальная кинетическая энергия данной системы:
(4)
т.к. максимальное значение .
С другой стороны для пружинного маятника можем записать потенциальную энергию деформации:
(5)
- где
Вспомним зависимость координаты от времени при гармоническом колебании:
(6)
Подставим (5) в (4) при условии (для упрощения):
=
(7)
Тогда максимальная потенциальная энергия данной системы:
(8)
т.к. максимальное значение .
Вывод: задачи школьной физики чаще всего связаны именно с максимальным значением энергии колебания. Её можно рассчитать и как кинетическую энергию в положении равновесия (4), и как потенциальную энергию в точке максимального отклонения (8).
Механические колебания и волны
Механические колебания – периодически повторяющееся перемещение материальной точки, при котором она движется по какой-либо траектории поочередно в двух противоположных направлениях относительно положения устойчивого равновесия.
Отличительными признаками колебательного движения являются:
- повторяемость движения;
- возвратность движения.
Для существования механических колебаний необходимо:
- наличие возвращающей силы – силы, стремящейся вернуть тело в положение равновесия (при малых смещениях от положения равновесия);
- наличие малого трения в системе.
Механические волны – это процесс распространения колебаний в упругой среде.
Содержание
- Виды волн
- Гармонические колебания
- Амплитуда и фаза колебаний
- Период колебаний
- Частота колебаний
- Свободные колебания (математический и пружинный маятники)
- Вынужденные колебания
- Резонанс
- Длина волны
- Звук
- Основные формулы по теме «Механические колебания и волны»
Виды волн
- Поперечная – это волна, в которой колебание частиц среды происходит перпендикулярно направлению распространения волны.
Поперечная волна представляет собой чередование горбов и впадин.
Поперечные волны возникают вследствие сдвига слоев среды относительно друг друга, поэтому они распространяются в твердых телах.
- Продольная – это волна, в которой колебание частиц среды происходит в направлении распространения волны.
Продольная волна представляет собой чередование областей уплотнения и разряжения.
Продольные волны возникают из-за сжатия и разряжения среды, поэтому они могут возникать в жидких, твердых и газообразных средах.
Важно!
Механические волны не переносят вещество среды. Они переносят энергию, которая складывается из кинетической энергии движения частиц среды и потенциальной энергии ее упругой деформации.
Гармонические колебания
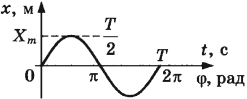
Гармонические колебания – простейшие периодические колебания, при которых координата тела меняется по закону синуса или косинуса:
где ( x ) – координата тела – смещение тела от положения равновесия в данный момент времени; ( A ) – амплитуда колебаний; ( omega t+varphi_0 ) – фаза колебаний; ( omega ) – циклическая частота; ( varphi_0 ) – начальная фаза.
Если в начальный момент времени тело проходит положение равновесия, то колебания являются синусоидальными.
Если в начальный момент времени смещение тела совпадает с максимальным отклонением от положения равновесия, то колебания являются косинусоидальными.
Скорость гармонических колебаний
Скорость гармонических колебаний есть первая производная координаты по времени:
где ( v ) – мгновенное значение скорости, т. е. скорость в данный момент времени.
Амплитуда скорости – максимальное значение скорости колебаний, это величина, стоящая перед знаком синуса или косинуса:
Ускорение гармонических колебаний
Ускорение гармонических колебаний есть первая производная скорости по времени:
где ( a ) – мгновенное значение ускорения, т. е. ускорение в данный момент времени.
Амплитуда ускорения – максимальное значение ускорения, это величина, стоящая перед знаком синуса или косинуса:
Если тело совершает гармонические колебания, то сила, действующая на тело, тоже изменяется по гармоническому закону:
где ( F ) – мгновенное значение силы, действующей на тело, т. е. сила в данный момент времени.
Амплитуда силы – максимальное значение силы, величина, стоящая перед знаком синуса или косинуса:
Тело, совершающее гармонические колебания, обладает кинетической или потенциальной энергией:
где ( W_k ) – мгновенное значение кинетической энергии, т. е. кинетическая энергия в данный момент времени.
Амплитуда кинетической энергии – максимальное значение кинетической энергии, величина, стоящая перед знаком синуса или косинуса:
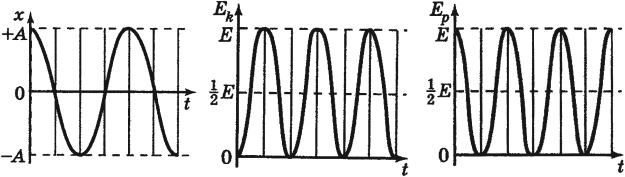
При гармонических колебаниях каждую четверть периода происходит переход потенциальной энергии в кинетическую и обратно.
В положении равновесия:
- потенциальная энергия равна нулю;
- кинетическая энергия максимальна.
При максимальном отклонении от положения равновесия:
- кинетическая энергия равна нулю;
- потенциальная энергия максимальна.
Полная механическая энергия гармонических колебаний
При гармонических колебаниях полная механическая энергия равна сумме кинетической и потенциальной энергий в данный момент времени:
Важно!
Следует помнить, что период колебаний кинетической и потенциальной энергий в 2 раза меньше, чем период колебаний координаты, скорости, ускорения и силы. А частота колебаний кинетической и потенциальной энергий в 2 раза больше, чем частота колебаний координаты, скорости, ускорения и силы.
Графики зависимости кинетической, потенциальной и полной энергий всегда лежат выше оси времени.
Если сила сопротивления отсутствует, то полная энергия сохраняется. График зависимости полной энергии от времени есть прямая, параллельная оси времени (в отсутствие сил трения).
Амплитуда и фаза колебаний
Амплитуда колебаний – модуль наибольшего смещения тела от положения равновесия.
Обозначение – ( A, (X_{max}) ), единицы измерения – м.
Фаза колебаний – это величина, которая определяет состояние колебательной системы в любой момент времени.
Обозначение – ( varphi ), единицы измерения – рад (радиан).
Фаза колебаний – это величина, стоящая под знаком синуса или косинуса. Она показывает, какая часть периода прошла от начала колебаний.
Фаза гармонических колебаний в процессе колебаний изменяется.
( varphi_0 ) – начальная фаза колебаний.
Начальная фаза колебаний – величина, которая определяет положение тела в начальный момент времени.
Важно!
Путь, пройденный телом за одно полное колебание, равен четырем амплитудам.
Период колебаний
Период колебаний – это время одного полного колебания.
Обозначение – ( T ), единицы измерения – с.
Период гармонических колебаний – постоянная величина.
Частота колебаний
Частота колебаний – это число полных колебаний в единицу времени.
Обозначение – ( nu ), единицы времени – с-1 или Гц (Герц).
1 Гц – это частота такого колебательного движения, при котором за каждую секунду совершается одно полное колебание:
Период и частота колебаний – взаимно обратные величины:
Циклическая частота – это число колебаний за 2π секунд.
Обозначение – ( omega ), единицы измерения – рад/с.
Свободные колебания (математический и пружинный маятники)
Свободные колебания – колебания, которые совершает тело под действием внутренних сил системы за счет начального запаса энергии после того как его вывели из положения устойчивого равновесия.
Условия возникновения свободных колебаний:
- при выведении тела из положения равновесия должна возникнуть сила, стремящаяся вернуть его в положение равновесия;
- силы трения в системе должны быть достаточно малы. При наличии сил трения свободные колебания будут затухающими.
При наличии сил трения свободные колебания будут затухающими.
Затухающие колебания – это колебания, амплитуда которых с течением времени уменьшается.
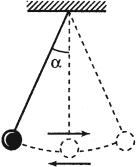
Математический маятник – это материальная точка, подвешенная на невесомой нерастяжимой нити.
Период колебаний математического маятника:
Частота колебаний математического маятника:
Циклическая частота колебаний математического маятника:
Максимальное значение скорости колебаний математического маятника:
Максимальное значение ускорения колебаний математического маятника:
Период свободных колебаний математического маятника, движущегося вверх с ускорением или вниз с замедлением:
Период свободных колебаний математического маятника, движущегося вниз с ускорением или вверх с замедлением:
Период свободных колебаний математического маятника, горизонтально с ускорением или замедлением:
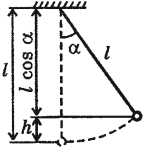
Мгновенное значение потенциальной энергии математического маятника, поднявшегося в процессе колебаний на высоту ( h ), определяется по формуле:
где ( l ) – длина нити, ( alpha ) – угол отклонения от вертикали.
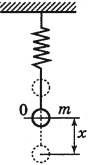
Пружинный маятник – это тело, подвешенное на пружине и совершающее колебания вдоль вертикальной или горизонтальной оси под действием силы упругости пружины.
Период колебаний пружинного маятника:
Частота колебаний пружинного маятника:
Циклическая частота колебаний пружинного маятника:
Максимальное значение скорости колебаний пружинного маятника:
Максимальное значение ускорения колебаний пружинного маятника:
Мгновенную потенциальную энергию пружинного маятника можно найти по формуле:
Амплитуда потенциальной энергии – максимальное значение потенциальной энергии, величина, стоящая перед знаком синуса или косинуса:
Важно!
Если маятник не является ни пружинным, ни математическим (физический маятник), то его циклическую частоту, период и частоту колебаний по формулам, применимым к математическому и пружинному маятнику, рассчитать нельзя. В данном случае эти величины рассчитываются из формулы силы, действующей на маятник, или из формул энергий.
Вынужденные колебания
Вынужденные колебания – это колебания, происходящие под действием внешней периодически изменяющейся силы.
Вынужденные колебания, происходящие под действием гармонически изменяющейся внешней силы, тоже являются гармоническими и незатухающими. Их частота равна частоте внешней силы и называется частотой вынужденных колебаний.
Резонанс
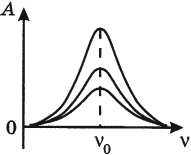
Резонанс – явление резкого возрастания амплитуды колебаний, которое происходит при совпадении частоты вынуждающей силы и собственной частоты колебаний тела.
Условие резонанса:
( v_0 ) – собственная частота колебаний маятника.
На рисунке изображены резонансные кривые для сред с разным трением. Чем меньше трение, тем выше и острее резонансная кривая.
Явление резонанса учитывается при периодически изменяющихся нагрузках в машинах и различных сооружениях.
Также резонанс используется в акустике, радиотехнике и т. д.
Длина волны
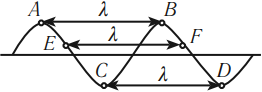
Длина волны – это расстояние, на которое волна распространяется за один период, т. е. это кратчайшее расстояние между двумя точками среды, колеблющимися в одинаковых фазах.
Обозначение – ( lambda ), единицы измерения – м.
Расстояние между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разряжениями в продольной волне равно длине волны.
Скорость распространения волны – это скорость перемещения горбов и впадин в поперечной волне и сгущений или разряжений в продольной волне.
Звук
Звук – это колебания упругой среды, воспринимаемые органом слуха.
Условия, необходимые для возникновения и ощущения звука:
- наличие источника звука;
- наличие упругой среды между источником и приемником звука;
- наличие приемника звука; • частота колебаний должна лежать в звуковом диапазоне;
- мощность звука должна быть достаточной для восприятия.
Звуковые волны – это упругие волны, вызывающие у человека ощущение звука, представляющие собой зоны сжатия и разряжения, передающиеся на расстояние с течением времени.
Классификация звуковых волн:
- инфразвук (( nu ) < 16 Гц);
- звуковой диапазон (16 Гц < ( nu ) < 20 000 Гц);
- ультразвук (( nu ) > 20 000 Гц).
Скорость звука – это скорость распространения фазы колебания, т. е. области сжатия и разряжения среды.
Скорость звука зависит
- от упругих свойств среды:
в воздухе – 331 м/с, в воде – 1400 м/с, в металле – 5000 м/с;
- от температуры среды:
в воздухе при температуре 0°С – 331 м/с,
в воздухе при температуре +15°С – 340 м/с.
Характеристики звуковой волны
- Громкость – это величина, характеризующая слуховые ощущения человека, зависящая от амплитуды колебаний в звуковой волне. Единицы измерения – дБ (децибел).
- Высота тона – это величина, характеризующая слуховые ощущения человека, зависящая от частоты колебаний в звуковой волне. Чем больше частота, тем выше звук. Чем меньше частота, тем ниже звук.
- Тембр – это окраска звука.
Музыкальный звук – это звук, издаваемый гармонически колеблющимся телом. Каждому музыкальному тону соответствует определенная длина и частота звуковой волны.
Шум – хаотическая смесь тонов.
Основные формулы по теме «Механические колебания и волны»
Механические колебания и волны
2.9 (58.68%) 152 votes
| Kinetic energy | |
|---|---|

The cars of a roller coaster reach their maximum kinetic energy when at the bottom of the path. When they start rising, the kinetic energy begins to be converted to gravitational potential energy. The sum of kinetic and potential energy in the system remains constant, ignoring losses to friction. |
|
|
Common symbols |
KE, Ek, K or T |
| SI unit | joule (J) |
|
Derivations from |
Ek = 1/2mv2 Ek = Et + Er |
In physics, the kinetic energy of an object is the form of energy that it possesses due to its motion.[1]
It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes. The same amount of work is done by the body when decelerating from its current speed to a state of rest. Formally, a kinetic energy is any term in a system’s Lagrangian which includes a derivative with respect to time and the second term in a Taylor expansion of a particle’s relativistic energy. [2][3]
In classical mechanics, the kinetic energy of a non-rotating object of mass m traveling at a speed v is 
The standard unit of kinetic energy is the joule, while the English unit of kinetic energy is the foot-pound.
History and etymology
The adjective kinetic has its roots in the Greek word κίνησις kinesis, meaning «motion». The dichotomy between kinetic energy and potential energy can be traced back to Aristotle’s concepts of actuality and potentiality.[4]
The principle in classical mechanics that E ∝ mv2 was first developed by Gottfried Leibniz and Johann Bernoulli, who described kinetic energy as the living force, vis viva. Willem ‘s Gravesande of the Netherlands provided experimental evidence of this relationship. By dropping weights from different heights into a block of clay, Willem ‘s Gravesande determined that their penetration depth was proportional to the square of their impact speed. Émilie du Châtelet recognized the implications of the experiment and published an explanation.[5]
The terms kinetic energy and work in their present scientific meanings date back to the mid-19th century. Early understandings of these ideas can be attributed to Gaspard-Gustave Coriolis, who in 1829 published the paper titled Du Calcul de l’Effet des Machines outlining the mathematics of kinetic energy. William Thomson, later Lord Kelvin, is given the credit for coining the term «kinetic energy» c. 1849–1851.[6][7] Rankine, who had introduced the term «potential energy» in 1853, and the phrase «actual energy» to complement it,[8] later cites William Thomson and Peter Tait as substituting the word «kinetic» for «actual».[9]
Overview
Energy occurs in many forms, including chemical energy, thermal energy, electromagnetic radiation, gravitational energy, electric energy, elastic energy, nuclear energy, and rest energy. These can be categorized in two main classes: potential energy and kinetic energy. Kinetic energy is the movement energy of an object. Kinetic energy can be transferred between objects and transformed into other kinds of energy.[10]
Kinetic energy may be best understood by examples that demonstrate how it is transformed to and from other forms of energy. For example, a cyclist uses chemical energy provided by food to accelerate a bicycle to a chosen speed. On a level surface, this speed can be maintained without further work, except to overcome air resistance and friction. The chemical energy has been converted into kinetic energy, the energy of motion, but the process is not completely efficient and produces heat within the cyclist.
The kinetic energy in the moving cyclist and the bicycle can be converted to other forms. For example, the cyclist could encounter a hill just high enough to coast up, so that the bicycle comes to a complete halt at the top. The kinetic energy has now largely been converted to gravitational potential energy that can be released by freewheeling down the other side of the hill. Since the bicycle lost some of its energy to friction, it never regains all of its speed without additional pedaling. The energy is not destroyed; it has only been converted to another form by friction. Alternatively, the cyclist could connect a dynamo to one of the wheels and generate some electrical energy on the descent. The bicycle would be traveling slower at the bottom of the hill than without the generator because some of the energy has been diverted into electrical energy. Another possibility would be for the cyclist to apply the brakes, in which case the kinetic energy would be dissipated through friction as heat.
Like any physical quantity that is a function of velocity, the kinetic energy of an object depends on the relationship between the object and the observer’s frame of reference. Thus, the kinetic energy of an object is not invariant.
Spacecraft use chemical energy to launch and gain considerable kinetic energy to reach orbital velocity. In an entirely circular orbit, this kinetic energy remains constant because there is almost no friction in near-earth space. However, it becomes apparent at re-entry when some of the kinetic energy is converted to heat. If the orbit is elliptical or hyperbolic, then throughout the orbit kinetic and potential energy are exchanged; kinetic energy is greatest and potential energy lowest at closest approach to the earth or other massive body, while potential energy is greatest and kinetic energy the lowest at maximum distance. Disregarding loss or gain however, the sum of the kinetic and potential energy remains constant.
Kinetic energy can be passed from one object to another. In the game of billiards, the player imposes kinetic energy on the cue ball by striking it with the cue stick. If the cue ball collides with another ball, it slows down dramatically, and the ball it hit accelerates as the kinetic energy is passed on to it. Collisions in billiards are effectively elastic collisions, in which kinetic energy is preserved. In inelastic collisions, kinetic energy is dissipated in various forms of energy, such as heat, sound and binding energy (breaking bound structures).
Flywheels have been developed as a method of energy storage. This illustrates that kinetic energy is also stored in rotational motion.
Several mathematical descriptions of kinetic energy exist that describe it in the appropriate physical situation. For objects and processes in common human experience, the formula ½mv² given by Newtonian (classical) mechanics is suitable. However, if the speed of the object is comparable to the speed of light, relativistic effects become significant and the relativistic formula is used. If the object is on the atomic or sub-atomic scale, quantum mechanical effects are significant, and a quantum mechanical model must be employed.
Newtonian kinetic energy
Kinetic energy of rigid bodies
In classical mechanics, the kinetic energy of a point object (an object so small that its mass can be assumed to exist at one point), or a non-rotating rigid body depends on the mass of the body as well as its speed. The kinetic energy is equal to 1/2 the product of the mass and the square of the speed. In formula form:
where 

For example, one would calculate the kinetic energy of an 80 kg mass (about 180 lbs) traveling at 18 metres per second (about 40 mph, or 65 km/h) as
When a person throws a ball, the person does work on it to give it speed as it leaves the hand. The moving ball can then hit something and push it, doing work on what it hits. The kinetic energy of a moving object is equal to the work required to bring it from rest to that speed, or the work the object can do while being brought to rest: net force × displacement = kinetic energy, i.e.,
Since the kinetic energy increases with the square of the speed, an object doubling its speed has four times as much kinetic energy. For example, a car traveling twice as fast as another requires four times as much distance to stop, assuming a constant braking force. As a consequence of this quadrupling, it takes four times the work to double the speed.
The kinetic energy of an object is related to its momentum by the equation:
where:
For the translational kinetic energy, that is the kinetic energy associated with rectilinear motion, of a rigid body with constant mass 

where:
The kinetic energy of any entity depends on the reference frame in which it is measured. However, the total energy of an isolated system, i.e. one in which energy can neither enter nor leave, does not change over time in the reference frame in which it is measured. Thus, the chemical energy converted to kinetic energy by a rocket engine is divided differently between the rocket ship and its exhaust stream depending upon the chosen reference frame. This is called the Oberth effect. But the total energy of the system, including kinetic energy, fuel chemical energy, heat, etc., is conserved over time, regardless of the choice of reference frame. Different observers moving with different reference frames would however disagree on the value of this conserved energy.
The kinetic energy of such systems depends on the choice of reference frame: the reference frame that gives the minimum value of that energy is the center of momentum frame, i.e. the reference frame in which the total momentum of the system is zero. This minimum kinetic energy contributes to the invariant mass of the system as a whole.
Derivation
Without vectors and calculus
The work W done by a force F on an object over a distance s parallel to F equals
.
Using Newton’s Second Law
with m the mass and a the acceleration of the object and
the distance traveled by the accelerated object in time t, we find with 
With vectors and calculus
The work done in accelerating a particle with mass m during the infinitesimal time interval dt is given by the dot product of force F and the infinitesimal displacement dx
where we have assumed the relationship p = m v and the validity of Newton’s Second Law. (However, also see the special relativistic derivation below.)
Applying the product rule we see that:
Therefore, (assuming constant mass so that dm = 0), we have,
Since this is a total differential (that is, it only depends on the final state, not how the particle got there), we can integrate it and call the result kinetic energy. Assuming the object was at rest at time 0, we integrate from time 0 to time t because the work done by the force to bring the object from rest to velocity v is equal to the work necessary to do the reverse:
This equation states that the kinetic energy (Ek) is equal to the integral of the dot product of the velocity (v) of a body and the infinitesimal change of the body’s momentum (p). It is assumed that the body starts with no kinetic energy when it is at rest (motionless).
Rotating bodies
If a rigid body Q is rotating about any line through the center of mass then it has rotational kinetic energy (
where:
(In this equation the moment of inertia must be taken about an axis through the center of mass and the rotation measured by ω must be around that axis; more general equations exist for systems where the object is subject to wobble due to its eccentric shape).
Kinetic energy of systems
A system of bodies may have internal kinetic energy due to the relative motion of the bodies in the system. For example, in the Solar System the planets and planetoids are orbiting the Sun. In a tank of gas, the molecules are moving in all directions. The kinetic energy of the system is the sum of the kinetic energies of the bodies it contains.
A macroscopic body that is stationary (i.e. a reference frame has been chosen to correspond to the body’s center of momentum) may have various kinds of internal energy at the molecular or atomic level, which may be regarded as kinetic energy, due to molecular translation, rotation, and vibration, electron translation and spin, and nuclear spin. These all contribute to the body’s mass, as provided by the special theory of relativity. When discussing movements of a macroscopic body, the kinetic energy referred to is usually that of the macroscopic movement only. However, all internal energies of all types contribute to a body’s mass, inertia, and total energy.
Fluid dynamics
In fluid dynamics, the kinetic energy per unit volume at each point in an incompressible fluid flow field is called the dynamic pressure at that point.[11]
Dividing by V, the unit of volume:
where 
Frame of reference
The speed, and thus the kinetic energy of a single object is frame-dependent (relative): it can take any non-negative value, by choosing a suitable inertial frame of reference. For example, a bullet passing an observer has kinetic energy in the reference frame of this observer. The same bullet is stationary to an observer moving with the same velocity as the bullet, and so has zero kinetic energy.[12] By contrast, the total kinetic energy of a system of objects cannot be reduced to zero by a suitable choice of the inertial reference frame, unless all the objects have the same velocity. In any other case, the total kinetic energy has a non-zero minimum, as no inertial reference frame can be chosen in which all the objects are stationary. This minimum kinetic energy contributes to the system’s invariant mass, which is independent of the reference frame.
The total kinetic energy of a system depends on the inertial frame of reference: it is the sum of the total kinetic energy in a center of momentum frame and the kinetic energy the total mass would have if it were concentrated in the center of mass.
This may be simply shown: let 
Then,
However, let 


Thus the kinetic energy of a system is lowest to center of momentum reference frames, i.e., frames of reference in which the center of mass is stationary (either the center of mass frame or any other center of momentum frame). In any different frame of reference, there is additional kinetic energy corresponding to the total mass moving at the speed of the center of mass. The kinetic energy of the system in the center of momentum frame is a quantity that is invariant (all observers see it to be the same).
Rotation in systems
It sometimes is convenient to split the total kinetic energy of a body into the sum of the body’s center-of-mass translational kinetic energy and the energy of rotation around the center of mass (rotational energy):
where:
- Ek is the total kinetic energy
- Et is the translational kinetic energy
- Er is the rotational energy or angular kinetic energy in the rest frame
Thus the kinetic energy of a tennis ball in flight is the kinetic energy due to its rotation, plus the kinetic energy due to its translation.
Relativistic kinetic energy
If a body’s speed is a significant fraction of the speed of light, it is necessary to use relativistic mechanics to calculate its kinetic energy. In special relativity theory, the expression for linear momentum is modified.
With m being an object’s rest mass, v and v its velocity and speed, and c the speed of light in vacuum, we use the expression for linear momentum 

Integrating by parts yields
Since 

Simplifying the expression we obtain



resulting in the formula
This formula shows that the work expended accelerating an object from rest approaches infinity as the velocity approaches the speed of light. Thus it is impossible to accelerate an object across this boundary.
The mathematical by-product of this calculation is the mass–energy equivalence formula—the body at rest must have energy content
At a low speed (v ≪ c), the relativistic kinetic energy is approximated well by the classical kinetic energy. This is done by binomial approximation or by taking the first two terms of the Taylor expansion for the reciprocal square root:
So, the total energy 
When objects move at a speed much slower than light (e.g. in everyday phenomena on Earth), the first two terms of the series predominate. The next term in the Taylor series approximation
is small for low speeds. For example, for a speed of 10 km/s (22,000 mph) the correction to the Newtonian kinetic energy is 0.0417 J/kg (on a Newtonian kinetic energy of 50 MJ/kg) and for a speed of 100 km/s it is 417 J/kg (on a Newtonian kinetic energy of 5 GJ/kg).
The relativistic relation between kinetic energy and momentum is given by
This can also be expanded as a Taylor series, the first term of which is the simple expression from Newtonian mechanics:[14]
This suggests that the formulae for energy and momentum are not special and axiomatic, but concepts emerging from the equivalence of mass and energy and the principles of relativity.
General relativity
Using the convention that
where the four-velocity of a particle is
and 
If the particle has momentum
as it passes by an observer with four-velocity uobs, then the expression for total energy of the particle as observed (measured in a local inertial frame) is
and the kinetic energy can be expressed as the total energy minus the rest energy:
Consider the case of a metric that is diagonal and spatially isotropic (gtt, gss, gss, gss). Since
where vα is the ordinary velocity measured w.r.t. the coordinate system, we get
Solving for ut gives
Thus for a stationary observer (v = 0)
and thus the kinetic energy takes the form
Factoring out the rest energy gives:
This expression reduces to the special relativistic case for the flat-space metric where
In the Newtonian approximation to general relativity
where Φ is the Newtonian gravitational potential. This means clocks run slower and measuring rods are shorter near massive bodies.
Kinetic energy in quantum mechanics
In quantum mechanics, observables like kinetic energy are represented as operators. For one particle of mass m, the kinetic energy operator appears as a term in the Hamiltonian and is defined in terms of the more fundamental momentum operator 
Notice that this can be obtained by replacing 

In the Schrödinger picture, 

The expectation value of the electron kinetic energy, 

where 

The density functional formalism of quantum mechanics requires knowledge of the electron density only, i.e., it formally does not require knowledge of the wavefunction. Given an electron density 
where ![T[rho ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9f33f6be9ea929173b30036aae6d57718be7b9c)
See also
- Escape velocity
- Foot-pound
- Joule
- Kinetic energy penetrator
- Kinetic energy per unit mass of projectiles
- Kinetic projectile
- Parallel axis theorem
- Potential energy
- Recoil
Notes
- ^ Jain, Mahesh C. (2009). Textbook of Engineering Physics (Part I). p. 9. ISBN 978-81-203-3862-3. Archived from the original on 2020-08-04. Retrieved 2018-06-21., Chapter 1, p. 9 Archived 2020-08-04 at the Wayback Machine
- ^ Landau, Lev; Lifshitz, Evgeny (15 January 1976). Mechanics (Third ed.). p. 15. ISBN 0-7506-2896-0.
- ^ Goldstein, Herbert (2002). Classical Mechanics (Third ed.). p. 62-33. ISBN 978-0201657029.
- ^ Brenner, Joseph (2008). Logic in Reality (illustrated ed.). Springer Science & Business Media. p. 93. ISBN 978-1-4020-8375-4. Archived from the original on 2020-01-25. Retrieved 2016-02-01. Extract of page 93 Archived 2020-08-04 at the Wayback Machine
- ^ Judith P. Zinsser (2007). Emilie du Chatelet: Daring Genius of the Enlightenment. Penguin. ISBN 978-0-14-311268-6.
- ^ Crosbie Smith, M. Norton Wise (1989-10-26). Energy and Empire: A Biographical Study of Lord Kelvin. Cambridge University Press. p. 866. ISBN 0-521-26173-2.
- ^ John Theodore Merz (1912). A History of European Thought in the Nineteenth Century. Blackwood. p. 139. ISBN 0-8446-2579-5.
- ^ William John Macquorn Rankine (1853). «On the general law of the transformation of energy». Proceedings of the Philosophical Society of Glasgow. 3 (5).
- ^ «… what remained to be done, was to qualify the noun ‘energy’ by appropriate adjectives, so as to distinguish between energy of activity and energy of configuration. The well-known pair of antithetical adjectives, ‘actual’ and ‘potential,’ seemed exactly suited for that purpose. … Sir William Thomson and Professor Tait have lately substituted the word ‘kinetic’ for ‘actual.‘» William John Macquorn Rankine (1867). «On the Phrase «Potential Energy,» and on the Definitions of Physical Quantities». Proceedings of the Philosophical Society of Glasgow. VI (III).
- ^ Goel, V. K. (2007). Fundamentals Of Physics Xi (illustrated ed.). Tata McGraw-Hill Education. p. 12.30. ISBN 978-0-07-062060-5. Archived from the original on 2020-08-03. Retrieved 2020-07-07. Extract of page 12.30 Archived 2020-07-07 at the Wayback Machine
- ^ A.M. Kuethe and J.D. Schetzer (1959) Foundations of Aerodynamics, 2nd edition, p.53. John Wiley & Sons ISBN 0-471-50952-3
- ^ Sears, Francis Weston; Brehme, Robert W. (1968). Introduction to the theory of relativity. Addison-Wesley. p. 127., Snippet view of page 127 Archived 2020-08-04 at the Wayback Machine
- ^ Physics notes — Kinetic energy in the CM frame Archived 2007-06-11 at the Wayback Machine. Duke.edu. Accessed 2007-11-24.
- ^ Fitzpatrick, Richard (20 July 2010). «Fine Structure of Hydrogen». Quantum Mechanics. Archived from the original on 25 August 2016. Retrieved 20 August 2016.
References
- Physics Classroom (2000). «Kinetic Energy». Retrieved 2015-07-19.
- School of Mathematics and Statistics, University of St Andrews (2000). «Biography of Gaspard-Gustave de Coriolis (1792-1843)». Retrieved 2006-03-03.
- Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (6th ed.). Brooks/Cole. ISBN 0-534-40842-7.
- Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics (5th ed.). W. H. Freeman. ISBN 0-7167-0809-4.
- Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics (4th ed.). W. H. Freeman. ISBN 0-7167-4345-0.
External links
Media related to Kinetic energy at Wikimedia Commons





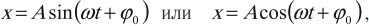
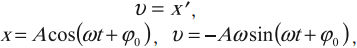
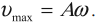
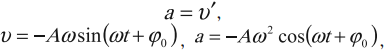
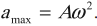
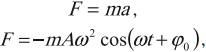
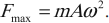
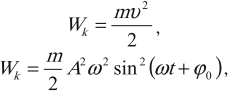
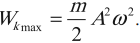
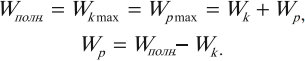
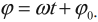




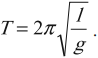
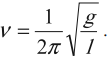
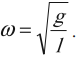
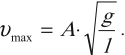
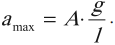
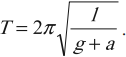
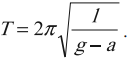
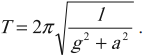
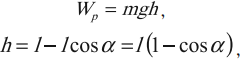
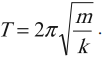
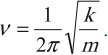
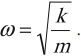
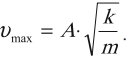
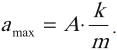
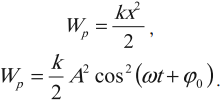
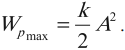
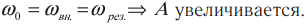
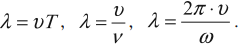
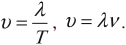


















































![{displaystyle T[rho ]={frac {1}{8}}int {frac {nabla rho (mathbf {r} )cdot nabla rho (mathbf {r} )}{rho (mathbf {r} )}}d^{3}r}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25c6547c29b24c193b6dc8a0276e1e820cfb8da6)