Обновлено: 29.05.2023
Так как функция линейная, то будет возрастать (или убывать) на всем множестве определения, поэтому достаточно найти значение функции на концах отрезка.
Ответ: наибольшее значение 1, наименьшее -5.
- Написать правильный и достоверный ответ;
- Отвечать подробно и ясно, чтобы ответ принес наибольшую пользу;
- Писать грамотно, поскольку ответы без грамматических, орфографических и пунктуационных ошибок лучше воспринимаются.
Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.
Применяя эту формулу, зная конкретное значение (x), можно вычислить соответствующее значение (y).
Чтобы построить график данной функции, нам нужны координаты двух точек, принадлежащих графику функции.
В жизни существует множество ситуаций, которые можно описать математической моделью с помощью линейных функций.
на овощной базе хранится (700) т картофеля. Каждый день запасы пополняют на (30) т. Сколько картофеля станет на овощной базе через (2); (4); (10) дней?
После (x) дней количество (y) картофеля на овощной базе можно записать в виде формулы (y = 700 + 30x).
Если функцию (y = kx + m) надо исследовать только для значений (x) из некоторого множества (X), то записывают y = kx + m , x ∈ X .
b) Во втором случае функция та же, только значения (x=-6) и (x=3) не рассматриваются, так как они не принадлежат интервалу ((-6;3)).
По графику линейной функции, можно определить наибольшее и наименьшее значения линейной функции на заданном отрезке.
b) y = 1 3 x + 1, x ∈ − 6 ; 3 , концы отрезка не рассматриваются, поэтому наибольшего и наименьшего значений нет.
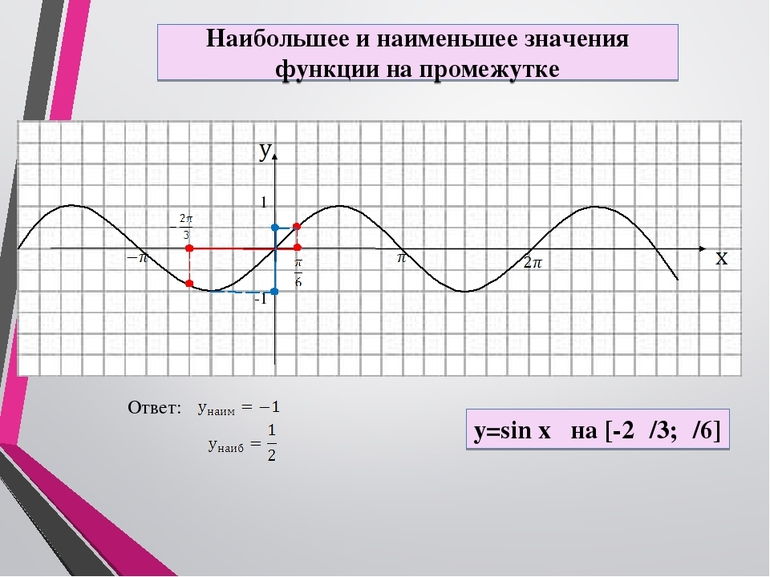
Наибольшее и наименьшее значения функции на множестве
(основные определения)
Пусть X – некоторое множество, входящее в область определения D ( f ) функции y = f (x) .
Определение 1. Значение f (x0) функции y = f (x) в точкеназывают наибольшим значением функции f (x) на множестве X , если для любой точки выполнено неравенство
Наибольшее значение функции f (x) на множестве X часто обозначают
Определение 2. Значение f (x0) функции y = f (x) в точке называют наименьшим значением функции f (x) на множестве X , если для любой точки выполнено неравенство
Наименьшее значение функции f (x) на множестве X часто обозначают
Определение 3. Наибольшее значение функции на множестве X часто называют максимальным значением функции f (x) на множестве X или максимумом функции f (x) на множестве X . Наименьшее значение функции на множестве X часто называют минимальным значением функции f (x) на множестве X или минимумом функции f (x) на множестве X .
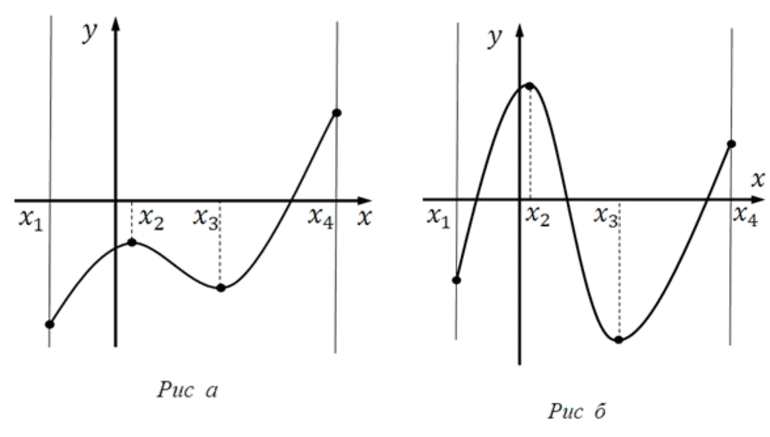
Пример 1. Минимальным значением функции y = x 2 на множестве является число 0 (рис. 1).
Максимального значения функция y = x 2 на множестве не имеет.
Пример 2. Максимальным значением функции y = – x 2 на множестве является число 0 (рис. 2).
Минимального значения функция y = – x 2 на множестве не имеет.
Пример 3. Функция y = x на множестве не имеет ни максимального, ни минимального значений (рис. 3).
Пример 4. Функция y = arctg x на множестве не имеет ни максимального, ни минимального значений (рис. 4).
Существование наибольшего и наименьшего значений функции на отрезке. Теорема Вейерштрасса
Как мы видели в примерах 1 — 4, даже такие хорошо известные функции, как
не имеют наибольших или наименьших значений на множестве. Однако, если бы в качестве множества X мы взяли произвольный отрезок, то ситуация стала бы принципиально иной, что вытекает из следующей теоремы.
Теорема Вейерштрасса. Если функция непрерывна на отрезке, то на этом отрезке существует точка, в которой функция принимает наибольшее значение, а также точка, в которой функция принимает наименьшее значение.
Доказательство теоремы Вейерштрасса выходит за рамки школьного курса математики и здесь не приводится.
Примеры решения задач
| y = 2x 3 + 3x 2 – 36x + 30 | (1) |
Из формулы (2) получаем, что критическими точками функции (1) являются точки x = – 3 , x = 2, причем только точка x = 2 принадлежит отрезку [–2, 4] . Вычисляя значения функции (1) в критической точке x = 2, а также на концах отрезка x = – 2 и x = 4 , получим:
| y (2) = – 14 , |
| y (– 2) = 98 , |
| y (4) = 62 . |
Ответ. Наибольшее значение функции (1) на отрезке [–2, 4] равно 98 , а наменьшее значение функции (1) на отрезке [–2, 4] равно – 14 .
на отрезке [–1, 27] .
Решая уравнение y’ = 0 , получим
Заметим также, что производная (4) функции (3) не существует в точке x = 0 . Следовательно, у функции (3) есть три критические точки: x = 0, и , причем все эти точки лежат на отрезке [–1, 27] . Вычисляя значения функции (3) в критических точках x = 0, и , а также на концах отрезка x = – 1 и x = 27 , получим:
| y (0) = 0 , |
| y (– 1) = – 1 , |
| y (27) = 99 . |
Ответ. Наибольшее значение функции (3) на отрезке [–1, 27] равно 99 , а наменьшее значение функции (3) на отрезке [–1, 27] равно – 1 .
Решение. Для того, чтобы найти критические точки функции (5), перепишем правую часть формулы (5), используя определение модуля:
В точке x = 0 производная функции (5) не существует. Критическими точками являются точки
Все критические точки принадлежат отрезку [–1, 6] . Вычисляя значения функции (5) в критических точках x = 0, x = 3, x = 5, а также на концах отрезка x = – 1 и x = 6 , получим:
| y (0) = – 4 , |
| y (3) = – e 3 , |
| y (5) = e 5 , |
| y (– 1) = – 5e , |
| y (6) = 2e 6 . |
Ответ. Наибольшее значение функции (5) на отрезке [–1, 6] равно 2e 6 , а наменьшее значение функции (5) на отрезке [–1, 6] равно – e 3 .
| y = (x – 27) e 28 – x | (6) |
на отрезке [23, 40] .
В некоторых задачах нужно найти наибольшее и наименьшее значения функции. Если неизвестен алгоритм и основные правила, то простое задание превращается в изнурительный труд, который очень редко приносит положительные результаты. В интернете существует множество информации, но не вся она достоверна. Самое страшное — применение неверных методик нахождения.
Общая информация
Исследование функции — распространенная задача, которая показывает ее поведение и свойства. Одним из элементов считается нахождение максимума и минимума функции. Существуют специальные программы для нахождения этих значений (онлайн-калькулятор). Однако каждому следует понимать принцип нахождения, поскольку это может пригодиться в жизни.
- Нахождение области определения функции (ОДФ).
- Понятие дифференциала и основные методы его нахождения.
- Умение решать уравнения.
- Знание графиков простых функций.
- Основные типы функций, полуинтервал и интервал.
Все пять навыков приобрести несложно, кроме второго. В этом нужно подробно разобраться, поскольку очень важно уметь находить производные (дифференциалы) не только табличных элементарных функций, но и сложных. Важно знать основные свойства, которые применяются для нахождения производной.
Область определения
Обозначение интервалов
Результатом решения задач на нахождение ОДЗ является определенный интервал. Важно правильно его обозначать, поскольку это существенно влияет на решение. Нужно руководствоваться следующими правилами:
Очень важно правильно читать интервалы. Например, запись (1;4) читается следующим образом: переменная принимает значения, которые находятся в интервале от 1 не включительно до 4 не включительно. Это числа 2 и 3, поскольку 1 и 4 не входят в промежуток. Запись вида [5;10) читается таким образом: некоторое значение принадлежит интервалу от 5 включительно, до 10 не включительно.
Зависимость от типа
Функции различаются между собой. От этого и зависит нахождение их области определения. Они бывают простыми и сложными. Первые состоят из единичных элементов, а сложные включают в себя несколько типов. Их еще называют составными. Простые классифицируются на три вида:
- Алгебраические: рациональные и иррациональные.
- Тригонометрические: sin, cos, tg и ctg.
- Трансцендентные: степенные, показательные и логарифмические.
Рациональные бывают целыми и дробными. Они не включают в себя выражения, содержащие такие элементы: корень, степень, логарифм и тригонометрические функции. D(f) этих функций — все действительные числа (Z). Если она является дробной, то это означает, что в ее числителе и (или) знаменателе находится аргумент, значение которого не должно обращать ее в пустое множество.
Когда под корнем находится выражение, содержащее независимую переменную, то она называется иррациональной. В этом случае D(f) — множество Z, кроме тех, которые превращают выражение под корнем четной степени в отрицательное значение. Функция, представленная степенными выражениями, имеет D(f) = Z, но только тогда, когда значение аргумента не превращает функцию в пустое множество.
Метод нахождения
Для решения любой задачи нужно применять определенные правила. Они называются алгоритмом. Для каждого типа функций существует конкретный вариант решения. Для дробной он является следующим:
- Найти корни уравнения знаменателя, приравнивая его к 0.
- Определить интервал, значения из которого может принимать аргумент.
В случае, когда выражение является иррациональной функцией, корень которой является четным, следует решать не уравнение, а неравенство. Его значение не должно быть меньше 0. Для логарифмического типа выражение натурального логарифма (ln) должно быть всегда больше 0.
Для sin(x) и cos(x) областью определения является множество значений Z. Однако для tg(x) и ctg(x) следует помнить, что аргумент не должен принимать значение x = (Pi / 2) + Pi * k и x = Pi * k соответственно. Следует отметить, что коэффициент k принадлежит множеству чисел Z.
Для примера нужно разобрать задачу, в которой следует найти D(3x / [(x — 1) * (x + 1) * (10 — x)^(1/2)]). Решать ее необходимо по такому алгоритму:
- Знаменатель является сложным. Он состоит из двух выражений: (x — 1) * (x + 1) и (10 — x)^(1/2).
- Первое выражение (решить уравнение): (x — 1) * (x + 1) = 0. Оно имеет два корня: x1 = -1 и x2 = 1. Числовой промежуток: (-бесконечность;-1) U (1;+бесконечность).
- Второе (неравенство): (10 — x) a). Например, (a;+inf): х = lim [f(x)], где x->a и x->+inf.
Для нахождения минимального и максимального значения функции достаточно материала, изложенного выше. Специалисты рекомендуют разобраться с теорией, а затем переходить к практике.
Примеры решений
Дана квадратичная функция y = x^2 + 6x + 9. Необходимо найти наименьшее значение функции квадратного уравнения на отрезке [1;5]. Для этой цели нужно воспользоваться алгоритмом:
- D(y): все множество Z.
- Отрезок входит в D(y).
- Производная: y’ = [x^2 + 6x + 9]’ = 2x + 6 (существует во всех точках).
- Стационарные точки (y’ = 0): 2x + 6 = 0. Отсюда, x = -3.
- Подставить в исходное выражение: y(-3) = (-3)^2 + 6 * (-3) + 9 = 9 — 18 + 9 = 0, y(1) = (1)^2 + 6 * (1) + 9 = 1 + 6 + 9 = 16 и y(5) = (5)^2 + 6 * (5) + 9 = 25 + 30 + 9 = 64.
- Максимум и минимум (с учетом стационарной точки и интервала): MIN(y) = 0 и MAX(y) = 64.
Одним из простейших типов задач является следующая: найдите наибольшее значение линейной функции z = 5x + 10 на отрезке [-3;3]. Для ее решения можно также воспользоваться алгоритмом:
- D(z) — все значения от бесконечно малого до бесконечно большого чисел.
- Промежуток, на котором нужно найти максимум и минимум, полностью входит в D(f).
- Дифференциал: z’ = 5 (существует во всех точках, а стационарных точек нет вообще).
- Минимум и максимум: MIN(z(-3)) = 5 * (-3) + 10 = -5 и MAX(z(3)) = 5 * (3) + 10 = 25.
Последнюю задачу необязательно решать по алгоритму, поскольку она считается простейшей. Математики рекомендуют тренироваться в нахождении MIN и MAX функции, поскольку только практика позволяет быстро решать задачи.
Таким образом, для нахождения максимального и минимального значений заданной функции необходимо пользоваться специальным универсальным алгоритмом. Кроме того, нужно правильно находить дифференциалы, область определения, а также разбираться в интервалах.
Читайте также:
- Обработка кокеток план урока
- Счастлив ли мечтатель белые ночи кратко
- План урока рог1аллин терахьдешнаш 6 класс
- Почему в русских школах учат немецкий язык
- Проект по вокалу в доу
Найдем наибольшее значение линейной функции:
при
следующих ограничениях:
Необходимо
найти начальное опорное (абсолютно
произвольное) решение для функции L,
которое бы удовлетворяло системе
наложенных ограничений. Далее, применяя
симплекс таблицы, будем получать решения,
при которых значение функции будет, как
минимум, не убывать. И так до тех пор,
пока не достигнем оптимально решения,
при котором функция достигает своего
максимума. Если, конечно, рассматриваемая
нами линейная функция обладаем
максимальным значением при заданной
системе ограничений. Перед применением
симплекс таблиц, необходимо преобразовать
систему линейных ограничений и
рассматриваемую нами функцию L к вполне
определенному виду.
•
Свободные члены
системы ограничений должны быть
неотрицательными.
Свободные
члены системы ограничений неотрицательные.
• Система
ограничений должна быть приведена к
каноническому виду.
К
левой части неравенства 1 системы
ограничений прибавляем неотрицательную
переменную y1 —
преобразуем неравенство 1 в равенство.
К левой части
неравенства 2 системы ограничений
прибавляем неотрицательную переменную
y2 —
преобразуем неравенство 2 в равенство.
К левой части
неравенства 3 системы ограничений
прибавляем неотрицательную переменную
y3 —
преобразуем неравенство 3 в равенство.
Система
ограничений приведена к каноническому
виду, т.е. все условия системы представляют
собой уравнения.
•
Определимся с
начальным опорным решением.
Переменная y1 входит
в уравнение 1 с коэффициентом 1, а в
остальные уравнения системы с коэффициентом
ноль, т.е. y1 —
базисная переменная.
Переменная y2 входит
в уравнение 2 с коэффициентом 1, а в
остальные уравнения системы с коэффициентом
ноль, т.е. y2 —
базисная переменная.
Переменная y3 входит
в уравнение 3 с коэффициентом 1, а в
остальные уравнения системы с коэффициентом
ноль, т.е. y3 —
базисная переменная.
Переменные,
которые не являются базисными называются
свободными переменными. Приравняв
свободные переменные нулю в получившийся
системе ограничений мы получим начальное
опорное решение.
X нач =
( 0 , 0 , 0 , 25 , 20 , 18 )
В
процессе дальнейших преобразований
возможны два случая. Если в симплекс
таблице, на каком-то шаге, мы получим
строку L состоящую из неотрицательных
элементов — задача решена, мы нашли
оптимальное решение. В противном случае
— функция не является ограниченной.
Обратите
внимание:
При составлении
исходной симплекс таблицы, коэффициенты
функции L записываются с противоположными
знаками, а свободный член со своим
знаком.
Правило 1:
-
в качестве
разрешающего выбираем столбец, в котором
нарушено условие неотрицательности
(для задачи на максимум) или отрицательности
(для задачи на минимум). Если таких
столбцов несколько, разрешающий будет
тот, которому соответствует наибольшее
по модулю значение элемента заключительной
строки, т.е.
.
За
ведущий выберем столбец 3 , так как -9
наименьший элемент в L строке. Элемент
L строки, принадлежащий столбцу свободных
членов не рассматриваем.
|
базисные |
x1 |
x2 |
x3 |
свободные |
|
y1 |
5 |
2 |
3 |
25 |
|
y2 |
1 |
6 |
2 |
20 |
|
y3 |
4 |
0 |
3 |
18 |
|
L |
— 6 |
— 5 |
— 9 |
0 |
построить график линейной функции:
a)
y=13x+1,x∈−6;3
; b)
y=13x+1,x∈−6;3
.
Составим таблицу значений функции:
| (x) | (-6) | (3) |
| (y) | (-1) | (2) |
Построим на координатной плоскости (xOy) точки ((-6;-1)) и ((3;2)) и
проведём через них прямую.
Далее выделим отрезок, соединяющий построенные точки.
Этот отрезок и есть график линейной функции
y=13x+1,x∈−6;3
.
Точки ((-6); (-1)) и ((3); (2)) на рисунке отмечены тёмными кружочками.
b) Во втором случае функция та же, только значения (x=-6) и (x=3) не рассматриваются, так как они не принадлежат интервалу ((-6;3)).
Поэтому точки ((-6); (-1)) и ((3); (2)) на рисунке отмечены светлыми кружочками.
По графику линейной функции, можно определить наибольшее и наименьшее значения линейной функции на заданном отрезке.
В случае
a)
y=13x+1,x∈−6;3
, имеем:
yнаиб
(= 2) и
yнаим
(= -1);
b)
y=13x+1,x∈−6;3
, концы отрезка не рассматриваются, поэтому наибольшего и наименьшего значений нет.
Экономическая и геометрическая интерпретация задачи целочисленного программирования. Экстремальная задача, переменные которой принимают лишь целочисленные значения, называется задачей целочисленного программирования.
В математической модели задачи целочисленного программирования как целевая функция, так и функции в системе ограничений могут быть линейными, нелинейными и смешанными. Ограничимся случаем, когда целевая функция и система ограничений задачи являются линейными.
1.20. В цехе предприятия решено установить дополнительное оборудование, для размещения которого выделено площади. На приобретение оборудования предприятие может израсходовать 10 тыс. руб., при этом оно может купить оборудование двух видов. Комплект оборудования I вида стоит 1000 руб., а II вида — 3000 руб. Приобретение одного комплекта оборудования I вида позволяет увеличить выпуск продукции в смену на 2 ед., а одного комплекта оборудования II вида — на 4 ед. Зная что для установки одного комплекта оборудования I вида требуется 2 м2 площади, а оборудования II вида — 1 м2 площади определить такой набор дополнительного оборудования, которых дает возможность максимально увеличить выпуск продукции
Решение. Составим математическую модель задачи. Предположим, что предприятие приобретет комплектов оборудования I вида и
комплектов оборудования II вида. Тогда переменные
и
должны удовлетворять следующим неравенствам:

Если предприятие приобретет указанное количество оборудоВания, то общее увеличение выпуска продукции составит
(9)
По своему экономическому содержанию переменные и
могу принимать лишь целые неотрицательные значения, т. е.
(10)
,
— целые. (11)
Таким образом, приходим к следующей математической задаче: найти максимальное значение линейной функции (9) при вы полнении условий (8), (10) и (11). Так как неизвестные могут принимать только целые значения, то задача (8) — (11) является задачей целочисленного программирования. Поскольку число неизвестных задачи равно двум, решение данной задачи можно найти, используя ее геометрическую интерпретацию. Для этого прежде всего построим многоугольник решений задачи, состоящей в определении максимального значения линейной функции (9) при выполнении условий (8) и (10) (рис. 11). Координаты всех точек построенного многоугольника решений ОАЕВС Удовлетворяют системе линейных неравенств (8) и условию неотрицательности переменных (10). Вместе с тем условию (11), т. е. условию целочисленности переменных, удовлетворяют координаты лишь 12 точек, отмеченных на рис. 11. Чтобы найти точку, координаты которой определяют решение исходной задачи, заменим многоугольник ОАВС многоугольником OKEMNF, содержащим все допустимые точки с целочисленными координатами и таким, что координаты каждой из вершин являются целыми числами. Значит, если найти точку максимума функции (9) на многоугольнике OKEMNF, то координаты этой точки и определят оптимальный план задачи.
Для этого построим вектор и прямую
проходящую через многоугольник решений OKEMNF (число 12 взято произвольно). Построенную прямую передвигаем в направлении вектора
до тех пор, пока она не пройдет через последнюю общую точку ее с данным многоугольником. Координаты этой точки и определяют оптимальный план, а значение целевой функции в ней является максимальным.
В данном случае искомой является точка E(1; 3), в которой целевая функция принимает максимальное значение Следовательно, координаты точки Е определяют оптимальный план задачи (8) — (11). В соответствии с этим планом предприятию следует приобрести один комплект оборудования 1 вида и три комплекта оборудования II вида. Это обеспечит предприятию при имеющихся у него ограничениях на производственные площади и денежные средства максимальное увеличение выпуск продукции, равное 14 ед. в смену.
1.21. Для выполнения работ могут быть использованы П механизмов. Производительность I-го механизма при выполнении J-Й работы
равна
. Предполагая, что каждый механизм может быть использован только на одной работе и каждая работа может выполняться только одним механизмом, определить закрепление механизмов за работами, обеспечивающее максимальную производительность. Построить математическую модель задачи.
Решение. Введем переменную , значение которой равно 1, если при выполнении I-й работы используется J-Й механизм, и равно 0 в противном случае. Тогда условия использования каждого механизма только на одной работе выражаются равенствами
(12)
А условия выполнения работы только одним механизмом — равенствами
(13)
(14)
Таким образом, задача состоит в определении таких значений неизвестных , удовлетворяющих системам уравнений (12) и (13) и условию (14), при которых достигается максимальное значение функции
(15)
Сформулированная задача является задачей целочисленного программирования.
Определение оптимального плана задачи целочисленного программирования. Рассмотрим задачи целочисленного программирования, в которых как целевая функция, так и функции в системе ограничений являются линейными. В связи с этим сформулируем основную задачу линейного программирования, в которой переменные могут принимать только целые значения. В общем виде эту задачу можно записать так: найти максимум функции
(16)
При условиях
(17)
(18)
— целые
(19)
Если найти решение задачи (16) — (19) симплексным методом, то оно может оказаться как целочисленным, так и нет (примером задачи линейного программирования, решение которой всегда является целочисленным, служит транспортная задача). В общем же случае для определения оптимального плана задачи (16) — (19) требуются специальные методы. В настоящее время существует несколько таких методов, из которых наиболее известным является метод Гомори, в основе которого лежит описанный выше симплексный метод.
Метод Гомори. Нахождение решения задачи целочисленного программирования методом Гомори начинают с определения симплексным методом оптимального плана задачи (16) — (18) без учета целочисленности переменных. После того как этот план найден, просматривают его компоненты. Если среди компонент нет дробных чисел, то найденный план является оптимальным планом задачи целочисленного программирования (16) — (19). Если же в оптимальном плане задачи (16) — (18) переменная принимает дробное значение, то к системе уравнений (17) добавляют неравенство
(20)
И находят решение задачи (16) — (18), (20).
В неравенстве (20) и
— преобразованные исходные величины
и
значения которых взяты из последней симплекс-таблицы, а
и
— дробные части чисел (под дробной частью некоторого числа а понимается наименьшее неотрицательное число B такое, что разность между А и B есть целое). Если в оптимальном плане задачи (16) — (18) дробные значения принимают несколько переменных, то дополнительное неравенство (20) определяется наибольшей дробной частью.
Если в найденном плане задачи (16) — (18), (20) переменные принимают дробные значения, то снова добавляют одно дополнительное ограничение и процесс вычислений повторяют. Проводя конечное число итераций, либо получают оптимальный план задачи целочисленного программирования (16) — (19), либо устанавливают ее неразрешимость.
Если требование целочисленности (19) относится лишь к некоторым переменным, то такие задачи называются Частично целочисленными. Их решение также находят последовательным решением задач, каждая из которых получается из предыдущей с помощью введения дополнительного ограничения. В этом случае такое ограничение имеет вид
(21)
Где определяются из следующих соотношений:
1) для , которые могут принимать нецелочисленные значения,

2) для , которые могут принимать только целочисленные значения,

Из изложенного выше следует, что процесс определения оптимального плана задачи целочисленного программирования методом Гомори включает следующие основные этапы:
1. Используя симплексный метод, находят решение задачи (16) — (18) без учета требования целочисленности переменных.
2. Составляют дополнительное ограничение для переменной, которая в оптимальном плане задачи (16) — (18) имеет максимальное дробное значение, а в оптимальном плане задачи (16) — (19) должна быть целочисленной.
3. Используя двойственный симплекс-метод, находят решение задачи, получающейся из задачи (16) — (18) в результате присоединения дополнительного ограничения.
4. В случае необходимости составляют еще одно дополнительное ограничение и продолжают итерационный процесс до получения оптимального плана задачи (16) — (19) или установления ее неразрешимости.
1.22. Методом Гомори найти максимальное значение функции
(24)
При условии

(26)
— целые
(27)
Дать геометрическую интерпретацию решения задачи.
Решение. Для определения оптимального плана задачи (24) — (27) сначала находим оптимальный план задачи (24) — (26) (табл. 22).
Как видно из табл. 22, найденный оптимальный план задачи (24) — (26) не является оптимальным планом задачи (24) — (27), поскольку две компоненты
и
имеют нецелочисленные значения. При этом дробные части этих чисел равны между собой. Поэтому для одной из этих переменных составляется дополнительное ограничение. Составим, например, такое ограничение для переменной
. Из последней симплекс-таблицы (табл. 22) имеем
Таким образом, к системе ограничений задачи (24) — (27) добавляем неравенство
или
Т. е.
(28)
Находим теперь максимальное значение функции (24) при выполнении условий (25), (26) и (28) (табл. 23).
Из таблицы 23 видно, что исходная задача целочисленного программирования имеет оптимальный план При этом плане значение целевой функции равно
. Дадим геометрическую интерпретацию решения задачи. Областью допустимых решений задачи (24) — (26) является многоугольник OABCD (рис. 12). Из рис. 12 видно, что максимальное значение целевая функция принимает в точке С (19/2; 7/2), т. e. что Х = (19/2; 7/2; 0; 0; 34) является оптимальным планом. Это непосредственно видно и из таблицы 22. Так как Х = (19/2; 7/2; 0; 0; 34) не является оптимальным планом задачи (24) — (27) (числа
и
— дробные), то вводится дополнительное ограничение
. Исключая из него
и
подстановкой вместо них соответствующих значений из уравнений системы ограничений (25), получим
отсекающий от многоугольника OABCD треугольник EFC.
Как видно из рис. 12, областью допустимых решений полученной задачи является многоугольник OABEFD. В точке Е(9; 4) этого многоугольника целевая функция данной задачи принимает максимальное значение. Так как координаты точки Е – целые числа и неизвестные ,
и
принимают целочисленные значения при подстановке в уравнение (25) значений
и
, то
является оптимальным планом задачи (24) — (27). Это следует и из таблицы 23.
2.5. Методом Гомори найти решение задачи, состоящей в определении максимального значения функции
(29)
При условиях

(31)
— целые. (32)
Дать геометрическую интерпретацию решения задачи.
Решение. Сформулированную задачу перепишем так: найти максимальное значение функции
(33)
При условиях

(35)
— целые. (36)
Задача (33) – (36) является частично целочисленной, так как переменные и
могут принимать нецелочисленные значения.
Находим симплексным методом решение задаяи (33) – (35) (таблица 24).
После II итерации получаем оптимальный план данной задачи При этом плане переменная
приняла нецелочисленное значение. Поэтому необходимо перейти к новой задаче, добавив к системе ограничений (33) – (35) еще одно ограничение
или
(37)
Находим теперь решение задачи, состоящей в определении максимального значения функции (33) при условиях (34), (35) и (37). Данную задачу решаем двойственным симплекс-методом (таблица 25).
Из таблицы 25 видно, что является оптимальным планом построенной задачи. Так как при этом плане переменные
и
принимают целые значения, то он также является оптимальным планом исходной задачи (33) – (36).
Дадим геометрическую интерпретацию решения задачи. На рис. 13 показана область допустимых решений задачи (33) – (35). Из рисунка видно, что максимальное значение целевая функция принимает в точке , т. е. что
является оптимальным планом задачи (33) – (35). В то же время
не является планом задачи (33) – (36), так как переменная
принимает дробное значение. Поэтому вводим дополнительное ограничение
откуда, подставляя вместо
его значение из второго уравнения системы уравнений (34), получаем
. Этому неравенству на рис. 13 соответствует полуплоскость, ограниченная прямой
, отсекающей от многоугольника ОАВС треугольник ADE. В области ODEBC находим точку Е(1; 1), в которой функция (33) принимает максимальное значение. Так как координаты точки Е — целые числа, то
является оптимальным планом задачи (33) — (37). Это видно и из таблицы 25.
| < Предыдущая | Следующая > |
|---|
Наибольшим или наименьшим значением функции в определенной области называют наибольшее или наименьшее значение, которое достигает эта функция на указанной области.
Чтобы найти наибольшее или наименьшее значение функции в данной области, нужно решить задачу на экстремум, то есть найти производную заданной функции, приравнять её к нулю и найти точки, в которых производная функции обращается в нуль. Потом из этих точек нужно выбрать только те, которые входят в нашу заданную область. Затем нужно вычислить значение функций в этих точках. Кроме этого, нужно найти значение функции в граничных точках заданной области (если это отрезок) и сравнить их со значениями в точках экстремума. Потом можно сделать вывод о наименьшем или наибольшем значении функции в данной области.
Определить наименьшее и наибольшее значения функции y=x3−6×2+9y=x^3-6x^2+9 на отрезке [−1;2][-1;2].
Решение
Сначала вычисляем производную исходной функции:
y′=3×2−12xy’=3x^2-12x
Затем приравниваем ее к нулевому значению и решаем уравнение:
3×2−12x=03x^2-12x=0
x(3x−12)=0x(3x-12)=0
x1=0x_1=0
x2=4x_2=4
Затем — непосредственный поиск максимального и минимального значений функции на заданном отрезке. Важно отметить, что точка x=4x=4 не входит в заданный отрезок, поэтому значение функции в этой точке вычислять не требуется.
Находим значение функции в точке x1x_1:
f(0)=9f(0)=9
Кроме этого, нужно найти значение функции в граничных точках нашего отрезка, то есть в точках x=−1x=-1 и x=2x=2:
f(−1)=−1−6+9=2f(-1)=-1-6+9=2
f(2)=8−24+9=−7f(2)=8-24+9=-7
Получаем, что на заданном отрезке, наименьшее значение функции, которое равно −7-7, достигается в точке x=2x=2 , а наибольшее значение, равное 99, достигается в точке x=0x=0.
Найти наибольшее и наименьшее значение функции-параболы y=3x2y=3x^2 на всей области её определения.
Решение
Функция y=3x2y=3x^2 определена на всем интервале от минус бесконечности к плюс бесконечности. Найдем производную этой функции:
y′=6xy’=6x
Приравниваем производную к нулю:
6x=06x=0
x=0x=0
Точка x=0x=0 — единственный экстремум этой функции. В этой точке функция равна f(0)=0f(0)=0. Остается решить максимум это или минимум.
Так как график нашей функции это парабола, ветви которой направлены вверх (поскольку 3>03>0), то точка x=0x=0 — точка минимума этой функции. Следовательно, функция y=3x2y=3x^2 достигает своего минимального значения в точке x=0x=0 равного 00. Максимального значения эта функция не имеет. Оно только приближается к сколь угодно большому числу когда значение аргумента стремится к плюс или минус бесконечности.
Тест по теме “Наибольшие и наименьшие значения функции”
Не можешь разобраться в этой теме?
Обратись за помощью к экспертам
Гарантированные бесплатные доработки
Быстрое выполнение от 2 часов
Проверка работы на плагиат









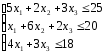
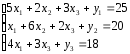
 .
.







