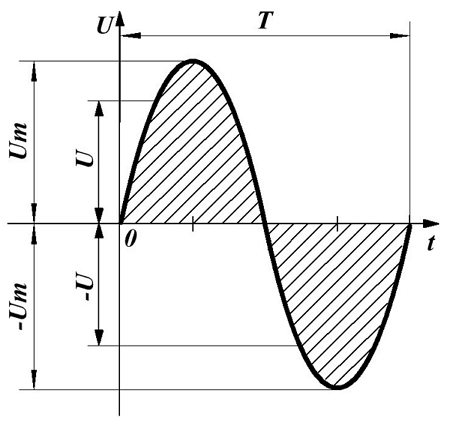
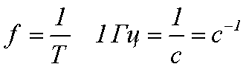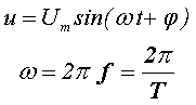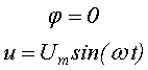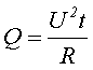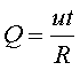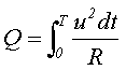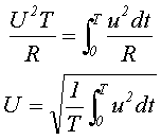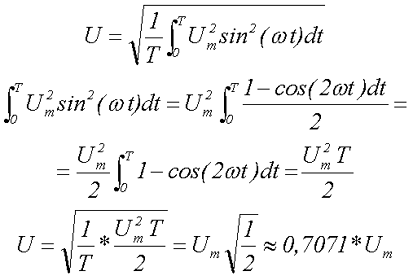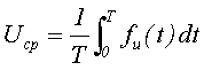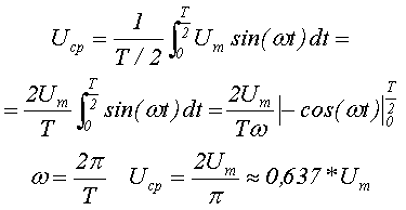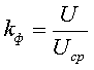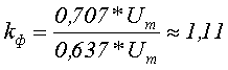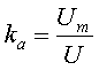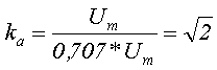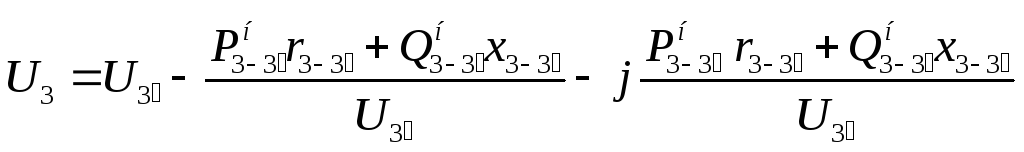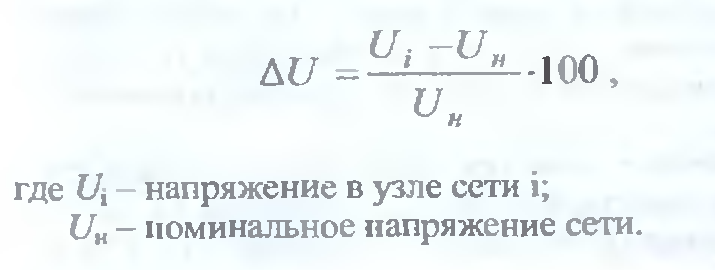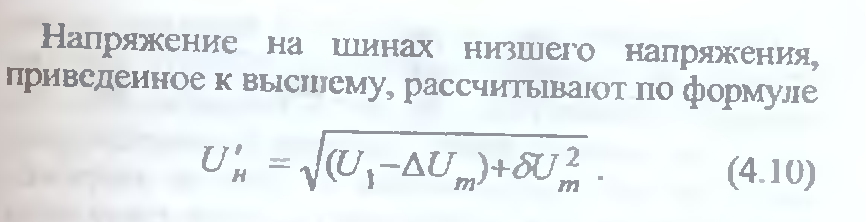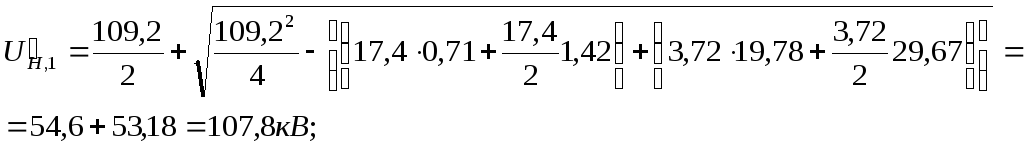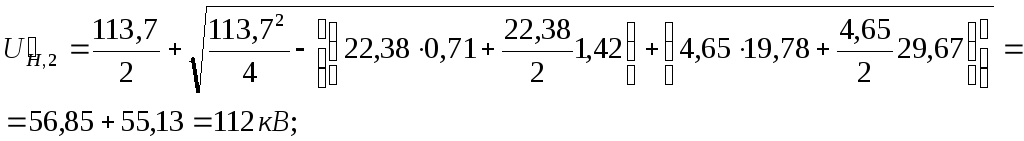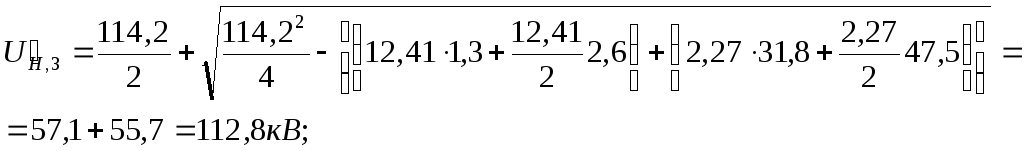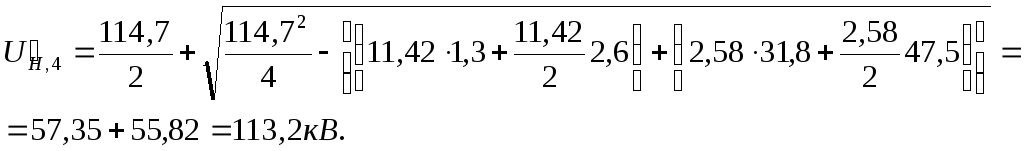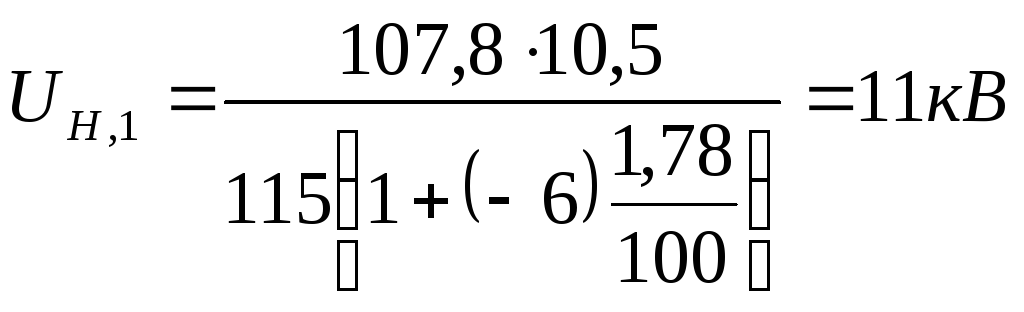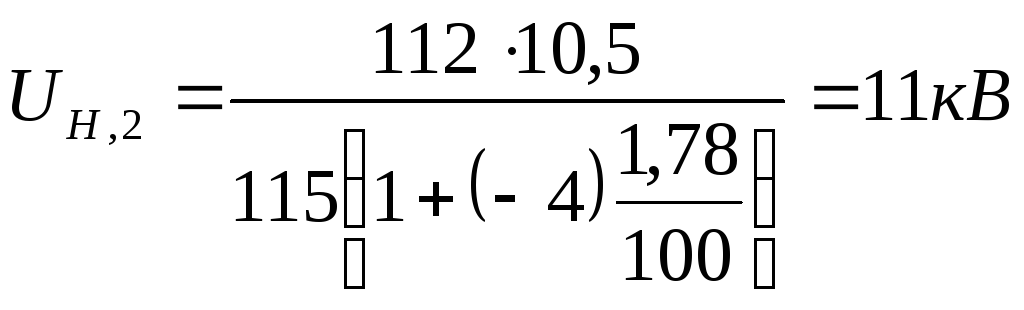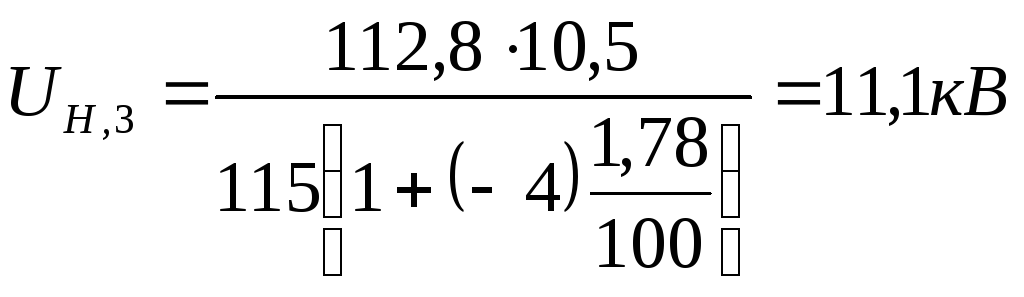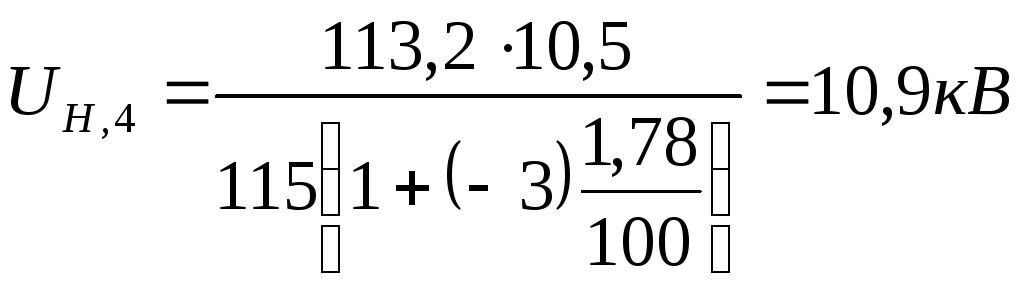Переменное напряжение — это напряжение, которое изменяется с течением времени. Далее будем рассматривать только гармоническое переменное напряжение (изменяется по синусоиде).
u = Umsin(2πt + Ψ ) = Umsin(ωt + Ψ )
Где u = u(t) — мгновенное значение переменного напряжения [В].
Um — максимальное значение напряжения (амплитудное значение) [В].
f — частота равная числу колебаний в 1 секунду (единица частоты f — герц (Гц) или с-1)
ω — угловая частота (омега) (единица угловой частоты — рад/с или с-1)
ω = 2πf = 2π/T
Аргумент синуса, т. е. (ωt + Ψ), называют фазой. Фаза характеризует состояние колебания (числовое значение) в данный момент времени t.
U — Действующее значение напряжения [В]:
Рассмотрим параметры напряжения в бытовой электросети.
Все мы знаем, что у нас дома в розетке поступает переменный ток, с напряжением 220 вольт и частотой 50 герц (в идеальных условиях) на самом деле допускается не большая погрешность как в меньшую, так и в большую сторону так, что не удивляйтесь если ваш вольтметр покажет не 220, а например 210 или даже 230 В.).
Большинство приборов измеряет не амплитудное, а действующее значение переменного напряжения, тока, мощности так, что если мы говорим что у нас напряжение сети 220, 380 В и т. д. то имеется виду именно действующие значения.
- Действующее значение напряжения U = 220 В.
- Амплитудное значение напряжения цепи переменного тока Um = U*√2 = 220 *√2 = 311 В.
- Угловая частота ω = 2πf = 3,14*2*50 = 314 рад/с.
- Начальная фаза Ψ = 0 град.
- Мгновенное значение u = 311sin(314t) В.
Всем доброго времени суток! В прошлой статье я рассказал, как рассчитать индуктивность катушки выполненной на разомкнутом сердечнике (например, ферритовой антенны, контурных катушек радиоприёмников, катушек с построечными сердечниками и т. д.). Сегодняшняя статья посвящена переменному напряжению и параметрам, которые его характеризуют.
Что такое переменное напряжение?
Как известно электрическим током называется упорядоченное движение заряженных частиц, которое возникает под действием разности потенциалов или напряжения. Одной из основных характеристик любого типа напряжения является его зависимость от времени. В зависимости от данной характеристики различают постоянной напряжение, значение которого с течением времени практически не изменяется и переменное напряжение, изменяющееся во времени.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Переменное напряжение в свою очередь бывает периодическим и непериодическим. Периодическим называется такое напряжение, значения которого повторяются через равные промежутки времени. Непериодическое напряжение может изменять своё значение в любой период времени. Данная статья посвящена периодическому переменному напряжению.
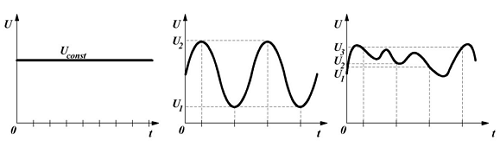
Постоянное (слева), периодическое (в центре) и непериодическое (справа) переменное напряжение.
Минимальное время, за которое значение переменного напряжения повторяется, называется периодом. Любое периодическое переменное напряжение можно описать какой-либо функциональной зависимостью. Если время обозначить через t, то такая зависимость будет иметь вид F(t), тогда в любой период времени зависимость будет иметь вид
где Т – период.
Величина обратная периоду Т, называется частотой f. Единицей измерения частоты является Герц, а единицей измерения периода является Секунда
Наиболее часто встречающаяся функциональная зависимость периодического переменного напряжения является синусоидальная зависимость, график которой представлен ниже
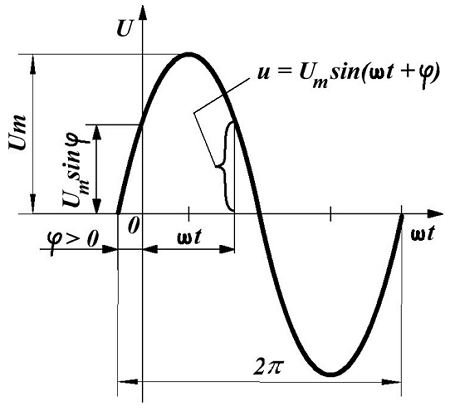
Из математики известно, что синусоида является простейшей периодической функцией, и все другие периодические функции, возможно, представить в виде некоторого количества таких синусоид, имеющих кратные частоты. Поэтому необходимо изначально рассмотреть особенности синусоидального напряжения.
Таким образом, синусоидальное напряжение в любой момент времени, мгновенное напряжение, описывается следующим выражением
где Um – максимальное значение напряжения или амплитуда,
ω –угловая частота, скорость изменения аргумента (угла),
φ – начальная фаза, определяемая смещением синусоиды относительно начала координат, определяется точкой перехода отрицательной полуволны в положительную полуволну.
Величина (ωt + φ) называется фазой, характеризующая значение напряжения в данный момент времени.
Таким образом, амплитуда Um, угловая частота ω и начальная фаза φ являются основными параметрами переменного напряжения и определяют его значение в каждый момент времени.
Обычно, при рассмотрении синусоидального напряжения считают, что начальная фаза равна нулю, тогда
В практической деятельности, довольно часто, используют ещё ряд параметров переменного напряжения, такие как, действующее напряжение, среднее напряжение и коэффициент формы, которые мы рассмотрим ниже.
Что такое действующее напряжение переменного тока?
Как я писал выше, одним из основных параметров переменного напряжения является амплитуда Um, однако использовать в расчётах данную величину не удобно, так как временной интервал в течение, которого значение напряжения u равно амплитудному Um ничтожно мал, по сравнению с периодом Т напряжения. Использовать мгновенное значение напряжения u, также не очень удобно, вследствие больших объёмов расчётов. Тогда возникает вопрос, какое значение переменного напряжения использовать при расчётах?
Для решения данного вопроса необходимо обратиться к энергии, которая выделяется под воздействием переменного напряжения, и сравнить её с энергией, которая выделяется под воздействием постоянного напряжения. Для решения данного вопроса обратимся к закону Джоуля – Ленца для постоянного напряжения
Для переменного напряжения мгновенное значение выделяемой энергии составит
где u – мгновенное значение напряжения
Тогда количество энергии за полный период от t0 = 0 до t1 = T составит
Приравняв выражения для количества энергии при переменном напряжении и постоянном напряжении и выразив полученное выражение через постоянное напряжение, получим действующее значение переменного напряжения
Получившееся выражение, позволяет вычислить действующее значение напряжение U для периодического переменного напряжения любой формы. Из выше изложенного можно сделать вывод, что действующее значение переменного напряжения называется такое постоянное напряжение, которое за такое же время и на таком же сопротивлении выделяет такую же энергию, которая выделяется данным переменным напряжением.
Действующее значение синусоидального напряжения.
Вычислим действующее значение синусоидального напряжения
Стоит отметить, все напряжения электротехнических устройств определяются, как правило, действующим значением напряжения.
Для определения амплитудного значения синусоидального напряжения необходимо преобразовать полученное выражение
Таким образом если в розетке у нас U = 230 В, следовательно, амплитудное значение данного напряжения
Действующее напряжение также имеет название эффективного напряжения и среднеквадратичного напряжения.
С действующим напряжением разобрались, теперь рассмотрим среднее значение напряжение.
Что такое среднее значение переменного напряжения?
Ещё одним параметром переменного напряжения, который его характеризует, является средним значением переменного напряжения. В отличие от действующего значения переменного напряжения, которое характеризует работу переменного напряжения, среднее значение напряжения характеризует количество электричества, которое перемещается из одной точки цепи в другую, под действием переменного напряжения. Среднее значение напряжения за период определяется следующим выражением
где Т – период переменного напряжения,
fu(t) – функциональная зависимость напряжения от времени.
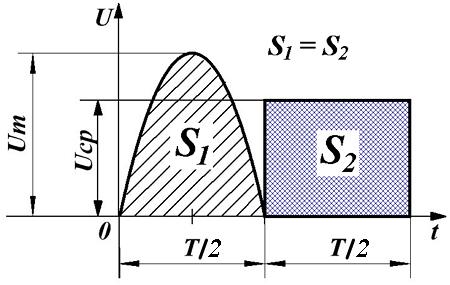
Таким образом, среднее значение переменного напряжения численно будет равно высоте прямоугольника с основанием T, площадь которого равна площади, ограниченной функцией fu(t) и осью Ox за период Т.
Среднее значение переменного напряжения.
В случае синусоидальной функции, можно говорить только о среднем значении за полупериод, так как в течение всего периода положительная полуволна компенсируется отрицательной полуволной, и тогда среднее за период напряжение будет равно нулю.
Таким образом, среднее за полупериод Т/2 значение переменного напряжения синусоидальной формы будет равно
где Um – максимальное значение напряжения или амплитуда,
ω –угловая частота, скорость изменения аргумента (угла).
Какие коэффициенты, характеризуют переменное напряжение?
Иногда возникает необходимость охарактеризовать форму переменного напряжения. Для этой цели существует ряд параметров данного переменного напряжения:
1. Коэффициент формы переменного напряжения kф – показывает как относится действующее значение переменного напряжения U к его среднему значению Ucp.
Так для синусоидального напряжения коэффициент формы составит
2. Коэффициент амплитуды переменного напряжения kа – показывает как относится амплитудное значение переменного напряжения Um к его действующему значению U
Так для синусоидального напряжения коэффициент амплитуды составит
На сегодня всё, в следующей статье я рассмотрю прохождение переменного напряжения через сопротивление, индуктивность и емкость.
Стефания Яковлева
28 января, 01:53
0
Для расчета величины максимального значения напряжения в указанной сети применим формулу: Umax = U * √2.
Данные: U — показываемое используемым вольтметром напряжение (U = 380 В).
Произведем расчет: Umax = U * √2 = 380 * √2 = 537,4 В.
Ответ: Максимальное напряжение в указанной сети составляет 537,4 В.
- Комментировать
- Жалоба
- Ссылка
Определение значения напряжения в узловых точках максимальном режиме
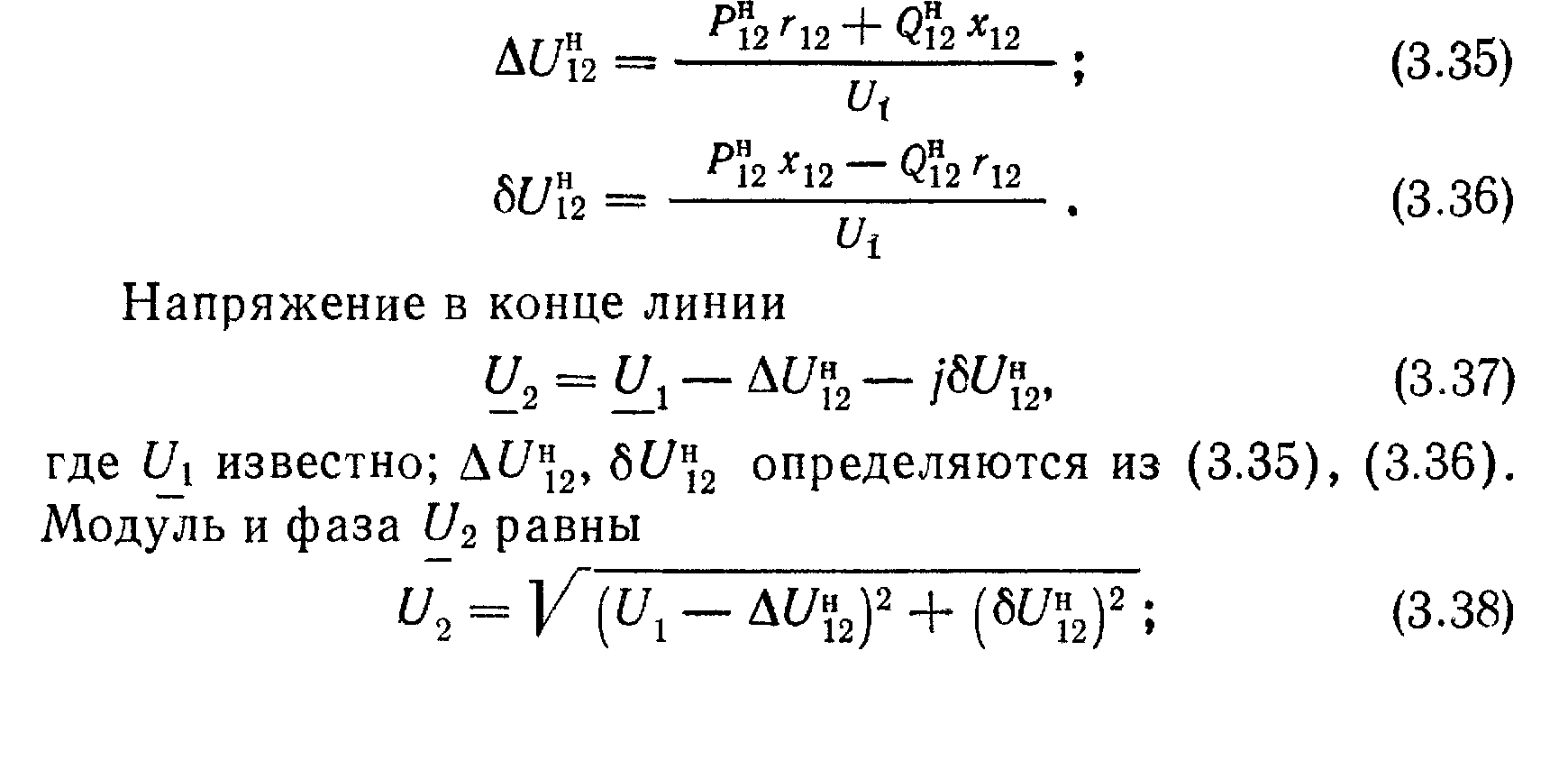
Отсюда:
,
где
Рн,
Qн– активная и
реактивная мощность нагрузки в
рассматриваемом режиме; Rab
, Хab– активное и
реактивное сопротивление линии на
данном участке.
Для расчетов сопротивления
r
и x
берем из таблицы 4.2
Пример
4
А
3
;
Для подстанций, которые
напрямую соединены с А берем максимальное
напряжение, а для тех, которые от других
подстанций, либо отпайки, из ранее
рассчитанных.
Регулирование напряжения в электрической сети в максимальном режиме
Понижающие
трансформаторы имеют РПН в нейтрали
обмотки высшего напряжения. Ответвление
регулируемой части обмотки, обеспечивающее
желаемое напряжение на шинах низшего
напряжения Uн
жел.,
может быть определено по выражению
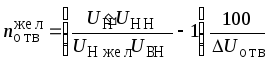
(5.1)
где
UНН,
UВН – номинальные
напряжения обмоток низшего и высшего
напряжения; DUотв
– ступень регулирования напряжения в
%.
Вычисленное
значение округляется до ближайшего
целого числа nотв
с учетом максимального числа ответвлений,
которое может колебаться от –9 до +9 для
трансформаторов типов ТДН, ТРДН. После
этого следует определить действительное
напряжение на шинах низшего напряжения
подстанций
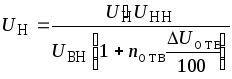
(5.2)
и
отклонения напряжения на этих шинах от
номинального напряжения (Uном=
10 кВ), %
. (5.3)
Аналог формулы
5.3
Отдельно
решается вопрос регулирования напряжения
на шинах низшего напряжения подстанций
с автотрансформаторами. Так как в
автотрансформаторах устройство РПН
осуществляется на стороне среднего
напряжения, то здесь отсутствует
возможность регулирования напряжения
на стороне низшего напряжения. На
крупных подстанциях требуемое напряжение
непосредственно на шинах низшего
напряжения может быть обеспечено с
помощью синхронных компенсаторов.
Другим способом регулирования напряжения
является использование линейных
регулировочных трансформаторов,
позволяющих регулировать напряжение
в пределах 101.5%
номинального напряжения.
Если
в результате расчета регулировочных
ответвлений трансформаторов выясняется,
что необходимо произвести корректировку
напряжения на шинах источника питания,
то новые значения напряжений на
подстанциях допускается оценивать
приближенно, ориентировочно считая,
что во всех точках сети напряжения
изменяются на столько же %, на сколько
было изменено напряжение на шинах
источника питания.
Результаты
расчетов ответвлений трансформаторов,
обеспечивающих желаемые напряжения на
шинах низшего напряжения подстанций в
режиме наименьших нагрузок и послеаварийном
режиме, сводятся в таблицы, в которых
указываются напряжения низшей стороны
трансформатора, приведенные к стороне
высшего напряжения, расчетный номер
ответвления обмотки, округленное
значение номера ответвления с учетом
возможного диапазона регулирования
напряжения, действительное напряжение
на шинах низшего напряжения подстанции
и отклонение этого напряжения от
номинального напряжения.
Напряжение на шинах низкого
напряжения, приведенное к стороне
высшего напряжения для трансформаторов
с не расщепленными обмотками типа ТДН,
ТДЦ, ТМН
,
определяется по формуле:
,
(5.4)
где— активная и реактивная мощности нагрузки
в рассматриваемом режиме;
— активное и реактивное сопротивление
трансформаторов, определенные по таблице
1.2.
На подстанциях, где установлены
трансформаторы с расщепленными обмотками,
поэтому
определяется
по формуле:
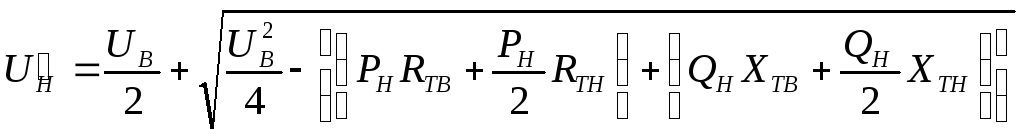
(8.21)
где
;
(8.22)
;
(8.23)
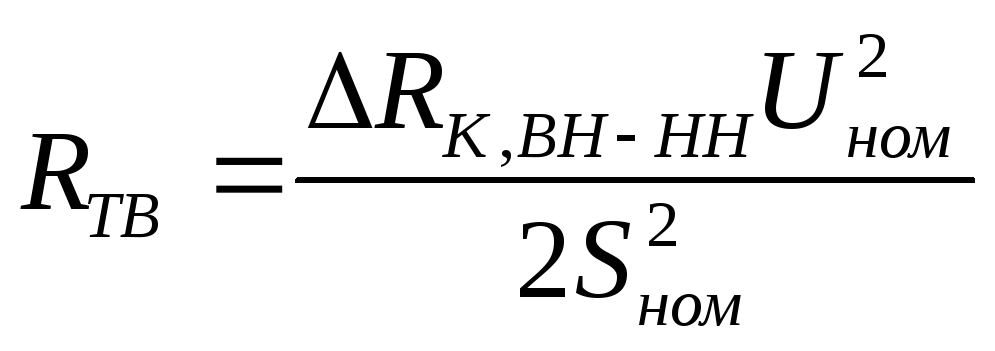
(8.24)
;
(8.25)
,
(8.26)
где
;
(8.27)
.
(8.28)
Используя вышеприведенные формулы
(8.21)-(8.28), определим соответствующие
показатели для всех подстанций.
Для ПС № 1 и 2 ():
;
;
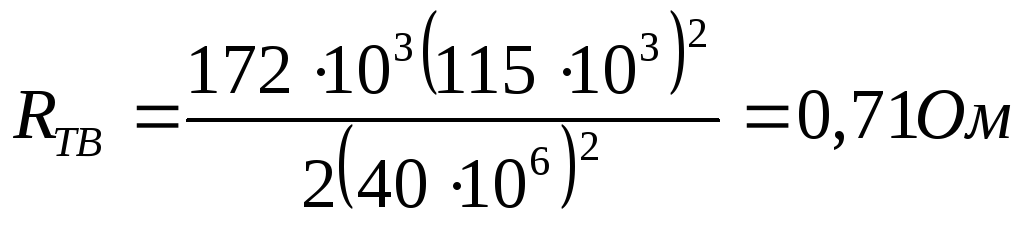
;
;
;
;
;
;
;
;
;
;
Для ПС № 3 и 4 ():
;
;
;
;
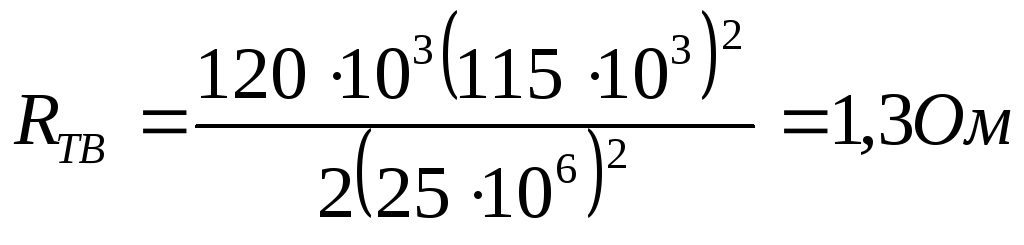
;
;
;
;
Ответвление регулируемой
части обмотки, обеспечивающее желаемое
напряжение на шинах низшего напряжения
,
определим по выражению (5.2):
Для ПС № 1:
,
округляем.
Действительное напряжение
на шинах низшего напряжения подстанций
определим по формуле (5.3):
По выражению (5.4) рассчитаем
отклонение напряжения на этих шинах от
номинального напряжения ():
Для ПС № 2:
,
округляем.
Для ПС № 3:
,
округляем.
Для ПС № 4:
,
округляем.
Результаты расчета запишем
в таблицу 8.5.
Таблица 8.5
|
№ ПС |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Переменный ток
(AC — Alternating Current) — электрический ток, меняющий свою величину и направление с течением времени.
Часто в технической литературе переменным называют ток, который меняет только величину, но не меняет направление, например, пульсирующий ток. Необходимо помнить при расчётах, что переменный ток в этом случае является лишь составляющей частью общего тока. Такой вариант можно представить как переменный ток AC
с постоянной составляющей
DC
. Либо как постоянный ток с переменной составляющей, в зависимости от того, какая составляющая наиболее важна в контексте.
DC
— Direct Current — постоянный ток, не меняющий своей величины и направления.
В реальности постоянный ток не может сохранять свою величину постоянной, поэтому существует условно в тех случаях, где можно пренебречь изменениями его постоянной величины, либо в качестве составляющей (DC
) для периодически меняющегося электрического тока любой формы. Тогда величина
DC
будет равна среднему значению тока за период, и будет являться нулевой линией для переменной составляющей
AC
.
При синусоидальной форме тока, например в электросети, постоянная составляющая DC
равна нулю.
Постоянный ток с переменной составляющей в виде пульсаций показан синей линией на верхнем графике рисунка. Запись AC+DC
в данном случае не является математической суммой, а лишь указывает на две составляющие тока. Суммируются мощности. Величина тока будет равна квадратному корню из суммы квадратов двух величин — значения постоянной составляющей
DC
и среднеквадратичного значения переменной составляющей
AC
.
Термины AC
и
DC
применимы как для тока, так и для напряжения.
Лампочка и постоянное напряжение
Для опытов нам также понадобится простая автомобильная лампа накаливания на напряжение 12 Вольт
Вот ее характеристики: рабочее напряжение U=12 Вольт, мощность Р = 21 Ватт.
Следовательно, зная мощность и напряжение лампы, можно узнать, какую силу тока будет потреблять лампочка. Из формулы P=IU, где I – сила тока, можно найти I. Значит I=P/U=21/12=1,75 Ампер.
Ладно, с лампочкой разобрались. Давайте ее зажжем. Для этого на нашем блоке питания выставляем рабочее напряжение для нашей лампы
Подаем напряжение с блока питания на лампу и вуаля!
Замеряем напряжение на клеммах-крокодилах блока питания с помощью мультиметра . Ровнехонько 12 Вольт, как и предполагалось.
К этим же клеммах цепляем и наш осциллограф
Смотрим осциллограмму:
Видите прямую линию? Это и есть осциллограмма постоянного напряжения. В течение времени у нас напряжение остается таким, каким и было и не меняется. Если посчитать, то можно вычислить, чему равняется напряжение. Так как одна клеточка у нас 5 Вольт (на фото внизу слева), то значит, наше напряжение 12 Вольт. Я также вывел это значение на дисплей осциллографа в самом нижнем левом углу: 12,03 Вольт. Все верно.
Замеряем силу тока. Как правильно замерить силу тока в цепи, можно узнать, прочитав статью как измерить ток и напряжение мультиметром?.
Получили 1,72 Ампер. А как вы помните, наше расчетное значение было 1,75 Ампер. Думаю, вину можно переложить на погрешность прибора или на лампочку
Максимальные напряжения при кручении
Из формулы для определения напряжений и эпюры распределения касательных напряжений при кручении видно, что максимальные напряжения возникают на поверхности.
Определим максимальное напряжение, учитывая, что ρта
х
= d/
2, где
d
— диаметр бруса круглого сечения.
Для круглого сечения полярный момент инерции рассчитывается по формуле (см. лекцию 25).
Максимальное напряжение возникает на поверхности, поэтому имеем
Обычно JP/pmax
обозначают
Wp
и называют
моментом сопротивления
при кручении, или
полярным моментом сопротивления
сечения
Таким образом, для расчета максимального напряжения на поверхности круглого бруса получаем формулу
Для круглого сечения
Для кольцевого сечения
Условие прочности при кручении
Разрушение бруса при кручении происходит с поверхности, при расчете на прочность используют условие прочности
где [τ
к] — допускаемое напряжение кручения.
Виды расчетов на прочность
Существует два вида расчета на прочность.
1. Проектировочный расчет — определяется диаметр бруса (вала) в опасном сечении:
Откуда
2. Проверочный расчет — проверяется выполнение условия прочности
3. Определение нагрузочной способности (максимального крутящего момента)
Расчет на жесткость
При расчете на жесткость определяется деформация и сравнивается с допускаемой. Рассмотрим деформацию круглого бруса над действием внешней пары сил с моментом т
(рис. 27.4).
При кручении деформация оценивается углом закручивания (см. лекцию 26):
Здесь φ
— угол закручивания;
γ
— угол сдвига;
l
— длина бруса;
R
— радиус;
R =d/2.
Откуда
Закон Гука имеет вид τ
к =
Gγ
. Подставим выражение для
γ
, получим
Откуда
Произведение GJP
называют жесткостью сечения.
Модуль упругости можно определить как G
= 0,4
Е.
Для стали
G
= 0,8 • 105 МПа.
Обычно рассчитывается угол закручивания, приходящийся на один метр длины бруса (вала) φ
o.
Условие жесткости при кручении можно записать в виде
где φ
o — относительный угол закручивания,
φ
о =
φ/l; [φо]
≈ 1град/м = 0,02рад/м — допускаемый относительный угол закручивания.
Примеры решения задач
Пример 1. Из расчетов на прочность и жесткость определить потребный диаметр вала для передачи мощности 63 кВт при скорости 30 рад/с. Материал вала — сталь, допускаемое напряжение при кручении 30 МПа; допускаемый относительный угол закручивания [φо]
= 0,02рад/м; модуль упругости при сдвиге
G
= 0,8 * 105 МПа.
Решение
1. Определение размеров поперечного сечения из расчета на прочность.
Условие прочности при кручении:
Определяем вращающий момент из формулы мощности при вращении:
Из условия прочности определяем момент сопротивления вала при кручении
Значения подставляем в ньютонах и мм.
Определяем диаметр вала:
2. Определение размеров поперечного сечения из расчета на жесткость.
Условие жесткости при кручении:
Из условия жесткости определяем момент инерции сечения при кручении:
Определяем диаметр вала:
3. Выбор потребного диаметра вала из расчетов на прочность и жесткость.
Для обеспечения прочности и жесткости одновременно из двух найденных значений выбираем большее.
Полученное значение следует округлить, используя ряд предпочтительных чисел. Практически округляем полученное значение так, чтобы число заканчивалось на 5 или 0. Принимаем значение dвала = 75 мм.
Для определения диаметра вала желательно пользоваться стандартным рядом диаметров, приведенном в Приложении 2.
Пример 2. В поперечном сечении бруса d
= 80 мм наибольшее касательное напряжение
τтах
= 40 Н/мм2. Определить касательное напряжение в точке, удаленной от центра сечения на 20 мм.
Решение
Эпюра касательных напряжений в поперечном сечении представлена на рис. 2.37, б
. Очевидно,
откуда
Пример 3. В точках внутреннего контура поперечного сечения трубы (d0 = 60 мм; d = 80 мм) возникают касательные напряжения, равные 40 Н/мм2. Определить максимальные касательные напряжения, возникающие в трубе.
Решение
Эпюра касательных напряжений в поперечном сечении представлена на рис. 2.37, в
. Очевидно,
Откуда
Пример 4. В кольцевом поперечном сечении бруса (d0
= 30 мм;
d =
70 мм) возникает крутящий момент
Мz
= 3 кН-м. Вычислить касательное напряжение в точке, удаленной от центра сечения на 27 мм.
Решение
Касательное напряжение в произвольной точке поперечного сечения вычисляется по формуле
В рассматриваемом примере Мz
= 3 кН-м = 3-106 Н• мм,
Подставляя числовые значения, получаем
Пример 5. Стальная труба (d0 = l00 мм; d = 120 мм) длиной l
= 1,8 м закручивается моментами
т
, приложенными в ее торцевых сечениях. Определить величину
т
, при которой угол закручивания
φ
= 0,25°. При найденном значении
т
вычислить максимальные касательные напряжения.
Решение
Угол закручивания (в град/м) для одного участка вычисляется по формуле
тогда
В данном случае
Подставляя числовые значения, получаем
Вычисляем максимальные касательные напряжения:
Пример 6. Для заданного бруса (рис. 2.38, а
) построить эпюры крутящих моментов, максимальных касательных напряжений, углов поворота поперечных сечений.
Решение
Заданный брус имеет участки I, II, III, IV, V
(рис. 2. 38,
а).
Напомним, что границами участков являются сечения, в которых приложены внешние (скручивающие) моменты и места изменения размеров поперечного сечения.
Пользуясь соотношением
строим эпюру крутящих моментов.
Построение эпюры Мz
начинаем со свободного конца бруса:
для участков III
и
IV
для участка V
Эпюра крутящих моментов представлена на рис, 2.38, б
. Строим эпюру максимальных касательных напряжений по длине бруса. Условно приписываем
τ
шах те же знаки, что и соответствующим крутящим моментам. На участке
I
на участке II
на участке III
на участке IV
на участке V
Эпюра максимальных касательных напряжений показана на рис. 2.38, в
.
Угол поворота поперечного сечения бруса при постоянных (в пределах каждого участка) диаметре сечения и крутящем моменте определяется по формуле
Строим эпюру углов поворота поперечных сечений. Угол поворота сечения А φ
л = 0, так как в этом сечении брус закреплен.
Эпюра углов поворота поперечных сечений изображена на рис. 2.38, г
.
Пример 7. На шкив В
ступенчатого вала (рис. 2.39,
а)
передается от двигателя мощность
N
B = 36 кВт, шкивы
А
и
С
соответственно передают на станки мощности
NA
= 15 кВт и
NC
= 21 кВт. Частота вращения вала
п
= 300 об/мин. Проверить прочность и жесткость вала, если [
τ
KJ = 30 Н/мм2, [Θ] = 0,3 град/м, G = 8,0-104 Н/мм2,
d1
= 45 мм,
d2
= 50 мм.
Вычислим внешние (скручивающие) моменты, приложенные к валу:
где
Строим эпюру крутящих моментов. При этом, двигаясь от левого конца вала, условно считаем момент, соответствующий N
А, положительным,
Nc
— отрицательным. Эпюра Mz показана на рис. 2.39,
б
. Максимальные напряжения в поперечных сечениях участка АВ
что меньше [тк] на
Относительный угол закручивания участка АВ
что значительно больше [Θ] ==0,3 град/м.
Максимальные напряжения в поперечных сечениях участка ВС
что меньше [тк] на
Относительный угол закручивания участка ВС
что значительно больше [Θ] = 0,3 град/м.
Следовательно, прочность вала обеспечена, а жесткость — нет.
Пример 8. От электродвигателя с помощью ремня на вал 1
передается мощность
N
= 20 кВт, С вала
1
поступает на вал
2
мощность
N1
= 15 кВт и к рабочим машинам — мощности
N2
= 2 кВт и
N3
= 3 кВт. С вала
2
к рабочим машинам поступают мощности
N4
= 7 кВт,
N5
= 4 кВт,
N6
= 4 кВт (рис. 2.40,
а).
Определить диаметры валов d1 и d2 из условия прочности и жесткости, если [
τ
KJ = 25 Н/мм2, [Θ] = 0,25 град/м, G = 8,0-104 Н/мм2. Сечения валов
1
и
2
считать по всей длине постоянными. Частота вращения вала электродвигателя
п =
970 об/мин, диаметры шкивов D1 = 200 мм, D2 = 400 мм, D3 = 200 мм, D4 = 600 мм. Скольжением в ременной передаче пренебречь.
Решение
Нарис. 2.40, б
изображен вал
I
. На него поступает мощность
N
и с него снимаются мощности
Nl
, N2,
N3.
Определим угловую скорость вращения вала 1
и внешние скручивающие моменты
m, m1, т2, т3:
Строим эпюру крутящих моментов для вала 1 (рис. 2.40, в
). При этом, двигаясь от левого конца вала, условно считаем моменты, соответствующие
N3
и
N1
, положительными, а
N
— отрицательным. Расчетный (максимальный) крутящий момент
Nx1
max = 354,5 H*м.
Диаметр вала 1 из условия прочности
Диаметр вала 1 из условия жесткости ([Θ], рад/мм)
Окончательно принимаем с округлением до стандартного значения d1 = 58 мм.
Частота вращения вала 2
На рис. 2.40, г
изображен вал
2;
на вал поступает мощность
N1
, а снимаются с него мощности
N4, N5, N6.
Вычислим внешние скручивающие моменты:
Эпюра крутящих моментов для вала 2
показана на рис. 2.40,
д.
Расчетный (максимальный) крутящий момент Мя max» = 470 H-м.
Диаметр вала 2
из условия прочности
Диаметр вала 2
из условия жесткости
Окончательно принимаем d2=
62 мм.
Пример 9. Определить из условий прочности и жесткости мощность N
(рис. 2.41,
а
), которую может передать стальной вал диаметром
d = 50
мм, если [тк] = 35 Н/мм2, [ΘJ = 0,9 град/м; G = 8,0* I04 Н/мм2,
n
= 600 об/мин.
Решение
Вычислим внешние моменты, приложенные к валу:
где
Расчетная схема вала показана на рис. 2.41, б
.
На рис. 2.41, в
представлена эпюра крутящих моментов. Расчетный (максимальный) крутящий момент
Mz
= 9,54
N
. Условие прочности
откуда
Условие жесткости
откуда
Лимитирующим является условие жесткости. Следовательно, допускаемое значение передаваемой мощности [N] = 82,3 кВт.
Лампочка и переменное напряжение
Теперь начинается самое интересное. Берем наш ЛАТР
Ставим прибор на измерение переменного напряжения и выставляем с помощью крутилки ЛАТРа напряжение в 12 Вольт. Обратите внимание, что крутилка на мультиметре находится в диапазоне измерения переменного напряжения. Забегая вперед, скажу, что мультиметр измеряет среднеквадратичное напряжение.
Цепляем осциллограф к клеммах ЛАТРа, не забывая на осциллографе выставить замеры переменного напряжения и смотрим получившуюся осциллограмму:
Смотрим, сколько силы тока кушает наша лампочка. Все как положено, 1,71 Ампер.
Переменное напряжение — это напряжение, которое изменяется с течением времени. Далее будем рассматривать только гармоническое переменное напряжение (изменяется по синусоиде).
Где u = u(t) — мгновенное значение переменного напряжения [В].
U
m — максимальное значение напряжения
(амплитудное значение) [В].
f — частота равная числу колебаний в 1 секунду (единица частоты f — герц (Гц) или с -1 )
ω — угловая частота (омега) (единица угловой частоты — рад/с или с -1 )
ω = 2πf = 2π/T
Аргумент синуса, т. е. (ωt + Ψ), называют фазой. Фаза характеризует состояние колебания (числовое значение) в данный момент времени t.
U — Действующее значение напряжения [В]:
Рассмотрим параметры напряжения в бытовой электросети.
Все мы знаем, что у нас дома в розетке поступает переменный ток, с напряжением 220 вольт и частотой 50 герц (в идеальных условиях) на самом деле допускается не большая погрешность как в меньшую, так и в большую сторону так, что не удивляйтесь если ваш вольтметр покажет не 220, а например 210 или даже 230 В.).
Большинство приборов измеряет не амплитудное, а действующее значение переменного напряжения, тока, мощности так, что если мы говорим что у нас напряжение сети 220, 380 В и т. д. то имеется виду именно действующие значения.
- Действующее значение напряжения U = 220 В.
- Амплитудное значение напряжения цепи переменного токаUm = U*√2 = 220 *√2 = 311 В.
- Угловая частота ω = 2πf = 3,14*2*50 = 314рад/с.
- Начальная фаза Ψ = 0град.
- Мгновенное значениеu= 311sin(314t)В.
Как вы помните из предыдущей статьи, переменное напряжение – это напряжение, которое меняется со временем. Оно может меняться с каким-то периодом, а может быть хаотичным. Но не стоит также забывать, что и переменное напряжение обладает своими особенными параметрами.
Среднее значение напряжения
Среднее значение переменного напряжения Uср – это, грубо говоря, площадь под осциллограммой относительно нуля за какой-то промежуток времени. Чтобы это понять, давайте рассмотрим вот такую осциллограмму.
Например,чему равняется среднее значение напряжения за эти два полупериода? В данном случае ноль вольт. Почему так? Площади S1 и S2 равны. Но все дело в том, что площадь S2 берется со знаком “минус”. А так как площади равны, то в сумме они дают ноль: S1+(-S2)=S1-S2=0. Для бесконечного по времени синусоидального сигнала среднее значение напряжения также равняется нулю.
То же самое касается и других сигналов, например, двухполярного меандра. Меандр – это прямоугольный сигнал, у которого длительности паузы и импульса равны. В этом случае его среднее напряжение также будет равняться нулю.