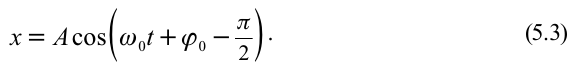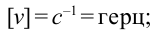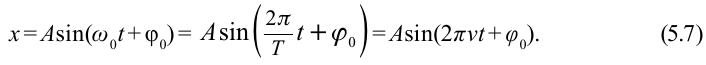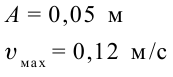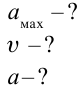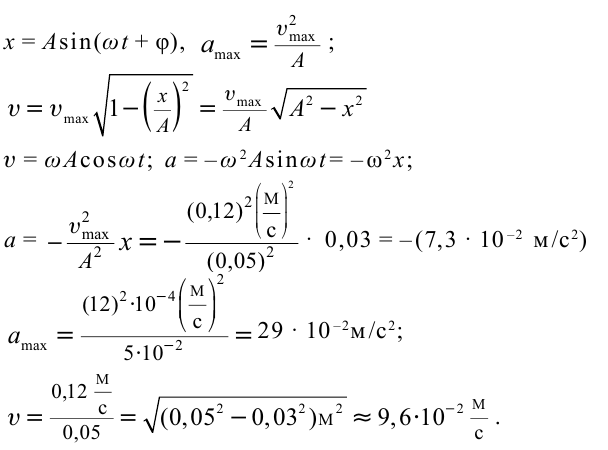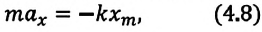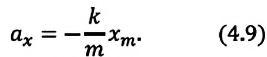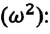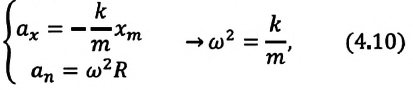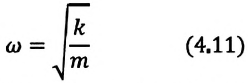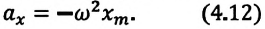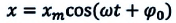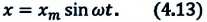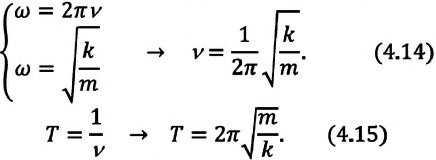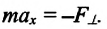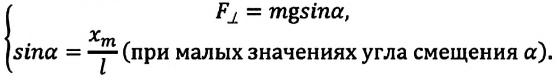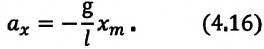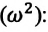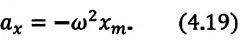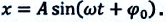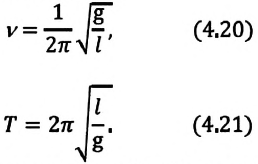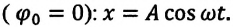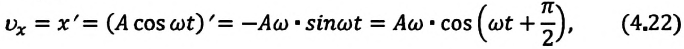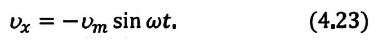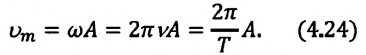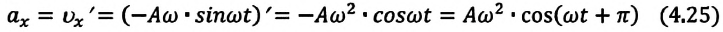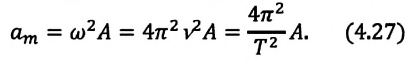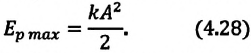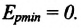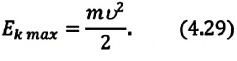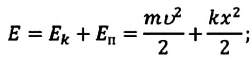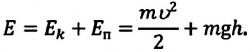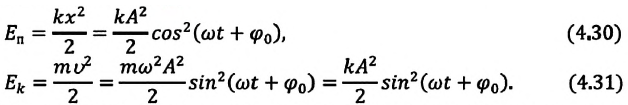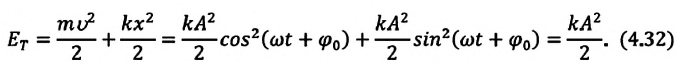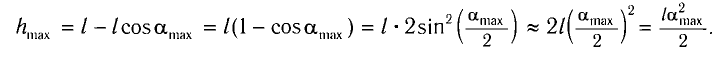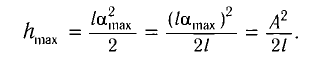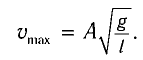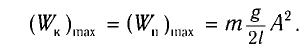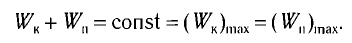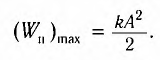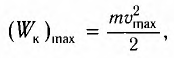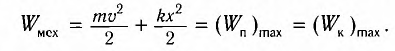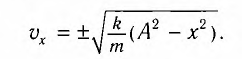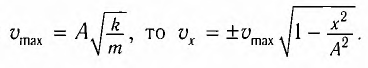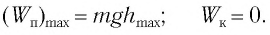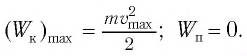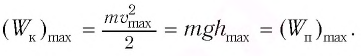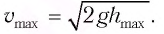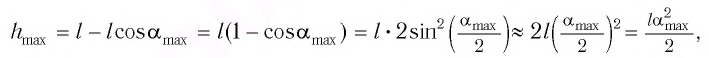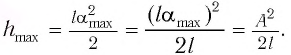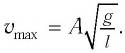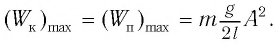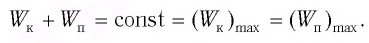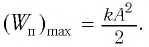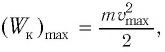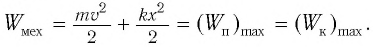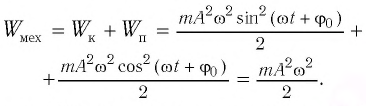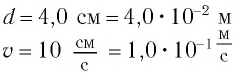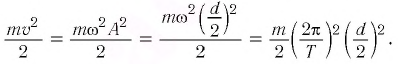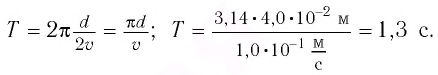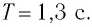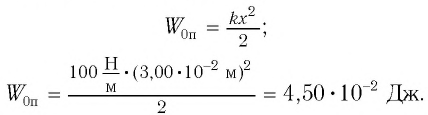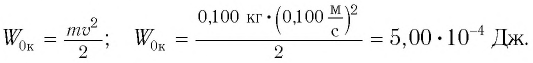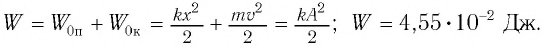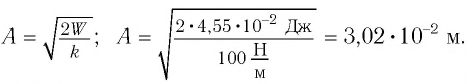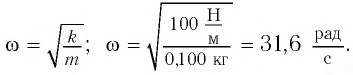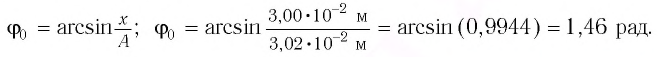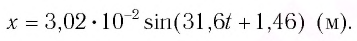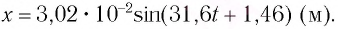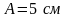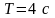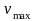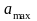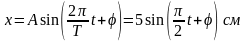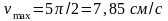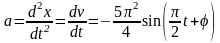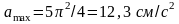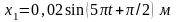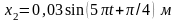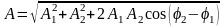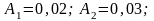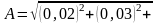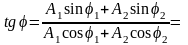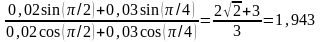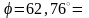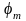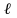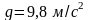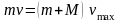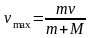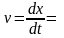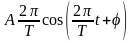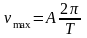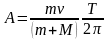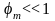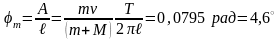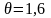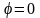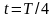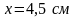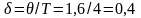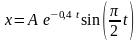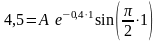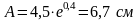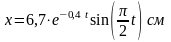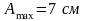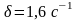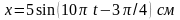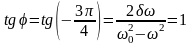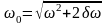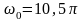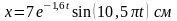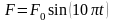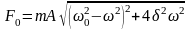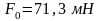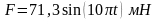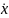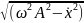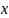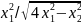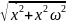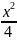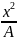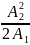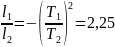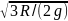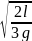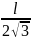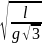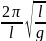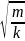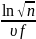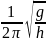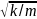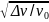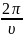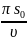Определить максимальное ускорение аmax материальной точки, совершающей гармонические колебания с амплитудой А =15 см, если наибольшая скорость точки v=30 см/с. Написать также уравнение колебаний.
Уравнение гармонических колебаний в общем виде выглядит так:
$x(t)=Asin(wt+phi_0)$ (1)
где x(t) — координата точки в момент времени t, А — амплитуда колебаний, w — круговая частота колебаний, фо — начальная фаза колебаний.
Первая производная по времени от (1) дает скорость, а вторая — ускорение:
$v=frac{d(x(t))}{dt}=Awcos(wt+phi_0)$ (2)
Из (2) очевидно, что наибольшего значения скорость достигнет при значении косинуса равном единице. Тогда можем записать:
$v_{max}=Aw$ (3)
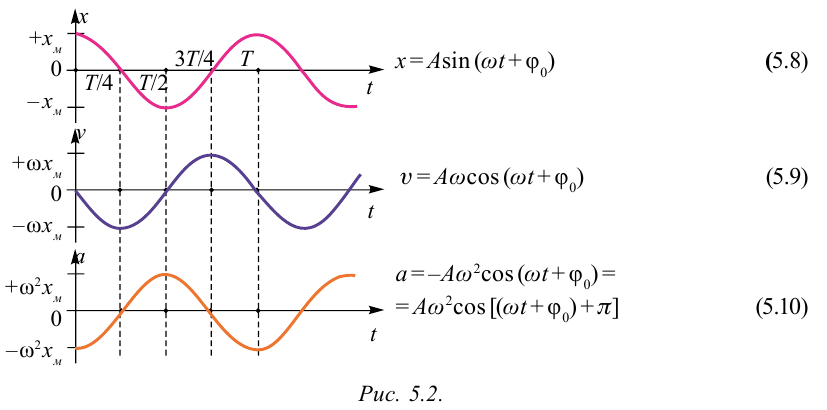
Из (3) можем найти $w=frac{v_{max}}{A}=frac{0,3}{0,15}=2$ рад/с
Производная от (2) даст нам значение ускорения:
$a=frac{d(Awcos(wt+phi_0))}{dt}=-Aw^2sin(wt+phi_0)$ (4)
Очевидно из (4), что максимальное значение ускорения будет при значении синуса равном -1.
$a_{max}=Aw^2$ (5)
$a_{max}=0,15*2^2=0,6$ м/с^2
Уравнение гармонических колебаний нашей точки будет выглядеть с учетом (1) и заданных и найденных значений:
$x(t)=0,15sin(2t+phi_0)$
Поскольку в условии ничего не сказано о начальной фазе, в случае если она равна нулю, уравнение будет иметь такой вид:
$x(t)=0,15sin(2t)$
Содержание:
Гармонические колебания:
Некоторые движения, встречающиеся в быту, за равные промежутки времени повторяются. Такое движение называется периодическим движением. Часто встречается движение, при котором тело перемещается то в одну, то в другую сторону относительно равновесного состояния. Такое движение тела называется колебательным движением или просто колебанием.
Колебания, совершаемые телом, которое выведено из равновесного состояния в результате действия внутренних сил, называются собственными (свободными) колебаниями. Величина удаления от равновесного состояния колеблющегося тела называется его смещением (
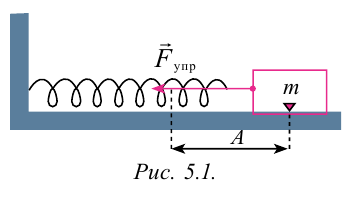
Для наблюдения механических колебаний ознакомимся с колебаниями груза, закрепленного на конце пружины (рис. 5.1). На этом рисунке груз, закрепленный на пружине, сможет двигаться без трения с горизонтальным стержнем, так как силу тяжести шарика приводит в равновесие реакционная сила стержня.
Коэффициент упругости пружины – 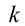
Если груз, который находится в равновесии, потянем вправо на расстояние 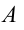
сторону равновесного состояния.
С течением времени смещение груза уменьшается относительно 
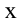
Для определения закономерности изменения в течение времени системы, которая периодически совершает колебания, заполним воронку песком, подвесим на веревке, подложим бумагу под систему и раскачаем воронку. В ходе колебания начинаем равномерно вытягивать бумагу из-под системы. В результате мы увидим, что следы песка на бумаге образуют синусоиду. Из этого можно сделать следующий вывод: смещение периодически колеблющегося тела по истечении времени изменяется по закону синусов и косинусов. При этом самое большое значение смещения равняется амплитуде (
здесь: 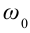
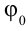
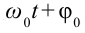
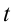
Из математики известно, что 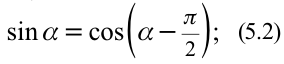
Колебания, в которых с течением времени параметры меняются по закону синуса или косинуса, называются гармоническими колебаниями.
Значит, пружинный маятник, вышедший из равновесного состояния, совершает гармоническое колебание. Для того чтобы система совершала гармоническое колебание: 1) при выходе тела из равновесного состояния, для возвращения его в равновесное состояние должна появиться внутренняя сила; 2) колеблющееся тело должно обладать инертностью и на него не должны оказывать воздействие силы трения и сопротивления. Эти условия называется условиями проявления колебательных движений.
Основные параметры гармонических колебаний
a) период колебания 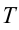

б) частота колебания 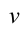
Единица
c) циклическая частота 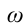
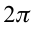
С учетом формул (5.5) и (5.6) уравнение гармонических колебаний (5.2) можно записать в следующей форме.
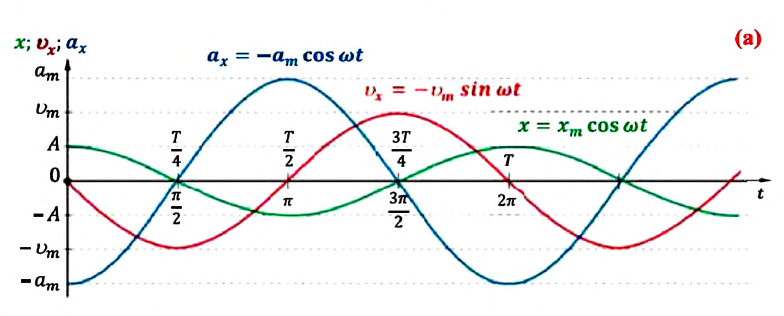
Большинство величин, количественно описывающих гармонические колебания, смещения которых с течением времени меняются по закону синусов или косинусов (скорость, ускорение, кинетическая и потенциальная энергия), тоже гармонически меняются.
Это подтверждается следующими графиками и уравнениями:
Пример решения задачи:
Точка совершает гармоническое колебательное движение. Максимальное смещение и скорость соответственно равны 0,05 м и 0,12 м/с. Найдите максимальное ускорение и скорость колебательного движения, а также ускорение точки в момент, когда смещение равно 0,03 м.
Дано:
Найти:
Формула и решение:
Гармонические колебания пружинного маятника
В 1985 году в городе Мехико произошла ужасная катастрофа, причина которой было землетрясение: 5526 человек погибли, 40 ООО человек ранены, 31000 человек остались без крова. Из проведенных затем исследований ученые выяснили, что главной причиной разрушений во время землетрясения является совпадение частоты свободных колебаний зданий с частотой вынужденных колебаний Земли. Поэтому при возведении новых зданий в сейсмически активной зоне необходимо, чтобы эти частоты не совпадали. Это даст возможность уменьшить последствия землетрясения. С этой целью важно знать, от чего зависят частота и период колебаний.
Одной из простейших колебательных систем, совершающих гармонические колебания, является пружинный маятник.
Пружинный маятник — это колебательная система, состоящая из пружины и закрепленного на ней тела. Колебания, возникающие в пружинном маятнике, являются гармоническими колебаниями:
Под гармоническими колебаниями подразумеваются колебания, возникающие под действием силы, прямо пропорциональной перемещению и направленной против направления перемещения.
Исследование колебаний пружинного маятника имеет большое практическое значение, например, при вычислении колебаний рессор автомобиля при езде; в исследовании воздействия колебаний на фундамент зданий и тяжелых станков, в определении эластичности ушных перепонок при диагностике лор-заболеваний. По этой причине изучение колебаний пружинного маятника является актуальной проблемой.
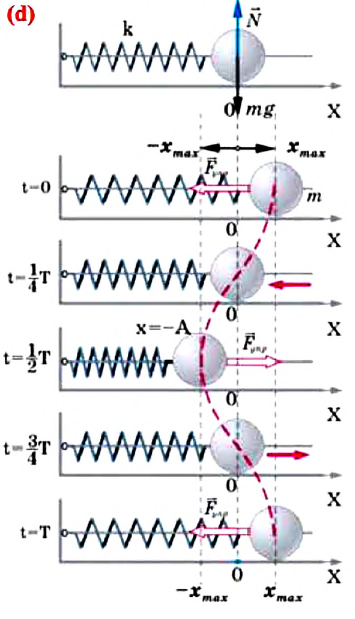
С целью уменьшения количества сил, действующих на колебательную систему, целесообразно использовать горизонтально расположенную колебательную систему пружина-шарик (d).
В этой системе действия силы тяжести и реакции опоры уравновешивают друг друга. При выведении шарика из состоянии равновесия, например, при растяжении пружины до положения 
или
Формула (4.9) является уравнением свободных гармонических колебаний пружинного маятника.
Где 
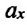
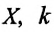
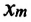
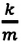
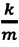
или
Таким образом, уравнение движения пружинного маятника можно записать и так:
Уравнение (4.12) показывает, что колебания пружинного маятника с циклической частотой 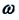
Так как тригонометрическая функция является гармонической функцией, то и колебания пружинного маятника являются гармоническими колебаниями.
Здесь 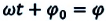
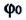
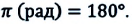
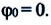

Из сравнения выражений (4.11) и (4.5) определяются величины, от которых зависят период и частота колебаний пружинного маятника:
Из выражений (4.14) и (4.15) видно, что период и частота пружинного маятника зависят от жесткости пружины и массы груза, подвешенного к нему.
Гармонические колебания математического маятника
До наших дней дошла такая историческая информация: однажды в 1583 году итальянский ученый Г. Галилей, находясь в храме города Пиза, обратил внимание на колебательное движение люстры, подвешенной на длинном тросе. Он, сравнивая колебания люстры со своим пульсом, определил, что, несмотря на уменьшение амплитуды колебания, время, затрачиваемое на одно полное колебание (период колебания) люстры, не изменяется. Затем Галилей в результате многочисленных проведенных исследований, изменяя длину нитевого маятника, массу подвешенного к нему груза, высоту расположения маятника (по сравнению с уровнем моря), определил, от чего зависят период и частота колебаний маятника.
Гармонические колебания возникают также под действием силы тяжести. Это можно наблюдать с помощью математического маятника.
Математический маятник — это идеализированная колебательная система, состоящая из материальной точки, подвешенной на невесомой и нерастяжимой нити.
Для исследования колебаний математического маятника можно использовать систему, состоящую из тонкой длинной нити и шарика (b).
Сила тяжести 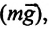
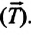
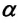
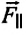
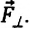
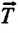
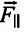
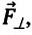
Приняв во внимание, что:
Для уравнения движения математического маятника получим:
Где 
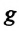
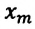
Для данной колебательной системы отношение 

или
Таким образом, уравнение движения математического маятника можно записать и так:
Уравнение (4.19) показывает, что колебания математического маятника являются гармоническими колебаниями с циклической частотой со. Из математики вы знаете, что решением этого уравнения является нижеприведенная функция:
Так как эта функция является гармонической, то и колебания математического маятника являются гармоническими колебаниями.
Отсюда определяются величины, от которых зависят период и частота колебаний математического маятника:
Таким образом, период и частота колебаний математического маятника зависят от длины маятника и напряженности гравитационного поля в данной точке.
Скорость и ускорение при гармонических колебаниях
Вы уже знакомы с основными тригонометрическими функциями и умеете строить графики тригонометрических уравнений, описывающих гармонические колебания.
При гармонических колебаниях маятника его смещение изменяется по гармоническому закону, поэтому не трудно доказать, что его скорость и ускорение также изменяются по гармоническому закону. Предположим, что смещение изменяется по закону косинуса и начальная фаза равна нулю
Так как скорость является первой производной смещения (координат) по времени, то:
или
Как видно из выражения (4.23), скорость, изменяющаяся по гармоническому закону, опережает колебания смещения по фазе на 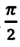
Максимальное (амплитудное) значение скорости зависит от амплитуды, частоты и периода колебаний:
Так как ускорение является первой производной скорости по времени, то получим:
или
Как видим, колебания ускорения, изменяющегося по гармоническому закону, опережают колебания скорости по фазе на 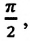
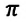
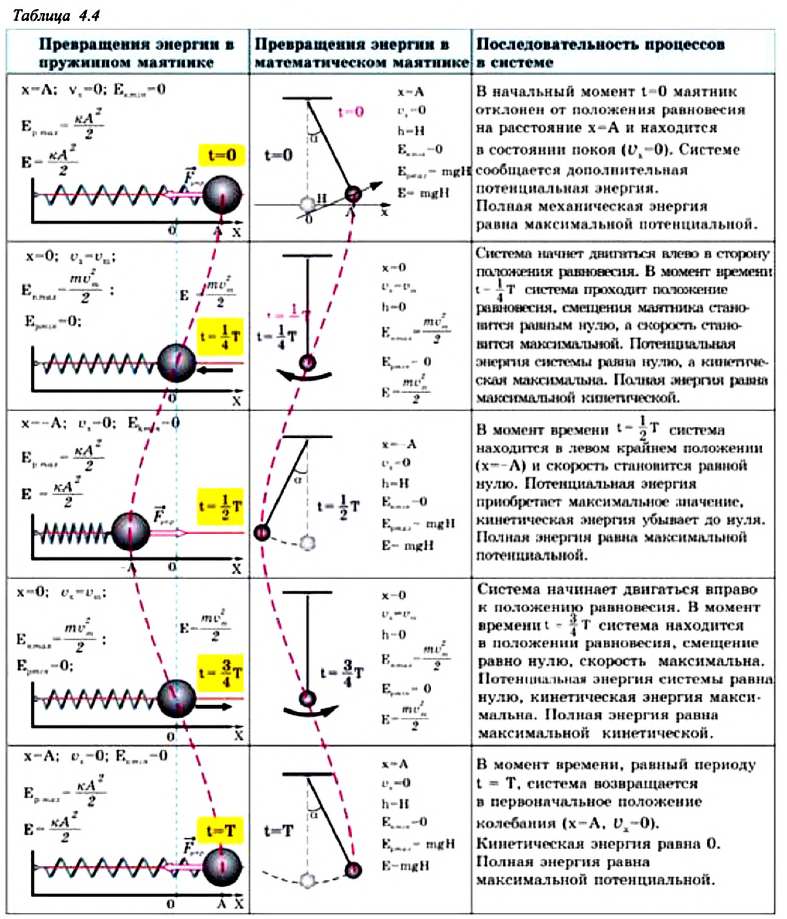
Превращения энергии при гармонических колебаниях
Теоретический материал
Потенциальная и кинетическая энергия свободных гармонических колебаний в замкнутой системе периодически превращаются друг в друга.
В таблице 4.4 дано сравнение превращений энергий в пружинном и математическом маятниках. Как видно из таблицы, потенциальная энергия колебательной системы в точке возвращения 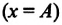
Если же маятник находится в точке равновесия, потенциальная энергия минимальна:
Кинетическая энергия системы, наоборот, в точке возвращения минимальна 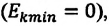
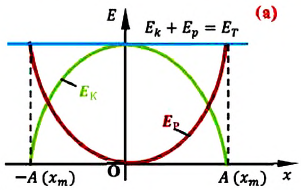
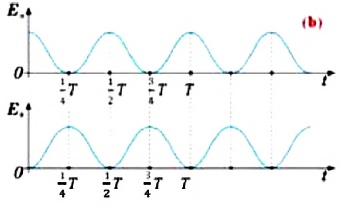
На рисунке (а) даны графики зависимости потенциальной и кинетической энергии при гармоническом колебательном движении от смещения.
Полная механическая энергия замкнутой колебательной системы в произвольный момент времени 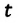
a) для пружинного маятника:
b) для математического маятника:
Если принять во внимание изменение смещения и скорости по гармоническому закону в формулах потенциальной и кинетической энергии колебательного движения, то станет очевидно, что при гармонических колебаниях эти энергии так же изменяются по гармоническому закону (b):
Как было отмечено выше, полная энергия системы не изменяется по гармоническому закону:
• Полная энергия гармонических колебаний прямо пропорциональна квадрату амплитуды колебаний.
Если же в системе существует сила трения, то его полная энергия не сохраняется — изменение полной механической энергии равно работе силы трения. В результате колебания затухают:
Превращения энергии при гармонических колебаниях
Механическая энергия системы равна сумме ее кинетической и потенциальной энергий. Кинетической энергией тело обладает вследствие своего движения, а потенциальная энергия определяется взаимодействием тела с другими телами или полями. Механическая энергия замкнутой системы, в которой не действуют силы трения (сопротивления), сохраняется.
Поскольку при колебаниях гармонического осциллятора силу трения не учитывают, то его механическая энергия сохраняется.
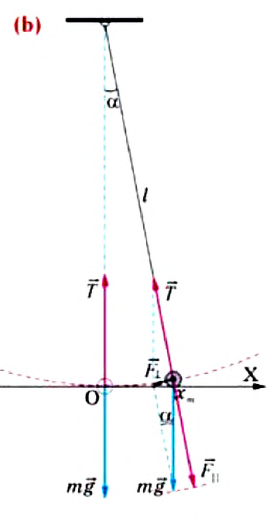
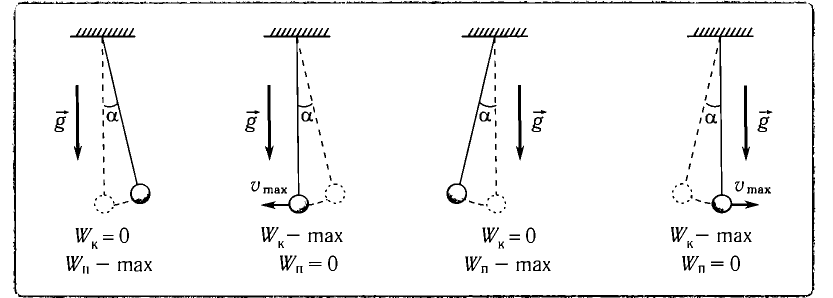
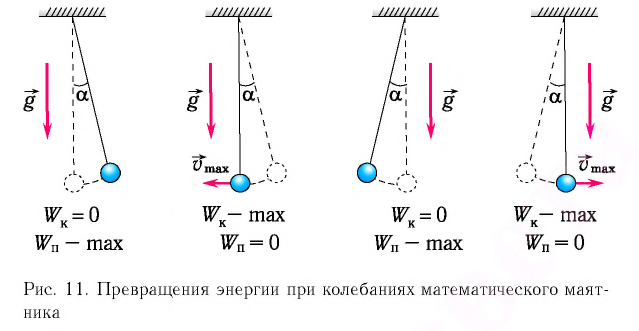
Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю.
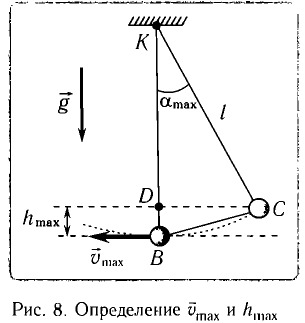
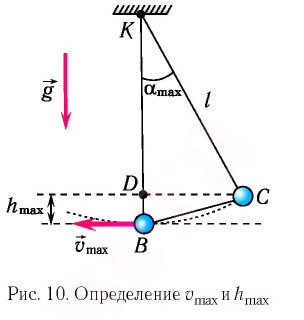
При отклонении маятника на угол а (рис. 7), соответствующий максимальному смещению от положения равновесия, потенциальная энергия максимальна, а кинетическая энергия равна нулю:
Рис. 7. Превращения энергии при колебаниях математического маятника
Поскольку при прохождении положения равновесия его потенциальная энергия равна нулю, то кинетическая энергия (а следовательно, и скорость) будет максимальна:
Из закона сохранения механической энергии следует (рис. 8), что
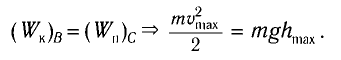
Отсюда найдем модуль максимальной скорости маятника:
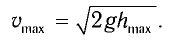
Высоту 
Если колебания малые, то 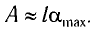
Отсюда
Подставив выражение для 
Подставляя выражения для 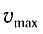

Таким образом, в положении равновесия потенциальная энергия полностью переходит в кинетическую, а в положениях максимального отклонения кинетическая энергия полностью переходит в потенциальную.
В любом промежуточном положении
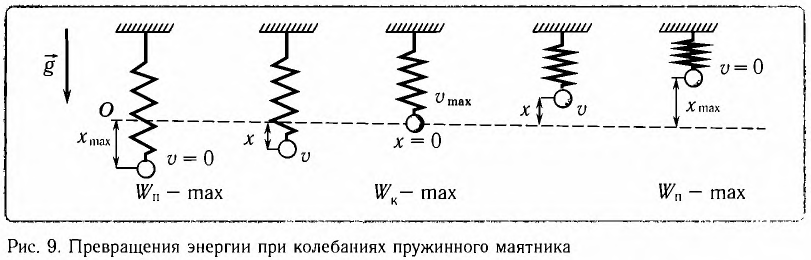
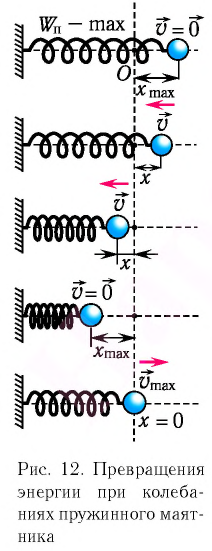
Покажем, что аналогичные превращения энергии имеют место и для пружинного маятника (рис. 9). В крайних точках, когда координата груза принимает значение 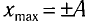
Таким образом, получаем, что механическая энергия гармонического осциллятора пропорциональна квадрату амплитуды колебаний.
В положении равновесия, когда x = 0, вся энергия осциллятора переходит в кинетическую энергию груза:
где 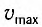
В промежуточных точках полная механическая энергия
Отсюда можно вывести выражение для модуля скорости 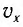
координатой х:
Так как
Энергия при гармонических колебаниях
Механическая энергия системы равна сумме ее кинетической и потенциальной энергии. Механическая энергия замкнутой системы, в которой не действуют силы трения (сопротивления), сохраняется.
Поскольку при колебаниях гармонического осциллятора силой трения пренебрегают, то его механическая энергия сохраняется. Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю.
При отклонении маятника на угол 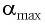
Поскольку при прохождении положения равновесия потенциальная энергия равна нулю 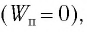
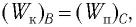
Запишем закон сохранения механической энергии, подставив в него выражения для потенциальной и кинетической энергии:
Отсюда найдем модуль максимальной скорости маятника:
Высоту 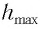
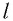
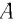
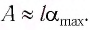
или
Подставив выражение (3) для 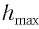
Подставляя выражения (3) для 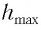
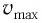
Таким образом, в положении равновесия потенциальная энергия полностью переходит в кинетическую, а в положениях максимального отклонения кинетическая энергия полностью переходит в потенциальную (рис. 11). В любом промежуточном положении
Покажем, что аналогичные превращения энергии имеют место и для пружинного маятника (рис. 12).
В крайних положениях, когда 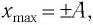
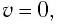
Таким образом, из соотношения (6) следует, что механическая энергия пружинного маятника пропорциональна квадрату амплитуды колебаний.
В положении равновесия, когда 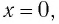
где 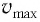
В положениях между крайними точками полная энергия
С учетом выражений для координаты 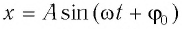
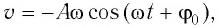
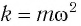
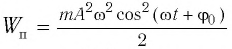
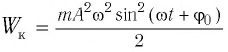
Тогда полная механическая энергия пружинного маятника в этот же. момент времени есть величина постоянная и равная:
Таким образом, начальное смещение 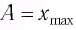
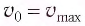
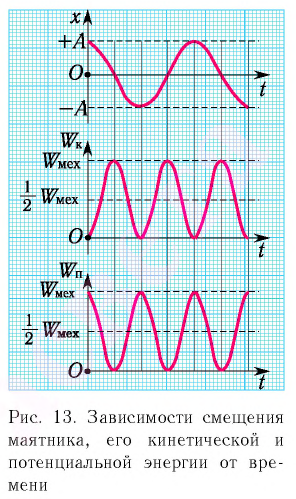
Заметим, что частота периодических изменений кинетической (потенциальной) энергии колеблющегося тела в два раза больше частоты колебаний маятника. Действительно, дважды за период механическая энергия тела будет полностью превращаться в потенциальную (в двух крайних положениях маятника) и дважды за период — в кинетическую (при его прохождении через положение равновесия) (рис. 13).
Пример №1
Математический маятник при колебаниях от одного крайнего положения до другого смещается на расстояние 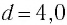
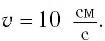
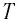
Дано:
Решение
По закону сохранения механической энергии
Отсюда:
Ответ:
Пример №2
Груз массой 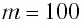
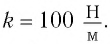
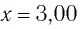
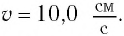
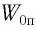
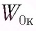
Дано:
Решение Потенциальная энергия груза:
Кинетическая энергия груза:
Начальное смещение груза не является амплитудой, так как вместе с начальным отклонением грузу сообщили и скорость. Однако полная энергия может быть выражена через амплитуду колебаний:
Отсюда
Циклическая частота:
В начальный момент времени 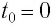
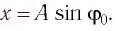
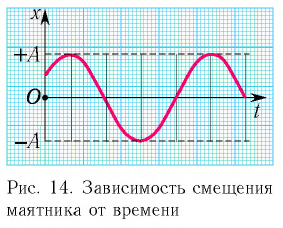
Тогда закон гармонических колебаний имеет вид (рис. 14):
Ответ:
- Вынужденные колебания в физике
- Электромагнитные колебания
- Свободные и вынужденные колебания в физике
- Вынужденные электромагнитные колебания
- Закон Архимеда
- Движение жидкостей
- Уравнение Бернулли
- Механические колебания и волны в физике
Как найти ускорение — определение и формулы расчета в физике
Содержание:
-
Что такое ускорение
- Единица измерения
-
Как рассчитать ускорение: формулы
- Для прямолинейного движения
- Для равноускоренного движения
- Для равнозамедленного движения
- Нахождение ускорения через массу и силу
- Мгновенное ускорение
- Максимальное ускорение
- Среднее ускорение
- Проекция ускорения
Что такое ускорение
Ускорение (overrightarrow а) — векторная величина в физике, характеризующая быстроту изменения скорости тела.
Ускорение является векторной величиной, показывающей, на сколько изменяется вектор скорости тела при его движении за единицу времени.
Единица измерения
В СИ (системе интернациональной) ускорение измеряется: ( begin{bmatrix}aend{bmatrix}=frac м{с^2})
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как рассчитать ускорение: формулы
Для прямолинейного движения
Прямолинейное движение — механическое движение, при котором траектория тела — прямая линия.
В этом случае ускорение находится по следующим формулам:
(a;=;frac{mathrm V}t)
(a;=;frac{2S}{t^2})
(a;=;frac{V^2}{2S})
Где (a) — достигнутое ускорение тела, (S) — пройденный путь (расстояние), (t) — затраченное время.
Время отсчитывается от начала движения тела.
При прямолинейном равномерном движении ускорение по модулю равняется нулю.
Для равноускоренного движения
Равноускоренное движение — прямолинейное движение с постоянным положительным ускорением (разгон).
При таком виде движения ускорение определяется по формуле: (a;=;frac{V-V_0}t), где (V_0) и (V) начальная и конечная скорости соответственно, (a) — достигнутое ускорение тела, (t) — затраченное время.
Для равнозамедленного движения
Равнозамедленное движение — прямолинейное движение с постоянным отрицательным ускорением (замедление).
При таком виде движения ускорение находим по формуле: (a;=-;frac{V-V_0}t), где V0 и V начальная и конечная скорости соответственно, a — достигнутое ускорение тела, t — затраченное время.
Нахождение ускорения через массу и силу
Принцип инерции Галилея:
Если не действовать на тело, то его скорость не будет меняться.
Система отсчета (СО) — система координат, точка отсчета и указание начала отсчета времени.
Инерциальная система отсчета (ИСО) — это СО, в которой наблюдается движение по инерции (соблюдается принцип инерции).
II закон Ньютона:
В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.
или
(overrightarrow a=frac{overrightarrow F}m)
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени — это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Другими словами — это ускорение, которое развивает тело за максимально короткий отрезок времени.
Выражается по формуле:
( overrightarrow a=lim_{trightarrow0}frac{triangleoverrightarrow V}{triangle t})
Максимальное ускорение
(a_{max}=omega v_{max},) где (a_{max}) — максимальное ускорение, (omega) — круговая (угловая, циклическая) частота, (v_{max}) — максимальная скорость.
Среднее ускорение
Среднее ускорение — это отношение изменения скорости к промежутку времени, за который это изменение произошло.
(overrightarrow{a_{ср}}=frac{triangleoverrightarrow V}{triangle t}), где (overrightarrow{a_{ср}}) — среднее ускорение, (triangleoverrightarrow V) — изменение скорости, ( triangle t) — изменение времени.
Проекция ускорения
Определение проекции ускорения на ось (х):
(a_x=frac{V_x-V_{0x}}t), где где (a_x) — проекция ускорения на ось (х), (V_x) — проекция текущей скорости на ось (х), (V_{0x}) — проекция начальной скорости на ось (х), (t) или (triangle t) — промежуток времени, за который произошло изменение проекции скорости.
Насколько полезной была для вас статья?
Рейтинг: 1.92 (Голосов: 36)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Примеры решения задач
Пример
1. Амплитуда
гармонического колебания
,
период
.
Найти максимальную скорость
колеблющейся точки и ее максимальное
ускорение
.
Решение.
Уравнение гармонического колебательного
движения точки имеет вид:
.
Начальная фаза
неизвестна
и далее будет показано, что она не
требуется для решения задачи. Скорость
v
колеблющейся точки по определению равна
.
Таким образом, скорость точки изменяется
по гармоническому закону с амплитудой
(максимальным значением)
.
Ускорение a
колеблющейся точки по определению равно
.
Следовательно, ускорение точки также
изменяется по гармоническому закону с
амплитудой (максимальным значением)
.
Пример
2. Найти
амплитуду A
и начальную фазу
гармонического колебания, полученного
от сложения одинаково направленных
колебаний, данных уравнениями
и
.
Решение.
Амплитуда суммы одинаково направленных
гармонических колебаний одинаковой
частоты (периода) рассчитывается по
формуле
.
По условию задачи:
.
Следовательно,
.
Начальная фаза суммарного колебания
определяется из уравнения
.
Следовательно,
.
Пример
3. Бревно
массы
висит на двух шнурах длины
каждый. В торец бревна попадает и
застревает в нем пуля массы
,
летящая со скоростью
.
Найти амплитуду
и период T
колебаний бревна. Трением пренебречь.
Решение.
Бревно на шнурах длиной
можно считать математическим маятником,
период колебаний T
которого
рассчитывается по формуле:
,
где
– ускорение свободного падения. Попадание
и застревание пули в бревне является
абсолютно неупругим ударом, для которого
закон сохранения импульса записывается
как:
.
Следовательно, максимальная скорость
бревна с пулей
.
Бревно с пулей будет совершать
гармонические колебания
.
Скорость бревна, в свою очередь,
.
Максимальная скорость бревна (амплитуда
скорости)
.
Следовательно,
.
Угловая амплитуда
малых колебаний бревна связана с
амплитудой A
линейных колебаний соотношением:
.
Приближенное равенство выполняется
для малых углов:
.
Окончательно для угловой амплитуды
колебаний бревна получаем
.
Пример
4. Период
затухающих колебаний
;
логарифмический декремент затухания
;
начальная фаза
.
При
смещение точки
.
Написать уравнение движения этого
колебания.
Решение.
Уравнение затухающего колебательного
движения имеет вид
.
Коэффициент затухания
.
Следовательно,
.
Амплитуду A
затухающих колебаний находим из условия
.
Следовательно,
.
Получаем, что
.
Окончательно уравнение затухающих
колебаний:
.
Пример
5. Тело массой
совершает затухающие колебания с
максимальной амплитудой
,
начальной фазой
и коэффициентом затухания
.
На это тело начала действовать внешняя
периодическая сила F,
под действием которой установились
вынужденные колебания. Уравнение
вынужденных колебаний имеет вид
.
Найти (с числовыми коэффициентами)
уравнение собственных колебаний и
уравнение внешней периодической силы.
Решение.
Уравнение собственных затухающих
колебаний имеет вид
.
Сдвиг фаз между собственными и вынужденными
колебаниями равен
.
Следовательно,
и
,
где частота вынужденных колебаний
и коэффициент затухания
.
Следовательно,
.
Тогда уравнение собственных колебаний:
.
Уравнение внешней периодической силы:
,
где
(
– амплитуда вынужденных колебаний).
Получаем
.
Следовательно, уравнение внешней
периодической силы:
.
Задачи
1.1.
Точка совершает колебания с амплитудой
А=4см
и периодом Т=2с.
Написать уравнение этих колебаний,
считая, что в момент t=0 смещения x(0)=0
и
(0)<0.
Определить фазу (ωt+φ) для двух моментов
времени: 1) когда смещение x=1 см и
>0;
2) когда скорость
=-6
см/с и х<0. (x= А cos
(ωt+φ), где А= 4 см, ω=2π/Т=π рад/с, φ=π/2 рад;
1)5π/3 рад; 2)0,842π рад).
1.2.
Определить максимальные значения
скорости
max
и
ускорения
max
точки, совершающей гармонические
колебания с амплитудой А=3
см и угловой частотой ω=π/2 с-1.
(4,71 см/с; 7,40 см/с2).
1.3.
Точка совершает колебания по закону
x=Аcosωt, где А
=5 см; ω = 2с-1.
Определить ускорение |
|
точки в момент времени, когда ее скорость
=
8 см/с. (|
|=
ω
=12
см/с2).
1.4.
Точка совершает гармонические колебания.
Наибольшее смещение xmax
точки равно 10 см, наибольшая скорость
max
= 20 см/с. Найти угловую частоту ω колебаний
и максимальное ускорение
max
точки. (2 с-1;
40 см/с2).
1.5.
Максимальная скорость
max
точки, совершающей гармонические
колебания, равна 10см/с, максимальное
ускорение
max=100
см/с2.
Найти угловую частоту ω колебаний, их
период Т
и амплитуду А.
Написать уравнение колебаний, приняв
начальную фазу равной нулю. (10 с-1;
0,628 с; 1 см;
=
А cos
ωt).
1.6.
Точка совершает колебания по закону
х=Аsinωt .В некоторый момент времени
смещение x1
точки оказалось равным 5 см. Когда фаза
колебаний увеличилась вдвое, смещение
x2
стало равным 8 см. Найти амплитуду А
колебаний. (А=2
=8,33 см).
1.7.
Колебания точки происходят по закону
х=Acos(ωt/+φ).В некоторый момент времени
смещение x точки равно 5 см, ее скорость
=20
см/с и ускорение
=-80
см/с2.
Найти амплитуду А,
угловую частоту ω, период Т
колебаний и фазу (ωt/+φ) в рассматриваемый
момент времени. (ω=
=4
с-1;
Т=2π/ω=1,57 с; А=
=7,07
см; ωt+φ=arcos(x/А)=
π/4 рад).
Сложение
колебаний
1.8.
Два
одинаково направленных гармонических
колебания одного периода с амплитудами
А1=10
см и А2=6
см складываются в одно колебание с
амплитудой А=14
см. Найти разность фаз ∆φ складываемых
колебаний. (π/3 рад).
1.9.
Два гармонических колебания, направленных
по одной прямой и имеющих одинаковые
амплитуды и периоды, складываются в
одно колебание той же амплитуды. Найти
разность фаз ∆φ складываемых колебаний.
(2π/3 рад или 4π/3 рад).
1.10.
Определить амплитуду А
и
начальную фазу φ результирующего
колебания, возникающего при сложении
двух колебаний одинаковых направления
и периода: x1=А1
sin
ωt
и x2=А2
sin
ω(t+τ),
где А1=А2=1
см; ω=π с-1;
τ=0,5 с. Найти уравнение результирующего
колебания. (А=1,41 см; φ=π/4 рад; x = А cos
(ωt+φ), где ω = π с-1).
1.11.
Точка участвует в двух одинаково
направленных колебаниях: x1=А1sinωt
и x2=А2cos
ωt, где А1=1
см; А2=2
см; ω=1 с-1.
Определить амплитуду А
результирующего колебания, его частоту
ν и начальную фазу φ. Найти уравнение
этого движения. (А=2,24 см; ν=0,159 Гц; φ=0,353π
рад; x= А cos
(ωt+φ), где ω=1 с-1).
1.12.
Складываются
два гармонических колебания одного
направления с одинаковыми периодами
Т1=Т2=1,5
с
и амплитудами А1=А2=2
см.
Начальные фазы колебаний φ1=π/2
и φ2=π/3.
Определить амплитуду А
и начальную фазу φ результирующего
колебания. Найти его уравнение и построить
с соблюдением масштаба векторную
диаграмму сложения амплитуд. (А=3,86 см;
φ=0,417π рад; x= А cos
(ωt+φ), где ω=2π/Т с-1
=
4,19 с-1).
1.13.
Складываются
три гармонических колебания одного
направления с одинаковыми периодами
Т1=Т2=Т3=2
с
и амплитудами А1=А2=А3=3
см. Начальные фазы колебаний φ1=0,
φ2=π/3,
φ3=2π/3.
Построить векторную диаграмму сложения
амплитуд. Определить из чертежа амплитуду
А
и начальную фазу φ результирующего
колебания. Найти его уравнение. (А= 6 см;
φ= π/3 рад; x= А cos
(ωt+φ), где ω=2π/Т с-1=π
с-1).
1.14.
Складываются
два гармонических колебания одинаковой
частоты и одинакового направления: x1=
А1cos(ωt+φ1)
и x2=А2cos(ωt+φ2).
Начертить векторную диаграмму для
момента времени t=0. Определить аналитически
амплитуду А
и
начальную фазу φ результирующего
колебания. Отложить А
и
φ на векторной диаграмме. Найти уравнение
результирующего колебания (в
тригонометрической форме через косинус).
Задачу решить для двух случаев: 1) А1=1
см, φ1=π/3;
А2=2
см, φ2=5π/6;
2) А1=1
см, φ1=2π/3;
А2=1
см, φ2=7π/6.
(1) А= 2,24см; φ= 0,686π рад; 2) А= 1,41см; φ=0,917π
рад).
1.15.
Два камертона звучат одновременно.
Частоты ν1
и ν2
их колебаний соответственно равны 440 и
440,5 Гц. Определить период Т
биений.
(2с).
1.16.
Складываются два взаимно перпендикулярных
колебания, выражаемых уравнениями
х=А1sin
ωt и y=А2cosω(t+τ),
где А1
=
2 см, А2=1
см, ω= π с-1,
τ=0,5 с. Найти уравнение траектории и
построить ее, показав направление
движения точки. (y=
— (А2/А1)x
или y=
— 1/2x).
1.17.
Точка совершает одновременно два
гармонических колебания, происходящих
по взаимно перпендикулярным направлениям
и
выражаемых
уравнениями х=А1cosωt
и y=А2cosω(t+τ),
где
А1=4
см, А2=8
см, ω=π с-1,
τ =1 с. Найти уравнение траектории точки
и построить график ее движения. (y=
— (А2/А1)x
или y=
— 2x).
1.18.
Точка
совершает одновременно два гармонических
колебания одинаковой частоты, происходящих
по взаимно перпендикулярным направлениям
и
выражаемых
уравнениями: 1)
х=Аcosωt
и y=Аcosωt;
2)
х=Асosωt
и y=А1cosωt;
3)
х=Аcosωt
и y=Аcos(ωt+φ1);
4)
х=А2cosωt
и y=Аcos(ωt+φ2);
5)
х=А1cosωt
и y=А1sinωt;
6)
х=Аcosωt
и y=А1sinωt;
7)
х=А2sinωt
и y=А1sinωt;

х=А2sinωt
и y=Аsin(ωt+φ2).
Найти для восьми случаев: уравнение
траектории точки, построить ее с
соблюдением масштаба и указать направление
движения. Принять: А=2
см, А1=3
см, А2=
1 см; φ1=π/2,
φ2=π.
(1) y=
x; 2) y
= (А2/А1)x,
y
=
x;
3) x2+y2=А2,
x2+y2=4;
4) y=
— (А2/А1)x,
y=
— 2x; 5) x2+y2=А2,
x2+y2=9;
6)
+
=1,
+
=1;
7) y= (А2/А1)x,
y=3x; 
y=-2x).
1.19.
Точка участвует одновременно в двух
взаимно перпендикулярных колебаниях,
выражаемых уравнениями х=А1cosωt
и y=А2
sinωt,
где А1=2
см, А2=1
см. Найти уравнение траектории точки и
построить ее, указав направление
движения. (
+
=1,
=1).
1.20.
Точка
одновременно совершает два гармонических
колебания, происходящих по взаимно
перпендикулярным направлениям и
выражаемых уравнениями
х=А1sinωt
и y=А2cosωt,
где А1=0,5
см; А2=2
см. Найти уравнение траектории точки и
построить ее, указав направление
движения. (
= 1).
1.21.
Движение точки задано уравнениями
х=А1sinωt
и y=А2sinω(t+τ),
где А1=10
см,
А2=5
см, ω=2
с-1,
τ=π/4 с. Найти уравнение траектории и
скорость точки в момент времени t =0,5с.
(
=1,
υ = 13,7
м/с).
1.22.
Материальная
точка участвует одновременно в двух
взаимно перпендикулярных колебаниях,
выражаемых уравнениями
х=А1cosωt
и y=-А2cos2ωt,
где А1=2
см,
А2=1
см. Найти уравнение траектории и построить
ее. (y=-2(А2/А1)x2+А2,
y=-(
x2+1).
1.23.
Точка участвует одновременно в двух
гармонических колебаниях, происходящих
по взаимно перпендикулярным направлениям
и описываемых уравнениями: 1)
х=Аsinωt
и y=Аcos2ωt;
2)
х=Аcosωt
и y=Аsin2ωt;
3)
х=Аcos2ωt
и y=А1cosωt;
4)
х=А1sinωt
и y=Аcosωt.
Найти уравнение траектории точки,
построить ее с соблюдением масштаба и
указать направление движения. Принять:
А=2 см; А1=3
см. (1)
y=А-2
,y=-x2+2;
2) y=2
-А,
y=x2-2;
3) 2Аy-А1x2=АА1,
y=¾x2+
;
4) x=2(А1/А)y
,
x=
y
).
1.24.
Точка участвует одновременно в двух
взаимно перпендикулярных колебаниях,
выражаемых уравнениями
х=А1cosωt
и y=А2sin0,5ωt,
где А1=
2 см, А2=3
см. Найти уравнение траектории точки
и построить ее, указав направление
движения. (y=
(А1-x),
x=
(2-x)).
1.25.
Смещение
светящейся точки на экране осциллографа
является результатом сложения двух
взаимно перпендикулярных колебаний,
которые описываются уравнениями: 1)
х=Аsin3ωt
и y=А
sin2ωt;
2)
х=Аsin3ωt
и y=Аcos2ωt;
3)
х=Аsin3ωt
и y=Аcosωt.
Применяя графический метод сложения и
соблюдая масштаб, построить траекторию
светящейся точки на экране. Принять А
=4см. (Самостоятельно).
Динамика
гармонических колебаний. Маятники
1.26.
Грузик массой m=250
г, подвешенный к пружине, колеблется по
вертикали с периодом Т=1
с. Определить жесткость k
пружины.
(9,87 Н/м).
1.27.
К спиральной пружине подвесили грузик,
в результате чего пружина растянулась
на х=9 см. Каков будет период Т
колебаний
грузика, если его немного оттянуть вниз
и затем отпустить? (0,6 с).
1.28.
Гиря, подвешенная к пружине, колеблется
по вертикали с амплитудой А=4
см. Определить полную энергию Е
колебаний
если жесткость k
пружины
равна 1 кН/м. (0,8 Дж).
1.29.
Найти
отношение длин двух математических
маятников, если отношение периодов их
колебаний равно 1,5. (
=
-(
)2=2,25
.
).
1.30.
Математический маятник длиной 𝓁=1
м установлен в лифте. Лифт поднимается
с ускорением а=2,5
м/с2.
Определить период Т
колебаний маятника. (Т=2π
=1,8
с).
1.31.
Тонкий
обруч, повешенный на гвоздь, вбитый
горизонтально в стену, колеблется в
плоскости, параллельной стене. Радиус
R
обруча
равен 30 см. Вычислить период Т
колебаний
обруча. (Т=2π
=1.55
c).
1.32.
Однородный
диск радиусом R=30
см
колеблется около горизонтальной
оси, проходящей через одну из образующих
цилиндрической поверхности диска. Каков
период Т
его
колебаний? (Т=2π
=1.35
c).
1.33.
Диск радиусом R=24
см колеблется около горизонтальной
оси, проходящей через середину одного
из радиусов перпендикулярно плоскости
диска. Определить приведенную длину L
и
период Т
колебаний
такого маятника. (36 см).
1.34.
Математический
маятник длиной 𝓁1=40
см и физический маятник в виде тонкого
прямого стержня длиной 𝓁2=60
см синхронно колеблются около одной и
той же горизонтальной оси. Определить
расстояние, a
центра
масс стержня от оси колебаний. (10 см).
1.35.
Верхний конец стальной проволоки
диаметром 0,5 мм и длинной 80 см защемлён.
К нижнему концу проволоки прикреплён
шар массой 2 кг и диаметром 10 см. Если
шар повернуть вокруг вертикальной оси
на небольшой угол и отпустить, он будет
совершать вращательные колебания.
Определите период колебаний шара. (11,5
с).
1.36.
Тонкая прямоугольная пластинка может
колебаться вокруг горизонтальной оси,
лежащей в ее плоскости и перпендикулярной
одной из ее сторон, длина которой равна
𝓁.
а)
Каков период колебаний, если ось совпадает
с верхней стороной пластинки?
б)
При каком расстоянии оси от середины
пластинки период колебаний пластинки
будет наименьшим? Каков этот период?
(1) 2π
;
2)
;
2π
).
1.37.
Шар радиусом 5 см подвешен на нити длиной
10 см. Определите погрешность, которую
мы делаем, приняв его за математический
маятник длиной 15 см.
(2,2%).
Затухающие
колебания
1.38.
Амплитуда
затухающих колебаний маятника за время
t1=5
мин уменьшилась в два раза. За какое
время t2,
считая от начального момента, амплитуда
уменьшится в восемь раз? (15
мин).
1.39.
За время t=8
мин
амплитуда затухающих колебаний маятника
уменьшилась в три раза. Определить
коэффициент затухания δ. (0,0023 с-1).
1.40.
Амплитуда колебаний маятника длиной
l=1 м за время t=10 мин уменьшилась в два
раза. Определить логарифмический
декремент колебаний Ө. (Ө =
ln
= 2,31·10-3).
1.41.
Логарифмический декремент колебаний
Ө маятника равен 0,003. Определить число
N
полных
колебаний, которые должен сделать
маятник, чтобы амплитуда уменьшилась
в два раза. (N=
ln
=231).
1.42.
Гиря массой m=500
г подвешена к спиральной пружине
жесткостью k
=20
Н/м и совершает упругие колебания в
некоторой среде. Логарифмический
декремент колебаний Ө=0,004. Определить
число N
полных
колебаний, которые должна совершить
гиря, чтобы амплитуда колебаний
уменьшилась в п=2
раза.
За какое время t
произойдет это уменьшение? (N=
ln
=173;
t=2πn
= 2 мин 52 с).
1.43.
Тело
массой m=5
г совершает затухающие колебания. В
течение времени t
=50 с тело потеряло 60% своей энергии.
Определить коэффициент сопротивления
b.
(9,16·10-5
кг/с).
1.44.Определить
период Т
затухающих
колебаний, если период Т0
собственных
колебаний системы равен 1с и логарифмический
декремент колебаний Ө =0,628. (1,005).
1.45.
Найти число N
полных
колебаний системы, в течение которых
энергия системы уменьшилась в п=2
раза. Логарифмический декремент колебаний
Ө =0,01. (35).
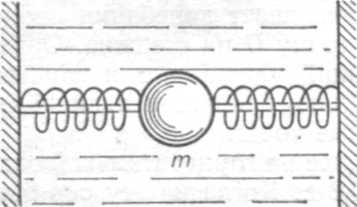
Рис.1
1.46.
Тело массой m=1
кг
находится в вязкой среде с коэффициентом
сопротивления b=0,05
кг/с. С помощью двух одинаковых пружин
жесткостью k=50
Н/м каждое тело удерживается в положении
равновесия, пружины при этом не
деформированы (рис. 1). Тело сместили от
положения равновесия и отпустили.
Определить: 1) коэффициент затухания δ;
2) частоту ν колебаний; 3) логарифмический
декремент
колебаний
Ө; 4) число N
колебаний,
по прошествии которых амплитуда
уменьшится в е
раз. (1) 0,025; 2) 1,59Гц; 3) 0,0157; 4) 64).
1.47.
Начальная амплитуда колебаний маятника
равна 3 см. Через 10 с она стала равной 1
см. Через сколько времени амплитуда
колебаний будет равна 0,3 см?
(21 с).
1.48.
Каков логарифмический декремент
затухания маятника длиной 0,8 м, если его
начальная амплитуда равна 5°, а через 5
мин она становится равной 0,5°? (0,014).
1.49.
Через сколько времени энергия колебаний
камертона с частотой f
=600
Гц уменьшится в n=106
раз, если логарифмический декремент
затухания равен 0,0008?
(t =
=14 с).
1.50.
Какова общая сумма путей, пройденных
колеблющейся точкой до полного затухания
колебаний, если амплитуда первого
колебания равна 1 мм, а логарифмический
декремент затухания равен 0,002?
(2 м).
Вынужденные
колебания. Резонанс
1.51.
Под действием силы тяжести электродвигателя
консольная балка, на которой он установлен,
прогнулась на
h=1 мм.
При какой частоте вращения n
якоря
электродвигателя может возникнуть
опасность резонанса? (n=
=16 с-1).
1.52.
Вагон массой m=80
т имеет четыре рессоры. Жесткость k
пружин
каждой рессоры равна 500 кН/м. При какой
скорости υ
вагон
начнет сильно раскачиваться вследствие
толчков на стыках рельс, если длина 𝓁
рельса
равна 12,8 м? (υ=(l/π)
=10,2
м/с).
1.53.
Колебательная система совершает
затухающие колебания с частотой ν=1000
Гц. Определить частоту ν0
собственных колебаний, если резонансная
частота vpeз=998
Гц. (1002 Гц).
1.54.
Определить,
на сколько резонансная частота отличается
от частоты ν0=l
кГц собственных колебаний системы,
характеризуемой коэффициентом затухания
δ=400 с-1.
(Δν= δ2/(4π2
ν0)=4,05
Гц).
1.55.
Определить логарифмический декремент
колебаний Ө колебательной системы, для
которой резонанс наблюдается при
частоте, меньшей собственной частоты
ν0=10
кГц на ∆ν=2 Гц. (θ=2π
=0,089).
1.56.
Период Т0
собственных
колебаний пружинного маятника равен
0,55 с. В вязкой среде период Т
того
же маятника стал равным 0,56 с. Определить
резонансную частоту νpeз
колебаний. (νpeз=
=1,75
с-1).
1.57.
Пружинный маятник (жесткость k
пружины
равна 10 Н/м, масса m
груза
равна 100 г) совершает вынужденные
колебания в вязкой среде с коэффициентом
сопротивления r=2·10-2
кг/с. Определить коэффициент затухания
δ и резонансную амплитуду Арез,
если
амплитудное значение вынуждающей силы
F0=10
мН.
(0,1 с-1;
5 см).
1.58.
Тело
совершает вынужденные колебания в среде
с коэффициентом сопротивления r=1
г/с. Считая затухание малым, определить
амплитудное значение вынуждающей силы,
если резонансная амплитуда Арез=0,5
см и частота ν0
собственных колебаний равна 10 Гц с-1.
(F0=2πν0rАрез=0,314
мН).
1.59.
Амплитуды
вынужденных гармонических колебаний
при частоте ν1=400
Гц и ν2=600
Гц равны между собой. Определить
резонансную частоту vpeз.
Затуханием пренебречь. (510 Гц).
1.60.К
спиральной пружине жесткостью
k=10
Н/м подвесили грузик массой m=10
г и погрузили всю систему в вязкую среду.
Приняв коэффициент сопротивления b
равным
0,1 кг/с, определить: 1) частоту ν0
собственных колебаний; 2) резонансную
частоту νpcз;
3) резонансную амплитуду Арез,
если
вынуждающая сила изменяется по
гармоническому закону и ее амплитудное
значение F0=0,02
Н; 4) отношение резонансной амплитуды к
статическому смещению под действием
силы F0.
(1) 5,03 Гц; 2) 4,91 Гц; 3) 6,4 мм; 4) 3,2).
1.61.
Во сколько раз амплитуда вынужденных
колебаний будет меньше резонансной
амплитуды, если частота изменения
вынуждающей силы будет больше резонансной
частоты: 1)на 10%? 2)в два раза? Коэффициент
затухания δ в обоих случаях принять
равным 0,1 ω0
(ω0
− угловая частота собственных колебаний).
(1) 1,53; 2) 15,2).
1.62.
Амплитуда смещения вынужденных колебаний
при очень малой частоте равна s0=2
мм, а при резонансе равна s=16 мм, Предполагая,
что декремент затухания меньше единицы,
определите его. (s
=
(
+
);
при υ<1 можно принять, что s =
,
откуда υ=
=0,4).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Условие задачи:
Материальная точка совершает гармонические колебания. Период колебаний 0,5 с, максимальное ускорение 15,8 м/с2. Определить амплитуду колебаний.
Задача №9.1.2 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(T=0,5) с, (a_{max}=15,8) м/с2, (A-?)
Решение задачи:
Если материальная точка совершает гармонические колебания, то уравнение этих колебаний можно представить в виде:
[x = Asin left( {omega t} right)]
В этой формуле (A) – амплитуда колебаний, (omega) – циклическая частота колебаний.
Чтобы найти уравнение ускорения точки при этих колебаниях, нужно дважды взять производную от уравнения колебаний. Сначала возьмем первую производную:
[x^{prime} = Aomega cos left( {omega t} right)]
Теперь берем вторую производную:
[x^{primeprime} = – A{omega ^2}sin left( {omega t} right)]
То есть мы имеем:
[a = – A{omega ^2}sin left( {omega t} right)]
Понятно, что максимальное по модулю значение ускорения в таком случае следует искать по формуле:
[{a_{max }} = A{omega ^2};;;;(1)]
Циклическая частота колебаний (omega) и период колебаний (T) связаны по известной формуле:
[omega = frac{{2pi }}{T}]
Тогда, учитывая это, формула (1) примет вид:
[{a_{max }} = frac{{4{pi ^2}A}}{{{T^2}}}]
Откуда искомая амплитуда колебаний (A) равна:
[A = frac{{{a_{max }}{T^2}}}{{4{pi ^2}}}]
Численный ответ задачи равен:
[A = frac{{15,8 cdot {{0,5}^2}}}{{4 cdot {{3,14}^2}}} = 0,1;м]
Ответ: 0,1 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
9.1.1 Уравнение гармонических колебаний имеет вид x=4*sin(2*pi*t) (м). Определить
9.1.3 За какое время от начала движения точка, колеблющаяся по закону x=7*sin(0,5*pi*t) (м)
9.1.4 Две точки совершают гармонические колебания. Максимальная скорость первой точки