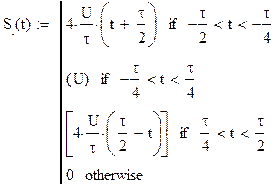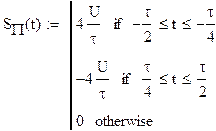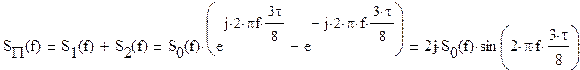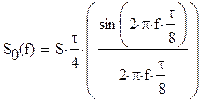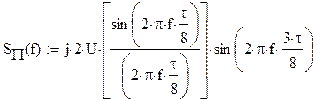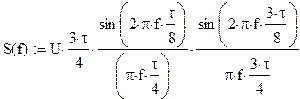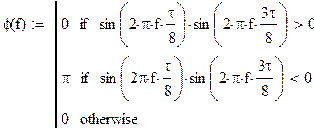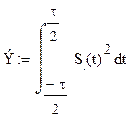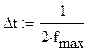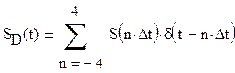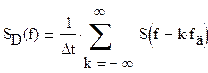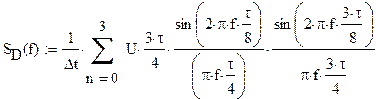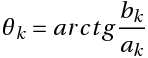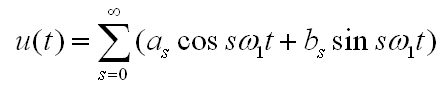Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
ТПИ Задания 14.doc
Скачиваний:
31
Добавлен:
31.03.2015
Размер:
171.01 Кб
Скачать
-
Сформировать
сигнал x(t),соответствующий
своему варианту. (
Здесь и в последующих заданиях номер
варианта равен номеру М в журнале
группы. М =п1п2. Символы п1 и п2 –это
первая и вторая цифры номера.)
Все сигналы рассматриваются только в
диапазоне изменения времени от -1 до
+1. За пределами этого диапазона значение
сигнала равно нулю. Частота ω0=π/2.
Варианты сигналов: 1) cos(ω0 *t); 2)cos2(ω0 *t); 3) 1 -t;
4) 1 –t2; 5)exp(- |t|); 6) 1 –t4;
7) 1 -t3; 
9)cos(2ω0*t);
10) 1/(1 +t2); 11)sin2(ω0
*t); 12) (sin2(ω0
*t))1/2 ; 13)cos2(ω0 *t); 14)cos(2*ω0 *t); 15)t;
16)t2 ; 17)t3
;18)sin(3*ω0*t);
19)sin(ω0*t);
20)t*sin(ω0*t); 21) 1; 22)
0.5 +cos(ω0 *t);
23) 1-cos2(ω0 *t);
24)cos2(2*ω0 *t).
-
Построить график
сигнала x(t)
в диапазоне от (-3 <t<3). -
Найти
прямое преобразование Фурье сигнала
x(t)
и его амплитудно-частотную
характеристику.
Пределы интегрирования ( -1 до +1)
F(f)
= ∫ x(t)*exp(-ј*2*π*f*t)dt
= ∫ x(t)*cos
(-ј*2*π*f*t)dt
+ ј∫ x(t)*sin
(-ј*2*π*f*t)dt.
Преобразование
Фурье имеет мнимую и действительную
части
F(f) = Re[F(f)] + ј*Im[F(f)].
Амплитудно-частотная характеристика
сигнала
A(f)
= {( Re[F(f)])2
+(
Im[F(f)])2
}1/2.
-
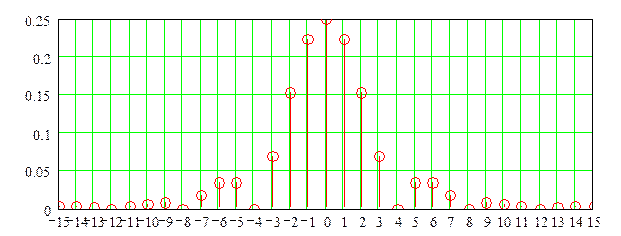
Построить
график A(f)
(частотный спектр сигнала). По графику
определить максимальную частоту fмакс.
в спектре
сигнала из условия А(fмакс
) < = 0.05 *
A(f)макс. -
Найти
обратное преобразование Фурье
x1(t) = ∫
F(f) *exp(-ј*2*π*f*t)df.
Интегрирование осуществляется в
диапазоне частот (-fмакс
до +fмакс
). Вычислить
и построить разность сигналов ε=x1(t)
— x(t).
Записать максимальное по модулю значение
εмакс.
Задание 2
Дискретизация сигналов во времени.
-
По
найденному в задании 1 п.4 fмакс
вычислитьT=1/(4*fмакс
). -
Построить периодическую функцию δT
(t) =∑ δ(t–n*T).
Суммирование ведётся поnв диапазоне его изменения от -20 до + 20
Функция δ (t) = 1,
если толькоt= 0, и равна
«0» приt≠ 0. -
Построить дискретный периодический
сигнал xД (t)=x1(t)* δT
(t). Функцияx1(t)
получена в задании 1 п.5. -
Вычислить максимальное значение второй
производной сигнала x(t)
(см. п.1 задания 1). -
При восстановлении сигнала по его
дискретным отсчётам путём линейной
интерполяции интервал квантования
выбирают из условия T1 =
(8*εмакс)/|x(2)(t)макс.Вычислить T1. Величина εмакс
берётся из п.5 задания 1,x(2)(t)
– вторая производная сигналаx(t). -
Выполнить п.2,3 задания, заменив TнаT1 иx1(t)
наx(t).
Контрольные вопросы к заданию
-
Суть дискретизации сигналов во времени
по Котельникову. -
Суть дискретизации сигналов во времени
по величине ошибки аппроксимации. -
Как соотносятся спектры сигналов x1(t)
наx(t)? -
Сигнал, квантованный по Котельников,
воспроизводиться с использованием
аппроксимации полиномом первой степени.
Какова при этом будет ошибка воспроизведения
сигнала x(t)? -
Целесообразно ли увеличивать степень
аппроксимирующего полинома при
квантовании сигнала по времени? -
При воспроизведении исходного сигнала
из квантованного по времени чаще всего
используют полиномы нулевой или первой
степени. Почему? -
Суть неравномерного квантования по
времени. -
Приведите несколько примеров, где
используются квантованные во времени
сигналы. -
С какой частотой дожжен квантоваться
речевой сигнал? -
Как непрерывный сигнал преобразуют в
цифровую форму? -
Имеются ли ограничения на число разрядов
при оцифровке речевых сигналов? -
Какова должна быть частота следования
в линии связи импульсов неизбыточного
кода при цифровой передачи речевого
сигнала? -
Возможно ли технически реализовать
сигнал x1(t)
наx(t)?
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
$begingroup$
Having
$$ f(x) = cos(x) + sin(10x)$$
How Can I know which is the max frequency of this signal?
I need it to set the right Nyquist frequency ($2cdotmaxtext{frequency}$)
I can use Matlab if it’s needed
asked Jun 4, 2013 at 17:24
$endgroup$
$begingroup$
The $sin(10x)$ term has a frequency of $frac {10}{2pi }$ because $x$ must increase be $frac {2pi }{10}$ to make a full cycle.
answered Jun 4, 2013 at 17:49
Ross MillikanRoss Millikan
369k27 gold badges252 silver badges444 bronze badges
$endgroup$
2
$begingroup$
In the more complicated case you can apply Fourier series. In this case the signal is already in the desired form and we have to pick the term with the last nonzero coefficient. In general the signal might not have any last term in which case you have to lowpass filter it first. There is also a mathematical form to the operation and it is convolution defined by
begin{equation}
(f*g)(x) = int_{-infty}^infty f(t) g(x-t) dt .
end{equation}
In the case of $T$-periodic functions its expression can be reduced somewhat. It is useful to take a look at the operation in $k$-space. For series coefficients we have
begin{equation}
c_k(f*g) = T cdot c_k(f)c_k(g) ,
end{equation}
where $T$ is the period. Hence by choosing a suitable impulse response $g$, that has $c_k(g)=0$ for every $k geq N$ the filtered signal $f*g$ has also coefficients
begin{equation}
c_k(f*g) = T cdot c_k(f)c_k(g) = T cdot c_k(f) cdot 0 = 0
end{equation}
for $n geq N$. Hence there is a maximum frequency $f_N = frac{N}{2pi}$ and you may set sampling frequency to $N/pi$. Here we have assumed that the Fourier series is of the form
begin{equation}
f(x) = sum_{k=-N}^N c_k e^{ikx} , k = 2pi f_k .
end{equation}
For the signal in the question $N = 10$ and the sampling frequency equals to $10/pi$.
answered Jun 4, 2013 at 20:21
$endgroup$
You must log in to answer this question.
Not the answer you’re looking for? Browse other questions tagged
.
Not the answer you’re looking for? Browse other questions tagged
.
Министерство образования и науки Российской Федерации
НОВОСИБИРСКИЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
_____________________________________________________________________
Кафедра теоретических основ радиотехники (ТОР)
РАДИОТЕХНИЧЕСКИЕ
ЦЕПИ И СИГНАЛЫ
ЗАДАНИЕ
N 2
СПЕКТРАЛЬНЫЙ АНАЛИЗ СИГНАЛОВ
ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ
Вариант N 2
Подвариант N 4
Факультет РЭФ Преподаватель: проф.
Яковлев А.Н.
Группа РТ- 5 — 45
Студент: Дашеев Р.В.
Дата сдачи « 14 » апреля 2006 г.
Новосибирск, 2006
2.4.1. Спектральный
анализ сигналов
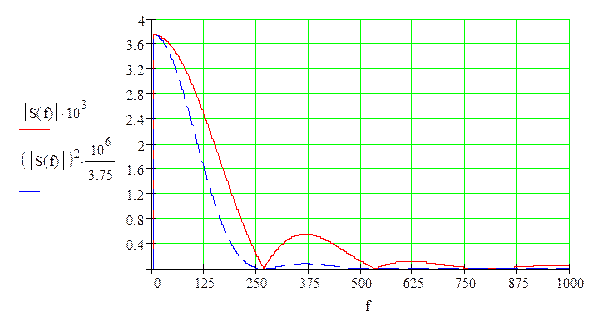
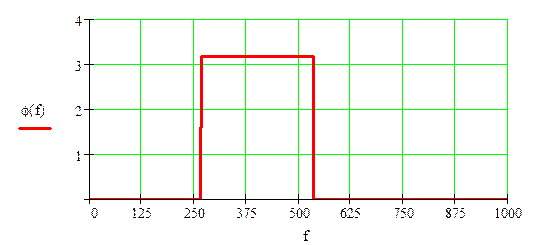
а) определить спектральную плостность S(f) сигнала S(t).
Построить спектральные диаграммы модуля |S(f)| и фазы f(f), диаграмму энергитического спектра |S(f)|2;
б) найти ширину «лепестка»
спектра одиночного импульса и сигнала;
в) вычислить энергию сигнала;
г) рассчитать коэффициенты Cn и Аn комплексного и тригонометрического ряда Фурье для
периодического сигнала ST(t),
полученного путем повторения заданного сигнала S(t) с периодом Tn . Построить соответствующие
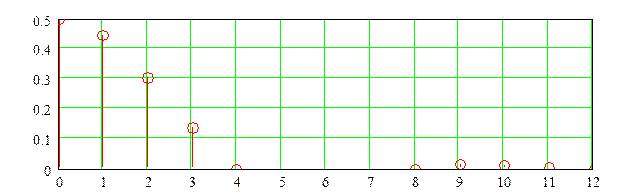
спектральные диаграммы |Cn|,
Fn
è |An|,fn .
Вароиант №
2 Подвариант № 4
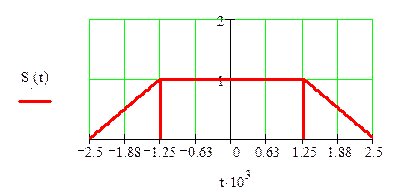
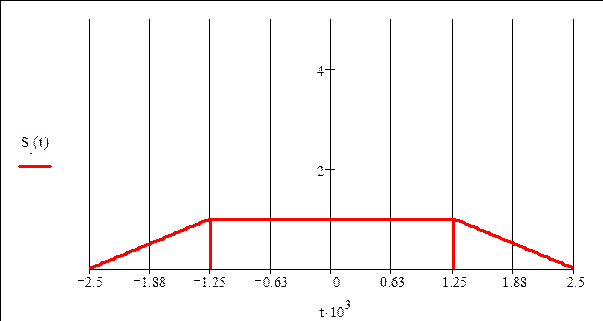
Запись исходного сигнала S(t) через временные интервалы:
а) Определим
спектральную плостность S(f) сигнала S(t)
Для того ,чтобы перейти от данного сигнала к
прямоугольному необходимо от данного сигнала взять производную
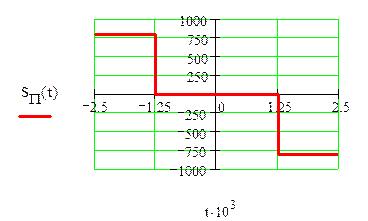
Имеем два прямоугольных импульса.Для определения
спектра S(t) воспользуемся теоремой о спектре суммы сигналов.
Для того , чтобы определить спектр S(t) сигнала S(t) необходимо воспользоваться
теоремой о интегрировании спектра сигнала.
б) Ширина
«лепестка» спектра одиночного импульса и сигнала
— ширина лепестка спектра одиночного импульса
— ширина лепестка спектра сигнала
в) Вычисление
энергии сигнала
г) Рассчет
коэффициентов Cn и Аn комплексного и
тригонометрического ряда Фурье для периодического сигнала ST(t)
Период повторения заданного импульса:
Частота периодического сигнала:
Число гармоник n возмем равным:
Определим коэффициенты комплексного ряда Фурье:
Коэффициенты комплексного ряда Фурье связанны с
коэффициентами тригононометрического ряда следующими соотношениями:
2.4.3.
Дискритизация непрерывных сигналов
а) вычислить максимальную частоту fmax в спектре сигнала;
б) определить интервал дискретизации;
в) построить графики дискретизированного сигнала, если за
дискретизирующую систему функций принять последовательность дельта-импульсов d(t);
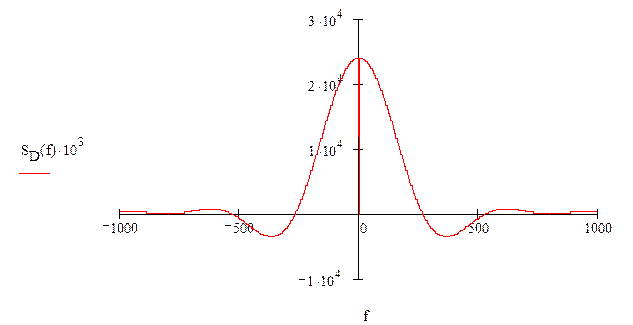
г) определить спектр SD(f) дискетизированного в
соответствии с п.»3″ сигнала. Построить диаграмму спектральной
плотности |SD(f)|.
а) Максимальная
частотя fmax в спектре
сигнала;
За максимальную частоту fmax в спектре сигнала можно принять ширену первого
«лепестка». Она будет равна:
б) Интервал
дискретизации;
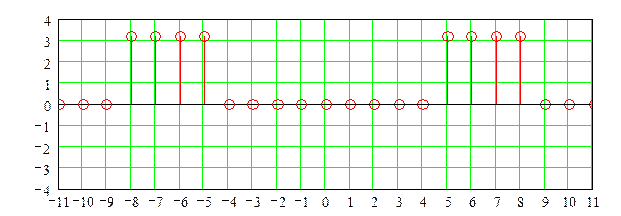
в) График
дискретизированного сигнала
г) Спектр SD(f) дискетизированного в
соответствии с п.»3″ сигнала
Спектр SD(f)
дискетизированного сигнала связан со спектром исходного сигнала следующим
соотношением:
Многие, смотря на описание ЧПУ контроллера, задаются вопросом о таком параметре, как максимальная частота импульсов. Давайте попробуем разобраться, что это такое и на что это влияет?
Влияет это, конечно, на конечную скорость станка. Разумеется, она зависит не только от электроники, но и от механики. Но в данном случае, мы будем рассматривать систему лишь с точки зрения электроники.
Для примера посчитаем максимальную скорость, которой нам позволит достичь электроника при использовании платы PCIMC-3D и драйверов DM556. У платы PCIMC-3D максимальная частота импульсов 47 kHz.
Для понимания расчетов произведем их под разный шаг ШВП, возьмем шаг 5, 10, 20. В конце это позволит нам определиться с тем, какой именно ШВП нам целесообразно использовать.
Итак, начнем «из далека». Шаговый двигатель имеет свой шаг. У биполярных шаговых двигателей два основных типа HS (к примеру 57HS76-3004) и НМ (к примеру 57HM76-3004). У двигателей HS один шаг это 1,8 градуса, у HM в половину меньше т.е. 0,9 градуса. В сфере ЧПУ станков в 90% используются шаговые двигатели HS, и мы также советуем вам остановиться именно на них. Таким образом, для шагового двигателя HS при одном шаге в 1,8 градуса требуется 200 импульсов на оборот.
Любой драйвер позволяет производить деление шага. Это необходимо для точности позиционирования и плавности перемещения. Деление шага на драйвере DM556, DM542 находятся либо на самом драйвере и называются Pulse/rev Table, либо в руководстве. Деление шага выставляется путем комбинации переключателей на драйвере, согласно таблице.
Пример таблицы на драйвере DM542:
Как таковое деление шага 1/1 (т.е. 200 шагов на оборот двигателя HS) никогда не используют. В данной таблице деление шага указано уже в имп./оборот для удобства. К примеру, 800 имп./оборот в данной таблице это деление шага ¼ (т.е. 200 х 4).
По нашему мнению, самые оптимальные значения деления шага 800, 1600, 3200. Помните, что чем выше деление шага, тем больше плавность перемещения, но тем большая потеря момента (стоит учесть что потеря момента крайне незначительна, но есть). Если вы планируете использовать ваш станок для работ на высоких скоростях (6000 мм/мин и выше), то стоит выбрать меньшее деление шага.
Итак, с шагами двигателя и делением шага на драйвере разобрались, поехали дальше.
В начале статье мы выяснили, что частота у нашей платы PCIMC-3D 47kHz.
47 kHz это частота 47000 импульсов в секунду. Скорость на нашем станке мы хотим узнать в мм/мин, поэтому частоту также переведем в импульсы в минуту, получим: 47000*60 = 2820000 импульсов в минуту.
Исходя из вышесказанного, мы решили, что будем использовать шаговый двигатель HS и на нашем драйвере выставим деление шага 1/8 т.е. 1600 импульсов на оборот.
Теперь узнаем, сколько оборотов в минуту, мы сможем достичь: 2820000/1600 = 1762,5 оборота в минуту.
Ранее мы говорили о том, что будем делать расчет для разных ШВП с шагом: 5, 10, 20.
Поскольку наш шаговый двигатель может достичь максимальных оборотов в 1762,5 об./мин, то при винте с шагом 5 мм/об. максимальная скорость станка будет равна 1762,5 х 5 = 8812,5 мм/мин. Подобным образом сделаем расчет для в винта с шагом 10. 1762,5 x 10 = 17625 мм/мин. И для винта с шагом 20. 1762,5 x 20 = 35250 мм/мин.
Разумеется, это максимальные параметры, и, как я и говорил, реальная максимальная скорость зависит не только от электроники, но и от механики.
Давайте приведем наши расчеты в «божеский вид» и выведем красивую формулу:
Частота контроллера (Hz)— характеристика контроллера ЧПУ, указывается в описании и руководстве к плате. Обратите внимание, что частота в описании указывается в kHz. Для того, чтобы перевести в Hz необходимо умножить на 1000.
Шаг передачи (мм) — расстояние в мм, которое проходит ваш станок за полный оборот шагового двигателя.
Деление шага — дробление шага, выставленное на драйвере шагового двигателя. Обратите внимание, что на некоторых драйвера указывается уже полученное значение деления шага, а не само дробление. К примеру, в таблице на драйвере DM556 значение 1600 есть ни что иное, как 200 х 8.
Вывод: надеюсь, данная статья поможет вам легко определить, стоит ли вам гнаться за платой с высокой частотой, или же вам достаточно бюджетного варианта со сравнительно низкими параметрами.
F.A.Q.
Надеюсь, данная рубрика будет постоянно пополняться вашими вопросами и нашими ответами на них.
1. Какая максимальная частота импульсов для драйвера шагового двигателя?
Производителями большинства драйверов установлена максимальная частота входных сигналов в 200 kHz. Однако, стоит сделать поправку. При проведении опытов установлено, что в 90% случаев уже на 170 kHz начинают проявляться уходы, пропуски и другие дефекты. Поэтому в случае, если вы планируете работать на высокой частоте, я бы советовал вам установить «порог надежности» в 150 kHz.
Но, как вы успели убедиться в статье, 150 kHz это более чем достаточно!
2. Какая частота у LPT плат?
Для примера возьмем плату LPT-DPTR 1.03. Она, как и большинство подобных плат по своей сути не является генератором импульсов. Она является всего лишь усилителем и элементом защиты. На самом деле импульсы в данном случае формирует компьютер.
Если обратиться к Mach3, то в настройках (Config — Ports&Pins) мы увидим возможность переключения частоты от 25 kHz до 100 kHz. Не стоит «на слово» верить голым цифрам.
Частота зависит на 100% от характеристик вашего компьютера. Делясь накопленным опытом, могу сказать, что большинство рядовых компьютеров могут поддерживать частоту в 45 kHz. Лишь некоторые, более мощные и совершенные, в 60 kHz. Компьютеров, стабильно работающих на частоте свыше 60 kHz, за всю историю встречено не было 
Практическое применение преобразования Фурье для анализа сигналов. Введение для начинающих
Время на прочтение
9 мин
Количество просмотров 256K
1. Преобразование Фурье и спектр сигнала
Во многих случаях задача получения (вычисления) спектра сигнала выглядит следующим образом. Имеется АЦП, который с частотой дискретизации Fd преобразует непрерывный сигнал, поступающий на его вход в течение времени Т, в цифровые отсчеты — N штук. Далее массив отсчетов подается в некую программку, которая выдает N/2 каких-то числовых значений (программист, который утянул из инета написал программку, уверяет, что она делает преобразование Фурье).
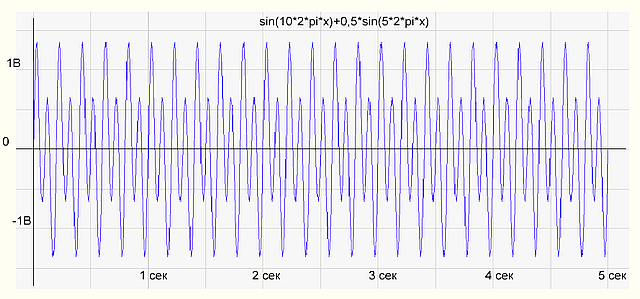
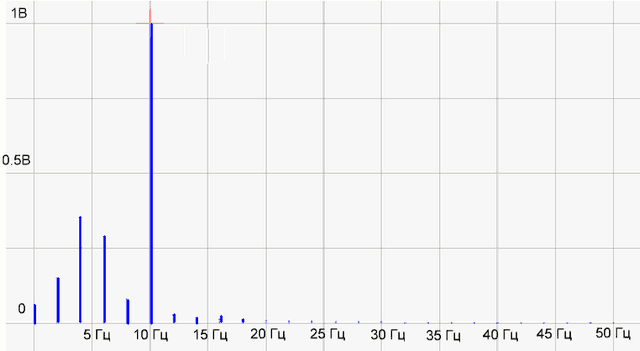
Чтобы проверить, правильно ли работает программа, сформируем массив отсчетов как сумму двух синусоид sin(10*2*pi*x)+0,5*sin(5*2*pi*x) и подсунем программке. Программа нарисовала следующее:
рис.1 График временной функции сигнала
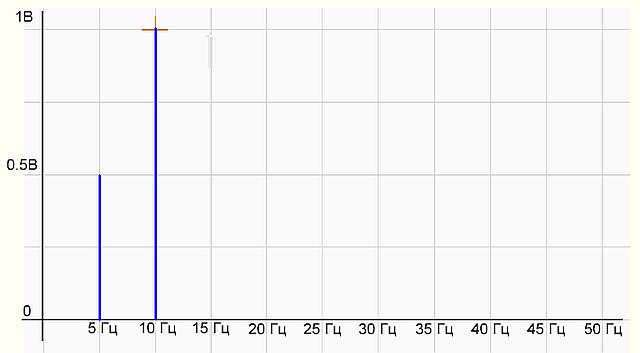
рис.2 График спектра сигнала
На графике спектра имеется две палки (гармоники) 5 Гц с амплитудой 0.5 В и 10 Гц — с амплитудой 1 В, все как в формуле исходного сигнала. Все отлично, программист молодец! Программа работает правильно.
Это значит, что если мы подадим на вход АЦП реальный сигнал из смеси двух синусоид, то мы получим аналогичный спектр, состоящий из двух гармоник.
Итого, наш реальный измеренный сигнал, длительностью 5 сек, оцифрованный АЦП, то есть представленный дискретными отсчетами, имеет дискретный непериодический спектр.
С математической точки зрения — сколько ошибок в этой фразе?
Теперь
начальство решило
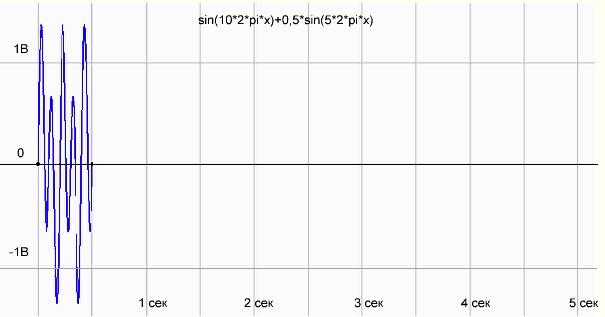
мы решили, что 5 секунд — это слишком долго, давай измерять сигнал за 0.5 сек.
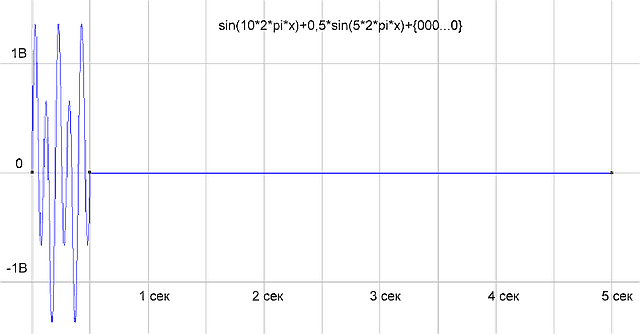
рис.3 График функции sin(10*2*pi*x)+0,5*sin(5*2*pi*x) на периоде измерения 0.5 сек
рис.4 Спектр функции
Что-то как бы не то! Гармоника 10 Гц рисуется нормально, а вместо палки на 5 Гц появилось несколько каких-то непонятных гармоник. Смотрим в интернетах, что да как…
Во, говорят, что в конец выборки надо добавить нули и спектр будет рисоваться нормальный.
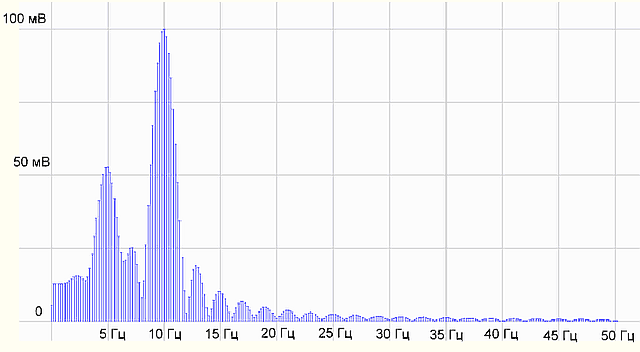
рис.5 Добили нулей до 5 сек
рис.6 Получили спектр
Все равно не то, что было на 5 секундах. Придется разбираться с теорией. Идем в Википедию — источник знаний.
2. Непрерывная функция и представление её рядом Фурье
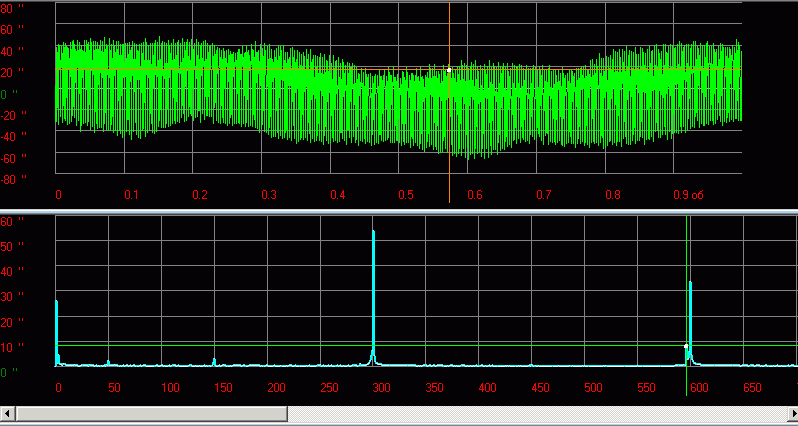
Математически наш сигнал длительностью T секунд является некоторой функцией f(x), заданной на отрезке {0, T} (X в данном случае — время). Такую функцию всегда можно представить в виде суммы гармонических функций (синусоид или косинусоид) вида:
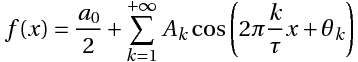
k — номер тригонометрической функции ( номер гармонической составляющей, номер гармоники)
T — отрезок, где функция определена (длительность сигнала)
Ak — амплитуда k-ой гармонической составляющей,
θk- начальная фаза k-ой гармонической составляющей
Что значит «представить функцию в виде суммы ряда»? Это значит, что, сложив в каждой точке значения гармонических составляющих ряда Фурье, мы получим значение нашей функции в этой точке.
(Более строго, среднеквадратичное отклонение ряда от функции f(x) будет стремиться к нулю, но несмотря на среднеквадратичную сходимость, ряд Фурье функции, вообще говоря, не обязан сходиться к ней поточечно. См. https://ru.wikipedia.org/wiki/Ряд_Фурье.)
Этот ряд может быть также записан в виде:
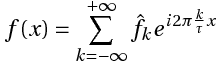
где 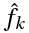
или
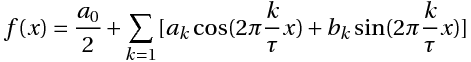
Связь между коэффициентами (1) и (3) выражается следующими формулами:
и
Отметим, что все эти три представления ряда Фурье совершенно равнозначны. Иногда при работе с рядами Фурье бывает удобнее использовать вместо синусов и косинусов экспоненты мнимого аргумента, то есть использовать преобразование Фурье в комплексной форме. Но нам удобно использовать формулу (1), где ряд Фурье представлен в виде суммы косинусоид с соответствующими амплитудами и фазами. В любом случае неправильно говорить, что результатом преобразования Фурье действительного сигнала будут комплексные амплитуды гармоник. Как правильно говорится в Вики «Преобразование Фурье (ℱ) — операция, сопоставляющая одной функции вещественной переменной другую функцию, также вещественной переменной.»
Итого:
Математической основой спектрального анализа сигналов является преобразование Фурье.
Преобразование Фурье позволяет представить непрерывную функцию f(x) (сигнал), определенную на отрезке {0, T} в виде суммы бесконечного числа (бесконечного ряда) тригонометрических функций (синусоид иили косинусоид) с определёнными амплитудами и фазами, также рассматриваемых на отрезке {0, T}. Такой ряд называется рядом Фурье.
Отметим еще некоторые моменты, понимание которых требуется для правильного применения преобразования Фурье к анализу сигналов. Если рассмотреть ряд Фурье (сумму синусоид) на всей оси Х, то можно увидеть, что вне отрезка {0, T} функция представленная рядом Фурье будет будет периодически повторять нашу функцию.
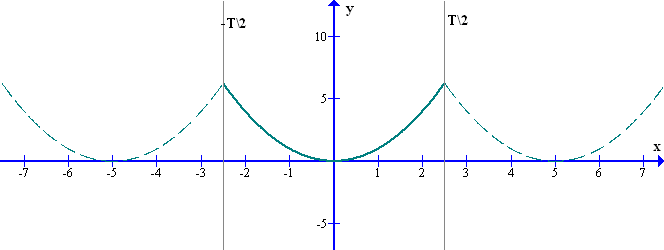
Например, на графике рис.7 исходная функция определена на отрезке {-T2, +T2}, а ряд Фурье представляет периодическую функцию, определенную на всей оси х.
Это происходит потому, что синусоиды сами являются периодическими функциями, соответственно и их сумма будет периодической функцией.
рис.7 Представление непериодической исходной функции рядом Фурье
Таким образом:
Наша исходная функция — непрерывная, непериодическая, определена на некотором отрезке длиной T.
Спектр этой функции — дискретный, то есть представлен в виде бесконечного ряда гармонических составляющих — ряда Фурье.
По факту, рядом Фурье определяется некоторая периодическая функция, совпадающая с нашей на отрезке {0, T}, но для нас эта периодичность не существенна.
Далее.
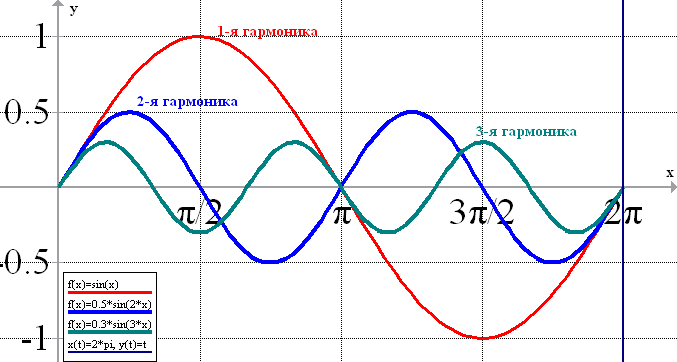
Периоды гармонических составляющих кратны величине отрезка {0, T}, на котором определена исходная функция f(x). Другими словами, периоды гармоник кратны длительности измерения сигнала. Например, период первой гармоники ряда Фурье равен интервалу Т, на котором определена функция f(x). Период второй гармоники ряда Фурье равен интервалу Т/2. И так далее (см. рис. 8).
рис.8 Периоды (частоты) гармонических составляющих ряда Фурье (здесь Т=2π)
Соответственно, частоты гармонических составляющих кратны величине 1/Т. То есть частоты гармонических составляющих Fk равны Fk= кТ, где к пробегает значения от 0 до ∞, например к=0 F0=0; к=1 F1=1T; к=2 F2=2T; к=3 F3=3T;… Fk= кТ (при нулевой частоте — постоянная составляющая).
Пусть наша исходная функция, представляет собой сигнал, записанный в течение Т=1 сек. Тогда период первой гармоники будет равен длительности нашего сигнала Т1=Т=1 сек и частота гармоники равна 1 Гц. Период второй гармоники будет равен длительности сигнала, деленной на 2 (Т2=Т/2=0,5 сек) и частота равна 2 Гц. Для третьей гармоники Т3=Т/3 сек и частота равна 3 Гц. И так далее.
Шаг между гармониками в этом случае равен 1 Гц.
Таким образом сигнал длительностью 1 сек можно разложить на гармонические составляющие (получить спектр) с разрешением по частоте 1 Гц.
Чтобы увеличить разрешение в 2 раза до 0,5 Гц — надо увеличить длительность измерения в 2 раза — до 2 сек. Сигнал длительностью 10 сек можно разложить на гармонические составляющие (получить спектр) с разрешением по частоте 0,1 Гц. Других способов увеличить разрешение по частоте нет.
Существует способ искусственного увеличения длительности сигнала путем добавления нулей к массиву отсчетов. Но реальную разрешающую способность по частоте он не увеличивает.
3. Дискретные сигналы и дискретное преобразование Фурье
С развитием цифровой техники изменились и способы хранения данных измерений (сигналов). Если раньше сигнал мог записываться на магнитофон и храниться на ленте в аналоговом виде, то сейчас сигналы оцифровываются и хранятся в файлах в памяти компьютера в виде набора чисел (отсчетов).
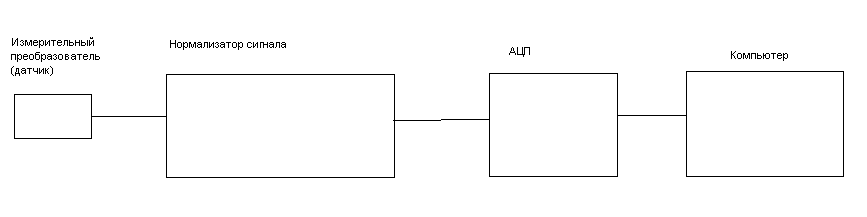
Обычная схема измерения и оцифровки сигнала выглядит следующим образом.
рис.9 Схема измерительного канала
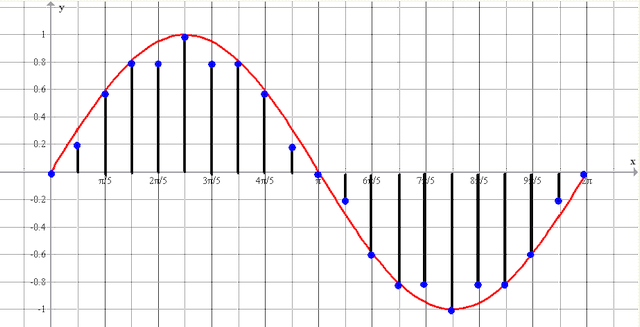
Сигнал с измерительного преобразователя поступает на АЦП в течение периода времени Т. Полученные за время Т отсчеты сигнала (выборка) передаются в компьютер и сохраняются в памяти.
рис.10 Оцифрованный сигнал — N отсчетов полученных за время Т
Какие требования выдвигаются к параметрам оцифровки сигнала? Устройство, преобразующее входной аналоговый сигнал в дискретный код (цифровой сигнал) называется аналого-цифровой преобразователь (АЦП, англ. Analog-to-digital converter, ADC) ( Wiki).
Одним из основных параметров АЦП является максимальная частота дискретизации (или частота семплирования, англ. sample rate) — частота взятия отсчетов непрерывного во времени сигнала при его дискретизации. Измеряется в герцах. (( Wiki))
Согласно теореме Котельникова, если непрерывный сигнал имеет спектр, ограниченный частотой Fмакс, то он может быть полностью и однозначно восстановлен по его дискретным отсчетам, взятым через интервалы времени 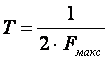
А что будет, если мы будем брать отсчеты с меньшей частотой, чем требуется по теореме Котельникова?
В этом случае возникает эффект «алиасинга» (он же стробоскопический эффект, муаровый эффект), при котором сигнал высокой частоты после оцифровки превращается в сигнал низкой частоты, которого на самом деле не существует. На рис. 11 красная синусоида высокой частоты — это реальный сигнал. Синяя синусоида более низкой частоты — фиктивный сигнал, возникающий вследствие того, за время взятия отсчета успевает пройти больше, чем пол-периода высокочастотного сигнала.
Рис. 11. Появление ложного сигнала низкой частоты при недостаточно высокой частоте дискретизации
Чтобы избежать эффекта алиасинга перед АЦП ставят специальный антиалиасинговый фильтр — ФНЧ (фильтр нижних частот), который пропускает частоты ниже половины частоты дискретизации АЦП, а более высокие частоты зарезает.
Для того, чтобы вычислить спектр сигнала по его дискретным отсчетам используется дискретное преобразование Фурье (ДПФ). Отметим еще раз, что спектр дискретного сигнала «по определению» ограничен частотой Fмакс, меньшей половине частоты дискретизации Fd. Поэтому спектр дискретного сигнала может быть представлен суммой конечного числа гармоник, в отличие от бесконечной суммы для ряда Фурье непрерывного сигнала, спектр которого может быть неограничен. Согласно теореме Котельникова максимальная частота гармоники должна быть такой, чтобы на нее приходилось как минимум два отсчета, поэтому число гармоник равно половине числа отсчетов дискретного сигнала. То есть если в выборке имеется N отсчетов, то число гармоник в спектре будет равно N/2.
Рассмотрим теперь дискретное преобразование Фурье (ДПФ).
Сравнивая с рядом Фурье
видим, что они совпадают, за исключением того, что время в ДПФ имеет дискретный характер и число гармоник ограничено величиной N/2 — половиной числа отсчетов.
Формулы ДПФ записываются в безразмерных целых переменных k, s, где k – номера отсчетов сигнала, s – номера спектральных составляющих.
Величина s показывает количество полных колебаний гармоники на периоде Т (длительности измерения сигнала). Дискретное преобразование Фурье используется для нахождения амплитуд и фаз гармоник численным методом, т.е. «на компьютере»
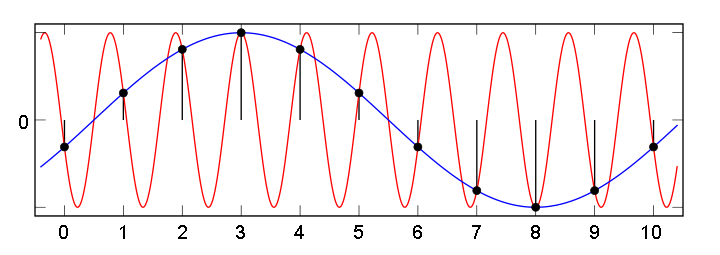
Возвращаясь к результатам, полученным в начале. Как уже было сказано выше, при разложении в ряд Фурье непериодической функции (нашего сигнала), полученный ряд Фурье фактически соответствует периодической функции с периодом Т. (рис.12).
рис.12 Периодическая функция f(x) с периодом Т0, с периодом измерения Т>T0
Как видно на рис.12 функция f(x) периодическая с периодом Т0. Однако из-за того, что длительность измерительной выборки Т не совпадает с периодом функции Т0, функция, получаемая как ряд Фурье, имеет разрыв в точке Т. В результате спектр данной функции будет содержать большое количество высокочастотных гармоник. Если бы длительность измерительной выборки Т совпадала с периодом функции Т0, то в полученном после преобразования Фурье спектре присутствовала бы только первая гармоника (синусоида с периодом равным длительности выборки), поскольку функция f(x) представляет собой синусоиду.
Другими словами, программа ДПФ «не знает», что наш сигнал представляет собой «кусок синусоиды», а пытается представить в виде ряда периодическую функцию, которая имеет разрыв из-за нестыковки отдельных кусков синусоиды.
В результате в спектре появляются гармоники, которые должны в сумме изобразить форму функции, включая этот разрыв.
Таким образом, чтобы получить «правильный» спектр сигнала, являющегося суммой нескольких синусоид с разными периодами, необходимо чтобы на периоде измерения сигнала укладывалось целое число периодов каждой синусоиды. На практике это условие можно выполнить при достаточно большой длительности измерения сигнала.
Рис.13 Пример функции и спектра сигнала кинематической погрешности редуктора
При меньшей длительности картина будет выглядеть «хуже»:
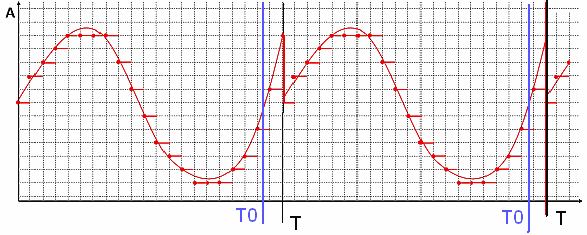
Рис.14 Пример функции и спектра сигнала вибрации ротора
На практике бывает сложно понять, где «реальные составляющие», а где «артефакты», вызванные некратностью периодов составляющих и длительности выборки сигнала или «скачками и разрывами» формы сигнала. Конечно слова «реальные составляющие» и «артефакты» не зря взяты в кавычки. Наличие на графике спектра множества гармоник не означает, что наш сигнал в реальности из них «состоит». Это все равно что считать, будто число 7 «состоит» из чисел 3 и 4. Число 7 можно представить в виде суммы чисел 3 и 4 — это правильно.
Так и наш сигнал… а вернее даже не «наш сигнал», а периодическую функцию, составленную путем повторения нашего сигнала (выборки) можно представить в виде суммы гармоник (синусоид) с определенными амплитудами и фазами. Но во многих важных для практики случаях (см. рисунки выше) действительно можно связать полученные в спектре гармоники и с реальными процессами, имеющими циклический характер и вносящими значительный вклад в форму сигнала.
Некоторые итоги
1. Реальный измеренный сигнал, длительностью T сек, оцифрованный АЦП, то есть представленный набором дискретных отсчетов (N штук), имеет дискретный непериодический спектр, представленный набором гармоник (N/2 штук).
2. Сигнал представлен набором действительных значений и его спектр представлен набором действительных значений. Частоты гармоник положительны. То, что математикам бывает удобнее представить спектр в комплексной форме с использованием отрицательных частот не значит, что «так правильно» и «так всегда надо делать».
3. Сигнал, измеренный на отрезке времени Т определен только на отрезке времени Т. Что было до того, как мы начали измерять сигнал, и что будет после того — науке это неизвестно. И в нашем случае — неинтересно. ДПФ ограниченного во времени сигнала дает его «настоящий» спектр, в том смысле, что при определенных условиях позволяет вычислить амплитуду и частоту его составляющих.
Использованные материалы и другие полезные материалы.
FourierScope — программа для построения радио сигналов и их спектрального анализа.
Graph — программа с открытым кодом, предназначенная для построения математических графиков.
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ – КАК ЭТО ДЕЛАЕТСЯ
Дискретное преобразование Фурье (ДПФ)