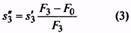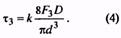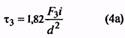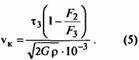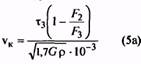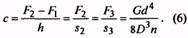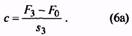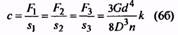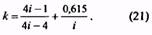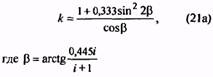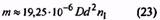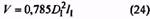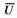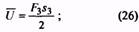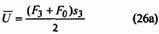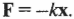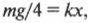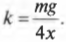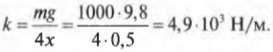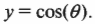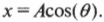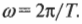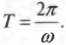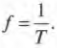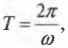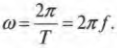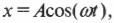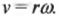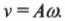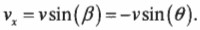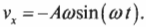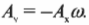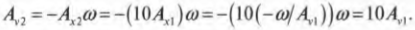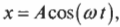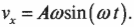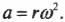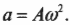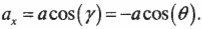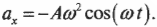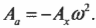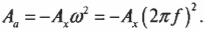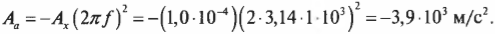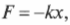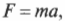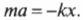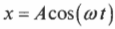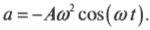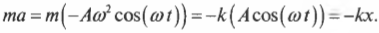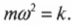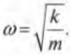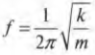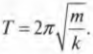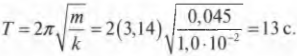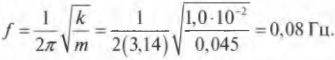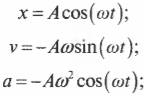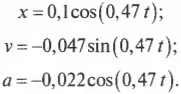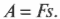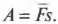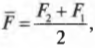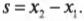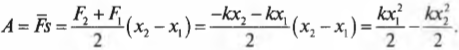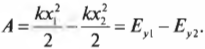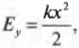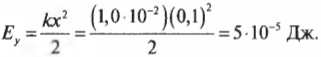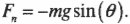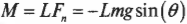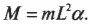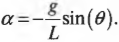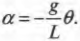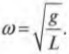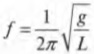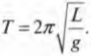Деформации. Силы упругости. Закон Гука
Пластическими деформациями называются деформации, полностью или частично сохраняющиеся после прекращения действии внешних сил.
Способность к упругим и пластическим деформациям зависит от природы вещества, из которого состоит тело, условий, в которых оно находится; способов его изготовления. Например, если взять разные сорта железа или стали, то у них можно обнаружить совершенно разные упругие и пластичные свойства. При обычных комнатных температурах железо является очень мягким, пластичным материалом; закаленная сталь, наоборот, — твердый, упругий материал. Пластичность многих материалов представляет собой условие для их обработки, для изготовления из них нужных деталей. Поэтому она считается одним из важнейших технических свойств твердого вещества.
При деформации твердого тела происходит смещение частиц (атомов, молекул или ионов) из первоначальных положений равновесия в новые положения. При этом изменяются силовые взаимодействия между отдельными частицами тела. В результате в деформированном теле возникают внутренние силы, препятствующие его деформации.
Различают деформации растяжения (сжатия), сдвига, изгиба, кручения.
Силы упругости
Силы упругости имеют электромагнитную природу. Они препятствуют деформациям и направлены перпендикулярно поверхности соприкосновения взаимодействующих тел, а если взаимодействуют такие тела, как пружины, нити, то силы упругости направлены вдоль их оси.
Силу упругости, действующую на тело со стороны опоры, часто называют силой реакции опоры.
где и
длина тела в деформированном и недеформированном состоянии соответственно.
Закон Гука
Небольшие и кратковременные деформации с достаточной степенью точности могут рассматриваться как упругие. Для таких деформаций справедлив закон Гука:
- Сила упругости, возникающая при деформации тела прямо пропорциональна абсолютному удлинению тела и направлена в сторону, противоположную смещению частиц тела:
где проекция силы на ось
жесткость тела, зависящая от размеров тела и материала, из которого оно изготовлено, единица жесткости в системе СИ Н/м.
Примеры решения задач
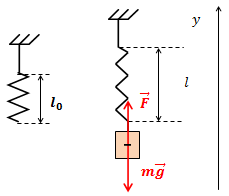
| Задание | Пружина жесткостью |
| Решение | Сделаем рисунок. |
На груз, подвешенный на пружине, действуют сила тяжести и сила упругости
.
Спроектировав это векторное равенство на координатную ось , получим:
По закону Гука сила упругости:
поэтому можно записать:
откуда длина деформированной пружины:
Переведем в систему СИ значение длины недеформированной пружины см
м.
Ускорение свободного падения м/с
.
Подставив в формулу численные значения физических величин, вычислим:
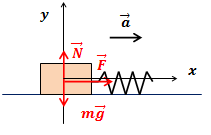
| Задание | По горизонтальной поверхности передвигают тело массой 3 кг с помощью пружины жесткостью |
| Решение | Сделаем рисунок. |
На тело действуют сила тяжести , сила реакции опоры
и сила упругости пружины
.
Выберем систему координат, как показано на рисунке и запишем это векторное равенство в проекциях на оси координат:
Как рассчитать пружину
Как найти коэффициент жёсткости пружины: формула, определение
Рано или поздно при изучении курса физики ученики и студенты сталкиваются с задачами на силу упругости и закон Гука, в которых фигурирует коэффициент жесткости пружины. Что же это за величина, и как она связана с деформацией тел и законом Гука?
Сила упругости и закон Гука
Для начала определим основные термины, которые будут использоваться в данной статье. Известно, если воздействовать на тело извне, оно либо приобретет ускорение, либо деформируется. Деформация — это изменение размеров или формы тела под влиянием внешних сил. Если объект полностью восстанавливается после прекращения нагрузки, то такая деформация считается упругой; если же тело остается в измененном состоянии (например, согнутом, растянутом, сжатым и т. д. ), то деформация пластическая.
Примерами пластических деформаций являются:
- лепка из глины;
- погнутая алюминиевая ложка.
В свою очередь, упругими деформациями будут считаться:
- резинка (можно растянуть ее, после чего она вернется в исходное состояние);
- пружина (после сжатия снова распрямляется).
В результате упругой деформации тела (в частности, пружины) в нем возникает сила упругости, равная по модулю приложенной силе, но направленная в противоположную сторону. Сила упругости для пружины будет пропорциональна ее удлинению. Математически это можно записать таким образом:
где F — сила упругости, x — расстояние, на которое изменилась длина тела в результате растяжения, k — необходимый для нас коэффициент жесткости. Указанная выше формула также является частным случаем закона Гука для тонкого растяжимого стержня. В общей форме этот закон формулируется так: «Деформация, возникшая в упругом теле, будет пропорциональна силе, которая приложена к данному телу». Он справедлив только в тех случаях, когда речь идет о малых деформациях (растяжение или сжатие намного меньше длины исходного тела).
Определение коэффициента жесткости
Коэффициент жесткости (он также имеет названия коэффициента упругости или пропорциональности) чаще всего записывается буквой k, но иногда можно встретить обозначение D или c. Численно жесткость будет равна величине силы, которая растягивает пружину на единицу длины (в случае СИ — на 1 метр). Формула для нахождения коэффициента упругости выводится из частного случая закона Гука:
Чем больше величина жесткости, тем больше будет сопротивление тела к его деформации. Также коэффициент Гука показывает, насколько устойчиво тело к действию внешней нагрузки. Зависит этот параметр от геометрических параметров (диаметра проволоки, числа витков и диаметра намотки от оси проволоки) и от материала, из которого она изготовлена.
Единица измерения жесткости в СИ — Н/м.
Расчет жесткости системы
Встречаются более сложные задачи, в которых необходим расчет общей жесткости. В таких заданиях пружины соединены последовательно или параллельно.
Последовательное соединение системы пружин
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:
1/k = 1/k1 + 1/k2 + … + 1/ki,
где k — общая жесткость системы, k1, k2, …, ki — отдельные жесткости каждого элемента, i — общее количество всех пружин, задействованных в системе.
Параллельное соединение системы пружин
В случае когда пружины соединены параллельно, величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:
k = k1 + k2 + … + ki.
Измерение жесткости пружины опытным путем — в этом видео.
Вычисление коэффициента жесткости опытным методом
С помощью несложного опыта можно самостоятельно рассчитать, чему будет равен коэффициент Гука. Для проведения эксперимента понадобятся:
- линейка;
- пружина;
- груз с известной массой.
Последовательность действий для опыта такова:
- Необходимо закрепить пружину вертикально, подвесив ее к любой удобной опоре. Нижний край должен остаться свободным.
- При помощи линейки измеряется ее длина и записывается как величина x1.
- На свободный конец нужно подвесить груз с известной массой m.
- Длина пружины измеряется в нагруженном состоянии. Обозначается величиной x2.
- Подсчитывается абсолютное удлинение: x = x2-x1. Для того чтобы получить результат в международной системе единиц, лучше сразу перевести его из сантиметров или миллиметров в метры.
- Сила, которая вызвала деформацию, — это сила тяжести тела. Формула для ее расчета — F = mg, где m — это масса используемого в эксперименте груза (переводится в кг), а g — величина свободного ускорения, равная приблизительно 9,8.
- После проведенных расчетов остается найти только сам коэффициент жесткости, формула которого была указана выше: k = F/x.
Примеры задач на нахождение жесткости
Задача 1
На пружину длиной 10 см действует сила F = 100 Н. Длина растянутой пружины составила 14 см. Найти коэффициент жесткости.
- Рассчитываем длину абсолютного удлинения: x = 14—10 = 4 см = 0,04 м.
- По формуле находим коэффициент жесткости: k = F/x = 100 / 0,04 = 2500 Н/м.
Ответ: жесткость пружины составит 2500 Н/м.
Задача 2
Груз массой 10 кг при подвешивании на пружину растянул ее на 4 см. Рассчитать, на какую длину растянет ее другой груз массой 25 кг.
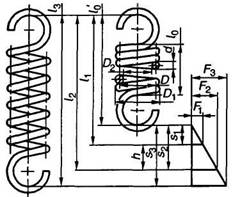
10. Формулы и способы расчета пружин из стали круглого сечения по ГОСТ 13765-86 в ред. 1990г.
Пружина сжатия
Пружина растяжения
|
Наименование параметра |
Обозначение |
Расчетные формулы и значения |
|
1. Сила пружины при предварительной деформации, Н |
F1 |
Принимаются в зависимости от нагрузки пружины |
|
2. Сила пружины при рабочей деформации (соответствует наибольшему принудительному перемещению подвижного звена в механизме), Н |
F2 |
|
|
3. Рабочий ход пружины, мм |
h |
|
|
4. Наибольшая скорость перемещения подвижного конца пружины при нагружении или разгрузке, м/с |
Vmax |
|
|
5. Выносливость пружины, число циклов до разрушения |
NF |
Продолжение табл. 10
|
Наименование параметра |
Обозначение |
Расчетные формулы и значения |
|
6. Наружный диаметр пружины, мм |
D1 |
Предварительно назначают с учетом конструкции узла. Уточняются по таблицам ГОСТ 13766-86-ГОСТ 13776-86 |
|
7. Относительный инерционный зазор пружины сжатия. Для пружин растяжения служит ограничением максимальной деформации |
δ |
δ = 1-F2/F3. (1) Для пружин сжатия классов I и IIδ=0,05…0,25; для пружин растяжения δ=0,05…0,10; для одножильных пружин класса IIIδ=0,10…0,40; для трехжильных класса IIIδ=0,15…0,40 |
|
8. Сила пружины при максимальной деформации, Н |
F3 |
F3=F2/(1-δ) (2) Уточняется по таблицам ГОСТ 13766-86-ГОСТ 13776-86 |
|
9. Сила предварительного напряжения (при навивке из холоднотянутой и термообработанной проволоки), Н |
F0 |
F0= (0,1… 0,25) F3 |
|
10. Диаметр проволоки, мм |
d |
Выбирается по таблицам ГОСТ 13764-86-ГОСТ 13776-86 |
|
11. Диаметр трехжильного троса, мм |
d1 |
|
|
12. Жесткость одного витка пружины, Н/мм |
c1 |
|
|
13. Максимальная деформация одного витка пружины, мм |
s’3 (при F0=0) s»3 (при F0>0) |
Выбирается по таблицам ГОСТ 13764-86-ГОСТ 13776-86 |
|
14. Максимальное касательное напряжение пружины, Н/мм2 (Коэффициент k см. п. 35) |
τ3 |
Назначается по табл. 2 ГОСТ 13764-86. При проверке Для трехжильных пружин |
|
15. Критическая скорость пружины сжатия, м/с (Максимальная скорость подвижного звена механизма vmax должна быть равна или меньше vK, т.е. vK > vmax) |
vк |
Для трехжильных пружин |
|
16. Модуль сдвига, Н/мм2 |
G |
Для пружинной стали G = 7,85·104 |
|
17. Динамическая (гравитационная) плотность материала, Н·с2/м4 |
Р |
p = γ/g, где g-ускорение свободного падения, м/с2; γ — удельный вес, Н/м3. Для пружиннойстали р = 8·103 |
|
18. Жесткость пружины, Н/мм |
с |
Для пружин с предварительным напряжением Для трехжильных пружин |
|
19. Число рабочих витков пружины |
n |
n = c1/c (7) |
|
20. Полное число витков пружины |
n1 |
n1 = n+ n2, (8) где n2 — число опорных витков |
|
21. Средний диаметр пружины, мм |
D |
D = D1 – d = D2 + d Для трехжильных пружин D = D1– d1= D2+ d1(9a) |
|
22. Индекс пружины |
i |
i = D/d (10) Для трехжильных пружин i= D/d1 (10а) Рекомендуется назначать от 4 до 12 |
Продолжение табл. 10
|
Наименование параметра |
Обозначение |
Расчетные формулы и значения |
||||
|
23. Коэффициент расплющивания троса в трехжильной пружине, учитывающий увеличение сечения витка вдоль оси пружины после навивки |
Δ |
Для трехжильного троса с углом свивкиβ=24° определяется по таблице, приведенной ниже |
||||
|
i |
40 |
45 |
50 |
55 |
60 |
7,0 и более |
|
Δ |
1,029 |
1,021 |
1,015 |
1,010 |
1,005 |
1,000 |
|
24. Предварительная деформация пружины, мм |
s1 |
s1=F1/c (11) |
||||
|
25. Рабочая деформация пружины, мм |
s2 |
s2= F2/c (12) |
||||
|
26. Максимальная деформация пружины, мм |
s3 |
s3= F3/c (13) |
||||
|
27. Длина пружины при максимальной деформации, мм |
l3 |
l3 = (n1 + 1 – n3)d, (14) где n3 — число обработанных витков. Для трехжильных пружин l3 = (n + l)d1Δ. (14а) Для пружин растяжения с зацепами l3 = l0 + s3 |
||||
|
28. Длина пружины в свободном состоянии, мм |
l0 |
l0=l3+s3 (15) |
||||
|
29. Длина пружины растяжения без зацепов в свободном состоянии, мм |
l0‘ |
l0‘ = (n1+1)d (15а) |
||||
|
30. Длина пружины при предварительной деформации, мм |
1l |
l1 = l0-s1. (16) Для пружин растяжения l1= l0+s1(16а) |
||||
|
31. Длина пружины при рабочей деформации, мм |
l2 |
l2=l0-s2. (17) Для пружин растяжения l2=l0+s2 (17а) |
||||
|
32. Шаг пружины в свободном состоянии, мм |
t |
t = s’3+d. (18) Для трехжильных пружин t = s’3+d1Δ. (18а) Для пружин растяжения t = d(18б) |
||||
|
33. Напряжение в пружине при предварительной деформации, Н/мм2 |
τ1 |
|
||||
|
34. Напряжение в пружине при рабочей деформации, Н/мм2 |
τ2 |
|
||||
|
35. Коэффициент, учитывающий кривизну витка пружины |
k |
Для трехжильных пружин |
||||
|
36. Длина развернутой пружины (для пружин растяжения без зацепов), мм |
l |
|
||||
|
37. Масса пружины (для пружин растяжения без зацепов), кг |
m |
|
||||
|
38. Объем, занимаемый пружиной (без учета зацепов пружины), мм3 |
V |
|
||||
|
39. Зазор между концом опорного витка и соседним рабочим витком пружины сжатия, мм |
λ |
Устанавливается в зависимости от формы опорного витка |
||||
|
40. Внутренний диаметр пружины, мм |
D2 |
D2=D1-2d (25) |
||||
|
41. Временное сопротивление проволоки при растяжении, Н/мм2 |
Rm |
Устанавливается при испытаниях проволоки или по ГОСТ 9389-75 и ГОСТ 1071-81 |
||||
|
42. Максимальная энергия, накапливаемая пружиной, или работа деформации, МДж |
|
Для пружин сжатия и растяжения без предварительного напряжения для пружин растяжения с предварительным напряжением |
Методика определения размеров пружин по ГОСТ 13765-86.
1. Исходными величинами для определения размеров пружин являются силы F1 и F2, рабочий ход h, наибольшая скорость перемещения подвижного конца пружины при нагружении или при разгрузке vmах, выносливость NF и наружный диаметр пружины D1 (предварительный).
Если задана только одна сила F2, то вместо рабочего хода h для подсчета берут величину рабочей деформации s2, соответствующую заданной силе.
2. По величине заданной выносливости NF предварительно определяют принадлежность пружины к соответствующему классу по табл. 1.
3. По заданной силе F2 и крайним значениям инерционного зазора δ вычисляют по формуле (2) значение силы F3.
4. По значению F3, пользуясь табл. 2, предварительно определяют разряд пружины.
5. По табл. 11-17 находят строку, в которой наружный диаметр витка пружины наиболее близок к предварительно заданному значению D1. В этой же строке находят соответствующие значения силы F3 и диаметра проволоки d.
6. Для пружин из закаливаемых марок сталей максимальное касательное напряжение τ3 находят по табл. 2, для пружин из холоднотянутой и термообработанной τ3 вычисляют с
учетом значений временного сопротивления Rm. Для холоднотянутой проволоки Rm определяют из ГОСТ 9389-75, для термообработанной — из ГОСТ 1071-81.
7. По полученным значениям F3 и τ3, aтакже по заданному значению F2 по формулам (5) и (5а) вычисляют критическую скорость vK и отношение vmax/vK, подтверждающее или
отрицающее принадлежность пружины к предварительно установленному классу.
При несоблюдении условий vmax/vK<1 пружины I и II классов относят к последующему классу или повторяют расчеты, изменив исходные условия. Если невозможно изменение исходных условий, работоспособность обеспечивается комплектом запасных пружин.
8. По окончательно установленному классу и разряду в соответствующей таблице на параметры витков пружин, помимо ранее найденных величин F3, D1, и d, находят величины c1 и s3, после чего остальные размеры пружины и габариты узла вычисляют по формулам (6)… (25).
Груз массой 45 кг с
помощью динамометра тянут равномерно по горизонтальной плоскости. Определите
деформацию пружины динамометра, если ее жесткость равна 7,8 кH/м, сила упругости направлена под углом 30 градусов к горизонту,
а коэффициент трения скольжения груза по поверхности равен 0,26.
Решение.
Деформация пружины x связана
с ее жесткостью l и модулем силы упругости F
соотношением F = kx (закон
Гука), откуда x = F/k. Силу F можно найти с помощью
второго закона Ньютона.
На груз действуют сила
тяжести mg, сила упругости пружины F,
сила нормальной реакции опоры N и сила трения Fтр . По второму закону
Ньютона получаем.
Запишем теперь его в
проекциях на координатные оси OX
и OY.
Кроме того, Fтр = mN. Решаем полученную систему уравнений и находим F.
Ответ: x = 15 мм.
Источник: Подготовка к тестированию по физике. Шепелевич. В. Г.
В этой главе …
- Изучаем закон Гука
- Осваиваем основы простого гармонического движения
- Изучаем особенности простого гармонического движения
- Измеряем энергию простого гармонического движения
- Вычисляем период колебаний маятника
Эта глава посвящена описанию еще одного типа движения, а именно: описанию периодического движения. Примерами такого движения являются колебания грузика на пружинке, качания маятника и даже прыжки с высоты с помощью эластичной веревки. В этой главе рассматриваются закономерности и особенности таких повторяющихся, т.е. периодических движений. Здесь мы научимся вычислять характеристики периодического движения: период колебаний пружинки и маятника, упругую энергию сжатой пружины и т.д.
Содержание
- Постигаем закон Гука
- Растягиваем и сжимаем пружины
- Изучаем особенности закона Гука
- Движется дальше: простое гармоническое движение
- Изучаем простое гармоническое движение по горизонтали и по вертикали
- Изучаем свойства простого гармонического движения
- Изучаем траекторию простого гармонического движения
- Определяем период простого гармонического движения
- Определяем скорость в простом гармоническом движении
- Определяем ускорение в простом гармоническом движении
- Определяем частоту колебаний груза на пружине
- Вычисляем энергию простого гармонического движения
- Качаемся вместе с маятником
Постигаем закон Гука
Все объекты природы могут деформироваться, т.е. менять свою форму или объем, под действием приложенной силы. Если такие деформации (т.е. изменения) исчезают после прекращения действия приложенной силы, то они называются упругими. Упругость играет важную роль в технике. Упругие пружины используются для гашения удара при посадке космического корабля на поверхность планеты. Свернутые в спираль упругие пластины применяются в заводных механизмах часов. Даже в мышеловке используется упругая деформация пружины.
Еще в XVII-M веке английский физик Роберт Гук, изучая упругие свойства разных материалов, вывел закон, названный его именем. Согласно закону Гука, для упругого деформирования материала требуется приложить силу, величина которой прямо пропорциональна его деформации. Например, чтобы растянуть пружину на величину ( x ), потребуется приложить внешнюю силу ( F_{вн} ), которая равна:
где ( k ) — это коэффициент пропорциональности.
Точнее говоря, вектор деформации ( mathbf{x} ) всегда направлен противоположно силе сопротивления пружины (или силе упругости) ( mathbf{F} ), а потому в векторную формулировку закона Гука обычно входит знак “минус”:
Растягиваем и сжимаем пружины
Следует помнить, что закон Гука относится только к упруго деформируемым материалам.
В реальном мире, помимо упругих деформаций, имеются еще и пластические деформации. Так называют деформации, которые остаются в объекте, хотя бы частично, даже после прекращения действия внешних сил. Если сила не превосходит некоторой известной величины, которая называется пределом упругости, то возникающая деформация будет пластической. Предел упругости имеет разные значения для разных материалов. Если деформируемый объект, например пружина, испытывает только упругие деформации, то его называют идеально упругим, например, идеально упругой пружиной. Коэффициент пропорциональности ( k ) в законе Гука ( F=kx ) называется коэффициентом упругости объекта, который зависит от материала объекта, его размеров и измеряется в Н/м.
Допустим, вам нужно спроектировать подвеску автомобиля массой 1000 кг, состоящую из 4 пружин, которые могут идеально упруго деформироваться на расстояние 0,5 м. Каким коэффициентом упругости должна обладать пружина, чтобы выдержать вес автомобиля?
Вес автомобиля равен ( mg ), где ( g ) — это ускорение свободного падения под действием силы гравитационного притяжения. Это значит, что на каждую пружину приходится вчетверо меньшая нагрузка ( mg/4 ).
Определим упругую деформацию пружины под действием этой нагрузки по формуле закона Гука:
т.е. коэффициент упругости равен:
Подставляя значения, получим:
Итак, чтобы выдержать вес автомобиля, потребуется пружина с коэффициентом упругости равным 4,9·103 Н/м. Не забудьте, что каждый элемент подвески автомобиля должен обладать определенным запасом прочности, чтобы выдерживать непредсказуемые превышения нагрузки, например на ухабах. Однако эта задача выходит за рамки данного курса.
Изучаем особенности закона Гука
Как уже упоминалось выше, в векторную формулировку закона Гука обычно входит знак “минус”:
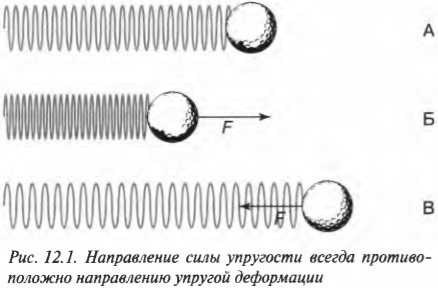
Таким образом, знак “минус” выражает следующую особенность упругой деформации: сила упругости всегда противоположна деформации. На рис. 12.1 схематически показаны направления силы упругости и деформации при сжатии и растяжении пружины.
Как видите, при отсутствии растяжении или сжатия нет и деформации (см. схему А на рис. 12.1). Если пружина сжимается влево, то сила упругости направлена вправо (см. схему Б на рис. 12.1), а если пружина растягивается вправо, то сила упругости направлена влево (см. схему В на рис. 12.1).
Сила упругости пружины не зря называется силой сопротивления, ведь она стремится установить равновесие.
Движется дальше: простое гармоническое движение
Простым гармоническим движением называется такое движение, при котором сила сопротивления движению пропорциональна перемещению. При этом сила трения не учитывается, и никакие другие внешние силы не оказывают никакого влияния на движение. Такое движение будет выполняться периодически и бесконечно долго. Конечно же, в реальной ситуации так не бывает, но здесь имеется в виду именно идеализированная ситуация.
Изучаем простое гармоническое движение по горизонтали и по вертикали
На рис. 12.1 показан пример движения мячика, прикрепленного к пружине. При сжатии пружины внешней силой справа налево в пружине возникает сила упругости, которая стремится вернуть мячик в исходное положение. После возврата мячика в исходное положение он останавливается не сразу, а спустя какое-то время. Оно необходимо для торможения ускорившегося мячика с помощью силы упругости, возникающей при растягивании вправо. Дело в том, что мячик обладает некоторой массой, и инерция (см. главу 11) не позволяет ему остановиться мгновенно. В результате имеем следующую последовательность событий (см. рис. 12.1).
- Схема А. Мячик находится в состоянии равновесия. Никакие силы не действуют на него. Пружина находится в нерастянутом и в несжатом состоянии.
- Схема Б. Внешняя сила сжала пружину справа налево. В пружине возникла упругая сила сопротивления ( F ).
- Схема В. Внешняя сила отпускает пружину (и далее не участвует в процессе движения). Упругая сила сопротивления пружины ( F ) стремится распрямить пружину, т.е. вернуть мячик в исходное состояние. Мячик начинает ускоренное движение.
Когда мячик проходит точку исходного положения, его скорость становится очень большой (фактически максимальной) и он продолжает движение вправо. При этом возникает деформация растяжения и соответственно направленная противоположно упругая сила сопротивления пружины. Именно так и происходит при повторяющихся движениях мячика слева направо и, наоборот, справа налево. После первоначального толчка из неподвижного состояния мячик начинает совершать периодические колебания из самого крайнего левого положения в самое крайнее правое положение.
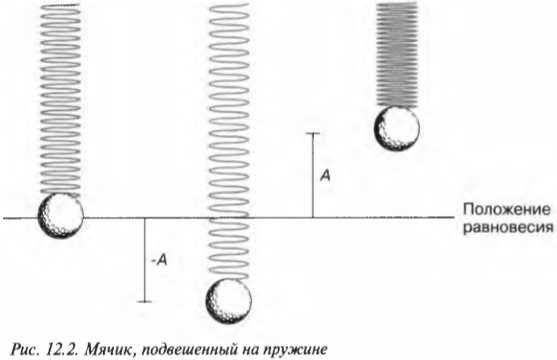
В примере на рис. 12.1 предполагается, что силы трения нет. А что будет, если пружинку с мячиком подвесить вертикально, как показано на рис. 12.2?
В подвешенном состоянии изменится положение равновесия, но после воздействия внешней силы мячик будет совершать аналогичные периодические движения, но теперь уже вверх-вниз.
Это новое равновесное положение определяется равенством веса мячика ( mg ) и силы упругости ( ky_0 ) растянутой пружины под действием этого веса:
Итак, новое положение исходного равновесия будет определяться формулой:
Теперь если потянуть мячик вниз с помощью внешней силы и отпустить мячик, то он начнет совершать периодическое движение, как и в прежнем примере (см. рис. 12.1), но теперь уже относительно нового положения равновесия.
Периодическое движение подобного рода называется периодическим колебанием, а крайние положения мячика при таком периодическом движении мячика называются амплитудами периодических колебаний. Амплитуда является важным элементом математического описания простого гармонического движения.
Изучаем свойства простого гармонического движения
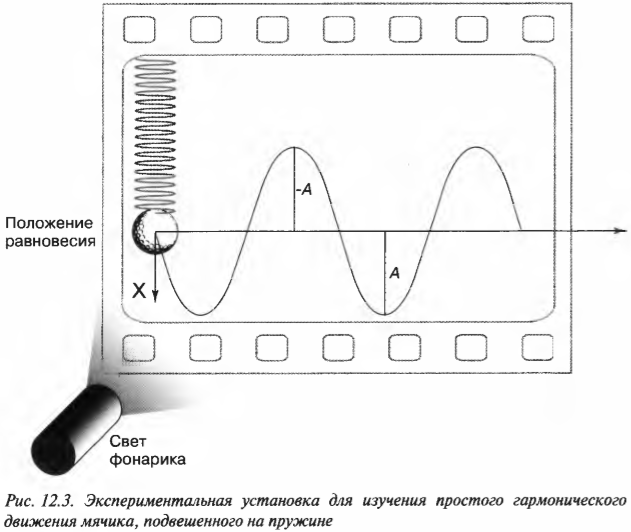
Представьте себе, что для изучения простого гармонического движения ученые решили освещенный фонариком мячик из предыдущего примера заснять на движущуюся по горизонтали фотопленку.
После проявки фотопленки на ней оказался четкий волнообразный след, который показан на рис. 12.3.
Оказывается, мячик действительно совершает периодические движения вверх-вниз относительно исходного равновесного положения с амплитудой А. Вблизи точки равновесия скорость мячика максимальна, а в точках амплитуды минимальна.
Траектория мячика очень похожа на синусоидальную кривую, т.е. след мячика на движущейся фотопленке описывается графиком функции ( sin ) (“синус”) либо ( cos ) (“косинус”) со сдвигом от начала координат. Действительно, решением уравнения простого гармонического движения является функция ( sin ) или ( cos ).
Изучаем траекторию простого гармонического движения
Построим и рассмотрим внимательно кривую функции:
Наверняка эта функция и ее графическое представление в виде синусоидальной кривой уже знакомо многим читателям этой книги из курса математики. Ее часто можно встретить на экранах разных приборов в реальной жизни или даже в виртуальном мире кино и компьютерных игр.
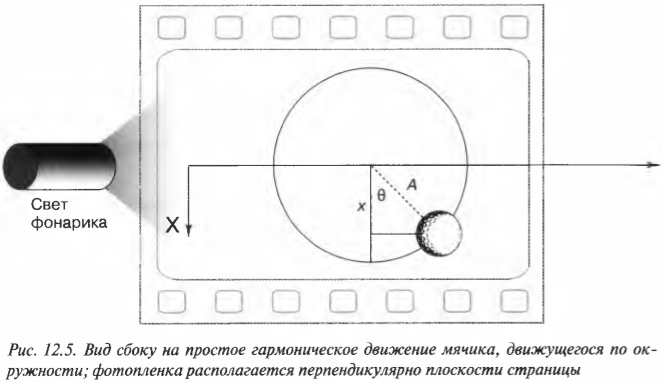
Пусть освещенный фонариком мячик движется по окружности перпендикулярной плоскости страницы и снимается на движущуюся по горизонтали фотопленку. Тогда после проявки фотопленки на ней снова появится синусоидальная кривая, как показано на рис. 12.4.
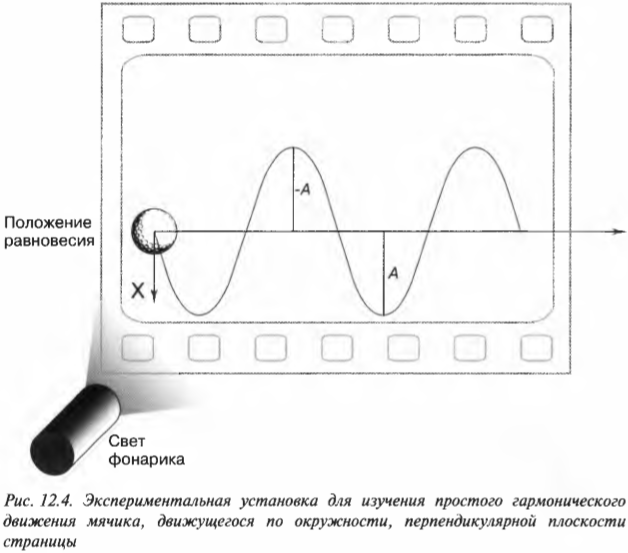
Если расположить окружность так, чтобы она была параллельна плоскости страницы (рис. 12.5), то можно легко заметить, что положение мячика определяется формулой:
где ( x ) — это текущее смещение мячика по оси X от положения равновесия, ( theta ) — это угол поворота мячика при вращении по окружности, а ( A ) — это амплитуда периодического движения.
Если мячик вращается по окружности с постоянной угловой скоростью, то ( theta=omega t ) и ( x=Acos(omega t) ).
Определяем период простого гармонического движения
Прохождение мячиком пути, равного длине окружности, называется циклом, а время его прохождения — периодом. Период обозначается символом ( T ) и измеряется в секундах.
На рис. 12.4 и 12.5 полный цикл соответствует движению мячика от исходного положения с амплитудой ( A ), затем к положению с амплитудой ( -A ), а потом снова к положению с амплитудой ( A ).
Как связан период с уже знакомыми нам параметрами движения? За один цикл мячик проходит угол величиной ( 2pi ) за период ( T ), т.е. его угловая скорость равна:
Откуда получаем выражение для периода:
Для характеристики периодического движения часто используют понятие частота, которое равно количеству циклов за единицу времени. Например, если мячик на рис. 12.4 совершает 1000 полных оборотов в секунду, то его частота равна 1000 с-1. В системе СИ частоту измеряют в герцах (или сокращенно Гц), т.е. 1 с-1 = 1 Гц. Таким образом, частота вращения мячика по окружности равна 1000 Гц.
Частота ( f ) и период ( T ) связаны очень простым соотношением:
Поскольку:
то теперь можно легко найти связь между частотой и угловой скоростью:
При описании периодических движений угловую скорость ( omega ) часто называют циклической частотой.
Определяем скорость в простом гармоническом движении
На рис. 12.5 мячик совершает движение по окружности, а координата перемещения по оси X определяется формулой:
где ( x ) — это текущее смещение мячика по оси X от положения равновесия, ( omega ) — это угловая скорость мячика при вращении по окружности, а ( A ) — это амплитуда периодического движения.
В любой точке с координатой х мячик обладает некоторой скоростью, которая зависит от времени. Как выразить ее с помощью математической формулы?
Очень просто, ведь для этого достаточно вспомнить о связи между угловой ( omega ) и тангенциальной ( v ) скоростью (см. главу 10):
Поскольку в данном случае ( r=A ), то в итоге получим для тангенциальной скорости:
Теперь для определения скорости периодических колебаний следа мячика по оси X на фотопленке нужно вычислить проекцию тангенциальной скорости на ось X:
(Здесь знак “минус” возникает, поскольку фотопленка движется вниз и ось Y направлена вниз, а потому угол ( beta ) между вектором скорости и осью X равен ( 180^circ+theta ), a ( sin(beta)=sin(180^circ+theta )=-sin(theta) ). — Примеч. ред.)
После подстановки выражений для ( theta=omega t ) и для ( v=Aomega ) получим:
Обратите внимание, что скорость меняется от исходного положения с амплитудой перемещения ( A ) и амплитудой скорости ( 0 ), затем к положению с амплитудой перемещения ( 0 ) и амплитудой скорости ( -Aomega ), потом к положению с амплитудой перемещения ( -A ) и амплитудой скорости ( 0 ), затем к положению с амплитудой перемещения ( 0 ) и амплитудой скорости ( Aomega ), а потом снова к положению с амплитудой перемещения ( A ) и амплитудой скорости ( 0 ).
Как видите, в простом гармоническом движении амплитуда скорости ( A_v=Aomega ) связана с амплитудой перемещения ( A_х=A ) формулой:
Рассмотрим следующий простой пример. Представьте себе, что несколько отчаянных парней и девушек прыгают с высоты с помощью эластичной веревки. Известно, что при прыжке с некоторой высоты относительно точки равновесия максимальная скорость в точке равновесия одного из смельчаков достигает величины 4 м/с. Он решает в 10 раз увеличить высоту прыжка. Какой будет его максимальная скорость в точке равновесия?
Итак, амплитуда скорости в первом прыжке ( A_{v1}=-A_{х1}omega ) равна 4 м/с. Амплитуда перемещения во втором прыжке (с новой высоты) в 10 раз больше амплитуды перемещения в начале, т.е. ( A_{х2}=10A_{х1} ). Вопрос: чему равна амплитуда скорости ( A_{v2}=-A_{х2}omega ) во втором прыжке? Подставляя выражение для ( A_{х2}=-omega/A_{v1} ) в формулу ( A_{х2}=10A_{х1} ), а затем в формулу ( A_{v2}=-A_{х2}omega ), получим:
Итак, при увеличении амплитуды прыжка в 10 раз амплитуда скорости возрастает тоже в 10 раз, т.е. становится равной 40 м/с.
Определяем ускорение в простом гармоническом движении
Вернемся к примеру на рис. 12.5, где мячик совершает движение по окружности. Его координата перемещения по оси X определяется формулой:
где ( x ) — это текущее смещение мячика по оси X от положения равновесия, ( omega ) — это угловая скорость мячика при вращении по окружности, а ( A ) — это амплитуда периодического движения.
Как мы уже выяснили в предыдущем разделе, его скорость перемещения по оси X определяется формулой:
Однако вращательное движение мячика также характеризуется центростремительным ускорением. Как выразить ее с помощью математической формулы?
Как известно (см. главу 10), угловая скорость ( omega ) центростремительное ускорение ( a ) связаны следующей формулой:
Поскольку в данном случае ( r=A ), то в итоге получим для центростремительного ускорения:
Теперь для определения ускорения периодических колебаний следа мячика по оси X на фотопленке нужно вычислить проекцию центростремительного ускорения на ось X:
(Здесь знак “минус” возникает, поскольку фотопленка движется вниз и ось Y направлена вниз, а потому угол ( gamma ) между вектором центростремительного ускорения и осью X равен ( 180^circ + theta ), a ( cos(gamma)=cos(180^circ + theta)=-cos(theta) ). — Примеч. ред.)
После подстановки выражений для ( theta=omega t ) и для ( a=Aomega^2 ) получим:
Как видите, в простом гармоническом движении амплитуда ускорения ( A_а=Aomega^2 ) связана с амплитудой перемещения ( A_х=A ) формулой:
Рассмотрим еще один простой пример. Пусть диафрагма (тоненькая пластинка) в трубке домашнего телефона совершает простое гармоническое движение с частотой ( theta=omega t ) величиной 1 кГц (т.е. 1000 Гц) и амплитудой перемещения ( A_х=A ) величиной 1,0·10-4 м. Чему равна амплитуда ускорения мембраны ( A_а )?
Поскольку ( omega=2pi!f ), то после подстановки этого выражения в предыдущую формулу ( A_а=-A_хomega^2 ) получим:
Подставляя численные значения, получим:
Как видите, мембрана обычного телефона испытывает очень большое ускорение, которое почти в 400 раз больше ускорения свободного падения ( g ) = 9,8 м/с2 под действием гравитационного притяжения Земли.
Определяем частоту колебаний груза на пружине
С математической точки зрения колебания груза на пружине и движение мячика по окружности (см. предыдущие разделы этой главы) принципиально не отличаются. Дело в том, что оба эти движения являются простыми гармоничными. Поэтому их основные характеристики (например, скорость, ускорение, частота и период колебаний) должны описываться аналогичными математическими формулами. Остановимся и подробно проследим за этой аналогией.
Как известно, согласно закону Гука (см. выше в этой главе), при растяжении пружины на величину ( x ) возникает упругая сила ( F ), которая равна:
где ( k ) — это коэффициент пропорциональности.
Согласно закону Ньютона (см. главу 5), сила и вызванное ею ускорение ( a ) связаны следующим соотношением:
откуда получаем:
Из предыдущего раздела нам уже известно, что в простом гармоническом движении перемещение и ускорение выражаются следующими формулами:
и
Подставляя эти выражения в предыдущую формулу, полученную на основе законов Гука и Ньютона, получим:
Сокращая некоторые переменные, получим:
Откуда легко можно выразить циклическую частоту:
Поскольку ( omega=2pi!f ) и ( omega=2pi/T ), то после подстановки предыдущего выражения в эти формулы получим:
и
Пусть пружина на рис. 12.1 обладает коэффициентом упругости ( k ), равным 1,0·10-2 Н/м, а к ней прикреплен груз массой 4 г. Чему будет равен период колебаний груза на пружине? Подставляя значения в предыдущую формулу для периода, получим:
А какова частота этих колебаний? Снова подставляя значения в предыдущую формулу для частоты, получим:
Используя формулы перемещения, скорости и ускорения для простого гармонического движения (см. ранее в этой главе):
можно вычислить координату, скорость и ускорение груза на пружине в произвольный момент времени. Как будут выглядеть эти формулы для задачи с грузиком на пружине?
Сначала вычислим циклическую частоту:
Если амплитуда ( A ) равна 10 см, то получим:
Вычисляем энергию простого гармонического движения
В простом гармоническом движении периодически происходит увеличение и уменьшение кинетической энергии, например груза на пружине. Ясно, что кинетическая энергия груза не пропадает, а преобразуется в энергию сжатой или растянутой пружины. Эта энергия называется упругой потенциальной энергией пружины. Сколько энергии запасено в сжатой или растянутой пружине?
Попробуем вычислить ее с помощью простых соображений. Как известно, работа ( A ) силы ( F ) при перемещении на расстояние ( s ) равна:
При сжатии или растяжении пружины сила ( F ) меняется линейно с расстоянием, поэтому работу этой силы по сжатию или растяжению пружины на расстояние ( s ) можно представить как произведение средней силы ( overline{F} ) на перемещение ( s ):
Средняя ( overline{F} ) сила определяется как:
где ( F_1=-kx_1 ) — это сила упругости в точке с координатой ( x_1 ), a ( F_2=-kx_2 ) — сила упругости в точке с координатой ( x_2 ). При этом перемещение ( s ) будет равно:
Подставляя выражения для ( s ) и ( overline{F} ) в формулу работы, получим:
Члены ( frac{kx^2_1}{2} ) и ( frac{kx^2_2}{2} ) выражают упругую потенциальную энергию пружины ( E_{у1} ) и ( E_{у2} ) в точках с координатами ( x_1 ) и ( x_2 ), соответственно. Таким образом, работа силы упругости равна изменению упругой потенциальной энергии пружины:
Рассмотрим простой пример. Насколько возрастет упругая потенциальная энергия пружины с коэффициентом упругости 1,0·10-2 Н/м при сжатии ее на 10 см? Подставляя значения в формулу
получим:
Учтите, что при изменении упругой потенциальной пружины с грузом (при отсутствии внешних сил) изменяется кинетическая энергия груза. Причем эти изменения происходят так, что неизменной остается полная энергия системы, состоящей из пружины и груза. Например, при достижении точки равновесия пружина полностью разжимается, и ее упругая потенциальная энергия становится равной нулю, а кинетическая энергия груза при этом становится максимальной. И наоборот, при максимальном сжатии или растяжении пружины ее упругая потенциальная энергия становится максимальной, а кинетическая энергия груза при этом становится равной нулю.
Качаемся вместе с маятником
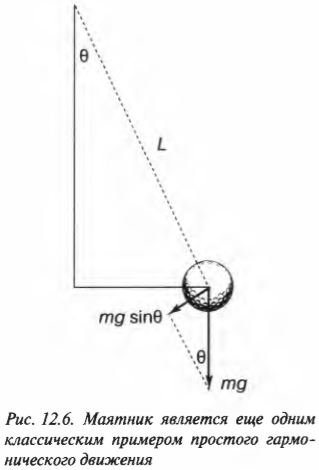
Еще одним типичным примером простого гармонического движения (кроме груза на пружине) является простой маятник, который показан на рис. 12.6.
Можно ли движение маятника описать математическими формулами простого гармонического движения, которые (выше в этой главе) использовались для описания движения груза на пружине? Да, и вот почему.
Дело в том, что на маятник, подвешенный на нити длиной ( L ) и отклоненный на угол ( theta ), действует сила гравитационного притяжения ( mathbf{F}=mmathbf{g} ). Перпендикулярная нити компонента силы создает сопротивление движению:
Момент этой компоненты силы
определяет угловое ускорение маятника ( alpha ):
Отсюда получаем формулу математического маятника:
(Математическим маятником называется идеализированная система, состоящая из невесомой и нерастяжимой нити, на которой подвешен груз с массой, сосредоточенной в одной точке. — Примеч. ред.)
При малых колебаниях, т.е. при малых значениях угла ( theta ); можно считать, что ( sin(theta)approxtheta ), и тогда прежняя формула приобретает следующий вид:
Эта формула связи ускорения и перемещения объекта очень похожа на прежние формулы простого гармонического движения груза на пружине и мячика по окружности (см. ранее в этой главе). Но прежде в эту формулу входило линейное перемещение, а теперь — угловое.
По аналогии с прежними формулами связи ускорения и перемещения объекта, совершающего простое гармоническое движение, коэффициент пропорциональности между ускорением и перемещением ( g/L ) равен квадрату циклической частоты ( omega^2 ). Отсюда получаем, что:
Далее, поскольку ( omega=2pi!f ) и ( omega=2pi/T ), то после подстановки предыдущего выражения в эти формулы получим:
и
Обратите внимание, что период качаний математического маятника не зависит от его массы!
Глава 12. Сжимаем пружины: простое гармоническое движение
3.6 (72%) 10 votes
Виды деформации
Деформация – это изменение формы, или размеров тела.
Есть несколько видов деформации:
- сдвиг;
- кручение;
- изгиб;
- сжатие/растяжение;
Деформация сдвига возникает, когда одни части тела сдвигаются относительно других его частей. Если подействовать на верхнюю часть картонного ящика, наполненного различными предметами, горизонтальной силой, то вызовем сдвиг верхней части ящика относительно его нижней части.
Сжатие или растяжение легко представить на примере прямоугольного куска тонкой резины. Такая деформация используется, к примеру, в резинках для одежды.
Примеры изгиба и кручения показаны на рисунке 1. Пластиковая линейка, деформированная изгибом, представлена на рис. 1а, а на рисунке 1б – эта же линейка, деформируемая кручением.
Рис. 1. пластиковая линейка, деформированная изгибом – а) и кручением – б)
В деформируемом теле возникают силы, имеющие электромагнитную природу и препятствующие деформации.
Расчет силы упругости
Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.
Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.
Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.
Разноцветная пластмассовая пружина-игрушка растяжению сопротивляется слабо
Закон Гука
Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал ( F_{text{упр}} ) силой упругости.
[ large boxed{ F_{text{упр}} = k cdot Delta L }]
Эту формулу назвали законом упругости Гука.
( F_{text{упр}} left( H right) ) – сила упругости;
( Delta L left(text{м} right) ) – удлинение пружины;
( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости).
Какие деформации называют малыми
Закон Гука применяют для малых удлинений (деформаций).
Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.
Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.
Как рассчитать коэффициент жесткости
Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему – по оси.
Рис. 4. Вес подвешенного на пружине груза уравновешивается силой упругости
Так как силы взаимно компенсируются, в правой части уравнения находится ноль.
[ large F_{text{упр}} — m cdot g = 0 ]
Подставим в это уравнение выражение для силы упругости
[ large k cdot Delta L — m cdot g = 0 ]
Прибавим к обеим частям вес груза и разделим на измеренное изменение длины (Delta L ) пружины. Получим выражение для коэффициента жесткости:
[ large boxed{ k = frac{ m cdot g }{Delta L} }]
(g) – ускорение свободного падения, оно связано с силой тяжести.
Расчет винтовых цилиндрических одножильных пружин растяжения и сжатия.
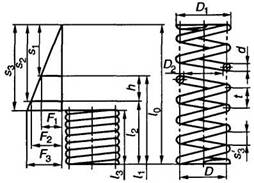
Рассмотрим расчет винтовых цилиндрических одножильных пружин растяжения и сжатия. Основные геометрические параметры винтовых цилиндрических пружин из проволоки круглого поперечного сечения (см. рис. 1): d — диаметр проволоки; Dн и D — наружный и средний диаметры пружины; c=D/d — индекс пружины; t — шаг пружины; α — угол подъема витков; L0 — длина развернутой пружины (без учета зацепов пружины). Податливость пружины прямо пропорциональна ее индексу c. Для увеличения податливости пружины индекс с принимают возможно большим; практически c=4…12.
Значения индекса с пружины принимают в зависимости от диаметра проволоки:
| d, мм | < 2,5 | 3…5 | 6…12 |
| c | 5…12 | 4…10 | 4…9 |
Рис. 1
С увеличением индекса пружины той же жесткости можно сократить ее длину путем увеличения диаметра, а с уменьшением индекса можно уменьшить диаметр пружины путем увеличения ее длины.
Рис. 2
В любом поперечном сечении витка пружины растяжения или сжатия при работе возникают (рис. 2, а) сила F, направленная по осевой линии пружины, и момент М=FD/2, вектор которого перпендикулярен осевой линии пружины. Сила F раскладывается на поперечную F1=F cos α и продольную F2=F sin α силы. При разложении момента М по осевой линии витка пружины и перпендикулярному ему направлению в поперечном сечении проволоки пружины возникают: крутящий T=FD cos α/2 и изгибающий Ми=FD sin α/2 моменты. Так как угол α<10…12°, то изгибающий момент Ми значительно меньше крутящего Т, а продольная сила F2 значительно меньше поперечной силы F1 но, как показывают расчеты, касательные напряжения сдвига значительно меньше касательных напряжений кручения, поэтому для упрощения расчета пружин на прочность обычно учитывают лишь крутящий момент T, при этом приближенно принимают cos α=1, т. е. T=М=FD/2. Таким образом, расчет винтовой цилиндрической пружины растяжения или сжатия из проволоки круглого поперечного сечения производят по формуле
где τ — расчетное максимальное напряжение в поперечных сечениях витков пружины; [τ] — допускаемое напряжение для проволоки пружины; k — коэффициент влияния на напряжение кривизны витков и поперечной силы; F — максимальная растягивающая или сжимающая сила. Формулой пользуются при проверочном расчете пружины, когда ее размеры известны.
Значения коэффициента k принимают в зависимости от индекса пружины:
| c | 4 | 5 | 6 | 8 | 10 | 12 |
| k | 1,37 | 1,29 | 1,24 | 1,17 | 1,14 | 1,11 |
Рис. 3
Допускаемое напряжение [τ] пружин при статических нагрузках можно принимать по графикам (рис. 3), где отдельные кривые относятся к пружинам из проволоки:
- 1 — вольфрамовой и рояльной;
- 2 — хромованадиевой;
- 3 — углеродистой, закаленной в масле;
- 4 — углеродистой холоднотянутой;
- 5 — моиель-металла;
- 6 — фосфористой бронзы;
- 7 — специальной латуни.
При пульсирующей нагрузке с небольшим числом циклов допускаемые напряжения [τ] следует принимать в 1,25…1,5 раза ниже, чем по графикам.
При проектировочном расчете пружины диаметр проволоки
значением индекса с пружины задаются. Диаметр d проволоки, вычисленный по формуле, окончательно согласовывают с соответствующим ГОСТом для пружинной проволоки.
Средний диаметр D пружины и наружный диаметр DH определяют по формулам
и
При расчетах различают следующие силы пружины (см. рис. 1 , а, б): при предварительной деформации — F1 при рабочей деформации (соответствует наибольшему принудительному перемещению подвижного звена в механизме) — F2; при максимальной деформации «(допускаемой) — F3. Соответственно в формулах F=F3.
Обычно пружину устанавливают с действующей на нее начальной нагрузкой F1=(0,1…0,5)F2. Максимальная сила пружины F3=(1,05..,1,66)F2. При изменении силы пружины от F1 до F2 жесткость пружины
где h — рабочий ход пружины, значение которого назначают или вычисляют по условиям работы механизма. Жесткость одного витка пружины где G — модуль сдвига материала проволоки пружины. Для стали G=80000 МПа и, следовательно, для стальной пружины где С1 — в Н/мм; d — в мм.
Число рабочих витков пружины
Полное число витков
где n2=1,5…2 — число опорных витков.
Деформация пружины
Подставив в формулу вместо F силы F1, F2, F3, получим деформации: λ1 — предварительную, λ2 — рабочую и λ3 — максимальную. Максимальная деформация одного витка пружины
Шаг пружины в ненагруженном состоянии: для пружины сжатия
для пружины растяжения
Высота пружины при максимальной деформации
где n3 — число зашлифованных витков. Высота пружины в свободном состоянии для пружины сжатия для пружины растяжения
Высоту пружины при предварительной и рабочей деформации легко определить из (рис. 1, а, б). Длина развернутой пружины (без учета зацепов пружины растяжения)
Более подробный геометрический расчет винтовых цилиндрических пружин сжатия и растяжения из стальной проволоки круглого сечения дан в ГОСТ 13765-68.
Соединяем две одинаковые пружины
В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.
Параллельное соединение пружин
На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину (Delta L). Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.
Рис. 5. Две пружины, соединенные параллельно, деформируются меньше одной такой пружины
Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом (mg).
Одна пружина:
[ large k_{1} cdot Delta L = m cdot g ]
Две параллельные пружины:
[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= m cdot g ]
Так как правые части уравнений совпадают, левые части тоже будут равны:
[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= k_{1} cdot Delta L ]
Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:
[ large k_{text{параллел}} cdot frac{1}{2}= k_{1} ]
Умножим обе части полученного уравнения на число 2:
[ large boxed{ k_{text{параллел}} = 2k_{1} } ]
Коэффициент жесткости (k_{text{параллел}}) двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной
Последовательное соединение пружин
Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину (Delta L). Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.
Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.
На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину (Delta L).
Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений
Рис. 6. Система, состоящая из двух одинаковых пружин, соединенных последовательно, деформируются больше одной пружины
Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом (mg).
Одна пружина:
[ large k_{1} cdot Delta L = m cdot g ]
Две последовательные пружины:
[ large k_{text{послед}} cdot Delta L cdot 2 = m cdot g ]
Так как правые части уравнений совпадают, левые части тоже будут равны:
[ large k_{text{послед}} cdot Delta L cdot 2 = k_{1} cdot Delta L ]
Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:
Not Found
Пример
1. Пружина сжатия. Дано: F1 = 20 Н; F2 = 80Н; h = 30мм; D1 = 10÷
12мм; Vmax = 5 м/с; NF ≥ 1∙107. Пользуясь табл. 1, убеждаемся, что при заданной выносливости пружину следует отнести к классу I. По формуле (2), пользуясь интервалом значений 8 от 0,05 до 0,25 (формула (1)], находим граничные значения силы F3, a именно:
F3 = F2/(1-0,05) ÷ F2/(1-0,25)=84 ÷ 107 Н
В интервале от 84 до 107 Н (ГОСТ 13766—86) пружин класса I, разряда 1 имеются следующие силы F3 ; 85; 90; 95; 100 и 106 Н (табл. 11). Исходя из заданных размеров диаметра и стремления обеспечить наибольшую критическую скорость, останавливаемся на витке со следующими данными (номер позиции 355): F3 = 106 H; d = 1,80 мм; D1 = 12 мм; с1 =97,05 Н/мм; s′3 = 1,092 мм. Учитывая, что для пружин класса I норма напряжений τ = 0,3Rm (см. табл. 2), находим, что для найденного диаметра проволоки из углеродистой холоднотянутой стали расчетное напряжение τ33 ≈ 0,3 · 2100 = = 630 Н/мм2. Принадлежность к классу I проверяем путем определения отношения vmax / vk , для чего предварительно определяем критическую скорость по формуле (5)при d = 0,25:
Полученная величина указывает на отсутствие соударения витков, и, следовательно, выбранная пружина удовлетворяет заданным условиям, но так как пружины класса II относятся к разряду ограниченной выносливости, то следует учитывать комплектацию машины запасными пружинами с учетом опытных данных. Определение остальных размеров производим по формулам табл. 10. По формуле (6) находим жесткость пружины c = (F2-F1)/h= (80-20)/30=2.0 Н/мм. Число рабочих витков пружины определяем по формуле (7): n = c1/c = 36,58/2,0 = 18,29 ≈ 18,5 Уточненная жесткость имеет значение c = c1/n = 36,58/18,5= 1,977 ≈ 2,0 Н/мм. При полутора нерабочих витках полное число витков находим по формуле (8): n1 = n + n2 = 18,5 + 1,5 = 20 По формуле (9) определяем средний диаметр пружины D =
11,5 — 1,40 = 10,1 мм. Деформации, длины и шаг пружины вычисляем по формулам [(11)-(18)]:
На этом определение размеров пружины и габарита узла (размер ℓ1) заканчивается. Следует отметить, что некоторое увеличение выносливости может быть достигнуто при использовании пружины с большей величиной силы F3 , чем найденная в настоящем примере. С целью выяснения габаритов, занимаемых такой пружиной, проделаем добавочный анализ: остановимся, например, на витке со следующими данными по ГОСТ 13770-86 (позиция 313); F3 = 106 H; d = 1,4 мм; D1 = 10,5 мм; с1 =50,01 Н/мм; s′3 = 2,119 мм. Находим τ = 1150 Н/мм2 и производим расчет в той же последовательности: d = 1- (F2/F3)=1- (80/106) = 0,245; vk= (1150 · 0,245) /35,1 = 8,05 м/с, vmax / vk = 5,0/8,05 =0,622 Очевидно, что у этой пружины создается большой запас на несоударяемость витков. Далее в рассмотренном ранее порядке находим n=50,01/2,0= 25,01 ≈ 25,0 Уточненная жесткость с =50,01/25,0
≈ 2,0 Н/мм;
Таким образом, устанавливаем, что применение пружины с более высокой силой F3
хотя и привело к большему запасу на несоударяемость витков, но оно сопровождается увеличением габарита узла (размер ℓ1) на 15,3 мм. Можно показать, что если выбрать виток с большим диаметром, например D1 = 16 мм (ГОСТ 13770-86, номер позиции 314), то тогда потребуется расширить узел по диаметру, но при этом соответственно уменьшится размер ℓ1.
Пример 2. Пружина сжатия. Дано: F1 = 100 Н; F2 =
250 Н; h
=
100 мм; D1 = 15 ÷ 25 мм; vmax = 10 м/с Независимо от заданной выносливости на основании формулы (5) можно убедиться, что при значениях d, меньших 0,25 [формула (1)], все одножильные пружины, нагружаемые со скоростью vmax более 9,4 м/с, относятся к III классу. По формуле (2) с учетом диапазона значений d для пружин класса III от 0,1 до 0,4 [формула (1)] находим границы сил
;
F3=F2/(1-0,1)÷ F2/(1-0,4) = 250/0,9 ÷ 250/0,6 =278÷417 Н Верхние значения силы F3
,
как видно из табл. 2 ГОСТ 13764—86, не могут быть получены из числа одножильных конструкций, поэтому, учитывая коэффициенты d = 0,15 ÷ 0,40 [формула (1)] для трехжильных пружин, устанавливаем новые пределы F3, по формуле (2): F3
=
294÷417 Н. Для указанного интервала в ГОСТ 13774-86 имеются витки со следующими силами
F3:
300; 315; 335; 375 и 400 (табл. 16а). Исходя из заданных размеров диаметра и наименьших габаритов узла, предварительно останавливаемся на витке со следующими данными (номер позиции 251): F3 = 300 Н; d = 1,4 мм; d1
=
3,10 ; D1
=
17 мм; с1 = 50,93 Н/мм; s′3= 5,900 мм. Согласно ГОСТ 13764—86 для пружин класса III τ3 = 0,6 Rm
.
Используя ГОСТ 9389-75, определяем напряжение для найденного диаметра проволоки τ3 = 0,6 · 2300 = 1380 МПа. Принадлежность к классу проверяем путем определения величины отношения vmax / vk для чего предварительно находим d и критическую скорость по формулам (1), (2) и (5а): d = 1-(F2/F3) = 1-(250/300)= 0,167; vk= (1380 · 0,167)/32,4 = 7 м/с vmax / vk= 10,0 /7,0=1,43 > 1. Полученное неравенство свидетельствует о наличии соударения витков и о принадлежности пружины к классу III. Определение остальных параметров производится по формулам табл. 10. По формуле (6) находим жесткость c = (F2- F1) / h = 250-100/100= 1,5 Н/мм. Число рабочих витков пружины вычисляют по формуле (7): n = c1/c = 50,9/1,5 = 33,9 ≈ 34,0 Уточненная жесткость
с
= c1 /n = 50,9/34,0 = 1,49 ≈ 1,5 Н/мм. Полное число витков находят по формуле (8): n1 = n + 1,5 = 34,0 + 1,5 = 35,5 . По формуле (9а) определяют средний диаметр пружины D
=
D1 — d1
=
17 — 3,10 = 13,90 мм. Деформации, длины и шаг пружины находят по формулам в табл. 10 [формулы (10а), (11)-(18а)]: s1 = F1/c = 100/1,5 = 66,7 мм; s2 = F2/c = 250/1,5 = 166,7 мм; s3 = F3/c = 300/1,5 =200 мм ; i = D/d1=13,90/3,10 =4,5; ℓ3
= (n1+1) d1∆ = (35,5 + 1) 3,10 · 1,021 = 115,5 мм; ℓ0=
ℓ3 + s3 = 115,5 + 200 = 315,5 мм; ℓ1 =ℓ0 — s1 = 315,5 — 66,7 = 248,8 мм; ℓ2 =ℓ0 — s2
=
315,5 — 166,7 = 148,8 мм
t
= s’3
+
d1∆ = 5,9 + 3,10 · 1,021 = 9,19 мм.Проанализируем пружины, соответствующие трем ближайшим значениям F3
,
взятым из ГОСТ 13774—86 (пружины класса III, разряда 1) для рассмотренного случая (табл. 16а). Вычисления, проделанные в аналогичном порядке, показывают, что для трех соседних сил F3 образуется шесть размеров пружин, удовлетворяющих требованиям по величине наружного диаметра. Сведения о таких пружинах приведены ниже.
| F3,H | 300 | 315 | 335 | |||
| d , мм | 1,4 | 1,6 | 1,4 | 1,6 | 1,4 | 1,6 |
| d1 , мм | 3,10 | 3,50 | 3,10 | 3,50 | 3,10 | 3,50 |
| D1 , мм | 17,0 | 24,0 | 16,0 | 22,0 | 15,0 | 21,0 |
| vmax / vk | 1,43 | 1,50 | 1,16 | 1,21 | 0,942 | 0,984 |
| ℓ0, мм | 317,0 | 273,9 | 355,1 | 309,0 | 405,1 | 337,0 |
| ℓ1, мм | 250,4 | 207,2 | 288,4 | 242,3 | 338,4 | 270,3 |
| ℓ2, мм | 150,4 | 107,2 | 188,4 | 142,3 | 238,4 | 170,3 |
| n1, мм | 36,0 | 20,0 | 44,5 | 27,0 | 56,0 | 31,0 |
| V,мм3 | 57000 | 93000 | 58000 | 92000 | 60000 | 93000 |
Из этих данных следует, что с возрастанием F3 уменьшается отношение vmax / vk и, в частности, может быть устранено соударение витков, но вместе с этим возрастают габариты по размерам ℓ1. С возрастанием диаметров пружин габариты по размерам ℓ1 уменьшаются, однако существенно возрастают объемы пространств, занимаемые пружинами. Следует отметить, что если бы для рассматриваемого примера, в соответствии с требованиями распространенных классификаций, была выбрана пружина класса I, то при одинаковом диаметре гнезда (
D1 ≈ 18 мм) даже самая экономная из них потребовала бы длину гнезда ℓ1 = 546 мм, т. е. в 2,2 раза больше, чем рассмотренная выше. При этом она была бы в 11,5 раза тяжелее и, вследствие малой критической скорости (vk = 0,7 м/с), практически неработоспособной при заданной скорости нагружения 10 м/с.
Пример
3. Пружина растяжения. Дано: F1 = 250 Н; F2 = 800 Н; h = 100 мм; D1 = 28 ÷ 32 мм; NF ≥ 1· 105.На основании ГОСТ 13764—86 по величине
NF
устанавливаем, что пружина относится к классу II (см. табл. 1.) По формуле (2) находим силы
F3
, cоответствующие предельной деформации: F3 = F2/(1-0,05) ÷ F2/(1-0,10) =842÷ 889 Н. В интервале сил 842—889 Н в ГОСТ 13770—86 для пружин класса II, разряда 1 (номер пружины 494) имеется виток со следующими параметрами: F3 = 850 Н; D1
=
30 мм; d = 4,5 мм; с1 = 242,2 Н/мм; s’3 =3,510 мм (см. табл. 14). По заданным параметрам с помощью формулы (6) определяем жесткость пружины:
с = (
F2- F1)/h = (800-250)/100 = 5,5 H/мм. Число рабочих витков находим по формуле (7): n = c1/c = 242,2 / 5,5 ≈ 44.Деформации и длины пружины вычисляют по формулам [(11)-(17а)]: s1=F1/c = 250/5,5 =45,5 мм; s2 = F2/c = 800/5,5 = 145,5 мм; s3 = F3/c = 850/5,5 = 154,5 мм ; ℓ’0
=
(n +1)d= (44+1)4,5 = 202,5 мм; ℓ1 =ℓ0 + s1 = 202,5 + 45,5 = 248,0 мм; ℓ2 =ℓ0 + s2
=
202,5 +145,5 = 348,0 мм; ℓ3 =ℓ0 + s3
=
202,5 +154,5 = 357,0 мм. Размер ℓ2 с учетом конструкций зацепов определяет длину гнезда для размещения пружины растяжения в узле. Размер ℓ3 с учетом конструкций зацепов ограничивает деформацию пружины растяжения при заневоливании. Трехжильные пружины (угол свивки 24º). Жесткость s1=F1/s1 = F2/s2 =F3/s3 = 30000d4k/D3n = H/мм; k= (1+ 0,333· sin22b)/ cosb b = arctg (0,445 i / i+1) , i = D/d1Напряжение τ3 = 1,82 F3 i /d2МПа Полученные значения жесткости должны совпадать с вычисленными по формуле (6). Полученные значения напряжений должны совпадать с указанными в ГОСТ 13764—86 для соответствующих разрядов с отклонениями не более + 10
%.
404 Not Found
The requested URL /bottom.php was not found on this server.
Additionally, a 404 Not Found error was encountered while trying to use an ErrorDocument to handle the request.
Потенциальная энергия сжатой или растянутой пружины
Пружина сжатая (левая часть рис. 7), или растянутая (правая часть рис. 7) на длину (Delta L ) обладает потенциальной возможностью вернуться в первоначальное состояние и при этом совершить работу, например, по перемещению груза. В таких случаях физики говорят, что пружина обладает потенциальной энергией.
Рис. 7. Деформированная — сжатая или растянутая пружина обладает потенциальной энергией
Эта энергия зависит от коэффициента жесткости пружины и от ее удлинения (или укорочения при сжатии).
Чем больше жесткость (упругость) пружины, тем больше ее потенциальная энергия. Увеличив удлинение пружины получим повышение ее потенциальной энергии по квадратичному закону:
[ large boxed{ E_{p} = frac{k}{2} cdot left( Delta L right)^{2} }]
( E_{p} left( text{Дж} right)) – потенциальная энергия сжатой или растянутой пружины;
( Delta L left(text{м} right) ) – удлинение пружины;
( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости) пружины.
Плоские спиральные пружины
Плоские спиральные пружины изготавливают из тонкой высококачественной углеродистой ленты. Применяют в качестве заводных, аккумулирующих энергию, что возможно благодаря высокой гибкости ленты, позволяющей иметь большой угол поворота валика до нескольких десятков оборотов. Пружины обычно помещают в барабан для обеспечения смазки и придания им определённых внешних размеров. В неответственныхмеханизмах используютспиральные пружины и без барабанов. Внутренний конец пружины крепят, как правило, к валику, а наружный к барабану.
КПД спиральных пружин определяется отношением работы, производимой пружиной при развёртывании к работе, затрачиваемой на заводку, и колеблется в пределах 0,6-0,7 в зависимости от смазки. Следует избегатьпружин повышенной толщины ленты, так как они работают не плавно, что ведёт к перенапряжению в материале пружины и к её поломке. Толщину ленты пружины b
следует выбирать из условия
, , где r
–
радиусвалика, на который наматывается пружина. Уравнение оси пружиннойленты, плотно навитой на валик, в полярных координатах ,где ρ–текущий полярный радиус, φ- полярный угол. Начальный радиус ρ1 соответствует углу φ1.Конечный радиус ρ2 соответствуетуглуφ2 = φ1 +2n, где n—число оборотов спирали пружины равное .
Рабочая длина ленты пружиныL
= .
При жёстком закреплении концов пружины в корпусе и на валике, она испытывает чистый изгиб. Напряжение изгиба ленты ,где h
–
высота ленты, М
– изгибающиймомент. Отсюда требуемая высота ленты
.
Суммарный угол закручивания ,где J
– момент инерции сечения ленты.
Максимальный момент на валике пружины ,где nр
– максимальное расчётноечисло витков пружины.
nр =n2 – n1 , где n2
– число витков заведенной пружины в барабане, n1 – число витков свободной пружины (вне барабана).
Рабочее число оборотов барабанаφпри расчёте следует увеличивать на 0,5-1,5 для покрытия потерь на трение.
Минимальный момент на валике пружины , где np.min = n – n1 ; n –число витков спущенной пружины (в барабане).
Тарельчатые пружины
выбирают равным 2-3, а угол подъема образующей конуса 2-60. В соответствии с ГОСТ 3957 тарельчатые пружины выполняют наружным диаметром 28-300мм, толщиной
s = 1-20мм
, высотой конуса
f= 0,6-9мм
. Рабочая нагрузка пружин до 520 кН. Упругая осадка пружин допускается до 0,8f.
Тарельчатые пружины, имея небольшие габариты по высоте, представляют значительные преимущества по сравнению с другими пружинами для больших нагрузок при высокой потребной жёсткости, что и определяет область их применения. На рис. б показано обычное выполнение пакета пружин для максимальной податливости. На рис. в
показан пакет с тройным набором односторонних пружин для повышения несущей способности. На рис.
г
пакет пружин с промежуточными шайбами, более активно демпфирующих энергию колебаний.
Тарельчатые пружины штампуют, как правило, из листовой кремнистой стали 60С2А. Для повышения несущей способности их обжимают пере закалкой до полного распрямления, в результате чего в них возникают остаточные напряжения обратного знака.
Точный расчёт пружин довольно сложен и их обычно подбирают по таблицам ГОСТа 3957.
Приближённая зависимость между осевой силой Р
и осевым сжатием
λ1
одного элемента пружины , где
E и μ
– модуль упругости и коэффициент Пуассона материала пружины;
А
– коэффициент, принимаемый по приведенному графику.
Наибольшее напряжение сжатия на внутренней кромке пружины .
Коэффициенты К, К0, К1
также принимают по графику. Допускаемые напряжения по приведенной формуле выбирают весьма высокими, достигающими при статической нагрузке для кремнистой стали
1600 – 2000 МПа
.
Выводы
- Упругие тела – такие, которые сопротивляются деформации;
- Во время деформации в упругих телах возникает сила, она препятствует деформации, ее называют силой упругости;
- Деформация – изменение формы, или размеров тела;
- Есть несколько видов деформации: изгиб, кручение, сдвиг, растяжение/сжатие;
- Удлинение пружины – это разность ее конечной и начальной длин;
- Сжатая или растянутая пружина обладает потенциальной энергией (вообще, любое упруго деформированное тело обладает потенциальной энергией);
- Система, состоящая из нескольких одинаковых пружин, будет иметь коэффициент жесткости, отличный от жесткости единственной пружины;
- Если пружины соединяют параллельно – коэффициент жесткости системы увеличивается;
- А если соединить пружины последовательно – коэффициент жесткости системы уменьшится.