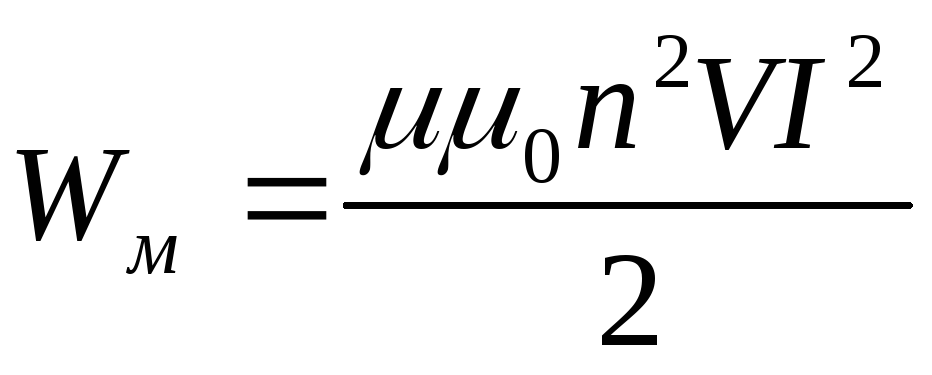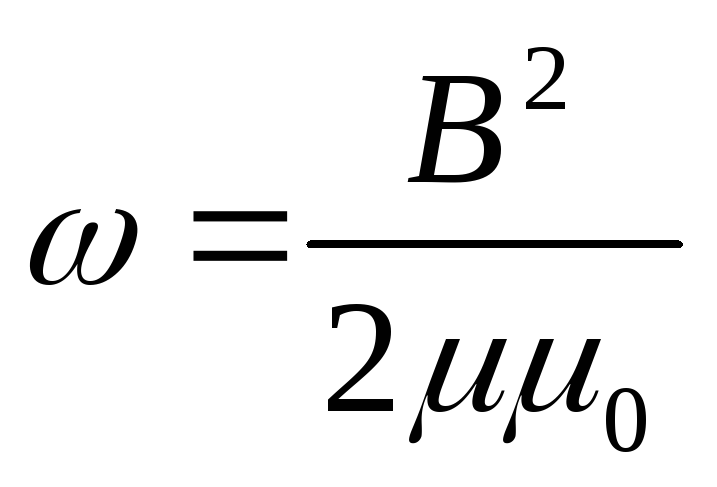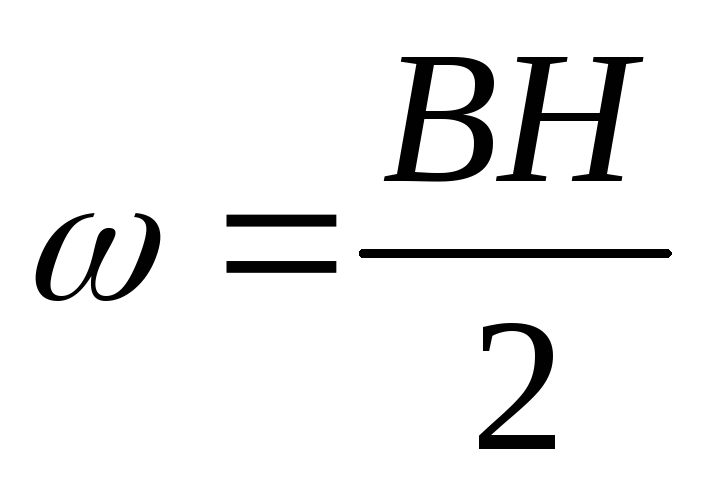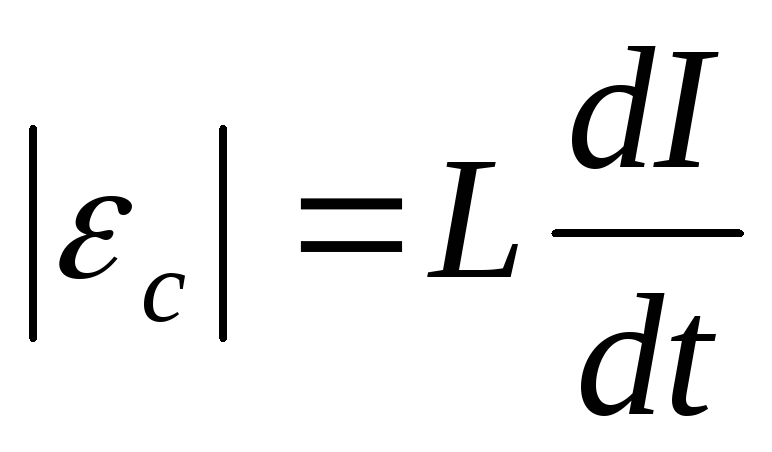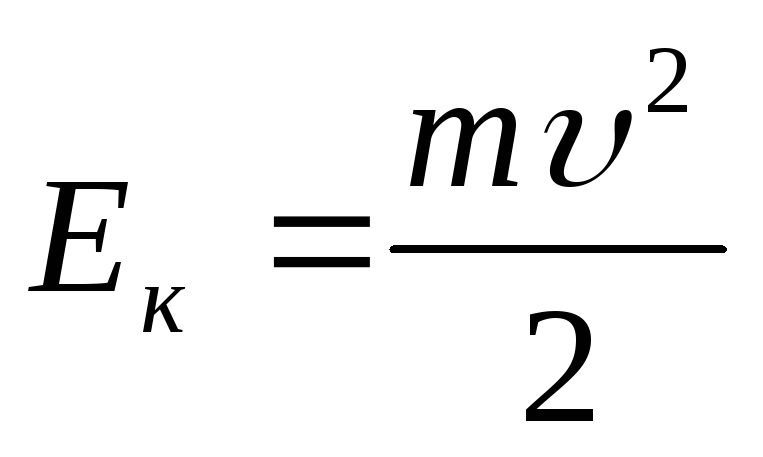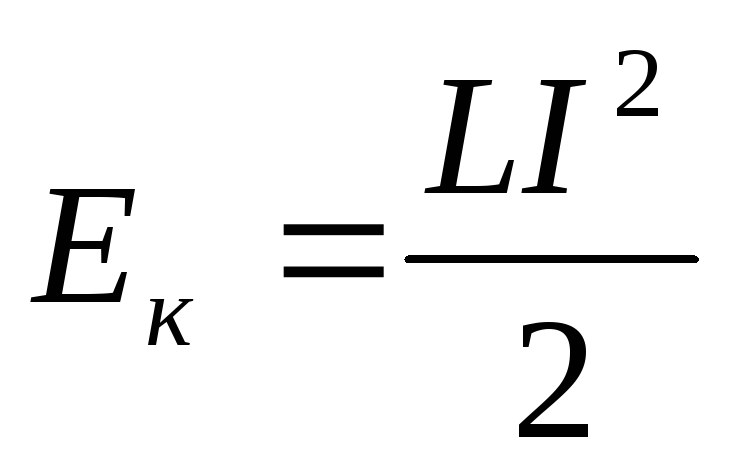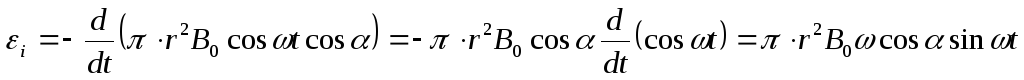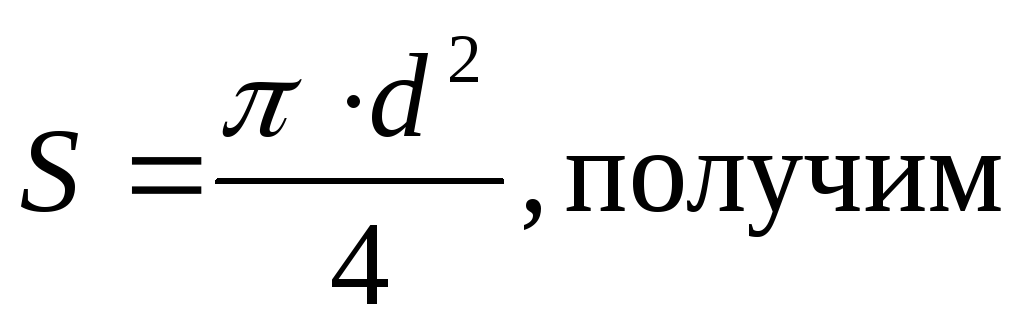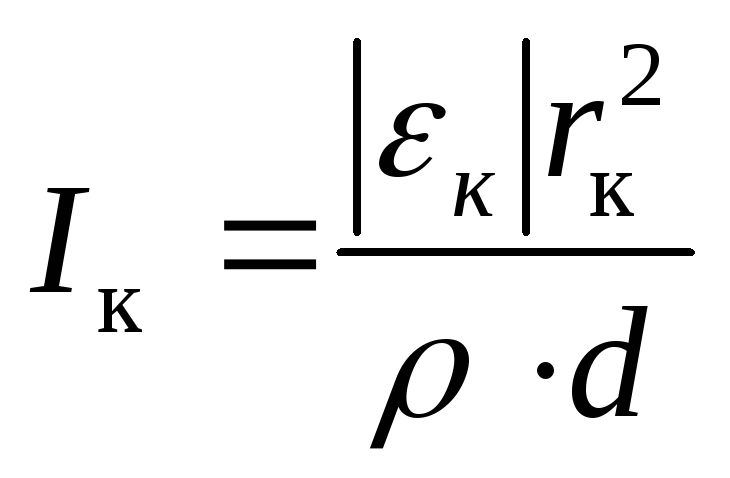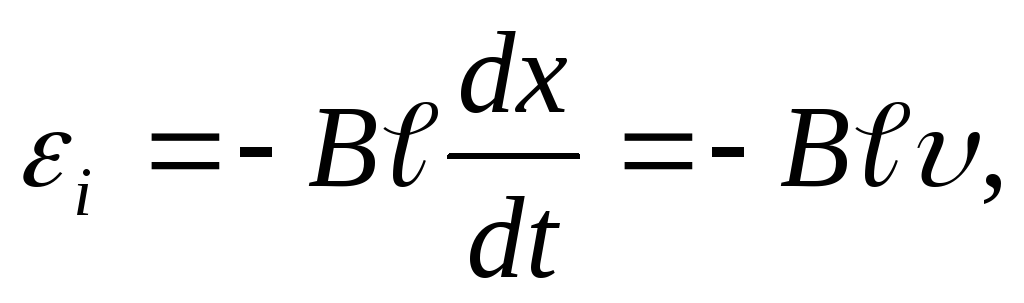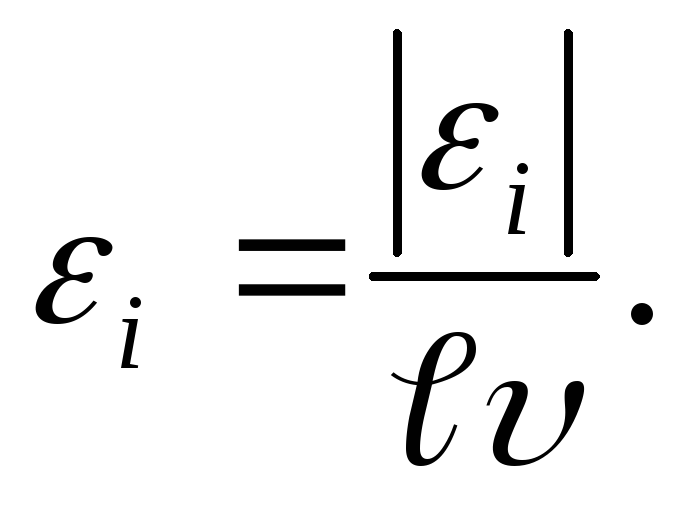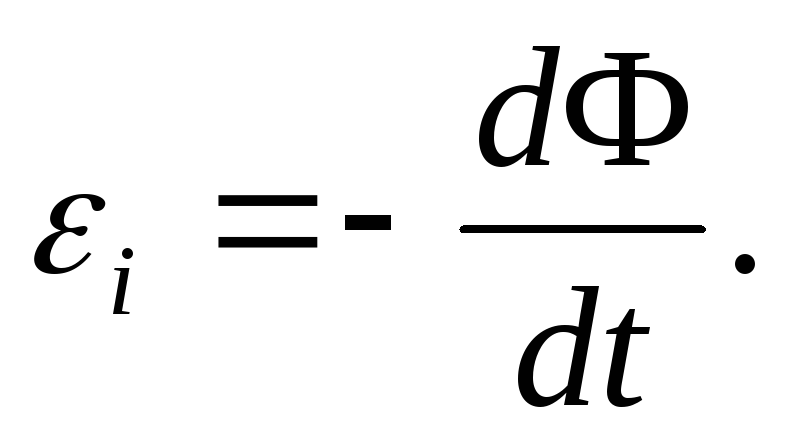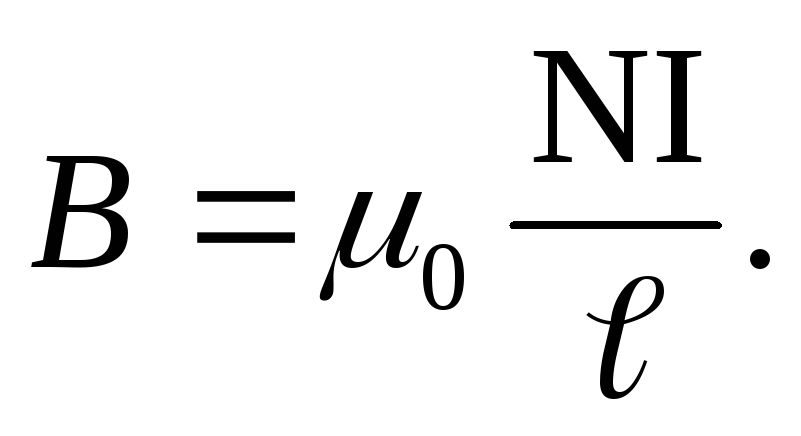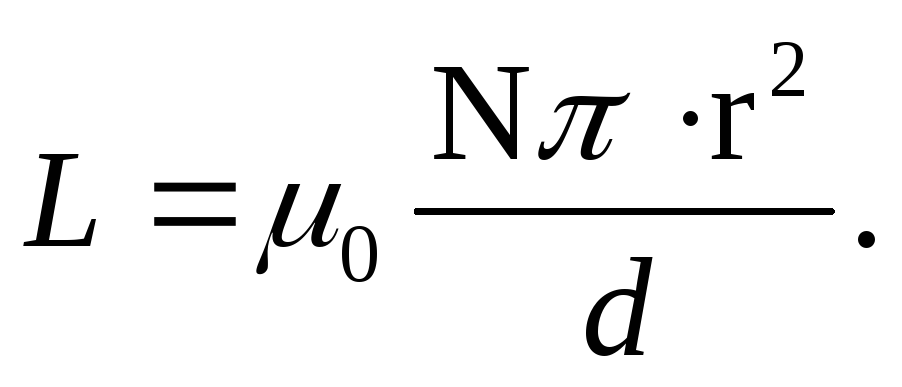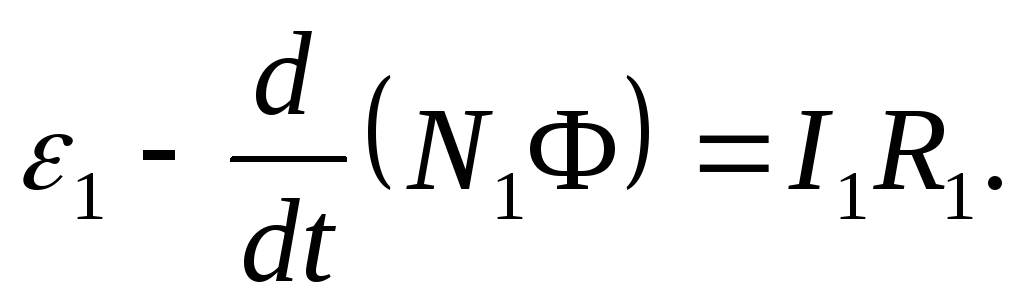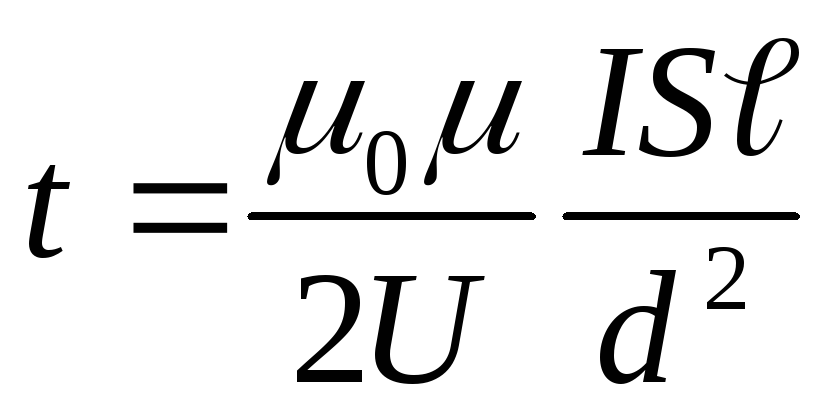Как найти максимальную энергию в катушке - Исправление недочетов и поиск решений вместе с Examum.ru

Задание:

Найти максимальную плотность энергии магнитного поля внутри катушки (без сердечника) идеального контура Томсона, если дифференциальное уравнение электромагнитных колебаний в контуре имеет вид q» + 10⁸ q = 0. Конденсатор емкостью С = 10^–6 Ф был заряжен до разности потенциалов Δφ₀ = 100 В, а начальный ток в контуре был равен нулю. Число витков катушки контура на единицу ее длины n = 10³ 1/м.

Решение:

Источник

Самоиндукция

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: самоиндукция, индуктивность, энергия магнитного поля.

Самоиндукция является частным случаем электромагнитной индукции. Оказывается, что электрический ток в контуре, меняющийся со временем, определённым образом воздействует сам на себя.

Ситуация 1 .Предположим, что сила тока в контуре возрастает. Пусть ток течёт против часовой стрелки; тогда магнитное поле этого тока направлено вверх и увеличивается (рис. 1).

Рис. 1. Вихревое поле препятствует увеличению тока

Таким образом, наш контур оказывается в переменном магнитном поле своего собственного тока. Магнитное поле в данном случае возрастает (вместе с током) и потому порождает вихревое электрическое поле, линии которого направлены по часовой стрелке в соответствии с правилом Ленца.

Как видим, вихревое электрическое поле направлено против тока, препятствуя его возрастанию; оно как бы «тормозит» ток. Поэтому при замыкании любой цепи ток устанавливается не мгновенно — требуется некоторое время, чтобы преодолеть тормозящее действие возникающего вихревого электрического поля.

Ситуация 2 . Предположим теперь, что сила тока в контуре уменьшается. Магнитное поле тока также убывает и порождает вихревое электрическое поле, направленное против часовой стрелки (рис. 2).

Рис. 2. Вихревое поле поддерживает убывающий ток

Теперь вихревое электрическое поле направлено в ту же сторону, что и ток; оно поддерживает ток, препятствуя его убыванию.

Как мы знаем, работа вихревого электрического поля по перемещению единичного положительного заряда вокруг контура — это ЭДС индукции. Поэтому мы можем дать такое определение.

Явление самоиндукции состоит в том, что при изменении силы тока в контуре возникает ЭДС индукции в этом же самом контуре.

При возрастании силы тока (в ситуации 1) вихревое электрическое поле совершает отрицательную работу, тормозя свободные заряды. Стало быть, ЭДС индукции в этом случае отрицательна.

При убывании силы тока (в ситуации 2) вихревое электрическое поле совершает положительную работу, «подталкивая» свободные заряды и препятствуя убыванию тока. ЭДС индукции в этом случае также положительна (нетрудно убедиться в том, что знак ЭДС индукции, определённый таким образом, согласуется с правилом выбора знака для ЭДС индукции, сформулированным в листке «Электромагнитная индукция»).

Индуктивность

Мы знаем, что магнитный поток, пронизывающий контур, пропорционален индукции магнитного поля: . Кроме того, опыт показывает, что величина индукции магнитного поля контура с током пропорциональна силе тока: B sim I . Стало быть, магнитный поток через поверхность контура, создаваемый магнитным полем тока в этом самом контуре, пропорционален силе тока: .

Коэффициент пропорциональности обозначается и называется индуктивностью контура:

(1)

Индуктивность зависит от геометрических свойств контура (формы и размеров), а также от магнитных свойств среды, в которую помещён контур (Улавливаете аналогию? Ёмкость конденсатора зависит от его геометрических характеристик, а также от диэлектрической проницаемости среды между обкладками конденсатора). Единицей измерения индуктивности служит генри (Гн).

Допустим, что форма контура, его размеры и магнитные свойства среды остаются постоянными (например, наш контур — это катушка, в которую не вводится сердечник); изменение магнитного потока через контур вызвано только изменением силы тока. Тогда , и закон Фарадея приобретает вид:

$mathcal E_i = -L frac{displaystyle Delta I}{displaystyle Delta t vphantom{1^a}} = -LI.$ (2)

Благодаря знаку «минус» в (2) ЭДС индукции оказывается отрицательной при возрастании тока и положительной при убывании тока, что мы и видели выше.

Рассмотрим два опыта, демонстрирующих явление самоиндукции при замыкании и размыкании цепи.

Рис. 3. Самоиндукция при замыкании цепи

В первом опыте к батарейке подключены параллельно две лампочки, причём вторая — последовательно с катушкой достаточно большой индуктивности (рис. 3).

Ключ вначале разомкнут.

При замыкании ключа лампочка 1 загорается сразу, а лампочка 2 — постепенно. Дело в том, что в катушке возникает ЭДС индукции, препятствующая возрастанию тока. Поэтому максимальное значение тока во второй лампочке устанавливается лишь спустя некоторое заметное время после вспыхивания первой лампочки.

Это время запаздывания тем больше, чем больше индуктивность катушки. Объяснение простое: ведь тогда больше будет напряжённость вихревого электрического поля, возникающего в катушке, и потому батарейке придётся совершить большую работу по преодолению вихревого поля, тормозящего заряженные частицы.

Во втором опыте к батарейке подключены параллельно катушка и лампочка (рис. 4). Сопротивление катушки много меньше сопротивления лампочки.

Рис. 4. Самоиндукция при размыкании цепи

Ключ вначале замкнут. Лампочка не горит — напряжение на ней близко к нулю из-за малости сопротивления катушки. Почти весь ток, идущий в неразветвлённой цепи, проходит через катушку.

При размыкании ключа лампочка ярко вспыхивает! Почему? Ток через катушку начинает резко убывать, и возникает значительная ЭДС индукции, поддерживающая убывающий ток (ведь ЭДС индукции, как видно из (2), пропорциональна скорости изменения тока).

Иными словами, при размыкании ключа в катушке появляется весьма большое вихревое электрическое поле, разгоняющее свободные заряды. Под действием этого вихревого поля через лампочку пробегает импульс тока, и мы видим яркую вспышку. При достаточно большой индуктивности катушки ЭДС индукции может стать существенно больше ЭДС батарейки, и лампочка вовсе перегорит.

Лампочку-то, может, и не жалко, но в промышленности и энергетике данный эффект является серьёзной проблемой. Так как при размыкании цепи ток начинает уменьшаться очень быстро, возникающая в цепи ЭДС индукции может значительно превышать номинальные напряжения и достигать опасно больших величин. Поэтому в агрегатах, потребляющих большой ток, предусмотрены специальные аппаратные меры предосторожности (например, масляные выключатели на электростанциях), препятствующие моментальному размыканию цепи.

Электромеханическая аналогия

Нетрудно заметить определённую аналогию между индуктивностью в электродинамике и массой в механике.

1. Чтобы разогнать тело до заданной скорости, требуется некоторое время — мгновенно изменить скорость тела не получается. При неизменной силе, приложенной к телу, это время тем больше, чем больше масса тела.

Чтобы ток в катушке достиг своего максимального значения, требуется некоторое время; мгновенно ток не устанавливается. Время установления тока тем больше, чем больше индуктивность катушки.

2. Если тело налетает на неподвижную стену, то скорость тела уменьшается очень быстро. Стена принимает на себя удар, и его разрушительное действие тем сильнее, чем больше масса тела.

При размыкании цепи с катушкой ток уменьшается очень быстро. Цепь принимает на себя «удар» в виде вихревого электрического поля, порождаемого убывающим магнитным полем тока, и этот «удар» тем сильнее, чем больше индуктивность катушки. ЭДС индукции может достичь столь больших величин, что пробой воздушного промежутка выведет из строя оборудование.

На самом деле эти электромеханические аналогии простираются довольно далеко; они касаются не только индуктивности и массы, но и других величин, и оказываются весьма полезными на практике. Мы ещё поговорим об этом в листке про электромагнитные колебания.

Энергия магнитного поля

Вспомним второй опыт с лампочкой, которая не горит при замкнутом ключе и ярко вспыхивает при размыкании цепи. Мы непосредственно наблюдаем, что после размыкания ключа в лампочке выделяется энергия. Но откуда эта энергия берётся?

Берётся она, ясное дело, из катушки — больше неоткуда. Но что за энергия была запасена в катушке и как вычислить эту энергию? Чтобы понять это, продолжим нашу электромеханическую аналогию между индуктивностью и массой.

Чтобы разогнать тело массы из состояния покоя до скорости , внешняя сила должна совершить работу . Тело приобретает кинетическую энергию, которая равна затраченной работе: .

Чтобы после замыкания цепи ток в катушке индуктивности достиг величины , источник тока должен совершить работу по преодолению вихревого электрического поля, направленного против тока. Работа источника идёт на создание тока и превращается в энергию магнитного поля созданного тока. Эта энергия запасается в катушке; именно эта энергия и выделяется потом в лампочке после размыкания ключа (во втором опыте).

Индуктивность служит аналогом массы ; сила тока является очевидным аналогом скорости . Поэтому естественно предположить, что для энергии магнитного поля катушки может иметь место формула, аналогичная выражению для кинетической энергии:

$W = frac{displaystyle LI^2}{displaystyle 2 vphantom{1^a}}.$ (3)

(тем более, что правая часть данной формулы имеет размерность энергии — проверьте!).

Формула (3) действительно оказывается справедливой. Уметь её выводить пока не обязательно, но если вы знаете, что такое интеграл, то вам не составит труда понять следующие рассуждения.

Пусть в данный момент сила тока через катушку равна . Возьмём малый промежуток времени . В течение этого промежутка приращение силы тока равно ; величина считается настолько малой, что много меньше, чем .

За время по цепи проходит заряд dq=Idt . Вихревое электрическое поле совершает при этом отрицательную работу:

$dA_B = mathcal E_i dq = mathcal E_i Idt = -L frac{displaystyle dI}{displaystyle dt vphantom{1^a}}Idt=-LIdI.$

Источник тока совершает такую же по модулю положительную работу (сопротивлением катушки, напомним, мы пренебрегаем, так что вся работа источника совершается против вихревого поля):

Интегрируя это от нуля до , найдем работу источника , которая затрачивается на создание тока :

$A = int_{0}^{I}LIdI=frac{displaystyle LI^2}{displaystyle 2 vphantom{1^a}}.$

Эта работа превращается в энергию магнитного поля созданного тока, и мы приходим к формуле (3).

Разберем задачи ЕГЭ по физике по темам: «Самоиндукция», «Магнитный поток», «Индуктивность», «Электромагнитная индукция».

Задача 1. На катушке сопротивлением 8,2 Ом и индуктивностью 25 мГн поддерживается постоянное напряжение 55 В. Сколько энергии выделится при размыкании цепи? Какая средняя ЭДС самоиндукции появится при этом в катушке, если энергия будет выделяться в течение 12 мс?

Дано:

R = 8,2 Ом;
L= 25 мГн = $25cdot 10^{-3}$ Гн;
t = 12 мс = 12;

Найти:
W_м — ? E_is — ?

Решение:

Решение любой задачи по физике должно начинаться с создания модели, которая поясняет ситуацию, описанную в данной задачи. В качестве модели может выступать чертеж, пояснительный рисунок, электрическая схема.

Для этой задачи необходимо начертить электрическую схему.

На схеме изображены катушка индуктивности, источник тока, поддерживающий на ней постоянное напряжение, ключ.

При замкнутом ключе через катушку протекает постоянный электрический ток, величину которого можно рассчитать, используя закон Ома для участка цепи. Катушка аналогична резистору, подключенному в эту цепь.

$displaystyle I=frac{U}{R}, I=frac{55}{8,2}approx 6,7(A).$

Энергия магнитного поля рассчитывается по формуле:

$displaystyle W_{M}=frac{Li^{2}}{2}, W_{M}=frac{25cdot 10^{-3}cdot 6,7^{2}}{2}approx 0,56$ (Дж).

Стоит обратить внимание, что эта формула аналогична формуле кинетической энергии в механике: $displaystyle E_{K}=frac{mv^{2}}{2}.$

При размыкании ключа, через катушку начинает протекать уже переменный ток. Поэтому магнитный поток, пронизывающий катушку, меняется. В самой катушке возникает ЭДС индукции, так как в ней течёт переменный ток. Тем самым, возникает явление самоиндукции.

Используя закон электромагнитной индукции в виде $displaystyle mathcal E _{is}=-Lfrac{Delta I}{Delta t},$ приходим к расчету второй неизвестной величины этой задачи:

$displaystyle mathcal E _{is}=25cdot 10^{-3}frac{6,7}{12cdot 10^{-3}}approx 14$ (B).

В этих расчетах мы не учитывали знак (-), который указан в законе электромагнитной индукции. Смысл этого знака заключен в учёте правила Ленца, определяющего направление индукционного тока. Но так как о направлении индукционного тока речь в задаче не идет, то в расчетах именно получено значение модуля ЭДС самоиндукции.

Ответ: 0,56 Дж, 14 В.

Задача 2. На рисунке приведён график зависимости силы тока от времени в электрической цепи, индуктивность которой 1 мГн. Определите модуль ЭДС самоиндукции в интервале времени от 5 до 15 с. Ответ выразите в мкВ.

Решение

Решение любых графических задач необходимо начинать с «чтения» самого графика. В этой задаче рассматривается зависимость силы тока от времени в цепи, содержащей катушку индуктивности. Необходимо обратить внимание на те интервалы времени, в течение которых происходит изменение силы тока. С изменением этой величины связано изменение магнитного потока и, как следствие, возникновение ЭДС самоиндукции. Сила тока меняется в интервале от 0 до 5 с, от 5 до 10 с и от 15 до 20 с. В интервале от 10 до 15 с сила тока постоянна, изменение магнитного потока не происходит, поэтому $mathcal E _{si}=0$ . Для участка от 5 до 10 с надо применить закон электромагнитной индукции $displaystyle mathcal E _{is}=-Lfrac{Delta I}{Delta t}$ .

Для модуля ЭДС самоиндукции, т.е. без учета направления индукционного тока, этот закон будет иметь вид:

$displaystyle |mathcal E _{is}|=left|Lfrac{Delta I}{Delta t} right|$ .

Данные для расчета необходимо взять из графической зависимости, учитывая при этом перевод в систему «СИ».

$displaystyle mathcal E_{is}=left| 1cdot 10^{-3} frac{20cdot 10^{-3}-30cdot 10^{-3}}{10-5}right|=2cdot 10^{-6}(B)=2$ (мкВ).

Ответ: 2 мкВ.

Задача 3. Катушка, обладающая индуктивностью , соединена с источником питания с ЭДС и двумя одинаковыми резисторами . Электрическая схема соединения показана на рис. 1. В начальный момент ключ в цепи разомкнут.

В момент времени t=0 ключ замыкают, что приводит к изменениям силы тока, регистрируемым амперметром, как показано на рис. 2. Основываясь на известных физических законах, объясните почему при замыкании ключа сила тока плавно увеличивается до некоторого нового значения — $I_{1}.$ Определите значение силы тока $I_{1}.$ Внутренним сопротивлением источника тока пренебречь.

Решение

В данной задаче необходимо рассмотреть две ситуации, которые происходят до и после замыкания ключа.

До замыкания ключа в цепи устанавливается постоянная сила тока, которая определяется законом Ома для полной цепи $displaystyle I=frac{mathcal E}{R+r}$ . Так как по условию внутренним сопротивлением источника можно пренебречь, то $displaystyle I=frac{mathcal E}{R}=3$ (A).
После замыкания ключа параллельно к первому резистору подключается второй, имеющий такое же сопротивление. Тогда общее сопротивление цепи можно рассчитать, как $displaystyle frac{1}{R_{ob}}=frac{1}{R}+frac{1}{R}=frac{2}{R}; R_{ob}=frac{R}{2}.$ Таким образом, внешнее сопротивление цепи уменьшается в 2 раза.
Наличие в цепи катушки индуктивности, в которой возникает ЭДС самоиндукции, препятствует мгновенному нарастанию силы тока (по аналогии с механикой – тело большой массы не может быстро изменить свою скорость). Поэтому сила тока плавно увеличивается до некоторого значения $I_{1}.$
Так как ЭДС самоиндукции с течением времени уменьшается до нулевого значения, то ток в цепи будет возрастать в 2 раза, так как общее сопротивление уменьшается также в 2 раза.
$displaystyle I_{1}=frac{mathcal E}{R/2}=frac{2mathcal E}{R}=6$ (A).

Ответ: 6 А.

Задача 4. Катушка Проволочная рамка площадью 60 см² помещена в однородное магнитное поле так, что плоскость рамки перпендикулярна вектору индукции vec{B} . Проекция $B_{n}$ индукции магнитного поля на нормаль к плоскости рамки изменяется во времени t согласно графику на рисунке.

Из приведенного ниже списка выберите все верные утверждения о процессах, происходящих в рамке.

Модуль ЭДС электромагнитной индукции, возникающий в рамке, максимален в интервале от 0 до 1мс.
Ответ. Согласно закону электромагнитной индукции $displaystyle mathcal E=-frac{Delta Phi }{Delta t}=-frac{Delta Bcdot S}{Delta t}.$
Т.е. максимальное значение ЭДС индукции будет наблюдаться на интервале максимального изменения $B_{n}$ с течением времени. В интервале от 0 до 1 мс скорость изменения проекции $B_{n}$ наибольшая.
Утверждение верное.
Магнитный поток через рамку в интервале от 2 до 4 мс равен 12 мВб.
Ответ. Формула для расчета магнитного потока имеет вид $Phi=B_{n}S.$
В данном временном интервале проекция $B_{n}$ постоянна и равна 2 Тл.
$displaystyle Phi=2cdot 60cdot 10^{-4}=12cdot 10^{-3}$ (Вб) = 12 (мВб).
Утверждение верное.
Модуль ЭДС электромагнитной индукции, возникающей в рамке, в интервале от 4 до 6 мс равен 6 В.
Ответ. Согласно закону электромагнитной индукции $displaystyle mathcal E=-frac{Delta Phi }{Delta t}=-frac{Delta Bcdot S}{Delta t}.$
$displaystyle mathcal E=left|frac{(-2-2)cdot 60cdot 10^{-4}}{2cdot 10^{-3}}right|=12$ (B).
Утверждение неверное.
Модуль скорости изменения магнитного потока через рамку минимален в интервале от 0 до 1 мс.
Ответ. В той задаче изменение магнитного потока связано с изменением проекции $B_{n}$ индукции магнитного поля. В интервале от 0 до 1 мс проекция $B_{n}$ меняется быстрее всего, потому и изменение магнитного потока максимальное.
Утверждение неверное.
Модуль ЭДС электромагнитной индукции, возникающей в рамке, равен нулю в интервале времени от 2 до 4 мс.
Ответ. Согласно закону электромагнитной индукции $displaystyle mathcal E=-frac{Delta Phi }{Delta t}=-frac{Delta Bcdot S}{Delta t}.$
В интервале от 2 до 4 мс проекция $B_{n}$ не изменяется, потому и .
Тогда в проволочной рамке ЭДС индукции не возникает.
Утверждение верное.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Самоиндукция» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Полная энергия электромагнитных колебаний в колебательном контуре

Теорема физики (формула) и словесная формулировка математической записи: полная энергия Е электромагнитных колебаний колебательного контура в каждый момент времени равна сумме энергии электрического поля в конденсаторе и энергии магнитного поля катушки индуктивности в этот момент времени. Полная энергия равна максимальной энергии электрического поля E_C_max (в момент, когда энергия магнитного поля катушки равна нулю) и максимальной энергии магнитного поля катушки E_L_max (в момент, когда энергия электрического поля равна нулю).

(% MathType!MTEF!2!1!+-% feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8% qacaWGfbGaeyypa0Jaamyra8aadaWgaaWcbaGaamitaiGac2gacaGG% HbGaaiiEaaqabaGcpeGaaiilaiaadweapaWaaSbaaSqaa8qacaWGmb% aapaqabaGcdaWgaaWcbaWdbiaad2gacaWGHbGaamiEaaWdaeqaaOWd% biabg2da98aadaWcaaqaaiaadYeacaWGXbWaa0baaSqaaiaaicdaae% aacaaIYaaaaOGaeqyYdC3aaWbaaSqabeaacaaIYaaaaaGcbaGaaGOm% aaaapeGaaiilaiaacckacaWGfbGaeyypa0Jaamyra8aadaWgaaWcba% Gaai4qaiGac2gacaGGHbGaaiiEaaqabaGcpeGaaiilaiaadweapaWa% aSbaaSqaaiaadoeaaeqaaOWaaSbaaSqaa8qacaWGTbGaamyyaiaadI% haa8aabeaak8qacqGH9aqppaWaaSaaaeaacaWGXbWaa0baaSqaaiaa% icdaaeaacaaIYaaaaaGcbaGaaGOmaiaadoeaaaaaaa!5E23!E = {E_{Lmax }},{E_L}_{max} = frac{{Lq_0^2{omega ^2}}}{2},E = {E_{Cmax }},{E_C}_{max} = frac{{q_0^2}}{{2C}})

Здесь L – индуктивность катушки, q₀– максимальный заряд конденсатора, ω – круговая частота электромагнитных колебаний контура, С – емкость конденсатора.

Доказательство теоремы (вывод формулы): значение электрической энергии колебательного контура, в котором совершаются гармонические колебания, в любой момент времени t равно

E_С(t)=(frac{{q_0^2{{cos }^2}(omega t + {phi _0})}}{{2C}})

Магнитная энергия контура, совершающего гармонические колебания, в любой момент времени t равна

E_L(t)=(% MathType!MTEF!2!1!+-% feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca% WGmbGaamyCamaaDaaaleaacaaIWaaabaGaaGOmaaaakiabeM8a3naa% CaaaleqabaGaaGOmaaaakiGacohacaGGPbGaaiOBamaaCaaaleqaba% GaaGOmaaaakiaacIcacqaHjpWDcaWG0bGaey4kaSIaeqy1dy2aaSba% aSqaaiaaicdaaeqaaOGaaiykaaqaaiaaikdaaaaaaa!487A!frac{{Lq_0^2{omega ^2}{{sin }^2}(omega t + {phi _0})}}{2})

В области гармонических колебаний, когда омическое сопротивление пренебрежимо мало (R=0), энергетических потерь нет, и заряд на обкладках восстанавливается через каждый период полностью. Магнитная энергия переходит в электрическую, и наоборот, электрическая в магнитную. По закону сохранения энергии полная энергия контура не изменяется и в любой момент времени равна сумме электрической и магнитной энергий. Найдем эту сумму:

Е=E_С+E_L=(frac{{q_0^2{{cos }^2}(omega t + {phi _0})}}{{2C}} + frac{{Lq_0^2{omega ^2}{{sin }^2}(omega t + {phi _0})}}{2})

Заменяя величину ({omega ^2})на ее значение во втором слагаемом ({omega ^2} = frac{1}{{LC}}), получим

Е=(frac{{q_0^2{{cos }^2}(omega t + {phi _0})}}{{2C}} + frac{{q_0^2{{sin }^2}(omega t + {phi _0})}}{{2C}} = frac{{q_0^2}}{{2C}}({cos ^2}(omega t + {phi _0}) + {sin ^2}(omega t + {phi _0})))

Выражение в скобках равно единице, поэтому (% MathType!MTEF!2!1!+-% feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyraiabg2% da9maalaaabaGaamyCamaaDaaaleaacaaIWaaabaGaaGOmaaaaaOqa% aiaaikdacaWGdbaaaaaa!3BFD!E = frac{{q_0^2}}{{2C}})

Максимального значения электрическая энергия достигает в те моменты времени, когда косинус фазы принимает значения, равные единице, поэтому E_Смах =(% MathType!MTEF!2!1!+-% feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca% WGXbWaa0baaSqaaiaaicdaaeaacaaIYaaaaaGcbaGaaGOmaiaadoea% aaaaaa!3A2D!frac{{q_0^2}}{{2C}})

Магнитная энергия достигает максимального значения в те моменты времени, когда синус фазы принимает значения, равные единице, поэтому E_L_мах=(% MathType!MTEF!2!1!+-% feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca% WGmbGaamyCamaaDaaaleaacaaIWaaabaGaaGOmaaaakiabeM8a3naa% CaaaleqabaGaaGOmaaaaaOqaaiaaikdaaaaaaa!3CF6!frac{{Lq_0^2{omega ^2}}}{2}), но (% MathType!MTEF!2!1!+-% feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqyYdC3aaW% baaSqabeaacaaIYaaaaOGaeyypa0ZaaSaaaeaacaaIXaaabaGaamit% aiaadoeaaaaaaa!3C20!{omega ^2} = frac{1}{{LC}}) и E_L_{мах=(% MathType!MTEF!2!1!+-% feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca% WGXbWaa0baaSqaaiaaicdaaeaacaaIYaaaaaGcbaGaaGOmaiaadoea% aaaaaa!3A2D!frac{{q_0^2}}{{2C}})}

Максимальная электрическая энергия электромагнитного колебания равна максимальной магнитной энергии. Сравнивая полученные значения с выражением для полной энергии, как и положено по закону сохранения энергии, имеем равенство полной энергии в любой момент времени максимальным значениям кинетической и потенциальной энергий. В те моменты времени, когда кинетическая энергия максимальна, потенциальная минимальна и наоборот, так один вид энергии периодически полностью без потерь переходит в другой.

Теорема доказана.

Условия выполнения: выполняется в области упругих растяжений пружины для случая, когда массой пружины пренебрегают по сравнению с массой подвеса. Кроме того, пренебрегают процессами затухания колебаний.

Источник

В электрической цепи (см. рис.) все элементы идеальные, их параметры указаны. Ключ К замыкают.

1)  Найти напряжение на катушке индуктивности сразу после замыкания ключа.

2)  Найти максимальную скорость изменения энергии N_m в катушке индуктивности.

3)  Найти скорость изменения тока в цепи в момент, когда скорость изменения

энергии в катушке равна от максимальной скорости N_m.

Спрятать решение

Решение.

1.  Найдем напряжение на катушке индуктивности сразу после замыкания ключа  — U₀  =  E.

2.  Пусть U  — напряжение на катушке, тогда

Максимальная скорость изменения энергии N_m при следовательно,

3.  Найдем скорость изменения тока в цепи:

Отсюда

Ответ: 1) U₀  =  E; 2) 3)

Спрятать критерии

Критерии проверки:

№	Критерий	Максимальный балл
1	Первый вопрос стоит  — 2 балла	2
2	Второй вопрос стоит  — 4 балла, правильно записаны все необходимые уравнения  — 1 балл	4
3	Третий вопрос стоит  — 4 балла, правильно записаны все необходимые уравнения  — 1 балл	4

Классификатор: Электродинамика. Самоиндукция. Катушка индуктивности

Источник

На чтение 12 мин. Опубликовано 12.12.2019

§ 101. Энергия магнитного поля катушки

При размыкании цепи в опыте (см. рис. 150, в) лампочка ярко вспыхивала. Откуда же бралась энергия, за счет которой в данном случае горела лампочка? Так как это происходило, когда цепь была отключена от источника тока, т. е. при уменьшении индукции магнитного поля катушки, то, следовательно, энергия, потребляемая лампочкой, была раньше запасена в виде энергии магнитного поля. При размыкании цепи оно начинает исчезать и запасенная в нем энергия в процессе самоиндукции превращается в энергию электрического тока, за счет которой горит лампочка. Из рассмотренного делаем вывод: магнитное поле обладает энергией.

Запас энергии магнитного поля катушки равен энергии, израсходованной источником тока на преодоление э. д. с. самоиндукции за весь тот промежуток времени, пока сила тока при замыкании цепи возрастала от нуля до некоторого значения I (см. рис. 150, б). Часть работы э. д. с. источника в катушке идет на нагревание ее проводов, а часть, равная э. д. с. самоиндукции Е_ист = Е_с, совершает работу против э. д. с. самоиндукции.

Работа тока, идущая на преодоление э. д. с. самоиндукции, равна энергии магнитного поля катушки:

Ток изменялся от 0 до I, следовательно, Поэтому Ток изменялся от 0 до I, тогда изменение тока ΔI = I. Значит,

Подставим Е_с и I_ср в формулу (3):

Получим формулу энергии магнитного поля катушки

Зависимость энергии магнитного поля катушки от ее индуктивности и силы тока в ней можно видеть на таком опыте. Увеличив реостатом силу тока в катушке, разомкнем цепь. В этом случае лампочка вспыхнула ярче, чем при малом токе в катушке. Значит, энергия магнитного поля катушки тем больше, чем больше сила тока в ней. Удалим из катушки половину сердечника, уменьшив тем самым ее индуктивность. Установим прежнюю силу тока в цепи и затем разомкнем ее. В этом случае лампочка вспыхивает менее ярко. Следовательно, энергия магнитного поля катушки тем больше, чем больше ее индуктивность. Энергия магнитного поля нами используется, например, в подъемном электромагнитном кране для притяжения кусков железа к сердечнику электромагнита крана, для получения тока во вторичной обмотке трансформатора.

Задача 36. В катушке без сердечника за 0,01 сек ток увеличился от 1 до 2 а, при этом в катушке возникла э. д. с. самоиндукции 20 в. Определить индуктивность катушки и изменение энергии ее магнитного поля.

Изменение энергии магнитного поля катушки Заменив получим

Если в контуре с индуктивностью L течёт ток I, то в момент размыкания цепи возникает индукционный ток и им совершается работа. Эта работа совершается за счёт энергии исчезнувшего при размыкании цепи магнитного поля. На основании закона сохранения и превращения энергию магнитного поля превращается главным образом в энергию электрического поля, за счёт которой происходит нагревание проводников. Работа может быть определена из соотношения

Так как 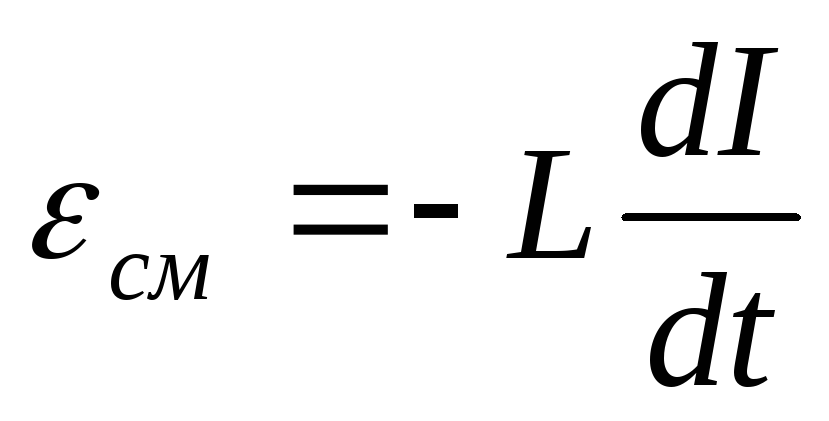, то

Уменьшение энергии магнитного поля равно работе тока, поэтому

(16.18)

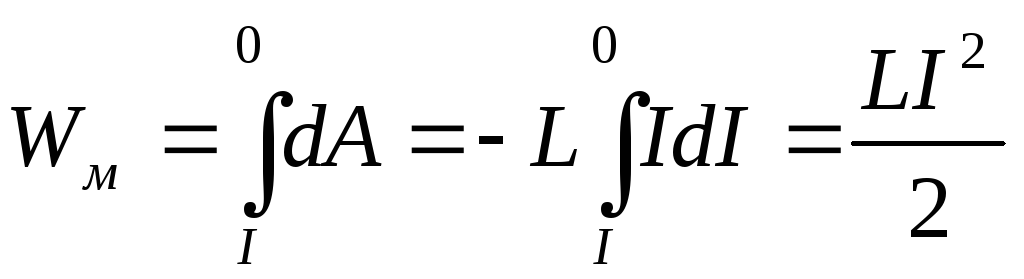
Формула справедлива для любого контура и показывает, что энергия магнитного поля зависит от индуктивности контура и силы тока, протекающего по нему.

Рассчитаем энергию однородного магнитного поля длинного соленоида, индуктивность которого определяется по формуле L = μμ₀n 2 V. B этом случае формула энергии примет вид

Учитывая, что напряжённость поля внутри бесконечно длинного соленоида Н=In, получаем

(16.19)

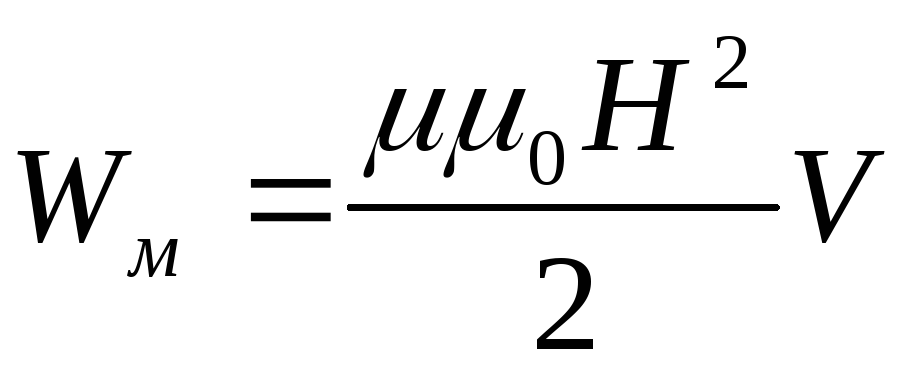
Выразим энергию через индукцию магнитного поля B= μμ₀H:

(16.20)

(16.21)

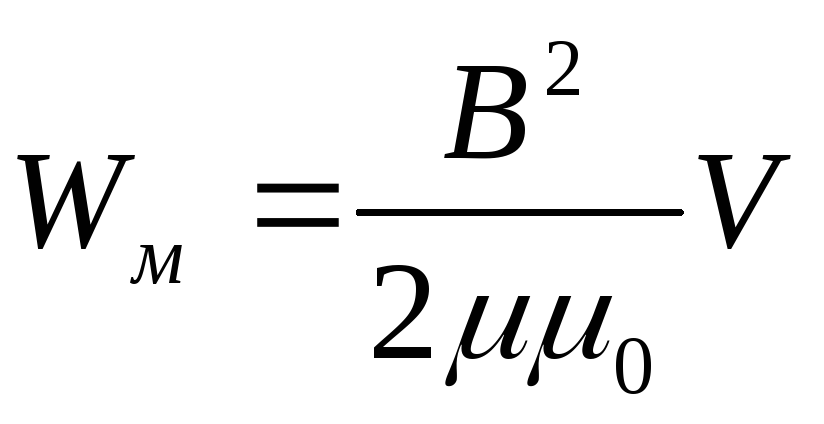
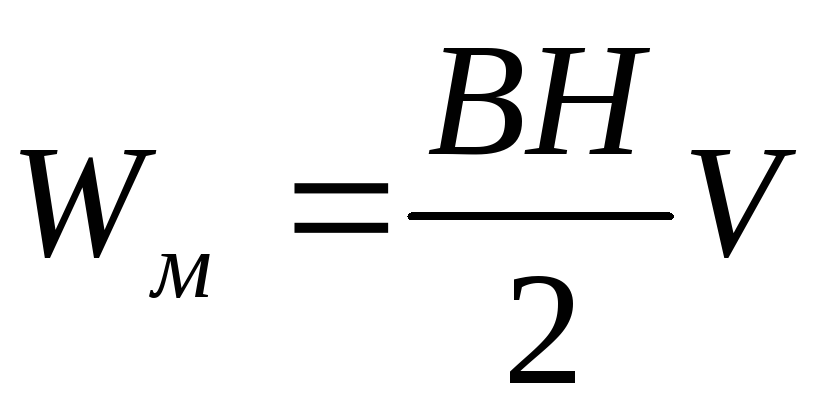
Вследствие того, что магнитное поле соленоида однородно и локализовано внутри соленоида, энергия распределена по объёму соленоида с постоянной плотностью

(16.22)

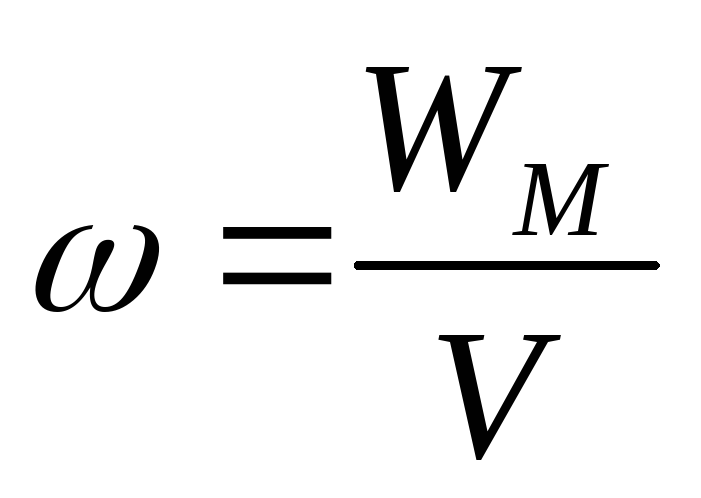
Учитывая последние три формулы, получаем

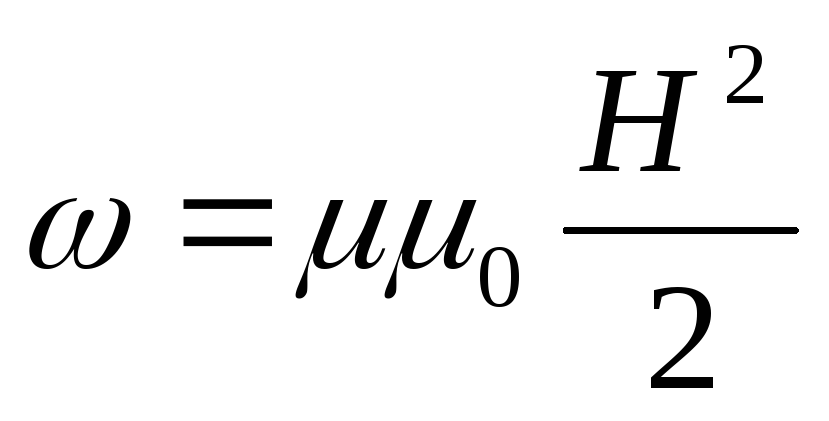
Учитывая правило Ленца, можно заметить, что явление самоиндукции аналогично проявлению инертности тел в механике. Так, вследствие инертности тело не мгновенно приобретает определённую скорость, а постепенно. Так же постепенно происходит и его торможение. То же самое, как мы видели, происходит и с силой тока при самоиндукции. Эту аналогию можно провести и дальше.

эти уравнения эквивалентны.

Эквивалентны и формулы

Примеры решения задач

Пример. В магнитном поле, изменяющемся по закону B=B₀cosωt (B₀=5мТл,

ω=5с -1 ), помещён круговой проволочный виток радиусом r=30см, причём нормаль к витку образует с направлением поля угол α=30º. Определите ЭДС индукции, возникающую в витке в момент времени t=10с.

Дано: B=B₀cosωt; B₀=5мТл=5∙10 -3 Тл; ω=5с -1 ; r=30см=0,3 м; α=30º; t=10 с.

Решение: Согласно закону Фарадея,

, (1)

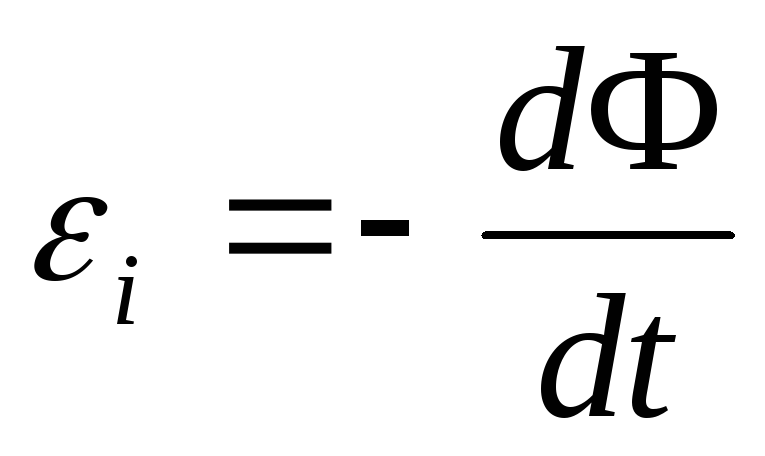
Где магнитный поток, сцепленный с витком при произвольном его расположении относительно магнитного поля.

По условию задачи B=B₀cosωt, а площадь кольца S=πr 2 , поэтому

Подставив выражение (2) в формулу (1) и продифференцировав, получаем искомую ЭДС индукции в заданный момент времени:

Пример В соленоиде длиной ℓ=50см и диаметром d=6см сила тока равномерно увеличивается на 0,3А за одну секунду. Определите число витков соленоида, если сила индукционного тока в кольце радиусом 3,1 см из медной проволоки (ρ=17нОм∙м), надетом на катушку, I_к=0,3 А.

Дано: ℓ=50см=0,5 м; d=6см=0,06м; 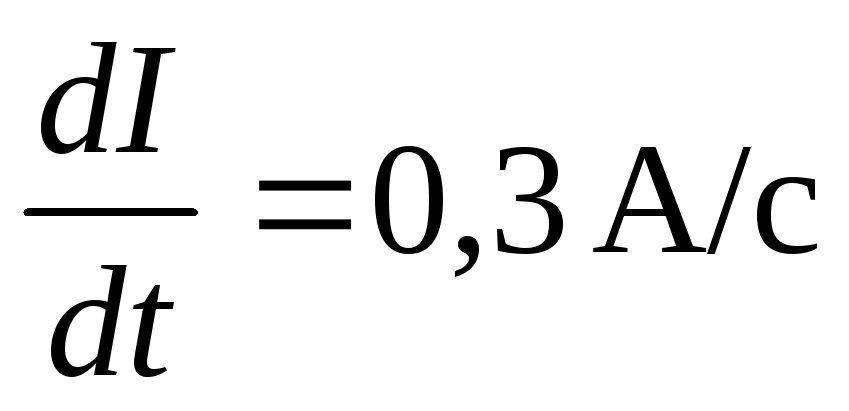;r_к=3,1см=3.1∙10 -2 м; ρ=17нОм∙м=17∙10 -9 Ом∙м; I_к=0,3 А.

Решение. При изменении силы тока в соленоиде возникает ЭДС самоиндукции

(1)

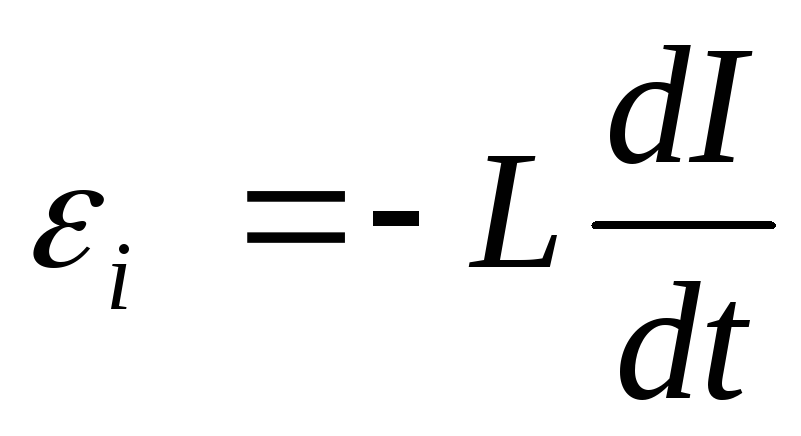
где 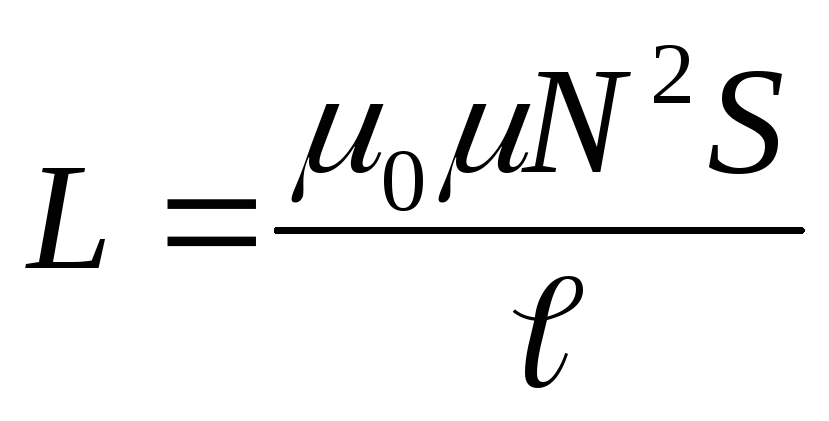— индуктивность соленоида. Подставив это выражение в (1)

с учётом

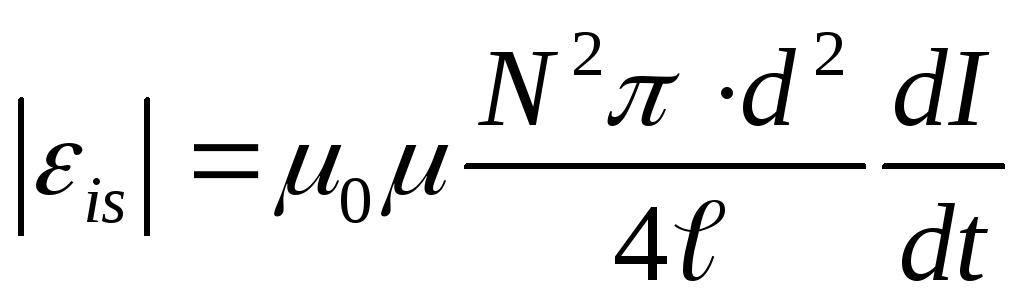
ЭДС индукции, возникающая в одном кольце, в N раз меньше, чем найденное значение ЭДС самоиндукции в соленоиде, состоящем из N витков, т.е.

. (2)

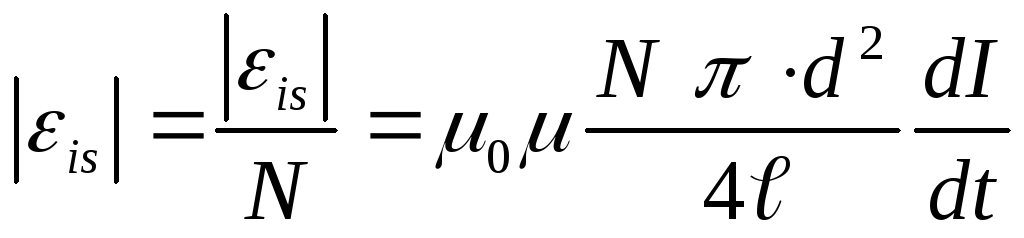
Согласно закону Ома, сила индукционного тока в кольце

, (3)

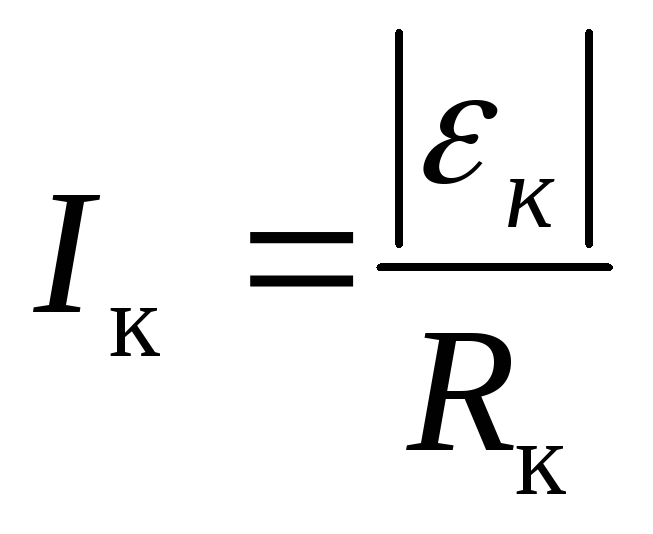
где 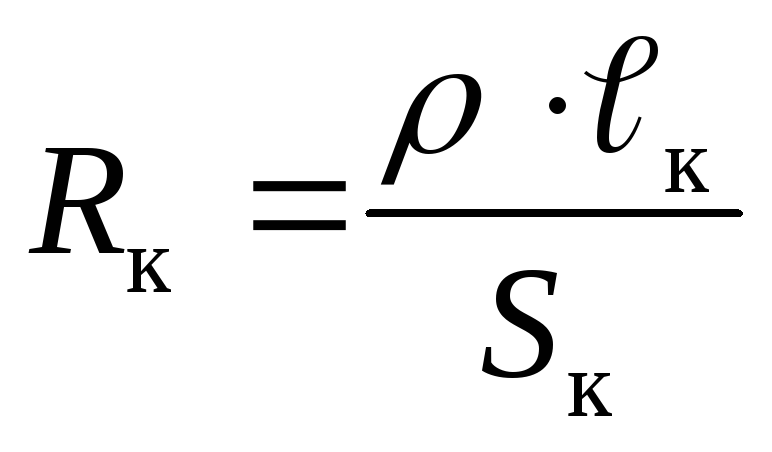— сопротивление кольца. Поскольку ℓ_к=πd, а S_к=πr_к 2 , выражение (3) примет вид

Подставив в эту формулу выражение (2), найдём искомое число витков соленоид

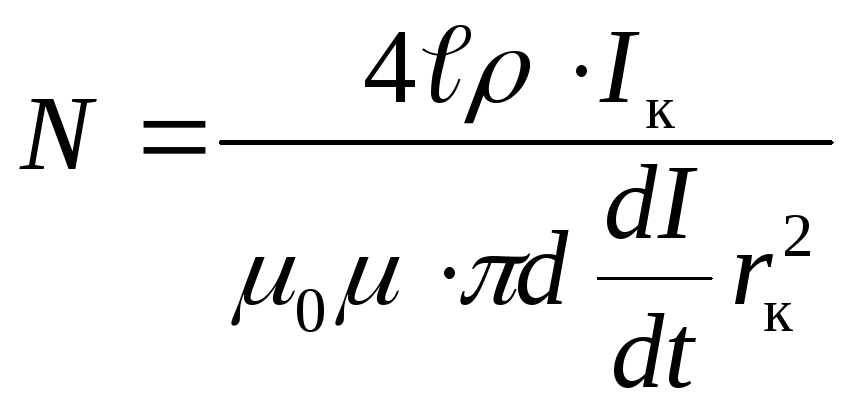
Пример В однородном магнитном поле подвижная сторона (её длина ℓ=20см) прямоугольной рамки (см. рисунок) перемещается перпендикулярно линиям магнитной индукции со скоростью υ=5 м/с. Определите индукцию В магнитного поля, если возникающая в рамке ЭДС индукции ε_i=0,2 В.

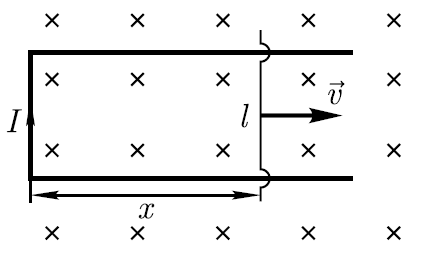
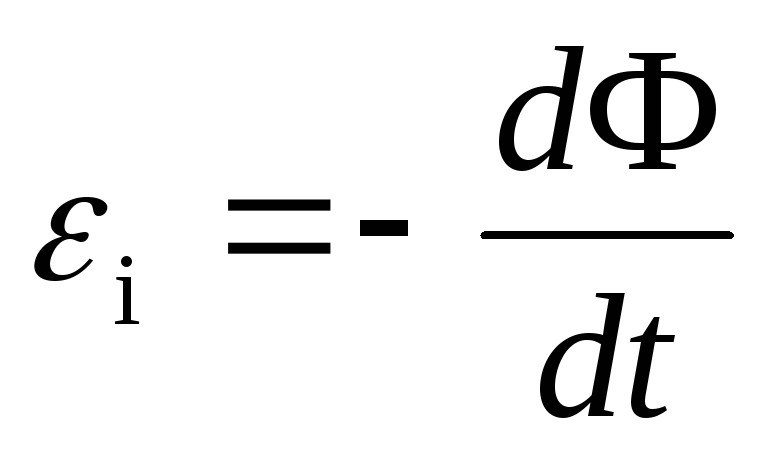
Решение. При движении в магнитном поле подвижной стороны рамки поток Ф вектора магнитной индукции сквозь рамку возрастает, что, согласно закону Фарадея,

, (1)

приводит к возникновению ЭДС индукции.

Поток вектора магнитной индукции, сцепленный с рамкой,

Подставив выражение (2) в формулу (1) и учитывая, что B и ℓ — величины постоянные, получаем

откуда искомая индукция магнитного поля

Пример В однородном магнитном поле с индукцией В=0,2 Тл равномерно вращается катушка, содержащая N=600 витков, с частотой n=6 с -1 . Площадь S поперечного сечения катушка 100см 2 . Ось вращения перпендикулярна оси катушки и направлению магнитного поля. Определите максимальную ЭДС индукции вращающейся катушки.

Дано: В=0,2 Тл; N=600; n=6 с -1 ; S=100см 2 =10 -2 м 2 .

Решение. Согласно закону Фарадея,

где Ф – полный магнитный поток, сцеплённый со всеми витками катушки. При произвольном расположении катушки относительно магнитного поля

где круговая частота ω=2πn. Подставив ω в (1), получим

Пример Однослойная длинная катушка содержит N=300 витков, плотно прилегающих друг к другу. Определите индуктивность катушки, если диаметр проволоки d=0,7 мм (изоляция ничтожной толщины) и она намотана на картонный цилиндр радиусом r=1 см. .

Дано: N=300; d=0,7 мм=7∙10 -4 м; r=1 см=10 -2 м.

Решение. Индуктивность катушки

(1)

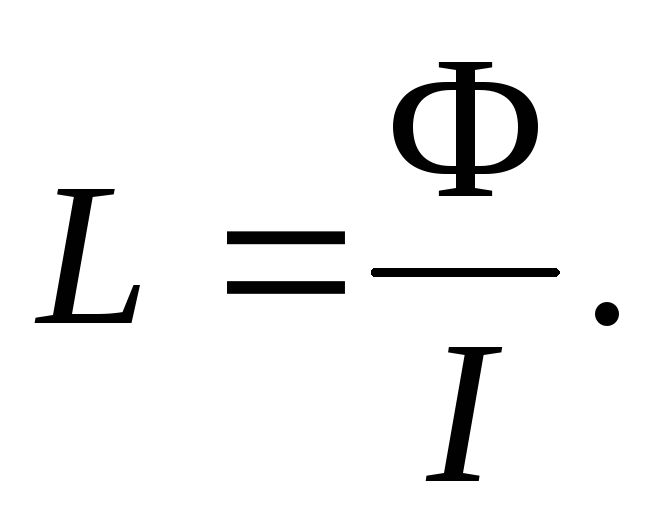
где Ф – полный магнитный поток, сцепленный со всеми витками катушки; I — сила тока в катушке.

Учитывая, что полный магнитный поток

(N-число витков катушки; В – магнитная индукция; S – площадь поперечного сечения катушки); магнитная индукция в катушке без сердечника

(μ₀ – магнитная постоянная; ℓ- длина катушки), длина катушки

(d-диаметр проволоки; витки вплотную прилегают друг к другу), площадь поперечного сечения катушки

Получим осле подстановки записанных выражений в формулу (1) искомую индуктивность катушки:

Пример Первичная обмотка понижающего трансформатора с коэффициентом трансформации k=0,1 включена в сеть с источником переменного напряжения с ЭДС ε₁=220 В. Пренебрегая потерями энергии в первичной обмотке, определите напряжение U₂ на зажимах вторичной обмотки, если её сопротивление R₂=5 Ом и сила тока в ней I₂=2А.

Решение. В первичной обмотке под действием переменной ЭДС ε₁ возникает переменный ток I₁, создающий в сердечнике трансформатора переменногый магнитный поток Ф, который пронизывает вторичную обмотку. Согласно закону Ома, для первичной обмотки

где R₁ – сопротивление первичной обмотки. Падение напряжения I₁R₁ при быстропеременных полях мало по сравнению с ε₁ и ε₂. Тогда можем записать:

(1)

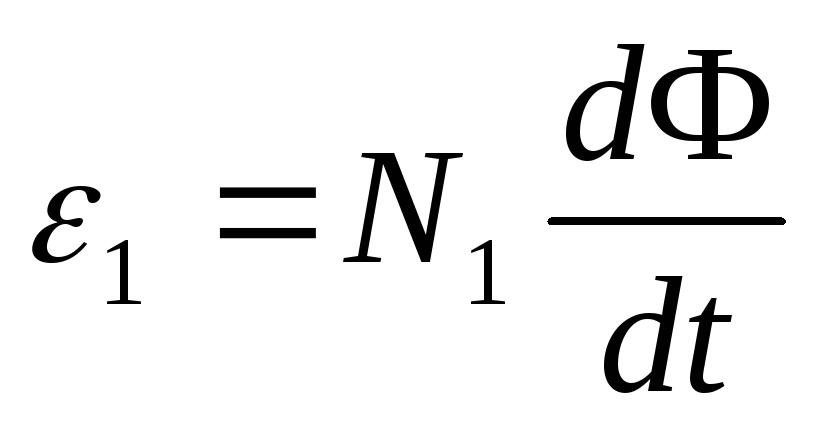
ЭДС взаимной индукции, возникающая во вторичной обмотке,

(2)

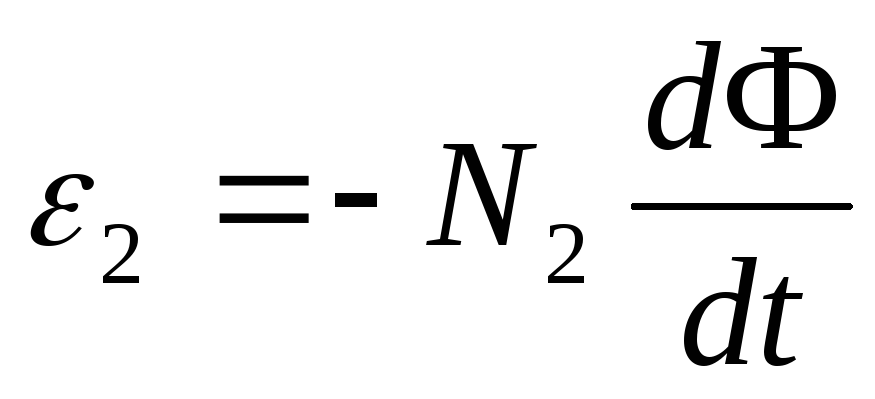
Из выражений (1) и (2) получаем

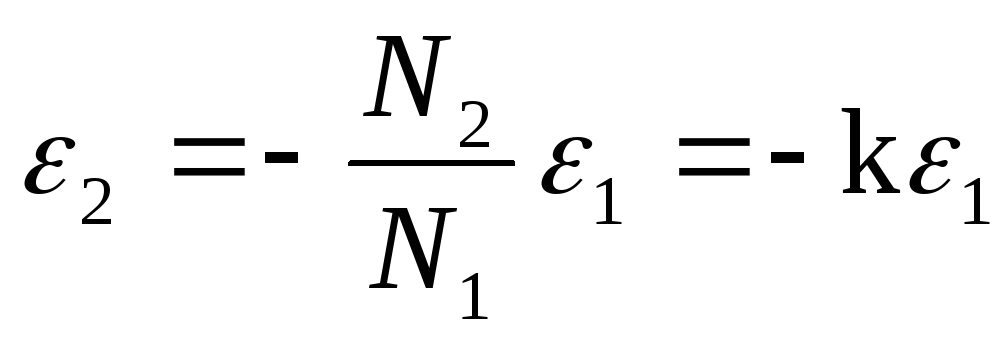
где 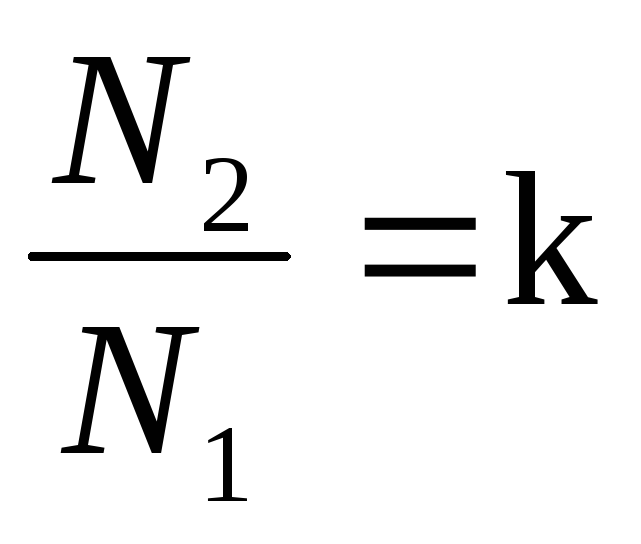— коэффициент трансформации, а знак «-» показывает, что ЭДС в первичной и вторичной обмотках противоположны по фазе. Следовательно, ЭДС во вторичной обмотке

Напряжение на зажимах вторичной обмотки

Пример Соленоид без сердечника с однослойной обмоткой из проволоки диаметром d=0,4 мм имеет длину ℓ=0.5 м и поперечное сечение S=60см 2 . За какое время при напряжении U=10 В и силе тока I=1,5 А в обмотке выделится количество теплоты, равное энергии поля внутри соленоида? Поле считать однородным.

Дано: d=0,4 мм=0,4∙10 -4 м; ℓ=0,5 м; S=60см 2 =6∙10 -3 м 2 ; I=1,5А; U=10В; Q=W.

Решение. При прохождении тока I при напряжении U в обмотке за время t выделяется теплота

Энергия поля внутри соленоида

(2)

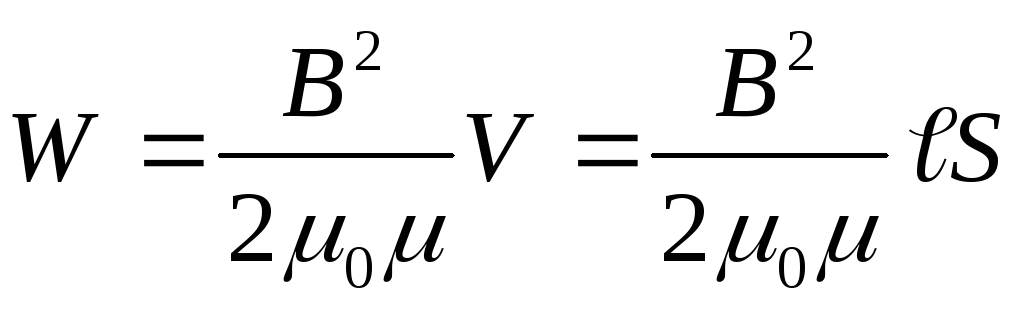
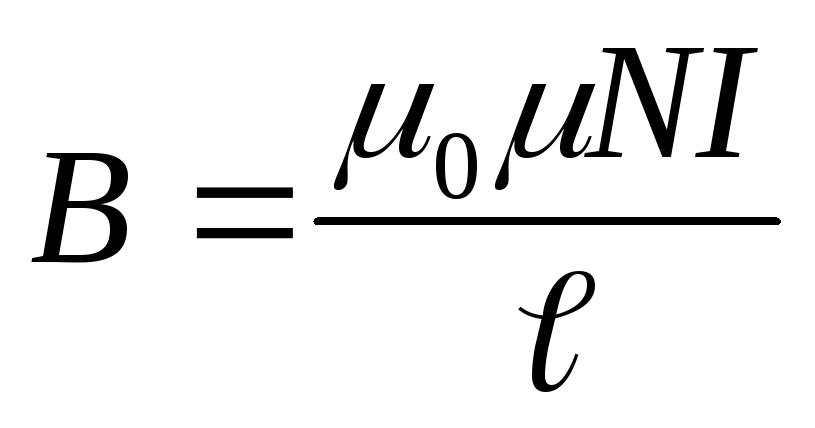
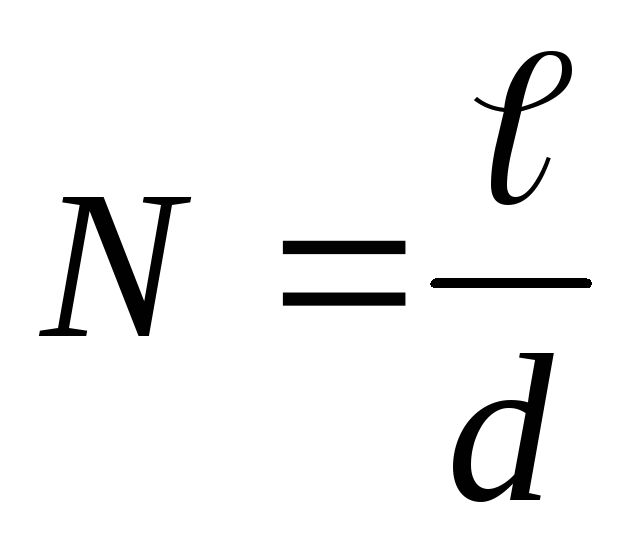
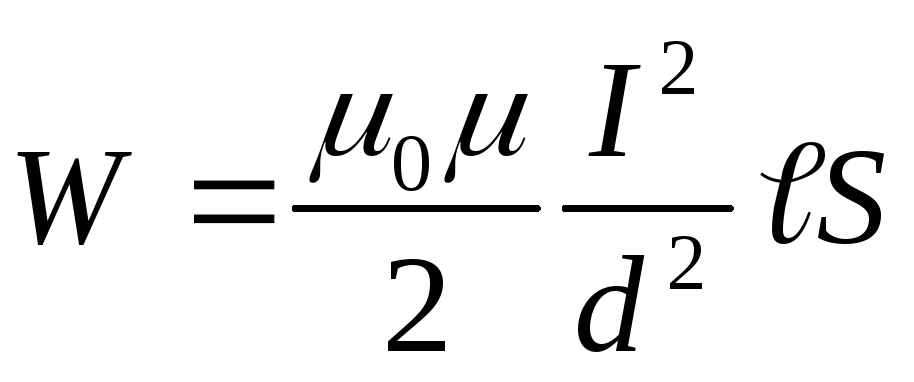
где (N – общее число витков соленоида). Если витки вплотную прилегают друг к другу, то ℓ=Nd, откуда . Подставив выражение для В иN в (2), получаем

. (3)

Согласно условию задачи, Q=W. Приравняв выражение (1) и (3),найдём искомое время:

Пример Катушка без сердечника длиной ℓ=50 см содержит N=200 витков. По катушке течёт ток I=1А. Определите объёмную плотность энергии магнитного поля внутри катушки..

Решение. Объёмная плотность энергии магнитного поля (энергия единицы объёма)

, (1)

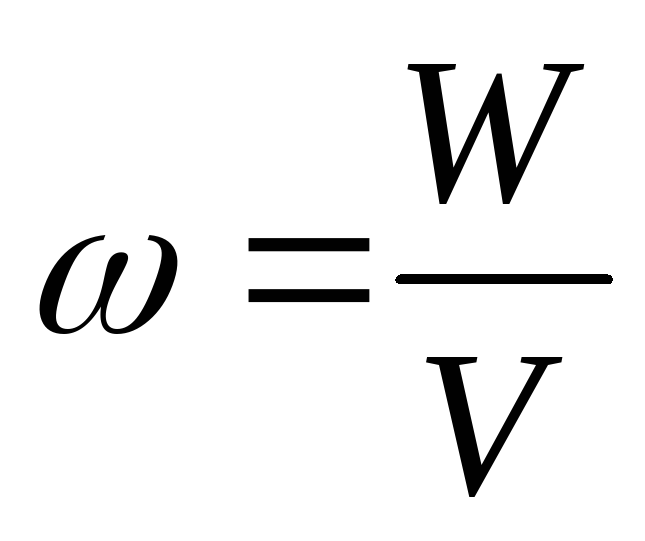
где 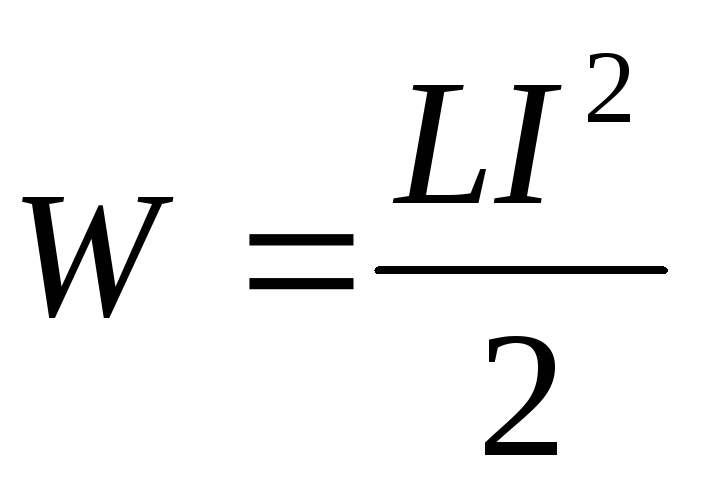— энергия магнитного поля (L — индуктивность катушки); V=Sℓ- объём катушки (S — площадь катушки; ℓ- длина катушки).

Магнитная индукция поля внутри соленоида с сердечником с магнитной проницаемостью μ равна

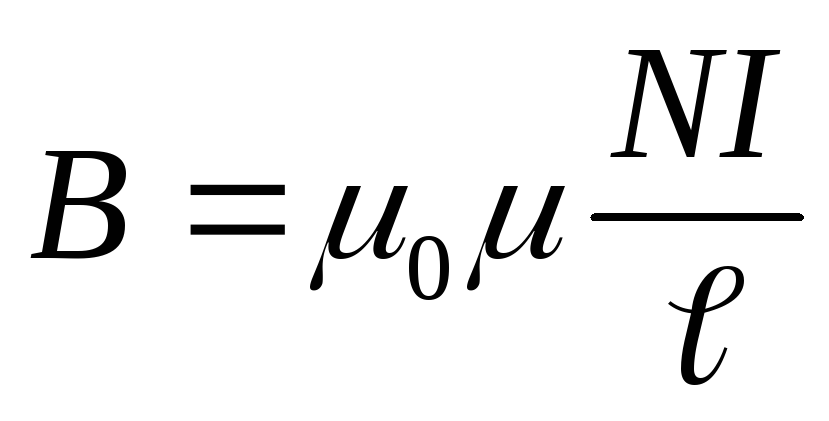
Полный магнитный поток, сцепленный со всеми витками соленоида,

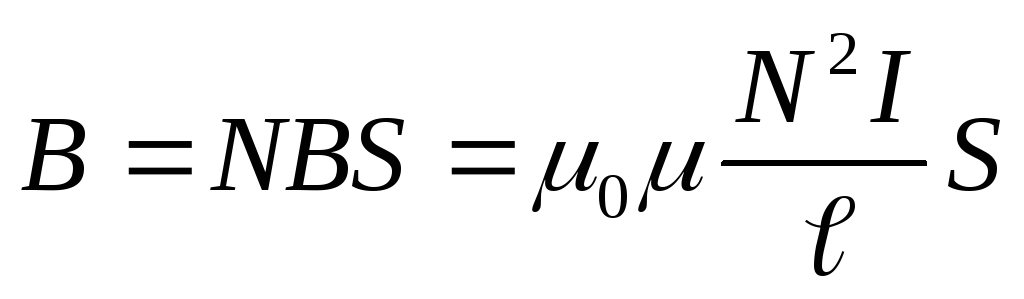
Учитывая, что Ф=LI, получаем формулу для индуктивности соленоида:

(2)

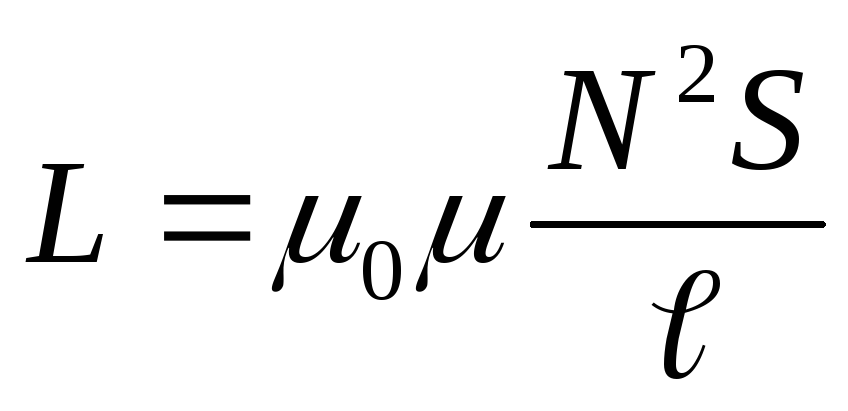
Подставив выражение (2) в формулу (1) с учётом того, что 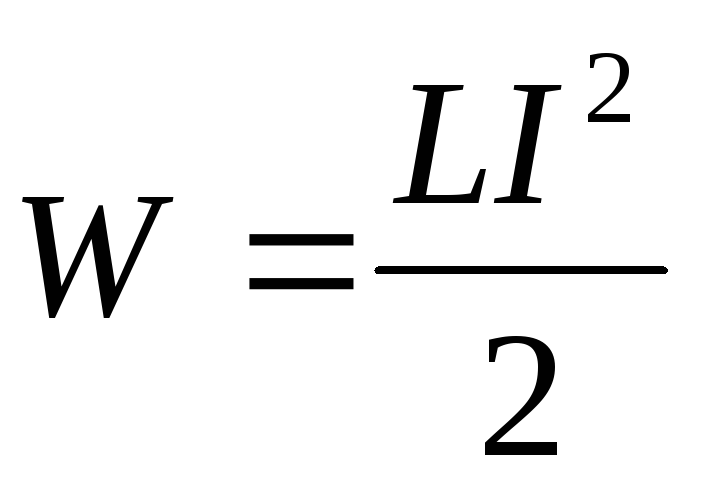, найдём искомую объёмную плотность энергии магнитного поля внутри катушки:

Почему возникает магнитное поле

Магнитные свойства некоторых веществ, позволяющие притягивать металлические предметы, были известны с давних времен. Но к пониманию сути этого явления удалось приблизиться только в начале XIX века. По аналогии с электрическими зарядами, были попытки объяснить магнитные эффекты с помощью неких магнитных зарядов (диполей). В 1820 г. датский физик Ханс Эрстед обнаружил, что магнитная стрелка отклоняется при пропускании электрического тока через проводник, находящийся около нее.

Тогда же французский исследователь Андре Ампер установил, что два проводника, расположенные параллельно друг другу, вызывают взаимное притяжение при пропускании через них электрического тока в одном направлении и отталкивание, если токи направлены в разные стороны.

Рис. 1. Опыт Ампера с проводами с током. Стрелка компаса вблизи провода с током

На основании этих наблюдений Ампер пришел к выводу, что взаимодействие тока со стрелкой, притяжение (и отталкивание) проводов и постоянных магнитов между собой можно объяснить, если предположить, что магнитное поле создается движущимися электрическими зарядами. Дополнительно Ампер выдвинул смелую гипотезу, согласно которой внутри вещества существуют незатухающие молекулярные токи, которые и являются причиной возникновения постоянного магнитного поля. Тогда все магнитные явления можно объяснить взаимодействием движущихся электрических зарядов, и никаких особенных магнитных зарядов не существует.

Математическую модель (теорию), с помощью которой стало возможным рассчитывать величину магнитного поля и силу взаимодействия, разработал английский физик Джеймс Максвелл. Из уравнений Максвелла, объединивших электрические и магнитные явления, следовало, что:

Магнитное поле возникает только в результате движения электрических зарядов;
Постоянное магнитное поле существует у природных магнитных тел, но и в этом случае причиной возникновения поля является непрерывное движение молекулярных токов (вихрей) в массе вещества;
Магнитное поле можно создать еще с помощью переменного электрического поля, но это тема будет рассмотрена в следующих наших статьях.

Магнитное поле катушки с током

Металлический провод, намотанный кольцами на любой цилиндрический стержень (деревянный, пластмассовый и т.п.) — это и есть электромагнитная катушка. Провод должен быть изолированным, то есть покрыт каким-либо изолятором (лаком или пластиковой оплеткой) во избежание замыкания соседних витков. В результате протекания тока магнитные поля всех витков складываются и получается, что суммарное магнитное поле катушки с током идентично (полностью похоже) магнитному полю постоянного магнита.

Рис. 2. Магнитное поле катушки и постоянного магнита.

Внутри катушки магнитное поле будет однородное, как в постоянном магните. Снаружи магнитные линии поля катушки с током можно обнаружить с помощью мелких металлических опилок. Линии магнитного поля замкнуты. По аналогии с магнитной стрелкой компаса, катушка с током имеет два полюса — южный и северный. Силовые линии выходят из северного полюса и заканчиваются в южном.

Для катушек с током существуют дополнительные, отдельные названия, которые используют в зависимости от области применения:

Катушка индуктивности, или просто — индуктивность. Термин используется в радиотехнике;
Дроссель (drossel — регулятор, ограничитель). Используется в электротехнике;
Соленоид. Это составное слово происходит от двух греческих слов: solen — канал, труба и eidos — подобный). Так называют специальные катушки с сердечниками из специальных магнитных сплавов (ферромагнетиков), которые используют в качестве электромеханических механизмов. Например, в автомобильных стартерах втягивающее реле — это соленоид.

Рис. 3. Катушки индуктивности, дроссель, соленоид

Энергия магнитного поля

В катушке с током запасается энергия от источника электропитания (батареи, аккумулятора), которая тем больше, чем больше ток I и величина L, которая называется индуктивностью. Энергия магнитного поля катушки с током W вычисляется с помощью формулы:

Эта формула напоминает формулу для кинетической энергии тела. Индуктивность аналогична массе тела, а сила тока аналогична скорости тела. Магнитная энергия пропорциональна квадрату силы тока, как кинетическая энергия пропорциональна квадрату скорости.

Для расчета величины индуктивности катушки существует следующая формула:

N — число витков катушки;

S — площадь поперечного сечения катушки;

l_к — длина катушки;

μ — магнитная проницаемость материала сердечника — справочная величина. Сердечник представляет собой металлический стержень, помещенный внутрь катушки. Он позволяет значительно увеличивать величину магнитного поля.

Что мы узнали?

Итак, мы узнали, что магнитное поле возникает только в результате движения электрических зарядов. Магнитное поле катушки с током похоже на магнитное поле постоянного магнита. Энергию магнитного поля катушки можно рассчитать, зная силу тока I и индуктивность L.

Источник