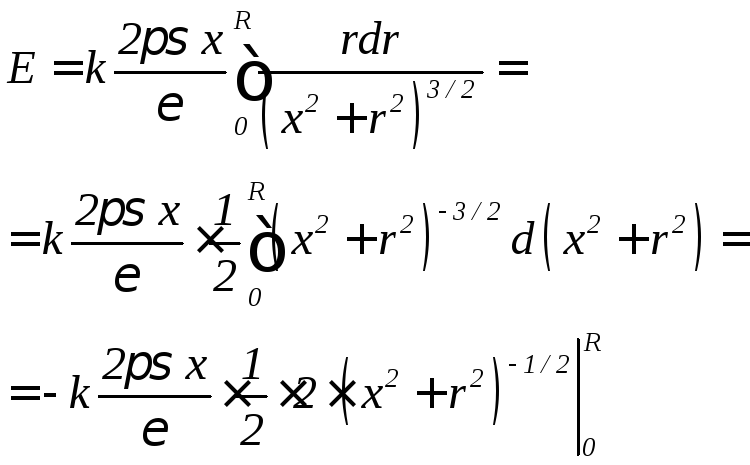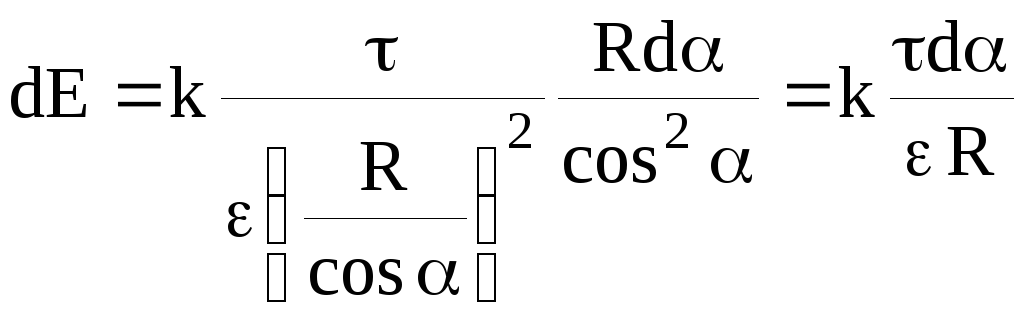2018-05-14
Кольцо радиуса $r$ из тонкой проволоки имеет заряд $q$. Найти модуль напряженности электрического поля на оси кольца как функцию расстояния $l$ до его центра. Исследовать полученную зависимость при $l gg r$. Определить максимальное значение напряженности и соответствующее расстояние $l$. Изобразить примерный график функции $E(l)$.
Решение:
Из симметрии условия ясно, что поле вдоль нормали будет равным нулю
то есть $E_{n} = 0$ и $E = E_{l}$
Тогда $dE_{l} = frac{dq}{ 4 pi epsilon_{0} (R^{2} + l^{2} ) } cos theta$
Но $dq = frac{q}{2 pi R} dx$ и $cos theta = frac{l}{ sqrt{R^{2} + l^{2} } }$
Следовательно $E = int dE_{l} = int_{0}^{2 pi R} frac{ql}{2 pi R} frac{dx}{4 pi epsilon_{0} (R^{2} + l^{2} )^{3/2} }$
или $E = frac{1}{4 pi epsilon_{0} } frac{ql}{ (l^{2} + R^{2} )^{3/2} }$
при $l gg R$ кольцо ведет себя как точечный заряд, создающий поле,
$E approx frac{1}{4 pi epsilon_{0} } frac{q}{l^{2} }$
Для максимального значения $E_{max}$, должно быть $frac{dE}{dl} = 0$
Итак, $(l^{2} + R^{2})^{3/2} — frac{3}{2}l sqrt{ l^{2} + R^{2} } 2l = 0$ или $l^{2} + R^{2} — 3l^{2} = 0$.
Таким образом, $l = frac{R}{ sqrt{2} }$ и $E_{max} = frac{q}{ 6 sqrt{3} pi epsilon_{0} R^{2} }$
Часть A. Кольцо (2.0 балл)
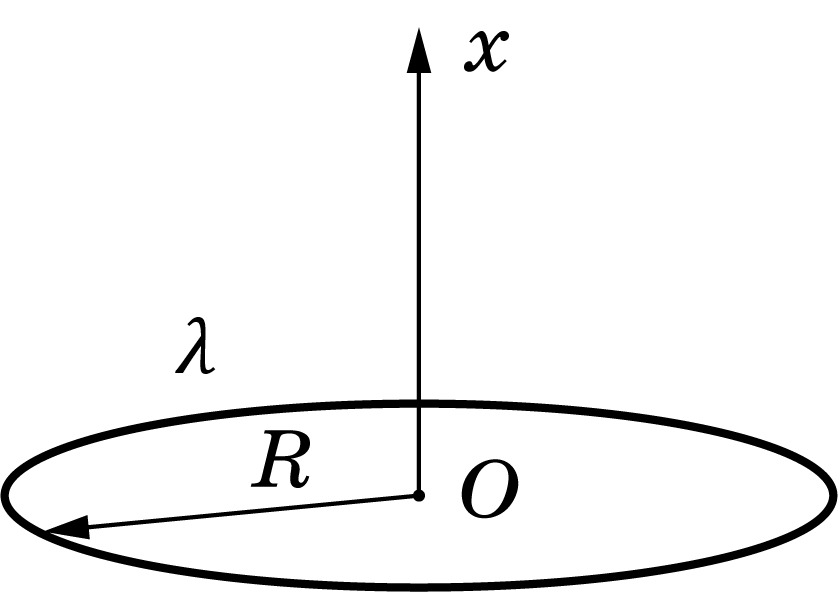
Кольцо радиуса $R$ равномерно заряжено по периметру с линейной плотностью заряда $lambda$.
A1
0.20
Найдите напряженность поля в центре заряженного кольца.
A2
0.30
Найдите потенциал на оси кольца на расстоянии $x$ от его центра.
A3
0.30
Найдите модуль напряженности поле на оси кольца на расстоянии $x$ от его центра.
A4
0.60
При каком значении $x$ напряженность поля на оси кольца максимальна? Найдите эту максимальную напряженность.
A5
0.60
Найдите напряженность поля, создаваемого диском радиуса $R$, равномерно заряженного по поверхности с плотностью заряда $sigma$ на его оси на расстоянии $x$ от центра.
Часть B. Две половины кольца (2.0 балла)
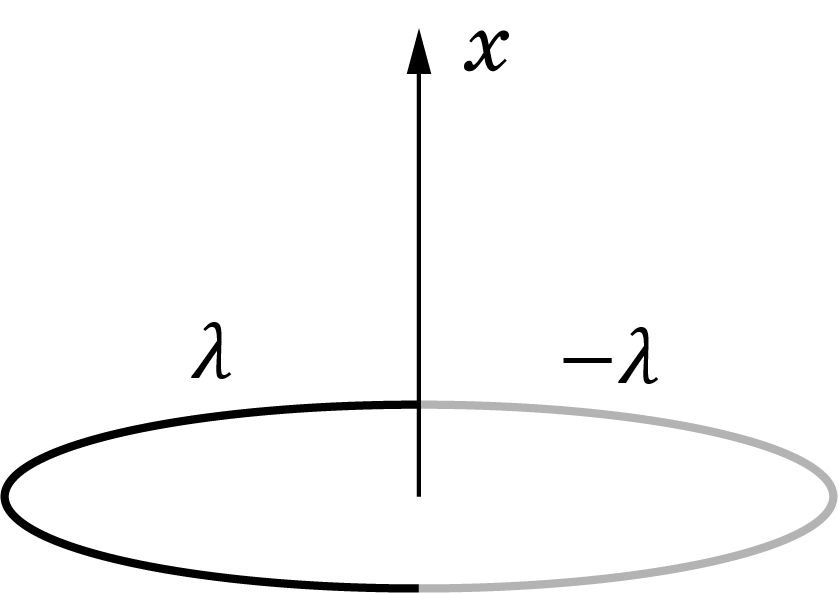
Кольцо состоит из двух половин радиуса $R$, одна из которых равномерно заряжена с линейной плотностью заряда $lambda$, а другая — с $-lambda$.
B1
0.20
Найдите потенциал на оси кольца на расстоянии $x$ от его центра.
B2
1.00
Найдите модуль напряженности поля в центре кольца.
B3
0.80
Найдите модуль напряженности поля на оси кольца на расстоянии $x$ от его центра.
Часть C. Цилиндр (6 баллов)
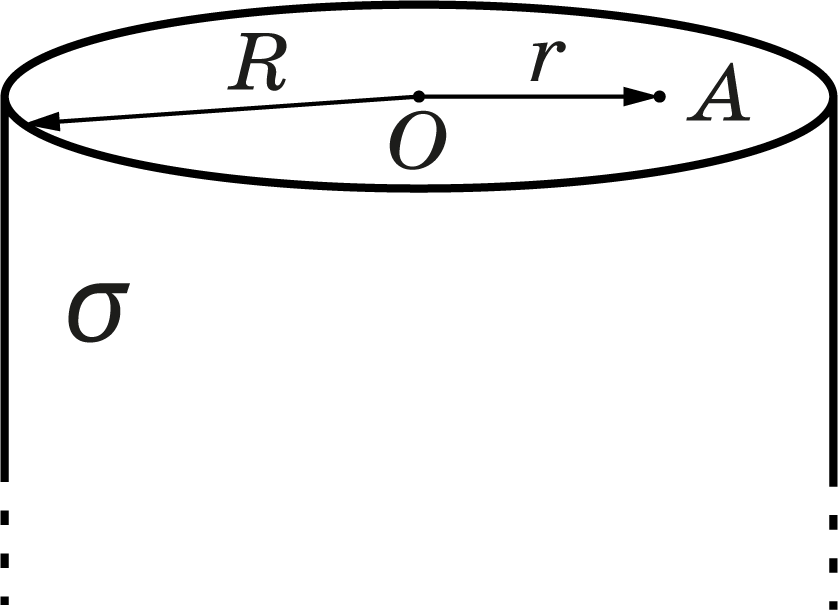
Бесконечный цилиндр радиуса $R$ равномерно заряжен по боковой поверхности с поверхностной плотностью заряда $sigma$.
C1
0.30
Чему равен модуль напряженности электрического поля на расстоянии $r < R$ от оси цилиндра?
Теперь рассмотрим полубесконечный цилиндр того же радиуса $R$, равномерно заряженного с той же поверхностной плотностью заряда $sigma$. От вас потребуется найти поле в каждой точке основания цилиндра (см. рис.).
C2
2.00
Найдите модуль напряженности поля в центре основания цилиндра $O$.
C3
0.70
Рассмотрим точку $A$ в основании цилиндра, находящуюся на расстоянии $r < R$ от точки $O$. Найдите проекцию вектора напряженности электрического поля на линию $OA$.
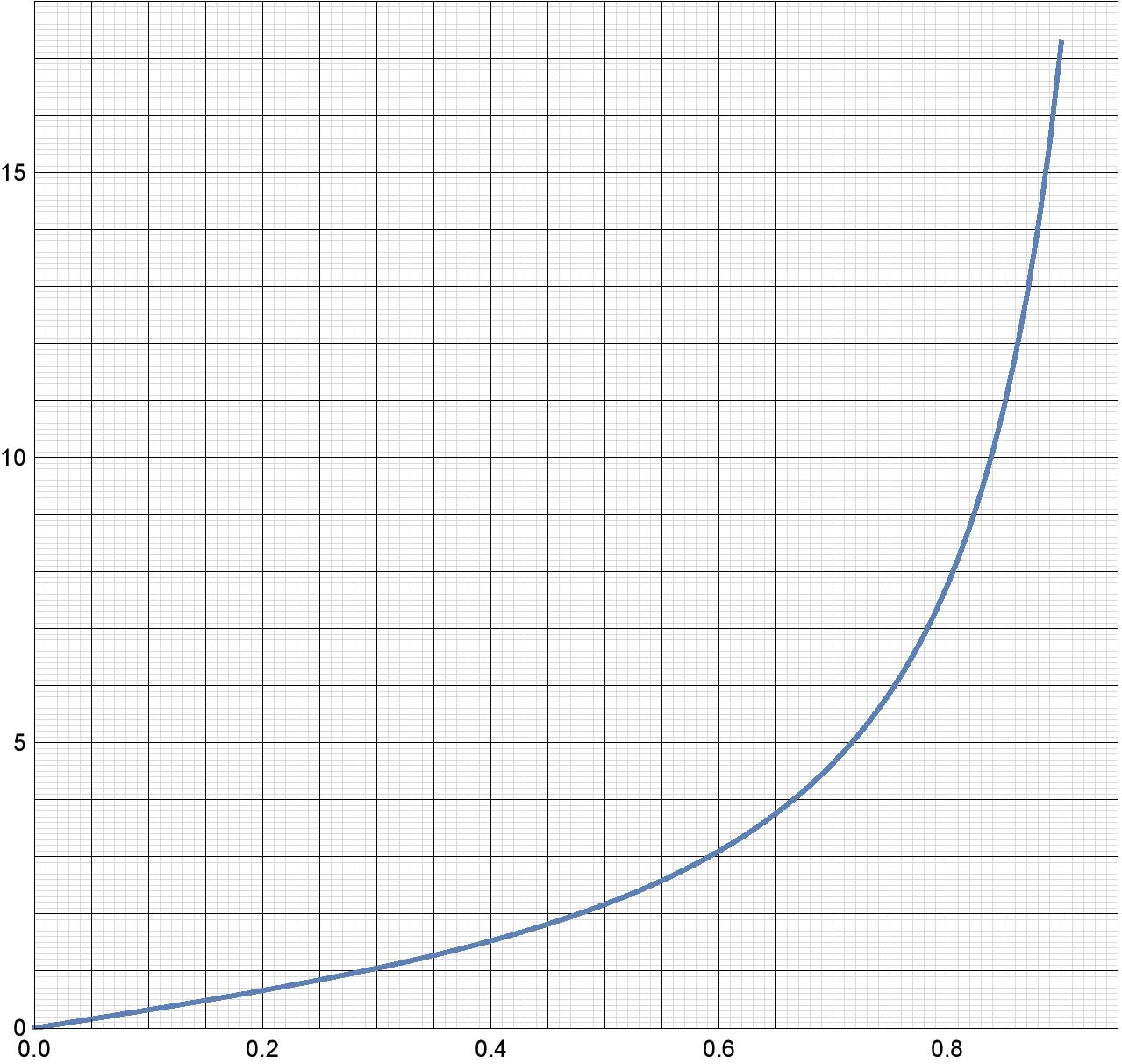
Для решения следующего пункта вам может понадобиться зависимость радиальной компоненты напряженности поля кольца в его плоскости. Если кольцо радиуса $R$ равномерно заряжено зарядом $Q$, то на расстоянии $r$ от его центра радиальная компонента напряженности поля равна
$$E_r=frac{kQ}{2{pi}R^2}cdot y(x)$$
где $x=r/R$. График зависимости $y(x)$ представлен на рисунке ниже.
C4
3.00
Для рассматриваемого полубесконечного цилиндра найдите модуль напряженности электрического поля в точке $A$, находящейся на расстоянии $r=0,!9R$ от точки $O$.
Особенности расчёта напряжённости электрического поля при непрерывном пространственном распределении заряда.
Можно выделить три типа непрерывного
распределения заряда: объёмное,
поверхностное, линейное.
Объёмное распределение характеризуется
объёмной плотностью заряда:
;
поверхностное – поверхностной плотностью
заряда:
;
линейное – линейной плотностью заряда:
.
При известных распределениях
,
,
конечный заряд находится интегрированием
соответственно по объёму, поверхности,
линии:
,
,
.
Считая элементарный заряд
точечным, для напряжённости поля
точечного заряда в диэлектрике следует
записать:
.
Результирующее поле находится
интегрированием:
,
.
Например, в случае объёмного распределения:
,
где интегрирование проводится по всему
пространству, в котором
отлично от нуля.
Таким образом, зная распределение
зарядов
,
,
,
можно полностью решить задачу о нахождении
напряжённости электрического поля. В
общем случае расчёт сопряжён со
значительными математическими
трудностями, так как связан с вычислением
трёх интегралов для нахождения проекций,
,
.
Задача облегчается в случаях, когда
распределение зарядов обладает некоторой
симметрией.
Электрическое поле на оси равномерно заряженного тонкого кольца.
Выделим элементарный участок кольца с
зарядом
,
где R- радиус кольца.
В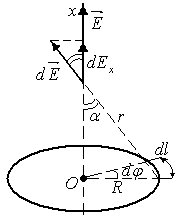
напряженность от элементарного участка
направлена вдольв случае
.
Очевидно, результирующее поле направлено
вдоль оси
.
Найдем проекцию:
;
Результирующая напряженность равна:
где
—
заряд кольца,.
Напряженность электрического поля
равна нулю в центре кольца и убывает до
нуля при
по
закону обратных квадратов:
,
так как для этих точек
.
Таким образом, величина напряженности
принимает максимальное значение в
некоторой точке на оси, которую можно
найти, используя необходимое условие
максимума:
.
Координата этой точки равна:
.
Убедитесь в этом самостоятельно.
Максимальное значение
равно:
.
Электрическое поле на оси равномерно заряженного круга.
Р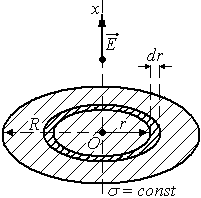
поле на оси круга можно вычислить как
сумму полей колец с радиусами отдо
–
радиус круга:
;
,
где
;
П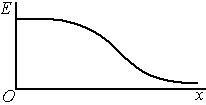
.
Зависимость
представлена на графике. Вблизи круга
или при
(неограниченная пластина). Напряженность
не зависит от расстояния:
.
Поле неограниченной пластины является
однородным. Вдали от круга при
электрическое поле убывает как поле
точечного заряда по закону обратных
квадратов:
,
где
— заряд круга.
Самостоятельно исследуйте электрическое
поле на оси круглого отверстия в
неограниченной равномерно заряженной
пластине.
Электрическое поле равномерно заряженной нити ().
а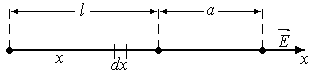
().
Введем обозначение,
где— длина нити,
– расстояние до точки от ближайшего
конца нити.
Н
от элементарного участка нитиравна:
.
Для результирующей напряженности
получаем:
.
Для точек, удаленных от нити, при условии
,
напряженность убывает по закону обратных
квадратов:
.
б) Электрическое поле прямой нити в
точках вне оси.
Геометрия положения точки пространства
относительно нити однозначно задается
расстоянием
и углами
и
.
Выделим элементарный участок
нити, который создает элементарную
напряженность в точке величиной
.
Здесь
,
– расстояние от элементарного участка
до
точки,—
полярный угол для элементарного участка,—
угловой размер элементарного участка.
В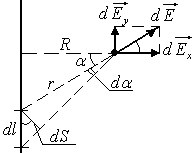
переменной интегрированияна полярный угол
.
Воспользуемся для этого геометрической
связью
,
— элементарный участок дуги окружности
радиусом
.
Для проекций
и
получаем:
,
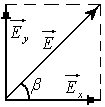
Интегрируя от
до
находим для проекций:
,
.
Модуль результирующего вектора равен
,
а направление вектора определяется
углом,
для которого выполняется условие:
.
Отметим, что электрическое поле прямой
нити обладает осевой симметрией.
Соседние файлы в папке Физика2
- #
- #
- #
- #
- #
- #
Максимальная напряженность поля в зависимости от расстояния
Решим несколько задач, связанных с определением напряженности поля на различных расстояниях от объекта, который является источником поля. Здесь потребуется вспомнить правила взятия производной сложной функции, а также и предел функции.
Задача 1.
При напряженности электрического поля В/м воздух перестает быть надежным изолятором и в нем происходит искровой разряд. Каким должен быть радиус металлического шара, чтобы на нем мог удержаться заряд в 1 Кл?
Напряженность поля заряженного шара выражается формулой
Отсюда найдем радиус:
Ответ: 94,9 м.
Задача 2.
В вершинах квадрата со стороной расположены четыре одинаковых заряда
. Определить максимальную напряженность поля на оси, проходящей через середину квадрата перпендикулярно его плоскости. На каком расстоянии от квадрата напряженность максимальна?
Задача 2
Каждый из зарядов будет делать вклад в суммарную напряженность поля в данной точке. Вектора напряженностей от пары зарядов, находящихся в противоположных углах, частично компенсируют друг друга: горизонтальные их составляющие (проекции на плоскость квадрата) в сумме дадут ноль. Поэтому складываться будут вертикальные составляющие – проекции напряженностей на вертикальную ось. Проекция напряженности поля на вертикальную ось от одного заряда равна:
От четырех зарядов:
Расстояние до заряда , определим его. Если сторона квадрата
, то диагональ равна
, а половина диагонали —
. Пусть от плоскости квадрата до точки
расстояние
:
. Тогда
А косинус угла
Подставим:
В этой формуле переменная величина – расстояние . Чтобы найти максимум функции
, возьмем производную:
Приравняем производную к нулю, чтобы найти экстремум:
Мы определили расстояние, на котором напряженность будет максимальной – можно убедиться в том, что это именно точка максимума, определив знак производной слева и справа от данной точки. Теперь можно подставить это расстояние в формулу напряженности поля и определить максимальную напряженность:
Ответ: максимальная напряженность достигается на расстоянии
от плоскости квадрата.
Задача 3.
Тонкое проволочное кольцо радиусом имеет заряд
. Найти напряженность поля на оси кольца на расстоянии
от его центра. Построить график зависимости
.
Задача похожа на предыдущую. Только теперь элементарные заряды распределены по кольцу, и каждый заряд создает вектор напряженности. Таким образом, получим поверхность в виде конуса, составленную из векторов напряженностей отдельных элементарных зарядов.
Если встать в центр кольца, то вектора полностью скомпенсируют друг друга, и суммарная напряженность будет нулевой. Однако, как только мы сдвинемся чуть вправо или влево из этой точки, то напряженность уже не будет нулевой, так как у векторов появится продольная составляющая, и именно сумма всех этих составляющих и даст напряженность поля в любой точке на оси кольца, удаленной от него на расстояние . Элементарный заряд можно найти как
. Напряженность, создаваемая им,
Где , а косинус угла
Напряженность поля ото всех зарядов:
Чтобы найти максимум функции , возьмем производную:
Приравняем производную к нулю, чтобы найти экстремум:
Определим максимальную напряженность поля в этой точке, подставив это расстояние в выражение для напряженности:
Мы выяснили, что в центре кольца напряженность поля нулевая и растет с расстоянием , пока не достигнет максимума на расстоянии
. Теперь посмотрим, чему будет равна напряженность на бесконечно большом расстоянии: устремим
к бесконечности.
Так как в этой функции и в числителе, и в знаменателе, и мы имеем неопределенность типа бесконечность на бесконечность, то определим предел по правилу Лопиталя:
Итак, можно строить график:
Задача 3, график