Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
Given four sides of quadrilateral a, b, c, d, find the maximum area of the quadrilateral possible from the given sides .
Examples:
Input : 1 2 1 2 Output : 2.00 It is optimal to construct a rectangle for maximum area .
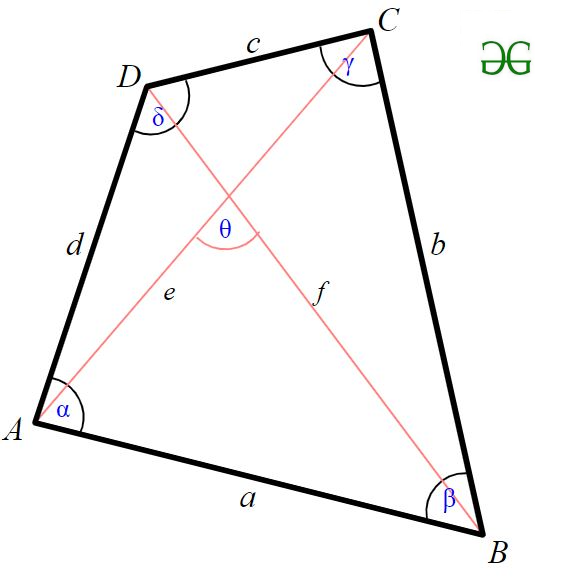
According to Bretschneider’s formula, the area of a general quadrilateral is given by
Here a, b, c, d are the sides of a quadrilateral, s is the semiperimeter of a quadrilateral and angles are two opposite angles.
So, this formula is maximized only when opposite angles sum to pi(180) then we can use a simplified form of Bretschneider’s formula to get the (maximum) area K.
This formula is called as Brahmagupta’s formula .
Below is the implementation of given approach
C++
#include <iostream>
#include <math.h>
using namespace std;
double maxArea(double a, double b,
double c, double d)
{
double semiperimeter = (a + b + c + d) / 2;
return sqrt((semiperimeter - a) *
(semiperimeter - b) *
(semiperimeter - c) *
(semiperimeter - d));
}
int main()
{
double a = 1, b = 2, c= 1, d = 2;
cout <<maxArea(a, b, c, d);
return 0;
}
C
#include <stdio.h>
#include <math.h>
double maxArea(double a, double b,
double c, double d)
{
double semiperimeter = (a + b + c + d) / 2;
return sqrt((semiperimeter - a) *
(semiperimeter - b) *
(semiperimeter - c) *
(semiperimeter - d));
}
int main()
{
double a = 1, b = 2, c= 1, d = 2;
printf("%.2fn",maxArea(a, b, c, d));
return 0;
}
Java
import java.io.*;
class GFG
{
static double maxArea(double a, double b,
double c, double d)
{
double semiperimeter = (a + b + c + d) / 2;
return Math.sqrt((semiperimeter - a) *
(semiperimeter - b) *
(semiperimeter - c) *
(semiperimeter - d));
}
public static void main (String[] args)
{
double a = 1, b = 2, c= 1, d = 2;
System.out.println(maxArea(a, b, c, d));
}
}
Python3
import math
def maxArea (a , b , c , d ):
semiperimeter = (a + b + c + d) / 2
return math.sqrt((semiperimeter - a) *
(semiperimeter - b) *
(semiperimeter - c) *
(semiperimeter - d))
a = 1
b = 2
c = 1
d = 2
print("%.2f"%maxArea(a, b, c, d))
C#
using System;
class GFG {
static double maxArea(double a, double b,
double c, double d)
{
double semiperimeter = (a + b + c + d) / 2;
return Math.Sqrt((semiperimeter - a) *
(semiperimeter - b) *
(semiperimeter - c) *
(semiperimeter - d));
}
public static void Main ()
{
double a = 1, b = 2, c= 1, d = 2;
Console.WriteLine(maxArea(a, b, c, d));
}
}
PHP
<?php
function maxArea( $a, $b, $c, $d)
{
$semiperimeter = ($a + $b + $c + $d) / 2;
return sqrt(($semiperimeter - $a) *
($semiperimeter - $b) *
($semiperimeter - $c) *
($semiperimeter - $d));
}
$a = 1; $b = 2; $c= 1; $d = 2;
echo(maxArea($a, $b, $c, $d));
?>
Javascript
<script>
function maxArea(a, b, c, d)
{
let semiperimeter = (a + b + c + d) / 2;
return Math.sqrt((semiperimeter - a) *
(semiperimeter - b) *
(semiperimeter - c) *
(semiperimeter - d));
}
let a = 1, b = 2, c= 1, d = 2;
document.write(maxArea(a, b, c, d));
</script>
Output:
2.00
Time Complexity: O(logn)
Auxiliary Space: O(1)
Please suggest if someone has a better solution which is more efficient in terms of space and time.
This article is contributed by Aarti_Rathi. Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above
Last Updated :
22 Jun, 2022
Like Article
Save Article
Порядок следования сторон не влияет на площадь. Допустим, у нас имеется выпуклый четырёхугольник $%ABCD$% с основанием $%AD$%. Отрежем от него треугольник $%ABC$%, а потом приставим его к $%AC$% с разворотом. При этом порядок следования длин изменится — например, с $%3,4,5$% на $%4,3,5$%. Легко видеть, что при помощи таких действий можно получить любую из шести перестановок.
Максимум площади четырёхугольника с заданными длинами наблюдается у вписанного четырёхугольника. Эта задача встречается во многих сборниках. Сама максимальная площадь $%S$% может быть вычислена по формуле $$S^2=(p-a)(p-b)(p-c)(p-d),$$ где $%p$% — полупериметр. Для случая длин $%3,4,5,6$% имеем $%p=9$%, а площадь равна $%S=6sqrt{10}$%.
Сообщения без ответов | Активные темы | Избранное
|
|
Максимальная площадь четырехугольника
|
|
29/07/08 |
Четырёхугольник имеет стороны длиной
|
|
|
|
|
мат-ламер |
Re: Максимальная площадь четырехугольника
|
||
30/01/09 |
(Оффтоп) Интересна физическая аналогия. Пусть мы внутрь четырёхугольника закачиваем газ. Одну сторону будем удерживать. Для остальных сторон рассмотреть условия их равновесия.
|
||
|
|
|||
|
slavav |
Re: Максимальная площадь четырехугольника
|
||
26/05/14 |
Интуиция подсказывает что четырехугольник будет вписан в окружность. — 05.11.2021, 20:55 — Ответ тут в комментарии.
|
||
|
|
|||
|
zykov |
Re: Максимальная площадь четырехугольника
|
|
18/09/21 |
Вписанный четырёхугольник Цитата: Вписанный четырёхугольник имеет максимальную площадь среди всех четырёхугольников, имеющих ту же последовательность длин сторон.
|
|
|
|
|
lel0lel |
Re: Максимальная площадь четырехугольника
|
|
20/04/10 |
Не безынтересен вопрос — какая может быть минимальная площадь?
|
|
|
|
|
zykov |
Re: Максимальная площадь четырехугольника
|
|
18/09/21 |
какая может быть минимальная площадь? Если выпуклый, то вырождается в треугольник — одна из сторон равна сумме двух из этих 4 величин.
|
|
|
|
|
vicvolf |
Re: Максимальная площадь четырехугольника
|
|
23/02/12 |
Не безынтересен вопрос — какая может быть минимальная площадь?
|
|
|
|
|
worm2 |
Re: Максимальная площадь четырехугольника
|
||
01/08/06 |
какая может быть минимальная площадь? Если выпуклый, то вырождается в треугольник — одна из сторон равна сумме двух из этих 4 величин. Да, это следует из той же обобщённой формулы Брахмагупты. Сумма противоположных углов должна быть минимальна (соответственно, сумма двух других противоположных углов — максимальна). Два локальных минимума, из которых выбирается тот, что меньше.
|
||
|
|
|||
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Задания Д27 C4 № 6906
На плоскости дан набор точек с целочисленными координатами. Необходимо найти четырёхугольник наибольшей площади с вершинами в этих точках, две вершины которого лежат на оси Ox, а две оставшиеся – по разные стороны от оси Ox.
Вам предлагается два задания с похожими условиями: задание А и задание Б. Вы можете решать оба задания или одно из них по своему выбору. Задание Б более сложное, его решение оценивается выше. Итоговая оценка выставляется как максимальная из оценок за задания А и Б.
Задание А. Имеется набор данных, состоящий из 10 пар координат.
Напишите программу для решения такой задачи. В этом варианте задания оценивается только правильность программы, время работы и размер использованной памяти не имеют значения.
Максимальная оценка за правильную программу – 2 балла.
Задание Б. Имеется набор данных, состоящий из пар координат. Пар может быть много.
Напишите программу для решения этой задачи.Постарайтесь сделать программу эффективной по времени и используемой памяти (или хотя бы по одной из этих характеристик).
Программа считается эффективной по времени, если время работы программы пропорционально количеству пар чисел N, т. е. при увеличении N в k раз время работы программы должно увеличиваться не более чем в k раз.
Программа считается эффективной по памяти, если размер памяти, использованной в программе для хранения данных, не зависит от числа N и не превышает 1 килобайта.
Максимальная оценка за правильную программу, эффективную по времени и памяти, — 4 балла.
Максимальная оценка за правильную программу, эффективную по времени, но неэффективную по памяти, — 3 балла.
Перед текстом программы кратко опишите алгоритм решения задачи и укажите используемый язык программирования и его версию. Описание входных данных.
В первой строке вводится одно целое положительное число — количество точек N. Каждая из следующих N строк содержит два целых числа: сначала координата x, затем координата y очередной точки.
Описание выходных данных.
Программа должна вывести одно число — максимальную площадь четырёхгольника, удовлетворяющего условиям задачи. Если такого четырёхугольника не существует, программа должна вывести ноль.
Пример входных данных:
6
0 0
2 0
0 2
3 -3
5 -5
6 6
Пример выходных данных для приведённого выше примера входных данных:
11
Рассматривайте только четырёхугольники со сторонами лежащими не на оси Ox.
Комментарий.
В оригинальной формулировке задачи последнего условия нет, что создаёт дополнительные трудности при поиске необходимых четырёхугольников.
Решение.
Искомый четырёхугольник состоит из двух треугольников с общим основанием, лежащим на оси Ox, при этом один треугольник лежит выше этой оси, другой – ниже. Площадь четырёхугольника будет максимальной, если вершины на оси Ox будут расположены как можно дальше друг от друга, а вершины, не лежащие на этой оси, — как можно дальше от неё. Программа читает исходные данные, не запоминая все точки в массиве. Для каждой точки проверяется её принадлежность оси Ox (условие y=0). Среди точек, лежащих на оси, необходимо найти наиболее далеко отстоящие друг от друга – они дадут наибольшее возможное общее основание двух треугольников. Это будут точки с наименьшим и наибольшим значением координаты x. Среди точек, не лежащих на оси Ox, надо найти две точки, расположенные по разные стороны от оси и как можно дальше от неё, — они дадут наибольшие возможные значения высот треугольников. Это будут точки с наибольшим положительным и
наименьшим отрицательным значением координаты y.
Таким образом, задача сводится к нахождению максимального и минимального x среди точек, у которых y=0, максимального и минимального y среди остальных точек и нахождению площади четырёхугольника на основе этих данных.
Перед выводом результата необходимо убедиться в существовании искомого четырёхугольника.
Пример правильной и эффективной программы на языке Паскаль
program c4;
var
n: integer;
x, y: integer;
xmin, xmax: integer;
xsearch: boolean;
ymin, ymax: integer;
i: integer;
s: real;
begin
xsearch := true;
xmin := 0; xmax := 0;
ymin:=0; ymax := 0;
readln(n);
for i:=1 to n do begin
readln(x,y);
if y=0 then begin
if xsearch or (x < xmin) then xmin:=x;
if xsearch or (x > xmax) then xmax:=x;
xsearch:=false;
end
else if y < ymin then ymin:=y
else if y > ymax then ymax:=y
end;
if (xmax>xmin) and (ymin<0) and (ymax>0)
then s := (xmax-xmin)*(ymax-ymin)/2
else s := 0;
writeln(s);
end.
Пример правильной и эффективной программы на языке Бейсик
DIM n AS INTEGER
DIM x, y AS INTEGER
DIM xmin, xmax AS INTEGER
DIM xsearch AS INTEGER
DIM ymin, ymax AS INTEGER
DIM i AS INTEGER
DIM s AS DOUBLE
xsearch = 1
xmin = 0: xmax = 0
ymin = 0: ymax = 0
INPUT n
FOR i = 1 TO n
INPUT x, y
IF y = 0 THEN
IF xsearch = 1 OR x < xmin THEN xmin = x
IF xsearch = 1 OR x > xmax THEN xmax = x
xsearch = 0
ELSEIF y < ymin THEN ymin = y
ELSEIF y > ymax THEN ymax = y
END IF
NEXT i
IF xmax > xmin AND ymin < 0 AND ymax > 0 THEN
s = (xmax — xmin) * (ymax – ymin) / 2
ELSE
s = 0
END IF
PRINT s
Пример правильной и эффективной программы на Алгоритмическом языке
алг c4
нач
цел n
цел x,y
цел xmin=0, xmax=0
лог xsearch=да
цел ymin=0, ymax=0
цел i
вещ s
ввод n
нц для i от 1 до n
ввод x, y
если y=0
то
если xsearch или xесли xsearch или x>xmax то xmax:=x все
xsearch:=нет
иначе
если yесли y>ymax то ymax:=y все
все
кц
если xmax > xmin и ymin < 0 и ymax > 0
то s:=(xmax-xmin)*(ymax-ymin)/2
иначе s:=0
все
вывод s
кон
Пример решения задачи А на языке Паскаль.
varcoord: array[1..10, 1..2] of integer; {исходные данные}
x, y: integer; {координаты очередной точки}
xminpos, xmaxpos, yminpos, ymaxpos: integer; {координаты точек четырёхугольника с наибольшей площадью}
s: real; {площадь четырёхугольника}
i, j: integer;
begin
xminpos := MaxInt; xmaxpos := -(MaxInt-1);
yminpos := MaxInt; ymaxpos := -(MaxInt-1);
for i := 1 to 10 do begin
read(x, y);
coord[i, 1] := x; coord[i, 2] := y;
end;
for i := 1 to 10 do begin
if (coord[i, 2] = 0) and (coord[i, 1] < xminpos) then xminpos := coord[i, 1];
if (coord[i, 2] = 0) and (coord[i, 1] > xmaxpos) then xmaxpos := coord[i, 1];
if (coord[i, 2] <> 0) and (coord[i, 2] < yminpos) then yminpos := coord[i, 2];
if (coord[i, 2] <> 0) and (coord[i, 2] > ymaxpos) then ymaxpos := coord[i, 2];
end;
if (xminpos = xmaxpos) or (yminpos = ymaxpos) or (xminpos = MaxInt) then
s := 0
else s := (xmaxpos - xminpos)*(ymaxpos-yminpos)/2;
writeln(s);
end.
�������
����� ������������ ������� ����� ����� ����ң���������,
����� ������ �������� ����� 1, 4, 7, 8?
�������
���������� ����ң���������, ��� �������� ������� ��������
����� 1 � 8. ����� ��� ������ �������� ������� ����� 4 � 7.
���� �������, ������ 1 � 8 ��������������, �� �����ģ� ���������
� �������� ������������ ţ ����������� �������������� ����
�� ��������� �������������. ����� �������, ������ 1 � 8 �����
���������, � ������� ����ң���������� �� ���������.
����� S — ������� ������� ����ң����������, α — ����
����� ��������� ���������, ������� 1 � 8, � ⠗ ���� �����
��������� ���������, ������� 4 � 7. �����
S = · 1· 8 sin α +
· 4· 7 sin β
· 1· 8+
· 4· 7
=4+14 = 18.
������ ������, ��� ��� ������ �������� ���������� ����ң���������,
������� �������� ����� 18. �������������, ���������
12+82=42+72 , ������� ������ ������������� ����ң���������,
������������ �� ���� ������������� ������������� � �������� 1, 8 �
4, 7 � ����� �����������, ������ .
�����
18.
��������� � ���������� �������������
| web-���� | |
| �������� | ������� ����� �� ��������� �.�.������� |
| URL | http://zadachi.mccme.ru |
| ������ | |
| ����� | 2581 |

 .
.  .
.  , когда
, когда  .
.
