Сообщения без ответов | Активные темы | Избранное
|
|
Максимальная площадь трапеции
|
|
20/02/16 |
Доброго времени суток. Задача: найти максимальную площадь трапеции с двумя углами по 60 градусов, вписанной в единичную окружность. Вроде бы естественно предположить, что решение состоит в нахождении условного экстремума, следовательно, в применении метода Лагранжа. Но здесь я не знаю как формализовать условие. И еще возникает следующий вопрос: можно ли решить эту задачу элементарными методами (на уровне школьной геометрии, например)?
|
|
|
|
|
DeBill |
Re: Максимальная площадь трапеции
|
||
10/01/16 |
sond Есть такая формула для площади чет-ка — через диагонали, и угол промеж них…
|
||
|
|
|||
|
redicka |
Re: Максимальная площадь трапеции
|
|
10/09/14 |
sond , можно решить по-школьному-найти наибольшее значение функции на промежутке.
|
|
|
|
|
ewert |
Re: Максимальная площадь трапеции
|
||
11/05/08 |
Можно ещё проще: найти максимальную из возможных площадей при условии, что эта площадь известна.
|
||
|
|
|||
|
Dmitriy40 |
Re: Максимальная площадь трапеции
|
||
20/08/14 |
А нужно ли решать алгебраически если задача несложно решается аналитически школьной тригонометрией? (Подсказка) Выбрав за переменную величину угол
|
||
|
|
|||
|
RikkiTan1 |
Re: Максимальная площадь трапеции
|
|
21/09/13 |
Какой ответ у этой задачи? к формуле что означает
|
|
|
|
|
sond |
Re: Максимальная площадь трапеции
|
|
20/02/16 |
Удалось получить следующее: Используем то, что вписанный угол равен половине центрального угла, опирающегося на ту же дугу: Остался лишь вопрос, как именно следует понимать одну из подсказок, приведенную выше. Конкретно, что
|
|
|
|
|
Dmitriy40 |
Re: Максимальная площадь трапеции
|
||
20/08/14 |
RikkiTan1 , sond Значком «
|
||
|
|
|||
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
В кругоиду произвольной степени х, сидящей на некотором отрезке d = const, можно вписать бесчисленной множество правильных трапеций (одна из сторон параллельна основанию), среди которых одна имеет наибольшую площадь. На этом отрезке можно построить бесчиленное множество кругоид. Какова будет степень х кругоиды, имеющей наибольшую площадь вписанной правильной трапеции, в сравнении со всеми трапециями максимальной площади, вписанными в другие кругоиды, построенные на том же отрезке d? $$18.06.2015$$ Итак, площадь трапеции в зависимости от показателя степени х изменяется таким образом:$$1)$$ при х, стремящемся к нулю, площадь трапеции S стремится к нулю; $%2)$% при х = 2 $%S = 3d^{2}(3^{1/2}/16)$% (falcao) или $%S = 2d^{2}2^{1/2}/9$% (nikolaykruzhilin1936); $%3)$% при х, стремящемся к бесконечности, $%S = 2d^{2}$%(falcao) или $%S = d^{2}3^{1/2}/4$% (nikolaykruzhilin1936)
If we have already known the perimeter of a trapezoid, what is its maximum area?
First, the equation I used to calculate the area of a trapezoid is:
$$A = frac{x+y}{2} times h$$
For my question, I suppose that the perimeter is $C$ and I have the relationship between the perimeter and bases and legs:
$$
C = x + y + a + b
$$
In this equation, $x$ and $y$ are the lengths of the bases and $a$ and $b$ are the lengths of the legs. Then we have these relationships:
$$h = a times sin{alpha} = b times sinbeta$$
$$y + atimes cosalpha + b times cosbeta = x$$
$$$$
wherein $alpha$ is the angle between base $x$ and leg $a$ and $beta$ is the angle between base $y$ and leg $b$. $h$ is the length of the height. Then I do not know how to continue my work.
Further thinking: If the sum of lengths of one base and two legs are fixed, that is:
$$C = x + a + b$$
what is the maximum area of the trapezoid? Anticipating your reply.
Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
|||
|
В окружности радиусом [math]R[/math] вписана трапеция с большим основанием [math]2R[/math] и острым углом [math]alpha[/math]. Найти при каком значении угла [math]alpha[/math] площадь трапеции будет максимальна. В общем задача не из трудных, интереснее будет графическое доказательство максимума площади.
|
||
| Вернуться к началу |
|
||
|
KOPMOPAH |
|
||
|
Нетрудно получить, что площадь трапеции [math]S=frac{2R+2R(sin^2alpha-cos^2alpha)}2.Rsin 2alpha[/math] С учетом дифференцирования результат представляем как [math]S=R^2left(sin2alpha -frac{sin4alpha}2right)[/math] Дальше [math]S'(alpha)=2cos 2alpha-2cos 4alpha=…=sin 3alpha sin alpha^*[/math] Поскольку [math]alpha > 0 Rightarrow sin alpha ne 0[/math]. Тогда [math]sin 3alpha=0[/math], откуда [math]3alpha=180^circ Rightarrow alpha=60^circ[/math].
|
|||
| Вернуться к началу |
|
||
| За это сообщение пользователю KOPMOPAH «Спасибо» сказали: 3axap, Andy |
|||
|
KOPMOPAH |
Заголовок сообщения: Re: Максимальная площадь вписанной трапеции
|
|
Andy писал(а): …Вам известно это доказательство? Меня со школьной скамьи учили, что графические построения сами по себе не являются доказательствами. Тем интереснее будет посмотреть, что Вы имели в виду. К великому сожалению мне неизвестно такое доказательство, поэтому я публиковал задачу. Полностью согласен с тем, чему Вас учили в школе насчет построений и доказательств. Тем не менее дополнительные построения часто дают побольше информации и намного понятнее, чем много «букаф».
|
|
| Вернуться к началу |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Максимальная площадь вписанного прямоугольника
в форуме Начала анализа и Другие разделы школьной математики |
vulpes |
13 |
651 |
18 май 2018, 11:42 |
|
Максимальная площадь параллелограмма, вписанного в эллипс
в форуме Геометрия |
pens |
1 |
183 |
17 ноя 2020, 21:45 |
|
Площадь трапеции
в форуме Геометрия |
Lord_Adwond |
41 |
1155 |
01 июл 2017, 20:57 |
|
Площадь трапеции
в форуме Геометрия |
Eppywppq |
1 |
244 |
11 ноя 2018, 13:02 |
|
Площадь трапеции
в форуме Геометрия |
A_5 |
22 |
1281 |
16 июн 2017, 22:39 |
|
Площадь трапеции
в форуме Геометрия |
_DiMoN4iK_ |
6 |
137 |
06 ноя 2019, 10:53 |
|
Найти площадь трапеции
в форуме Геометрия |
oduv |
3 |
1172 |
18 янв 2014, 18:13 |
|
Найти площадь трапеции
в форуме Геометрия |
ceos |
6 |
643 |
25 май 2014, 21:27 |
|
Площадь криволинейной трапеции
в форуме Интегральное исчисление |
Cinnabar |
3 |
276 |
03 июл 2019, 16:18 |
|
Найти площадь криволинейной трапеции
в форуме Интегральное исчисление |
Mr_Math_Men |
1 |
222 |
05 июн 2014, 16:48 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 8 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
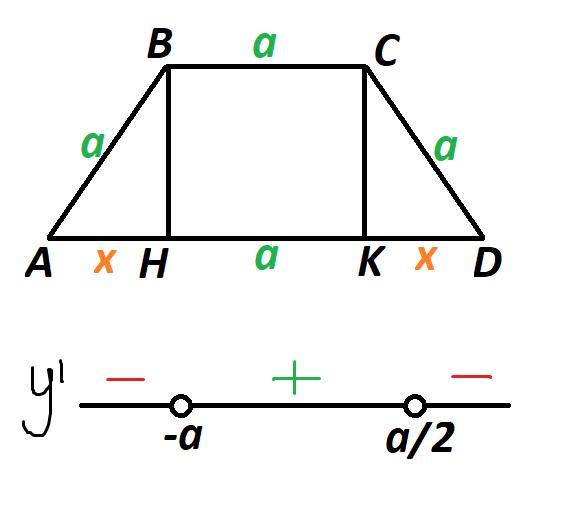
Рассмотрим трапецию ABCD.
Основания трапеции не могут иметь одинаковую длину, так как в противном случае это будет параллелограмм. Значит, одно из оснований BC и две боковые стороны AB и CD равны по а. Заметим, что рассматриваемая трапеция равнобедренная.
Проведем высоты BH и CK. Тогда, HK=а.
Обозначим AH=KD=х.
Высоту трапеции найдем по теореме Пифагора:
Запишем выражение для площади трапеции:
Исследуем на экстремумы функцию S. Найдем производную:
Найдем нули производной:
При переходе через точку производная меняет знак с минуса на плюс, значит это точка минимума.
При переходе через точку производная меняет знак с плюса на минус, значит это точка максимума.
Таким образом, наибольшую площадь трапеция имеет при . Эта площадь равна:
Ответ:
Приложения:

 , под которым боковая сторона трапеции видна из центра описанной окружности, после дополнительных построений (радиусов и перпендикуляров) и математических преобразований придём к формуле
, под которым боковая сторона трапеции видна из центра описанной окружности, после дополнительных построений (радиусов и перпендикуляров) и математических преобразований придём к формуле ![$Ssim R^2 sin alpha, alpha in [0°..120°]$ $Ssim R^2 sin alpha, alpha in [0°..120°]$](https://dxdy-03.korotkov.co.uk/f/2/4/f/24f6e5fcb1fa33734794f0cdc64e809382.png) , что сразу даёт величину максимума площади при
, что сразу даёт величину максимума площади при  и величину площади трапеции.
и величину площади трапеции. . Но тут
. Но тут  ?
? 
 Максимум, действительно, достигается при
Максимум, действительно, достигается при  , и, соответственно, максимальная площадь получается равной
, и, соответственно, максимальная площадь получается равной 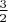 .
.  .
. .
.


