|
25 / 25 / 7 Регистрация: 02.12.2010 Сообщений: 824 |
|
|
1 |
|
Полная энергия и максимальная сила груза, подвешенного на пружине09.06.2012, 20:29. Показов 8277. Ответов 5
Привет. Помогите, пожалуйста решить задачу, осталось 2-3 до зачета
0 |
|
4444 / 2448 / 227 Регистрация: 20.08.2011 Сообщений: 3,108 |
|
|
10.06.2012, 01:44 |
2 |
|
.. А может кто-то подсказать поподробнее? Подсказать всегда пожалуйста, но решать — вам! К тому же пишу сейчас в спешке, могут быть ошибки.
1 |
|
25 / 25 / 7 Регистрация: 02.12.2010 Сообщений: 824 |
|
|
24.06.2012, 17:43 [ТС] |
3 |
|
спасибо за подсказку. но пару уточнений.
та же полная энергия та же за счет чего? за счет закона сохранения энергии или что? решая задачу как сказали вы получается, что расстояние x3 больше расстояния x2. такое разве может быть? или это за счет того, что мы его отпустили не из положения равновесия, а из точки x = x-2? где x — положение равновесия, а x-2 груз, когда его отпустили на 1 см вниз и подняли на 3 вверх ( то есть в общем подняли на 3 см от положения равновесия).
0 |
|
Комп_Оратор) 8849 / 4591 / 619 Регистрация: 04.12.2011 Сообщений: 13,703 Записей в блоге: 16 |
|
|
24.06.2012, 20:22 |
4 |
|
Мне кажется, что положение равновесия задано ее начальным растяжением на 1см (ось OX направлена вниз). То что пружина натянута, значения не имеет. Главное, что равнодействующая равна нулю и система придет в это состояние, когда израсходуется энергия колебаний. Давайте докажем это: Добавлено через 14 минут
Равнодействующая от принятого положения когда пружина не растянута X: Надо было бы:
0 |
|
25 / 25 / 7 Регистрация: 02.12.2010 Сообщений: 824 |
|
|
25.06.2012, 00:08 [ТС] |
5 |
|
равна по модулю: почему не учитывается сила тяжести? Добавлено через 1 минуту
Полная энергия пружины, груза или колебаний? груза.
0 |
|
Комп_Оратор) 8849 / 4591 / 619 Регистрация: 04.12.2011 Сообщений: 13,703 Записей в блоге: 16 |
|
|
25.06.2012, 00:34 |
6 |
|
почему не учитывается сила тяжести? Смотрите:
Раскрыв скобки: Сила тяжести равна kX0 по модулю. Грузик, ведь взвешен пружинкой как пружинными весами, и по его показаниям, вес соответствует деформации Х0 (1 см), то есть эта сила учтена. Посчитайте сами равнодействующую в верхней и нижней точке. Должно получиться kXм, где Xм=3 см.
груза. Так ведь груза, это «колебаний» и есть, не от центра ж Земли считать.
0 |
Механическая колебательная система, состоящая из пружины с коэффициентом упругости (жёсткостью) (k), один конец которой жёстко закреплён, а на втором находится груз массы (m), называется пружинным маятником.
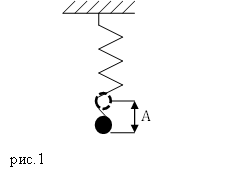
Рис. (1). Колебания пружинного маятника
Рассмотрим простейший пружинный маятник — движущееся по горизонтальной плоскости твёрдое тело (груз), прикреплённое пружиной к стене (рис. (1)). Допустим, что силы трения не оказывают существенного влияния на движение груза.
Первоначально пружина не деформирована (не растянута и не сжата), поэтому никакие силы в горизонтальном направлении на груз не действуют. Точка О — положение равновесия груза.
Переместим груз вправо. Пружина при этом растянется, и в ней возникнет сила упругости, направленная влево, к положению равновесия, и по модулю равная:
где (x=A) — максимальное (амплитудное) отклонение груза от положения равновесия.
Если отпустить груз, то под действием силы упругости он начнёт ускоренно перемещаться влево, к точке (О), по мере приближения к которой скорость груза будет возрастать от нуля до некоторого максимального значения. При приближении к точке равновесия деформация пружины уменьшается, а значит, уменьшается и сила упругости. Так как груз имеет скорость при прохождении положения равновесия, то он по инерции продолжает свое движение влево. Теперь пружина начинает сжиматься (деформация сжатия), что приводит к возникновению силы упругости, направленной вправо, т.е. к положению равновесия. По мере возрастания степени деформации пружины сила растет и все больше тормозит движение груза. В конце концов, груз останавливается.
Но сила упругости, направленная к точке (О), будет продолжать действовать, поэтому груз вновь придёт в движение в обратную сторону, вправо, и на обратном пути его скорость будет возрастать от нуля до максимального значения в точке (О).
Движение груза от точки (О) к крайней правой точке снова приведёт к растяжению пружины, опять возникнет сила упругости, направленная к положению равновесия и замедляющая движение груза до полной его остановки.
Мы описали одно полное колебание.
В каждой точке траектории, кроме положения равновесия, на груз действует сила упругости пружины, которая направлена к положению равновесия.
Второй закон Ньютона для такой системы при условии отсутствия внешних сил и сил трения имеет вид:
— ускорение пружинного маятника.
Обрати внимание!
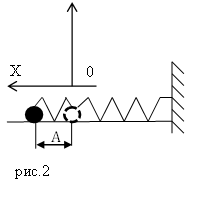
Данная формула справедлива и для вертикального пружинного маятника (рис. (2)) в котором действуют сила тяжести груза и сила упругости пружины.
Рис. (2). Колебания вертикального пружинного маятника
Обрати внимание!
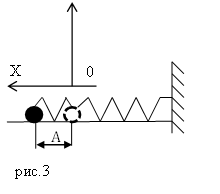
Ускорение тела, колеблющегося на пружине, не зависит от силы тяжести, действующей на это тело. Сила тяжести только приводит к первоначальному изменению (смещению вниз) положения равновесия (рис. (3)).
Рис. (3). Изображение смещения маятника
Период свободных колебаний пружинного маятника определяется по формуле Гюйгенса:
(m) — масса груза,
(k) — коэффициент жёсткости пружины.
Пружинные маятники широко используются в качестве акселерометра в системах управления баллистических ракет, контактных взрывателях артиллерийских и авиационных боеприпасов и т. п.
Акселерометр (лат. accelero — «ускоряю» и др.-греч. μετρέω — «измеряю») — прибор, измеряющий проекцию кажущегося ускорения (разности между истинным ускорением объекта и гравитационным ускорением). Как правило, акселерометр представляет собой чувствительную массу, закреплённую в упругом подвесе. Отклонение массы от её первоначального положения при наличии кажущегося ускорения несёт информацию о величине этого ускорения.
Рис. (4). Схема акселерометра
На рисунке (4) — схема простейшего акселерометра. Груз закреплён на пружине. Демпфер подавляет колебания груза. Чем больше кажущееся ускорение, тем сильнее деформируется пружина, изменяя показания прибора.
Источники:
Рис. 1. Колебания пружинного маятника. © ЯКласс.
Рис. 2. Колебания вертикального пружинного маятника. © ЯКласс.
Рис. 3. Изображение смещения маятника.
Рис. 4. Схема акселерометра.
Дифференциальное уравнение колебаний.
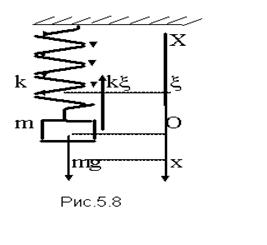
Свободные колебания. Рассмотрим колебания груза массы m, висящего на пружине, жесткость которой. Направим ось координат Х вертикально вниз,
причем за начало отсчета примем точку О (рис.5.8), лежащую на одном уровне с центром масс m, когда груз неподвижен. При этом пружина растянута на величину x по сравнению с недеформированном состоянием. Величина упругой силы, действующей на массу m, равна kx. В положении равновесия
Если теперь сместить груз из положения равновесия, то он начнет совершать колебательное движение. Колебания, которые происходят в системе, выведенной из положения равновесия и затем предоставленной самой себе, называются свободными или собственными колебаниями,а частота, с которой происходят эти колебания, называется собственной частотой.Пусть в некоторый момент времени смещение груза равно х. Тогда второй закон Ньютона в проекции на ось Х может быть записан в следующем виде:
max = mg — k (x +x) или с учетом (5-13)
В свою очередь, уравнение (5-14) можно записать иначе, если представить ускорение тела через вторую производную смещения по времени ax = d 2 x/dt 2 и обозначить величину k/m = 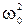
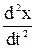
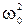
Уравнение (5-15) является дифференциальным уравнением второго порядка, однако его решение можно просто угадать простым перебором всех элементарных функций, из которых только функции синуса и косинуса удовлетворяют решению этого уравнения. Действительно, если
смещение x = A sin(w0t + j), (5-16)
то скорость тела 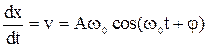
и ускорение тела 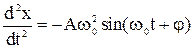
Сравнение (5-16) и (5-18) показывает, что действительно (5-16) является решением уравнения (5-15). Величины А и j остаются произвольными, для их определения необходимо использовать начальные условия, т.е. значения смещения и скорости тела в начальный момент времени. Например, если при t = 0 x (0)= 0, а v(0) = v0, то из (5-16 ) следует, что sinj = 0 и j = 0, a из (5-17) величина А = v0/w0. При этих условиях решением уравнения (5-15) служит функция х(t) = 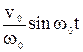
Затухающие колебания. В реальной жизни любой колебательный процесс постепенно затухает из-за наличия сил трения. Для колебаний груза на пружине существенную роль играет так называемое вязкое трение, сила которого при малых смещениях оказывается пропорциональной величине скорости тела:
Fтрен = — bv = — b 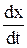
В этом случае второй закон Ньютона (уравнение движения) для груза, колеблющегося на пружине, приобретает такой вид:

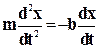
Вводя обозначения 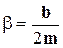
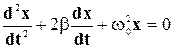
где по-прежнему 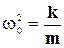
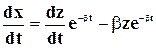
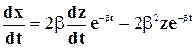
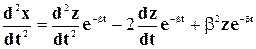
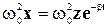
С учетом этого уравнение (5-21) может быть записано в таком виде:
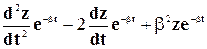
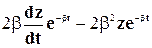
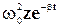
После сокращения на величину 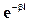
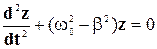
Сравнивая полученное уравнение с выражением (5-15), нетрудно заметить их почти полную идентичность; различие состоит лишь в том, что частота колебаний в (5-22) определяется из формулы 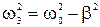
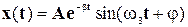
где как и ранее величины А и j определяются из начальных условий. В большинстве случаев b
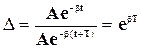
т.е. декремент затухания равен относительному уменьшению амплитуды за время, равное периоду колебания. Натуральный логарифм D называют логарифмическим декрементом затухания d, т.е. d = ln D = bТ.
Дата добавления: 2015-04-15 ; просмотров: 2782 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Свободные колебания пружинного маятника. Общие сведения
Цель работы. Ознакомиться с основными характеристиками незатухающих и затухающих свободных механических колебаний.
Задача. Определить период собственных колебаний пружинного маятника; проверить линейность зависимости квадрата периода от массы; определить жесткость пружины; определить период затухающих колебаний и логарифмический декремент затухания пружинного маятника.
Приборы и принадлежности. Штатив со шкалой, пружина, набор грузов различной массы, сосуд с водой, секундомер.
1. Свободные колебания пружинного маятника. Общие сведения
Колебаниями называются процессы, в которых периодически изменяется одна или несколько физических величин, описывающих эти процессы. Колебания могут быть описаны различными периодическими функциями времени. Простейшими колебаниями являются гармонические колебания – такие колебания, при которых колеблющаяся величина (например, смещение груза на пружине) изменяется со временем по закону косинуса или синуса. Колебания, возникающие после действия на систему внешней кратковременной силы, называются свободными.
Рассмотрим одну из простейших колебательных систем – пружинный маятник, представляющий собой груз массой m, подвешенный на абсолютно упругой пружине с коэффициентом жесткости k
(рис. 1). Пусть l0 – длина пружины без подвешенного к ней груза. При подвешивании груза под действием силы тяжести пружина растянется на x1 так, что маятник будет находиться в положении равновесия вследствие равенства модулей силы тяжести mg и упругой силы Fупр: mg = kx1, стремящейся вернуть груз в положение равновесия (полагается, что деформации пружины идеально упругие и подчиняются закону Гука).
Если груз вывести из положения равновесия, отклонив на величину x, то сила упругости возрастает: Fупр = – kx2= – k(x1 + x). Дойдя до положения равновесия, груз будет обладать отличной от нуля скоростью и пройдет положение равновесия по инерции. По мере дальнейшего движения будет увеличиваться отклонение от положения равновесия, что приведет к возрастанию силы упругости, и процесс повторится в обратном направлении. Таким образом, колебательное движение системы обусловлено двумя причинами: 1) стремлением тела вернуться в положении равновесия и 2) инерцией, не позволяющей телу мгновенно остановиться в положении равновесия. В отсутствии сил трения колебания продолжались бы сколь угодно долго. Наличие силы трения приводит к тому, что часть энергии колебаний переходит во внутреннюю энергию и колебания постепенно затухают. Такие колебания называются затухающими.
Незатухающие свободные колебания
Сначала рассмотрим колебания пружинного маятника, на который не действуют силы трения – незатухающие свободные колебания. Согласно второму закону Ньютона c учетом знаков проекций на ось X

Из условия равновесия смещение, вызываемое силой тяжести: 



Это уравнение называется дифференциальным уравнением гармонических колебаний пружинного маятника. Из этого уравнения следует, что после прекращения внешнего воздействия, приводящего к первоначальному отклонению системы от положения равновесия, движение груза обусловлено только действием упругой силы (сила тяжести вызывает постоянное смещение).
Общее решение однородного дифференциального уравнения второго порядка (2) имеет вид

Данное уравнение называется уравнением гармонических колебаний. Наибольшее отклонение груза от положения равновесия А0 называется амплитудой колебаний. Величина 

есть круговая или циклическая частота собственных колебаний, связанная с периодом колебаний Т соотношением 

Рассмотрим свободные колебания пружинного маятника при наличии силы трения (затухающие колебания). В простейшем и вместе с тем наиболее часто встречающемся случае сила трения пропорциональна скорости υ движения:
где r – постоянная, называемая коэффициентом сопротивления. Знак минус показывает, что сила трения и скорость имеют противоположные направления. Уравнение второго закона Ньютона в проекции на ось Х при наличии упругой силы и силы трения
Данное дифференциальное уравнение с учетом υ = dx/dt можно записать

где 

Чтобы получить зависимость смещения x от времени t, необходимо решить дифференциальное уравнение (8). В случае малых затуханий (

где А0 и φ0 – начальная амплитуда и начальная фаза колебаний;


Движение груза в этом случае можно рассматривать как гармоническое колебание с частотой ω и переменной амплитудой, меняющейся по закону:

На графике функции (9), рис. 2, пунктирными линиями показано изменение амплитуды (10) затухающих колебаний.
Рис. 2. Зависимость смещения х груза от времени t при наличии силы трения
Для количественной характеристики степени затухания колебаний вводят величину, равную отношению амплитуд, отличающихся на период, и называемую декрементом затухания:

Часто используют натуральный логарифм этой величины. Такой параметр называется логарифмическим декрементом затухания:

Если за время t‘ амплитуда уменьшается в n раз, то из уравнения (10) следует, что

Отсюда для логарифмического декремента получаем выражение

Если за время t‘ амплитуда уменьшается в е раз (е = 2,71 – основание натурального логарифма), то система успеет совершить число колебаний

Следовательно, логарифмический декремент затухания – величина, обратная числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в е раз. Чем больше θ, тем быстрее происходит затухание колебаний.
2. Методика эксперимента и экспериментальная установка
Рис. 3. Схема установки
Установка состоит из штатива 1 с измерительной шкалой 2. К штативу на пружине 3 подвешиваются грузы 4 различной массы. При изучении затухающих колебаний в задании 2 для усиления затухания используется кольцо 5, которое помещается в прозрачный сосуд 6 с водой.
В задании 1 (выполняется без сосуда с водой и кольца) в первом приближении затуханием колебаний можно пренебречь и считать гармоническими. Как следует из формулы (5) для гармонических колебаний зависимость T 2 = f (m) – линейная, из которой можно определить коэффициент жесткости пружины k по формуле

где 
Задание 1. Определение зависимости периода собственных колебаний пружинного маятника от массы груза.
1. Определить период колебаний пружинного маятника при различных значениях массы груза m. Для этого с помощью секундомера для каждого значения m трижды измерить время t полных n колебаний (n ≥10) и по среднему значению времени 

2. По результатам измерений построить график зависимости квадрата периода T2 от массы m. Из углового коэффициента графика определить жесткость пружины k по формуле (16).
Результаты измерений для определения периода собственных колебаний


Дифференциальное уравнение гармонических колебаний пружинного маятника и его решение
Пусть сила трения равна нулю. В этом случае, если тело вывести из положения равновесия и отпустить, то оно будет ускоренно двигаться под действием упругой силы пружины .
Примеры решения задач
Пример № 1. Гармонические колебания материальной точки описываются уравнением м. Определите амплитуду А колебаний, циклическую частоту ω0, частоту ν и период Т колебаний.
| Дано:
м. |
Решение
Уравнение гармонических колебаний имеет вид: x(t)=A∙cos(ω0∙t+φ0) (1) |
| А — ? ω0 — ? ν0 — ? Т — ? | Сравнение уравнения (1) с уравнением, приведённым в условии задачи, показывает, |
что А=0,02 м, ω0=6∙π ≈18,8 рад/с.
Поскольку ω0=2∙π∙ν0, то 3 Гц.
Период колебаний =0,33 с.
Ответ: А=0,02 м, ω0=6∙π ≈18,8 рад/с, ν0 =3 Гц, Т=0,33 с.
Пример № 2. Груз массой т=50 г, привязанный к пружине, удлиняет её на х0=4,9 см. Пружину дополнительно растянули на х=8 см и отпустили. Определите максимальную силу, действующую на груз.
| Дано:
х=8 см |
СИ:
8∙10 -2 м . |
Решение
Максимальная сила определяется уравнением: Fmax =т∙аmax. Ускорение есть вторая производная |
| Fmax — ? | Н | переменной х по времени. |
Таким образом, для решения задачи необходимо установить вид зависимости х(t)=А∙sin(ω0∙t+φ0). (1)
Амплитуду А можно определить из условия: А=х0=4,9∙10 -2 м.
Циклическая частота . (2)
Сила тяжести груза компенсируется силой упругости пружины: m∙g=k∙x0, следовательно = . Подстановка данного равенства в формулу (2) позволяет выразить циклическую частоту: .
Дифференцируя выражение (1) по времени, можно найти скорость колебательного движения: υ(t)=А∙ω0∙cos(ω0∙t+φ0). (3)
Ускорение – производная скорости по времени: а(t)=А∙ω0 2 ∙sin(ω0∙t+φ0).
Максимальное значение ускорение достигает при синусе равном единице:
Amax=А∙ω0 2 . Тогда действующая на груз максимальная сила .
Подстановка численных значений даёт: Fmax =0,8 Н.
Пример № 3. Шарик массой т=10 г совершает гармонические колебания с амплитудой А=20 см и периодом T=4 с. В момент времени t0=0 координата шарика х0=А. Определите потенциальную и кинетическую энергию в момент времени t1=1 c.
| Дано:
t1=1 c. |
СИ: | Решение
Поскольку в момент времени t0=0 координата шарика х0=А гармонические колебания шарика удобно описывать функцией косинуса без начальной фазы: x(t)=A∙cosωt. Здесь А=0,2 м, , то есть ω=π/2, следовательно x(t)=0,2∙cos(π t/2) м. |
| Ек1 — ?
Еп1 — ? |
Дж | , где |
Подстановка численных значений даёт: Ек1=4,9∙10 -4 Дж.
Потенциальная энергия . Еп1=0.
Задачи для самостоятельного решения
71. Запишите решение уравнения гармонического колебания с амплитудой А= =5 см, если за время t=1 мин совершается N=150 колебаний, а начальная фаза колебаний φ0=π/4.
72. Колебательное движение материальной точки задано уравнением: м. Определите амплитуду, начальную фазу, максимальную скорость и максимальное ускорение колебательного движения.
73. Материальная точка массой т=20 г совершает гармонические колебания с амплитудой А=5 см. Период колебаний Т=10 с. Определите значение скорости и ускорения материальной точки в момент времени, которому соответствует фаза φ=60°.
74. Движение материальной точки описывается уравнением: . Определите моменты времени, когда скорость и ускорение достигают максимальных значений.
75. Тело массой т=10 г совершает гармонические колебания по закону: м. Определите максимальные значения возвращающей силы и кинетической энергии.
76. Материальная точка массой т=50 г совершает гармонические колебания по закону: м. Определите возвращающую силу F в момент времени t=0,5 c и полную энергию материальной точки.
77. Материальная точка массой т=20 г совершает гармонические колебания по закону: м. Определите полную энергию материальной точки.
78. Полная энергия материальной точки, совершающей гармонические колебания Е=10 мкДж, а максимальная возвращающая сила Fmax=0,5 мH. Запишите кинематическое уравнение движения материальной точки, если период колебаний Т=4 с, а начальная фаза колебаний φ0=π/6.
79. К пружине, имеющей коэффициент упругости k=800 Н/м, подвешен груз и приведён в колебательное движение. Максимальная кинетическая энергия груза Е=2,5 Дж. Определите амплитуду колебаний.
80. Уравнение колебаний материальной точки массой т=10 г имеет вид: см. Определите максимальную силу Fmax, действующую на материальную точку и её полную энергию Е.
Затухающие механические колебания и их характеристики
http://pandia.ru/text/77/494/49063.php
http://knigi.studio/obschaya-fizika/differentsialnoe-uravnenie-garmonicheskih-191854.html
2017-03-10
На груз массы $M$, висящий на пружине, кладут перегрузок массы $m$, удерживая груз в первоначальном положении, а затем его отпускают. Найдите максимальное значение силы, действующей на перегрузок со стороны груза.
Решение:
Начальное равновесие дает $kx_{0} = Mg$. По закону сохранения энергии имеем
$frac{kx_{0}^{2}}{2} + (M + m)g(v_{max} — x_{0}) = frac{kx_{max}^{2}}{2}; x_{max} neq x_{0}$.
Подставляя $x_{0} = Mg/k$, получаем
$x_{max} = (M + 2m) g/k$.
Из второго закона Ньютона
$ma = mg — N$,
$(M + m)a = (M + m)g — kx$.
Отсюда $N = frac{mkx}{M+m}$ т. е.
$N_{max} = frac{mkx_{max}}{M+m} = mg frac{M + 2m}{M+m}$.
Формулы пружинного маятника в физике
Формулы пружинного маятника
Определение и формулы пружинного маятника
Определение
Пружинным маятником называют систему, которая состоит из упругой пружины, к которой прикреплен груз.
Допустим, что масса груза равна $m$, коэффициент упругости пружины $k$. Масса пружины в таком маятнике обычно не учитывается. Если рассматривать вертикальные движения груза (рис.1), то он движется под действием силы тяжести и силы упругости, если систему вывели из состояния равновесия и предоставили самой себе.
Уравнения колебаний пружинного маятника
Пружинный маятник, совершающий свободные колебания является примером гармонического осциллятора. Допустим, что маятник совершает колебания вдоль оси X. Если колебания малые, выполняется закон Гука, то уравнение движения груза имеет вид:
[ddot{x}+{omega }^2_0x=0left(1right),]
где ${щu}^2_0=frac{k}{m}$ — циклическая частота колебаний пружинного маятника. Решением уравнения (1) является функция:
[x=A{cos left({omega }_0t+varphi right)=A{sin left({omega }_0t+{varphi }_1right) } }left(2right),]
где ${omega }_0=sqrt{frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ — амплитуда колебаний; ${(omega }_0t+varphi )$ — фаза колебаний; $varphi $ и ${varphi }_1$ — начальные фазы колебаний.
В экспоненциальном виде колебания пружинного маятника можно записать как:
[Re tilde{x}=Releft(Acdot exp left(ileft({omega }_0t+varphi right)right)right)left(3right).]
Формулы периода и частоты колебаний пружинного маятника
Если в упругих колебаниях выполняется закон Гука, то период колебаний пружинного маятника вычисляют при помощи формулы:
[T=2pi sqrt{frac{m}{k}}left(4right).]
Так как частота колебаний ($nu $) — величина обратная к периоду, то:
[nu =frac{1}{T}=frac{1}{2pi }sqrt{frac{k}{m}}left(5right).]
Формулы амплитуды и начальной фазы пружинного маятника
Зная уравнение колебаний пружинного маятника (1 или 2) и начальные условия можно полностью описать гармонические колебания пружинного маятника. Начальные условия определяют амплитуда ($A$) и начальная фаза колебаний ($varphi $).
Амплитуду можно найти как:
[A=sqrt{x^2_0+frac{v^2_0}{{omega }^2_0}}left(6right),]
начальная фаза при этом:
[tg varphi =-frac{v_0}{x_0{omega }_0}left(7right),]
где $v_0$ — скорость груза при $t=0 c$, когда координата груза равна $x_0$.
Энергия колебаний пружинного маятника
При одномерном движении пружинного маятника между двумя точками его движения существует только один путь, следовательно, выполняется условие потенциальности силы (любую силу можно считать потенциальной, если она зависит только от координат). Так как силы, действующие на пружинный маятник потенциальны, то можно говорить о потенциальной энергии.
Пусть пружинный маятник совершает колебания в горизонтальной плоскости (рис.2). За ноль потенциальной энергии маятника примем положение его равновесия, где поместим начало координат. Силы трения не учитываем. Используя формулу, связывающую потенциальную силу и потенциальную энергию для одномерного случая:
[E_p=-frac{dF}{dx}(8)]
учитывая, что для пружинного маятника $F=-kx$,
тогда потенциальная энергия ($E_p$) пружинного маятника равна:
[E_p=frac{kx^2}{2}=frac{m{{omega }_0}^2x^2}{2}left(9right).]
Закон сохранения энергии для пружинного маятника запишем как:
[frac{m{dot{x}}^2}{2}+frac{m{{omega }_0}^2x^2}{2}=const left(10right),]
где $dot{x}=v$ — скорость движения груза; $E_k=frac{m{dot{x}}^2}{2}$ — кинетическая энергия маятника.
Из формулы (10) можно сделать следующие выводы:
- Максимальная кинетическая энергия маятника равна его максимальной потенциальной энергии.
- Средняя кинетическая энергия по времени осциллятора равна его средней по времени потенциальной энергии.
Примеры задач с решением
Пример 1
Задание. Маленький шарик, массой $m=0,36$ кг прикреплен к горизонтальной пружине, коэффициент упругости которой равен $k=1600 frac{Н}{м}$. Каково было начальное смещение шарика от положения равновесия ($x_0$), если он при колебаниях проходит его со скоростью $v=1 frac{м}{с}$?
Решение. Сделаем рисунок.
По закону сохранения механической энергии (так как считаем, что сил трения нет), запишем:
[E_{pmax}=E_{kmax }left(1.1right),]
где $E_{pmax}$ — потенциальная энергия шарика при его максимальном смещении от положения равновесия; $E_{kmax }$ — кинетическая энергия шарика, в момент прохождения положения равновесия.
[E_{kmax }=frac{mv^2}{2}left(1.2right).]
Потенциальная энергия равна:
[E_{pmax}=frac{k{x_0}^2}{2}left(1.3right).]
В соответствии с (1.1) приравняем правые части (1.2) и (1.3), имеем:
[frac{mv^2}{2}=frac{k{x_0}^2}{2}left(1.4right).]
Из (1.4) выразим искомую величину:
[x_0=vsqrt{frac{m}{k}}.]
Вычислим начальное (максимальное) смещение груза от положения равновесия:
[x_0=1cdot sqrt{frac{0,36}{1600}}=1,5 cdot {10}^{-3}(м).]
Ответ. $x_0=1,5$ мм
Пример 2
Задание. Пружинный маятник совершает колебания по закону: $x=A{cos left(omega tright), } $где $A$ и $omega $ — постоянные величины. Когда возвращающая сила в первый раз достигает величины $F_0,$ потенциальная энергия груза равна $E_{p0}$.
В какой момент времени это произойдет?
Решение. Возвращающей силой для пружинного маятника является сила упругости, равная:
[F=-kx=-kA{cos left(omega tright)left(2.1right). }]
Потенциальную энергию колебаний груза найдем как:
[E_p=frac{kx^2}{2}=frac{kA^2{{cos }^2 left(omega tright) }}{2}left(2.2right).]
В момент времени, который следует найти $F=F_0$; $E_p=E_{p0}$, значит:
[frac{E_{p0}}{F_0}=-frac{A}{2}{cos left(omega tright) }to t=frac{1}{omega } arc{cos left(-frac{2E_{p0}}{AF_0}right) }.]
Ответ. $t=frac{1}{omega } arc{cos left(-frac{2E_{p0}}{AF_0}right) }$
Читать дальше: формулы равноускоренного прямолинейного движения.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!




 Стало быть, те же kX02/2 или mgXм
Стало быть, те же kX02/2 или mgXм