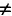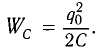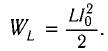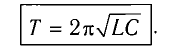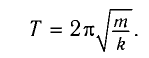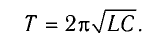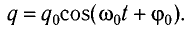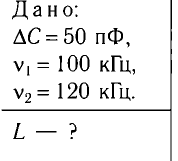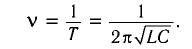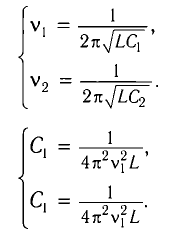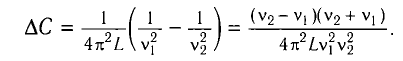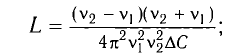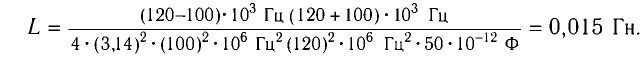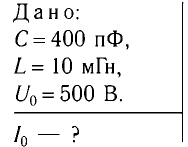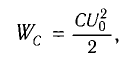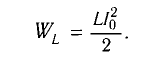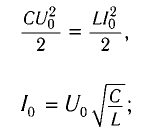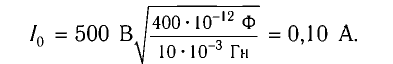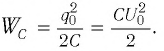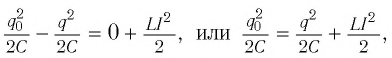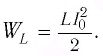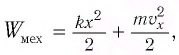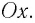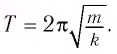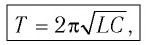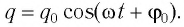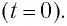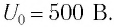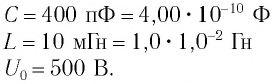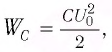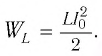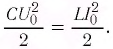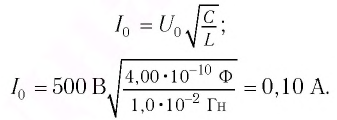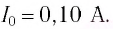Как найти максимальную силу тока в контуре

Условие задачи:

Определите максимальный ток в контуре, если длина электромагнитной волны в вакууме, на которую настроен колебательный контур – 75,36 м, а максимальный заряд конденсатора равен 10 нКл.

Задача №9.13.4 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(lambda=75,36) м, (q_m=10) нКл, (I_m-?)

Решение задачи:

Известно, что максимальная энергия магнитного поля тока катушки колебательного контура равна максимальной энергии электрического поля конденсатора этого же контура, поэтому из закона сохранения энергии следует, что:

[frac{{LI_m^2}}{2} = frac{{q_m^2}}{{2C}}]

Откуда максимальный ток в контуре (I_m) равен:

[{I_m} = frac{{{q_m}}}{{sqrt {LC} }};;;;(1)]

Частоту электромагнитных волн, излучаемых колебательным контуром, можно определить по формуле:

[nu = frac{1}{{2pi sqrt {LC} }};;;;(2)]

В этой формуле (L) – индуктивность катушки, (C) – электроемкость конденсатора.

Известно, что электромагнитные волны распространяются со скоростью света (c) (в вакууме она равна 3·10⁸ м/с). Между скоростью распространения электромагнитных волн (скоростью света (c)), их частотой колебаний (nu) и длиной волны (lambda) существует следующее соотношение:

[c = lambda nu ]

Откуда длина волны (lambda) равна:

[lambda = frac{c}{nu }]

В эту формулу поставим выражение (2):

[lambda = 2pi csqrt {LC} ]

Отсюда следует, что:

[sqrt {LC} = frac{lambda }{{2pi c}}]

Учитывая последнее полученное равенство, формула (1) примет вид:

[{I_m} = frac{{2pi c{q_m}}}{lambda }]

Посчитаем численный ответ задачи:

[{I_m} = frac{{2 cdot 3,14 cdot 3 cdot {{10}^8} cdot 10 cdot {{10}^{ – 9}}}}{{75,36}} = 0,25;А]

Ответ: 0,25 А.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

9.13.3 При изменении тока в катушке индуктивности на 1 А за 0,6 с в ней индуцируется ЭДС
9.13.5 В каком диапазоне длин волн можно улавливать радиопередачи приемником
9.13.6 Радиопередатчик искусственного спутника Земли работает на частоте 20 МГц

Колебательный контур:

Явление возникновения ЭДС индукции при изменении магнитного потока через площадь, ограниченную контуром, называется явлением электромагнитной индукции.

Под явлением самоиндукции понимают возникновение в контуре ЭДС индукции, создаваемой вследствие изменения силы тока в самом контуре. Правило Ленца: возникающий в замкнутом контуре индукционный ток имеет такое направление, при котором созданный им собственный магнитный поток через площадь, ограниченную контуром, стремится компенсировать изменение внешнего магнитного потока, вызвавшее данный ток.

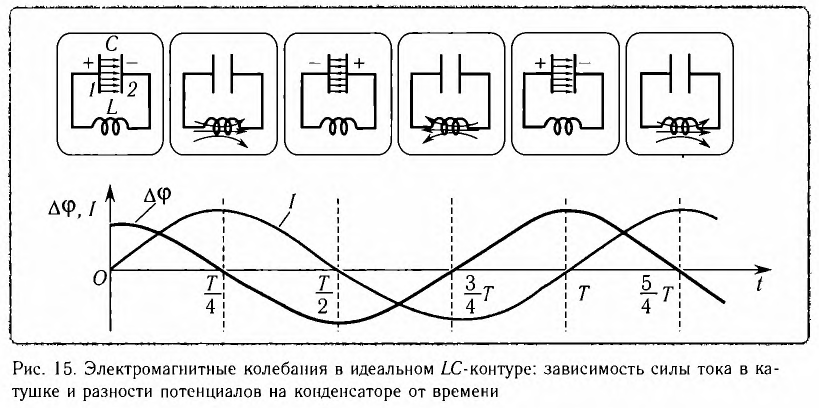
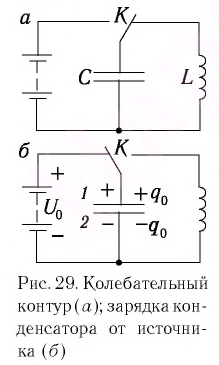
Рассмотрим электрическую цепь, содержащую конденсатор электроемкостью С и катушку (соленоид) индуктивностью L (рис. 15). Такая цепь называется идеальным колебательным контуром или LC-контуром.

В отличие от реального колебательного контура, который всегда обладает некоторым электрическим сопротивлением (R

Пусть в начальный момент времени (t = 0) конденсатор С заряжен так, что на его первой обкладке находится заряд +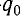, а на второй —. При этом конденсатор обладает энергией

С течением времени конденсатор начнет разряжаться, и в цепи появится электрический ток, сила l(t) которого будет меняться с течением времени. Поскольку при прохождении такого электрического тока в катушке индуктивности возникнет изменяющийся во времени магнитный поток, то это вызовет появление ЭДС самоиндукции, препятствующей изменению силы тока.

Вследствие этого сила тока в колебательном контуре будет возрастать от нуля до максимального значения в течение некоторого промежутка времени, определяемого индуктивностью катушки.

В момент полной разрядки конденсатора (q = 0) сила тока в катушке I(t) достигнет своего максимального значения . В соответствии с законом сохранения энергии первоначально запасенная в конденсаторе энергия электростатического поля перейдет в энергию магнитного поля, запасенную в этот момент в катушке:

После разрядки конденсатора сила тока в катушке начнет убывать. Это также произойдет не мгновенно, поскольку вновь возникающая ЭДС самоиндукции согласно правилу Ленца создаст индукционный ток. Он будет иметь такое же направление, как и уменьшающийся ток в цепи, и поэтому будет «поддерживать» его. Индукционный ток, создаваемый ЭДС самоиндукции катушки, перезарядит конденсатор до начального напряжения обратной полярности — знак заряда на каждой обкладке окажется противоположным начальному.

Соответственно, к моменту исчезновения тока заряд конденсатора достигнет максимального значения . При этом его обкладка, первоначально заряженная положительно, будет заряжена отрицательно (см. рис. 15). Далее процесс повторится с той лишь разницей, что электрический ток будет проходить в противоположном направлении.

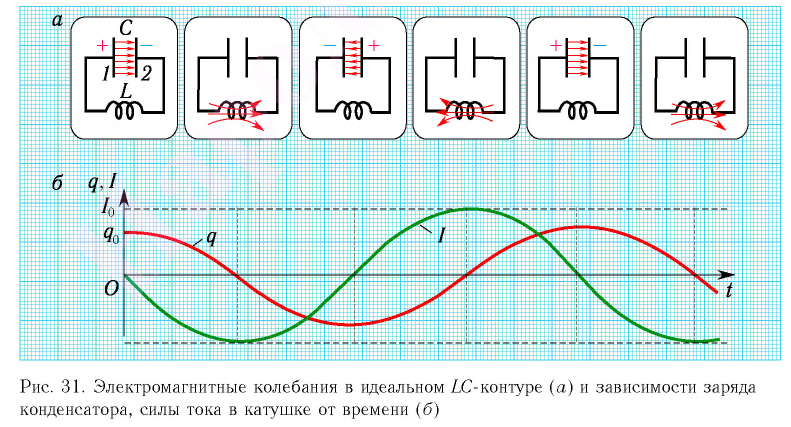
Таким образом, в идеальном LC-контуре будут происходить периодические изменения значений силы тока и напряжения, причем полная энергия контура будет оставаться постоянной. В этом случае говорят, что в контуре возникли свободные электромагнитные колебания.

Свободные электромагнитные колебания в LC-контуре — это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без потребления энергии от внешних источников.

Таким образом, возникновение свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора и возникновением в катушке ЭДС самоиндукции, которая «обеспечивает» эту перезарядку. Заметим, что заряд q(t) конденсатора и сила тока I(t) в катушке достигают своих максимальных значений и в различные моменты времени (см. рис. 15).

Наименьший промежуток времени, в течение которого LC-контур возвращается в исходное состояние (к начальному значению заряда данной обкладки), называется периодом свободных (собственных) электромагнитных колебаний в контуре.

Период свободных электромагнитных колебаний в контуре определяется по формуле Томсона:

Получим эту формулу, используя закон сохранения энергии. Поскольку полная энергия идеального LC-контура, равная сумме энергий электростатического поля конденсатора и магнитного поля катушки, сохраняется, то в любой момент времени справедливо равенство

 (1)

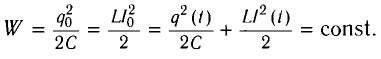
Поскольку закономерности гармонических колебаний носят универсальный характер, то можно сравнить колебания в LC-контуре с колебаниями пружинного маятника.

Для пружинного маятника полная механическая энергия в любой момент времени    2 ,

(2)

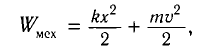
и период его колебаний

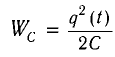
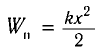
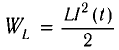
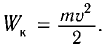
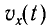
Проанализируем соотношения (1) и (2). Сравним выражения для энергии электростатического поля конденсатора и потенциальной энергии упругой деформации пружины энергии магнитного поля катушки  и кинетической энергии груза Аналогом координаты x(t) при колебаниях в электрическом контуре является заряд конденсатора q(t), а аналогом проекции скорости груза служит сила тока I(t) в колебательном контуре.

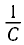
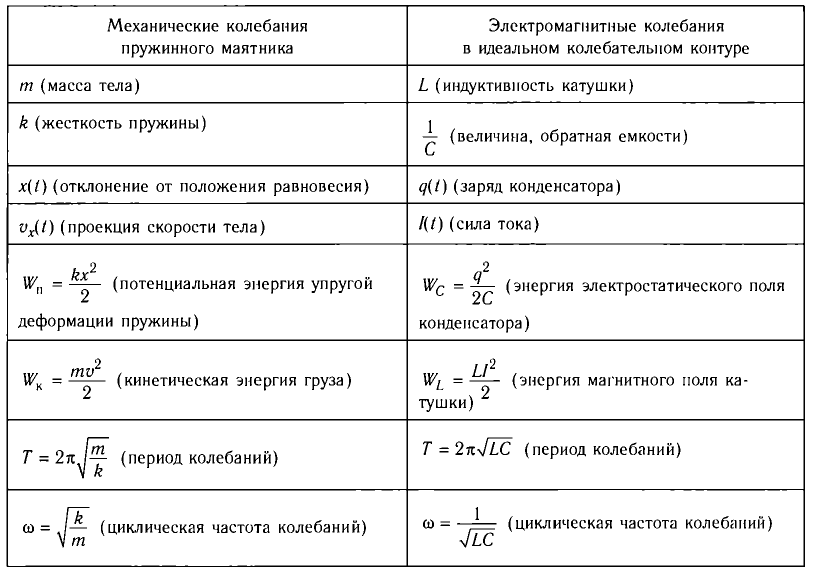
Следуя аналогии, заменим в формуле для периода колебаний пружинного маятника т на L и k на , тогда для периода свободных колебаний в LC-контуре получим формулу Томсона: 

Несложные дальнейшие рассуждения позволяют установить аналогии между физическими величинами при электромагнитных и механических колебаниях (табл. 4).

Таблица 4

Сопоставление физических величин, характеризующих электромагнитные и механические колебания

Соответственно, зависимость заряда конденсатора от времени будет иметь такой же характер, как и зависимость координаты (смещения) тела, совершающего гармонические колебания, от времени:

Также по гармоническому закону (но с другими начальными фазами) будут изменяться сила тока в цепи, напряжение на конденсаторе.

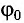
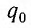
Для определения начальной фазы и амплитуды колебаний заряда необходимо знать заряд конденсатора и силу тока в катушке в начальный момент времени (t = 0).

Полная энергия идеального колебательного контура (R = 0) с течением времени сохраняется, поскольку в нем при прохождении тока теплота не выделяется.

Как уже отмечалось, реальный колебательный контур всегда имеет некоторое сопротивление R, обусловленное сопротивлением катушки, соединительных проводов и т. д. Это приводит к тому, что электромагнитные колебания в реальном контуре с течением времени затухают, тогда как в идеальном контуре они «будут происходить» сколь угодно долго.

Таким образом, механическим аналогом идеального колебательного контура является пружинный маятник без трения, а механическим аналогом реального колебательного контура — пружинный маятник с трением.

Пример №1

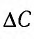
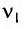
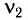
При изменении емкости конденсатора идеального LC-контура на = 50 пФ частота свободных электромагнитных колебаний в нем увеличилась с = 100 кГц до = 120 кГц. Определите индуктивность L контура.

Решение

Частота колебаний в контуре

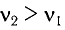
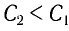
Поскольку частота колебаний в контуре увеличилась (), то электроемкость должна уменьшится, т. е. .

Из условия задачи получаем систему уравнений

Откуда 
 

Вычитая из первого уравнения второе, получаем

Откуда находим

Ответ: L = 0,015 Гн.

Пример №2

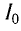
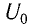
Колебательный контур состоит из конденсатора емкостью С = 400пФ и катушки индуктивностью L=10 мГн. Определите амплитудное значение силы тока в контуре, если амплитудное значение напряжения на конденсаторе = 500 В.

Решение

Максимальная энергия электростатического поля конденсатора

а максимальная энергия магнитного поля катушки

Так как контур идеальный (R = 0), то его полная энергия не меняется с течением времени. Кроме того, в момент, когда заряд конденсатора максимален, сила тока в катушке равна нулю, а в момент, когда заряд конденсатора равен нулю, сила тока в ней максимальна. Это позволяет утверждать, что максимальные энергии в конденсаторе и катушке равны: 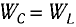, т. е.

откуда 

Ответ: .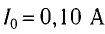

Колебательный контур и свободные электромагнитные колебания в контуре

Явление возникновения ЭДС в любом контуре при изменении магнитного потока через поверхность, ограниченную контуром, называется явлением электромагнитной индукции.

Под явлением самоиндукции понимают возникновение в замкнутом проводящем контуре ЭДС индукции, создаваемой вследствие изменения силы тока в самом контуре.

Правило Ленца: возникающий в замкнутом проводящем контуре индукционный ток имеет такое направление, при котором созданный им магнитный поток через поверхность, ограниченную контуром, стремится компенсировать изменение магнитного потока, вызвавшее данный ток.

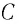
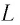
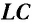
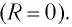
Рассмотрим электрическую цепь, состоящую из последовательно соединенных конденсатора электроемкостью  и катушки (соленоида) индуктивностью  (рис. 29, а), называемую идеальным колебательным контуром или -контуром. Электрическое сопротивление идеального контура считают равным нулю  Следовательно, идеальный колебательный контур является упрощенной моделью реального колебательного контура.

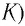
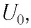
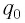
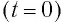
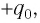
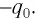
Подключив (при помощи ключа  источник тока, зарядим конденсатор до напряжения  сообщив ему заряд  (рис. 29, б). Следовательно, в начальный момент времени  конденсатор заряжен так, что на его обкладке 1 находится заряд  а на обкладке 2 — заряд  При этом электростатическое поле, создаваемое зарядами обкладок конденсатора, обладает энергией 

Рассмотрим процесс разрядки конденсатора в колебательном контуре. После соединения заряженного конденсатора с катушкой (при помощи ключа 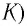 (рис. 30) он начнет разряжаться, так как под действием электрического поля, создаваемого зарядами на обкладках конденсатора, свободные электроны будут перемещаться по цепи от отрицательно заряженной обкладки к положительно заряженной. На рисунке 30 стрелкой показано начальное направление тока в электрической цепи.

Таким образом, в контуре появится нарастающий по модулю электрический ток, сила 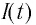 которого будет изменяться с течением времени (рис. 31, а). Но мгновенная разрядка конденсатора невозможна, так как изменение магнитного поля катушки, создаваемое нарастающим по модулю током, вызывает возникновение вихревого электрического поля. Действительно, в катушке индуктивности возникнет изменяющийся во времени магнитный поток, который вызовет появление ЭДС самоиндукции. Согласно правилу Ленца ЭДС самоиндукции стремится противодействовать вызвавшей ее причине, т. е. увеличению силы тока по модулю.

Вследствие этого модуль силы тока в колебательном контуре будет в течение некоторого промежутка времени плавно возрастать от нуля до максимального значения 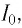 определяемого индуктивностью катушки и электроемкостью конденсатора (рис. 31, б).

При разрядке конденсатора энергия его электростатического поля превращается в энергию магнитного поля катушки с током. Согласно закону сохранения энергии суммарная энергия идеального колебательного контура остается постоянной с течением времени (уменьшение энергии электростатического поля конденсатора равно увеличению энергии магнитного поля катушки):

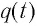
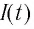
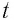
где  — мгновенное значение заряда конденсатора и  — сила тока в катушке в некоторый момент времени  после начала разрядки конденсатора.

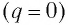
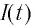
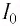
В момент полной разрядки конденсатора  сила тока в катушке  достигнет своего максимального по модулю значения  (см. рис. 31, б). В соответствии с законом сохранения энергии запасенная в конденсаторе энергия электростатического поля перейдет в энергию магнитного поля, запасенную в этот момент в катушке:

После разрядки конденсатора сила тока в катушке начинает убывать по модулю. Это также происходит не мгновенно, поскольку вновь возникающая ЭДС самоиндукции согласно правилу Ленца создает индукционный ток. Он имеет такое же направление, как и уменьшающийся по модулю ток в цепи, и поэтому «поддерживает» его. 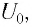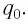Индукционный ток, создаваемый ЭДС самоиндукции катушки, перезаряжает конденсатор до начального напряжения  но знак заряда на каждой обкладке оказывается противоположным знаку начального заряда. Соответственно, к моменту исчезновения тока заряд конденсатора достигнет максимального значения  При этом его обкладка, первоначально заряженная положительно, будет заряжена отрицательно. Далее процесс повторится с той лишь разницей, что электрический ток в ко туре будет проходить в противоположном направлении, что отражено на рисунке 31, а.

Таким образом, в идеальном 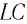-контуре будут происходить периодические изменения значений силы тока и напряжения, причем полная энергия контура будет оставаться постоянной. В этом случае говорят, что в контуре возникли свободные электромагнитные колебания.

Свободные электромагнитные колебания в LC-контуре — это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без пополнения энергии от внешних источников.

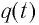
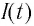
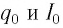
Таким образом, существование свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора, вызванной возникновением ЭДС самоиндукции в катушке. Заметим, что заряд  конденсатора и сила тока  в катушке достигают своих максимальных значений  в различные момента времени (см. рис. 31 а, б).

Наименьший промежуток времени, в течение которого LC-контур возвращается в исходное состояние (к начальным значениям заряда на каждой из обкладок), называется периодом свободных (собственных) электромагнитных колебаний в контуре.

Получим формулу для периода свободных электромагнитных колебаний в контуре, используя закон сохранения энергии. Поскольку полная энергия идеального -контура, равная сумме энергий электростатического поля конденсатора и магнитного поля катушки, сохраняется, то в любой момент времени справедливо равенство: 
 

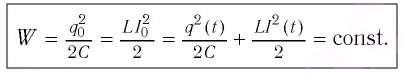
Процессы, происходящие в колебательном контуре, аналогичны колебаниям пружинного маятника. Для полной механической энергии пружинного маятника в любой момент времени:

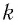
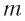
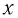
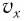
где  — жесткость пружины,  — масса груза,  — проекция смещения тела от положения равновесия,  — проекция его скорости на ось 

Период его колебаний:

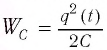
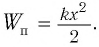
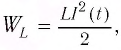
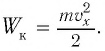
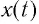
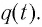
Проанализируем соотношения (1) и (2). Видно, что энергия электростатического поля конденсатора  является аналогом потенциальной энергии упругой деформации пружины  Соответственно, энергия магнитного поля катушки  которая обусловлена упорядоченным движением зарядов, является аналогом кинетической энергии груза  Следовательно, аналогом координаты  пружинного маятника при колебаниях в электрическом контуре является заряд конденсатора  Тогда, соответственно, аналогом проекции скорости груза будет сила тока в колебательном контуре, поскольку сила тока характеризует скорость изменения заряда конденсатора с течением времени.

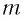
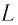
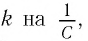
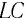
Следуя проведенной аналогии, заменим в формуле для периода колебаний пружинного маятника массу  на индуктивность  и жесткость  тогда для периода свободных колебаний в -контуре получим формулу:

которая называется формулой Томсона.

Несложные дальнейшие рассуждения позволяют установить аналогии между физическими величинами при электромагнитных и механических колебаниях (табл. 4).

Для наблюдения и исследования электромагнитных колебаний применяют электронный осциллограф, на экране которого получают временную развертку колебаний (рис. 32).

Зависимость заряда конденсатора от времени имеет такой же вид, как и зависимость координаты (проекции смещения) тела, совершающего гармонические колебания, от времени:

Также по гармоническому закону изменяются сила тока (но с другой начальной фазой) в цепи и напряжение на конденсаторе.

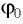
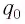
Для определения начальной фазы  и максимального заряда  необходимо знать заряд конденсатора и силу тока в катушке в начальный момент времени 

Отметим, что колебательный контур, в котором происходит только обмен энергией между конденсатором и катушкой, называется закрытым.

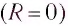
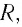
Полная энергия идеального колебательного контура  с течением времени сохраняется, поскольку в нем при прохождении тока теплота не выделяется. Реальный колебательный контур всегда имеет некоторое электрическое сопротивление  которое обусловлено сопротивлением катушки и соединительных проводов. Это приводит к тому, что электромагнитные колебания в реальном контуре с течением времени затухают, тогда как в идеальном контуре они будут происходить сколь угодно долго.

Таким образом, механическим аналогом идеального колебательного контура является пружинный маятник без учета трения, а механическим аналогом реального колебательного контура — пружинный маятник с учетом трения.

Пример решения задачи:

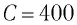
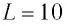
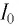
Идеальный колебательный контур состоит из конденсатора емкостью  пФ и катушки индуктивностью  мГн. Определите максимальное значение силы тока  в контуре, если максимальное значение напряжения на конденсаторе 
Дано:

Решение

Максимальная энергия электростатического поля конденсатора:

а максимальная энергия магнитного поля катушки:

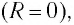
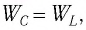
Так как контур идеальный  то его полная энергия сохраняется с течением времени. По закону сохранения энергии  т. е.

Отсюда

Ответ: 

Колебательный контур состоит из катушки индуктивностью 1 мГн к конденсатора емкостью 10 мкФ. Определить максимальную силу тока в контуре, если конденсатор заряжен до максимального напряжения 100 В

Закон сохранения энергии для колебательного контура:

$frac{CU^2}{2}=frac{LI^2}{2}$

$I=U*sqrt{frac{C}{L}}=100*sqrt{frac{10*10^{-6}}{1*10^{-3}}}=10;A$

Закон сохранения энергии для колебательного контура и анализ графика колебаний

Вадим Муранов, победитель всероссийского конкурса «Учитель года», преподаватель физики с 24-летним опытом работы.

Всем добрый день! Рад приветствовать вас на нашем очередном уже 26-ом воскресном мастер-классе!

Тема нашего сегодняшнего мастер-класса «Колебания»

«Сила тока в идеальном колебательном контуре меняется со временем так, как показано на рисунке. Определите заряд конденсатора в момент времени 7 мкс.

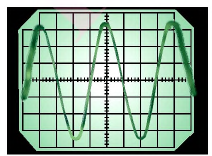
Вместо таблицы в этой задаче график колебаний. Что можно определить по данному графику? Прежде всего, любой график колебаний – это зависимость некой величины (не важно какой) от времени. В данном случае, если мы внимательно посмотрим, увидим, что здесь синусоида

Первое, что определяется по графику – это промежуток по времени между двумя пиками или впадинами этого графика. И этот промежуток является периодом колебаний

Второе, что можно определить, – это максимальное значение величины, чей график изображен на рисунке. В данном случае это сила тока, поэтому по максимальной точке можно определить максимальное или амплитудное значение силы тока. Иными словами, верхняя точка графика – это амплитуда той величины, чей это график

Необходимо найти заряд на конденсаторе в момент времени t=7 мкс. Но моменту времени 7 мкс соответствует некое значение силы тока, которое мы можем легко определить по графику. Находим 7 мкс, опускаемся вниз, видим, что это соответствует силе тока

Сразу должен сказать, что этот минус нам ни о чем не говорит, это просто обозначает, что ток течет в другом направлении, поэтому минус для нас неважен. И сам заряд мы так же определим, это будет положительный ответ.

Можно по-разному находить этот заряд: можно составить уравнение заряда в зависимости заряда от времени, и с помощью него определить величину этого заряда, но мы поступим по-другому.

Вспомним, что в нашей задаче написано, что контур идеальный, а, на самом деле, все задачи, с которыми вы будете встречаться в школе, будут связаны с идеальными маятниками и идеальными колебательными контурами.

Для идеального колебательного контура выполняется следующая вещь: в любой момент времени суммарная энергия, сосредоточенная в этом контуре (в конденсаторе и в катушке), будет равна любой из максимальных, то есть максимальной энергии электрического поля или максимальной энергии магнитного поля

W_э + W_м = W_эм = W_Мм

Вот это равенство является законом сохранения энергии для идеального колебательного контура. Запомните это равенство, оно вам пригодится в грядущих событиях. Сейчас мы тоже это равенство применим, и даже не один раз.

Еще раз: суммарная энергия, запасенная в контуре, равна максимальным значениям энергии электрического поля конденсатора или максимальному значению энергии магнитного поля. В данном случае нам удобнее приравнять это к максимальной энергии магнитного поля, т. к. нам известна максимальная сила тока.

Запишем

и домножим это равенство на 2С, чтобы полностью убрать все знаменатели.

В итоге получаем

Замечаем, что произведение LC присутствует в формуле периода , знаменитая формула Томсона.

Отсюда выражаем произведение LC и получаем

Заменим LC на , но сначала выразим заряд в квадрате

А теперь вместо LC подставляем и получаем

Далее убираем квадрат у заряда

Теперь подставляем все известные значения и вычисляем по инженерному калькулятору

Получаем приблизительный ответ Кл. Теперь переводим это в микрокулоны 0,57 мкКл. Вот таким должен быть ответ!

Все видео по физике