Решение: Рассмотрим уравнение координаты:
x = Xm∙соs(ω∙t + φ0),
где: х – координата тела, Хm – амплитуда, ω – угловая скорость, φ0 – начальная фаза. Хm = 0,2 м, ω = 2π.
Для нахождения скорости возьмем первую производную по времени от х:
υ = — ω∙Хm∙sin(ω∙t+ φ0), υ = — 0,4∙π∙sin(2πt+π/ 6).
υmax = ω∙Хm = 1,256 м/с.
Полная энергии частицы равна максимальной кинетической энергии:
[ {{E}_{max }}={{E}_{Kmax }}=frac{mcdot upsilon _{_{max }}^{2}}{2}. ]
Еmax = 0,016 Дж. Ответ: 1,256 м/с, 0,016 Дж.
« Последнее редактирование: 06 Октября 2014, 13:48 от alsak »
Записан
Формула скорости волны в физике
Формула скорости волны
Определение
Фронт волны (волновая поверхность) — это геометрическое место точек среды, для которых в некоторый момент времени фаза волны
имеет одно и то же значение.
Скоростью волны называют скорость, с которой движется фронт волны.
Формула фазовой скорости волны
Рассмотрим одномерный случай для гармонической волны. Уравнение волновой поверхности при это запишем как:
[Ф_s=omega t-kx+varphi left(1right),]
где${ Ф}_s$ — фаза волны; $k=frac{2pi }{lambda }$ — волновое число; $lambda $ — длина волны; $omega $ — циклическая частота; $varphi $ — начальная фаза. Уравнению (1) в каждый момент времени соответствует только одна точка оси X координата которой, равна:
[x=frac{omega t+varphi -Ф_s}{k}left(2right).]
Разным значениям фазы волны $Ф_s$ соответствуют разные волновые поверхности, каждая из которых в одномерной волне превращается в точку. Из формулы (2) видно, что волновые поверхности перемещаются в среде со скоростью:
[frac{dx}{dt}=frac{omega }{k}=frac{lambda }{T}=v left(3right),]
где $T$ — период колебаний точек в волне.
Если волны гармонические, то скорость движения волновой поверхности равна скорости распространения волны. Скорость, которую определяет выражение (3) является фазовой скоростью.
Фазовая скорость гармонической волны совпадает со скорость распространения энергии волны.
Скорость волны зависит от вещества, в котором распространяется волна и типа волны. Скорость волны — это не то же самое, что скорость колебания частиц среды в волне.
Формула для вычисления фазовой скорости распространения продольных волн
Скорость распространения продольных упругих волн в однородных в газах или жидкостях может быть вычислена как:
[v=sqrt{frac{K}{rho }}left(4right),]
где $K$ — модуль объемной упругости вещества; $rho =const$ — плотность среды. В газах формула (4) выполняется, если избыточное давление много меньше, равновесного давление газа в невозмущенном состоянии.
Для нахождения скорости распространения продольных волн в газе применяют выражение:
[v=sqrt{frac{gamma p}{rho }}left(5right),]
где $gamma $ — показатель адиабаты; $p$ — давление газа.
Продольные механические волны могут распространяться в твердых телах, их фазовая скорость равна:
[v=sqrt{frac{E}{rho }}left(6right),]
где $E$ — модуль Юнга вещества стержня.
Формула для фазовой скорости распространения поперечных волн
Поперечные механические волны способны распространяться только в твердых телах. Скорость ($v$) распространения поперечных волн в бесконечной изотропной среде при этом можно найти как:
[v=sqrt{frac{G}{rho }left(7right),}]
где $G$ — модуль сдвига среды; $rho $ — плотность вещества.
Упругие свойства и плотность твердого тела зависит от химического состава вещества, и она несущественно изменяется при изменении давления и температуры. Поэтому в большинстве случаев скорость распространения волны можно считать постоянной.
Формула для групповой скорости волн
Кроме фазовой скорости для описания распространения диспергирующих волн применяют понятие групповой скорости. При этом фазовая скорость может зависеть от частоты, при этом в веществе распространяются волны сложного негармонического характера, тогда с групповую скорость проще использовать, как характеристику скорости распространения волн.
Групповой скоростью называют скорость перемещения группы (цуга) волн, которые создают в каждый момент времени, локализованный в пространстве, волновой пакет. Любая реальная волна представляет собой суперпозицию гармонических волн. Скорость, с которой такая волна распространяется в веществе, имеющем дисперсию, равна фазовой скорости накрадывающихся волн. Распространение волны определяют перемещением энергии колебаний, которую переносит группа вол от источника.
Групповая скорость ($u$) связана с фазовой скоростью ($v$) формулой:
[u=v-frac{dv}{dlambda }left(8right).]
Если дисперсия отсутствует, то $frac{dv}{dlambda }=0$, тогда фазовая и групповая скорости равны и не зависят от длины волны.
Примеры задач с решением
Пример 1
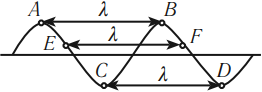
Задание. За время равное $t=20$ c волне совершается $N=$100 колебаний, при этом расстояние между соседними максимумами волны составляет 1 м. Какова скорость распространения волны?
Решение. Сделаем рисунок.
В качестве основы для решения задачи используем формулу для вычисления фазовой скорости волны вида:
[v=frac{lambda }{T} left(1.1right).]
Найдем период колебаний как время одного полного колебания:
[T=frac{t}{N} left(1.2right).]
Используя формулу (1.2) скорость будем вычислять, применяя формулу:
[v=frac{lambda N}{t}.]
Вычислим искомую скорость:
[v=frac{1cdot 100}{20}=5left(frac{м}{с}right).]
Ответ. $v=5frac{м}{с}$
Пример 2
Задание. Уравнение плоской волны, которая распространяется вдоль положительного направления оси X, имеет вид: $xi left(x,tright)=2{cos left[omega left(t-frac{x}{v}right)right] }left(мright).$ Частота колебаний $nu =450$Гц, длина волны $lambda =0,8 $м. Какова скорость распространения волны, какой будет максимальная скорость колебания частиц среды?
Решение. Фазовую скорость движения волны найдем как:
[v=frac{lambda }{T}=lambda nu left(2.1right),]
где период — величина обратная частоте колебаний:
[T=frac{1}{nu }left(2.2right).]
Вычислим фазовую скорость:
[v=450cdot 0,8=360 left(frac{м}{с}right).]
Скорость колебания частиц равна:
[frac{dxi }{dt}=frac{d}{dt}left(2{cos left[omega left(t-frac{x}{v}right)right] }right)=-2omega {sin left[omega left(t-frac{x}{v}right)right]left(2.3right). }]
Максимальное значение скорости колебаний частиц в волне из (2.3) равно:
[{left(frac{dxi }{dt}right)}_{max}=left|2omega right|left(2.4right).]
Циклическую частоту найдем как:
[omega =2pi nu ,]
тогда:
[{left(frac{dxi }{dt}right)}_{max}=left|2cdot 2pi nu right|=4pi nu .]
Вычислим максимальную скорость колебаний частиц:
[{left(frac{dxi }{dt}right)}_{max}=4pi cdot 450=5,65cdot {10}^3left(frac{м}{с}right).]
Ответ. $v=360 frac{м}{с}$, ${left(frac{dxi }{dt}right)}_{max}=5,65cdot {10}^3frac{м}{с}$
Читать дальше: формула скорости свободного падения.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Формула скорости волны
Фронт волны (волновая поверхность) — это геометрическое место точек среды, для которых в некоторый момент времени фаза волны имеет одно и то же значение.
Скоростью волны называют скорость, с которой движется фронт волны.
Формула фазовой скорости волны
Рассмотрим одномерный случай для гармонической волны. Уравнение волновой поверхности при это запишем как:
[Ф_s=omega t-kx+varphi left(1right),]
где$< Ф>_s$ — фаза волны; $k=frac<2pi ><lambda >$ — волновое число; $lambda $ — длина волны; $omega $ — циклическая частота; $varphi $ — начальная фаза. Уравнению (1) в каждый момент времени соответствует только одна точка оси X координата которой, равна:
Разным значениям фазы волны $Ф_s$ соответствуют разные волновые поверхности, каждая из которых в одномерной волне превращается в точку. Из формулы (2) видно, что волновые поверхности перемещаются в среде со скоростью:
где $T$ — период колебаний точек в волне.
Если волны гармонические, то скорость движения волновой поверхности равна скорости распространения волны. Скорость, которую определяет выражение (3) является фазовой скоростью.
Фазовая скорость гармонической волны совпадает со скорость распространения энергии волны.
Скорость волны зависит от вещества, в котором распространяется волна и типа волны. Скорость волны — это не то же самое, что скорость колебания частиц среды в волне.
Формула для вычисления фазовой скорости распространения продольных волн
Скорость распространения продольных упругих волн в однородных в газах или жидкостях может быть вычислена как:
где $K$ — модуль объемной упругости вещества; $rho =const$ — плотность среды. В газах формула (4) выполняется, если избыточное давление много меньше, равновесного давление газа в невозмущенном состоянии.
Для нахождения скорости распространения продольных волн в газе применяют выражение:
где $gamma $ — показатель адиабаты; $p$ — давление газа.
Продольные механические волны могут распространяться в твердых телах, их фазовая скорость равна:
где $E$ — модуль Юнга вещества стержня.
Формула для фазовой скорости распространения поперечных волн
Поперечные механические волны способны распространяться только в твердых телах. Скорость ($v$) распространения поперечных волн в бесконечной изотропной среде при этом можно найти как:
где $G$ — модуль сдвига среды; $rho $ — плотность вещества.
Упругие свойства и плотность твердого тела зависит от химического состава вещества, и она несущественно изменяется при изменении давления и температуры. Поэтому в большинстве случаев скорость распространения волны можно считать постоянной.
Формула для групповой скорости волн
Кроме фазовой скорости для описания распространения диспергирующих волн применяют понятие групповой скорости. При этом фазовая скорость может зависеть от частоты, при этом в веществе распространяются волны сложного негармонического характера, тогда с групповую скорость проще использовать, как характеристику скорости распространения волн.
Групповой скоростью называют скорость перемещения группы (цуга) волн, которые создают в каждый момент времени, локализованный в пространстве, волновой пакет. Любая реальная волна представляет собой суперпозицию гармонических волн. Скорость, с которой такая волна распространяется в веществе, имеющем дисперсию, равна фазовой скорости накрадывающихся волн. Распространение волны определяют перемещением энергии колебаний, которую переносит группа вол от источника.
Групповая скорость ($u$) связана с фазовой скоростью ($v$) формулой:
Если дисперсия отсутствует, то $frac=0$, тогда фазовая и групповая скорости равны и не зависят от длины волны.
Примеры задач с решением
Задание. За время равное $t=20$ c волне совершается $N=$100 колебаний, при этом расстояние между соседними максимумами волны составляет 1 м. Какова скорость распространения волны?
Решение. Сделаем рисунок.
В качестве основы для решения задачи используем формулу для вычисления фазовой скорости волны вида:
Найдем период колебаний как время одного полного колебания:
Используя формулу (1.2) скорость будем вычислять, применяя формулу:
Вычислим искомую скорость:
Ответ. $v=5frac<м><с>$
Задание. Уравнение плоской волны, которая распространяется вдоль положительного направления оси X, имеет вид: $xi left(x,tright)=2<cos left[omega left(t-fracright)right] >left(мright).$ Частота колебаний $nu =450$Гц, длина волны $lambda =0,8 $м. Какова скорость распространения волны, какой будет максимальная скорость колебания частиц среды?
Решение. Фазовую скорость движения волны найдем как:
где период — величина обратная частоте колебаний:
Вычислим фазовую скорость:
[v=450cdot 0,8=360 left(frac<м><с>right).]
Скорость колебания частиц равна:
Максимальное значение скорости колебаний частиц в волне из (2.3) равно:
Циклическую частоту найдем как:
Вычислим максимальную скорость колебаний частиц:
Длина и скорость волны.
Любая волна распространяется с некоторой скоростью. Под скоростью волны понимают скорость распространения возмущения. Например, удар по торцу стального стержня вызывает в нем местное сжатие, которое затем распространяется вдоль стержня со скоростью около 5 км/с.
Скорость волны определяется свойствами среды, в которой эта волна распространяется. При переходе волны из одной среды в другую ее скорость изменяется.
Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней.
Поскольку скорость волны — величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней:
,
где v — скорость волны, Т — период колебаний в волне, λ (греческая буква лямбда) — длина волны.
Формула выражает связь длины волны с ее скоростью и периодом. Учитывая, что период колебаний в волне обратно пропорционален частоте v, т. е. Т = 1/v, можно получить формулу, выражающую связь длины волны с ее скоростью и частотой:
,
Полученная формула показывает, что скорость волны равна произведению длины волны на частоту колебаний в ней.
Длина волны — это пространственный период волны. На графике волны (рис. выше) длина волны определяется как расстояние между двумя ближайшими точками гармонической бегущей волны, находящимися в одинаковой фазе колебаний. Это как бы мгновенные фотографии волн в колеблющейся упругой среде в моменты времени t и t + Δt. Ось х совпадает с направлением распространения волны, на оси ординат отложены смещения s колеблющихся частиц среды.
Частота колебаний в волне совпадает с частотой колебаний источника, т. к. колебания частиц в среде являются вынужденными и не зависят от свойств среды, в которой распространяется волна. При переходе волны из одной среды в другую ее частота не изменяется, меняются лишь скорость и длина волны.
Длина волны. Скорость распространения волны (Ерюткин Е.С.)
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
В ходе урока вы сможете самостоятельно изучить тему «Длина волны. Скорость распространения волны». На этом уроке вы сможете познакомиться с особенными характеристиками волн. В первую очередь вы узнаете, что такое длина волны. Мы рассмотрим ее определение, способ ее обозначения и измерения. Затем мы также подробно рассмотрим скорость распространения волны.
http://www.calc.ru/Dlina-I-Skorost-Volny.html
http://interneturok.ru/lesson/physics/9-klass/mehanicheskie-kolebaniya-i-volny/dlina-volny-skorost-rasprostraneniya-volny-eryutkin-e-s
Механические колебания и волны
Механические колебания – периодически повторяющееся перемещение материальной точки, при котором она движется по какой-либо траектории поочередно в двух противоположных направлениях относительно положения устойчивого равновесия.
Отличительными признаками колебательного движения являются:
- повторяемость движения;
- возвратность движения.
Для существования механических колебаний необходимо:
- наличие возвращающей силы – силы, стремящейся вернуть тело в положение равновесия (при малых смещениях от положения равновесия);
- наличие малого трения в системе.
Механические волны – это процесс распространения колебаний в упругой среде.
Содержание
- Виды волн
- Гармонические колебания
- Амплитуда и фаза колебаний
- Период колебаний
- Частота колебаний
- Свободные колебания (математический и пружинный маятники)
- Вынужденные колебания
- Резонанс
- Длина волны
- Звук
- Основные формулы по теме «Механические колебания и волны»
Виды волн
- Поперечная – это волна, в которой колебание частиц среды происходит перпендикулярно направлению распространения волны.
Поперечная волна представляет собой чередование горбов и впадин.
Поперечные волны возникают вследствие сдвига слоев среды относительно друг друга, поэтому они распространяются в твердых телах.
- Продольная – это волна, в которой колебание частиц среды происходит в направлении распространения волны.
Продольная волна представляет собой чередование областей уплотнения и разряжения.
Продольные волны возникают из-за сжатия и разряжения среды, поэтому они могут возникать в жидких, твердых и газообразных средах.
Важно!
Механические волны не переносят вещество среды. Они переносят энергию, которая складывается из кинетической энергии движения частиц среды и потенциальной энергии ее упругой деформации.
Гармонические колебания
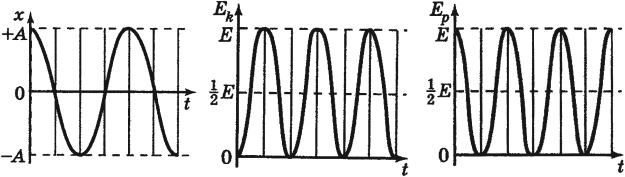
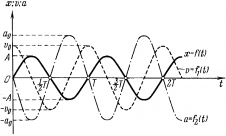
Гармонические колебания – простейшие периодические колебания, при которых координата тела меняется по закону синуса или косинуса:
где ( x ) – координата тела – смещение тела от положения равновесия в данный момент времени; ( A ) – амплитуда колебаний; ( omega t+varphi_0 ) – фаза колебаний; ( omega ) – циклическая частота; ( varphi_0 ) – начальная фаза.
Если в начальный момент времени тело проходит положение равновесия, то колебания являются синусоидальными.
Если в начальный момент времени смещение тела совпадает с максимальным отклонением от положения равновесия, то колебания являются косинусоидальными.
Скорость гармонических колебаний
Скорость гармонических колебаний есть первая производная координаты по времени:
где ( v ) – мгновенное значение скорости, т. е. скорость в данный момент времени.
Амплитуда скорости – максимальное значение скорости колебаний, это величина, стоящая перед знаком синуса или косинуса:
Ускорение гармонических колебаний
Ускорение гармонических колебаний есть первая производная скорости по времени:
где ( a ) – мгновенное значение ускорения, т. е. ускорение в данный момент времени.
Амплитуда ускорения – максимальное значение ускорения, это величина, стоящая перед знаком синуса или косинуса:
Если тело совершает гармонические колебания, то сила, действующая на тело, тоже изменяется по гармоническому закону:
где ( F ) – мгновенное значение силы, действующей на тело, т. е. сила в данный момент времени.
Амплитуда силы – максимальное значение силы, величина, стоящая перед знаком синуса или косинуса:
Тело, совершающее гармонические колебания, обладает кинетической или потенциальной энергией:
где ( W_k ) – мгновенное значение кинетической энергии, т. е. кинетическая энергия в данный момент времени.
Амплитуда кинетической энергии – максимальное значение кинетической энергии, величина, стоящая перед знаком синуса или косинуса:
При гармонических колебаниях каждую четверть периода происходит переход потенциальной энергии в кинетическую и обратно.
В положении равновесия:
- потенциальная энергия равна нулю;
- кинетическая энергия максимальна.
При максимальном отклонении от положения равновесия:
- кинетическая энергия равна нулю;
- потенциальная энергия максимальна.
Полная механическая энергия гармонических колебаний
При гармонических колебаниях полная механическая энергия равна сумме кинетической и потенциальной энергий в данный момент времени:
Важно!
Следует помнить, что период колебаний кинетической и потенциальной энергий в 2 раза меньше, чем период колебаний координаты, скорости, ускорения и силы. А частота колебаний кинетической и потенциальной энергий в 2 раза больше, чем частота колебаний координаты, скорости, ускорения и силы.
Графики зависимости кинетической, потенциальной и полной энергий всегда лежат выше оси времени.
Если сила сопротивления отсутствует, то полная энергия сохраняется. График зависимости полной энергии от времени есть прямая, параллельная оси времени (в отсутствие сил трения).
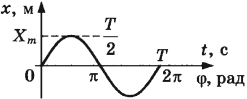
Амплитуда и фаза колебаний
Амплитуда колебаний – модуль наибольшего смещения тела от положения равновесия.
Обозначение – ( A, (X_{max}) ), единицы измерения – м.
Фаза колебаний – это величина, которая определяет состояние колебательной системы в любой момент времени.
Обозначение – ( varphi ), единицы измерения – рад (радиан).
Фаза колебаний – это величина, стоящая под знаком синуса или косинуса. Она показывает, какая часть периода прошла от начала колебаний.
Фаза гармонических колебаний в процессе колебаний изменяется.
( varphi_0 ) – начальная фаза колебаний.
Начальная фаза колебаний – величина, которая определяет положение тела в начальный момент времени.
Важно!
Путь, пройденный телом за одно полное колебание, равен четырем амплитудам.
Период колебаний
Период колебаний – это время одного полного колебания.
Обозначение – ( T ), единицы измерения – с.
Период гармонических колебаний – постоянная величина.
Частота колебаний
Частота колебаний – это число полных колебаний в единицу времени.
Обозначение – ( nu ), единицы времени – с-1 или Гц (Герц).
1 Гц – это частота такого колебательного движения, при котором за каждую секунду совершается одно полное колебание:
Период и частота колебаний – взаимно обратные величины:
Циклическая частота – это число колебаний за 2π секунд.
Обозначение – ( omega ), единицы измерения – рад/с.
Свободные колебания (математический и пружинный маятники)
Свободные колебания – колебания, которые совершает тело под действием внутренних сил системы за счет начального запаса энергии после того как его вывели из положения устойчивого равновесия.
Условия возникновения свободных колебаний:
- при выведении тела из положения равновесия должна возникнуть сила, стремящаяся вернуть его в положение равновесия;
- силы трения в системе должны быть достаточно малы. При наличии сил трения свободные колебания будут затухающими.
При наличии сил трения свободные колебания будут затухающими.
Затухающие колебания – это колебания, амплитуда которых с течением времени уменьшается.
Математический маятник – это материальная точка, подвешенная на невесомой нерастяжимой нити.
Период колебаний математического маятника:
Частота колебаний математического маятника:
Циклическая частота колебаний математического маятника:
Максимальное значение скорости колебаний математического маятника:
Максимальное значение ускорения колебаний математического маятника:
Период свободных колебаний математического маятника, движущегося вверх с ускорением или вниз с замедлением:
Период свободных колебаний математического маятника, движущегося вниз с ускорением или вверх с замедлением:
Период свободных колебаний математического маятника, горизонтально с ускорением или замедлением:
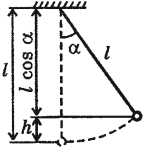
Мгновенное значение потенциальной энергии математического маятника, поднявшегося в процессе колебаний на высоту ( h ), определяется по формуле:
где ( l ) – длина нити, ( alpha ) – угол отклонения от вертикали.
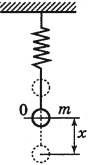
Пружинный маятник – это тело, подвешенное на пружине и совершающее колебания вдоль вертикальной или горизонтальной оси под действием силы упругости пружины.
Период колебаний пружинного маятника:
Частота колебаний пружинного маятника:
Циклическая частота колебаний пружинного маятника:
Максимальное значение скорости колебаний пружинного маятника:
Максимальное значение ускорения колебаний пружинного маятника:
Мгновенную потенциальную энергию пружинного маятника можно найти по формуле:
Амплитуда потенциальной энергии – максимальное значение потенциальной энергии, величина, стоящая перед знаком синуса или косинуса:
Важно!
Если маятник не является ни пружинным, ни математическим (физический маятник), то его циклическую частоту, период и частоту колебаний по формулам, применимым к математическому и пружинному маятнику, рассчитать нельзя. В данном случае эти величины рассчитываются из формулы силы, действующей на маятник, или из формул энергий.
Вынужденные колебания
Вынужденные колебания – это колебания, происходящие под действием внешней периодически изменяющейся силы.
Вынужденные колебания, происходящие под действием гармонически изменяющейся внешней силы, тоже являются гармоническими и незатухающими. Их частота равна частоте внешней силы и называется частотой вынужденных колебаний.
Резонанс
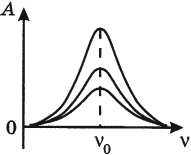
Резонанс – явление резкого возрастания амплитуды колебаний, которое происходит при совпадении частоты вынуждающей силы и собственной частоты колебаний тела.
Условие резонанса:
( v_0 ) – собственная частота колебаний маятника.
На рисунке изображены резонансные кривые для сред с разным трением. Чем меньше трение, тем выше и острее резонансная кривая.
Явление резонанса учитывается при периодически изменяющихся нагрузках в машинах и различных сооружениях.
Также резонанс используется в акустике, радиотехнике и т. д.
Длина волны
Длина волны – это расстояние, на которое волна распространяется за один период, т. е. это кратчайшее расстояние между двумя точками среды, колеблющимися в одинаковых фазах.
Обозначение – ( lambda ), единицы измерения – м.
Расстояние между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разряжениями в продольной волне равно длине волны.
Скорость распространения волны – это скорость перемещения горбов и впадин в поперечной волне и сгущений или разряжений в продольной волне.
Звук
Звук – это колебания упругой среды, воспринимаемые органом слуха.
Условия, необходимые для возникновения и ощущения звука:
- наличие источника звука;
- наличие упругой среды между источником и приемником звука;
- наличие приемника звука; • частота колебаний должна лежать в звуковом диапазоне;
- мощность звука должна быть достаточной для восприятия.
Звуковые волны – это упругие волны, вызывающие у человека ощущение звука, представляющие собой зоны сжатия и разряжения, передающиеся на расстояние с течением времени.
Классификация звуковых волн:
- инфразвук (( nu ) < 16 Гц);
- звуковой диапазон (16 Гц < ( nu ) < 20 000 Гц);
- ультразвук (( nu ) > 20 000 Гц).
Скорость звука – это скорость распространения фазы колебания, т. е. области сжатия и разряжения среды.
Скорость звука зависит
- от упругих свойств среды:
в воздухе – 331 м/с, в воде – 1400 м/с, в металле – 5000 м/с;
- от температуры среды:
в воздухе при температуре 0°С – 331 м/с,
в воздухе при температуре +15°С – 340 м/с.
Характеристики звуковой волны
- Громкость – это величина, характеризующая слуховые ощущения человека, зависящая от амплитуды колебаний в звуковой волне. Единицы измерения – дБ (децибел).
- Высота тона – это величина, характеризующая слуховые ощущения человека, зависящая от частоты колебаний в звуковой волне. Чем больше частота, тем выше звук. Чем меньше частота, тем ниже звук.
- Тембр – это окраска звука.
Музыкальный звук – это звук, издаваемый гармонически колеблющимся телом. Каждому музыкальному тону соответствует определенная длина и частота звуковой волны.
Шум – хаотическая смесь тонов.
Основные формулы по теме «Механические колебания и волны»
Механические колебания и волны
3 (59.17%) 145 votes
|
ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ |
|
|
Колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону), наз. гармоническими колебаниями. Например, в случае механических гармонических колебаний:. В этих формулах ω – частота колебания, xm – амплитуда колебания, φ0 и φ0’ – начальные фазы колебания. Приведенные формулы отличаются определением начальной фазы и при φ0’ = φ0 +π/2 полностью совпадают. |
|
|
Это простейший вид периодических колебаний. Конкретный вид функции (синус или косинус) зависит от способа выведения системы из положения равновесия. Если выведение происходит толчком (сообщается кинетическая энергия), то при t=0 смещение х=0, следовательно, удобнее пользоваться функцией sin, положив φ0’=0; при отклонении от положения равновесия (сообщается потенциальная энергия) при t=0 смещение х=хm, следовательно, удобнее пользоваться функцией cos и φ0=0. |
|
|
Выражение, стоящее под знаком cos или sin, наз. фазой колебания: Фаза колебания измеряется в радианах и определяет значение смещения (колеблющейся величины) в данный момент времени. |
|
|
Амплитуда колебания зависит только от начального отклонения (начальной энергии, сообщенной колебательной системе). |
|
|
Скорость и ускорение при гармонических колебаниях. |
|
|
Согласно определению скорости, скорость – это производная от координаты по времени |
|
|
Таким образом, мы видим, что скорость при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания скорости опережают колебания смещения по фазе на π/2. |
|
|
Величина |
|
|
Следовательно, для скорости при гармоническом колебании имеем: |
|
|
Согласно определению ускорения, ускорение – это производная от скорости по времени:
Ускорение при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания ускорения опережают колебания скорости на π/2 и колебания смещения на π (говорят, что колебания происходят в противофазе). |
|
|
Величина — максимальное ускорение (амплитуда колебаний ускорения). Следовательно, для ускорения имеем: |
|
|
Из анализа процесса колебательного движения, графиков и соответствующих математических выражений видно, что при прохождении колеблющимся телом положения равновесия (смещение равно нулю) ускорение равно нулю, а скорость тела максимальна (тело проходит положение равновесия по инерции), а при достижении амплитудного значения смещения – скорость равна нулю, а ускорение максимально по модулю (тело меняет направление своего движения). |
|
|
Сравним выражения для смещения и ускорения при гармонических колебаниях:
|
|
|
Можно записать: т.е. вторая производная смещения прямо пропорциональна (с противоположным знаком) смещению. Такое уравнение наз. уравнением гармонического колебания. Эта зависимость выполняется для любого гармонического колебания, независимо от его природы. Поскольку мы нигде не использовали параметров конкретной колебательной системы, то от них может зависеть только циклическая частота. |
|
|
Часто бывает удобно записывать уравнения для колебаний в виде: где T – период колебания. Тогда, если время выражать в долях периода подсчеты будут упрощаться. Например, если надо найти смещение через 1/8 периода, получим: |
|





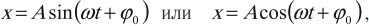
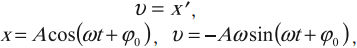
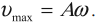
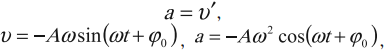
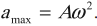
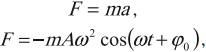
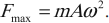
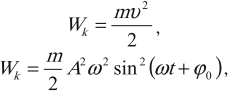
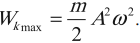
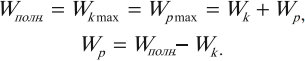
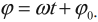




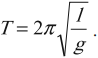
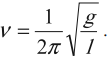
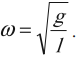
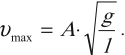
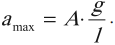
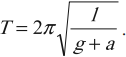
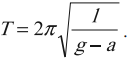
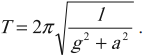
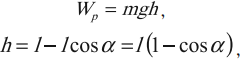
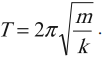
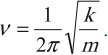
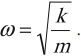
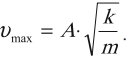
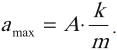
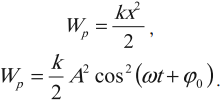
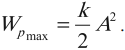
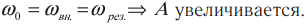
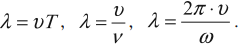
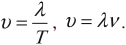



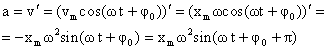 .
.