Как найти максимальную скорость по уравнению ускорения
Гармоническое колебательное движение и волны
Уравнение движения точки дано в виде . Найти период колебаний Т, максимальную скорость vmax и максимальное ускорение amax точки.
Дано:
Решение:
Уравнение колебаний запишем в виде
Скорость колеблющейся точки
Ускорение колеблющейся точки
Период колебаний Т выразим через циклическую частоту
Уравнение движения точки дано в виде x = 0,2 sin(пt + п/3), м. Найти максимальные значения скорости и ускорения.






Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.
Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!
Описание и исходные данные задания, 50% решения + фотография:
№3 2.1. Уравнение движения точки дано в виде x = 0,2 sin(пt + п/3), м. Найти максимальные значения скорости и ускорения.
Уравнение гармонических колебаний точки: , где – амплитуда колебаний; – круговая частота колебаний; – начальная фаза колебаний. Из заданного уравнения колебаний точки делаем вывод: м, рад/с, рад. Найдём зависимость скорости точки от времени:
Если вам нужно решить физику, тогда нажмите ➔ заказать контрольную работу по физике.
- Гармоническое колебание материальной точки задано уравнением x = 0,2 sin(10пt + п/4) м. Определить момент времени, при котором точка будет находиться в положении равновесия, и максимальную скорость колебания.
- Материальная точка совершает гармонические колебания по закону x = 0,9 cos (2п/3 t + п/4). Максимальное значение ускорения точки равно … 1) 0,6п м/с2; 2) 2/3 п м/с2; 3) 4п2 м/с2; 4) 0,4п2 м/с2.
- Уравнение движения точки дано в виде x = 2 sin(п/2 t + п/4), см. Определить период колебаний, максимальную скорость аmax и максимальное ускорение amax точки.
- Определить максимальные значения скорости и ускорения материальной точки, колеблющейся по закону: X = 0,04 sin п(t + 1/2) (м). Чему равна фаза колебаний спустя 10 сек после начала движения?
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Найти максимальное значение скорости точки, уравнение движения которой
Условие задачи:
Найти максимальное значение скорости точки, уравнение движения которой (x = 0,02sin left( <frac<<14pi t>><3>> right)).
Задача №9.1.13 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Решение задачи:
Чтобы найти уравнение скорости точки при колебаниях, нужно взять производную от данного в условии уравнения колебаний. Тогда:
То есть мы имеем:
Понятно, что максимальное по модулю значение скорости в таком случае равно (оно имеет место, когда косинус по модулю равен 1):
Ответ: 0,29 м/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
http://natalibrilenova.ru/uravnenie-dvizheniya-tochki-dano-v-vide-x—02-sinpt—p3-m-najti-maksimalnyie-znacheniya-skorosti-i-uskoreniya-/
http://easyfizika.ru/zadachi/kolebaniya-i-volny/najti-maksimalnoe-znachenie-skorosti-tochki-uravnenie-dvizheniya-kotoroj/
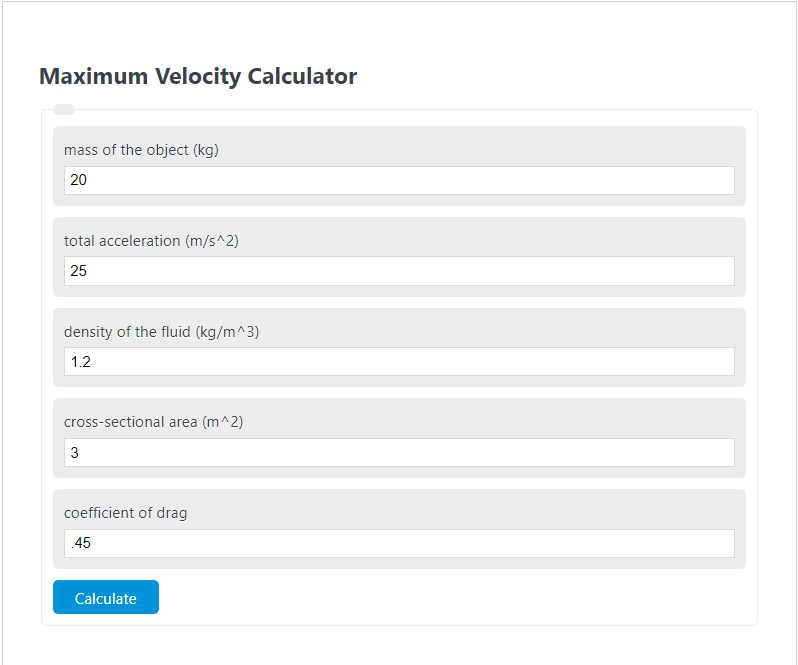
Enter the mass, acceleration, density of fluid, cross-sectional area, and drag coefficient into the calculator to determine the maximum velocity.
- All Velocity Calculators
- Velocity Calculator
- Free Fall Velocity Calculator
- Terminal Velocity Calculator
- Drag Coefficient Calculator
- Height to Velocity Calculator
- Gravity To Velocity Calculator
- Theoretical Velocity Calculator
Maximum Velocity Formula
The following equation is used to calculate the Maximum Velocity.
Vmax = SQRT ( 2*m*a / (p*A*C) )
- Where Vmax is the maximum velocity (m/s)
- m is the mass of the object (kg)
- a is the total acceleration (m/s^2)
- p is the density of the fluid (kg/m^3)
- A is the cross-sectional area (m^2)
- C is the coefficient of drag
What is a Maximum Velocity?
Definition:
A Maximum Velocity measures the peak velocity that an object will reach under a specific acceleration. This peak velocity is reached when the acceleration equals the force of drag divided by the mass.
How to Calculate Maximum Velocity?
Example Problem:
The following example outlines the steps and information needed to calculate Maximum Velocity.
First, determine the mass of the object. In this example, the mass is found to be 20kg.
Next, determine the total acceleration. For this problem, the total acceleration is found to be 25 m/s^2.
Next, determine the density of the fluid. In this case, the density of the fluid is measured to be 1.2 kg/m^3.
Next, determine the cross-sectional area exposed to drag. In this problem, the area is 3 m^2.
Next, determine the coefficient of drag. This is determined to be .45.
Finally, calculate the Maximum Velocity using the formula above:
Vmax = SQRT ( 2*m*a / (p*A*C) )
Vmax = SQRT ( 2*20*25 / (1.2*3*.45) )
Vmax = 24.845 m/s
Если вам дали уравнение для скорости, чтобы найти ее максимум (и, возможно, время, когда этот максимум наступил), навыки исчисления работают в вашу пользу. Однако, если ваша математика останавливается на алгебре, используйте калькулятор, чтобы найти ответ. Проблемы со скоростью включают в себя все, что движется, от бейсбола до ракеты.
Использование исчисления
-
Возьмите производную уравнения
-
Решите уравнение для времени
-
Тестовые решения
Возьмем производную уравнения скорости по времени. Эта производная является уравнением для ускорения. Например, если уравнение для скорости v = 3sin (t), где t — время, уравнение для ускорения a = 3cos (t).
Установите уравнение ускорения равным нулю и решите за время. Может существовать более одного решения, и это нормально. Помните, что ускорение — это наклон уравнения скорости, а производная — это наклон исходной линии. Когда наклон равен нулю, линия горизонтальна. Это происходит в экстремуме, то есть в максимуме или минимуме. В этом примере a = 3cos (t) = 0, когда t = pi ÷ 2 и t = (3pi) ÷ 2.
Протестируйте каждое решение, чтобы определить, является ли оно максимальным или минимальным. Выберите точку слева от экстремума, а другую точку справа. Если ускорение отрицательно слева и положительно справа, точка является минимальной скоростью. Если ускорение положительно влево и отрицательно вправо, точка является максимальной скоростью. В этом примере a = 3cos (t) является положительным как раз перед t = pi ÷ 2 и отрицательным сразу после, так что это максимум; однако (3pi) ÷ 2 является минимумом, потому что a = 3cos (t) является отрицательным непосредственно перед (3pi) ÷ 2 и положительным сразу после.
Если вы найдете более одного максимума, просто подключите время к исходному уравнению скорости, чтобы сравнить скорости в этих экстремумах. Какая бы ни была скорость, это абсолютный максимум.
Использование калькулятора
-
Введите уравнение скорости
-
Функция графика
-
Угадай позицию максимума
-
Записать значения
Нажмите кнопку «Y =» и введите уравнение скорости.
График функции. Посмотрите на график, чтобы оценить, где находится максимум.
Нажмите «2-й», «Calc», «Макс.» Используйте кнопки со стрелками для перемещения по графику слева от максимума и нажмите ввод. Стрелка справа от максимума и снова нажмите «Enter». Стрелка между этими точками и введите ваше лучшее предположение о позиции максимума.
Запишите время (значение x) и скорость (значение y) более точного решения максимума в калькуляторе.
Если исходное уравнение скорости включает синус или косинус, следите за временем, которое калькулятор сообщает, используя много десятичных знаков. Ваш реальный ответ на время может быть связан с пи. Разделите десятичное время на пи. Если частное близко к дроби, это, вероятно, та дробь, округленная калькулятором до десятичной дроби. Вернитесь к графику, нажмите «Trace» и введите точную дробь — включая кнопку «пи» на вашем калькуляторе. Если вы получите тот же максимум, который изначально нашел калькулятор, тогда этот максимум действительно будет получен при дробном кратном пи.
Как найти предельную скорость
wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 11 человек(а).
Количество просмотров этой статьи: 34 506.
Вы никогда не задумывались, почему при падении парашютисты в конечном итоге достигают предельной максимальной скорости, хотя сила тяжести в вакууме заставляет тело постоянно ускоряться? Падающее тело достигает предельной скорости, когда есть некая сдерживающая сила, такая, как сопротивление воздуха. Сила тяжести действует на тело с постоянной величиной, но сила сопротивления воздуха увеличивается с увеличением скорости падения тела. Если свободное падение длится достаточно долго, то скорость падения тела достигнет такой величины, при которой сила сопротивления станет равна силе тяжести, и эти силы будут компенсировать друг друга; в результате этого тело будет продолжать падение с постоянной скоростью, пока не коснется земли. Такая скорость называется предельной скоростью.
Как определить максимальную и минимальную скорости движущихся объектов — манекены — Бизнес — 2022
Одним из наиболее практических применений дифференциации является поиск максимальных или минимальных значений функции реального мира, например максимальной и минимальной скоростей движущегося объекта.
Вы можете представить v elocity как более техническую версию скорость .
Вот пример. Йо-йо движется прямо вверх и вниз. Его высота над землей, как функция времени, задается функцией H ( t ) = t 3 — 6 t 2 + 5 t + 30, где t находится в секундах и H ( t ) находится в дюймов. При t = 0 yo-yo составляет 30 дюймов над землей, а через 4 секунды он находится на высоте 18 дюймов, как показано на этом рисунке.
Высота yo-yo, от 0 до 4 секунд.
Чтобы определить общее расстояние, пройденное yo-yo, вам нужно добавить расстояния, пройденные на каждой ноге поездки yo-yo: вверх нога, нога и вторая нога.
Во-первых, йо-йо поднимается с высоты от 30 дюймов до 31 дюймов (где первая точка поворота). Это расстояние около 1,1 дюйма. Затем он опускается примерно с 31. 1 до 16. 9 (высота второй точки поворота). Это расстояние 31. 1 минус 16. 9, или около 14. 2 дюйма. Наконец, yo-yo снова поднимается с 16 дюймов до конечной высоты 18 дюймов. Это еще 1 дюйм. Добавьте эти три расстояния, чтобы получить общее пройденное расстояние:
Примечание: Сравните этот ответ с общим объемом перемещения — 12, который вы получаете от вычитания конечной высоты yo-yo, 18 дюймов, от ее начальная высота 30 дюймов. Смещение отрицательно, потому что движение сети вниз. И положительная величина смещения (а именно 12) меньше расстояния, пройденного 16. 4, потому что при смещении верхние ноги рейса yo-yo отменяют часть расстояния вниз. Посмотрите математику:
Средняя скорость yo-yo определяется общим пройденным пройденным расстоянием, деленным на прошедшее время. Таким образом,
Скажем, вы определяете, что максимальная скорость yo-yo составляет 5 дюймов в секунду, а ее минимальная скорость составляет -7 дюймов в секунду. Скорость -7 — это скорость 7, так что это максимальная скорость yo-yo. Его минимальная скорость равна нулю в двух оборотных точках.
Хорошим способом анализа максимальной и минимальной скорости является рассмотрение функции скорости и ее графика. (Или, если вы являетесь обжором для наказания, ознакомьтесь со следующим mumbo jumbo.) Скорость равна абсолютному значению скорости.
Velocity, V ( t ), является производной от позиции (высота, в этой задаче). Таким образом:
Итак, для задачи yo-yo, функция скорости,
Посмотрите на график S ( t ) на следующем рисунке.
Функция скорости yo-yo S ( t )
Глядя на этот график , легко видеть, что максимальная скорость yo-yo происходит при t = 2
и что минимальная скорость равна нулю на двух x -перехватах.
Минимальная и максимальная скорость: Для непрерывной функции скорость минимальная скорость равна нулю всякий раз, когда максимальная и минимальная скорости имеют противоположные знаки или когда один из них нуль. Когда максимальная и минимальная скорости являются как положительными, так и отрицательными, скорость минимум меньше абсолютных значений максимальной и минимальной скоростей. Во всех случаях максимальная скорость представляет собой больше абсолютных значений максимальной и минимальной скоростей. Это глоток или что?
Как найти максимальную скорость по графику
Чтобы узнать знак производной, рисуем координатную прямую, отмечаем точку 1/2 и определяем знаки производной подбором.
Берем любую точку, например, 0.
— 60 * 0 + 30 = 30 (производная положительна, функция возрастает)
Берем например, точку 1.
— 60 * 1 + 30 = — 30 (производная отрицательна, функция убывает)
Значит, t = 1/2 — это точка максимума.
Подставим это значение в уравнение скорости.
v = — 30t 2 + 30t + 2
v = — 30(1/2) 2 + 30 * 1/2 + 2 = — 7,5 + 15 + 2 = 9,5.
Ответ: максимальная скорость движения равна 9,5.
Из уравнения S = — 10t^3 + 15t^2 + 2t сначала найдем производную пути по времени(это будет уравнение скорости точки): S'(t) = V(t) = — 30t^2 + 30t + 2. Графиком функции данного уравнения является парабола и как видим около t^2(то есть коэффициент а) стоит отрицательное число, значит ветки параболы направлены вниз и максимальное значение t достигается на вершине параболы, найдем ее: tmax = — b / 2a = 30 / 30 * 2 = 0,5. Подставим в уравнение скорости и найдем Vmax получим Vmax = — 30 * 0,5^2 + 30 * 0,5 + 2 = 9,5.
- Попроси больше объяснений
- Следить
- Отметить нарушение
Ответ
Ответ:
Объяснение:
Находим L. Разделим путь на три отрезка(как на графике)(с 0 по 1 секунду, потом с 1 до 4 секунды и с 4 по 5 секунду)
1. S = Vot(начальная скорость умноженная на время) + at²/2 ; a(ускорение) = ΔV/Δt = 15 м/с²
S = 0 + 15*1/2 = 7,5 м
2. S = V*t = 15*3 = 45 м
3. S = Vot + at²/2 ; a = ΔV/Δt = — 15 м/с² (тело тормозит)
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
То есть ускорение – это величина, которая определяется изменением скорости за время, в течение которого это изменение произошло.
Еще раз о том, что такое равноускоренное движение
Автомобиль за каждую секунду увеличивает свою скорость на 
На первый взгляд, кажется, да, ведь за равные промежутки времени скорость увеличивается на равные величины. Давайте рассмотрим подробнее движение на протяжении 1 с. Возможен такой случай, что первые 0,5 с автомобиль двигался равномерно и увеличил свою скорость на Часто равноускоренным называют такое движение, при котором тело двигается с постоянным ускорением 
Уравнение скорости
Воспользовавшись уравнением, определяющим ускорение 
Уравнение скорости в проекциях имеет вид:
Это уравнение дает возможность определить скорость в любой момент движения тела. При работе с законом изменения скорости от времени необходимо учитывать направление скорости по отношению к выбранной СО.
К вопросу о направлении скорости и ускорения
В равномерном движении направление скорости и перемещения всегда совпадают. В случае равноускоренного движения направление скорости не всегда совпадает с направлением ускорения и не всегда направление ускорения указывает направление движения тела.
Рассмотрим наиболее типичные примеры направления скорости и ускорения.
1. Скорость и ускорение направлены в одну сторону вдоль одной прямой (рис. 1).
Рис. 1. Скорость и ускорение направлены в одну сторону вдоль одной прямой
В данном случае тело разгоняется. Примерами такого движения могут быть свободное падение, начало движения и разгон автобуса, старт и разгон ракеты.
2. Скорость и ускорение направлены в разные стороны вдоль одной прямой (рис. 2).
Рис. 2. Скорость и ускорение направлены в разные стороны вдоль одной прямой
Такое движение иногда называют равнозамедленным. В таком случае говорят, что тело тормозит. В конечном итоге оно либо остановится, либо начнет двигаться в противоположном направлении. Пример такого движения – камень, подброшенный вертикально вверх.
3. Скорость и ускорение взаимно перпендикулярны (рис. 3).
Рис. 3. Скорость и ускорение взаимно перпендикулярны
Примерами такого движения является движение Земли вокруг Солнца и движение Луны вокруг Земли. В этом случаи траекторией движения будет окружность.
Таким образом, направление ускорения не всегда совпадает с направлением скорости, но всегда совпадает с направлением изменения скорости.
График скорости
График скорости (проекции скорости) представляет собой закон изменения скорости (проекции скорости) от времени для равноускоренного прямолинейного движения, представленный графически.
Рис. 4. Графики зависимости проекции скорости от времени для равноускоренного прямолинейного движения
Проанализируем различные графики.
Первый. Уравнение проекции скорости:
Второй – это зависимость при отрицательном значении проекции ускорения, когда движение замедленно, то есть скорость по модулю сначала уменьшается. В этом случае уравнение выглядит так:
График начинается в точке
Где
Рис. 5. График функции
Это уравнение прямой, что подтверждается графиками, рассмотренными нами.
Некоторые частные случаи
Чтобы окончательно разобраться с графиком скорости, рассмотрим частные случаи. На первом графике зависимость скорости от времени связана с тем, что начальная скорость, 
Запись этого уравнения 
Рис. 6. Различные случаи равноускоренного движения
Еще два случая равноускоренного движения представлены на следующих двух графиках. Второй случай – это ситуация, когда сначала тело двигалось с отрицательной проекцией ускорения, а затем начало разгоняться в положительном направлении оси
Третий случай – это ситуация, когда проекция ускорения меньше нуля и тело непрерывно движется в направлении, противоположном положительному направлению оси 
График зависимости ускорения от времени
Равноускоренное движение – это движение, при котором ускорение тела не меняется.
Рис. 7. График зависимости проекций ускорения от времени
Если какая-либо зависимость является постоянной, то на графике она изображается прямой, параллельной оси абсцисс. Прямые I и II – прямые движения для двух разных тел. Обратите внимание, что прямая I лежит выше прямой абсцисс (проекция ускорения положительна), а прямая II – ниже (проекция ускорения отрицательна). Если бы движение было равномерным, то проекция ускорения совпала бы с осью абсцисс.
Рассмотрим рис. 8. Площадь фигуры, ограниченной осями, графиком и перпендикуляром к оси абсцисс, равна:
Произведение ускорения и времени –это изменение скорости за данное время.
Рис. 8. Изменение скорости
Площадь фигуры, ограниченной осями, зависимостью и перпендикуляром к оси абсцисс, численно равна изменению скорости тела.
Мы использовали слово «численно», поскольку единицы измерения площади и изменения скорости не совпадают.
Заключение
На данном уроке мы познакомились с уравнением скорости и научились графически изображать данное уравнение.
- Кикоин И.К., Кикоин А.К. Физика: Учебник для 9 класса средней школы. – М.: «Просвещение».
- Перышкин А.В., Гутник Е.М., Физика. 9 кл.: учебник для общеобразоват. учреждений/А.В. Перышкин, Е.М. Гутник. – 14-е изд., стереотип. – М.: Дрофа, 2009. – 300 с.
- Соколович Ю.А., Богданова Г.С. Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «class-fizika.narod.ru» (Источник)
- Интернет-портал «youtube.com» (Источник)
- Интернет-портал «fizmat.by» (Источник)
- Интернет-портал «sverh-zadacha.ucoz.ru» (Источник)
1. Что такое равноускоренное движение?
2. Охарактеризуйте движение тела и определите пройденный путь тела по графику за 2 с от начала движения:
3. На каком из графиков изображена зависимость проекции скорости тела от времени при равноускоренном движении при 
I. Механика
Тестирование онлайн
Гармоническое колебание
Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.
График гармонического колебания
График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.
Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.
Уравнение гармонического колебания
Уравнение гармонического колебания устанавливает зависимость координаты тела от времени
График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой 
Изменение скорости и ускорения при гармоническом колебании
Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия — достигает максимального значения.
Если колебание описывать по закону косинуса
Если колебание описывать по закону синуса
Максимальные значения скорости и ускорения
Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле












































