Прямолинейное равноускоренное движение — это прямолинейное движение, при котором скорость тела изменяется (увеличивается или уменьшается) на одну и ту же величину за равные промежутки времени.
Ускорение — физическая величина, характеризующая быстроту изменения скорости тела. То есть, показывает, на какую величину изменяется скорость за единицу времени.
Примеры равноускоренного движения:
- разгон самолета перед взлетом;
- падающая с крыши сосулька;
- торможение лыжника на горном склоне;
- разгоняющийся на склоне сноубордист;
- свободное падение в результате прыжка с парашютом;
- камень брошенный под углом к горизонту;
Равномерное прямолинейное движение является частным случаем равноускоренного движения, при котором ускорение равно нулю.
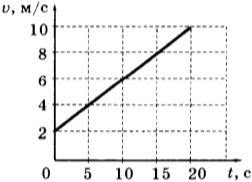
Равноускоренное движение: формулы
Формула для скорости при равноускоренном движении:
Vк=Vн+at
где: Vк — конечная скорость тела,
Vн — начальная скорость тела,
a=const — ускорение (a>0 при ускорении, a<0 при замедлении)
t — время.
Формула для ускорения при равноускоренном движении:
a=(Vк-Vн)/t
Во время движения тела ускорение остается постоянным.
Задача 1
Кирилл ехал на велосипеде со скоростью 6 м/с, затем начал разгоняться на горке. Чему будет равна его скорость через 10 секунд, если ускорение равно 0,5 м/с?
Решение. Vн=6м/с, ускорение a=0,5м/с, время разгона t=10 секунд.
Получаем: Vн= 6 + 0,5 · 10 = 11 м/с.
Ответ: за 10с Кирилл разгонится до скорости 11 м/с.
Формула расстояния при равноускоренном движении
- Если известны время, скорость начальная и скорость конечная
S = t*(Vн+ Vк)/2
- Если известны время, скорость начальная и ускорение
S = Vнt + at2/2 = t*(Vн + at/2)
где: S — путь, пройденный за время t,
Vн — начальная скорость,
Vк — конечная скорость,
a — ускорение тела,
t — время.
В случае равноускоренного движения с неизвестным временем движения, но с заданными начальной и конечной скоростями пройденный путь можно найти с помощью следующей формулы:
2аS = Vк2−Vн2
где S — путь, пройденный за время t ,
V0 — начальная скорость,
V — скорость в момент времени t,
a — ускорение тела.
Задача 2
Таксист получил заказ и начал движение с ускорением 0,1 м/с2. На каком расстоянии от начала движения его скорость станет равной 15м/с?
Решение. Так как таксист начал движение, начальная скорость равна нулю (Vн=0), Vк=15м/с, ускорение a=0,1м/с2.
Получаем:
S = 15^2 — 0^2 =1125 м.
Ответ: на расстоянии 1 125 м от начала движения скорость такси станет равной 15 м/с.
Перемещение при равноускоренном движении
Важно напомнить разницу между путем и перемещением тела.
- Путь — длина траектории. Если тело движется в любом направлении, то его путь увеличивается. Путь — всегда положительное значение.
- Перемещение — вектор, соединяющий начальное и конечное положение тела. Проекция перемещения может принимать отрицательное значение.
Например, если путник прошел в одну сторону расстояние S1, а обратно — S2, то: путь тела равен S1 + S2, а перемещение равно S1 − S2. В некоторых задачах путь и перемещение могут совпадать, но не всегда.
Равноускоренное движение: графически
График зависимости ускорения от времени:
Во время движения тела ускорение остается постоянным.
Взаимосвязь скорости, времени и расстояния:
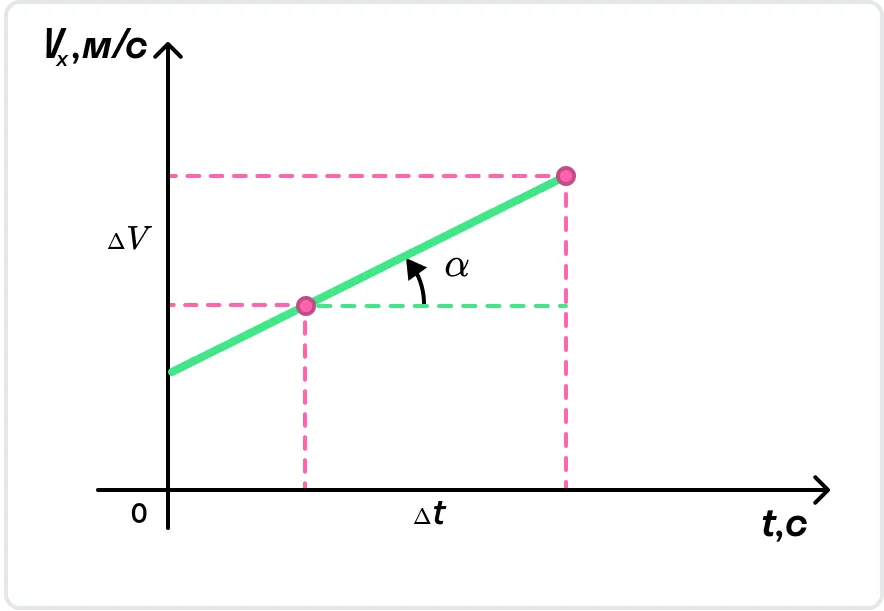
На рисунке показан график, в котором скорость равномерно увеличивается.
С помощью графика скорости можно определить ускорение тела как тангенс угла наклона графика к оси времени.
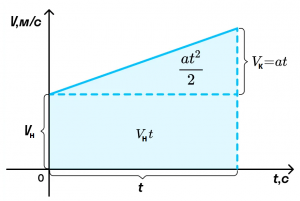
Из графика скорости получим формулу пути при равноускоренном движении тела.
Пройденный телом путь при равноускоренном движении численно равен площади фигуры под графиком зависимости скорости от времени. Вычислим площадь трапеции как сумму площадей прямоугольника Vнt и треугольника at2/2. Получим: S = Vнt + at2/2.
Математически зависимость координаты от времени при равноускоренном движении представляет собой квадратичную функцию, ее график — парабола.
Задача 3
Лыжник подъехал со скоростью 3 м/с к спуску длиной 36 м и съехал с него за несколько секунд, при этом его конечная скорость составила 15 м/с. Определите местонахождение лыжника спустя 2с после начала движения из начала координат.
Дано:
Vн = 3 м/с, начальная координата (t) равна нулю,
Vк = 15м/с,
a — скорость лыжника увеличивается, поэтому ускорение — положительное число,
S = 36м — путь с горы,
t — 2с.
Решение:
Найдем ускорение из формулы пути при равноускоренном движении: 2аS = Vк2−Vн2
Получим: а = (Vк2−Vн2 )/2S = (225-9)/(2*36) = 3 м/с2.
Составим уравнение движения лыжника исходя из формулы: S = Vнt + at2/2.
Получаем: x(t) = 3t + 1,5t2
По уравнению определим координату лыжника в момент времени t = 2с:
Получаем: x(2) = 3*2 + 1,5*22 =6+6=12 м.
Ответ: через 2 с после начала движения координата лыжника будет равна 12 м.
Для того, чтобы проверить правильность решения задач на равноускоренное движение, воспользуйтесь калькулятором равноускоренного движения.
Для того, чтобы перевести единицы измерения, воспользуйтесь конвертерами единиц измерения:
- Конвертер единиц измерения расстояния (длины)
- Конвертер единиц измерения скорости
- Конвертер единиц измерения времени
Равноускоренное движение

4.7
Средняя оценка: 4.7
Всего получено оценок: 68.
Обновлено 28 Июля, 2021
4.7
Средняя оценка: 4.7
Всего получено оценок: 68.
Обновлено 28 Июля, 2021
Одним из видов движения, изучаемых кинематикой, является равноускоренное движение. Равноускоренное движение — это достаточно распространённый вид движения, даже большинство равномерных движений начинались с разгона и были некоторое время равноускоренными. Рассмотрим эту тему подробнее, получим формулу равноускоренного движения, приведём примеры такого движения.
Ускорение
Если некоторое тело начинает движение из состояния покоя, то его скорость изменяется от нуля до некоторого максимального значения. Следовательно, при таком движении можно указать быстроту изменения скорости.
Например, в рекламе автомобилей указывается время разгона до 100 км/ч. Ясно, что модель, достигающая такой скорости за 5 секунд, значительно резвее, чем модель со временем разгона 15 секунд, хотя конечная скорость в обоих случаях одинакова. В чем же здесь разница, с точки зрения кинематики?
Разница в быстроте набора скорости.
Быстрота набора скорости называется ускорением. Ускорение (обозначается латинской буквой $a$) равно отношению величины набранной скорости ко времени этого увеличения:
$$overrightarrow a={overrightarrow {Δv}over t}={overrightarrow v- overrightarrow {v_0} over t}$$
где:
- $overrightarrow a$ — ускорение тела;
- $overrightarrow v$ — скорость тела в момент $t$;
- $overrightarrow {v_0}$ — начальная скорость тела (при $t=0$).
Из данной формулы можно получить размерность ускорения. Скорость измеряется в метрах в секунду, а время — в секундах, значит, ускорение измеряется в метрах в секунду за секунду (или метров в секунду в квадрате).
В приведённом примере первый автомобиль разгоняется с ускорением 5,56 метров в секунду за секунду, а второй — с ускорением 1,85 метров в секунду за секунду.
Равноускоренное движение
Движение, при котором ускорение тела постоянно, называется равноускоренным. При этом знак ускорения не играет роли. Движение с постоянным отрицательным ускорением также является равноускоренным, несмотря на то, что скорость уменьшается.
Наиболее частым примером равноускоренного движения является свободное падение тел в первые секунды, когда сопротивление воздуха ещё не играет большой роли. Другим примером может служить разгон автомобиля при постоянном нажатии на педаль «газа», пока не будет набрана необходимая скорость.
Формулы равноускоренного движения
Найдём формулы скорости и координаты при равноускоренном движении. Из приведённого выше определения ускорения следует, что скорость при постоянном ускорении равна:
$$overrightarrow v= overrightarrow {v_0} + overrightarrow a t$$
Это — линейная зависимость. Её график представляет собой прямую, наклон которой зависит от значения $a$. Чем оно больше, тем круче поднимается график.
Из курса физики 9 класса известно, что перемещение тела равно площади под графиком скорости. А площадь под данной прямой представляет собой трапецию с высотой $t$ и основаниями $v$ и $v_0$. Как известно из геометрии, площадь трапеции равна произведению полусуммы оснований на высоту. То есть:
$$overrightarrow x= {(overrightarrow {v_0} + overrightarrow v)over 2} t$$
Подставив значение $v$ из предыдущей формулы и учтя, что в начальный момент времени координата была равна $x_0$, мы получим:
$$overrightarrow x= overrightarrow {x_0}+overrightarrow {v_0}t + {overrightarrow at^2 over 2}$$
Это основная формула равноускоренного движения, позволяющая найти координату $overrightarrow x$ материальной точки в момент времени $t$ при условии, что начальная координата была равна $overrightarrow x_0$, начальная скорость — $overrightarrow {v_0}$, а ускорение — $overrightarrow a$. В задачах она используется, как правило, совместно с предыдущей.
Что мы узнали?
Ускорение — это физическая величина, характеризующая быстроту набора скорости материальной точкой. Движение с постоянным ускорением называется равноускоренным. Хорошим примером равноускоренного движения является свободное падение тел.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.7
Средняя оценка: 4.7
Всего получено оценок: 68.
А какая ваша оценка?
На чтение 4 мин Просмотров 3к. Опубликовано 25.11.2021
Содержание
- Ответ или решение 2
- Скорость движения рассчитывается по формуле
- Найдем уравнение скорости
- Ответ
- Уравнение скорости
- График скорости
- Некоторые частные случаи
- Заключение
Ответ или решение 2
Скорость движения рассчитывается по формуле
- Скорость движения равна производной формулы пути;
- чтобы найти максимальную скорость, нужно найти производную скорости;
- затем нужно определить точки максимума;
- подставить их в уравнение скорости.
Нам дано уравнение пути s = -10t 3 + 15t 2 + 2t
Найдем уравнение скорости
S` = — 10 * 3t 2 + 15 * 2t + 2 = — 30t 2 + 30t + 2
v = — 30t 2 + 30t + 2
Найдем точки максимума этой функции
Для этого найдем производную этой функции.
v`= — 30 * 2t + 30 = — 60t + 30
Приравняем ее к нулю.
Переносим 30 в правую часть, меняя знак.
Делим все уравнение на (- 30).
Чтобы узнать знак производной, рисуем координатную прямую, отмечаем точку 1/2 и определяем знаки производной подбором.
Берем любую точку, например, 0.
— 60 * 0 + 30 = 30 (производная положительна, функция возрастает)
Берем например, точку 1.
— 60 * 1 + 30 = — 30 (производная отрицательна, функция убывает)
Значит, t = 1/2 — это точка максимума.
Подставим это значение в уравнение скорости.
v = — 30t 2 + 30t + 2
v = — 30(1/2) 2 + 30 * 1/2 + 2 = — 7,5 + 15 + 2 = 9,5.
Ответ: максимальная скорость движения равна 9,5.
Из уравнения S = — 10t^3 + 15t^2 + 2t сначала найдем производную пути по времени(это будет уравнение скорости точки): S'(t) = V(t) = — 30t^2 + 30t + 2. Графиком функции данного уравнения является парабола и как видим около t^2(то есть коэффициент а) стоит отрицательное число, значит ветки параболы направлены вниз и максимальное значение t достигается на вершине параболы, найдем ее: tmax = — b / 2a = 30 / 30 * 2 = 0,5. Подставим в уравнение скорости и найдем Vmax получим Vmax = — 30 * 0,5^2 + 30 * 0,5 + 2 = 9,5.
- Попроси больше объяснений
- Следить
- Отметить нарушение
Vazgen1312 05.07.2019
Ответ
Ответ:
Объяснение:
Находим L. Разделим путь на три отрезка(как на графике)(с 0 по 1 секунду, потом с 1 до 4 секунды и с 4 по 5 секунду)
1. S = Vot(начальная скорость умноженная на время) + at²/2 ; a(ускорение) = ΔV/Δt = 15 м/с²
S = 0 + 15*1/2 = 7,5 м
2. S = V*t = 15*3 = 45 м
3. S = Vot + at²/2 ; a = ΔV/Δt = — 15 м/с² (тело тормозит)
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
То есть ускорение – это величина, которая определяется изменением скорости за время, в течение которого это изменение произошло.
Еще раз о том, что такое равноускоренное движение
Автомобиль за каждую секунду увеличивает свою скорость на 
На первый взгляд, кажется, да, ведь за равные промежутки времени скорость увеличивается на равные величины. Давайте рассмотрим подробнее движение на протяжении 1 с. Возможен такой случай, что первые 0,5 с автомобиль двигался равномерно и увеличил свою скорость на 

Уравнение скорости
Воспользовавшись уравнением, определяющим ускорение 
Уравнение скорости в проекциях имеет вид:
Это уравнение дает возможность определить скорость в любой момент движения тела. При работе с законом изменения скорости от времени необходимо учитывать направление скорости по отношению к выбранной СО.
К вопросу о направлении скорости и ускорения
В равномерном движении направление скорости и перемещения всегда совпадают. В случае равноускоренного движения направление скорости не всегда совпадает с направлением ускорения и не всегда направление ускорения указывает направление движения тела.
Рассмотрим наиболее типичные примеры направления скорости и ускорения.
1. Скорость и ускорение направлены в одну сторону вдоль одной прямой (рис. 1).
Рис. 1. Скорость и ускорение направлены в одну сторону вдоль одной прямой
В данном случае тело разгоняется. Примерами такого движения могут быть свободное падение, начало движения и разгон автобуса, старт и разгон ракеты.
2. Скорость и ускорение направлены в разные стороны вдоль одной прямой (рис. 2).
Рис. 2. Скорость и ускорение направлены в разные стороны вдоль одной прямой
Такое движение иногда называют равнозамедленным. В таком случае говорят, что тело тормозит. В конечном итоге оно либо остановится, либо начнет двигаться в противоположном направлении. Пример такого движения – камень, подброшенный вертикально вверх.
3. Скорость и ускорение взаимно перпендикулярны (рис. 3).
Рис. 3. Скорость и ускорение взаимно перпендикулярны
Примерами такого движения является движение Земли вокруг Солнца и движение Луны вокруг Земли. В этом случаи траекторией движения будет окружность.
Таким образом, направление ускорения не всегда совпадает с направлением скорости, но всегда совпадает с направлением изменения скорости.
График скорости
График скорости (проекции скорости) представляет собой закон изменения скорости (проекции скорости) от времени для равноускоренного прямолинейного движения, представленный графически.
Рис. 4. Графики зависимости проекции скорости от времени для равноускоренного прямолинейного движения
Проанализируем различные графики.
Первый. Уравнение проекции скорости:
Второй – это зависимость при отрицательном значении проекции ускорения, когда движение замедленно, то есть скорость по модулю сначала уменьшается. В этом случае уравнение выглядит так:
График начинается в точке
Где
Рис. 5. График функции
Это уравнение прямой, что подтверждается графиками, рассмотренными нами.
Некоторые частные случаи
Чтобы окончательно разобраться с графиком скорости, рассмотрим частные случаи. На первом графике зависимость скорости от времени связана с тем, что начальная скорость, 
Запись этого уравнения 
Рис. 6. Различные случаи равноускоренного движения
Еще два случая равноускоренного движения представлены на следующих двух графиках. Второй случай – это ситуация, когда сначала тело двигалось с отрицательной проекцией ускорения, а затем начало разгоняться в положительном направлении оси
Третий случай – это ситуация, когда проекция ускорения меньше нуля и тело непрерывно движется в направлении, противоположном положительному направлению оси 
График зависимости ускорения от времени
Равноускоренное движение – это движение, при котором ускорение тела не меняется.
Рис. 7. График зависимости проекций ускорения от времени
Если какая-либо зависимость является постоянной, то на графике она изображается прямой, параллельной оси абсцисс. Прямые I и II – прямые движения для двух разных тел. Обратите внимание, что прямая I лежит выше прямой абсцисс (проекция ускорения положительна), а прямая II – ниже (проекция ускорения отрицательна). Если бы движение было равномерным, то проекция ускорения совпала бы с осью абсцисс.
Рассмотрим рис. 8. Площадь фигуры, ограниченной осями, графиком и перпендикуляром к оси абсцисс, равна:
Произведение ускорения и времени –это изменение скорости за данное время.
Рис. 8. Изменение скорости
Площадь фигуры, ограниченной осями, зависимостью и перпендикуляром к оси абсцисс, численно равна изменению скорости тела.
Мы использовали слово «численно», поскольку единицы измерения площади и изменения скорости не совпадают.
Заключение
На данном уроке мы познакомились с уравнением скорости и научились графически изображать данное уравнение.
- Кикоин И.К., Кикоин А.К. Физика: Учебник для 9 класса средней школы. – М.: «Просвещение».
- Перышкин А.В., Гутник Е.М., Физика. 9 кл.: учебник для общеобразоват. учреждений/А.В. Перышкин, Е.М. Гутник. – 14-е изд., стереотип. – М.: Дрофа, 2009. – 300 с.
- Соколович Ю.А., Богданова Г.С. Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «class-fizika.narod.ru» (Источник)
- Интернет-портал «youtube.com» (Источник)
- Интернет-портал «fizmat.by» (Источник)
- Интернет-портал «sverh-zadacha.ucoz.ru» (Источник)
1. Что такое равноускоренное движение?
2. Охарактеризуйте движение тела и определите пройденный путь тела по графику за 2 с от начала движения:
3. На каком из графиков изображена зависимость проекции скорости тела от времени при равноускоренном движении при 
«>
Содержание:
- Определение и формула равноускоренного движения
- Основные кинематические величины при равноускоренном движении
- Примеры решения задач
Определение и формула равноускоренного движения
Определение
Движение, при котором за любые равные промежутки времени скорость меняется на одну величину, называют равнопеременным.
Если скорость при этом увеличивается, то такое движение носит название равноускоренного движения.
Равноускоренное движение можно определить еще как движение, при котором модуль касательного ускорения
($a_{tau}=$ const $>0$).
Основные кинематические величины при равноускоренном движении
Ускорение $bar{a}$ при равноускоренном движении находят как:
$$bar{a}=frac{bar{v}_{2}-bar{v}_{1}}{t}(1)$$
где v2 – конечная скорость, v1— начальнаяскорость движения, t–время движения.
Скорость в любой момент равноускоренного прямолинейного движения можно найти как:
$$bar{v}=bar{v}_{0}+bar{a} t(2)$$
где $bar{v}_0$ – начальная скорость движения.
Уравнение для координаты материальной при равноускоренном движении записывают как:
$$x=x_{0}+v_{0 x} t+frac{a_{x} t^{2}}{2}(2)$$
где v0x – проекция начальной скорости на ось X, ax – проекция ускорения на ось X.
Перемещение при равноускоренном движении является функцией вида:
$$bar{s}=bar{s}_{0}+bar{v}_{0} t+frac{bar{a} t^{2}}{2}(3)$$
где $bar{s}_0$ – перемещение в начальный момент времени.
Или $bar{s}$ еще можно представить как:
$$bar{s}=frac{bar{v}^{2}-bar{v}_{0}^{2}}{2 bar{a}}(4)$$
Примеры решения задач
Пример
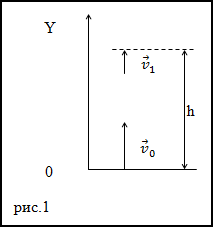
Задание. Тело было брошено вертикально вверх. Оно возвратилось на землю через промежуток времени, равный t.
Какой была начальная скорость тела, и на какую высоту оно поднялось?
Решение. Тело в поле тяжести Земли движется с постоянным ускорением равным ускорению свободного
падения, на рис.1 оно направлено вниз.
В качестве основы для решения задачи используем формулу для перемещения при равноускоренном движении:
$$bar{s}=bar{s}_{0}+bar{v}_{0} t+frac{bar{a} t^{2}}{2}$$
Все движение происходит только по оси Y, поэтому проекция выражения (1.1) примет вид:
$$y(t)=v_{0} t-frac{g t^{2}}{2}(1.2)$$
Формула для скорости при равноускоренном движении записывается как:
$$bar{v}=bar{v}_{0}+bar{a} t(1.3)$$
В проекции на ось она преобразуется к виду:
$$v(t)=v_{0}-g t(1.4)$$
Точке максимального подъема мы имеем y(t1)=h и v(t1)=0 (t1 — время поъема), тогда выражения (1.2)
и (1.4) перепишем как:
$$h=v_{0} t_{1}-frac{gleft(t_{1}right)^{2}}{2}, 0=v_{0}-g t_{1}(1.5)$$
где $t_{1}=frac{t}{2}$ . Следовательно,
$$v_{0}=frac{g t}{2}(1.6)$$
Подставляя выражение (1.6) вместо начальной скорости в формулу h, имеем:
$$h=frac{g t}{2} cdot frac{t}{2}-frac{gleft(frac{t}{2}right)^{2}}{2}=frac{g t^{2}}{8}$$
Ответ. $v_{0}=frac{g t}{2} ; h=frac{g t^{2}}{8}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Расстояние между двумя точками равно l. Первую половину пути тело проходит равноускорено,
вторую равнозамедленно. Максимальная скорость тела равна v. Каков модуль ускорения тела и время его перемещения, если
ускорения на обоих участках пути равны по модулю.
Решение. Данную задачу можно решить двумя способами.
1 способ аналитический.
В качестве основы для решения задачи используем формулу для перемещения при равноускоренном движении:
$$bar{s}=bar{s}_{0}+bar{v}_{0} t+frac{bar{a} t^{2}}{2}(2.1)$$
Для первой половины пути, учитывая, что мы рассматриваем прямолинейное движение, запишем:
$$s=frac{a t_{1}^{2}}{2}(2.2)$$
где учтено, что $bar{s}_{0}=0, bar{v}_{0}=0, s=frac{l}{2}$ .
Для второй половины пути получаем:
$$s^{prime}=v t_{2}-frac{a t_{2}^{2}}{2}(2.3)$$
где $s^{prime}=frac{l}{2}$ .
Суммарное время, которое провело тело в пути равно:
$$t=t_{1}+t_{2}(2.4)$$
Наибольшая скорость движения равна:
$$v=a t_{1}=a t_{2} rightarrow t_{1}=t_{2}(2.5)$$
Суммарный путь равен:
$$l=frac{a t_{1}^{2}}{2}+v t_{2}-frac{a t_{2}^{2}}{2} rightarrow t_{2}=frac{l}{v}$$
Ускорение выразим из (2.2), имеем:
$$a=frac{l}{t_{1}^{2}}=frac{v^{2}}{l}$$
2.графический способ решения задачи.
Для этого построим график зависимости v(t).
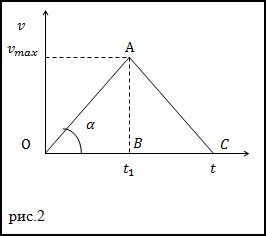
Путь равен площади под кривой или в нашем случае сумме площадей треугольниковOABи ABC. Значит можно записать:
$$
begin{array}{c}
l=frac{v_{max } t_{1}}{2}+frac{v_{max } t_{2}}{2} rightarrow t=frac{2 l}{v_{max }}=frac{2 l}{v} \
a=operatorname{tg} alpha=frac{v_{max }}{t / 2}=frac{v^{2}}{l}
end{array}
$$
Ответ. $t=frac{2 l}{v}, a=frac{v^{2}}{l}$
Читать дальше: Формула силы Лоренца.
Скорость. Ускорение. Равноускоренное прямолинейное движение
1. Реальное механическое движение — это движение с изменяющейся скоростью. Движение, скорость которого стечением времени изменяется, называют неравномерным движением.
При неравномерном движении координату тола уже нельзя определить но формуле ( x=x_0+v_xt ), так как значение скорости движения не является постоянным. Поэтому для характеристики быстроты изменения положения тела с течением времени при неравномерном движении вводят величину, называемую средней скоростью.
Средней скоростью ( vec{v}_{ср} ) неравномерного движения называют физическую величину, равную отношению перемещении ( vec{s} ) тела ко времени ( t ), за которое оно произошло: ( vec{v}_{ср}=frac{s}{t} ).
Записанная формула определяет среднюю скорость как векторную величину. В практических целях этой формулой можно воспользоваться для определения модуля средней скорости лишь в том случае, когда тело движется вдоль прямой в одну сторону. Если же нужно определить среднюю скорость движения автомобиля от Москвы до Санкт-Петербурга и обратно, чтобы рассчитать расход бензина, то эту формулу применить нельзя, поскольку перемещение в этом случае равно нулю и средняя скорость тоже равна нулю. Поэтому на практике при определении средней скорости пользуются величиной, равной отношению пути ( l ) ко времени ( t ), за которое этот путь пройден: ( v_{ср}=frac{l}{t} ). Эта скорость обычно называется средней путевой скоростью.
2. Важно, что, зная среднюю скорость неравномерного движения на каком-либо участке траектории, нельзя определить положение тела на этой траектории в любой момент времени. Например, если средняя скорость движения автомобиля за 2 часа 50 км/ч, то мы не можем сказать, где он находился через 0,5 часа от начала движения, через 1 час, 1,5 часа и т.п., поскольку он мог первые полчаса двигаться со скоростью 80 км/ч, затем какое-то время стоять, а какое-то время ехать в пробке со скоростью 20 км/ч.
3. Двигаясь по траектории, тело проходит последовательно все её точки. В каждой точке траектории оно находится в определённые моменты времени и имеет какую-то скорость.
Мгновенной скоростью называют скорость тела в данный момент времени в данной точке траектории.
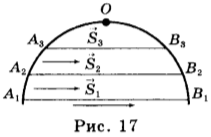
Предположим, некоторое тело совершает неравномерное прямолинейное движение (рис. 17), его скорость в точке О можно определить следующим образом: выделим на траектории участок AB, внутри которого находится точка О. Перемещение тела на этом участке — ( vec{s}_1 ) совершено за время ( t_1 ). Средняя скорость движения на этом участке – ( vec{v}_{ср.1}=frac{s_1}{t_1} ). Уменьшим перемещение тела. Пусть оно равно ( vec{s}_2 ), а время движения — ( t_2 ). Тогда средняя скорость за это время: ( vec{v}_{ср.2}=frac{s_2}{t_2} ). Еще уменьшим перемещение, средняя скорость на этом участке: ( vec{v}_{ср.3}=frac{s_3}{t_3} ).
При дальнейшем уменьшении перемещения и соответственно времени движения тела они станут такими маленькими, что прибор, например спидометр, перестанет фиксировать изменение скорости, и движение за этот малый промежуток времени можно считать равномерным. Средняя скорость на этом участке и есть мгновенная скорость тела в т.О.
Таким образом, мгновенной скоростью называют векторную физическую величину, равную отношению малого перемещения (( Delta{vec{s}} )) к малому промежутку времени ( Delta{t} ), за которое это перемещение произошло: ( vec{v}=frac{Delta{s}}{Delta{t}} ).
4. Одним из видов неравномерного движения является равноускоренное движение. Равноускоренным движением называют движение, при котором скорость тела за любые равные промежутки времени изменяется на одно и то же значение.
Слова «любые равные промежутки времени» означают, что какие бы равные промежутки времени (2 с, 1 с, доли секунды и т.п.) мы ни взяли, скорость всегда будет изменяться одинаково. При этом её модуль может как увеличиваться, так и уменьшаться.
5. Характеристикой равноускоренного движения, помимо скорости и перемещения, является ускорение.
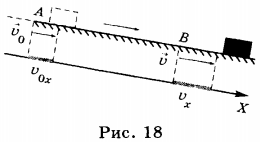
Пусть в начальный момент времени ( t_0=0 ) скорость тела равна ( vec{v}_0 ). В некоторый момент времени ( t ) она стала равной ( vec{v} ). Изменение скорости за промежуток времени ( t-t_0=t ) равно ( vec{v}-vec{v}_0 ) (рис.18). Изменение скорости за единицу времени равно: ( frac{vec{v}-vec{v}_0}{t} ). Эта величина и есть ускорение тела, она характеризует быстроту изменения скорости ( vec{a}=frac{vec{v}-vec{v}_0}{t} ).
Ускорение тела при равноускоренном движении — векторная физическая величина, равная отношению изменения скорости тела к промежутку времени, за который это изменение произошло.
Единица ускорения ( [a]=[v]/[t] ); ( [a] ) = 1 м/с/1 с = 1 м/с2. 1 м/с2 — это такое ускорение, при котором скорость тела изменяется за 1 с на 1 м/с.
Направление ускорения совпадает с направлением скорости движения, если модуль скорости увеличивается, ускорение направлено противоположно скорости движения, если модуль скорости уменьшается.
6. Преобразовав формулу ускорения, можно получить выражение для скорости тела при равноускоренном движении: ( vec{v}=vec{v}_0+vec{a}t ). Если начальная скорость тела ( v_0=0 ), то ( vec{v} = vec{a}t ).
Чтобы определить значение скорости равноускоренного движения в любой момент времени, следует записать уравнение для проекции скорости на ось ОХ. Оно имеет вид: ( v_x = v_{0x} + a_xt ); если( v_{0x}=0 ), то ( v_x = a_xt ).
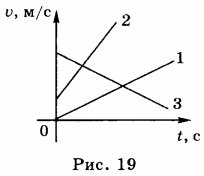
7. Как видно из формулы скорости равноускоренного движения, она линейно зависит от времени. Графиком зависимости модуля скорости от времени является прямая, составляющая некоторый угол с осью абсцисс (осью времени). На рисунке 19 приведены графики зависимости модуля скорости от времени.
График 1 соответствует движению без начальной скорости с ускорением, направленным так же, как и скорость; график 2 — движению с начальной скоростью ( v_{02} ) и с ускорением, направленным так же, как и скорость; график 3 — движению с начальной скоростью ( v_{03} ) и с ускорением, направленным в сторону, противоположную направлению скорости.
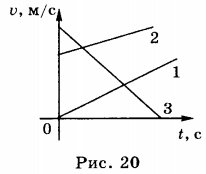
8. На рисунке приведены графики зависимости проекции скорости равноускоренного движения от времени (рис. 20).
График 1 соответствует движению без начальной скорости с ускорением, направленным вдоль положительного направления оси X; график 2 — движению с начальной скоростью ( v_{02} ), с ускорением и скоростью, направленными вдоль положительного направления оси X; график 3 — движению с начальной скоростью ( v_{03} ) : до момента времени ( t_0 ) направление скорости совпадает с положительным направлением оси X, ускорение направлено в противоположную сторону. В момент времени ( t_0 ) скорость равна нулю, а затем и скорость, и ускорение направлены в сторону, противоположную положительному направлению оси X.
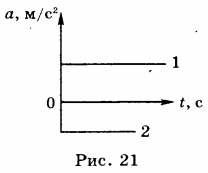
9. На рисунке 21 приведены графики зависимости проекции ускорения равноускоренного движения от времени.
График 1 соответствует движению, проекция ускорения которого положительна, график 2 — движению, проекция ускорения которого отрицательна.
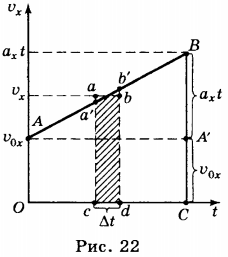
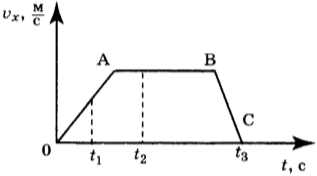
10. Формулу перемещения тела при равноускоренном движении можно получить, используя график зависимости проекции скорости этого движения от времени (рис. 22).
Выделим на графике малый участок ( ab ) и опустим перпендикуляры из точек ( a ) и ( b ) на ось абсцисс. Если промежуток времени ( Delta{t} ), соответствующий участку ( cd ) на оси абсцисс мал, то можно считать, что скорость в течение этого промежутка времени не изменяется и тело движется равномерно. В этом случае фигура ( cabd ) мало отличается от прямоугольника и её площадь численно равна проекции перемещения тела за время, соответствующее отрезку ( cd ).
На такие полоски можно разбить всю фигуру ОАВС, и её площадь равна сумме площадей всех полосок. Следовательно, проекция перемещения тела за время ( t ) численно равна площади трапеции ОАВС. Площадь трапеции равна произведению полусуммы её оснований на высоту: ( S_x= frac{1}{2}(OA+BC)OC ).
Как видно из рисунка, ( OA=v_{0x},BC=v_x,OC=t ). Отсюда следует, что проекция перемещения выражается формулой ( S_x= frac{1}{2}(v_{0x}+v_x)t ). Так как ( v_x = v_{0x} + a_{xt} ), то ( S_x= frac{1}{2}(2v_{0x} + a_xt)t ), отсюда ( S_x=v_{0x}t+ frac{a_xt^2}{2} ). Если начальная скорость равна нулю, то формула имеет вид ( S_x=frac{at^2}{2} ). Проекция перемещения равна разности координат ( S_x=x-x_0 ), поэтому: ( x-x_0=v_{0x}t+frac{at^2}{2} ), или ( x=x_{0x}+v_{0x}t+frac{at^2}{2} ).
Полученная формула позволяет определить положение (координату) тела в любой момент времени, если известны начальная скорость, начальная координата и ускорение.
11. На практике часто используют формулу или ( v^2_x-v^2_{0x}=2a_xs_x ), или ( v^2-v^2_{0}=2as ).
Если начальная скорость тела равна нулю, то: ( v^2_x=2a_xs_x ).
Полученная формула позволяет рассчитать тормозной путь транспортных средств, т.е. путь, который проезжает, например, автомобиль до полной остановки. При некотором ускорении движения, которое зависит от массы автомобиля и силы тяги двигателя, тормозной путь тем больше, чем больше начальная скорость автомобиля.
Содержание
- ПРИМЕРЫ ЗАДАНИЙ
- Часть 1
- Часть 2
- Ответы
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
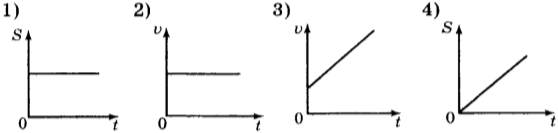
1. Hа рисунке приведены графики зависимости пути и скорости тела от времени. Какой график соответствует равноускоренному движению?
2. Автомобиль, начав двигаться из состояния покоя но прямолинейной дороге, за 10 с приобрел скорость 20 м/с. Чему равно ускорение автомобиля?
1) 200 м/с2
2) 20 м/с2
3) 2 м/с2
4) 0,5 м/с2
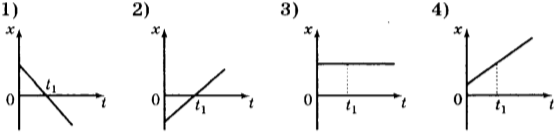
3. На рисунках представлены графики зависимости координаты от времени для четырёх тел, движущихся вдоль оси ( Оx ). У какого из тел в момент времени ( t_1 ) скорость движения равна нулю?
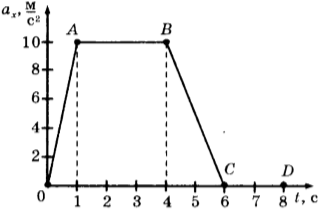
4. На рисунке представлен график зависимости проекции ускорения от времени для тела, движущегося прямолинейно вдоль оси ( Оx ).
Равноускоренному движению соответствует участок
1) только ОА
2) только АВ
3) только ОА и ВС
4) только CD
5. При изучении равноускоренного движения измеряли путь, пройденный телом из состояния покоя за последовательные равные промежутки времени (за первую секунду, за вторую секунду и т.д.). Полученные данные приведены в таблице.
Чему равен путь, пройденный телом за третью секунду?
1) 4 м
2) 4,5 м
3) 5 м
4) 9 м
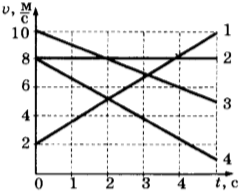
6. На рисунке представлены графики зависимости скорости движения от времени для четырёх тел. Тела движутся по прямой.
Для какого(-их) из тел — 1, 2, 3 или 4 — вектор ускорения направлен противоположно вектору скорости?
1) только 1
2) только 2
3) только 4
4) 3 и 4
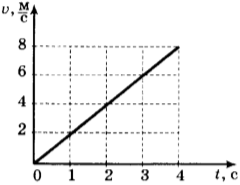
7. Используя график зависимости скорости движения тела от времени, определите его ускорение.
1) 1 м/с2
2) -1 м/с2
3) 2 м/с2
4) -2 м/с2
8. При изучении равноускоренного движения измеряли скорость тела в определённые моменты времени. Полученные данные, приведены в таблице. Чему равна скорость тела в момент времени 3 с?
1) 0 м/с
2) 2 м/с
3) 4 м/с
4) 14 м/с
9. На рисунке приведены графики зависимости скорости движения четырёх тел от времени. Ускорение какого из тел равно -1,5 м/с?
1) 1
2) 2
3) 3
4) 4
10. Используя график зависимости скорости движения тела от времени, определите скорость тела в конце 30-й секунды. Считать, что характер движения тела не изменился.
1) 14 м/с
2) 20 м/с
3) 62 м/с
4) 69,5 м/с
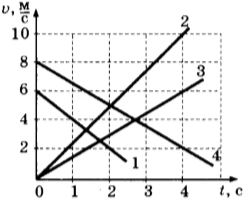
11. Два тела движутся по оси ( Оx ). На рисунке представлены графики зависимости проекции скорости движения тел 1 и 2 от времени.
Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера.
1) В промежутке времени ( t_3-t_5 ) тело 2 движется равноускоренно.
2) К моменту времени ( t_2 ) от начала движения тела прошли одинаковые пути.
3) В промежутке времени ( 0-t_3 ) тело 2 находится в покое.
4) В момент времени ( t_5 ) тело 1 останавливается.
5) В промежутке времени ( t_3-t_4 ) ускорение ( a_x ) тела 1 отрицательно.
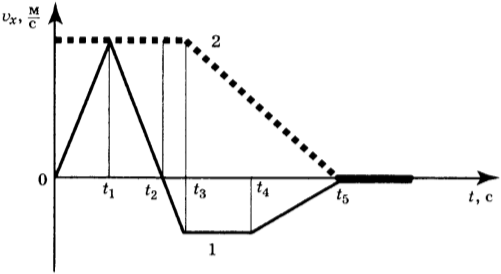
12. На рисунке представлен график зависимости проекции скорости от времени для тела, движущегося вдоль оси Ох.
Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера.
1) Участок ОА соответствует ускоренному движению тела.
2) Участок АВ соответствует состоянию покоя тела.
3) В момент времени ( t_1 ) тело имело максимальное по модулю ускорение.
4) Момент времени ( t_3 ) соответствует остановке тела.
5) В момент времени ( t_2 ) тело имело максимальное по модулю ускорение.
Часть 2
13. Зависимость координаты от времени для некоторого тела описывается уравнением ( x=12t-t^2 ). В какой момент времени скорость движения равна нулю?
Ответы
Скорость. Ускорение. Равноускоренное прямолинейное движение
3.3 (66.32%) 152 votes