Груз,
подвешенный на пружине, растягивает ее на 25 мм. Какова будет максимальная
скорость, если он будет совершать колебания вдоль вертикально направленной оси
с амплитудой, равной также 25 мм?
Решение.
Предположим,
что масса груза и жесткость пружины равны соответственно m и
k. Тогда для покоящегося груза, подвешенного на пружине, в состоянии равновесия выполняется равенство mg = kx0 , откуда k/m = g/x0 .
Если теперь этот
груз отклонить вверх или вниз от его положения равновесия, он начнет совершать
вдоль вертикальной оси OX гармонические
колебания. Действительно, если за x = 0 принять координату
точки, находясь в которой груз не деформирует пружину, то проекция на ось OX результирующей силы, действующей на груз, находящихся в точке x, будет равна mg – kx = kx0 – kx = —k(x – x0) = —kx’ , где x’ – x – x0 . Поскольку координаты
x’ и x отличаются
друг от друга только на постоянную величину x0 , проекции ускорения груза на оси OX и OX’ будут равны: ax = a’x
. Поэтому уравнение второго закона Ньютона, записанное в проекциях на ось OX’, принимает вид: ma’x = —kx, совпадающий с уравнением гармонических колебаний. Отсюда
следует, что груз будет совершать гармонические колебания.
Согласно
закону сохранения энергии максимальная кинетическая энергия тела, совершающего гармонические
колебания, равна его максимальной потенциальной энергии.
A – амплитуда колебаний.
Отсюда находим vmax .
Подставляем
сюда найденное выше выражение для k/m учитывая, что по условию задачи A
= x0 .
Ответ:
umax = 0,5 м/с.
Источник: Подготовка к тестированию по физике. Шепелевич. В. Г.
Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.
Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению (см. §2.1):
В этом соотношении – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука:
Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими .
Таким образом, груз некоторой массы , прикрепленный к пружине жесткости , второй конец которой закреплен неподвижно (рис. 2.2.1), составляют систему, способную в отсутствие трения совершать свободные гармонические колебания. Груз на пружине называют линейным гармоническим осциллятором .
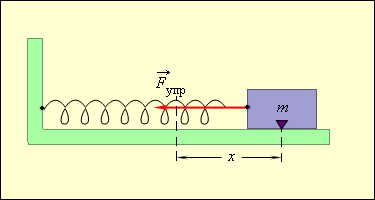 |
| Рисунок 2.2.1. |
Круговая частота свободных колебаний груза на пружине находится из второго закона Ньютона:
откуда
Частота называется собственной частотой колебательной системы.
Период гармонических колебаний груза на пружине равен
При горизонтальном расположении системы пружина–груз сила тяжести, приложенная к грузу, компенсируется силой реакции опоры. Если же груз подвешен на пружине, то сила тяжести направлена по линии движения груза. В положении равновесия пружина растянута на величину , равную
и колебания совершаются около этого нового положения равновесия. Приведенные выше выражения для собственной частоты и периода колебаний справедливы и в этом случае.
Строгое описание поведения колебательной системы может быть дано, если принять во внимание математическую связь между ускорением тела и координатой : ускорение является второй производной координаты тела по времени :
Поэтому второй закон Ньютона для груза на пружине может быть записан в виде
или
(*)
где
Все физические системы (не только механические), описываемые уравнением (*), способны совершать свободные гармонические колебания, так как решением этого уравнения являются гармонические функции вида
Уравнение (*) называется уравнением свободных колебаний . Следует обратить внимание на то, что физические свойства колебательной системы определяют только собственную частоту колебаний или период . Такие параметры колебательного процесса, как амплитуда m и начальная фаза , определяются способом, с помощью которого система была выведена из состояния равновесия в начальный момент времени.
Если, например, груз был смещен из положения равновесия на расстояние и затем в момент времени отпущен без начальной скорости, то m = , .
Если же грузу, находившемуся в положении равновесия, с помощью резкого толчка была сообщена начальная скорость 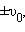
Таким образом, амплитуда m свободных колебаний и его начальная фаза определяются начальными условиями .
Существует много разновидностей механических колебательных систем, в которых используются силы упругих деформаций. На рис. 2.2.2 показан угловой аналог линейного гармонического осциллятора, совершающий крутильные колебания. Горизонтально расположенный диск висит на упругой нити, закрепленной в его центре масс. При повороте диска на угол возникает момент сил упругой деформации кручения:
Это соотношение выражает закон Гука для деформации кручения. Величина аналогична жесткости пружины . Второй закон Ньютона для вращательного движения диска записывается в виде (см. §1.23)
где – момент инерции диска относительно оси, проходящий через центр масс, – угловое ускорение.
По аналогии с грузом на пружине можно получить:
Крутильный маятник широко используется в механических часах. Его называют балансиром. В балансире момент упругих сил создается с помощью спиралевидной пружинки.
Пружинный маятник представляет собой материальную точку массой 
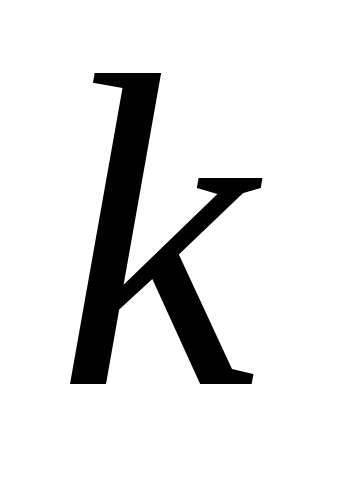
а) Горизонтальный маятник (рис. 15,а). При смещении груза 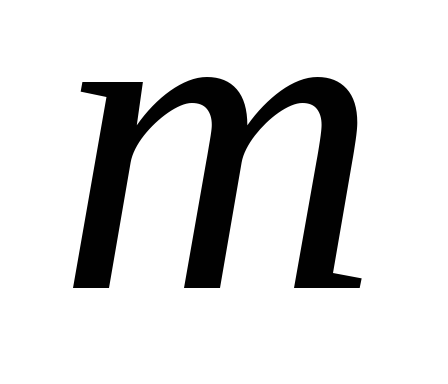
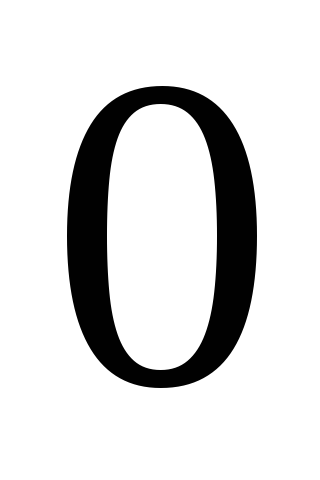
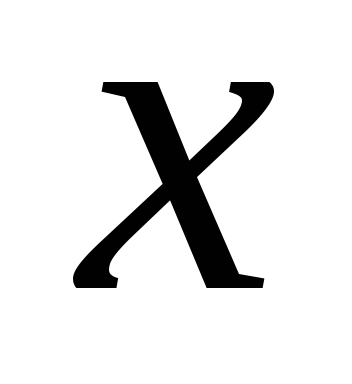
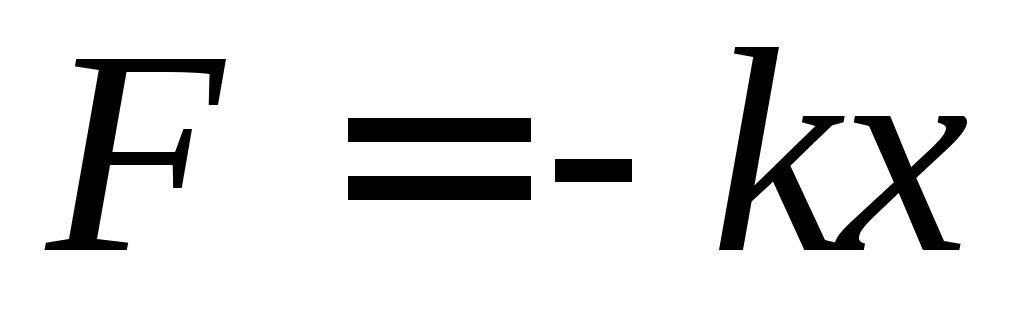
Предполагается, что горизонтальная опора, по которой скользит груз 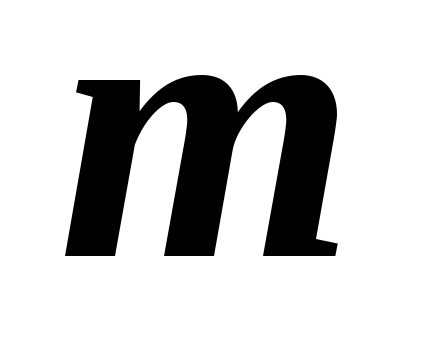
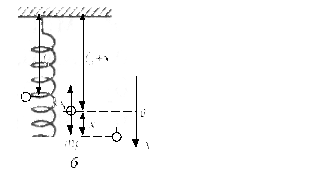
б) Вертикальный маятник (рис.15, б). Положение равновесия в этом случае характеризуется условием:
где 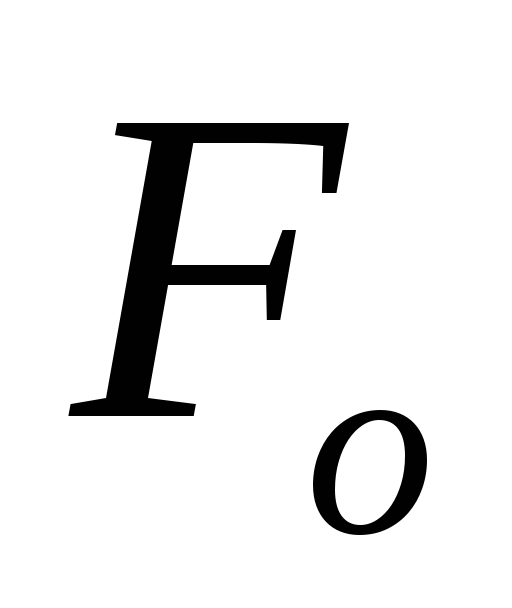
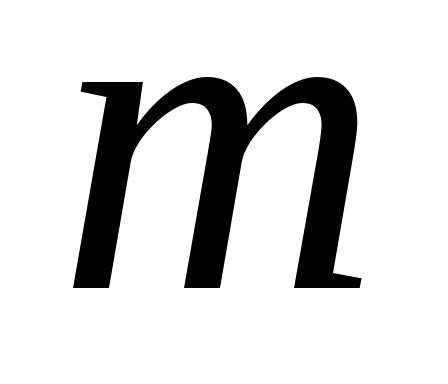
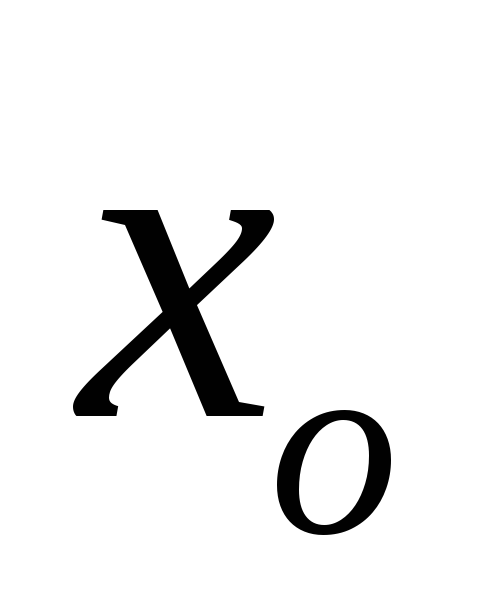
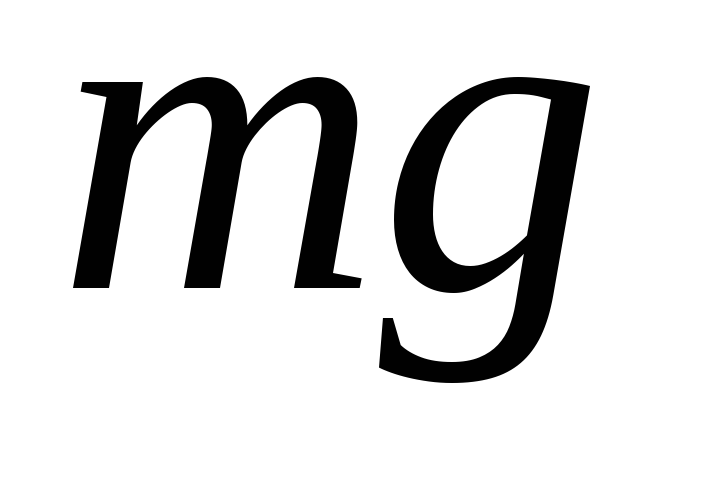
Рис.15. Пружинный маятник: а – горизонтальный и б – вертикальный
Если растянуть пружину и отпустить груз, то он начнет совершать вертикальные колебания. Если смещение в какой-то момент времени будет 
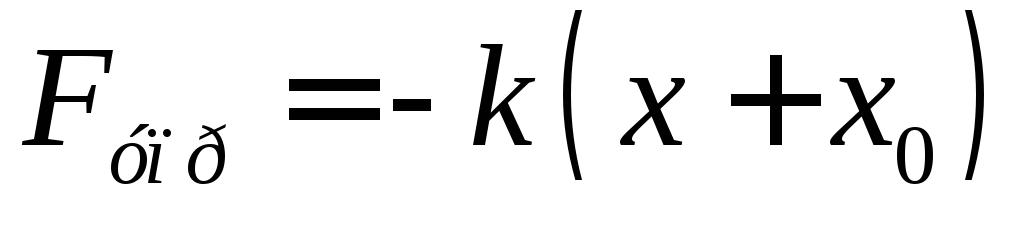
В обоих рассмотренных случаях пружинный маятник совершает гармонические колебания с периодом
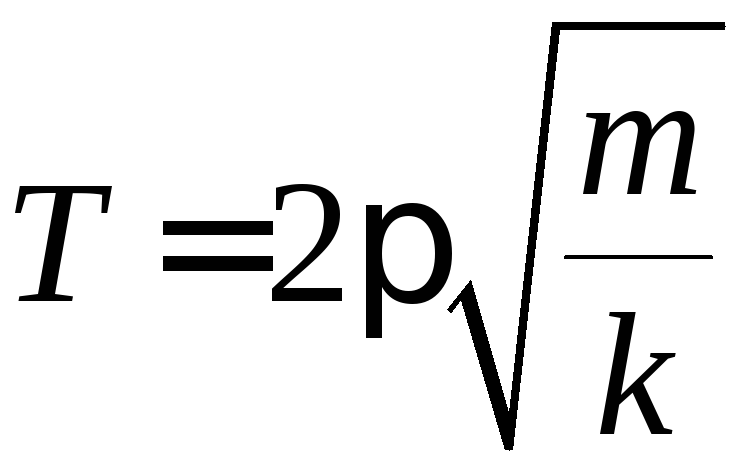
и циклической частотой
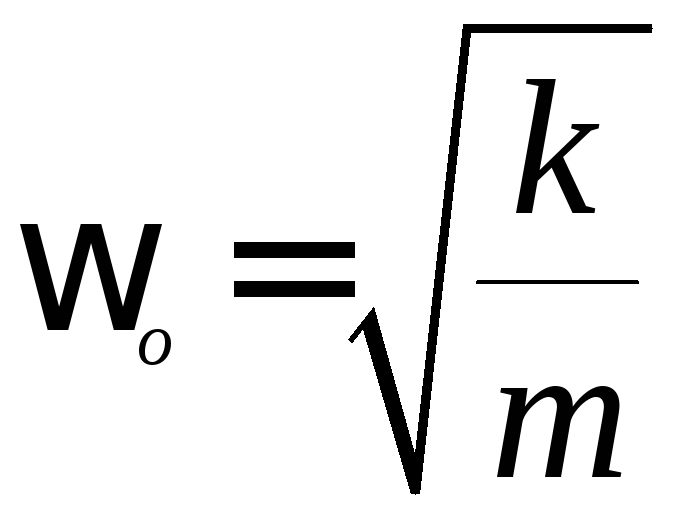
На примере рассмотрения пружинного маятника можно сделать вывод о том, что гармонические колебания – это движение, вызванное силой, возрастающей пропорционально смещению 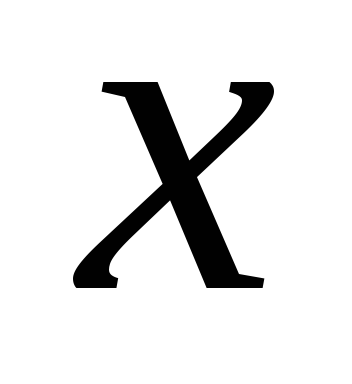
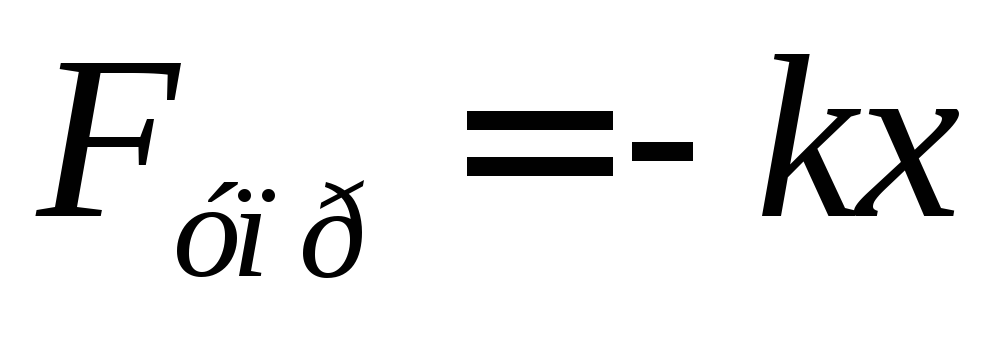
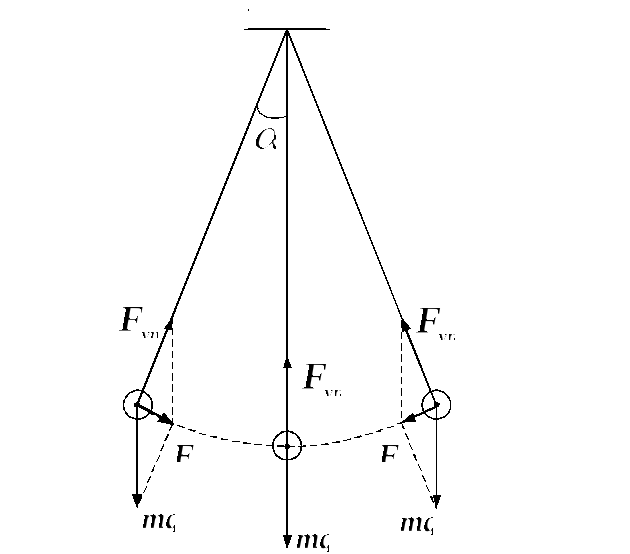
Математический маятник
Рис.16. Математический маятник
Математический маятник представляет собой идеализированную систему в виде материальной точки, подвешенной на невесомой нерастяжимой нити длиной 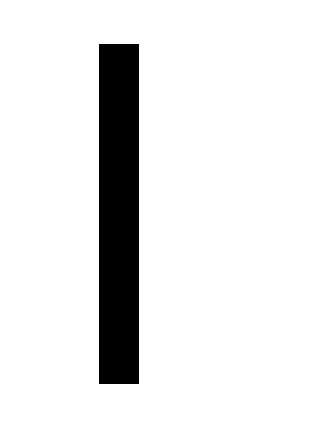
Колебания такого маятника при малых углах отклонения 
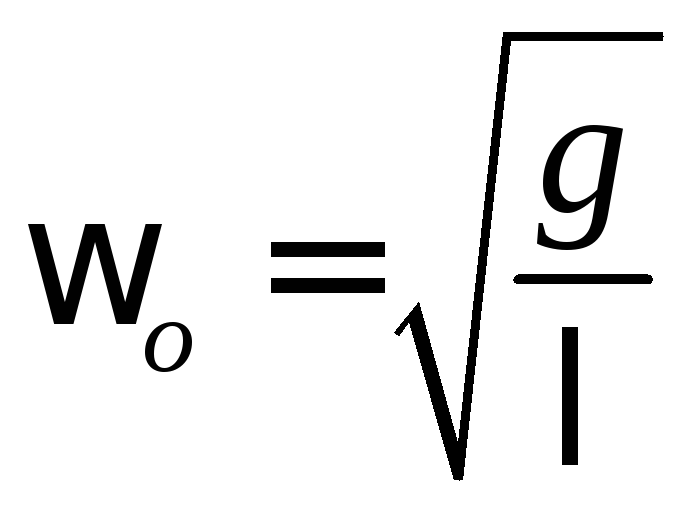

2.3. Энергия тела при гармонических колебаниях
Энергия, сообщенная колебательной системе при начальном толчке, будет периодически преобразовываться: потенциальная энергия деформированной пружины будет переходить в кинетическую энергию движущегося груза и обратно.
Пусть пружинный маятник совершает гармонические колебания с начальной фазой 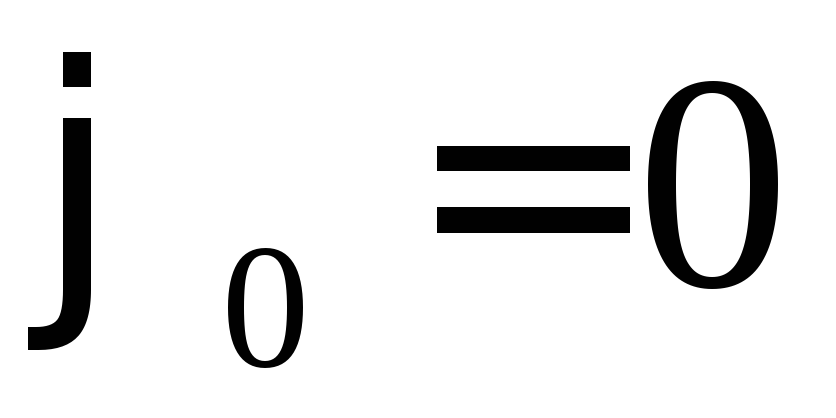

Рис.17. Закон сохранения механической энергии
при колебаниях пружинного маятника
При максимальном отклонении груза от положения равновесия полная механическая энергия маятника (энергия деформированной пружины с жесткостью 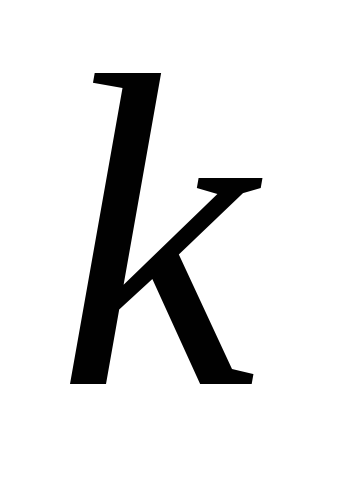
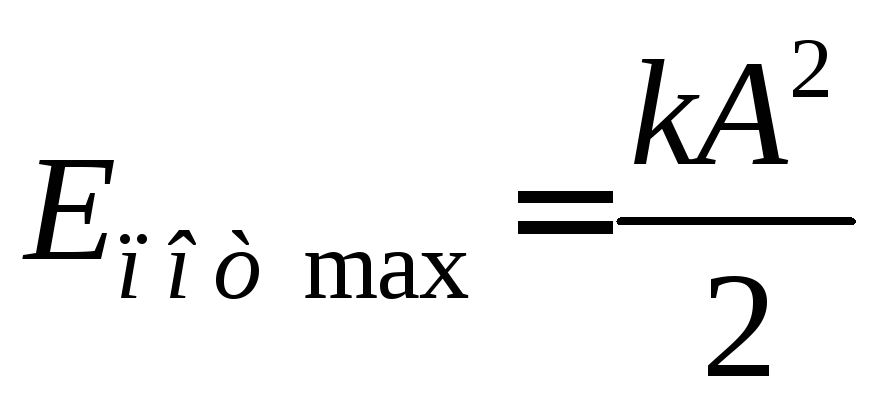
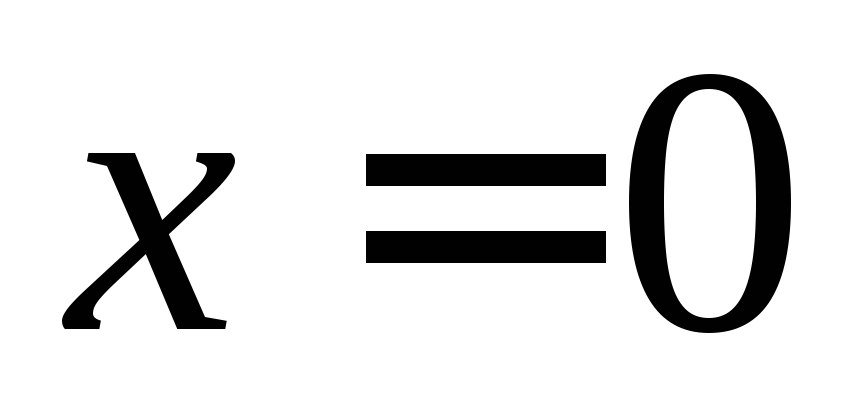
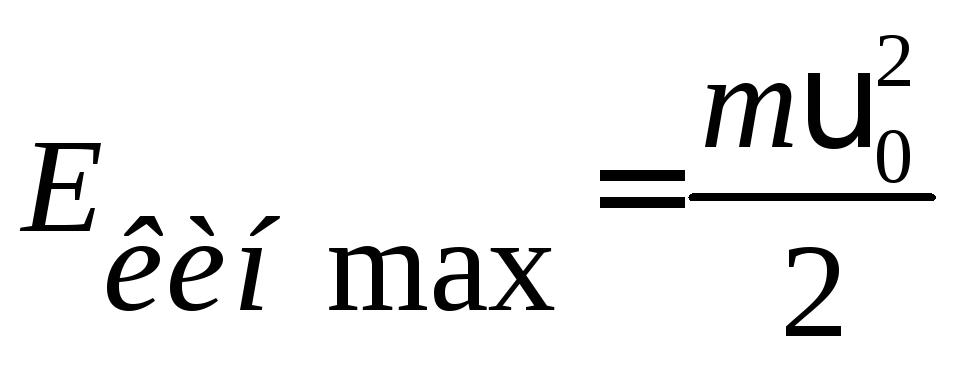
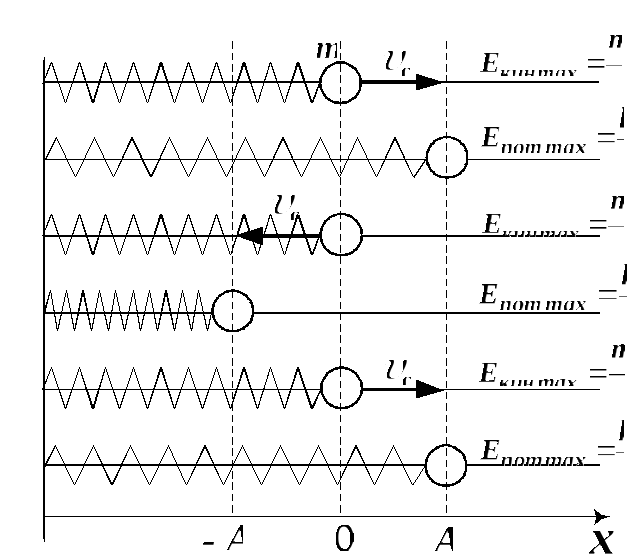
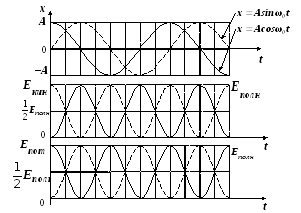
На рис.18 представлены графики зависимостей кинетической, потенциальной и полной энергии в случаях, когда гармонические колебания описываются тригонометрическими функциями синуса (пунктирная линия) или косинуса (сплошная линия).
Рис.18. Графики временной зависимости кинетической
и потенциальной энергии при гармонических колебаниях
Из графиков (рис.18) следует, что частота изменения кинетической и потенциальной энергии в два раза выше собственной частоты гармонических колебаний.
Маятник на пружине — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m.
Период колебаний пружинного маятника может быть вычислен по следующей формуле:
T = 2 π m k <displaystyle T=2pi <sqrt <frac >>> 
Когда на массивное тело действует упругая сила, возвращающая его в положение равновесия, оно совершает колебания около этого положения. Такое тело называют пружинным маятником. Колебания возникают под действием внешней силы. Колебания, которые продолжаются после того, как внешняя сила перестала действовать, называют свободными. Колебания, обусловленные действием внешней силы, называют вынужденными. При этом сама сила называется вынуждающей.
В простейшем случае пружинный маятник представляет собой движущееся по горизонтальной плоскости твердое тело, прикрепленное пружиной к стене.
Второй закон Ньютона для такой системы при условии отсутствия внешних сил и сил трения имеет вид:
m a = − k x ⟺ x ¨ + k m x = 0 <displaystyle ma=-kxiff <ddot >+<frac >x=0>
Если на систему оказывают влияние внешние силы, то уравнение колебаний перепишется так:
x ¨ + k m x = f ( x ) <displaystyle <ddot >+<frac >x=f(x)> 
В случае наличия затухания, пропорционального скорости колебаний с коэффициентом c:
x ¨ + c m x ˙ + k m x = f ( x ) <displaystyle <ddot >+<frac ><dot >+<frac >x=f(x)>
2020-11-28
Тело массой $m$ подвешен к потолку с помощью пружины. Жесткость пружины $k$. Какой максимальной скорости достигает тело во время движения, если его отпустить из положения, когда пружина не растянута?
Решение:
На тело действует сила тяжести $mg$ и сила натяжения пружины $F = kx$, тогда второй закон механики для движения этого тела можно записать так: $mg — kx = ma$.
Из этого уравнения следует, что ускорение тела $a$ сначала направлено вниз и уменьшается при опускании тела, достигая значение 0 при $x = frac{mg}{k}$; затем снова растет по величине, но направлено уже вверх.
Скорость тела растет, пока его ускорение направлено вниз, и уменьшается, когда ускорение направлено вверх. Поэтому скорость тела максимальна при $x = frac{mg}{k}$. Для поиска этой максимальную скорость, запишем закон сохранения энергии:
$mgx = frac{kx^{2} }{2} + frac{mv_{м}^{2} }{2}$,
отсюда, подставим $x = frac{mg}{k}$, получим: $v_{м} = g sqrt{ frac{m}{k} }$.
Найти частоту и максимальную скорость, которую имеет груз, совершающий колебания на пружине жѐсткостью 20 Н/м, если его масса 5 кг.
Амплитуду колебаний можем найти из выражения закона Гука. Поскольку сила, которая действует на пружину равна силе тяжести, то можем записать уравнение:
$mg=kA$ где m, g, k , A — масса, ускорение земного притяжения, эжесткость пружины, амплитуда колебаний. Откуда амплитуда:
Период гармонических колебаний пружинного маятника: $T=2pisqrt{frac{m}{k}}$
Частота $f=frac{1}{T}=frac{1}{2pisqrt{frac{m}{k}}}$
$f=frac{1}{2*3,14*sqrt{frac{5}{20}}}approx 0,31$ Гц
Круговая частота колебаний:
$w=frac{2pi}{T}=frac{2pi}{2pisqrt{frac{m}{k}}}=sqrt{frac{k}{m}}$
$w=sqrt{frac{29}{5}}=2$ рад/с
Уравнение гармонических колебаний: $x(t)=Asin(wt+phi_0)$
В нашем случае это уравнение приобретает вид:
$x(t0=frac{mg}{k}sin(t*sqrt{frac{k}{m}})$
Максимальная скорость груза в процессе колебаний равна произведению амплитуды на круговую частоту:
$v_{max}=frac{mg}{k}*sqrt{frac{k}{m}}$
$v_{max}=frac{5*10}{20}*sqrt{frac{20}{5}}=5$ м/с
Сообщения без ответов | Активные темы | Избранное
|
|
Колебания двух тел на пружине
|
|
10/12/15 |
|
|
|
|
|
Mihr |
Re: Колебания двух тел на пружине
|
||
18/09/14 |
mindroz , недостаточно заявить: я нашёл то-то и то-то. Продемонстрируйте, что у Вас получилось, тогда можно будет продолжить.
|
||
|
|
|||
|
Munin |
Re: Колебания двух тел на пружине
|
||
30/01/06 |
Вы можете найти максимальную скорость в системе отсчёта центра масс?
|
||
|
|
|||
|
Pphantom |
Posted automatically
|
||
09/05/12 |
|||
|
|
|||
|
Pphantom |
Posted automatically
|
||||
09/05/12 |
|
||||
|
|
|||||
|
Mihr |
Re: Колебания двух тел на пружине
|
||
18/09/14 |
mindroz , подумайте: в момент отрыва второго груза от своего упора пружина деформирована или нет?
|
||
|
|
|||
|
mindroz |
Re: Колебания двух тел на пружине
|
|
10/12/15 |
В момент отрыва второго груза пружина не деформирована. А его скорость относительно центра масс равна
|
|
|
|
|
Munin |
Re: Колебания двух тел на пружине
|
||
30/01/06 |
Меня сильно тормозит то, что два груза колеблются и я путаюсь. Я вам предложил простой способ рассуждения. Повторяю: Вы можете найти максимальную скорость в системе отсчёта центра масс? Путь рассуждений Mihr тоже ведёт к ответу, но именно на нём вы путаетесь.
|
||
|
|
|||
|
Mihr |
Re: Колебания двух тел на пружине
|
||
18/09/14 |
mindroz ,
|
||
|
|
|||
|
Skeptic |
Re: Колебания двух тел на пружине
|
||
|
01/12/11 |
(колеблются вокруг общего центра масс с одинаковой частотой) Период колебаний груза на пружине
|
||
|
|
|||
|
Cos(x-pi/2) |
Re: Колебания двух тел на пружине
|
||
29/09/14 |
Mihr выше дал правильный ответ и хорошее объяснение. При этом формула, указанная Skeptic -ом, не нужна для ответа на вопрос о максимальной скорости в задаче ТС; а чтобы по ней найти (если захочется) период колебаний двух грузов в данной задаче, надо подставить в роли Ещё замечание для ТС о небольшой путанице в обозначениях; если в условии задачи сказано про пружину, что сначала она сжата на то в формуле для скорости
|
||
|
|
|||
|
mindroz |
Re: Колебания двух тел на пружине
|
|
10/12/15 |
mindroz , Большое спасибо за подробное объяснение! Теперь я разобрался:).
|
|
|
|
Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |

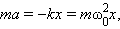
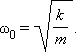
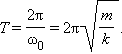
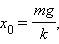
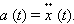
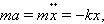
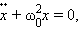
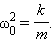
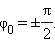
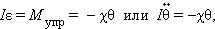
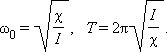
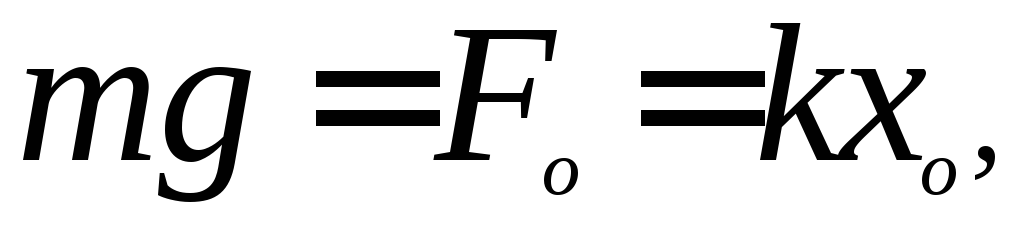
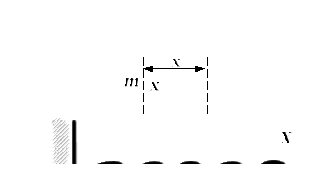

 . Затем, при растягивании пружины, скорость второго груза будет увеличиваться. После того, как пружина растянется максимально и начнет сжиматься и до момента её не растянутого состояния скорость второго груза тоже будет увеличиваться, т.к. сила упругости пружинки, действующая на второй груз будет направлена в направлении движения центра масс.
. Затем, при растягивании пружины, скорость второго груза будет увеличиваться. После того, как пружина растянется максимально и начнет сжиматься и до момента её не растянутого состояния скорость второго груза тоже будет увеличиваться, т.к. сила упругости пружинки, действующая на второй груз будет направлена в направлении движения центра масс.  .
. . Верно говорите, что в этот момент пружина не деформирована. Но ведь в тот момент, когда потенциальная энергия осциллятора равна нулю, его кинетическая энергия максимальна. А так как оба груза движутся согласованно (колеблются вокруг общего центра масс с одинаковой частотой), то скорость каждого из них в этой системе отсчёта в момент отрыва 2-го груза по модулю максимальна. Через полпериода она вновь будет максимальна, но теперь уже второй груз будет двигаться обратно, и его скорость в системе отсчёта, связанной со столом будет не вычитаться из скорости центра масс, а прибавляться к ней. Таким образом, максимальная скорость 2-го груза равна
. Верно говорите, что в этот момент пружина не деформирована. Но ведь в тот момент, когда потенциальная энергия осциллятора равна нулю, его кинетическая энергия максимальна. А так как оба груза движутся согласованно (колеблются вокруг общего центра масс с одинаковой частотой), то скорость каждого из них в этой системе отсчёта в момент отрыва 2-го груза по модулю максимальна. Через полпериода она вновь будет максимальна, но теперь уже второй груз будет двигаться обратно, и его скорость в системе отсчёта, связанной со столом будет не вычитаться из скорости центра масс, а прибавляться к ней. Таким образом, максимальная скорость 2-го груза равна  (в Ваших обозначениях).
(в Ваших обозначениях). .
. «приведённую массу» системы:
«приведённую массу» системы:

 входящей в
входящей в  должно быть написано
должно быть написано  а не
а не 