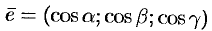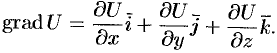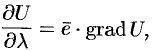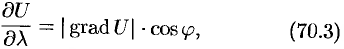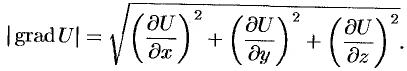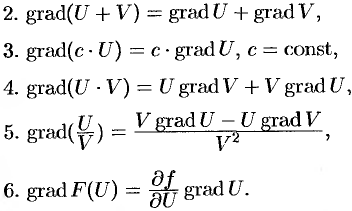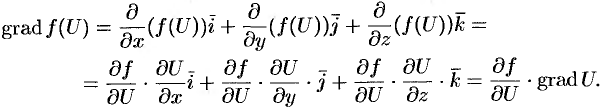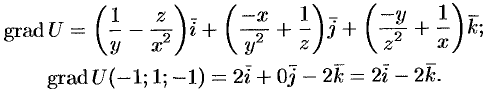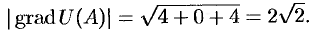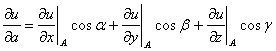При изучении скалярных полей наряду с функций 
рассматривается некоторый вектор, тесно связанный с этой функцией, — градиент скалярного поля.
Градиентом в точке 
скалярного поля, заданного дифференцируемой функцией , называется вектор, равный
.
Таким образом, каждой точке скалярного поля, заданного дифференцируемой функцией , соответствует не только значение этой функции, но и вполне определенный вектор 
.
Между градиентом функции в данной точке и производной по направлению в той же точке имеется связь, которая устанавливается следующей теоремой.
Теорема. Проекция вектора 
На единичный вектор 
равна производной функции 
по направлению 
:
.
Доказательство. Пусть . Из векторной алгебры известно, что проекция какого-либо вектора на другой вектор равна скалярному произведению этих векторов.
Так как 
, , то
.
Учитывая, что производная по направлению 
выражает скорость изменения скалярного поля в этом направлении, можно сказать, что проекция на вектор равна скорости изменения поля в направлении вектора .
Обозначим через 
угол между единичным вектором и . Тогда 
.
Поэтому 
.
Если направления векторов и совпадают (
), то производная по направлению имеет, очевидно, наибольшее значение, равное 
.
Таким образом, есть вектор, указывающий Направление наибольшего возрастания поля в данной точке и имеющий Модуль равный скорости этого возрастания.
Рассмотрим кривую 
, лежащую на поверхности уровня 
и проходящую через точку 
. Градиент функции в точке обладает следующими свойствами: 
перпендикулярен к вектору 
, направленному по касательной к кривой в точке .
В случае плоского скалярного поля, заданного дифференцируемой функцией двух переменных 
, градиент определяется формулой
.
Его связь с производной по направлению 
выражается равенством
,
Где — угол между единичным вектором и 
. Вектор 
перпендикулярен к касательной, проведенной к линии уровня в точке .
Пример 16. Найти наибольшую скорость возрастания функции
в точке 
.
Решение. Наибольшая скорость возрастания функции равна модулю градиента этой функции. Найдем градиент функции 
:
, 
.
В точке имеем 
.
Тогда наибольшая скорость возрастания функции равна
.
Пример 17. Найти скорость изменения скалярного поля, определяемого функцией 
в точке 
в направлении касательной, проведенной к параболе 
в этой точке в сторону возрастания координаты 
, и наибольшую скорость изменения поля в этой точке.
Решение. Скорость изменения скалярного поля в заданном направлении есть производная скалярного поля по направлению вектора , задающего направление.
,
Где 
; 
— направляющие косинусы вектора , 
. Вектор 
возьмем на касательной к параболе в , для чего составим уравнение касательной
,
, 
— уравнение касательной.
На найденной касательной возьмем точку 
с любой координатой 
(
), например 
. Тогда
.
Найдем значения производной по направлению в точке :
,
.
Тогда 
.
Наибольшая скорость изменения поля в точке 
есть 
.
Так как 
, то
.
Величина наибольшей скорости
.
| < Предыдущая | Следующая > |
|---|
Градиент скалярного поля и его свойства
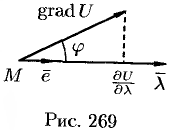
В каком направлении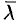 
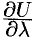
производная 
имеет наибольшее значение? Это направление указывает вектор, называемый градиентом скалярного ноля.
Можно заметить, что правая часть равенства (70.2) представляет собой скалярное произведение единичного вектора
и некоторого вектора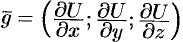 
.
Вектор, координатами которого являются значения частных производных функции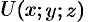 
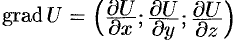
в точке 
, называют градиентом функции и обозначают 
, т. е. 
или
Отметим, что 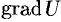есть векторная величина. Говорят: скалярное поле 
порождает векторное поле градиента . Теперь равенство (70.2) можно записать в виде
или
где 
— угол между вектором и направлением (см. рис. 269).
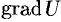
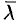
Из формулы (70.3) сразу следует, что производная но направлению достигает наибольшего значения, когда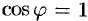 
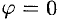
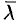
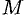
, т. е. при 
. Таким образом, направление градиента совпадает с направлением , вдоль которого функция (поле) меняется быстрее всего, т. е. градиент функции указывает направление наибыстрейшего возрастания функции. Наибольшая скорость изменения функции в точке 
равна
В этом состоит физический смысл градиента. На указанном свойстве градиента основано его широкое применение в математике и других дисциплинах.
Приведем важные свойства градиента функции.
Градиент направлен по нормали к поверхности уровня, проходящей через данную точку.
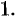
Действительно, по любому направлению вдоль поверхности уровня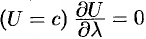 
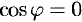
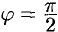
. Но тогда из (70.3) следует, что 
, т. е. 
.
Доказываются эти свойства на основании определения градиента. Докажем, например, последнее свойство. Имеем:
Замечание. Приведенные свойства градиента функции остаются справедливыми и для плоского поля.
Пример №70.2.
Найти наибольшую скорость возрастания функции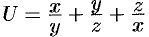 
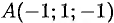
в точке 
.
Решение:
Имеем:
Наибольшая скорость возрастания функции равна
Отметим, что функция будет убывать с наибольшей скоростью 
, если точка 
движется в направлении — 
(антиградиентное направление).
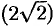
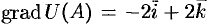
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
- Решение задач по высшей математике
Другие темы по высшей математике возможно вам они будут полезны:
Градиент функции
Градиент — вектор, своим направлением указывающий направление наискорейшего возрастания некоторой величины u. Другими словами, направление градиента есть направление наибыстрейшего возрастания функции.
Назначение сервиса. Онлайн калькулятор используется для нахождения градиента функции нескольких переменных. (см. пример) При этом решаются следующие задачи:
- нахождение частных производных функции, запись формулы градиента, вычисление наибольшой скорости возрастания функции в указанной точке;
- вычисление градиента в точке A, нахождение производной в точке A по направлению вектора a;
- нахождение полного дифференциала функции.
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
Решение со всеми исходными формулами сохраняется в формате Word.
Полный дифференциал для функции двух переменных: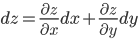 
Полный дифференциал для функции трех переменных равен сумме частных дифференциалов: d f(x,y,z)=dxf(x,y,z)dx+dyf(x,y,z)dy+dzf(x,y,z)dz
Алгоритм нахождения градиента
- Вычисление частных производных по формуле:
- Вычисление частных производных в точке A.
- Нахождение направляющих углов вектора a.
- Вычисление производной в точке A по направлению вектора a по формуле;
- Наибольшая скорость возрастания функции в указанной точке равна модулю градиента функции в этой точке.
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).