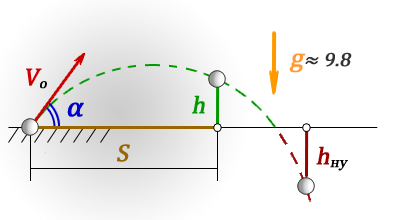
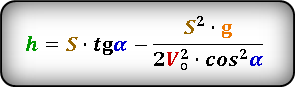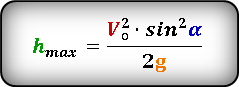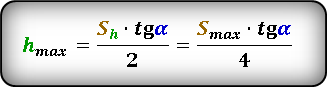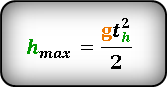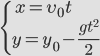Как найти максимальную точку полета - Исправление недочетов и поиск решений вместе с Examum.ru

1. Определить, на какой высоте находится тело, в любой точке траектории движения

h — высота тела в момент времени t

h_ну — высота ниже уровня броска (принимает отрицательное значение)

S — дальность полета по горизонтали

t — время полета

V_o — начальная скорость тела

α — угол под которым брошено тело

g ≈ 9,8 м/с² — ускорение свободного падения

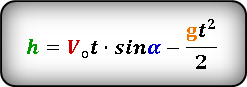
Формула для определения значения высоты тела в момент времени t

Формула для определения значения высоты тела через расстояние S по горизонтали

h_ну — высота ниже уровня броска, принимает отрицательное значение

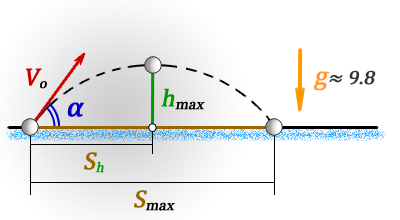
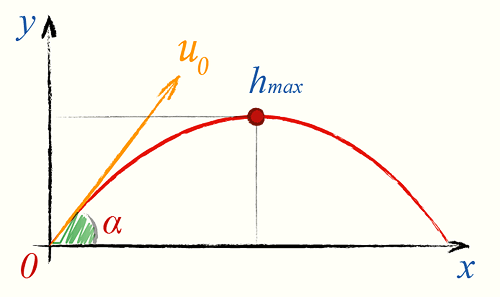
2. Найти максимальную высоту, на которую поднялось тело

h_max — максимальная высота

S_max — максимальная дальность полета, если бросок и падение на одном уровне

S_h — расстояние пройденное по горизонтали до момента максимального подъема

t_max — время всего полета

t_h — время за которое тело поднялось на максимальную высоту

V_o — начальная скорость тела

α — угол под которым брошено тело

g ≈ 9,8 м/с² — ускорение свободного падения

Формула для расчета максимальной высоты достигнутое телом, если даны, начальная скорость V_oи угол α под которым брошено тело. :

Формула для вычисления максимальной высоты, если известны, максимальное расстояние S _maxили расстояние по горизонтали при максимальной высоте S_hи угол α под которым брошено тело. :

По этой формуле, можно определить максимальную высоту, если известно время t_h за которое тело поднялось на эту высоту. :

Подробности

Опубликовано: 11 августа 2015

Обновлено: 13 августа 2021

Источник

Движение тела, брошенного горизонтально или под углом к горизонту.

Это движение в плоскости, поэтому для описания движения необходимо 2 координаты.
Считаем, что движение происходит вблизи поверхности Земли, поэтому ускорение тела – ускорение свободного падения (a = g).

Так как мы пренебрегаем сопротивлением воздуха, то ускорение направлено только к поверхности Земли (g) – вдоль вертикальной оси (y), вдоль оси х движение равномерное и прямолинейное.

Движение тела, брошенного горизонтально.

Выразим проекции скорости и координаты через модули векторов.

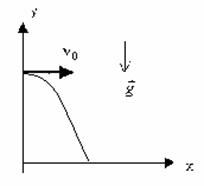
Для того чтобы получить уравнение траектории, выразим время tиз уравнения координаты x и подставим в уравнение для y:

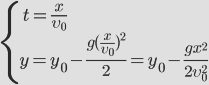
— между координатами квадратичная зависимость, траектория – парабола!

Движение тела, брошенного под углом к горизонту.

Порядок решения задачи аналогичен предыдущей.

Решим задачу для случая х₀=0 и y₀=0.

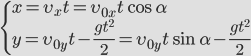
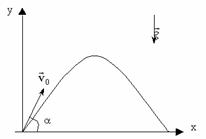
Движение тела, брошенного под углом к горизонту.

Докажем, что траекторией движения и в этом случае будет парабола. Для этого выразим координату Y через X (получим уравнение траектории):

Мы получили квадратичную зависимость между координатами. Значит траектория — парабола.

Найдем время полета тела от начальной точки до точки падения. В точке падения координата по вертикальной оси у=0.

Время полета:

Следовательно, для решения этой задачи необходимо решить уравнение

Оно будет иметь решение при t=0 (начало движения) и

Зная время полета, найдем максимальное расстояние, которое пролетит тело:

Дальность полета:

Из этой формулы следует, что:

— максимальная дальность полета будет наблюдаться при бросании тела (при стрельбе, например) под углом 45⁰;

— на одно и то же расстояние можно бросить тело (с одинаковой начальной скоростью) двумя способами – т.н. навесная и настильная баллистические траектории.

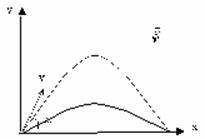
Используя то, что парабола – это симметричная кривая, найдем максимальную высоту, которой может достичь тело.
Время, за которое тело долетит до середины, равно: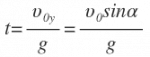

Время подъема:

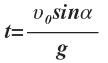
Тогда:

Максимальная высота:

Скорость тела в любой момент времени направлена по касательной к траектории движения (параболе) и равна

Угол, под которым направлен вектор скорости в любой момент времени:

Источник

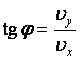
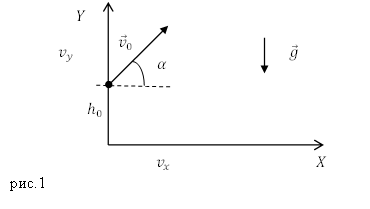
Движение тела, брошенного под углом к горизонту, — движение тела в двумерной системе координат (по двум осям) при изначальном направлении начальной скорости под углом к горизонту. Данное движение является сложным видом механического движения с криволинейной траекторией. Такие типы движений принято рассматривать в проекции на оси выбранной системы координат. В нашем конкретном случае возьмём декартову систему координат и запустим тело под углом displaystyle alpha к оси ОХ (рис. 1).

Рис. 1. Тело бросили под углом к горизонту

Классическая постановка задач на подобную тематику: тело бросили под углом $displaystyle {{upsilon }_{0}}$ к горизонту с начальной скоростью $displaystyle {{upsilon }_{0}}$ , найти различные параметры движения.

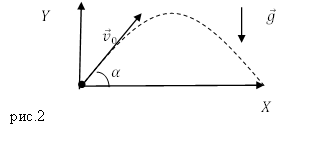
Первое, что мы сделаем, это попробуем данное сложное движение представить как сумму простых (рис. 2).

Рис. 2. Тело бросили под углом к горизонту (максимальная высота подъёма, путь по горизонтали, движение)

Рассмотрим само движение. После броска траектория движущегося тела представляет собой параболу (докажем позже). Выберем произвольную точку на параболе и укажем ускорение, с которым движется тело в данный момент (ускорение свободного падения). Направление данного ускорения — вертикально вниз. Проекции данного ускорения на ось ОХ ( $displaystyle {{c}^{2}}$ (м/ $displaystyle {{g}_{y}}=-10$ ), а на ось OY ( $displaystyle {{c}^{2}}$ (м/ $displaystyle {{c}^{2}}$ ).

Тогда, вдоль оси ОХ, тело движется равномерно (т.к. ускорение вдоль этой оси равно 0). Более сложным является движение тела вдоль оси OY: между точками A и B тело движется замедляясь, при этом движение равнозамедленное. Между точками B и C движение равноускоренное (рис.2, подписи). Исходя из установленного вида движения, можем решать задачу.

Рис. 3. Тело бросили под углом к горизонту (проекции скоростей)

Для рассмотрения движения тела вдоль осей, введём начальные скорости движения тела вдоль выбранных нами осей (рис. 3). На рисунке представлена часть траектории в самом начале движения. Начальные скорости движения вдоль осей обозначим $displaystyle {{upsilon }_{0y}}$ и $displaystyle left| {{{vec{upsilon }}}_{0}} right|$ . Исходя из треугольника, катетами которого являются наши проекции (можно построить параллельным переносом), а гипотенузой — модуль вектора начальной скорости ( $displaystyle left| {{{vec{upsilon }}}_{0}} right|$ ), можем найти значения необходимых нам проекций:

Вернёмся к рисунку 2. Попробуем найти полное время полёта ( $displaystyle {{t}_{max }}$ ). Для этого воспользуемся тем, что вдоль оси OY тело движется равнозамедленно, а в точке B движение вдоль этой оси и вовсе останавливается. Таким образом, конечная скорость в этой точке вдоль оси OY равна 0. Тогда, исходя из движения:

$displaystyle 0={{upsilon }_{0y}}-gfrac{{{t}_{max }}}{2}$ (3)

$displaystyle frac{{{t}_{max }}}{2}$ — т.к. время движения от точки А до B, и от B до C одинаково. Тогда:

$displaystyle {{t}_{max }}=frac{2{{upsilon }_{0y}}}{g}$ (4)

И, учитывая (2):

$displaystyle {{t}_{max }}=frac{2{{upsilon }_{0}}sin alpha }{g}$ (5)

Перейдём к вопросу о максимальной дальности броска в горизонтальном направлении ( $displaystyle {{S}_{max }}$ ).

Вдоль горизонта тело движется равномерно (рис. 2). Тогда путь, проделанный телом за время $displaystyle {{t}_{max }}$ :

$displaystyle {{S}_{max }}={{upsilon }_{0x}}{{t}_{max }}$ (6)

А с учётом (1) и (5):

$displaystyle frac{2upsilon _{0}^{2}sin alpha cos alpha }{g}$ = $displaystyle frac{upsilon _{0}^{2}sin (2alpha )}{g}$ = $displaystyle frac{upsilon _{0}^{2}sin (2alpha )}{g}$ (7)

Перейдём к максимальной высоте полёта ( $displaystyle {{H}_{max }}$ ). Данный параметр связан с движением тела вдоль оси OY, которое, как мы выяснили, является равноускоренным/равнозамедленным. Рассмотрим участок BC: для него вдоль соответствующей оси тело без начальной скорости движется с ускорением ( $displaystyle frac{{{t}_{max }}}{2}$ ) в течение времени $displaystyle frac{{{t}_{max }}}{2}$ , формируем уравнение:

$displaystyle {{H}_{max }}=frac{g{{left( {}^{{{t}_{max }}}!!diagup!!{}_{2}; right)}^{2}}}{2}=frac{g{{left( {{t}_{max }} right)}^{2}}}{8}$ (8)

С учётом (5):

$displaystyle frac{upsilon _{0}^{2}{{sin }^{2}}alpha }{2g}$ = $displaystyle frac{upsilon _{0}^{2}{{sin }^{2}}alpha }{2g}$ (9)

Таким образом, ряд параметров движения при броске под углом к горизонту можно вычислить, зная лишь начальные параметры броска.

Рис. 4. Тело бросили под углом к горизонту (конечная скорость)

Далее попробуем найти конечную скорость движения (при таких движениях, конечная скорость — скорость при подлёте к Земле). Рассмотрим конечную точку движения С (рис. 4). Скорость тела направлена под неким углом displaystyle beta . Построим проекции данного вектора на оси OX и OY. На основании построенного треугольника реализуем теорему Пифагора для поиска модуля полной конечной скорости:

$displaystyle left| {vec{upsilon }} right|=sqrt{upsilon _{x}^{2}+upsilon _{y}^{2}}$ (10)

Найдём компоненты вектора displaystyle left| {vec{upsilon }} right| . Т.к. движение вдоль оси OX равномерное, значит, $displaystyle {{upsilon }_{x}}={{upsilon }_{0x}}$ , используя (1):

$displaystyle {{upsilon }_{x}}={{upsilon }_{0}}cos alpha$ (11)

Движение вдоль оси OY от точки B в точку C равноускоренное, причём, без начальной скорости за время $displaystyle frac{{{t}_{max }}}{2}$ , тогда:

$displaystyle {{upsilon }_{y}}=gfrac{{{t}_{max }}}{2}$ (12)

Используя (5), получим:

$displaystyle {{upsilon }_{y}}=gfrac{2{{upsilon }_{0}}sin alpha }{2g}={{upsilon }_{0}}sin alpha$ (13)

Подставим (12) и (13) в (10):

$displaystyle {{upsilon }_{0}}sqrt{{{(cos alpha )}^{2}}+{{(sin alpha )}^{2}}}$ = $displaystyle {{upsilon }_{0}}$ = $displaystyle {{upsilon }_{0}}$ (14)

Для избавления от тригонометрических функций мы воспользовались основным тригонометрическим тождеством. Таким образом, доказано, что конечная скорость такого движения равна начальной, кроме того, из треугольника видно, что тело подлетело к земле под углом displaystyle beta =alpha .

Вывод:

для движения тела, брошенного под углом к горизонту, выведены добавочные формулы: (5), (7), (9), которые могут существенно упростить решение задачи.
представлен один из общих способов нахождения скорости при криволинейном движении (через теорему Пифагора и поиск компонент вектора).

Источник

Максимальная высота подъема тела, брошенного под углом к горизонту, формула

Максимальная высота подъема тела, брошенного под углом к горизонту определяется из формул времени максимального подъема и формулы координат тела

Максимальная высота подъема тела, брошенного под углом к горизонту

[
h_{max} = y(t_{hmax}) = u_0 t_{hmax} sin(α) — frac{gt_{hmax}^2}{2}
]

и после подстановки t_hmax в выражение (1) и его упрощения получим

[
h_{max} = frac{(u_0 sin(α))^2}{2g}
]

Здесь:
u₀ — начальная скорость тела (м/с),
α — угол, под которым брошено тело к горизонту (°),
g — ускорение свободного падения 9.81 (м/c²),
t_hmax — время подъема на максимальную высоту (c)

Вычислить, найти максимальную высоту подъема тела, брошенного под углом к горизонту по формуле (2).

Максимальная высота подъема тела, брошенного под углом к горизонту	стр. 420

Источник

Движение тела под углом к горизонту, теория и онлайн калькуляторы

Движение тела под углом к горизонту

Начальные условия

Рассмотрим движение тела (материальной точки) брошенного под углом к горизонту с некоторой высоты $h_0$. Начальная
скорость тела равна ${overline{v}}_0$, вектор ${overline{v}}_0$ составляет угол $alpha $ с горизонтом (рис.1). Систему отсчета, в которой движется тело, свяжем с Землей. Ось X направим параллельно земле, ось Y вертикально вверх.

Движение тела под углом к горизонту происходит в поле тяжести Земли под воздействием силы тяжести. Силой сопротивления воздуха пренебрежём. В этом случае ускорение тела ($overline{a}$) совпадает с ускорением свободного падения ($overline{g}$):

[overline{a}=overline{g}left(1right),]

где $g=9,8 frac{м}{с^2}$.

Запишем начальные условия движения тела (рис.1):

[ left{ begin{array}{c}
xleft(t=0 right)=0, \
yleft(t=0 right)=h, \
v_xleft(t=0 right){=v}_{0x}=v_0{cos alpha , } \
v_yleft(t=0 right){=v}_{0y}=v_0{sin alpha . } end{array}
right.left(2right).]

Уравнение для перемещения тела, брошенного под углом к горизонту. Траектория его движения

Перемещение тела, которое бросили под углом к горизонту является равноускоренным, следовательно, для написания уравнения движения воспользуемся векторным уравнением для перемещения ($overline{s}$) при равнопеременном движении в виде, учтем равенство (1):

[overline{s}(t)={overline{s}}_0+{overline{v}}_0t+frac{overline{g}t^2}{2}left(3right).]

Векторное уравнение (3) в проекции на оси координат X и Y даст нам два скалярных уравнения:

[left{ begin{array}{c}
x(t)=v_0{cos alpha }t \
y(t)=h_0+v_0{sin alpha }t-frac{gt^2}{2} end{array}
right.left(4right).]

Из системы уравнений (4) мы видим, что при рассматриваемом нами движении происходит наложение двух прямолинейных движений.
Причем по оси X тело под углом к горизонту движется с постоянной скоростью ${ v}_{0x}=v_0{cos alpha , }$ а по оси Y материальная точка перемещается с постоянным ускорением $overline{g}$. Уравнение траектории движения тела можно получить, если из первого уравнения системы (4) выразить время ($t$) полученный результат подставить во вторую формулу системы:

[t=frac{x}{v_0{cos alpha }};; ]

[y(x)=h_0 tg alpha -frac{g}{2}{left(frac{x}{v_0{cos б }}right)}^2left(5right).]

Уравнение $y(x)$ (функция (5)) показывает, что тело движется по параболе в плоскости, в которой лежат векторы $overline{g}$ и ${overline{v}}_0.$

Уравнение скорости движения тела брошенного под углом к горизонту

В векторном виде уравнение для скорости движения рассматриваемого нами тела в произвольный момент времени запишем:

[overline{v}(t)={overline{v}}_0+overline{g}tleft(6right).]

В скалярном виде уравнение (6) представим в виде системы уравнений:

[left{ begin{array}{c}
v_xleft(tright)=v_0{cos alpha , } \
v_yleft(tright)=v_0{sin alpha }-gt end{array}
right.left(7right).]

В системе уравнений (7) мы еще раз видим, что движение тела под углом к горизонту по оси X равномерное, по оси Y равнопеременное. Причем, двигаясь вверх, тело уменьшает свою скорость от $v_{0y}$ до нуля, затем падая вниз скорость тела увеличивается.

Модуль вектора скорости в производный момент времени для рассматриваемого нами движения найдем как:

[v=sqrt{v^2_x{+v}^2_y left(8right).}]

Время подъема и полета тела

Время, которое тело тратит на полет вверх в рассматриваемом движении можно найти из второго уравнения системы (7). В точке максимального подъема вектор скорости точки параллелен оси X, значит $v_y=0$, тогда время подъема ($t_p$):

[t_p=frac{v_0{sin alpha }}{g}left(9right).]

Время, которое тело находилось в воздухе (время полета($t_{pol}$)) получим из второго уравнения системы (4), приравняв ординату $y$ к нулю:

[t_{pol}=frac{v_0{sin alpha +sqrt{v^2_0{sin}^2alpha +2gh_0} }}{g}left(10right).]

При $h_0=0$ мы видим, что $t_{pol}=2t_p.$

Дальность полета и высота подъема

Для того чтобы найти горизонтальную дальность полета тела ($s$) при заданных нами условиях в уравнение координаты $x$ системы уравнений (4) подставим время полета ($t_{pol}$) (10). При $h_0=0,$ дальность полета равна:

[s=frac{v^2_0{sin left(2alpha right) }}{g}left(11right).]

Максимальную высоту подъема тела под углом к горизонту ($h_{max}$) находят из второго уравнения системы (4), подставляя в него время подъема ($t_p$) (9):

[h_{max}=h_0+frac{{v_0}^2{{sin}^2 б }}{2g}left(12right).]

Примеры задач с решением

Пример 1

Задание. Каким будет угол ($alpha $) под которым бросили тело к горизонту, если оказалось, что максимальная высота подъема ($h$) тела в четыре раза меньше, чем дальность его полета ($s$)? Сопротивление воздуха можно не учитывать.

Решение. Выберем систему отсчета связанную с Землей. Будем считать, что тело бросили из начала координат (рис.2).

Запишем кинематические уравнения движения тела в поле тяжести земли:

[overline{s}(t)={overline{s}}_0+{overline{v}}_0t+frac{overline{g}t^2}{2}left(1.1right).]

[overline{v}(t)={overline{v}}_0+overline{g}tleft(1.2right)]

Исходя из начальных условий, нашей задачи:

[left{ begin{array}{c}
{overline{s}}_0=0 \
v_{0x}=v_0{cos alpha , } \
v_{0y}=v_0{sin alpha } end{array}
right. left(1.3right).]

В проекциях на оси уравнения (1.1) и (1.2)предстанут в виде:

[left{ begin{array}{c}
x(t)=v_0{cos alpha }t \
y(t)=v_0{sin alpha }t-frac{gt^2}{2} end{array}
right.left(1.4right).]

[left{ begin{array}{c}
v_xleft(tright)=v_0{cos alpha , } \
v_yleft(tright)=v_0{sin alpha }-gt end{array}
right.left(1.5right).]

Время подъема из второго уравнения системы (1.5) равно:

[t_p=frac{v_0{sin alpha }}{g} left(1.6right).]

Тогда максимальная высота подъема равна:

[h=yleft(t_pright)=frac{v^2_0{sin}^2alpha }{2g}left(1.7right).]

Если тело бросили из начала координат, то $t_{pol}=2t_p,$ дальность полета найдем, подставив время полета в первое уравнение системы (1.4):

[s=xleft(t_{pol}right)=2v^2_0frac{{{cos alpha }sin alpha }}{g} left(1.8right).]

По условию задачи: $h=frac{s}{4}$, используем уравнения (1.7) и (1.8):

[frac{v^2_0{sin}^2alpha }{2g}=v^2_0frac{{{cos alpha }sin alpha }}{2g}to {sin alpha }={cos alpha }to alpha =frac{pi }{4}.]

Ответ. $alpha =frac{pi }{4}$

Пример 2

Задание. Какова скорость падения тела брошенного под углом горизонта $alpha $ со скоростью $v_0$? Если тело бросили с земли. Сопротивление воздуха можно не учитывать.

Решение. За основу решения задачи примем кинематическое уравнение для скорости движения тела в поле тяжести Земли:

[overline{v}left(tright)={overline{v}}_0+overline{g}tleft(2.1right).]

Начальные условия движения нашего тела:

[left{ begin{array}{c}
{overline{s}}_0=0 \
v_{0x}=v_0{cos alpha , } \
v_{0y}=v_0{sin alpha } end{array}
right. left(2.2right).]

В проекциях на оси X и Y уравнение (2.1):

[left{ begin{array}{c}
v_xleft(tright)=v_0{cos alpha , } \
v_yleft(tright)=v_0{sin alpha }-gt end{array}
right.left(2.3right).]

Время подъёма тела, принимая во внимание, что $v_yleft(t_pright)=0$ из второго уравнения (2.3) равно:

[t_p=frac{v_0{sin alpha }}{g} left(2.4right).]

Если тело бросили из начала координат, то $t_{pol}=2t_p:$

[t_{pol}=frac{2v_0{sin alpha }}{g}left(2.5right).]

Зная время полета, найдем $v_yleft(t_{pol}right)$, подставив его во второе уравнение (2.3):

[v_yleft(t_{pol}right)=-v_0{sin alpha left(2.6right). }]

Модуль вектора скорости в момент падения найдем как:

[v(t_{pol})=sqrt{v^2_x{+v}^2_y }=v_0.]

Ответ. При заданных условиях величина скорости падения равна модулю скорости бросания.

Читать дальше: динамика прямолинейного движения связанных тел.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Источник