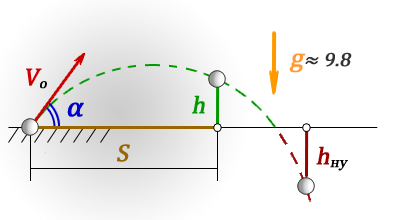
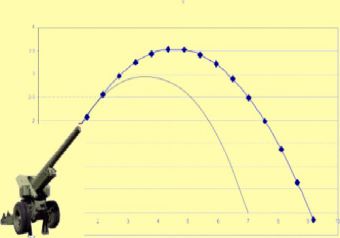
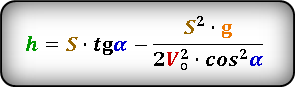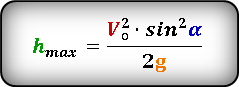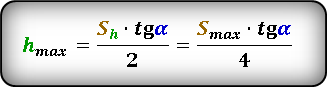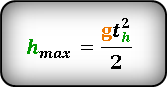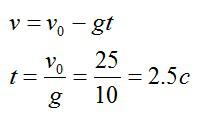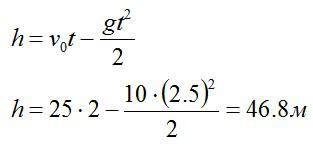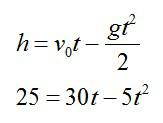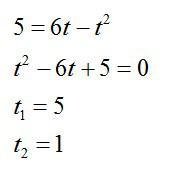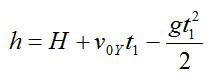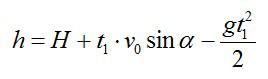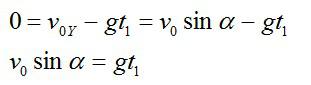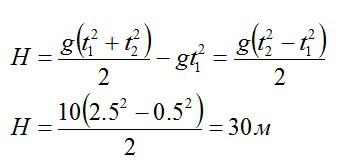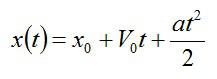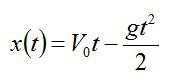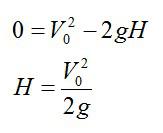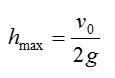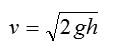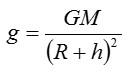1. Определить, на какой высоте находится тело, в любой точке траектории движения
h — высота тела в момент времени t
hну — высота ниже уровня броска (принимает отрицательное значение)
S — дальность полета по горизонтали
t — время полета
Vo — начальная скорость тела
α — угол под которым брошено тело
g ≈ 9,8 м/с2 — ускорение свободного падения
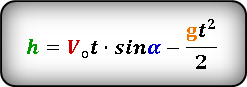
Формула для определения значения высоты тела в момент времени t
Формула для определения значения высоты тела через расстояние S по горизонтали
hну — высота ниже уровня броска, принимает отрицательное значение
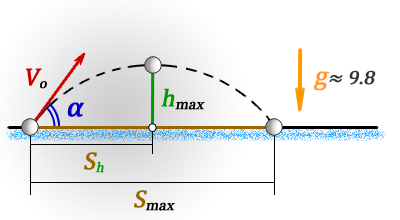
2. Найти максимальную высоту, на которую поднялось тело
hmax — максимальная высота
Smax — максимальная дальность полета, если бросок и падение на одном уровне
Sh — расстояние пройденное по горизонтали до момента максимального подъема
tmax — время всего полета
th — время за которое тело поднялось на максимальную высоту
Vo — начальная скорость тела
α — угол под которым брошено тело
g ≈ 9,8 м/с2 — ускорение свободного падения
Формула для расчета максимальной высоты достигнутое телом, если даны, начальная скорость Vo и угол α под которым брошено тело. :
Формула для вычисления максимальной высоты, если известны, максимальное расстояние S max или расстояние по горизонтали при максимальной высоте Sh и угол α под которым брошено тело. :
По этой формуле, можно определить максимальную высоту, если известно время th за которое тело поднялось на эту высоту. :
- Подробности
-
Опубликовано: 11 августа 2015
-
Обновлено: 13 августа 2021
Максимальная высота подъема тела, брошенного под углом к горизонту, формула
Максимальная высота подъема тела, брошенного под углом к горизонту определяется из формул времени максимального подъема и формулы координат тела
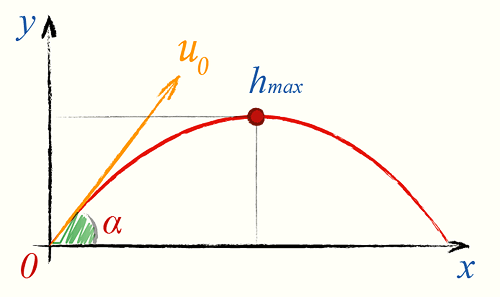
Максимальная высота подъема тела, брошенного под углом к горизонту
[
h_{max} = y(t_{hmax}) = u_0 t_{hmax} sin(α) — frac{gt_{hmax}^2}{2}
]
и после подстановки thmax в выражение (1) и его упрощения получим
[
h_{max} = frac{(u_0 sin(α))^2}{2g}
]
Здесь:
u0 — начальная скорость тела (м/с),
α — угол, под которым брошено тело к горизонту (°),
g — ускорение свободного падения 9.81 (м/c2),
thmax — время подъема на максимальную высоту (c)
Вычислить, найти максимальную высоту подъема тела, брошенного под углом к горизонту по формуле (2).
Максимальная высота подъема тела, брошенного под углом к горизонту |
стр. 420 |
|---|
Как найти максимальную высоту подъема
При броске тела вверх оно замедляется с ускорением g≈9,8 м/с², обусловленным гравитационным притяжением Земли. Именно поэтому в некоторый момент времени подброшенное тело останавливается и начинает движение в обратном направлении, вниз. Расстояние от точки смены направления движения тела до поверхности Земли и будет равно максимальной высоте подъема.
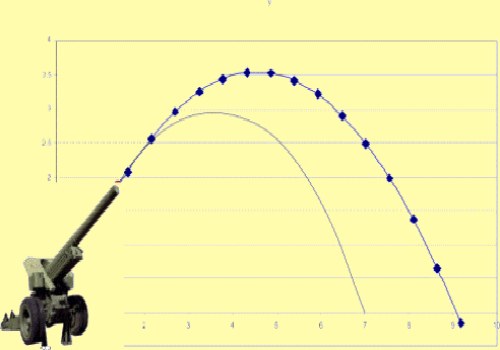
Вам понадобится
- — секундомер;
- — радар;
- — калькулятор;
- — угломер.
Инструкция
Найдите максимальную высоту подъема тела, брошено вверх при помощи секундомера. Не имеет значения, брошено ли тело вертикально вверх или под углом к горизонту. При помощи секундомера, засеките время, которое тело находилось в полете. Измеряйте значение времени в секундах. Поскольку половину времени, проведенного в полете тело поднимается, во вторую половину опускается, полученное значение поделите на 2.
Рассчитайте максимальную высоту подъема тела Н. Для этого возведите поделенное на 2 время полета t в квадрат. Полученное значение умножьте на ускорение свободного падения g≈9,8 м/с², а результат поделите на число 2, H=g∙t²/2. Высоту получите в метрах.
Пример. После броска с поверхности Земли тело снова упало на нее через 4 с, на какую максимальную высоту оно поднялось? Найдите время подъема тела на максимальную высоту. Оно равно половине всего времени движения 4/2=2 с. Подставьте значение в формулу H=g∙t²/2=9,8∙2²/2≈20 м. Если не требуется повышенная точность, значение ускорения свободного падения можно брать 10 м/с².
Определите максимальную высоту подъема тела, если известна его начальная скорость. Ее можно измерить специальным радаром. В некоторых устройствах, она изначально известна. В том случае, если тело запущено вертикально вверх с начальной скоростью v0, чтобы найти максимальную высоту подъема этого тела поделите квадрат этой начальной скорости на удвоенное значение ускорения свободного падения, H=v0²/2∙g. Скорость должна быть измерена в метрах в секунду.
Найдите максимальную высоту подъема тела, начальная скорость v0 которого направлена под углом к горизонту. При расчете учитывайте, что за подъем тела отвечает только вертикальная составляющая скорости, которая равна v0y= v0∙sin(α), где α – угол к горизонту, под которым тело начало свое движение, его измерьте угломером. Тогда для расчета максимальной высоты подъема тела можно использовать формулу, описанную в предыдущем пункте, а получившийся результат умножит на синус α, возведенный в квадрат H=(v0²/2∙g)∙sin²(α).
Источники:
- максимальная высота
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Вторник, а это значит, что сегодня мы снова решаем задачи. На это раз, на тему «свободное падение тел».
Присоединяйтесь к нам в телеграм и получайте актуальную рассылку каждый день!
Задачи на свободное падение тел с решением
Задача №1. Нахождение скорости при свободном падении
Условие
Тело падает с высоты 20 метров. Какую скорость оно разовьет перед столкновением с Землей?
Решение
Высота нам известна по условию. Для решения применим формулу для скорости тела в момент падения и вычислим:
Ответ: примерно 20 метров в секунду.
Задача №2. Нахождение высоты и времени движения тела, брошенного вертикально.
Условие
Индеец выпускает стрелу из лука вертикально вверх с начальной скоростью 25 метров в секунду. За какое время стрела окажется в наивысшей точке и какой максимальной высоты она достигнет стрела?
Решение
Сначала запишем формулу из кинематики для скорости. Как известно, в наивысшей точке траектории скорость стрелы равна нулю:
Теперь запишем закон движения для вертикальной оси, направленной вертикально вверх.
Ответ: 2,5 секунды, 46 метров.
Задача №3. Нахождение времени движения тела, брошенного вертикально вверх
Условие
Мячик бросили вертикально вверх с начальной скоростью 30 метров в секунду. Через какое время мяч окажется на высоте 25 метров?
Решение
Запишем уравнение для движения мячика:
Мы получили квадратное уравнение. Упростим его и найдем корни:
Как видим, уравнение имеет два решения. Первый раз мячик побывал на высоте через 1 секунду (когда поднимался), а второй раз через 5 секунд (когда падал обратно).
Ответ: 1с, 5с.
Задача №4. Нахождение высоты при движении тела под углом к горизонту
Условие
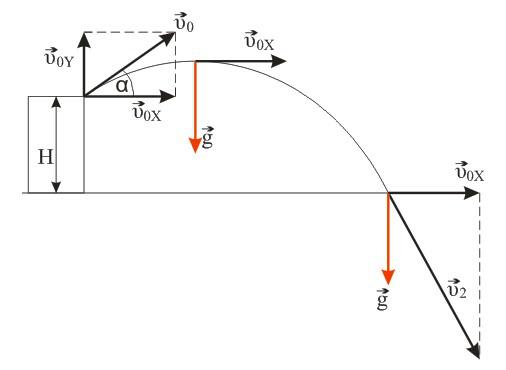
Камень, брошенный с крыши дома под углом альфа к горизонту, через время t1=0,5c достиг максимальной высоты, а еще через время t2=2,5c упал на землю. Определите высоту Н дома. Сопротивлением воздуха пренебречь. Ускорение свободного падения g = 10 м/с2.
Решение
Камень брошен со скоростью v0 под углом α к горизонту с дома высотой Н. Эту скорость можно разложить на две составляющие: v0X (горизонтальная) и v0Y (вертикальная). В горизонтальном направлении на камень не действует никаких сил (сопротивлением воздуха пренебрегаем), поэтому горизонтальная составляющая скорости неизменна на протяжении всего времени полета камня (равномерное движение). Максимальная точка траектории камня над уровнем земли (исходя из кинематических соотношений):
Здесь t1 – время подъема камня с высоты Н на высоту h; g – ускорение свободного падения.
Вертикальную составляющую скорости можно вычислить исходя из геометрических соображений:
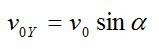
Подставив выражение для скорости в первое уравнение, получим:
Также высоту h можно выразить через время t2 падения камня с высоты h на землю (исходя из кинематических соотношений и учитывая, что с вертикальная составляющая скорости в наивысшей точке равна нулю):
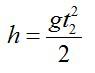
Для высоты дома можно записать:
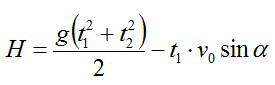
Так как вертикальная составляющая скорости камня в максимальной точке траектории равна нулю:
Подставляем в формулу для высоты H и вычисляем:
Ответ: H = 30 м.
Задача №5. Нахождение закона движения тела
Условие
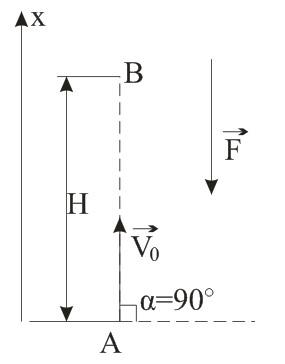
Найти закон движения тела против силы тяжести, при начальной скорости V0. И на какую максимальную высоту поднимется тело? Тело бросили под углом 90 градусов.
Решение
Тело брошено под углом α=90° к горизонту. Другими словами, тело брошено вертикально вверх с начальной скоростью V0. Направим координатную ось х вертикально вверх, так ее направление совпадает с вектором начальной скорости. F – сила тяжести, направленная вниз. В начальный момент тело находится в точке А.
В задаче нужно найти закон движения тела, то есть зависимость координаты тела от времени. В общем случае этот закон задается кинематическим соотношением:
где х0 – начальная координата тела; a – ускорение.
Так как мы поместили начало координат в точку А, х0=0. Тело движется с ускорением свободного падения g, при этом сила тяжести направлена против начальной скорости, поэтому в проекции на вертикальную ось a=-g. Таким образом, искомый закон движения перепишется в виде:
Далее будем использовать еще одно общее кинематическое соотношение:
где V – конечная скорость.
Максимальная высота подъема тела указана на рисунке точной B, в этот момент конечная скорость V равна нулю, а координата х равна максимальной высоте Н подъема тела. Отсюда можно найти выражение для этой величины:
Полезные формулы для решения задач на свободное падение
Свободное падение описывается формулами кинематики. Мы не будем приводить их вывод, но запишем самые полезные.
Формула для максимальной высоты подъема тела, брошенного вертикально вверх c некоторой начальной скоростью:
Кстати, как выводится именно эта формула можно посмотреть в последней задаче.
Формула для времени подъема и падения тела, брошенного вертикально вверх:
Скорость тела в момент падения с высоты h:
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Вопросы с ответами на свободное падение тел
Вопрос 1. Как направлен вектор ускорения свободного падения?
Ответ: можно просто сказать, что ускорение g направлено вниз. На самом деле, если говорить точнее, ускорение свободного падения направлено к центру Земли.
Вопрос 2. От чего зависит ускорение свободного падения?
Ответ: на Земле ускорение свободного падения зависит от географической широты, а также от высоты h подъема тела над поверхностью. На других планетах эта величина зависит от массы M и радиус R небесного тела. Общая формула для ускорения свободного падения:
Вопрос 3. Тело бросают вертикально вверх. Как можно охарактеризовать это движение?
Ответ: В этом случае тело движется равноускоренно. Причем время подъема и время падения тела с максимальной высоты равны.
Вопрос 4. А если тело бросают не вверх, а горизонтально или под углом к горизонту. Какое это движение?
Ответ: можно сказать, что это тоже свободное падение. В данном случае движение нужно рассматривать относительно двух осей: вертикальной и горизонтальной. Относительно горизонтальной оси тело движется равномерно, а относительно вертикальной – равноускоренно с ускорением g.
Баллистика – наука, изучающая особенности и законы движения тел, брошенных под углом к горизонту.
Вопрос 5. Что значит «свободное» падение.
Ответ: в данном контексте понимается, что тело при падении свободно от сопротивления воздуха.
Свободное падение тел: определения, примеры
Свободное падение – равноускоренное движение, происходящее под действием силы тяжести.
Первые попытки систематизированно и количественно описать свободное падение тел относятся к средневековью. Правда, тогда было широко распространено заблуждение, что тела разной массы падают с разной скоростью. На самом деле, в этом есть доля правды, ведь в реальном мире на скорость падения сильно влияет сопротивление воздуха.
Однако, если им можно пренебречь, то скорость падающих тел разной массы будет одинакова. Кстати, скорость при свободном падении возрастает пропорционально времени падения.
Ускорение свободно падающих тел не зависит от их массы.
Рекорд свободного падения для человека на данный момент принадлежит австрийскому парашютисту Феликсу Баумгартнеру, который в 2012 году прыгнул с высоты 39 километров и находился в свободном падении 36 402,6 метра.
Примеры свободного падения тел:
- яблоко летит на голову Ньютона;
- парашютист выпрыгивает из самолета;
- перышко падает в герметичной трубке, из которой откачан воздух.
При свободном падении тела возникает состояние невесомости. Например, в таком же состоянии находятся предметы на космической станции, движущейся по орбите вокруг Земли. Можно сказать, что станция медленно, очень медленно падает на планету.
Конечно, свободное падение возможно не только не Земле, но и вблизи любого тела, обладающего достаточной массой. На других комических телах падения также будет равноускоренным, но величина ускорения свободного падения будет отличаться от земной. Кстати, раньше у нас уже выходил материал про гравитацию.
При решении задач ускорение g принято считать равным 9,81 м/с^2. В реальности его величина варьируется от 9,832 (на полюсах) до 9,78 (на экваторе). Такая разница обусловлена вращением Земли вокруг своей оси.
Нужна помощь в решении задач по физике? Обращайтесь в профессиональный студенческий сервис в любое время.
Обновлено: 24.05.2023
Если тело бросить вертикально вверх при наличии начальной скорости υ 0 , оно будет двигаться равнозамедленно с ускорением, равным a = — g = — 9 , 81 υ c 2 .
Формулы вычисления показателей движения брошенного тела
Высота подбрасывания h за время t и скорость υ через промежуток t можно определить формулами:
t m a x — это время, за которое тело достигает максимальной высоты h m a x = h , при υ = 0 , а сама высота h m a x может быть определена при помощи формул:
Когда тело достигает высоты, равной h m a x , то оно обладает скоростью υ = 0 и ускорением g . Отсюда следует, что тело не сможет оставаться на этой высоте, поэтому перейдет в состояние свободного падения. То есть, брошенное вверх тело – это равнозамедленное движение, при котором после достижения h m a x изменяются знаки перемещения на противоположные. Важно знать, какая была начальная высота движения h 0 . Общее время тела примет обозначение t , время свободного падения — t п , конечная скорость υ к , отсюда получаем:
Если тело брошено вертикально вверх от уровня земли, то h 0 = 0 .
Время, необходимое для падения тела с высоты, куда предварительно было брошено тело, равняется времени его подъема на максимальную высоту.
Так как в высшей точке скорость равняется нулю видно:
Конечная скорость υ к тела, брошенного от уровня земли вертикально вверх, равна начальной скорости υ 0 по величине и противоположна по направлению, как показано на ниже приведенном графике.
Примеры решения задач
Тело было брошено вертикально вверх с высоты 25 метров со скоростью 15 м / с . Через какой промежуток времени оно достигнет земли?
Дано: υ 0 = 15 м / с , h 0 = 25 м , g = 9 , 8 м / с 2 .
Найти: t .
Решение
t = υ 0 + υ 0 2 + g h 0 g = 15 + 15 2 + 9 , 8 · 25 9 , 8 = 3 , 74 с
Ответ: t = 3 , 74 с .
Был брошен камень с высоты h = 4 вертикально вверх. Его начальная скорость равняется υ 0 = 10 м / с . Найти высоту, на которую сможет максимально подняться камень, его время полета и скорость, с которой достигнет поверхности земли, пройденный телом путь.
Дано: υ 0 = 10 м / с , h = 4 м , g = 9 , 8 м / с 2 .
Найти: H , t , v 2 , s .
Решение
H = h 0 υ 0 2 2 g = 4 + 10 2 9 , 8 = 14 , 2 м .
t = υ 0 + υ 0 2 + g h 0 g = 10 + 10 2 + 9 , 8 · 4 9 , 8 = 1 , 61 с .
υ 2 = υ k = 2 g H = 2 · 9 , 8 · 14 , 2 = 16 , 68 м / с .
s = H — h 0 + H = 2 H — h 0 = 2 · 14 , 2 = 24 , 4 м .
Ответ: H = 14 , 2 м ; t = 1 , 61 с ; v 2 = 16 , 68 м / с ; s = 24 , 4 м .
Согласно второму закону Ньютона, сила тяжести, обусловленная гравитационным притяжением, действует на все тела на поверхности Земли и вблизи неё вне зависимости от того, покоятся они или движутся.
При свободном падении тело движется равноускоренно. Это значит, что скорость свободно падающего тела увеличивается при приближении к поверхности Земли. Этому способствует ускорение свободного падения (рис. (1)).
Если подбросить тело вверх, то при отсутствии сопротивления воздуха, тело будет двигаться только под действием силы тяжести (рис. (2)), которая направлена вниз (к центру Земли). В эту же сторону направлено и ускорение свободного падения.
Чем большую начальную скорость получило тело при броске, тем больше будет время подъёма, и тем на большую высоту оно поднимется к моменту остановки.
После того как тело поднялось на наибольшую высоту, оно под действием силы тяжести начинает равноускоренно падать вниз.
Вдоль оси (Oy) тело движется равноускоренно с ускорением свободного падения g y и начальной скоростью υ 0 .
При движении вверх с начальной скоростью υ 0 значение скорости будет уменьшаться, тело будет замедляться. Направления проекций скорости и ускорения свободного падения на ось (Oy) будут противоположными.
При броске тела вверх оно замедляется с ускорением g≈9,8 м/с², обусловленным гравитационным притяжением Земли. Именно поэтому в некоторый момент времени подброшенное тело останавливается и начинает движение в обратном направлении, вниз. Расстояние от точки смены направления движения тела до поверхности Земли и будет равно максимальной высоте подъема.
- Как найти максимальную высоту подъема
- Как рассчитать скорость падения
- Как найти время падения тела
- — секундомер;
- — радар;
- — калькулятор;
- — угломер.
Найдите максимальную высоту подъема тела, брошено вверх при помощи секундомера. Не имеет значения, брошено ли тело вертикально вверх или под углом к горизонту. При помощи секундомера, засеките время, которое тело находилось в полете. Измеряйте значение времени в секундах. Поскольку половину времени, проведенного в полете тело поднимается, во вторую половину опускается, полученное значение поделите на 2.
Рассчитайте максимальную высоту подъема тела Н. Для этого возведите поделенное на 2 время полета t в квадрат. Полученное значение умножьте на ускорение свободного падения g≈9,8 м/с², а результат поделите на число 2, H=g∙t²/2. Высоту получите в метрах.
Пример. После броска с поверхности Земли тело снова упало на нее через 4 с, на какую максимальную высоту оно поднялось? Найдите время подъема тела на максимальную высоту. Оно равно половине всего времени движения 4/2=2 с. Подставьте значение в формулу H=g∙t²/2=9,8∙2²/2≈20 м. Если не требуется повышенная точность, значение ускорения свободного падения можно брать 10 м/с².
Определите максимальную высоту подъема тела, если известна его начальная скорость. Ее можно измерить специальным радаром. В некоторых устройствах, она изначально известна. В том случае, если тело запущено вертикально вверх с начальной скоростью v0, чтобы найти максимальную высоту подъема этого тела поделите квадрат этой начальной скорости на удвоенное значение ускорения свободного падения, H=v0²/2∙g. Скорость должна быть измерена в метрах в секунду.
Найдите максимальную высоту подъема тела, начальная скорость v0 которого направлена под углом к горизонту. При расчете учитывайте, что за подъем тела отвечает только вертикальная составляющая скорости, которая равна v0y= v0∙sin(α), где α – угол к горизонту, под которым тело начало свое движение, его измерьте угломером. Тогда для расчета максимальной высоты подъема тела можно использовать формулу, описанную в предыдущем пункте, а получившийся результат умножит на синус α, возведенный в квадрат H=(v0²/2∙g)∙sin²(α).
На какую высоту поднимется тело, брошенное вертикально вверх с начальной скоростью 800 м/с. Сопротивлением воздуха пренебречь.
Решение задачи:
Первый способ решения – длинный.
Тело бросают вертикально вверх с начальной скоростью, из-за ускорения свободного падения оно равно или поздно достигнет максимально высоты, остановится и устремится обратно к земле. Для того, чтобы определить эту высоту запишем уравнения движения и уравнение скорости тела:
В точке максимального подъема скорость тела (upsilon) равна нулю. Из выражения (2) определим время полета:
[upsilon = 0 Rightarrow 0 = <upsilon _0>– gt Rightarrow t = frac<<<upsilon _0>>>]
Подставим полученную формулу в выражение (1):
Второй способ решения – короткий.
Используем известную формулу без времени (знак “минус” справа присутствует из-за того, что движение замедленное!):
Конечная скорость (upsilon) равна нулю, поэтому формула станет короче. Выразим оттуда искомую высоту (h).
[upsilon _0^2 = 2gh Rightarrow h = frac<<upsilon _0^2>>>]
Видно, что если в задаче не дано времени, то лучше использовать второй способ.
Ответ: 32 км.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
помогите пожалуйста решить задачи:
1) Определите на какую максимальную высоту поднимется тело, если его подбросили вертикально вверх со скоростью 30 м/с.
2) Определите скорость пули через 2,5 с после выстрела вертикально вверх, если скорость в момент вылета из ствола была 300 м/с.
1) Используем формулу кинематики без времени: [ <upsilon ^2>– upsilon _0^2 = – 2gH]На максимальной высоте скорость тела будет равна нулю, тогда:[upsilon _0^2 = 2gH]Максимальная высота равна:[H = frac<<upsilon _0^2>>>][H = frac^2>>>> = 45;м]
2) Скорость пули в любой момент, движущейся вертикально вверх, можно найти по формуле:[upsilon = <upsilon _0>– gt][upsilon = 300 – 10 cdot 2,5 = 275;м/с]
Спасибо за ответ я понял как теперь решать
Можете сказать название формулы, использованной в первом шаге второго способа?υ
v2—v02=—2gh
По сути это закон сохранения энергии Ещё называют формулой кинематики без времени
Я взял формулу h_max = v_0^2*sin^2a/2*g a = 90. У меня вышло тот же самый ответ только, боюсь что я взял не правильную формулу. Или нет?
Да, Вы взяли формулу максимальной высоты для тела, брошенного под углом к горизонту, а в задаче тело брошено вертикально вверх. Правильная формула показана в решении выше (как и вывод этой формулы).
у меня вместо формул что-то вроде ^2>>>><<<<562<>[]
Для корректного отображения формул на сайте в браузере должны быть разрешены запуски скриптов js
С какой максимальной скоростью человек может бросить камень или мячик своей рукой?
Для решения задачи используем информацию о рекордной скорости бейсбольного мяча на подаче, равный v ≈ 45 м/сек. Масса бейсбольного мяча известна и приближенно равна m = 0,145 кг. Соответствующую кинетическую энергию (Е), затраченную на бросок мяча рукой, оценим из формулы Е ≈ (δМ + m)v²/2, где М — масса человека, а δМ = 0,005М — масса кисти руки.
Подставив в формулу массу среднего человека, M ≈ 70 кг, получим, что энергия рекордного броска равнялась E ≈ 500 Дж. Зафиксировав это значение как предел, решим теперь задачу в обратном направлении — найдём приближённую формулу для максимальной скорости (v) произвольного предмета с массой m, брошенного человеком с массой М, при фиксированной максимальной энергии E = 500 Дж.
Ответ: v ≈ √ ≈ √, [м/сек], где m и М в единицах кг. Подставив числовые значения, определим скорость,с которой человек может кинуть бейсбольный мяч. V= √1000/0.005×70+0.145=45 м/с=162км/ч
Можно сказать,что проверили информацию о рекордной скорости бейсбольного мяча на подаче, равный v ≈ 45 м/сек.
В газете прочитал такую статью: “Насколько высоко человек может что-либо подбросить?. Возьмем,например, бейсбольный мяч.Питчер, кидающий фастбол на скорости 130 км/, сумеет добросить его до высоты 50 метров. Я решил взять вышеуказанную задачу и проверить результат в 50 метров. Перевел в м/с: 130 км/час=36м/с
Выбрав вторую формулу, находим h=36^2/2×10=64.8 метра.
Правильно я проверил?
Думаю, да.
Проблема в том, что питчер не кидает мяч вертикально вверх, а формула справедлива только для мяча, брошенного вертикально вверх.
У меня получилось вот так:
Уравнение движения тела y = v_0 * t – (g * t^2 )/2. (*)
Время t можно найти из этого уравнения g = (v – v_0)/t => t = (v – v_0)/g. t = 81,6c
Подставим все известные значения в уравнение (*) и получим y = 32653 м.
Разница между вашими моим ответом 653 м.
В решении я принял, что (g = 10;м/с^2), а у Вас по всей видимости (g = 9,81;м/с^2). Разница в 600 с лишним метров в таком случае нормальна. Это всего лишь 2% от 32000 м.
Ваше решение тоже правильно (как и моё), хотя мне не нравится один момент. Вы решает по действиям и накапливаете ошибку. Если использовать мою конечную формулу и принять (g = 9,81;м/с^2), то:
[h = frac^2>>>> = 32619,8;м]
Тогда у нас с Вами разница 40 м, а её вообще не должно быть.
Читайте также:
- Что такое потолок кратко
- Кластер что это в экономике кратко и понятно
- Модели здоровьесберегающей деятельности школы типичная недостаточная
- Что рассказывается о повести временных лет о начале руси кратко
- Комплексный анализ текста 2 класс школа россии