Формулы математического маятника в физике
Формулы математического маятника
Определение и формулы математического маятника
Определение
Математический маятник — это колебательная система, являющаяся частным случаем физического маятника, вся масса которого
сосредоточена в одной точке, центре масс маятника.
Обычно математический маятник представляют как шарик, подвешенный на длинной невесомой и нерастяжимой нити. Это идеализированная система, совершающая гармонические колебания под действием силы тяжести. Хорошим приближением к математическому маятнику массивный маленький шарик, осуществляющий колебания на тонкой длинной нити.
Галилей первым изучал свойства математического маятника, рассматривая качание паникадила на длинной цепи. Он получил, что период колебаний математического маятника не зависит от амплитуды. Если при запуске мятника отклонять его на разные малые углы, то его колебания будут происходить с одним периодом, но разными амплитудами. Это свойство получило название изохронизма.
Уравнение движения математического маятника
Математический маятник — классический пример гармонического осциллятора. Он совершает гармонические колебания, которые описываются дифференциальным уравнением:
[ddot{varphi }+{omega }^2_0varphi =0 left(1right),]
где $varphi $ — угол отклонения нити (подвеса) от положения равновесия.
Решением уравнения (1) является функция $varphi (t):$
[varphi (t)={varphi }_0{cos left({omega }_0t+alpha right)left(2right), }]
где $alpha $ — начальная фаза колебаний; ${varphi }_0$ — амплитуда колебаний; ${omega }_0$ — циклическая частота.
Колебания гармонического осциллятора — это важный пример периодического движения. Осциллятор служит моделью во многих задачах классической и квантовой механики.
Циклическая частота и период колебаний математического маятника
Циклическая частота математического маятника зависит только от длины его подвеса:
[ {omega }_0=sqrt{frac{g}{l}}left(3right).]
Период колебаний математического маятника ($T$) в этом случае равен:
[T=frac{2pi }{{omega }_0}=2pi sqrt{frac{l}{g}}left(4right).]
Выражение (4) показывает, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения.
Уравнение энергии для математического маятника
При рассмотрении колебаний механических систем с одной степенью свободы часто берут в качестве исходного не уравнения движения Ньютона, а уравнение энергии. Так как его проще составлять, и оно является уравнением первого порядка по времени. Предположим, что трение в системе отсутствует. Закон сохранения энергии для совершающего свободные колебания математического маятника (колебания малые) запишем как:
[E=E_k+E_p=frac{mv^2}{2}+mgh=frac{mv^2}{2}+frac{mgx^2}{2l}=constleft(5right),]
где $E_k$ — кинетическая энергия маятника; $E_p$ — потенциальная энергия маятника; $v$ — скорость движения маятника; $x$ — линейное смещение груза маятника от положения равновесия по дуге окружности радиуса $l$, при этом угол — смещение связан с $x$ как:
[varphi =frac{x}{l}left(6right).]
Максимальное значение потенциальной энергии математического маятника равно:
[E_{pmax}=mgh_m=frac{mg{x^2}_m}{2l}left(7right);;]
Максимальная величина кинетической энергии:
[E_{kmax}=frac{mv^2_m}{2}=frac{m{omega }^2_0{x^2}_m}{2l}=E_{pmax}left(8right),]
где $h_m$ — максимальная высота подъема маятника; $x_m$- максимальное отклонение маятника от положения равновесия; $v_m={omega }_0x_m$ — максимальная скорость.
Примеры задач с решением
Пример 1
Задание. Какова максимальная высота подъема шарика математического маятника, если его скорость движения при прохождении положения равновесия составляла $v$?
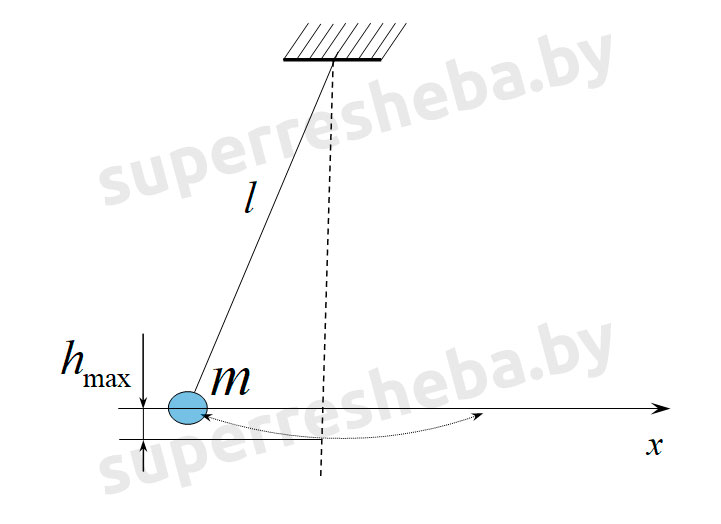
Решение. Сделаем рисунок.
Пусть ноль потенциальной энергии шарика в его положении равновесия (точка 0).В этой точке скорость шарика максимальна и равна по условию задачи $v$. В точке максимального подъема шарика над положением равновесия (точка A), скорость шарика равна нулю, потенциальная энергия максимальна. Запишем закон сохранения энергии для рассмотренных двух положений шарика:
[frac{mv^2}{2}=mgh left(1.1right).]
Из уравнения (1.1) найдем искомую высоту:
[h=frac{v^2}{2g}.]
Ответ. $h=frac{v^2}{2g}$
Пример 2
Задание. Каково ускорение силы тяжести, если математический маятник имеющий длину $l=1 м$, совершает колебания с периодом равным $T=2 с$? Считайте колебания математического маятника малыми.textit{}
Решение. За основу решения задачи примем формулу для вычисления периода малых колебаний:
[T=2pi sqrt{frac{l}{g}}left(2.1right).]
Выразим из нее ускорение:
[g=frac{4{pi }^2l}{T^2} .]
Проведем вычисления ускорения силы тяжести:
[g=frac{4{pi }^2cdot 1}{2^2}={pi }^2approx 9,87 left(frac{м}{с^2}right).]
Ответ. $g=9,87 frac{м}{с^2}$
Читать дальше: формулы пружинного маятника.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Вася Иванов
Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.
Определите максимальную высоту на которую поднимется математический маятник если тело проходит положение равновесия со скорость 1 м / с.
На этой странице сайта размещен вопрос Определите максимальную высоту на которую поднимется математический маятник если тело проходит положение равновесия со скорость 1 м / с? из категории
Физика с правильным ответом на него. Уровень сложности вопроса
соответствует знаниям учеников 5 — 9 классов. Здесь же находятся ответы по
заданному поиску, которые вы найдете с помощью автоматической системы.
Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по
заданной теме. На этой странице можно обсудить все варианты ответов с другими
пользователями сайта и получить от них наиболее полную подсказку.
Мария Зубкова
28 июля, 19:52
0
Данные задачи: V (скорость заданного маятника в положении равновесия) = 2 м/с.
Чтобы определить максимальную высоту подъема заданного маятника, применим закон сохранения энергии (кинетическая энергия в положении равновесия равна полной энергии, которая на максимальной высоте перейдет в потенциальную) : m * V² / 2 = m * g * h и h = V² / 2g.
Расчет: h = 2² / (2 * 10) = 0,2 м.
Ответ: Заданный маятник сможет подняться на высоту 0,2 м.
- Комментировать
- Жалоба
- Ссылка
Дано:
g=9.8 мс;g=9.8,dfrac{м}{с};
m=100 г=0.1 кг;m=100,г=0.1,кг;
v=4.0 мс.v=4.0,dfrac{м}{с}.
Найти:
Wмех−?W_{мех}-?
hmax−?h_{max}-?
Решение:
а) При прохождения маятником положения равновесия его кинетическая энергия Wк=mv22W_к=dfrac{mv^2}{2} максимальна и равна полной энергии:
Wмех=mv22.W_{мех}=dfrac{mv^2}{2}.
Подставим численные значения физических величин и произведём вычисления:
Wмех=0.1⋅422=0.8 Дж.W_{мех}=dfrac{0.1cdot 4^2}{2}=0.8,Дж.
б) Учитывая закон сохранения энергии, максимальная кинетическая энергия математического маятника равна максимальной потенциальной энергии (Wп)max=mghmax(W_п)_{max}=mgh_{max} и равна полной энергии. Следовательно, можно записать:
Wмех=mghmax;W_{мех}=mgh_{max};
hmax=Wмехmg.h_{max}=dfrac{W_{мех}}{mg}.
Подставим численные значения физических величин и вычислим максимальную высоту hmax,h_{max}, на которую поднимется маятник:
hmax=0.80.1⋅9.8=0.816 м=81.6 см.h_{max}=dfrac{0.8}{0.1cdot9.8}=0.816,м=81.6,см.
Ответ: а) Wмех=0.8 Дж;W_{мех}=0.8,Дж; б) hmax=81.6 см.h_{max}=81.6,см.