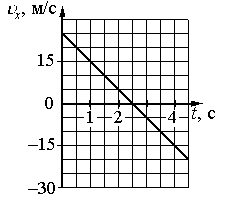Как найти максимальный модуль ускорения по графику - Исправление недочетов и поиск решений вместе с Examum.ru

Содержание

Что такое ускорение?
Движение по прямой и ускорение
Полное ускорение и его компоненты при движении тела по кривой
Угловое ускорение
Пример решения задачи
Что такое ускорение?
Движение по прямой и ускорение
Полное ускорение и его компоненты при движении тела по кривой
Угловое ускорение
Пример решения задачи

Автомобиль движется по прямой улице. На графике представлена зависимость скорости автомобиля от времени. Чему равен максимальный модуль ускорения? Ответ выразите в м/с 2 .

На всех рассматриваемых интервалах времени скорость автомобиля меняется равномерно, следовательно, ускорение на каждом интервале постоянно. Рассчитаем ускорения:

в интервале от 0 до 10 с:

в интервале от 10 до 20 с:

в интервале от 20 до 30 с:

в интервале от 30 до 40 с:

Максимальный модуль ускорения равен 2 м/с 2 .

В физике существует несколько видов ускорения, которые используются для описания того или иного типа механического перемещения тел в пространстве. Все эти виды являются векторными величинами. В данной статье не будем рассматривать вопрос, куда направлено ускорение, а сосредоточим свое внимание на формулах модуля ускорения.

Что такое ускорение?

Максимально полное определение этой кинематической характеристики можно привести следующее: ускорение — это величина, показывающая быстроту изменения скорости во времени. Речь идет об изменении как модуля, так и направления. Математически ускорение вычисляют так:

Оно называется мгновенным, то есть справедливым для конкретного момента времени t. Чтобы найти среднее значение модуля ускорения, формулу такую необходимо использовать:

Где v₂ и v₁ — скорости в моменты времени t₂ и t₁ соответственно.

Единицами измерения изучаемой физической величины являются метры в квадратную секунду (м/с 2 ). Многих может смутить возведение во вторую степень единиц времени, тем не менее, понять смысл единицы м/с 2 несложно, если ее представить в виде [м/с]/с. Последняя запись означает изменение скорости на одну единицу за одну единицу времени.

Движение по прямой и ускорение

Самой простой траекторией для перемещения тел в пространстве является прямая линия. Если скорость при движении по такой траектории не изменяется, то говорить об ускорении не приходится, поскольку оно будет равно нулю.

В технике широко распространено прямолинейное равноускоренное (равнозамедленное) движение. Например, при старте автомобиля или при его торможении мы имеем именно этот вид движения. Для его математического описания пользуются следующими равенствами:

Здесь v — некоторая начальная скорость тела, которая может быть также равна нулю, l — пройденный телом путь к моменту времени t. Знак + говорит об ускорении тела, знак — — о его торможении. Важно запомнить, что время t при использовании записанных формул начинает отсчитываться от момента появления у тела постоянного ускорения a. С учетом записанных равенств, формулы модуля ускорения тела принимают вид:

Как правило, если тело ускоряется, то говорят о положительном ускорении, если же оно замедляет свое движение, то говорят об отрицательной величине a. Нетрудно проверить, что обе формулы приводят к одной и той же единице измерения ускорения (м/с 2 ).

Полное ускорение и его компоненты при движении тела по кривой

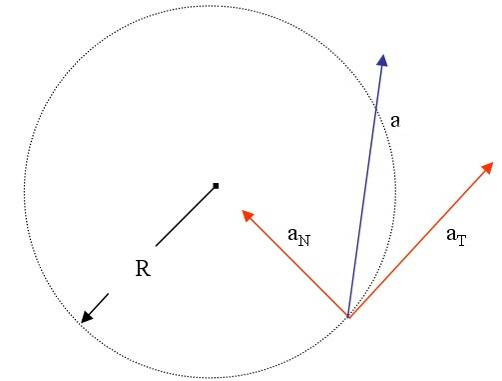
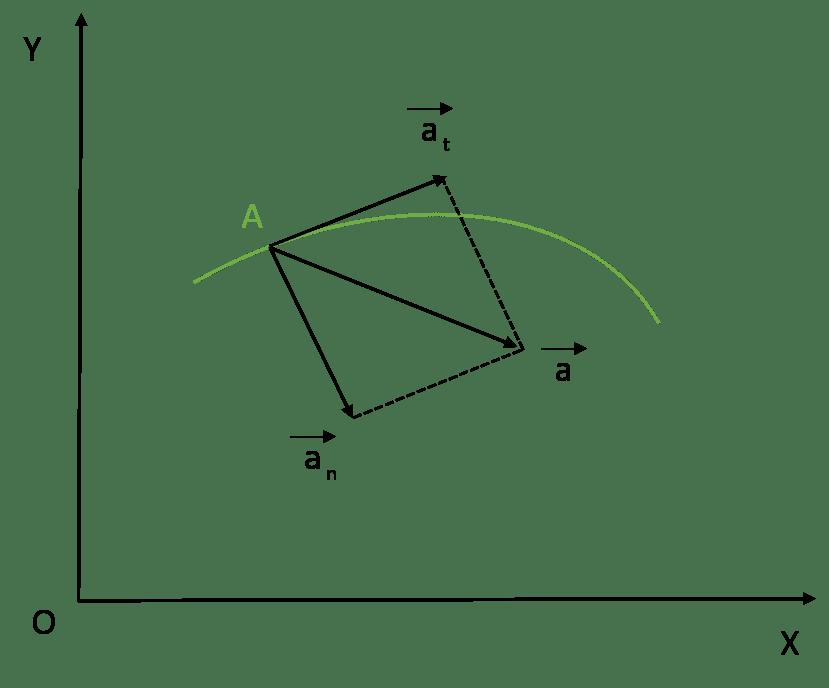
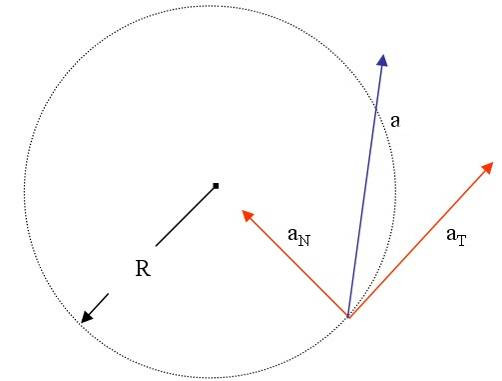
В случае перемещения тела по криволинейной траектории, величину a удобно представить в виде двух взаимно перпендикулярных составляющих. Они называются тангенциальным a_t и нормальным a_n ускорениями. Для такого случая формула модуля ускорения точки принимает вид:

Тангенциальную компоненту следует рассчитывать через производную функции v(t) по времени. Нормальная же компонента определяется не изменением модуля скорости, а самой ее величиной. Для ее расчета пользуются таким выражением:

Здесь r — радиус кривизны траектории, который в случае вращения по окружности совпадает с радиусом последней.

Для полноты информации отметим, что криволинейность траектории перемещения тела является достаточным признаком присутствия ненулевой нормальной составляющей ускорения. При этом величина a_t может быть равна нулю, что является справедливым для равномерного вращения тел.

Угловое ускорение

Как было отмечено во введении, существуют несколько видов ускорения. Одним из них является угловая кинематическая величина. Обозначим ее α. По аналогии с линейным ускорением, формула модуля ускорения углового имеет вид:

Где греческой буквой ω (омега) обозначена скорость угловая, единицами измерения которой являются радианы в секунду. Величина α показывает, как быстро тело увеличивает или замедляет скорость своего вращения.

Ускорение угловое можно связать с линейной величиной. Делается это с помощью такой формулы:

Важно понимать, что угловое ускорение является удобным способом представления тангенциальной составляющей полного ускорения в случае вращательного движения. Удобство здесь заключается в независимости величины α от расстояния до оси вращения r. В свою очередь, компонента a_t линейно возрастает при увеличении радиуса кривизны r.

Пример решения задачи

Известно, что тело вращается по окружности, радиус которой составляет 0,2 метра. Вращение является ускоренным, при этом скорость изменяется во времени по следующему закону:

Необходимо определить тангенциальное, нормальное, полное и угловое ускорения в момент времени 3 секунды.

Начнем решать эту задачу по порядку. Тангенциальная компонента определяется через производную скорости. Имеем:

Отметим, что это очень большое ускорение по сравнению с ускорением свободного падения (9,81 м/с 2 ).

Нормальная компонента вычисляется так:

a_n = v 2 /r = 1/r*(2 + 3*t 2 + 2*t 3 ) 2 = 1/0,2*(2+27+54) 2 = 34445 м/c 2 .

Теперь можно рассчитать полное ускорение. Оно будет равно:

То есть, полное ускорение практически полностью образовано нормальной компонентой.

Наконец, ускорение угловое определяется по формуле:

Полученное значение соответствует увеличению скорости угловой приблизительно на 60 оборотов за каждую секунду.

Что такое ускорение?

Вам будет интересно: Смоленский государственный институт искусств: факультеты, специальности, сроки обучения, документы для поступления

a = (v2 — v1)/(t2 — t1).

Где v2 и v1 — скорости в моменты времени t2 и t1 соответственно.

Единицами измерения изучаемой физической величины являются метры в квадратную секунду (м/с2). Многих может смутить возведение во вторую степень единиц времени, тем не менее, понять смысл единицы м/с2 несложно, если ее представить в виде [м/с]/с. Последняя запись означает изменение скорости на одну единицу за одну единицу времени.

Движение по прямой и ускорение

Здесь v0 — некоторая начальная скорость тела, которая может быть также равна нулю, l — пройденный телом путь к моменту времени t. Знак + говорит об ускорении тела, знак — — о его торможении. Важно запомнить, что время t при использовании записанных формул начинает отсчитываться от момента появления у тела постоянного ускорения a. С учетом записанных равенств, формулы модуля ускорения тела принимают вид:

Полное ускорение и его компоненты при движении тела по кривой

В случае перемещения тела по криволинейной траектории, величину a удобно представить в виде двух взаимно перпендикулярных составляющих. Они называются тангенциальным at и нормальным an ускорениями. Для такого случая формула модуля ускорения точки принимает вид:

Для полноты информации отметим, что криволинейность траектории перемещения тела является достаточным признаком присутствия ненулевой нормальной составляющей ускорения. При этом величина at может быть равна нулю, что является справедливым для равномерного вращения тел.

Угловое ускорение

Ускорение угловое можно связать с линейной величиной. Делается это с помощью такой формулы:

Важно понимать, что угловое ускорение является удобным способом представления тангенциальной составляющей полного ускорения в случае вращательного движения. Удобство здесь заключается в независимости величины α от расстояния до оси вращения r. В свою очередь, компонента at линейно возрастает при увеличении радиуса кривизны r.

Пример решения задачи

Необходимо определить тангенциальное, нормальное, полное и угловое ускорения в момент времени 3 секунды.

at = dv/dt = 6*t + 6*t2 = 6*3 + 6*9 = 76 м/с2.

Отметим, что это очень большое ускорение по сравнению с ускорением свободного падения (9,81 м/с2).

Нормальная компонента вычисляется так:

an = v2/r = 1/r*(2 + 3*t2 + 2*t3)2 = 1/0,2*(2+27+54)2 = 34445 м/c2.

Теперь можно рассчитать полное ускорение. Оно будет равно:

a = √(at2 + an2) = √(76 2 + 34445 2) = 34445,1 м/с2.

То есть, полное ускорение практически полностью образовано нормальной компонентой.

Наконец, ускорение угловое определяется по формуле:

α = at/r = 76/0,2 = 380 рад/с2.

Источник

В этой статье мы узнаем, как найти ускорение на графике скорости от времени, используя несколько примеров, и решим некоторые задачи.

Ускорение — это разность скоростей, изменяющаяся во времени; следовательно, по графику скорость-время мы можем найти ускорение, измерив наклон графика.

График скорости во времени для положительного ускорения

Давайте посмотрим, как найти ускорение по графику скорость-время. Ниже приводится график зависимости скорости от времени.

как найти ускорение на графике скорость-время

График зависимости скорости от времени для положительного ускорения

По оси x отложено время в секундах, а по оси y отложена скорость объекта в разное время. Наклон графика определяется выражением m=Δy/Δt. Здесь наклон графика скорость-время дает ускорение объекта.

а = м = ΔV/ΔT = v₂-v₁/t₂-t₁

Из приведенного выше графика ускорение будет положительным, если V₂>V₁ то есть, если скорость объекта увеличивается со временем. То же самое будет отрицательным, если V₂<V₁, то есть если скорость объекта уменьшается со временем. Это тот случай, когда объект замедляется. Так и в том случае, даже когда объект движется в противоположном направлении от направления его движения.

Подробнее о Как найти ускорение с постоянной скоростью: факты и примеры задач.

1 задачи: Рассмотрим объект круглой формы, покоящийся на вершине холма. К объекту прикладывают силу, чтобы сместить его с места. При приложении силы объект ускоряется вниз к подножию холма. Скорость объекта увеличивается до 4 м/с после прохождения расстояния 16 метров. Постройте график для того же, а затем рассчитайте ускорение объекта, учитывая начальную скорость объекта 2 м/с в определенный момент времени.

Решение: Изменение скорости объекта определяется как.

Скорость, равная 4 м/с, наблюдалась после того, как объект прошел расстояние 16 метров. Следовательно, время, затрачиваемое на перемещение 16 м и ускорение тела, равно

2м/с=16м/т

t=16м/2м/с=8с

Следовательно, скорость объекта в момент времени t = 8 секунд была 4 м/с. Теперь мы можем построить график для того же, что и ниже.

График скорости-времени

Судя по графику, скорость v₁=2 м/с при t₁=4 сек и скорость v₂=4 м/с при t₁=8 сек.

Следовательно, ускорение объекта между временными интервалами от 4 до 8 секунд равно

а = v₂-v₁/t₂-t₁ = 4-2/8-4 = 2/4 = 1/2 = 0.5 м/с²

Ускорение тела равно 0.5 м/с.².

График зависимости скорости от времени для нулевого ускорения

Приведенный ниже график показывает, что скорость объекта не меняется со временем и остается постоянной. Это означает, что между этими интервалами времени ускорения объекта не было.

График зависимости скорости от времени для Постоянная скорость

Приведенный выше график показывает, что скорость объекта остается неизменной все время, поэтому мы получаем прямую линию на графике зависимости скорости от времени. Это ясно указывает на то, что в этом случае график зависимости скорости от времени не дает наклона. Поскольку наклон графика отсутствует, ускорение, равное наклону, равно нулю.

Это означает, что перемещение объекта одинаково для разных интервалов времени, следовательно, скорость постоянна.

2 задачи:Скорость объекта, движущегося по плоской поверхности, оказалась равной 0.5 м/с. Через 5 минут другой наблюдатель обнаружил, что скорость равна 0.5 м/с. Тогда каково ускорение объекта на основе наблюдения?

Решение: V₁=0.5 м/с; В₂=0.5 м/с, временной интервал t=5 минут=300 секунд.

а=в₂-v₁/t₂-t₁= 0.5-0.5/300 =0

Поскольку изменений скорости объекта не наблюдалось, ускорение объекта равно нулю.

Подробнее о ускорение.

График зависимости скорости от времени для отрицательного ускорения

Если объект замедляется со временем, то наклон графика скорость-время будет отрицательным. Это показано на приведенном ниже графике зависимости скорости от времени.

График зависимости скорости от времени для отрицательного ускорения

Поскольку разница между конечной и начальной рассматриваемой точкой по оси ординат отрицательна, наклон графика ускорения объекта будет отрицательным.

3 задачи: Рассмотрим объект, замедляющийся со временем, как показано на графике ниже.

График скорости-времени

Вычислите ускорение тела на пути от А до В.

Решение: Скорость объекта в точке А в момент времени t₁= 2 секунды v₁=10 м/с и в момент времени t₂= 5 секунд v₂=4м/с. Поэтому ускорение тела равно

а = v₂-v₁/t₂-t₁ = 4-10/5-2= -6/3= -2m/s²

Поскольку скорость объекта со временем уменьшается, ускорение объекта отрицательно и равно -2 м/с.².

Подробнее о График постоянного отрицательного ускорения: что, как, примеры.

График отрицательной скорости для отрицательного ускорения

Когда объект удаляется от точки назначения по отрицательной оси, смещение объекта принимается как отрицательное по отрицательной оси Y. Если положение объекта отклоняется от направления его движения, то считается, что смещение объекта происходит в отрицательном направлении.

Отрицательная скорость В/с График времени

Выше приведен график зависимости скорости от времени для отрицательного ускорения. Видно, что скорость со временем уменьшается, наклон графика оказывается отрицательным, а значит, и ускорение отрицательное.

График отрицательной скорости во времени для положительного ускорения

Ниже приведен график зависимости отрицательной скорости от времени в секунду, который дает положительное ускорение.

Отрицательный график зависимости скорости от времени

Поскольку замедляющийся объект однажды начинает ускоряться обратно за счет какого-то внешнего силы, то ускорение, равное наклону График зависимости скорости от времени положителен, потому что скорость объекта продолжает расти со временем.

Подробнее о Отрицательная скорость и нулевое ускорение: как, когда, пример и проблемы.

Часто задаваемые вопросы

Q1. Из приведенного ниже графика вычислите ускорение объекта из точки О в А, из А в В и из В в С; а затем вычислить среднее ускорение объекта от O до C.

График скорости-времени

Решение: От О до А, v₁=0 при t₁=0; в₂=8 м/с при t₂= 4s

Следовательно, ускорение тела из точки О в точку А равно

а = v₂-v₁/t₂-t₁=8-0/4-0=8/4=2m/s²

От А до Б, в₁=8 м/с при t₁=4с; в₂=5 м/с при t₂= 8s

Следовательно, ускорение тела из точки А в точку В равно

а=в₂-v₁/t₂-t₁=5-8/8-4=-3/4=-0.75m/s²

От B до C, v₁=5 м/с при t₁=8с; в₂=5 м/с при t₂= 12s

Следовательно, ускорение тела из точки В в С равно

а=в₂-v₁/t₂-t₁=5-5/12-8=0/4=0

Среднее ускорение графика от O до C равно

A_{средний}= a_oa+a_ab+a_bc/3

=2-0.75+0/3=1.25/3=0.42m/s²

Следовательно, среднее ускорение тела от О до А равно 0.42 м/с.².

Почему ускорение является векторной величиной?

Ускорение имеет величину и направление.

Направление ускорения такое же, как и направление скорости после изменения; следовательно, это векторная величина.

Источник

Равноускоренное прямолинейное движение — движение по прямой линии с постоянным ускорением (a=const).
Ускорение — векторная физическая величина, показывающая изменение скорости тела за 1 с. Обозначается как a.
Единица измерения ускорения — метр в секунду в квадрате (м/с²).
Акселерометр — прибор для измерения ускорения.

Формула ускорения

Ускорение тела равно отношению изменения вектора скорости ко времени, в течение которого это изменение произошло:

v — скорость тела в данный момент времени, v₀ — скорость тела в начальный момент времени, t — время, в течение которого изменялась скорость

Пример №1. Состав тронулся с места и через 20 секунд достиг скорости 36 км/ч. Найти ускорение его разгона.

Сначала согласуем единицы измерения. Для этого переведем скорость в м/с: умножим километры на 1000 и поделим на 3600 (столько секунд содержится в 1 часе). Получим 10 м/с.

Начальная скорость состава равно 0 м/с, так как изначально он стоял на месте. Имея все данные, можем подставить их в формулу и найти ускорение:

Проекция ускорения

Проекция ускорения на ось ОХ

v_x — проекция скорости тела в данный момент времени, v_0x — проекция скорости в начальный момент времени, t — время, в течение которого изменялась скорость

Знак проекции ускорения зависит от того, в какую сторону направлен вектор ускорения относительно оси ОХ:

Если вектор ускорения направлен в сторону оси ОХ, то его проекция положительна.
Если вектор ускорения направлен в сторону, противоположную направлению оси ОХ, его проекция отрицательная.

При решении задач на тему равноускоренного прямолинейного движения проекции величин можно записывать без нижнего индекса, так как при движении по прямой тело изменяет положение относительно только одной оси (ОХ). Их обязательно нужно записывать, когда движение описывается относительно двух и более осей.

Направление вектора ускорения

Направление вектора ускорения не всегда совпадает с направлением вектора скорости!

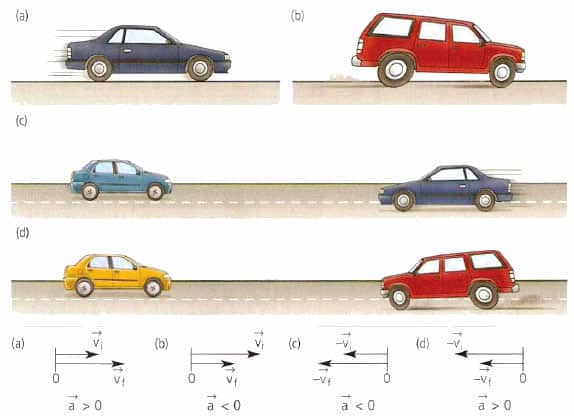
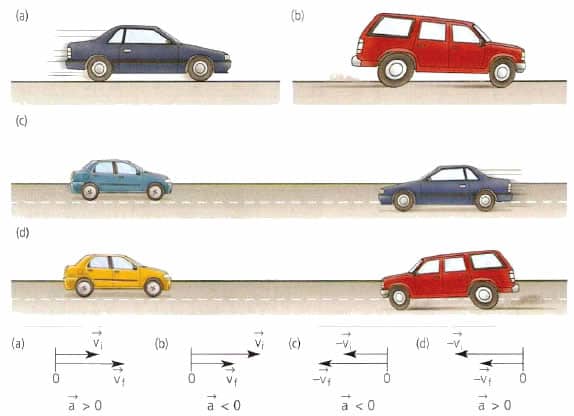
Равноускоренным движением называют такое движение, при котором скорость за одинаковые промежутки времени изменяется на одну и ту же величину. При этом направления векторов скорости и ускорения тела совпадают (а↑↑v).

Равнозамедленное движение — частный случай равноускоренного движения, при котором скорость за одинаковые промежутки времени уменьшается на одну и ту же величину. При этом направления векторов скорости и ускорения тела противоположны друг другу (а↑↓v).

Пример №2. Автомобиль сначала разогнался, а затем затормозил. Во время разгона направления векторов его скорости и ускорения совпадают, так как скорость увеличивается. Но при торможении скорость уменьшается, потому что вектор ускорения изменил свое направление в противоположную сторону.

График ускорения

График ускорения — график зависимости проекции ускорения от времени. Проекция ускорения при равноускоренном прямолинейном движении не изменяется (a_x=const). Графиком ускорения при равноускоренном прямолинейном движении является прямая линия, параллельная оси времени.

Зависимость положения графика проекции ускорения относительно оси ОХ от направления вектора ускорения:

Если график лежит выше оси времени, движение равноускоренное (направление вектора ускорения совпадает с направлением оси ОХ). На рисунке выше тело 1 движется равноускорено.
Если график лежит ниже оси времени, движение равнозамедленное (вектор ускорения направлен противоположно оси ОХ). На рисунке выше тело 2 движется равнозамедлено.

Если график ускорения лежит на оси времени, движение равномерное, так как ускорение равно 0. Скорость в этом случае — величина постоянная.

Чтобы сравнить модули ускорений по графикам, нужно сравнить степень их удаленности от оси времени независимо от того, лежат они выше или ниже нее. Чем дальше от оси находится график, тем больше его модуль. На рисунке график 2 находится дальше от оси времени по сравнению с графиком один. Поэтому модуль ускорения тела 2 больше модуля ускорения тела 1.

Пример №3. По графику проекции ускорения найти участок, на котором тело двигалось равноускорено. Определить ускорение в момент времени t₁= 1 и t₂= 3 с.

В промежуток времени от 0 до 1 секунды график ускорения рос, с 1 до 2 секунд — не менялся, а с 2 до 4 секунд — опускался. Так как при равноускоренном движении ускорение должно оставаться постоянным, ему соответствует второй участок (с 1 по 2 секунду).

Чтобы найти ускорение в момент времени t, нужно мысленно провести перпендикулярную прямую через точку, соответствующую времени t. От точки пересечения с графиком нужно мысленно провести перпендикуляр к оси проекции ускорения. Значение точки, в которой пересечется перпендикуляр с этой осью, покажет ускорение в момент времени t.

В момент времени t₁= 1с ускорение a = 2 м/с². В момент времени t₂= 3 ускорение a = 0 м/с².

Задание EF18774

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения

Определить, какому типу движения соответствует график зависимости координаты тела от времени.
Определить величины, которые характеризуют такое движение.
Определить характер изменения величин, характеризующих это движение.
Установить соответствие между графиками А и Б и величинами, характеризующими движение.

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

перемещение и путь;
скорость;
ускорение.

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

Ответ: 24

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17992

Начальная скорость автомобиля, движущегося прямолинейно и равноускоренно, равна 5 м/с. После прохождения расстояния 40 м его скорость оказалась равной 15 м/c. Чему равно ускорение автомобиля?

Алгоритм решения

Записать исходные данные.
Записать формулу, связывающую известные из условия задачи величины.
Выразить из формулы искомую величину.
Вычислить искомую величину, подставив в формулу исходные данные.

Решение

Запишем исходные данные:

Начальная скорость v₀ = 5 м/с.
Конечная скорость v = 15 м/с.
Пройденный путь s = 40 м.

Формула, которая связывает ускорение тела с пройденным путем:

Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».

Выразим из формулы ускорение:

Подставим известные данные и вычислим ускорение автомобиля:

Ответ: 2,5

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18202

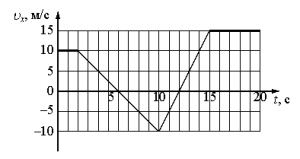
Внимательно прочитайте текст задания и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела v_x от времени.

Какой из указанных ниже графиков совпадает с графиком зависимости от времени проекции ускорения этого тела a_x в интервале времени от 6 с до 10 с?

Алгоритм решения

Охарактеризовать движение тела на участке графика, обозначенном в условии задачи.
Вычислить ускорение движение тела на этом участке.
Выбрать график, который соответствует графику зависимости от времени проекции ускорения тела.

Решение

Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.

Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:

t₁ = 6 с. Этой точке соответствует скорость v₁ = 0 м/с.
t₂ = 10 с. Этой точке соответствует скорость v₂ = –10 м/с.

Используем для вычислений следующую формулу:

Подставим в нее известные данные и сделаем вычисления:

Этому значению соответствует график «г».

Ответ: г

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18027

На графике приведена зависимость проекции скорости тела от времени при прямолинейном движении по оси х. Определите модуль ускорения тела.

Алгоритм решения

Записать формулу ускорения.
Записать формулу для вычисления модуля ускорения.
Выбрать любые 2 точки графика.
Определить для этих точек значения времени и проекции скорости (получить исходные данные).
Подставить данные формулу и вычислить ускорение.

Решение

Записываем формулу ускорения:

По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:

Выбираем любые 2 точки графика. Пусть это будут:

t₁ = 1 с. Этой точке соответствует скорость v₁ = 15 м/с.
t₂ = 2 с. Этой точке соответствует скорость v₂ = 5 м/с.

Подставляем данные формулу и вычисляем модуль ускорения:

Ответ: 10

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 13.9k

Источник

Что такое ускорение?

a = dv/dt.

a = (v₂ — v₁)/(t₂ — t₁).

Где v₂ и v₁— скорости в моменты времени t₂ и t₁ соответственно.

Единицами измерения изучаемой физической величины являются метры в квадратную секунду (м/с²). Многих может смутить возведение во вторую степень единиц времени, тем не менее, понять смысл единицы м/с² несложно, если ее представить в виде [м/с]/с. Последняя запись означает изменение скорости на одну единицу за одну единицу времени.

Движение по прямой и ускорение

v = v₀±a*t;

l = v₀*t±a*t²/2.

Здесь v₀ — некоторая начальная скорость тела, которая может быть также равна нулю, l — пройденный телом путь к моменту времени t. Знак + говорит об ускорении тела, знак — — о его торможении. Важно запомнить, что время t при использовании записанных формул начинает отсчитываться от момента появления у тела постоянного ускорения a. С учетом записанных равенств, формулы модуля ускорения тела принимают вид:

±a = (v — v₀)/t;

±a = 2*(l — v₀*t)/t².

Полное ускорение и его компоненты при движении тела по кривой

a = √(a_t² + a_n²).

a_n = v²/r.

Угловое ускорение

α = dω/dt.

Ускорение угловое можно связать с линейной величиной. Делается это с помощью такой формулы:

α = a_t/r.

Пример решения задачи

v = 2 + 3*t² + 2*t³.

Необходимо определить тангенциальное, нормальное, полное и угловое ускорения в момент времени 3 секунды.

a_t = dv/dt = 6*t + 6*t² = 6*3 + 6*9 = 76 м/с².

Отметим, что это очень большое ускорение по сравнению с ускорением свободного падения (9,81 м/с²).

Нормальная компонента вычисляется так:

a_n = v²/r = 1/r*(2 + 3*t² + 2*t³)² = 1/0,2*(2+27+54)² = 34445 м/c².

Теперь можно рассчитать полное ускорение. Оно будет равно:

a = √(a_t² + a_n²) = √(76 ² + 34445 ²) = 34445,1 м/с².

То есть, полное ускорение практически полностью образовано нормальной компонентой.

Наконец, ускорение угловое определяется по формуле:

α = a_t/r = 76/0,2 = 380 рад/с².

Источник

Задача. Определите наибольшие значения модулей (амплитуду) скорости $displaystyle {{a}_{max }}$ и ускорения колеблющейся материальной точки, если амплитуда её колебаний см, а период колебаний displaystyle T=2,0 с.

Решение

Думаем: будем считать колебания гармоническими (мы других не знаем), тогда

$displaystyle {{upsilon }_{max }}=Aomega$ (1)

$displaystyle {{a}_{max }}=A{{omega }^{2}}$ (2)

где displaystyle omega — циклическая частота колебаний. Её можно найти исходя из нашего последнего неиспользованного дано:

$displaystyle omega =frac{2pi }{T}$ (3)

Решаем: подставим (3) в (1) и в (2)

$displaystyle {{upsilon }_{max }}=Afrac{2pi }{T}$ (4)

$displaystyle {{a}_{max }}=A{{left( frac{2pi }{T} right)}^{2}}=Afrac{4{{pi }^{2}}}{{{T}^{2}}}$ (5)

Считаем: обязательный перевод амплитуды в единицы СИ ( $displaystyle =8,0*{{10}^{-2}}$ см м. Также вспомним о константе displaystyle pi approx 3,14 . Исходя из (4):

$displaystyle {{upsilon }_{max }}=8,0*{{10}^{-2}}*frac{2*3,14}{2,0}=25,1*{{10}^{-2}}$ м/с

$displaystyle ^{2}$ м/с $displaystyle ^{2}$

Ответ: $displaystyle {{a}_{max }}=78,9*{{10}^{-2}}$ м/с, $displaystyle ^{2}$ м/с $displaystyle ^{2}$ .

Ещё задачи на тему «Уравнение гармонических колебаний».

Источник