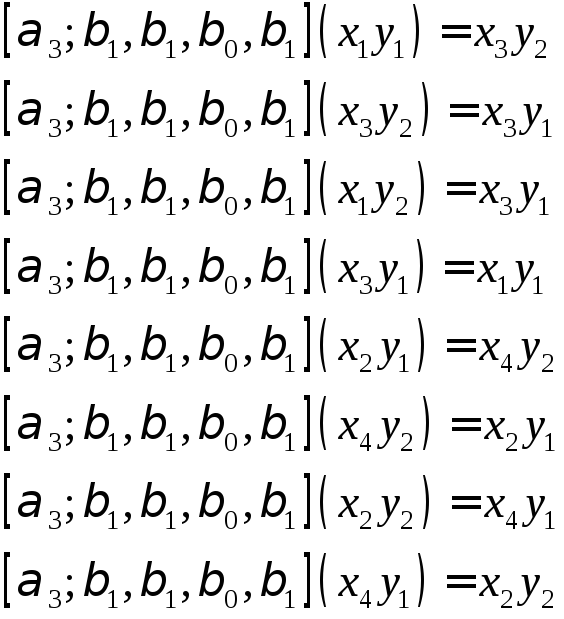Внутренняя устойчивость графа
Подмножество
вершин графа называется внутренне
устойчивым, если они попарно несмежны
между собой. Внутренне устойчивое
множество вершин называетсяпустым
подграфом, если при добавлении хотя
бы одной вершины свойство внутренней
устойчивости пропадает.
Пример
|
|
|
Мощность максимального
пустого подграфа называется числом
внутренней устойчивости графа.
Пусть
— некоторый граф,
— некоторая вершина,
— окрестность вершины
.
Неокрестность (коокрестность) вершиныграфа
обозначим
— подграф графа
,
порожденный.
ТеоремаПустой
подграф, содержащий вершинусодержит по крайней мере одну вершину
из коокрестности вершины.
Алгоритм нахождения пустых подграфов
Начальный шаг:строится вершина – корень дерева,
которой сопоставляется граф.Итерационный
шаг:на-ом
ярусе есть вершина, которой сопоставлен
граф.
а)
Извыбирается любая вершина
и выносится на
ярус.
б) Наярус выносятся все вершины, которые
входят в.
в)
Каждая из вершиняруса взвешивается соответствующим
графом – коокрестностью от графа.Заключительный
шаг:вершина дерева будет висячей,
если соответствующий ей граф – пустой
граф.Замечание
В пункте
а) желательно выбирать ту вершину,
которая имеет минимальную степень.
Пример
|
|
|
Полные подграфы. Плотность графа
Пусть
— некоторый граф. Максимальный по
включению вершин подграф графа, любые
две вершины которого смежны называетсяполным подграфом. Мощность
максимального полного подграфа называетсяплотностью графа.
Алгоритм нахождения полных подграфов
Начальный шаг:строится вершина – корень дерева,
которой сопоставляется граф.Итерационный
шаг:на-ом
ярусе есть вершина, которой сопоставлен
граф.
а)
Извыбирается любая вершина
и выносится на
ярус.
б) Наярус выносятся все вершины, которые
входят в.
в)
Каждая из вершиняруса взвешивается соответствующим
графом – окрестностью от графа.Заключительный
шаг:вершина дерева будет висячей,
если соответствующий ей граф – пустой
граф.Замечание
В пункте
а) желательно выбирать ту вершину,
которая имеет максимальную степень.
Задачу нахождения
полных подграфов в
можно свести к задаче нахождения пустых
подграфов в.
Пример
|
|
|
Полные подграфы
графа
(или пустые подграфы графа
):
Пример
|
|
Пример
|
|
|
Выделяем пустые
подграфы:
|
|
|
Реберные
графы.
Графы со свойством реберности
Пусть
— некоторый граф. Назовем граф
реберным графом
,
если носитель графасовпадает с множеством ребер графа
,
и две вершины всмежны, если соответствующие ребра
смежны в
.
Пример
|
(это |
Граф
обладает свойством реберности, если
существует некоторый граф, реберный
для которого является изоморфным для.
Пример
|
|
ТеоремаГрафобладает свойством реберности, если
существует разложение ребер графа на
полные подграфы такое, что каждая вершина
графа принадлежит не более чем двум
полным подграфам.
Замечание1.
Не для любого графа существует такое
разложение ребер.
2. В разложении ребер
каждое ребро принадлежит ровно одному
подграфу.
Пример
|
|
|
Пример
|
|
|
|
не |
Если граф обладает
свойством реберности, то как найти его
образ (т.е. граф, для которого данный
является реберным)?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример
:
:
Пример
|
|
|
|
Укладки графа.
Планарность
Исследуются
топологические свойства графа.
Гомеоморфизм графов– еще одно
отношение эквивалентности на графах.
Два графаи
гомеоморфны, если они изоморфны с
точностью до цепей степени 2.
Пример
|
|
|
|
Гомеоморфны. |
Пусть
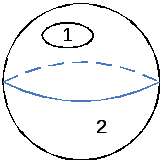
— некоторая поверхность.Род поверхности
— это максимальное число простых замкнутых
кривых, не разделяющих эту поверхность.
|
Род |
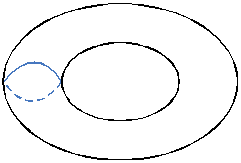
|
|
Род |
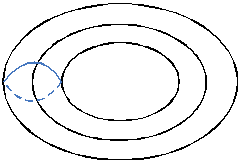
|
|
Род |
|
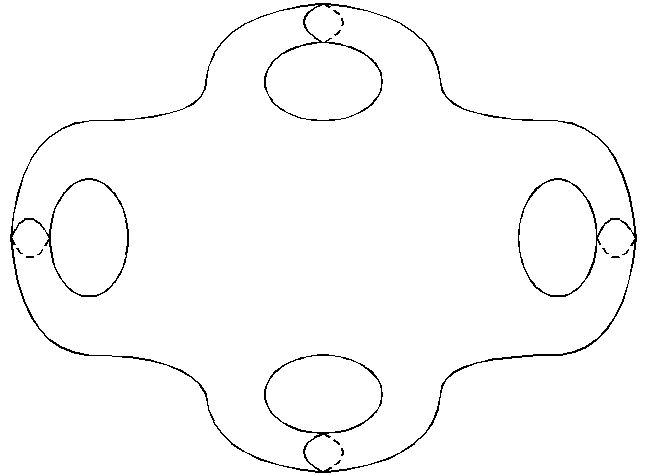
Поверхности,
которые имеют род 4:
Род графа
—
— минимальный род поверхности, на которой
можно «уложить» графбез взаимных пересечений ребер (ребра
пересекаются только в вершинах).
Пример
Граф
называетсяпланарным (плоским),
если.
-
печатные платы –
планарные графы; -
микросхемы (на
уровне технологии их изготовления) –
планарные графы.
Критерий
планарности графа (критерий
Понтрягина-Куратовского)
Граф планарен
тогда и только тогда, когда в нем
отсутствуют подграфы, гомеоморфные
или
.
|
|
|
Алгоритм приведения
графа
к планарному
1) Найти все подграф,
гомеоморфные
и
.
2)
Построить таблицу покрытия найденных
в п.1 подграфов ребрами, которые их
образуют.
3) Найти минимальное покрытие
подграфов ребрами (удалив ребра,
образующие покрытие, получим планарный
граф).
Раскраска графов
Пусть
— некоторый граф и
— разбиение
на
внутренне устойчивых множеств (разбиение
означает, что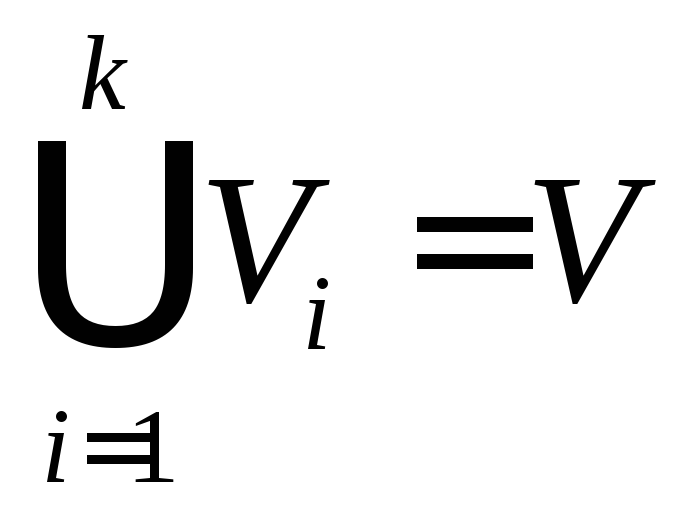
,
если).
В этом случае говорят, чтовершины
графа допускают раскраску в
цветов(цвета по номерам
).Хроматическое число
— минимальное значение
,
которое допускает раскраску графа.
Хроматическое
число пустого графа равно 1.
Хроматическое
число
.
Хроматическое
число.
Алгоритм нахождения
раскраски (хроматического числа)
1) Выделить все
пустые подграфы графа.
2) Построить
таблицу покрытий вершин графа пустыми
подграфами.
3) Найти минимальное
покрытие вершин графа пустыми подграфами
(мощность минимального покрытия – это
,
а само покрытие определяет раскраску).
Пример
|
|
|
|
|
Оценки хроматического
числа
1.
Теорема
Кенига
Граф бихроматичен ()
тогда и только тогда, когда внет циклов нечетной длины.
2.Теорема
,
где— плотность графа
.
3.Теорема
,
где— степень графа
.
4.Оценка
Бержа
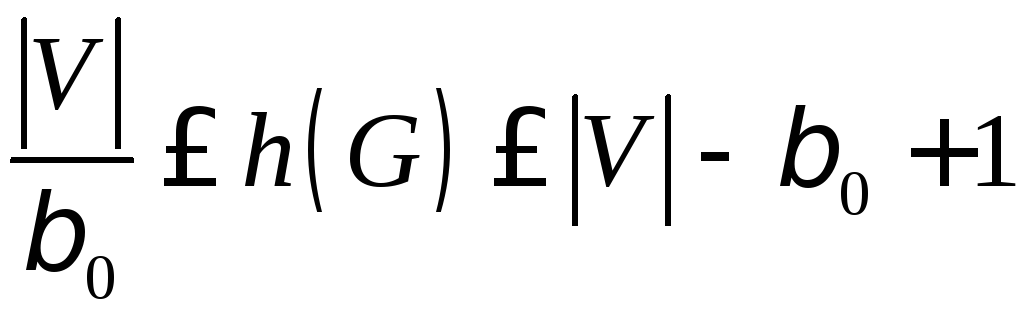
где— число внешней устойчивости графа
.
5.
Теорема
,
где,
.
,
где,
.
,
где,
.
,
где.
Примеры
а) Графы не имеют
общих вершин.
По теореме выше
.
б)
Графы имеют по одной общей вершине.
Отметим
для нечетного цикла следующую раскраску:
одна вершина в 3-й цвет, остальные в 1-й
и 2-й цвета поочередно. На нашем графе
вначале раскрасим в два цвета четный
цикл (вместе с общей вершиной). Теперь
рассмотрим нечетный цикл. В нем общая
вершина оказалась закрашена каким-то
цветом. Считаем этот цвет 3-им и закрашиваем
все остальные вершины поочередно в два
цвета (отличные от ранее выбранных, так
как имеем граф суммы). Итого использовали
четыре цвета..
в)
Графы имеют по две общие, не смежные
между собой вершины.
Так как между
двумя смежными вершинами в обоих графах
будет располагаться цепь длиной, по
крайней мере,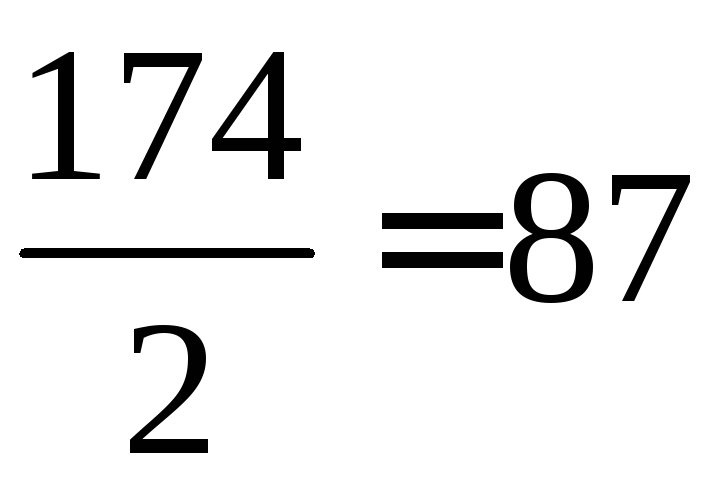
соединенная с аналогичной цепью в другой
части графа всеми возможными связями,
то.
Для четырех цветов раскраска существует
всегда: сначала раскрашиваем четный
цикл в два цвета, затем оставшиеся цепи
нечетного цикла закрашиваем в другие
два цвета..
Алгоритм
приближенной раскраски графа (алгоритм
Ершова)
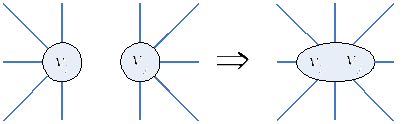
Алгоритм основан
на стягивании несмежных вершин:
Стягивание проводить
до тех пор, пока не получим полный граф.
Мощность этого полного графа является
оценкой хроматического числа сверху,
а сам полный граф определяет приближенную
раскраску графа.
ЗамечаниеВ
первую очередь желательно стягивать
те вершины, расстояние между которыми
четно.
Пример
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача
Есть
3 предприятия, на которых должны
выпускаться 11 изделий. Каждый тип изделий
должен выпускаться только на одном
предприятии. При выпуске изделий разного
типа ()
могут использоваться общие детали и
материалы. Для каждой пары изделий
указан процент общих деталей и материалов.
Необходимо распределить изделия по
предприятиям так, чтобы на одном
предприятии выпускались детали с
наибольшим процентом общих деталей.Критерий: Минимум общих поставок
для изделий, выпускаемых на одном
предприятии был как можно больше.
|
|
||||||||||
|
|
55 |
|
||||||||
|
|
60 |
80 |
|
|||||||
|
|
85 |
65 |
40 |
|
||||||
|
|
45 |
90 |
35 |
80 |
|
|||||
|
|
80 |
75 |
30 |
90 |
90 |
|
||||
|
|
50 |
30 |
70 |
35 |
65 |
30 |
|
|||
|
|
50 |
60 |
90 |
40 |
35 |
70 |
30 |
|
||
|
|
60 |
45 |
40 |
80 |
30 |
70 |
20 |
25 |
|
|
|
|
45 |
40 |
45 |
35 |
80 |
20 |
90 |
25 |
85 |
|
|
|
80 |
70 |
85 |
30 |
35 |
40 |
25 |
75 |
75 |
60 |
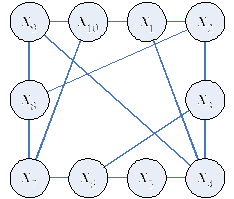
Граф несовместимости
изделий
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Перечисление
графов
Группа. Группа
подстановки
Группа–
алгебра с одно бинарной операцией (),
которая обладает следующими свойствами:
1) замкнутость
и
2)
ассоциативность3)
наличие нейтрального элемента4)
существование обратного элемента
для
Группа подстановки.Пусть.
Подстановкой назовем.


|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Операция:
произведение подстановок
Пример
Пример
Группа автоморфизмов
графа
Пусть
— некоторый граф.Автоморфизм графа
— это изоморфизм на себя (с, сохраняющая
отношение смежности между вершинами
графа).
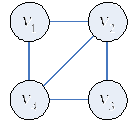
Пример
— не является
автоморфизмом.
— автоморфизм.
Группа автоморфизмов
графа
—
,
где— множество всех автоморфизмов графа,
— операция произведения.
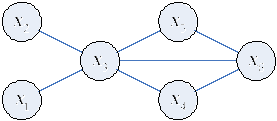
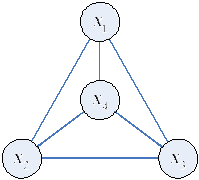
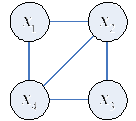
Пример
:
Пример
|
|
|
|
Пример |
|
Задание
Задан автоморфизм.
Определить все графы, которые допускают
данный автоморфизм.
|
|
|
|
|
|
Операции над
группами
Пусть даны группы
автоморфизмов
,
.
— порядок группы
,
— порядок группы
.
Группадействует на множестве
.
Группадействует на множестве
(
).
— степень группы
.
— степень группы
.
Рассмотрим три операции над группами:
-
Сложение
(объединение) групп – «».
-
Умножение групп
– «».
-
Композиция групп
– «».
Рассмотрение
проведем на примере:
|
|
|
-
Сложение
групп.
действует на
Степень
равна
,
порядокравен
.Пример
-
Произведение
групп
действует на
Степень
равна
,
порядокравен
.Пример
-
Композиция
групп
Действует
на.
Степень
равна
,
порядокравен
.
63
Document from www.cyberfac.ru
Соседние файлы в предмете Дискретная математика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- Авторы
- Резюме
- Файлы
- Ключевые слова
- Литература
Попов С.В.
1
1 ООО «Научно-внедренческая фирма БП+»
Практическая значимость комбинаторных задач связана с развитием искусственного интеллекта, который из теоретической области переместился в востребованную практическую сферу. Большое число интеллектуальных задач достаточно естественно переформулируются на языке графов, и для их решения требуется использование теоретико-графовых методов. В частности, большое число задач по описанию разнообразных предметных областей сводится к так называемым графам ортогональности, которые очень естественно позволяют описывать различные соотношения объектов предметной области. В свою очередь для исследования графов ортогональности необходимо проводить исследование совокупностей их максимальных пустых подграфов, что требует достаточно эффективной процедуры порождения последних. При этом должны учитываться определенные условия, которым должны удовлетворять пустые подграфы. Как правило, условия суть следствия, вытекающие из содержательных ограничений на объекты предметной области. Поэтому актуальным представляется создание процедуры порождения в определенном смысле полной совокупности пустых подграфов по заданному графу ортогональности, которая позволила бы учитывать содержательные особенности предметной области. К последним следует отнести в первую очередь отношение близости объектов, которое позволяет существенно снижать перебор при порождении пустых подграфов. В статье представлен теоретический базис такой процедуры, порождающей полную совокупность максимальных пустых подграфов заданного графа ортогональности, и краткое ее описание. Процедура получает на входе матрицу смежности графа, реализована на языке С++ и показала неплохие результаты при порождении объектов предметной области, заданной графом ортогональности. Отличительной ее особенностью является возможность учитывать различные соотношения локальности объектов предметной области, что существенно ускоряет работу.
комбинаторика
графы
предметные области
пустые подграфы
векторы
порождение пустых графов
1. Хопкрофт Д., Мотвани Р., Ульман Д. Введение в теорию автоматов, языков и вычислений. М.: Вильямс, 2012. 528 с.
2. F?redi Zolt?n. The number of maximal independent sets in connected graphs. Journal of Graph Theory. 2014. Vol. 19, no. 4. P. 463–470.
3. Попов С.В., Синтез предметных областей. Решение одного класса переборных задач. LAP LAMBERT Academic Publishing. 2017. 96 с.
4. Гашков С.Б. Графы-расширители и их применения в теории кодирования. М: МЦНМО, 2009. С. 70–122
5. Зыков А.А. Основы теории графов. М: Вузовская книга, 2012. 664 с.
Для большого числа прикладных задач, сводящихся к задачам на графах, интерес представляет исследование пустых подграфов [1, 2]. Особенно это важно при принятии решений в сложных предметных областях. Поэтому эффективная процедура построения всех нетривиальных пустых подграфов, удовлетворяющих определенным требованиям, представляется актуальной. Исходя из этого, в статье введена система преобразований графов и, в конечном итоге, – предложена процедура построения всех искомых пустых подграфов. Идея процедуры построения пустых подграфов выглядит так. Мы последовательно рассматриваем подграфы исходного графа, увеличивая их сложность и определяя для каждого пустые подграфы с искомыми свойствами. Процедура полна, поэтому по окончании работы выдаются все нетривиальные пустые подграфы.
Будем представлять пустые подграфы исходного графа, используя следующие признаки его узлов: узел входит в пустой подграф, узел не входит в пустой подграф и неизвестно, входит ли узел в пустой подграф. Причина возникновения последнего параметра такова. Решаемая здесь задача состоит в построении пустых подграфов, для которых выполняются определенные ограничения (например, на нижнюю оценку числа узлов). Построение осуществляется, переходя от подграфов меньшей сложности к подграфам с большей сложностью. В этом случае возможна ситуация, когда для некоторых подграфов непонятно, принадлежит ли конкретный узел его пустому подграфу, если факт принадлежности или непринадлежности можно установить лишь в последующем. Именно в этом случае используется термин неопределённость относительно вхождения конкретного узла.
Цель статьи: привести теоретический базис процедуры порождения полной совокупности максимальных пустых подграфов по заданному графу ортогональности.
1. Векторное представление графов. Построение максимальных пустых подграфов осуществляем относительно подграфов исходного графа ортогональности [3]. В частности, пусть G1 есть подграф графа G. Тогда пустой граф G’1⊆G1 называется максимальным в G1, если невозможно расширить множество его узлов за счет узлов только графа G1. Если G’1⊆G1 есть максимальный пустой подграф, то часть узлов G1 принадлежит G’1, а оставшиеся – не принадлежат. Принадлежность узлов подграфа G G1 расширению пустого подграфа G’1 характеризуется неопределенностью.
Пусть G’1 есть максимальный пустой подграф графа G1⊆G, N1 – есть множество узлов G’1, N0 – узлы подграфа G1 G’1. Обозначим N_ – множество узлов графа G, которые не входят в G1. Очевидно, что каждый узел из N0 смежный хотя бы с одним узлом из N1, и каждый узел из N1 смежный хотя бы с одним узлом из N0.
Пусть G1 и G2 суть подграфы графа G, и G1∪G2 есть их объединение, включающее ребра только этих подграфов. В исходном графе G могут встречаться ребра, инцидентные одновременно узлам G1 и G2, но в объединение G1∪G2 они не включены. Тем самым объединение G1∪G2 не расширяет множества ребер графов G1 и G2.
Пусть G’1⊆G1⊆G и G’2⊆G2⊆ G – максимальные пустые подграфы. Опишем максимальный в G1∪G2 пустой подграф, который есть подграф объединения G’1∪G’2. В него не включены узлы, которые не принадлежит хотя бы одному из подграфов G’1 или G’2. Таким образом, результирующему пустому подграфу принадлежат лишь часть узлов объединения G’1∪G’2, именно те, которые не принадлежат множеству G1G’1∪G2G’2. Тем не менее обозначим результирующий граф, полученный из пустых подграфов G’1 и G’2, как описано выше, также G’1∪G’2.
Распространим операцию ∪ на множества пустых подграфов. Пусть G*1 и G*2 суть множества максимальных пустых подграфов. Тогда G*1∪G*2 = {G1∪G2| G1∈G*1, G2∈G*2}.
Введем векторное обозначение подграфов. Пусть в графе G имеются N узлов, которые перенумерованы числами от 1 до N, и подграф G1⊆ G включает пустой подграф G’. Тогда подграф G’ определяет вектор νG’ = (ν1, ν2, …, νN) длины N, компоненты которого суть <0, 1, _>. Если узлы n1, n2, …, nq принадлежат G’, то в векторе nG’ на соответствующих местах n1, n2, …, nq стоит 1. Эти компоненты вектора nG’ cуть единичные. Если узлы m1, m2, …, ms принадлежат дополнению G1 G’, то в векторе nG’ на соответствующих местах m1, m2, …, ms стоит 0. Эти компоненты вектора nG’ суть нулевые. Иным узлам подграфа G G1 в векторе nG’ соответствуют компоненты «_». Будем называть их не значащими, так как мы не знаем, будут ли входить эти узлы в расширение пустого подграфа G’ по мере расширения графа G1.
Элементы базиса <0, 1, _> упорядочены следующим образом 0 < _, 1 < _. Компоненты 0 и 1 называются ортогональными. Это позволяет ввести лексикографический порядок на множестве векторов: векторы n1 и n2 находятся в отношении n1 < n2 тогда и только тогда, когда каждая пара (n’,n») соответствующих компонентов векторов соответственно n1 и n2 находятся в отношении n’ < n». В этом случае говорим, что вектор n2 поглощает вектор n1.
Введем произведение векторов над базисом <0, 1, _>: произведение ортогональных элементов равно 0, в остальных случаях ν1×ν2 = min(n1,n2). Затем распространим ее на векторы: произведение ν1×ν2 векторов n1 и n2 вычисляется покомпонентным умножением. Теперь распространим операцию×на множества векторов. Если n*1 и n*2 суть два множества векторов, то ν*1×ν*2 = {ν1×ν2| ν1∈ν*1, ν2 ∈ν*2}.
Пример 1. Пусть ν1 = (0, 1, _, 1, _), ν2 = (_, 1, 1, 0, _). Тогда ν1×ν2 = (0, 1, 1, 0, _).
Установим соответствие между операцией объединения пустых подграфов и произведением векторов. Пусть пустые подграфы G’1 и G’2 определяют векторы соответственно ν1 и ν2. Если узел n∈G’1, (компонент νn = 1), а в векторе, определяемом подграфом G’2, компонент νn ≠ 0, то узел n входит в объединение G’1∪G’2. И в векторе, определяемом G’1∪G’2, этому узлу соответствует единичный компонент. Аналогично, если узел n∈G’2 и в векторе 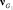
Таким образом, узел входит в объединение G’1∪G’2 подграфов, если он входит хотя бы в один подграф, а в другом отсутствует указание, что он в него не входит. Это обозначает, что единичный компонент, определяемый объединением, появляется лишь в случае, когда в одном векторе соответствующий компонент равен 1, а в другом он не нулевой.
Пример 2. Пусть подграф G’1 определяет вектор (1, 1, 0, _), а G’2 – (_, 0, _, 1). Тогда объединение G’1∪G’2 определяет вектор (1, 0, 0, 1).
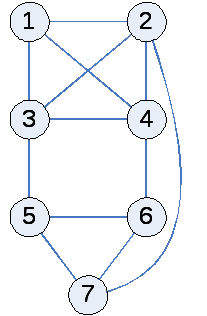
Пример 3. Пусть полный подграф G с узлами 1, 2, 3, 4 является подграфом в графе с 5 узлами и не известно, какие ребра инцидентны узлу 5. Пустые подграфы подграфа G, определяют векторы: (1, 0, 0, 0, _), (0, 1, 0, 0, _), (0, 0, 1, 0, _), (0, 0, 0, 1, _). Здесь пятый компонент есть _, так как не известно отношение инцидентности узла 5. К этим векторам следует добавить вектор (0, 0, 0, 0, _), исходя из того, что узлы 1, 2, 3, 4 могут не входить в пустой подграф, когда в него входит узел 5. Учитывая наличие последнего вектора, можно ввести обобщение: теперь векторы образуют множество (_, 0, 0, 0, _), (0, _, 0, 0, _), (0, 0, _, 0, _), (0, 0, 0, _, _).
Пример 4. Пусть G есть веник с вершиной 1 и висячими узлами 2, 3, 4, имеется еще узел 5, для которого не известно отношение инцидентности. В этом случае пустые подграфы определяют векторы (1, 0, 0, 0, _), (0, _, _, _, _). Во втором векторе первые три не значащих компонента обозначают, что вхождение узлов 2, 3, 4 в пустой подграф определяется не известным отношением инцидентности узла 5.
Пример 5. Пусть два подграфа определяют векторы (0, _, _, 0) и (_, 0, _, _). Это значит, что в первый подграф не входят узлы 1 и 4, а во второй – узел 2. Про остальные узлы расширений этих подграфов ничего сказать нельзя. Тогда (0, _, _, 0)×(_, 0, _, _) = = (0, 0, _, 0). То есть в объединение соответствующих пустых графов не входят узлы 1, 2, 4. Про узел 3 ничего сказать нельзя.
Докажем теорему.
Теорема 1. Пусть подграфы G1, G2, …, Gq графа G, покрывают все его ребра. Каждый из них определяет множество максимальных пустых подграфов, соответственно G*1, G*2, …, G*q. Тогда G*1∪G*2∪ …∪G*q представляет собой множество пустых графов, которое включает все максимальные пустые подграфы графа G.
Доказательство проведем от противного. Допустим, имеется пустой подграф G’, не принадлежащий объединению G*1∪G*2∪ …∪G*q и имеющий непустые вершинные пересечения G’1, G’2, …, G’m, соответственно с графами Gi1, Gi2, …, Gim совокупности G1, G2, …, Gq. Не уменьшая общности, можно считать, что G’1, G’2, …, G’m суть максимальные пустые подграфы соответственно в Gi1, Gi2, …, Gim. Но тогда G’ = G’1∪G’2∪… ∪G’m принадлежит объединению G*1∪G*2∪ …∪G*q. Противоречие. Теорема доказана.
Таким образом, любая полная совокупность подграфов, покрывающая все ребра исходного графа, позволяет получить совокупность всех максимальных пустых подграфов. И для построения совокупности максимальных пустых графов, удовлетворяющих определенным условиям, необходимо выбирать наиболее рациональное покрытие графа подграфами G1, G2, …, Gq.
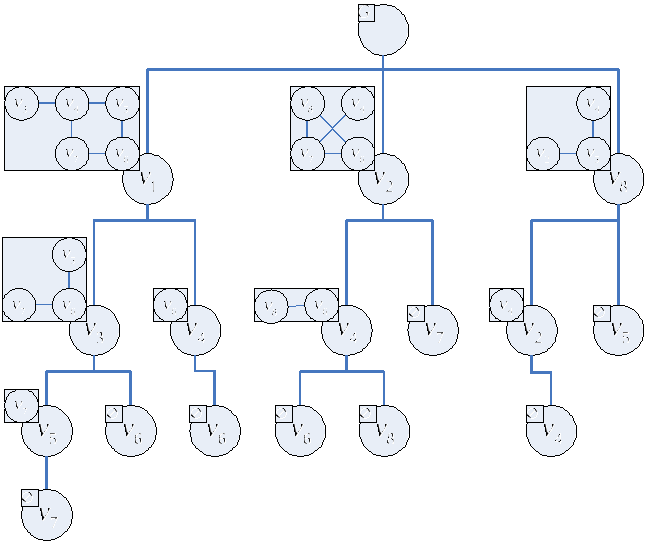
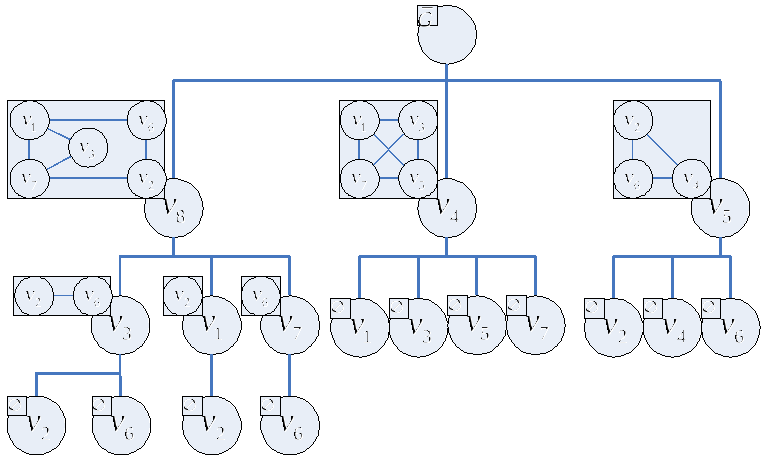
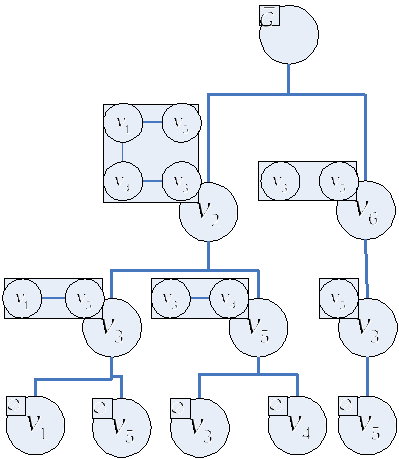
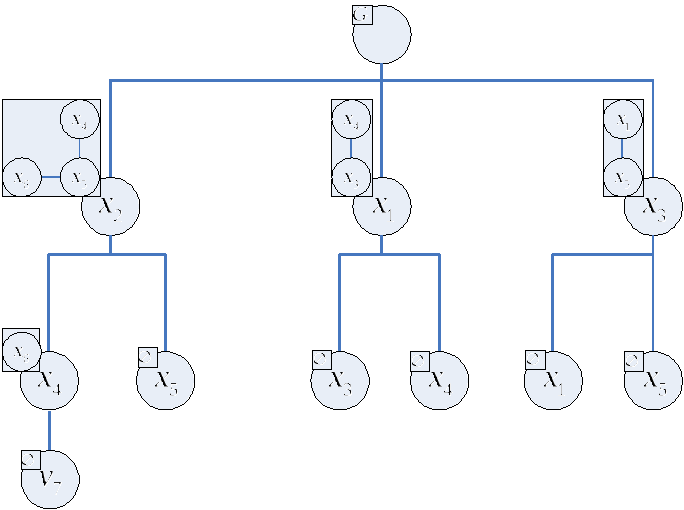
2. Вывод на графах. Используя операцию×на множестве векторов, определим понятие вывода, основываясь на бинарном правиле вывода: ν1×ν2⇒ν. Всякий вывод вектора ν из множества посылок {ν1, ν2, …, νq} можно представлять в виде однокорневого, растущего вверх бинарного дерева T, корню которого приписан вектор n. В T выше располагаются посылки, ниже заключения соответствующих правил, и листьям приписаны посылки {ν1, ν2, …, νq}.
Введем определение. Пусть ν есть вектор, определяемый некоторым подграфом. Результат ν* замены в нем всех единичных компонентов на несущественные компоненты назовем обобщением вектора ν. Очевидно отношение ν < ν*.
Следующий шаг состоит в том, что по выводу T вектора n строится, так называемое обобщенное дерево T* вектора n*, получающееся из T заменой всех векторов на их обобщения.
Справедливо утверждение.
Теорема 2. Обобщенное дерево T* является выводом вектора ν* из посылок, полученных обобщением всех посылок вывода T.
Доказательство. Рассмотрим правило вывода ν1×ν2⇒ν. Пусть ν*1 и ν*2 есть обобщения этих векторов. Покажем, что обобщение ν* вектора ν получается в результате применения правила ν*1×ν*2⇒ν*. Рассмотрим покомпонентные преобразования векторов, которые могут изменяться в результате применения операции ×. Операции, не содержащие 1, не меняются. Произведения 0×1 и 1×0 заменяются соответственно на 0×_ = 0 и _×0 = 0. Во всех случаях результат равен 0. Операция 1×1 заменяется на _×_, т.е. результатом является обобщение. Операции 1×_ = 1 и _×1 = 1 заменяются на _×_, что также является их обобщением. Таким образом, каждое правило вывода ν1×ν2⇒ν из T, превращается в правило вывода ν*1×ν*2⇒ν*. И, следовательно, вывод T превращается в вывод T* обобщения заключительного вектора вывода T. Теорема доказана.
3. Построение максимальных пустых подграфов. Введем такое определение. Два вектора n1 и n2 0-эквивалентны (обозначается n1 = 0n2), если совпадают их 0-компоненты.
Справедливы следующие утверждения:
Теорема 3. Пусть T есть вывод вектора n, и T* – обобщенный вывод вектора n*, полученный из T. Тогда выполняются отношения: n < n*и n = 0n*.
Теорема 4. Пусть имеется совокупность {n1, n2, …, nn} векторов таких, что их обобщения совпадают и равны n*. Тогда они принадлежат одному классу эквивалентности =0. Справедливо и обратное: если {n1, n2, …, nn} есть множество попарно =0–эквивалентных векторов, то их обобщения совпадают.
Переход к обобщающему вектору позволяет получить более экономные выводы. Справедливо утверждение 1.
Теорема 5. Пусть T* есть обобщенный вывод вектора n*, и n1 – его посылка. Тогда замена посылки n1 на вектор n2, такой что n1<n2 приводит к обобщённому выводу T1* вектора n1* такого, что выполняются отношения: n*<n1* и n* =0 n1*.
Таким образом, если в выводе вектора n* любой его вектор n и предшествующий ему вывод заменить на вывод поглощающего его вектора n’, то заключением вывода будет вектор n’*, поглощающий первоначальный n*.
Пример 6. Рассмотрим граф K3, узлы которого перенумерованы 1, 2, 3. Ребро (1, 2) определяет следующие пустые графы: (0, 1, _), (1, 0, _), (0, 0, _); ребро (2, 3) – пустые графы: (_, 0, 1), (_, 1, 0), (0, 0, 0); ребро 1,3 – пустые графы: (0, _, 1), (1, _, 0), (0, _, 0). Если перейти к обобщающим векторам и отбросить поглощаемые, то получим векторы: {(0, _, _), (_, 0, _)}, {(_, 0, _), (_, _, 0),}, {(0, _, _), (_, _, 0)}. В результате из этого множества векторов выводятся следующие векторы: (_, 0, 0), (0, _, 0), (0, 0, _). Выводится еще вектор (0, 0, 0), но он поглощается каждым из первых трех.
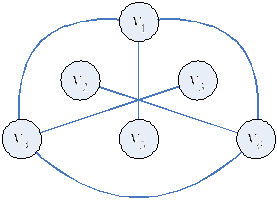
Пример 7. Полный двудольный граф (1; 3) определяет в точности два попарно несравнимых вектора (_, 0, 0, 0) и (0, _, _. _).
Введем такие определения.
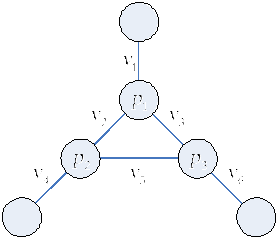
Пусть все пустые подграфы граф G определяют совокупность V попарно не сравнимых обобщенных векторов. Тогда V называется базисом графа G. Пусть G1, G2, …, Gm совокупность подграфов графа G и V1, V2, …, Vm суть базисы этих подграфов. Тогда максимальная совокупность всех обобщенных попарно не сравнимых векторов в множестве V1×V2×… ×Vm называется базисом совокупности G1, G2, …, Gm . Если G1, G2, …, Gm покрывает все ребра графа G, то он называется базисом графа G.
Пример 8. Для полного двудольного графа (n; m), базис состоит из двух векторов: в первом вначале расположены m нулевых компонентов, за которыми следуют n компонентов _, у второго наоборот – вначале m компонентов _, а затем n нулевых.
Справедлива теорема.
Теорема 6. Базис графа не зависит от выбора подграфов, покрывающих все его ребра.
Это утверждение представляет собой основу процедуры построения совокупности всех максимальных пустых подграфов по заданному графу, что имеет существенное значение при решении различных задач [4, 5]. Вкратце процедура получения пустых подграфов выглядит так. Пусть по заданному графу необходимо построить все его пустые подграфы, удовлетворяющие определенному условию. Таким условием может быть, например, нижняя граница числа узлов каждого пустого подграфа.
1. На вход поступает матрица смежности графа ортогональности. Каждая ее строка определяет веник, которому сопоставляется пара обобщенных векторов, описывающих его пустые подграфы.
2. В цикле, до получения неподвижной точки, строим попарные произведение этих векторов, попутно выбрасывая поглощаемые столбцы. При этом используется стратегия, минимизирующая число промежуточных подграфов, делая перебор управляемым содержательными особенностями предметной области.
3. На каждом шаге построения проверяются заданные условия, которым должны удовлетворять искомые пустые подграфы. Тем самым, поиск ведется только среди подграфов, которые удовлетворяют заданным условиям.
Заключение
Приведено теоретическое обоснование процедуры построения базиса графа, определяемого максимальными пустыми подграфами. Процедура реализована на языке C++ и работает на персональных компьютерах при решении практически значимых задач. Она использует различные стратегии поиска, что позволяет снизить перебор до приемлемого.
Библиографическая ссылка
Попов С.В. О ПРОЦЕДУРЕ ПОРОЖДЕНИЯ МАКСИМАЛЬНЫХ ПУСТЫХ ПОДГРАФОВ // Научное обозрение. Технические науки. – 2019. – № 2.
– С. 34-37;
URL: https://science-engineering.ru/ru/article/view?id=1239 (дата обращения: 28.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
1. Структурный анализ графов
Максимальные полные и
максимальные пустые
подграфы
1
2.
Ключевые понятия к данной теме:
─ подграф графа;
─ пустой граф (подграф);
─ полный граф (подграф).
3.
Постановка задачи
3
4.
Требуется найти в графе G =(X,U) все максимальные
пустые подграфы.
Определение максимального пустого подграфа
………
G=(X,U)
4
2
G1=(X1): X1= {(3,2)}
G2=(X2): X2 = {(4,1)}
3
Максимальные
пустые
подграфы
графа G
1
4
5.
G=(X,U)
2
4
G1=(X,U): X={(3,2)}; U =Ø
G2=(X,U): X= {(4,1)}; U = Ø
5
G3=(X,U): X= {(5)}; U = Ø
3
1
5
6.
максимальные пустые подграфы
Независимое множество вершин
(внутренне устойчивое множество)
7.
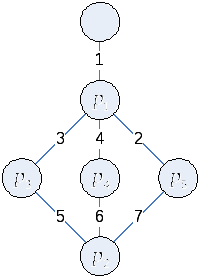
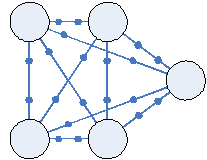
граф G = (X,U)
u1
x3
x1
x4
u6
u2
x5
u5
u3
x2
x6
u7
x7
u4
Рисунок 4.
7
8.
Рассмотрим алгоритм Х.Магу,
Дж.Уэйсмана
нахождения в графе G всех
максимальных пустых подграфов
8
9. Законы алгебры логики
f = x1x2 v x1x2
x v xy = x
xy x y x
Эквивалентные преобразования
(a+b) (a+c)… (a+p)= a+bc…p
x(x v y) = x (xx v xy) = x v xy = x
9
10.
Эквивалентные преобразования
(a+b) (a+c)… (a+p)= a+bc…p
x v xy = x
операция
поглощения
x(x v y) = (xx v xy) = x v xy = x
xy x y x
xx…x = x
операция склеивания
Закон идемпотентности
x+x+…+x = x
10
11.
Дан граф
G=(X,U)
u1
Матрица инциденций А графа G=(X,U )
3
А
x4
1
u1
u2
u3
u4
u5
u6
u7
1
u6
u2
5
u5
u3
2
x6
u7
u4
2
3
7
4
5
Рисунок 4.
6
7
11
12.
граф G=(X,U)
u1
Матрица инциденций А графа G=(X,U )
А
4
3
1
u6
u2
u5
6
u7
u2
u3
u4
u5
u6
u7
1
1
0
0
0
0
0
0
2
0
1
1
1
0
0
0
3
1
1
1
0
0
0
0
4
0
0
0
0
1
1
0
5
0
0
0
0
0
1
0
6
0
0
0
0
1
0
1
7
0
0
0
1
0
0
1
5
u3
2
u1
7
u4
Рисунок 4.
12
13.
Усовершенствованная матрица
инциденций графа G=(X, U).
Для её получения вводится система
«псевдобулевских» переменных
{xi}, где i = 1,n (n — число вершин графа G).
Каждая строка матрицы инциденций умножается на
соответствующую переменную из {xi }.
13
14.
Усовершенствованная матрица
инциденций графа G=(X,U)
граф G=(X,U)
u1
u6
u2
u5
5
u3
2
6
u7
u4
Рисунок 4.
u2
u3
u4
u5
u6
u7
x1
x1
0
0
0
0
0
0
x2
0
x2
x2
x2
0
0
0
x3
x3
x3
x3
0
0
0
0
x4
0
0
0
0
x4
x4
0
x5
0
0
0
0
0
x5
0
x6
0
0
0
0
x6
0
x6
x7
0
0
0
x7
0
0
x7
4
3
1
u1
7
14
15.
Составим произведение П:
ПG П ai , j xi 1
j
i
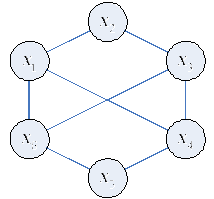
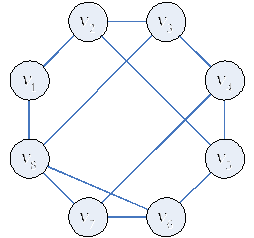
ПG = (x1 + x3) (x2 + x3) (x2 + x3) (x2 + x7) (x4 + x6) (x4 + x5) (x6 + x7) =
= (x1 + x3) (x2 + x3) (x2 + x7) (x4 + x6) (x4 + x5) (x6 + x7) =
= (x1 + x3) (x2 + x3) (x2 + x7) (x4 + x6) (x4 + x5) (x6 + x7) =
= (x1 + x3) (x2 + x3x7) (x4 + x5x6) (x6 + x7) =
= (x1x2 + x1x3x7 + x2x3 + x3x7)(x4x6+ x4x7+ x5x6 + x5x6x7)=
= (x1x2 + x2x3 + x3x7)(x4x6+ x4x7+ x5x6) =
= x1x2x4x6 + x1x2x4x7 + x1x2x5x6 + x2x3x4x6 + x2x3x4x7 + x2x3x5x6 +
+ x3x4x6x7 + x3x4x7 + x3x5x6x7 =
= x1x2x4x6 + x1x2x4x7 + x1x2x5x6 + x2x3x4x6 + x2x3x5x6 + x3x4x7 +
+x3x5x6x7.
15
16.
Получили произведение П:
ПG П ai , j xi 1
j
i
ПG = x1x2x4x6 + x1x2x4x7 + x1x2x5x6 + x2x3x4x6 + x2x3x5x6 +
+ x3x4x7 + +x3x5x6x7 = 1.
16
17.
Усовершенствованная матрица
инциденций графа G=(X,U)
x1
x2
u1
u1
u2
u3 u4
u5 u6
u7
x1
0
0
0
0
0
x2
x2
x2
0
0
0
0
3
1
u6
u2
0
4
u5
u3
x3
x3
x3
x3
0
0
0
0
x4
0
0
0
0
x4
x4
0
x5
0
0
0
0
0
x5
0
x6
0
0
0
0
x6
0
X6
2
6
5
u7
7
u4
Рисунок 4.
x7
0
0
0
x7
0
0
x7
П = x1x2x4x6 + x1x2x4x7 + x1x2x5x6 + x2x3x4x6 + x2x3x5x6 + x3x4x7 + +x3x5x6x7.
Алгебраические дополнения:
S=
(x3x5x7), (x3x5x6), (x3x4x7), (x1x2 x5x6), (x1x2x4),
(x1x5x7), (x1x4x7).
17
18.
Усовершенствованная матрица
инциденций графа G=(X,U)
x1
x2
u1
u1
u2
u3
u4
u5
u6
u7
x1
0
0
0
0
0
0
0
x2
x2
x2
0
0
x3
x3
0
0
0
0
x4
0
0
0
0
x4
x4
0
x5
0
0
0
0
0
x5
0
x6
0
0
0
0
x6
0
X6
0
0
0
0
x7
u5
u3
x3
0
4
u6
u2
0
x3
x7
3
1
2
6
5
u7
7
u4
Рисунок 4.
x7
П = x1x2x4x6 + x1x2x4x7 + x1x2x5x6 + x2x3x4x6 + x2x3x5x6 + x3x4x7 + +x3x5x6x7.
Максимальные пустые подграфы графа G:
S=
(x3x5x7), (x3x5x6), (x3x4x7), (x1x2 x5x6), (x1x2x4),
(x1x5x7), (x1x4x7)
18
19. Раскраска графа
Правильная раскраска вершин графа
Хроматическое число графа
Хроматическое число графа — минимальное
количество цветов, требуемое для раскраски вершин
графа, при которой любые вершины, соединенные
ребром раскрашены в разный цвет.
Применение алгоритма
20.
u1
3
1
u1
4
1
4
3
u6
u2
u5
u3
2
6
u6
u2
u5
5
u7
u4
7
u3
6
2
5
u7
7
u4
Рисунок 4.
Рисунок 4a.
Максимальные пустые подграфы:
S=
(x3x5x7), (x3x5x6), (x3x4x7), (x1x2 x5x6), (x1x2x4),
(x1x5x7), (x1x4x7).
20
21.
u1
u1
3
1
4
u6
u2
u5
2
6
u3
5
u7
7
4
u6
u2
u5
u3
3
1
6
2
5
u7
7
u4
u4
Рисунок 4.
Рисунок 4a.
Алгебраические дополнения:
S=
(x3x5x7), (x3x5x6), (x3x4x7), (x1x2 x5x6), (x1x2x4),
(x1x5x7), (x1x4x7).
21
22.
u1
3
1
u1
4
4
3
1
u6
u2
u5
u3
2
6
u6
u2
u5
5
u7
u4
7
u3
6
2
5
u7
7
u4
Рисунок 4.
Рисунок 4a.
Алгебраические дополнения:
S=
(x3x5x7), (x3x5x6), (x3x4x7), (x1x2 x5x6), (x1x2x4),
(x1x5x7), (x1x4x7).
22
23. Максимальные полные подграфы
24.
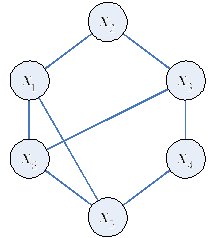
Задача : найти в графе G все максимальные полные подграфы.
Решение.
1
G
5
2
G
4
3
G
1
2
3
4
5
G
1
2
3
4
5
1
0
1
0
0
1
1
0
0
1
1
0
2
1
0
1
1
1
2
0
0
0
0
0
3
0
1
0
1
0
3
1
0
0
0
1
4
0
1
1
0
1
4
1
0
0
0
0
5
1
1
0
1
0
5
0
0
1
0
0
24
25.
1
G
G
1
2
3
4
5
1
0
0
1
1
0
2
0
0
0
0
0
3
1
0
0
0
1
4
1
0
0
0
0
5
0
0
1
0
0
u1
5
u2
G
2
u3
4
3
G – граф, дополняющий G до полного
G
u1 u2 u3
G
u1 u2 u3
1
1
1
0
1
x1
x1
0
2
0
0
0
2
0
0
0
3
0
1
1
3
0
x3
x3
4
1
0
0
4
x4
0
0
5
0
0
1
5
0
0
x5
П= (x1+x4x3)(x3 + x5) = x1x3 +x1x5 +
+x4x3 +x4x3x5.
Алгебраические дополнения:
S = x2x4x5; x2x4x3; x1x2x5
Максимальные полные подграфы графа G :
x2x4x5; x2x4x3; X1x2x5 .
25
26. Раскраска графа
Пример рёберной правильной раскраски с
помощью алгоритма Дж.Магу, Х.Уэйсмана
1
G
3
1
2
2
G*
3
4
5
4
5
П = (1 + 23)(3+ 245)(4+5) = (13+1245+23+2345)(4+5) =
= 134+135+1245+234+2345+2345 + 235 =
= 134 +135+ 1245 +234 + 235.
26
27.
G
3
1
2
G*
G*
4
5
Пg*
= (1 + 23)(3+ 245)(4+5) = (13+1245+23+2345)(4+5) =
= 134+135+1245+234+2345+2345 + 235 =
= 134+ 135 + 1245+234+235.
G
Алгебраические
дополнения:
S = { 25; 24; 3; 15;14 }
Раскраска G*:
2, 5 —
1, 4 —
3—
3
1
2
4
5
27
28.
Пример 2
U1
G2
G1
U3
U2
U1
U2
U3
U6
U4
U6
U4
U5
U5
U1
G1
U1
G2
U3
U2
U2
U3
U6
U4
U6
U5
U4
U5
28
29.
U1
G1
U1
G2
U3
U2
U2
U3
U6
U4
U6
U5
U4
U5
29
30.
30
31.
Усовершенствованная матрица
инциденций графа G=(X,U)
ПG =
u1
u2
u3
u4
u5
u6
u7
x1
x1
0
0
0
0
0
0
x2
0
x2
x2
x2
0
0
0
x3
x3
x3
x3
0
0
0
0
x4
0
0
0
0
x4
x4
0
x5
0
0
0
0
0
x5
0
x6
0
0
0
0
x6
0
x6
x7
0
0
0
x7
0
0
x7
31
-
-
November 27 2004, 11:10
- История
- Cancel
Кто-нибудь знает алгоритм поиска всех пустых подграфов в заданном графе, таким образом, чтобы после окончания поиска не было необходимости в поглощении?
В «Фундаментальных основах дискретной математике» В.А. Горбатова этот алгоритм есть, но для моей бедной головы он там слишком абстрактно описан.
Consider the following standard definitions. Given a graph G = (V, E)
- A circuit is a sequence of adjacent vertices starting and ending at
the same vertex. Circuits do not allow repeated edges but they do allow
repeated vertices. - A cycle is a special case of a circuit in which vertices also do not
repeat.
Note that circuits and Eulerian subgraphs are the same thing. This means that finding the longest circuit in G is equivalent to finding a maximum Eulerian subgraph of G. As noted above, this problem is NP-hard. So, unless P=NP, an efficient (i.e. polynomial time) algorithm for finding a maximal Eulerian subgraph in an arbitrary graph is impossible.
For undirected graphs, one way of randomly producing an Eulerian subgraph is to identify a cycle basis for G. A cycle basis is a set of cycles that, when combined using symmetric differences, can be used to form every Eulerian subgraph of the original graph G. Hence, we only need to take a random selection of cycles from this set and combine them to get our arbitrary Eulerian subgraph.
Given that an Eulerian subgraph is basically a collection of overlapping cycles, here is a greedy, polynomial-time algorithm that I’d like to suggest for finding large (but not necessarily maximum) Eulerian subgraphs. This works for both directed and undirected graphs and produces a set of edges (or arcs) E’ that define an Eulerian subgraph containing a user-defined source vertex s. The following steps are for directed graphs but can be easily modified for the undirected case.
Let U = {s} and E' = {}
while U is not empty
Let u be a random element in U
Form a cycle C from u in G
if no such cycle C exists
Remove u from U
else
Add the arcs of C to E'
Remove the arcs of C from G
Add the vertices of C to U
Here’s a few points to note about this algorithm.
- Here, the set U holds the vertices that are yet to be fully considered by the algorithm.
- To apply this method to undirected graphs, just replace the word
«arcs» with «edges» - This method can be seen as a generalisation of
Hierholzer’s algorithm. Hence, if the input graph G is already
an Eulerian graph, then the returned set E’ will contain all of the
edges from G. - Various methods can be used to generate a cycle C from
vertex u. For directed graphs, a simple method is to create an
additional dummy vertex u’ and temporarily redirect all of the incoming arcs
from u to u’. Various algorithms can then be used to determine a
u-u’-path (which represents a cycle), such as BFS, DFS, or
Wilson’s algorithm.
This algorithm can be said to produce a maximal Eulerian subgraph with respect to G and s. This is because, on termination, no further cycles can be added to the solution contained in E’. Note that we should not confuse the terms maximal and maximum here: finding a maximal Eulerian subgraph is easy (using the above method); finding a maximum Eulerian subgraph is NP-hard. Similar terminology is used with matchings.

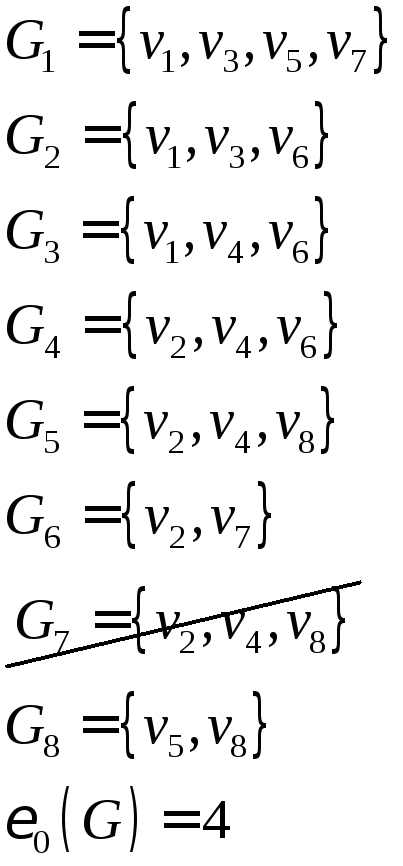
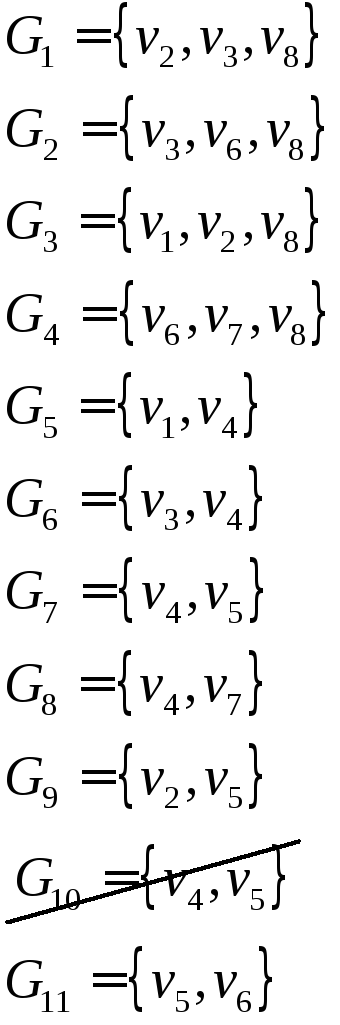
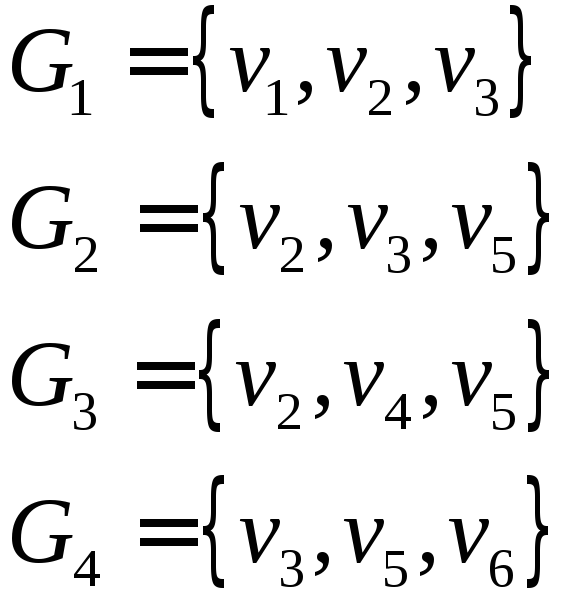
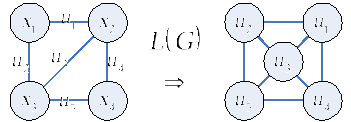
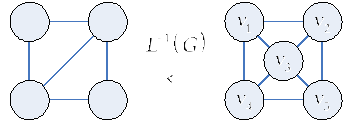
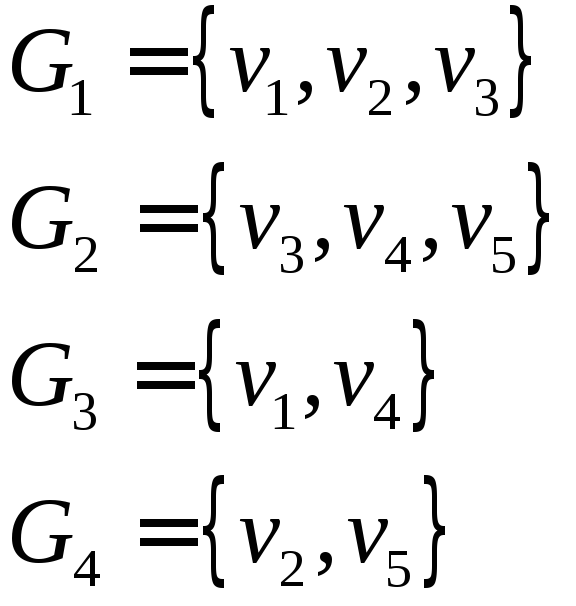
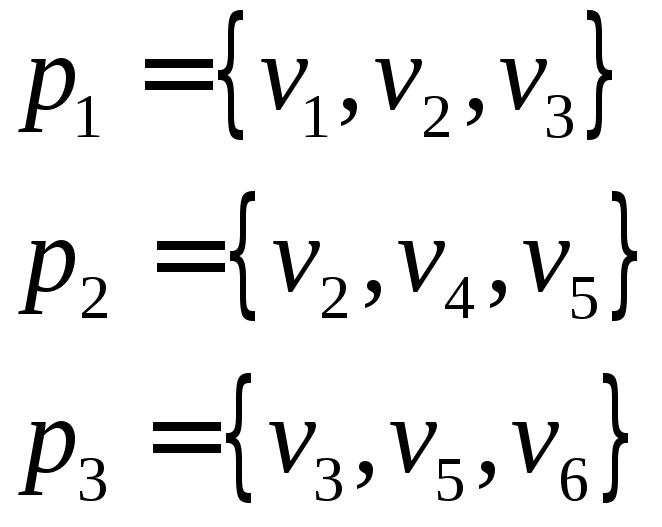
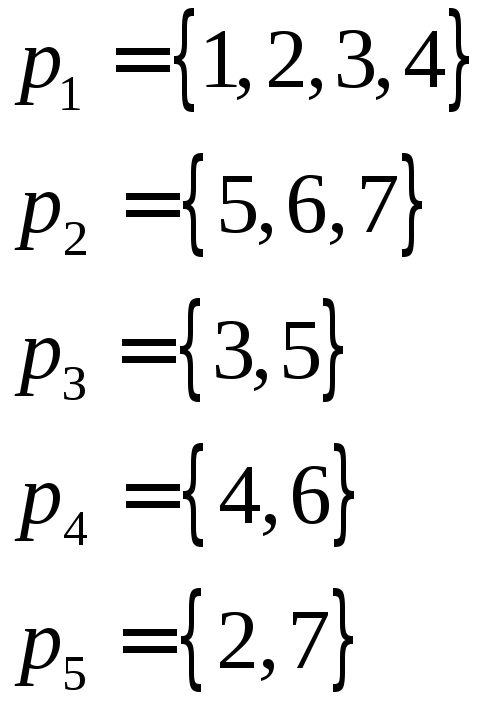
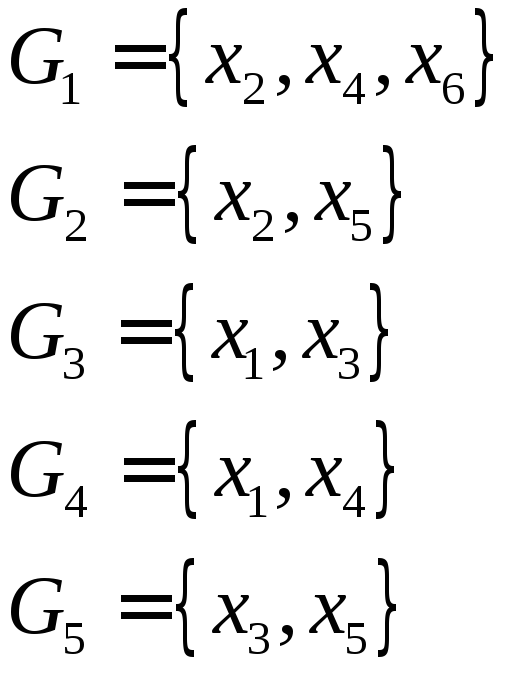
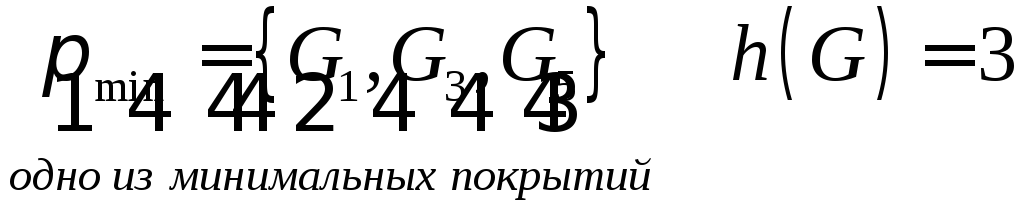

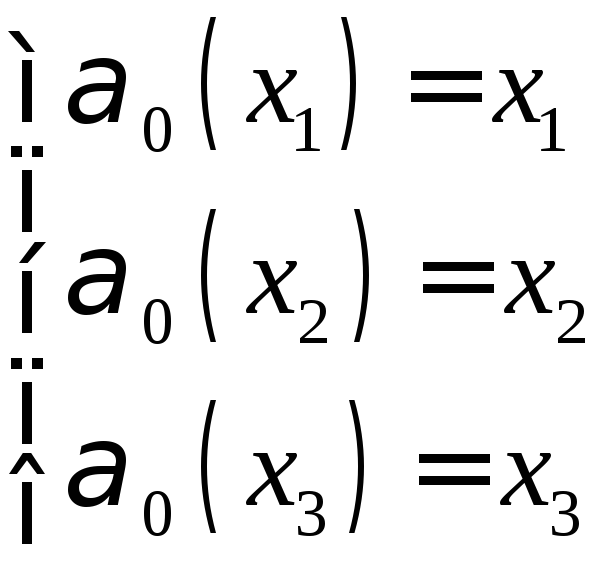
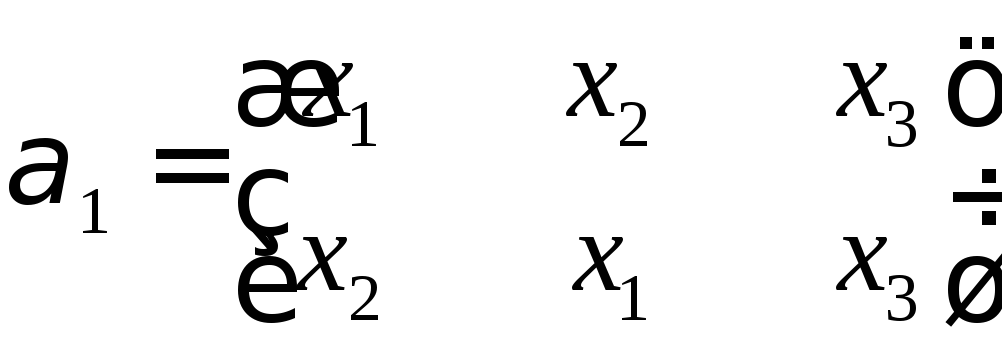
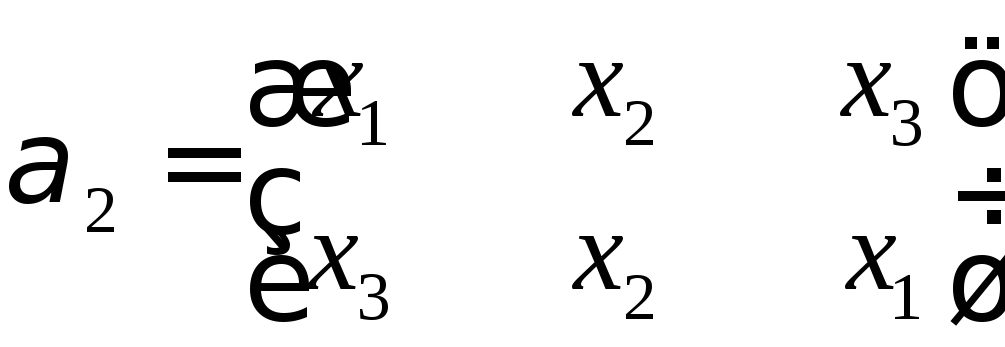

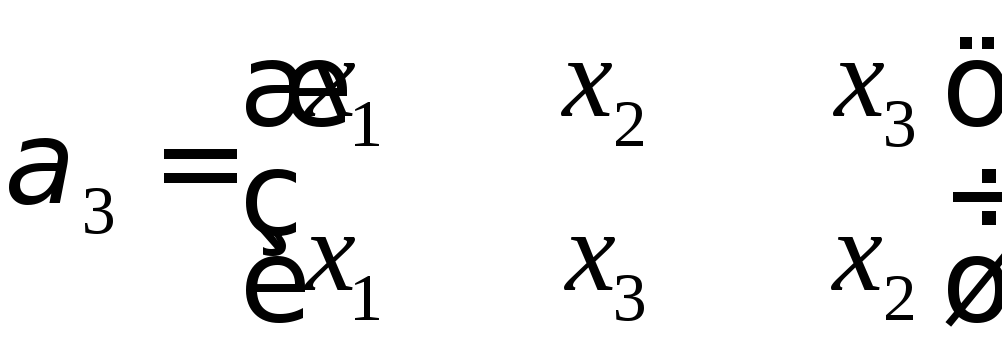
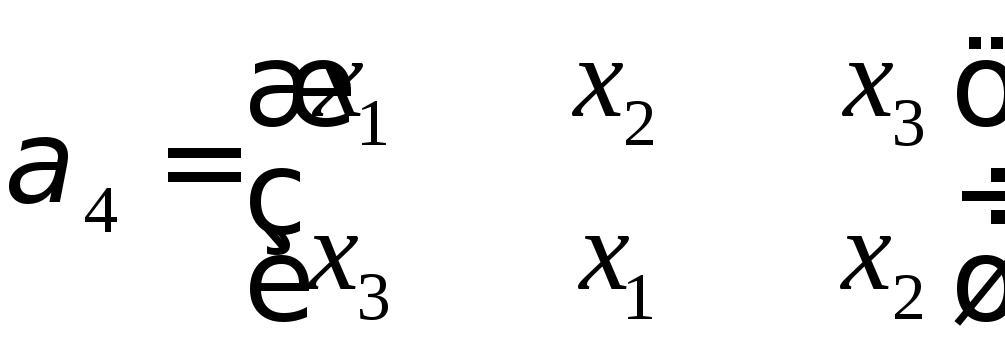
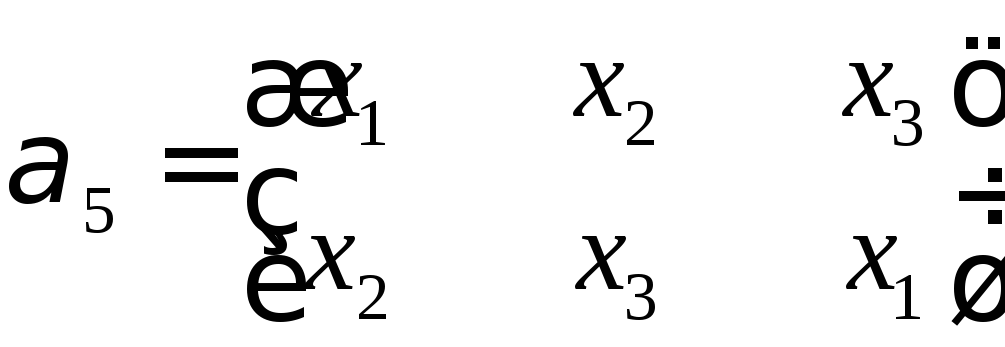
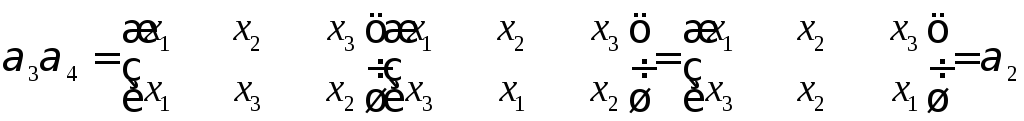
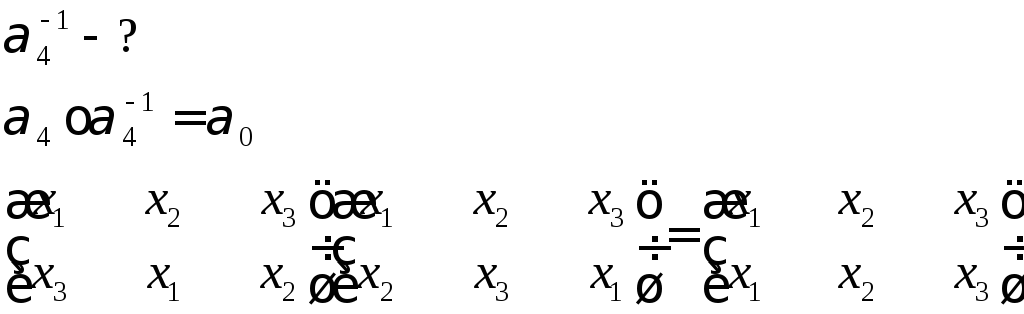
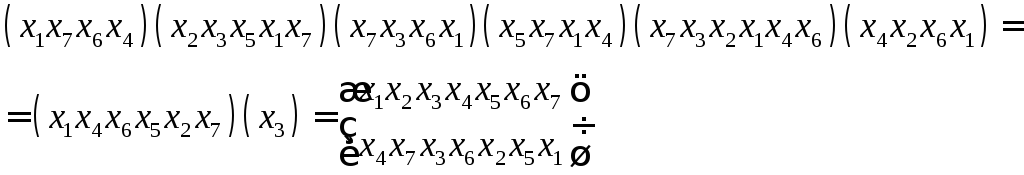
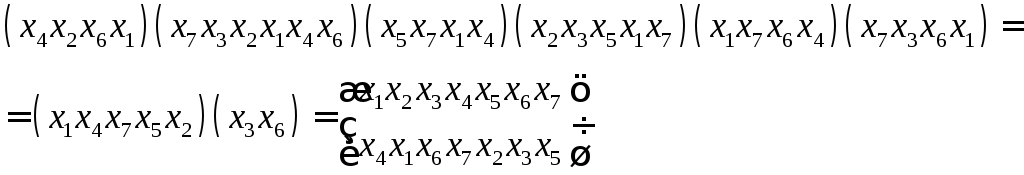
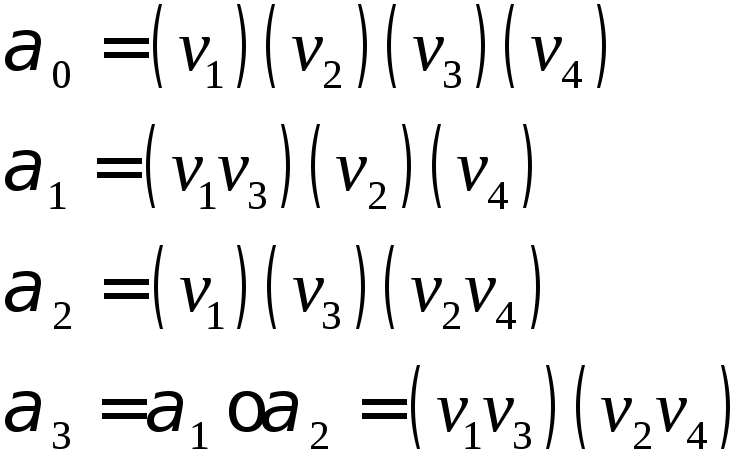
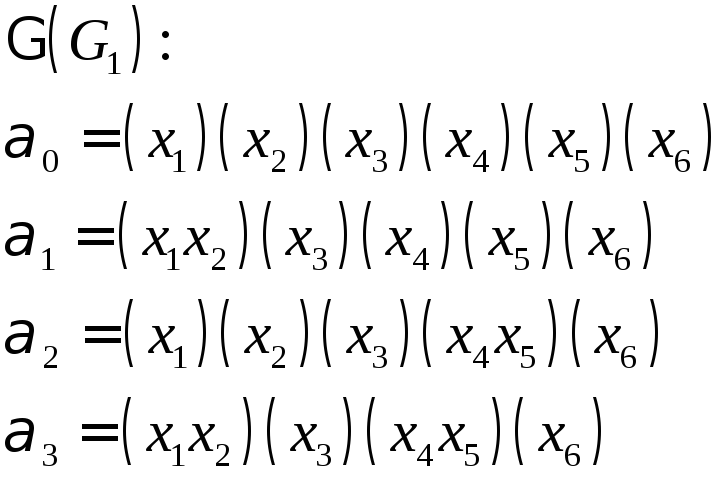
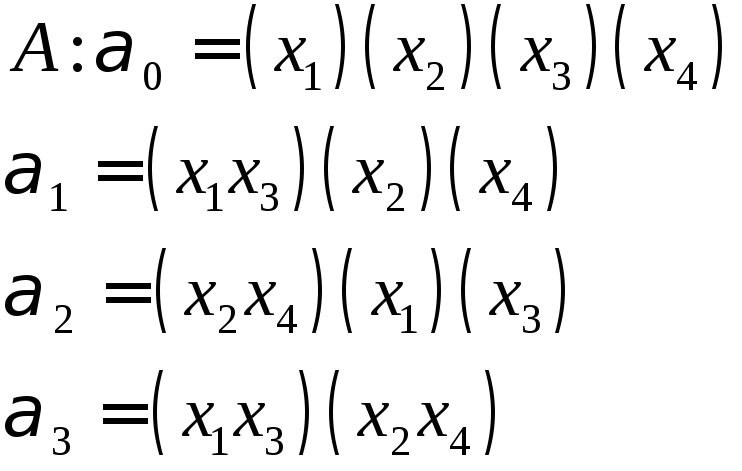
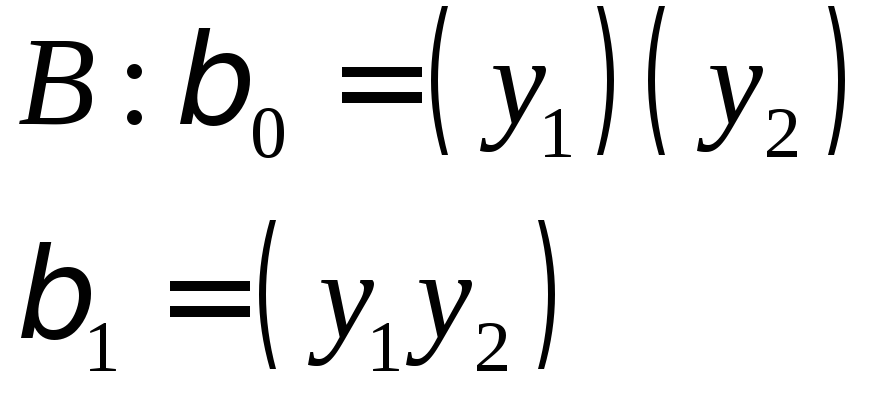
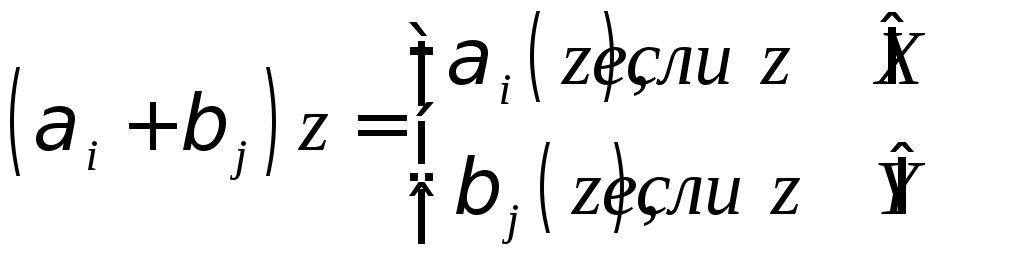 Степень
Степень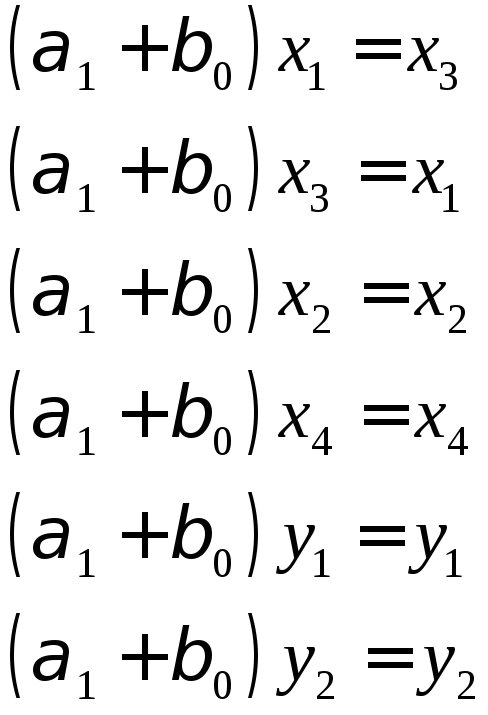
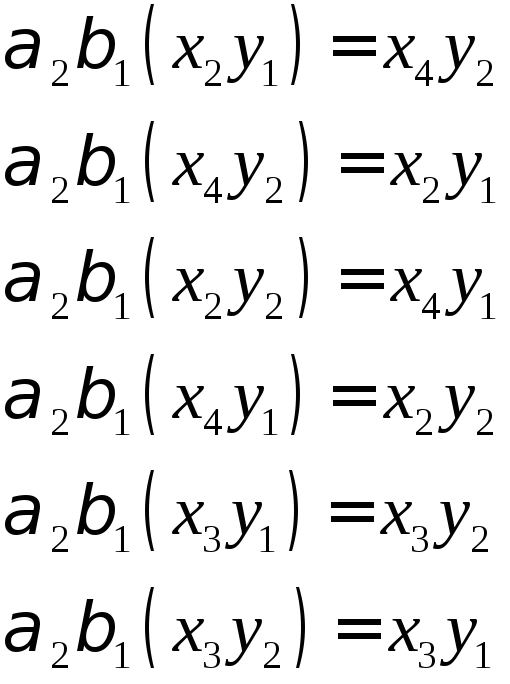
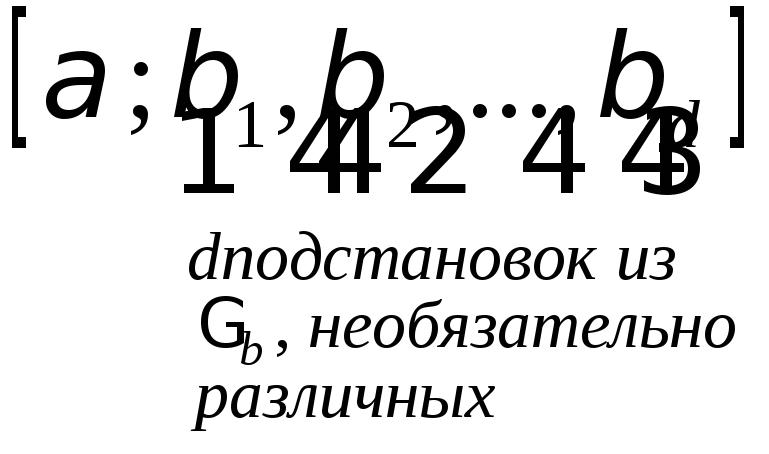 Действует
Действует