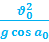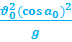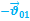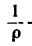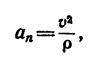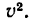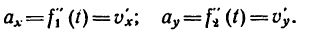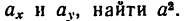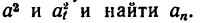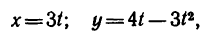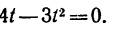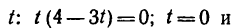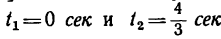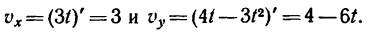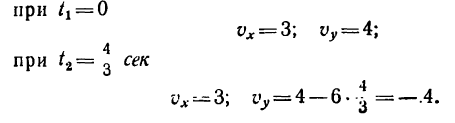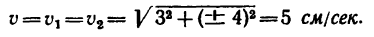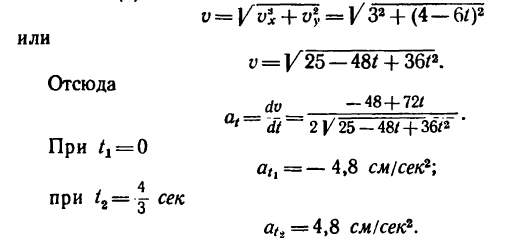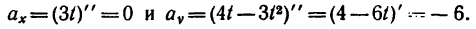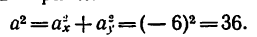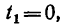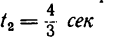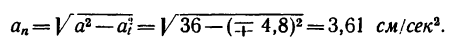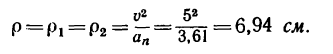Радиус кривизны траектории
В этой статье приведены две задачи, которые помогут вам научиться определять радиус кривизны траектории при движении тела под углом к горизонту. Каждая из задач представляет собой целый набор, поэтому неясностей не должно остаться.
Задача 1.
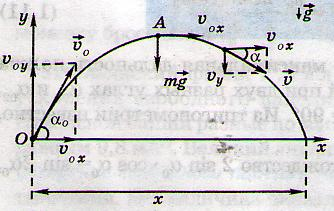
Тело брошено со скоростью 10 м/с под углом к горизонту. Найти радиусы кривизны траектории тела в начальный момент его движения, спустя время 0,5 с и в точке наивысшего подъема тела над поверхностью земли.
Как известно, радиус кривизны траектории связан с нормальным ускорением и скоростью формулой:
Откуда :
То есть, чтобы найти радиус кривизны траектории в любой точке, необходимо лишь знать скорость и нормальное ускорение, то есть ускорение, перпендикулярное вектору скорости. Рассмотрим все заданные точки и определим в них скорости и нужные составляющие ускорения.
К задаче 1
Самое простое – это определение этих величин в точке наивысшего подъема. Действительно, вертикальная составляющая скорости здесь равна нулю, поэтому скорость тела в данной точке равна горизонтальной составляющей, а ускорение, нормальное к вектору этой скорости – это ускорение свободного падения, поэтому
Вторая по простоте расчета – точка начала движения. Скорость в ней нам уже известна, осталось с ускорением разобраться. Ускорение свободного падения разложим на две составляющие: и
. Первая – перпендикулярна скорости, она-то нам и нужна. Определяем радиус:
Наконец, точка, в которой тело окажется через пол-секунды.
Наше тело будет лететь по горизонтали с постоянной скоростью, равной . По вертикали тело будет двигаться равнозамедленно до середины траектории (наивысшей точки), а затем равноускоренно. Определим, успеет ли тело добраться до апогея:
Простой прикидочный расчет показывает, что нужная нам точка находится на первой половине траектории, где тело еще двигается вверх. Тогда его скорость по оси :
Определим полную скорость тела в момент времени :
Угол наклона вектора скорости к горизонту в этот момент равен:
А можно было сразу и косинус найти:
Тогда искомый радиус кривизны траектории равен:
Ответ: м,
м,
м.
Задача 2.
Под каким углом к горизонту нужно бросить шарик, чтобы а) радиус кривизны траектории в начальный момент времени был в 8 раз больше, чем в вершине; б) центр кривизны вершины траектории находился бы на поверхности земли?
Запишем условие задачи так: а) , б)
.
а)Как и в предыдущей задаче, определяем радиус кривизны траектории в точке броска. Скорость нам известна, а нормальным ускорением будет проекция ускорения свободного падения:
Определим теперь радиус кривизны в вершине:
По условию :
б) Мы уже определили , осталась максимальная высота подъема.
Время определяем из условия равенства нулю вертикальной составляющей скорости так же, как мы это делали в предыдущей задаче:
Приравниваем и
:
Откуда .
Ответ: а) , б)
.
2 комментария
Есин из Хотам и ПВ
✉️
17.02.2022 15:20:44
Thank you very much
Jahongir
✉️
12.04.2022 19:14:12
Спасибо огромное! Полностью разобрался 
1) найти радиус кривизны траектории в наивысшей точке полета.

2)найти радийс кривизны траектории в начальной точке полета.
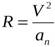
3) найти радиус траектории.
Центр масс твёрдого тела движется так же как двигалась бы материальная точка, масса которой равна массе тела, под действием внешних сил, приложенных к данному телу.
Тело состоит из нескольких элементов. Уравнение i-го элемента массой m записывается так:
Где Fi внешняя сила, а ∑Fik это сумма внутренних сил, действующих на i-ый элемент со стороны всех других элементов.
Сложим все аналогичные уравнения для всех элементов. Т.к. Fik = -Fki третьему закону Ньютона, то их сумма равна нулю.
После сложения получим:
Устойчивое равновесие — это равновесие, при котором, тело, выведенное из положения равновесия, вернётся в то же положение.
Неустойчивое равновесие — если тело, после смещения, не вернётся в это положение.
Скорость точки, движущейся по окружности ,часто называют Линейной скоростью ,чтобы подчеркнуть ее отличие от угловой скорости. Между линейной скоростью точки, обращающейся по окружности, и ее угловой скоростью существует связь. При равномерном движении точки по любой траектории модуль скорости равен s/∆t
Точка A, движущаяся по окружности радиуса R,за время ∆t проходит путь равный дуге A1A2
S=A1A2=∆ϕR .Модуль линейной скорости движения v= s/∆t ==∆ϕR/∆t=ωR
Итак , модуль линейной скорости точки, движущейся по окружности, равен произведению угловой скорости на радиус окружности :
Эта формула справедлива как для равномерного, так и для неравномерного движения точки по окружности.
Модуль ускорения точки, движущейся по окружности, можно выразить через угловую скорость тела и радиус окружности. Так как a=v²/R и v= ωR


















Очевидно, что модуль ускорения при равномерном движении точки по окружности есть постоянная величина, так как U и r не изменяются при движении
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студентов недели бывают четные, нечетные и зачетные. 9614 — 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
1.59. Радиус кривизны траектории в точке бросания: 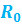
1.60. Радиус кривизны траектории в точке максимальной высоты А :

Замечание1: радиус кривизны 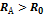
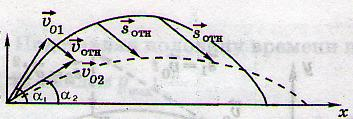
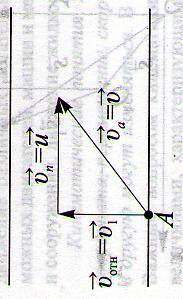
Как будут двигаться относительно друг друга два тела брошенные одновременно под разными углами к горизонту?
1.61.
… —второе тело относительно первого тела будет двигаться равномерно и прямолинейно, и вектор перемещения, соединяющий тела, в любой момент времени будет параллелен вектору относительной скорости:

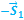

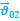
Относительность механического движения
§ 1.6.
1.63. Относительность скорости.
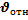
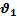
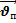
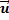
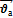
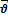


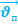
…- формула сложения скоростей



…- формула сложения перемещений.
Замечание: формулы (1) и (2) формулы преобразования Галилея.
Пойдем в обратном порядке.
gh=3/4*(2/3*(g*t)^2);
t=(3*h/*g)^0,5, где g – ускорение свободно падения;
t
0,3 c
А Митин Андрей, по-моему, проврался: в выражении t=2/(h*(8*g*h/5)^0.5) проблемы с размерностью.
2) Аппроксимируем движение точки равномерным движением по окружности.
v=w*R; a=w^2*R; m=p/v=p/(w*R);
F=m*a=(p*w^2*R)/(w*R)=p*w;
F=0,1*0,5*pi Н=0,05*pi Н, где pi – число пи.
1) Тут пока выкладки получаются громоздкие – утомительно писать в подобном окне. Может, потом чего-нибудь попроще придумаю. Но ответ такой: максимальны радиус в крайних точках траектории (начальной и конечной моменты движения), а минимальный – в точке, что делит траекторию пополам и в которой движение горизонтально.
Конечные соотношения:
R(t)=v(t)^3/(g*v(0)*cos(A)), где g – ускорение свободного падения.
Преподаватель который помогает студентам и школьникам в учёбе.
Кинематический способ определения радиуса кривизны траектории в теоретической механике
Кинематический способ определения радиуса кривизны траектории:
При решении многих технических задач возникает необходимость знать радиус кривизны р (или
Таким образом, если закон движения точки задан уравнениями
то при определении радиуса кривизны траектории рекомендуется произвести следующее:
1. Продифференцировав уравнения движения, найти выражения проекций на оси координат вектора скорости:
2. Подставив в (б’) выражения 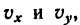
3. Продифференцировав по t уравнение (б), полученное непосредственно из (б’), найти касательное ускорение 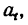
4. Продифференцировав вторично уравнения движения, найти выражения проекций на оси координат вектора ускорения
5. Подставив в (г) выражения
6. Подставить в (в) значения
7. Подставив в (а) найденные значения 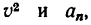
Задача:
Движение точки задано уравнениями
(х, у—в см, t — в сек). Определить радиус кривизны траектории в те моменты, когда она пересекает ось Ох.
Решение.
1. В те моменты, когда траектория пересекает ось Ох, ордината у—0. Поэтому, подставив во второе уравнение движения значение у = 0, получим
Отсюда [решая уравнение относительно 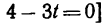
2. Находим выражения проекций скорости:
Как видно, проекция скорости на ось Ох — постоянная величина (не зависит от времени).
3. Определяем значение этих проекций в моменты пересечения траекторией оси Ох:
4. Числовое значение скорости точки в моменты пересечения траекторией оси Ох в данном случае одинаковы
5. Находим касательное ускорение точки. Для этого получим общее выражение (уравнение) скорости, воспользовавшись зависимостью (б):
6. Находим проекции полного ускорения точки:
Следовательно, в данном случае полное ускорение точки — постоянная величина. Причем
7. Определяем нормальное ускорение точки. Как при
так и при
8. Зная, что в моменты пересечения траекторией оси 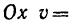
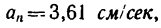
Решение этой задачи рекомендуется самостоятельно иллюстрировать чертежом, изобразив на нем траекторию точки, векторы скорости 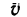
- Равномерное вращательное движение
- Равнопеременное вращательное движение
- Неравномерное вращательное движение
- Плоскопараллельное движение тела
- Равномерное криволинейное движение точки
- Равнопеременное движение точки
- Неравномерное движение точки по любой траектории
- Определение траектории, скорости и ускорения точки