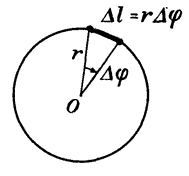
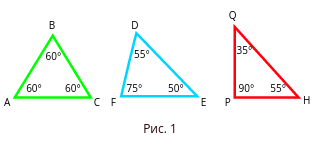Для описания движения по окружности наряду с линейной скоростью вводят понятие угловой скорости. Если точка при движении по окружности за время (Delta t) описывает дугу, угловая мера которой (Delta varphi), то угловая скорость (omega = frac{{Delta varphi }}{{Delta t}}).
Угловая скорость (omega) связана с линейной скоростью (upsilon) соотношением (upsilon = omega r), где (r) — радиус окружности, по которой движется точка (рис. 1). Понятие угловой скорости особенно удобно для описания вращения твердого тела вокруг оси. Хотя линейные скорости у точек, находящихся на разном расстоянии от оси, будут неодинаковыми, их угловые скорости будут равны, и можно говорить об угловой скорости вращения тела в целом.
Задача
Диск, радиуса (r) катится без проскальзывания по горизонтальной плоскости. Скорость центра диска постоянная и равна (upsilon_п). С какой угловой скоростью при этом вращается диск?
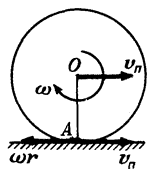
Каждая точка диска участвует в двух движениях — в поступательном движении со скоростью (upsilon_п) вместе с центром диска и во вращательном движении вокруг центра с некоторой угловой скоростью (omega).
Для нахождения (omega) воспользуемся отсутствием проскальзывания, то есть тем, что в каждый момент времени скорость точки диска, соприкасающейся с плоскостью, равна нулю. Это означает, что для точки А (рис. 2) скорость поступательного движения (upsilon_п) равна по величине и противоположна по направлению линейной скорости вращательного движения ({upsilon _{вр}} = omega r). Отсюда сразу получаем (omega = frac{{{upsilon _п}}}{r}).
Задача
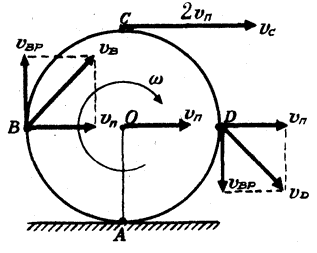
Найти скорости точек В, С и D того же диска (рис. 3).
Рассмотрим вначале точку В. Линейная скорость ее вращательного движения направлена вертикально вверх и равна ({upsilon _{вр}} = omega r = frac{{{upsilon _п}}}{R}r = {upsilon _п}), то есть по величине равна скорости поступательного движения, которая, однако, направлена горизонтально. Складывая векторно эти две скорости, находим, что результирующая скорость (upsilon_B) по величине равна ({upsilon _п}sqrt 2 ) и образует угол 45° с горизонтом. У точки С скорости вращательного и поступательного движения направлены в одну сторону. Результирующая скорость (upsilon_C) равна (2upsilon_п), и направлена горизонтально. Аналогично находится и скорость точки D (см. рис. 3).
Даже в том случае, когда скорость точки, движущейся по окружности, не меняется по величине, точка имеет некоторое ускорение, так как меняется направление вектора скорости. Это ускорение называется центростремительным. Оно направлено к центру окружности и равно
[{a_ц} = {omega ^2}r = frac{{{upsilon ^2}}}{R}]
((R) — радиус окружности, (omega) и (upsilon) — угловая и линейная скорости точки).
Если же скорость точки, движущейся по окружности, меняется не только по направлению, но и по величине, то наряду с центростремительным ускорением существует и так называемое тангенциальное ускорение. Оно направлено по касательной к окружности и равно отношению (frac{{Delta upsilon }}{{Delta t}}) (({Delta upsilon }) — изменение величины скорости за время (Delta t)).
Задача
Найти ускорения точек А, В, С и D диска радиуса (r), катящегося без проскальзывания по горизонтальной плоскости. Скорость центра диска постоянна и равна (upsilon_п) (рис. 3).
В системе координат, связанной с центром диска, диск вращается с угловой скоростью (omega), а плоскость движется поступательно со скоростью (upsilon_п). Проскальзывание между диском и плоскостью отсутствует, следовательно, (omega = frac{{{upsilon _п}}}{r}). Скорость поступательного движения (upsilon_п) не меняется, поэтому угловая скорость вращения диска постоянная и точки диска имеют только центростремительное ускорение ({a_ц} = {omega ^2}r = frac{{{upsilon_п^2}}}{R}), направленное к центру диска. Так как система координат движется без ускорения (с постоянной скоростью (upsilon_п)), то в неподвижной системе координат ускорения точек диска будут теми же.
Перейдем теперь к задачам на динамику вращательного движения. Вначале рассмотрим простейший случай, когда движение по окружности происходит с постоянной скоростью. Так как ускорение тела при этом направлено к центру, то и векторная сумма всех сил, приложенных к телу, должна быть тоже направлена к центру, и по II закону Ньютона (m{a_ц} = sum F).
Следует помнить, что в правую часть этого уравнения входят только реальные силы, действующие на данное тело со стороны других тел. Никакой центростремительной силы при движении по окружности не возникает. Этим термином пользуются просто для обозначения равнодействующей сил, приложенных к телу, движущемуся по окружности. Что касается центробежной силы, то она возникает только при описании движения по окружности в неинерциальной (вращающейся) системе координат. Мы пользоваться здесь понятием центростремительной и центробежной силы вообще не будем.
Задача
Определить наименьший радиус закругления дороги, которое автомобиль может пройти при скорости (upsilon=70) км/ч и коэффициенте трения шин о дорогу (k=0,3).
На автомобиль действуют сила тяжести (P=mg), сила реакции дороги (N) и сила трения (F_{тр}) между шинами автомобиля и дорогой. Силы (P) и (N) направлены вертикально и равны по величине: (P=N). Сила трения, препятствующая проскальзыванию («заносу») автомобиля, направлена к центру поворота и сообщает центростремительное ускорение: ({F_{тр}} = frac{{m{upsilon ^2}}}{R}). Максимальное значение силы трения ({F_{трmax}} = kN = kmg), поэтому минимальное значение радиуса окружности, по которой еще возможно движение со скоростью (upsilon), определяется из уравнения (frac{{m{upsilon ^2}}}{R} = kmg). Отсюда (R = frac{{{upsilon ^2}}}{{kg}} approx 130;м).
Сила реакции дороги (N) при движении автомобиля по окружности не проходит через центр тяжести автомобиля. Это связано с тем, что ее момент относительно центра тяжести должен компенсировать момент силы трения, стремящийся опрокинуть автомобиль. Величина силы трения тем больше, чем больше скорость автомобиля (left( {{F_{тр}} = frac{{m{upsilon ^2}}}{R}} right)). При некотором значении скорости момент силы трения превысит момент силы реакции и автомобиль опрокинется.
Задача
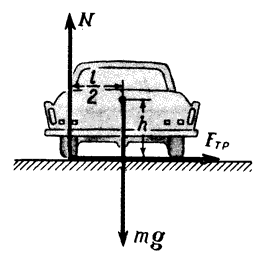
При какой скорости автомобиль, движущийся по дуге окружности радиуса (R=130) м, может опрокинуться? Центр тяжести автомобиля находится на высоте (h=1) м над дорогой, ширина следа автомобиля (l=1,5) м (рис. 4).
В момент опрокидывания автомобиля как сила реакции дороги (N), так и сила трения (F_{тр}) приложены к «внешнему» колесу. При движении автомобиля по окружности со скоростью (upsilon) на него действует сила трения (left( {{F_{тр}} = frac{{m{upsilon ^2}}}{R}} right)). Эта сила создает момент относительно центра тяжести автомобиля ({M_{тр}} = frac{{m{upsilon ^2}}}{R}h). Максимальный момент силы реакции дороги (N=mg) относительно центра тяжести равен (mgfrac{l}{2}) (в момент опрокидывания сила реакции проходит через внешнее колесо). Приравнивая эти моменты, найдем уравнение для максимальной скорости, при которой автомобиль еще не опрокинется:
[frac{{m{upsilon ^2}}}{R}h = frac{{mgl}}{2},]
откуда
[upsilon = sqrt {frac{{glR}}{{2h}}} approx 30;м/с approx 110;км/ч.]
Чтобы автомобиль мог двигаться с такой скоростью, необходим коэффициент трения (k geq frac{{{upsilon ^2}}}{{gR}}) (см. предыдущую задачу).
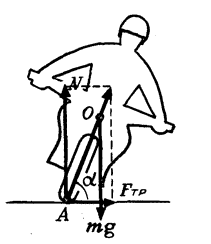
Аналогичная ситуация возникает при повороте мотоцикла или велосипеда. Сила трения, создающая центростремительное ускорение, имеет момент относительно центра тяжести, стремящийся опрокинуть мотоцикл. Поэтому для компенсации этого момента моментом силы реакции дороги мотоциклист наклоняется в сторону поворота (рис. 5).
Задача
Мотоциклист едет по горизонтальной дороге со скоростью (upsilon=70) км/ч, делая поворот радиусом (R=100) м. На какой угол (alpha) к горизонту он должен при этом наклониться, чтобы не упасть?
Сила трения между мотоциклом и дорогой ({{F_{тр}} = frac{{m{upsilon ^2}}}{R}}), так как она сообщает мотоциклисту центростремительное ускорение. Сила реакции дороги (N=mg). Условие равенства моментов силы трения и силы реакции относительно центра тяжести дает уравнение: ({F_{тр}} cdot lsin alpha = Nlcos alpha), где (l) — расстояние OA от центра тяжести до следа мотоцикла (см. рис. 5).
Подставляя сюда значения (F_{тр}) и (N), находим что ({text{tg}}alpha = frac{{gR}}{{{upsilon ^2}}}) или (alpha = {text{arctg}}frac{{gR}}{{{upsilon ^2}}} approx 70^circ). Отметим, что равнодействующая сил (N) и (F_{тр}) при этом угле наклона мотоцикла проходит через центр тяжести, что и обеспечивает равенство нулю суммарного момента сил (N) и (F_{тр}).
Для того, чтобы увеличить скорость движения по закруглению дороги, участок дороги на повороте делают наклонным. При этом в создании центростремительного ускорения, кроме силы трения, участвует и сила реакции дороги.
Задача
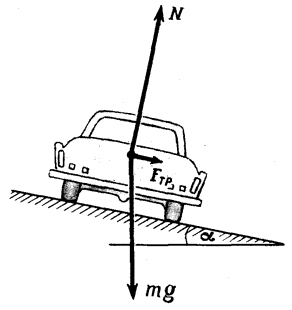
С какой максимальной скоростью (upsilon) может двигаться автомобиль по наклонному треку с углом наклона (alpha) при радиусе закругления (R) и коэффициенте трения шин о дорогу (k)?
На автомобиль действуют сила тяжести (mg), сила реакции (N), направленная перпендикулярно плоскости трека, и сила трения (F_{тр}), направленная вдоль трека (рис. 6). Так как нас не интересуют в данном случае моменты сил, действующих на автомобиль, мы нарисовали все силы приложенными к центру тяжести автомобиля. Векторная сумма всех сил должна быть направлена к центру окружности, по которой движется автомобиль, и сообщать ему центростремительное ускорение. Поэтому сумма проекций сил на направление к центру (горизонтальное направление) равна (frac{{m{upsilon ^2}}}{R}), то есть (frac{{m{upsilon ^2}}}{R} = Nsin alpha + {F_{тр}}cos alpha).
Сумма проекций всех сил на вертикальное направление равна нулю:
[Ncos alpha – mg – {F_{тр}}sin alpha = 0.]
Подставляя в эти уравнения максимальное возможное значение силы трения (F_{тр}=kN) и исключая силу (N), находим максимальную скорость (upsilon = sqrt {gRfrac{{k + {text{tg}}alpha }}{{1 – k{text{tg}}alpha }}}), с которой еще возможно движение по такому треку. Это выражение всегда больше значения (sqrt {kgR}), соответствующего горизонтальной дороге.
Разобравшись с динамикой поворота, перейдем к задачам на вращательное движение в вертикальной плоскости.
Задача
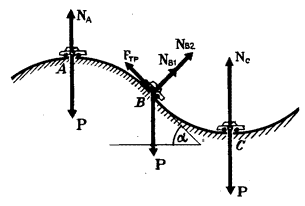
Автомобиль массы (m=1,5) т движется со скоростью (upsilon=70) км/ч по дороге, показанной на рисунке 7. Участки дороги АВ и ВС можно считать дугами окружностей радиуса (R=200) м, касающимися друг друга в точке В. Определить силу давления автомобиля на дорогу в точках А и С. Как меняется сила давления при прохождении автомобилем точки В?
В точке A на автомобиль действуют сила тяжести (P=mg) и сила реакции дороги (N_A). Векторная сумма этих сил должна быть направлена к центру окружности, то есть вертикально вниз, и создавать центростремительное ускорение: (frac{{m{upsilon ^2}}}{R} = P – {N_A}), откуда ({N_A} = mg – frac{{m{upsilon ^2}}}{R} approx 12 cdot {10^3};Н). Сила давления автомобиля на дорогу равна по величине и противоположна по направлению силе реакции. В точке С векторная сумма сил направлена вертикально вверх: (frac{{m{upsilon ^2}}}{R} = {N_C} – P) и ({N_C} = mg + frac{{m{upsilon ^2}}}{R} = 18 cdot {10^3};Н).
Таким образом, в точке А сила давления меньше силы тяжести, а в точке С — больше.
В точке В автомобиль переходит с выпуклого участка дороги на вогнутый (или наоборот). При движении по выпуклому участку проекция силы тяжести на направление к центру должна превышать силу реакции дороги (N_{B1}), причем (Pcos alpha – {N_{B1}} = frac{{m{upsilon ^2}}}{R}). При движении по вогнутому участку дороги, наоборот, сила реакции дороги (N_{B2}) превосходит проекцию силы тяжести:
[{N_{B2}} – Pcos alpha = frac{{m{upsilon ^2}}}{R}.]
Из этих уравнений получаем, что при прохождении точки В сила давления автомобиля на дорогу меняется скачком на величину (frac{{2m{upsilon ^2}}}{R} approx 6 cdot {10^3}) Н. Разумеется, такие ударные нагрузки действуют разрушающе как на автомобиль, так и на дорогу. Поэтому дороги и мосты всегда стараются делать так, чтобы их кривизна менялась плавно.
При движении автомобиля по окружности с постоянной скоростью сумма проекций всех сил на направление, касательное к окружности, должна быть равна нулю. В нашем случае касательная составляющая силы тяжести уравновешивается силой трения между колесами автомобиля и дорогой.
Величина силы трения регулируется вращательным моментом, прикладываемым к колесам со стороны мотора. Этот момент стремится вызвать проскальзывание колес относительно дороги. Поэтому возникает сила трения, препятствующая проскальзыванию и пропорциональная приложенному моменту. Максимальное значение силы трения равно (kN), где (k) — коэффициент трения между шинами автомобиля и дорогой, (N) — сила давления на дорогу. При движении автомобиля вниз сила трения играет роль тормозящей силы, а при движении вверх, наоборот, роль силы тяги.
Задача
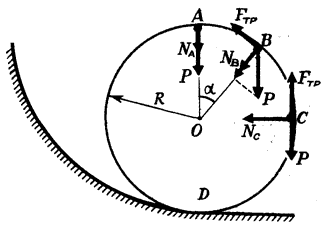
Автомобиль массой (m=0,5) т, движущийся со скоростью (upsilon=200) км/ч, совершает «мертвую петлю» радиуса (R=100) м (рис. 8). Определить силу давления автомобиля на дорогу в верхней точке петли A; в точке B, радиус-вектор которой составляет угол (alpha=30^circ) с вертикалью; в точке С, в которой скорость автомобиля направлена вертикально. Возможно ли движение автомобиля по петле с такой постоянной скоростью при коэффициенте трения тин о дорогу (k=0,5)?
В верхней точке петли сила тяжести и сила реакции дороги (N_A) направлены вертикально вниз. Сумма этих сил создает центростремительное ускорение: (frac{{m{upsilon ^2}}}{R} = {N_A} + mg).
Поэтому ({N_A} = frac{{m{upsilon ^2}}}{R} – mg approx {10^4};Н).
Сила давления автомобиля на дорогу равна по величине и противоположна по направлению силе (N_A).
В точке В центростремительное ускорение создается суммой силы реакции и проекции силы тяжести на направление к центру: (frac{{m{upsilon ^2}}}{R} = {N_B} + mgcos alpha). Отсюда
[{N_B} = frac{{m{upsilon ^2}}}{R} – mgcos alpha approx 11 cdot {10^3};Н]
Легко видеть, что ({N_B} > {N_A}); с увеличением угла (alpha) сила реакции дороги увеличивается.
В точке С сила реакции ({N_C} = frac{{m{upsilon ^2}}}{R} approx 15 cdot {10^3}) Н; центростремительное ускорение в этой точке создается только силой реакции, а сила тяжести направлена по касательной. При движении по нижней части петли сила реакции будет превышать (frac{{m{upsilon ^2}}}{R}) и максимальное значение (frac{{m{upsilon ^2}}}{R} – mg approx 20 cdot {10^3}) Н сила реакции имеет в точке D. Значение ({N_A} = frac{{m{upsilon ^2}}}{R} – mg), таким образом, является минимальным значением силы реакции.
Скорость автомобиля будет постоянной, если касательная составляющая силы тяжести не превышает максимальной силы трения (kN) во всех точках петли. Это условие заведомо выполняется, если минимальное значение (kN = k{N_A} = kmleft( {frac{{{upsilon ^2}}}{R} – g} right)) превосходит максимальное значение касательной составляющей силы веса. В нашем случае это максимальное значение равно (mg) (оно достигается в точке С), и условие (kmleft( {frac{{{upsilon ^2}}}{R} – g} right) > mg) выполняется при (k=0,5), (upsilon=200) км/ч, (R=100) м.
Таким образом, в нашем случае движение автомобиля по «мертвой петле» с постоянной скоростью возможно.
Рассмотрим теперь движение автомобиля по «мертвой петле» с выключенным мотором. Как уже отмечалось, обычно момент силы трения противодействует моменту, приложенному к колесам со стороны мотора. При движении автомобиля с выключенным мотором этого момента нет, и силой трения между колесами автомобиля и дорогой можно пренебречь.
Скорость автомобиля уже не будет постоянной — касательная составляющая силы тяжести замедляет или ускоряет движение автомобиля по «мертвой петле». Центростремительное ускорение тоже будет меняться. Создается оно, как обычно, равнодействующей силы реакции дороги и проекции силы тяжести на направление к центру петли.
Задача
Какую наименьшую скорость должен иметь автомобиль в нижней точке петли D (см. рис. 8 ) для того, чтобы совершить ее с выключенным мотором? Чему будет равна при этом сила давления автомобиля на дорогу в точке В? Радиус петли (R=100) м, масса автомобиля (m=0,5) т.
Посмотрим, какую минимальную скорость может иметь автомобиль в верхней точке петли А, чтобы продолжать двигаться по окружности?
Центростремительное ускорение в этой точке дороги создается суммой силы тяжести и силы реакции дороги (frac{{mupsilon _A^2}}{R} = mg + {N_A}). Чем меньшую скорость имеет автомобиль, тем меньшая возникает сила реакции (N_A). При значении ({upsilon _A} = sqrt {gR}) эта сила обращается в нуль. При меньшей скорости сила тяжести превысит значение, необходимое для создания центростремительного ускорения, и автомобиль оторвется от дороги. При скорости ({upsilon _A} = sqrt {gR}) сила реакции дороги обращается в нуль только в верхней точке петли. В самом деле, скорость автомобиля на других участках петли будет большей, и как легко видеть из решения предыдущей задачи, сила реакции дороги тоже будет большей, чем в точке А. Поэтому, если автомобиль в верхней точке петли имеет скорость ({upsilon _A} = sqrt {gR}), то он нигде не оторвется от петли.
Теперь определим, какую скорость должен иметь автомобиль в нижней точке петли D, чтобы в верхней точке петли А его скорость ({upsilon _A} = sqrt {gR}). Для нахождения скорости (upsilon_D) можно воспользоваться законом сохранения энергии, как если бы автомобиль двигался только под действием силы тяжести. Дело в том, что сила реакции дороги в каждый момент направлена перпендикулярно перемещению автомобиля, а следовательно, ее работа равна нулю (напомним, что работа (Delta A = FDelta Scos alpha), где (alpha) — угол между силой (F) и направлением перемещения (Delta S)). Силой трения между колесами автомобиля и дорогой при движении с выключенным мотором можно пренебречь. Поэтому сумма потенциальной и кинетической энергии автомобиля при движении с выключенным мотором не меняется.
Приравняем значения энергии автомобиля в точках А и D. При этом будем отсчитывать высоту от уровня точки D, то есть потенциальную энергию автомобиля в этой точке будем считать равной нулю. Тогда получаем
[frac{{mupsilon _D^2}}{2} = frac{{mupsilon _A^2}}{2} + 2mgR.]
Подставляя сюда значение ({upsilon _A} = sqrt {gR}) для искомой скорости (upsilon _D), находим:
[{upsilon _D} = sqrt {5gR} approx 70;м/с approx 260;км/ч.]
Если автомобиль въедет в петлю с такой скоростью, то он сможет совершить ее с выключенным мотором.
Определим теперь, с какой силой при этом автомобиль будет давить на дорогу в точке В. Скорость автомобиля в точке В опять легко находится из закона сохранения энергии:
[frac{{mupsilon _D^2}}{2} = frac{{mupsilon _B^2}}{2} + mgRleft( {1 + cos alpha } right).]
Подставляя сюда значение ({upsilon_D} = sqrt {5gR}), находим, что скорость ({upsilon _B} = sqrt {gRleft( {3 – 2cos alpha } right)}).
Воспользовавшись решением предыдущей задачи, по заданной скорости находим силу давления в точке В:
[{N_B} = frac{{mupsilon _B^2}}{R} – mgcos alpha = 3mgleft( {1 – cos alpha } right) approx 2 cdot {10^3};Н]
Аналогично можно найти силу давления в любой другой точке «мертвой петли».
Упражнения
- Найти угловую скорость искусственного спутника Земли, вращающегося по круговой орбите с периодом обращения (T=88) мин. Найти линейную скорость движения этого спутника, если известно, что его орбита расположена на расстоянии (R=200) км от поверхности Земли.
- Диск радиуса (R) помещен между двумя параллельными рейками. Рейки движутся со скоростями (upsilon_1) и (upsilon_2). Определить угловую скорость вращения диска и скорость его центра. Проскальзывание отсутствует.
- Диск катится по горизонтальной поверхности без проскальзывания. Показать, что концы векторов скоростей точек вертикального диаметра находятся на одной прямой.
- Самолет движется по окружности с постоянной горизонтальной скоростью (upsilon=700) км/ч. Определить радиус (R) этой окружности, если корпус самолета наклонен на угол (alpha=5^circ).
- Груз массы (m=100) г, подвешенный на нити длины (l=1) м, равномерно вращается по кругу в горизонтальной плоскости. Найти период обращения груза, если при его вращении нить отклонена по вертикали на угол (alpha=30^circ). Определить также натяжение нити.
- Автомобиль движется со скоростью (upsilon=80) км/ч по внутренней поверхности вертикального цилиндра радиуса (R=10) м по горизонтальному кругу. При каком минимальном коэффициенте трения между шинами автомобиля и поверхностью цилиндра это возможно?
- Груз массой (m) подвешен на нерастяжимой нити, максимально возможное натяжение которой равно (1,5mg). На какой максимальный угол (alpha) можно отклонить нить от вертикали, чтобы при дальнейшем движении груза нить не оборвалась? Чему будет равно при этом натяжение нити в тот момент, когда нить составит угол (frac{alpha}{2}) с вертикалью?
Источник: Журнал “Квант”, №5 1972 г. Автор: Л. Асламазов.
Сумма углов треугольника
Сумма углов треугольника — это сумма
всех внутренних углов треугольника.
Так, как углы измеряются в градусах, соответственно значение
суммы углов треугольника также измеряется в градусах.
Сумма углов треугольника есть величина постоянная,
неизменяемая, она равна 180 градусам, вне зависимости
от вида рассматриваемого треугольника.
На рисунке 1 изображены равносторонний,
разносторонний и прямоугольный треугольники,
их суммы внутренних углов равны 180 градусам.
Также, существует теорема, которая доказывает
утверждение о том, что сумма углов треугольника
180 градусов, она называется теоремой
о сумме углов треугольника.
Теорема о сумме углов треугольника — это теорема в
геометрии о сумме углов произвольного треугольника на плоскости.
Каков максимально возможный угол в треугольнике?
Вы предполагаете, что наименьший возможный угол равен 1, а наибольший возможный угол равен 178 для треугольника.
Треугольник с такими углами имеет углы 1, 1, 178, так как сумма всех углов треугольника равна 180.
Мы можем взять угол меньше 1.
Какой угол в треугольнике самый большой?
В треугольнике: самая короткая сторона всегда противоположна наименьшему внутреннему углу. Самая длинная сторона всегда противоположна наибольшему внутреннему углу.
Какой правильный многоугольник имеет наибольший внутренний угол?
Многоугольник с наименьшим числом сторон — это треугольник. Правильный треугольник будет равносторонним треугольником, и каждый из его углов будет составлять 60 градусов, и это наименьший внутренний угол. Наибольший внутренний угол правильного многоугольника не ограничен.
Как найти угол треугольника?
Ответ: Если вы знаете два угла, вы можете вычислить третий, поскольку сумма всех углов равна 180 градусам. Если стороны — a, b, а гипотенуза — c (противоположный угол A), а углы — A, B и C, то Sin A = a / c, поэтому a = cSin A. Также Cos A = b / c, так что b = cCos A.
Какой угол самый маленький?
Всегда помните, что самый маленький угол в треугольнике всегда противоположен самой короткой стороне. Кроме того, самый большой угол всегда противоположен самой длинной стороне. Ответ: Наименьший угол составляет 55.49 градуса с округлением до двух знаков после запятой.
Какая сторона треугольника самая длинная?
Гипотенуза всегда противоположна прямому углу и всегда является самой длинной стороной треугольника.
Как найти недостающий угол в треугольнике?
Шаг 2: сложите два известных угла внутри треугольника. Чтобы определить неизвестный угол, обязательно используйте общую сумму 180 °. Если даны два угла, сложите их, а затем вычтите из 180 °. Если два угла одинаковы и неизвестны, вычтите известный угол из 180 °, а затем разделите на 2.
Могут ли 22 градуса быть внутренним углом правильного многоугольника?
Если 22 ° — внутренний угол, то 180 ° — 22 °, т.е. 158 ° — внешний угол. Таким образом, 22 ° не может быть внутренним углом правильного многоугольника.
Как называется 50-сторонний многоугольник?
В геометрии пятиугольник, или пятиугольник, или 50-угольник — это многоугольник с пятидесяти гранями.
Есть ли минимальное количество острых внутренних углов?
Любой выпуклый многоугольник может иметь не более трех острых внутренних углов. Для любого острого внутреннего угла внешний угол будет больше 3 градусов. Сумма всех внешних углов в многоугольнике всегда равна 90 градусам, поэтому не может быть 360 или более острых внутренних углов.
Как найти угол треугольника с 3 сторонами?
Пример
- Шаг 1 Нам известны две стороны: Соседняя (6,750) и Гипотенуза (8,100).
- Шаг 2 SOHCAHTOA сообщает нам, что мы должны использовать косинус.
- Шаг 3 Вычислить смежное значение / гипотенуза = 6,750 / 8,100 = 0.8333.
- Шаг 4 Найдите угол на вашем калькуляторе, используя cos-1 0.8333:
Как найти угол треугольника с двумя углами?
Чтобы найти третий угол треугольника, когда известны два других угла, вычтите количество градусов в двух других углах из 180o.
Как найти угол прямоугольного треугольника?
Ключевые моменты
- Теорема Пифагора, a2 + b2 = c2, a 2 + b 2 = c 2, используется для определения длины любой стороны прямоугольного треугольника.
- В прямоугольном треугольнике один из углов имеет значение 90 градусов.
- Самая длинная сторона прямоугольного треугольника называется гипотенузой, и это сторона, противоположная углу в 90 градусов.
Почему самая длинная сторона противоположна наибольшему углу?
Как вы могли догадаться, наибольший угол будет противоположным 18, потому что это самая длинная сторона. Следовательно, величина угла в середине будет противоположной 13. Теорема: если одна сторона треугольника длиннее другой стороны, то угол, противоположный длинной стороне, будет больше, чем угол, противоположный более короткой стороне.
Как называется самая длинная сторона треугольника?
Какой треугольник имеет максимальную площадь?
Свойство максимальной площади равносторонних треугольников. Частный случай изопериметрической теоремы говорит нам, что среди всех треугольников с одинаковым периметром равносторонний имеет наибольшую площадь.
Какая самая короткая сторона прямоугольного треугольника?
Третья сторона — сторона, противоположная прямому углу — называется гипотенузой прямоугольного треугольника. Две более короткие стороны обычно называют «ногами». Эта формула называется теоремой Пифагора в честь Пифагора.
Какая сторона треугольника A?
Стороны треугольника известны следующим образом: гипотенуза — это сторона, противоположная прямому углу, или определяемая как самая длинная сторона прямоугольного треугольника, в данном случае h. Противоположная сторона — это сторона, противоположная интересующему нас углу, в данном случае a.
Работает ли теорема Пифагора для каждого треугольника?
Теорема Пифагора утверждает, что для всех прямоугольных треугольников «квадрат гипотенузы равен сумме квадратов на двух других сторонах». Теорема Пифагора работает только для прямоугольных треугольников, поэтому вы можете использовать ее, чтобы проверить, имеет ли треугольник прямой угол или нет.
Как определить угол наклона?
Если два угла треугольника имеют размеры 60 и 80 градусов, сложите числа вместе, чтобы получить сумму 140. Затем вычтите эту сумму из общей меры углов для треугольника, которая составляет 180 градусов: 180 — 140 = 40 градусов.
Как решить треугольник SSA?
Решение треугольников SSA
- сначала используйте Закон синусов, чтобы вычислить один из двух других углов;
- затем добавьте три угла к 180 °, чтобы найти другой угол;
- наконец, снова используйте Закон синуса, чтобы найти неизвестную сторону.
Как решить треугольник SAS?
Решение треугольников SAS
- используйте Закон косинусов для вычисления неизвестной стороны,
- затем используйте Закон синусов, чтобы найти меньший из двух других углов,
- а затем добавьте три угла к 180 °, чтобы найти последний угол.
Может ли треугольник иметь только один острый угол?
Ни одного острого угла !! Потому что один острый означает два тупых угла, каждый больше 90 градусов. Два тупых угла в сумме составляют более 180 градусов. Но три угла треугольника должны составлять ровно 180 градусов. Таким образом, должно быть как минимум два острых угла.
Может ли треугольник не иметь острых углов?
Поскольку сумма углов треугольника в евклидовой геометрии должна составлять 180 °, ни один евклидов треугольник не может иметь более одного тупого угла. Острый и тупой треугольники — это два разных типа наклонных треугольников — треугольники, которые не являются прямыми треугольниками, потому что у них нет угла 90 °.
Треугольник. Формулы определения и свойства треугольников.
В данной статье мы расскажем о классификаци и свойствах основной геометрической фигуры — треугольника. А также разберем некоторе примеры решения задач на треугольники.
Содержание:
Определение треугольника
Треугольник — это фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами. В геометрических задачах треугольник обычно изображают специальным симовлом — △, после которго пишут названия вершин треугольника напр. △ABC.
Треугольник ABC (△ABC)
- Точки A, B и C — вершины треугольника. Принято писать их большими буквами.
- Отрезки AB, BC и СА — стороны треугольника. Обычно сторонам присваивают свои названия маленькими буквами. Имя выбирают по первой вершине каждой стороны. Напр. у стороны AB первая вершина А поэтому эта сторона называется а. Тоесть AB = a, BC = b, CА = c.
- Стороны треугольника в местах соединения образуют три угла, которым обычно дают названия буквами греческого алфавита α, β, γ. Причем напротив стороны a лежит угол α, b — β, с — γ.
Углы треугольника, также, можно обозначать специальным символом — ∠. После которого пишут вершины треугольника в таком порядке чтобы вершина обозначающегося угла была в серединке. Например:
Классификация треугольников
Все треугольники можно разделить на несколько видов, различающихся между собой величиной углов или длинами сторон. Такая классификация позволяет выделить особенности каждого из них.
1.Разносторонний – треугольник, у которого все стороны имеют разную длину.
2. Равнобедренный – треугольник, у которого длины двух сторон равны. Они называются боковыми сторонами AB и BC. Третья сторона называется основание СА. В данном треугольнике углы при основании равны ∠ α = ∠ β
3.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.
4.Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°
5.Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.
6. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и BC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (CА).
Свойства треугольника
1.Свойства углов и сторон треугольника.
- Сумма всех углов треугольника равна 180°:
- Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
- В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
2.Теорема синусов.
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c |
| sin α | sin β | sin γ |
3. Теорема косинусов.
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
4. Теорема о проекциях
Для остроугольного треугольника:
Медианы треугольника
Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.
Свойства медиан треугольника:
1. Медианы треугольника пересекаются в одной точке O. (Точка пересечения медиан называется центроидом)
2. В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
| AO | = | BO | = | CO | = | 2 |
| OD | OE | OF | 1 |
3. Медиана треугольника делит треугольник на две равновеликие по площади части
4. Треугольник делится тремя медианами на шесть равновеликих треугольников.
5. Из векторов, образующих медианы, можно составить треугольник.
Формулы медиан треугольника
Формулы медиан треугольника через стороны:
http://bigbangpokemon.com/ru/%D0%BB%D1%8E%D0%B4%D0%B8/%D0%BA%D0%B0%D0%BA%D0%BE%D0%B9-%D0%BD%D0%B0%D0%B8%D0%B1%D0%BE%D0%BB%D1%8C%D1%88%D0%B8%D0%B9-%D1%83%D0%B3%D0%BE%D0%BB-%D0%B2-%D1%82%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA%D0%B5.html
http://binary2hex.ru/triangle.html
Как найти угол альфа формула
Содержание
- Синус, косинус, тангенс и котангенс. Определения
- Угол поворота
- Числа
- Тригонометрические функции углового и числового аргумента
- Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Синус угла ( sin α ) — отношение противолежащего этому углу катета к гипотенузе.
Косинус угла ( cos α ) — отношение прилежащего катета к гипотенузе.
Тангенс угла ( t g α ) — отношение противолежащего катета к прилежащему.
Котангенс угла ( c t g α ) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.
Угол поворота
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от — ∞ до + ∞ .
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами ( 1 , 0 ) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 . Определение дается через координаты точки A 1 ( x , y ).
Синус (sin) угла поворота
Синус угла поворота α — это ордината точки A 1 ( x , y ). sin α = y
Косинус угла поворота α — это абсцисса точки A 1 ( x , y ). cos α = х
Тангенс угла поворота α — это отношение ординаты точки A 1 ( x , y ) к ее абсциссе. t g α = y x
Котангенс угла поворота α — это отношение абсциссы точки A 1 ( x , y ) к ее ординате. c t g α = x y
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой ( 0 , 1 ) и ( 0 , — 1 ). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Синус и косинус определены для любых углов α .
Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z )
Котангенс определен для всех углов, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z )
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности — точка A c координатами ( 1 , 0 ).
Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус (sin) числа t
Синус числа t — ордината точки единичной окружности, соответствующей числу t. sin t = y
Косинус числа t — абсцисса точки единичной окружности, соответствующей числу t. cos t = x
Тангенс числа t — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. t g t = y x = sin t cos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).
Можно сказать, что sin α , cos α , t g α , c t g α — это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Основные функции тригонометрии
Синус, косинус, тангенс и котангенс — основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A ( 1 , 0 ) на угол величиной до 90 градусов и проведем из полученной точки A 1 ( x , y ) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 ( x , y ) . Длина катета, противолежащего углу, равна ординате точки A 1 ( x , y ) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α , при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
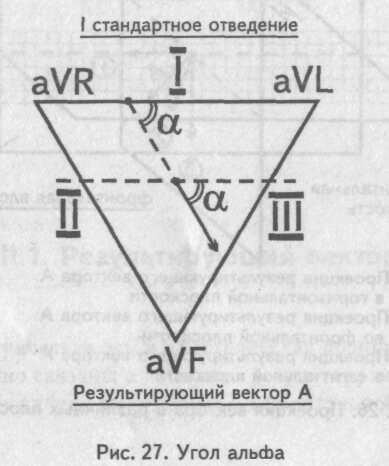
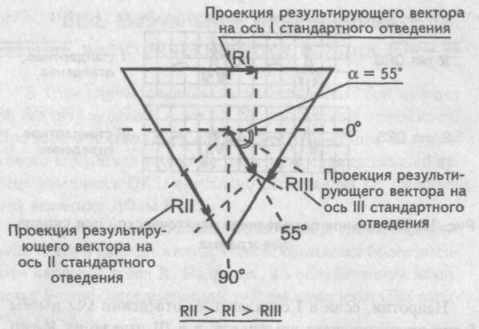
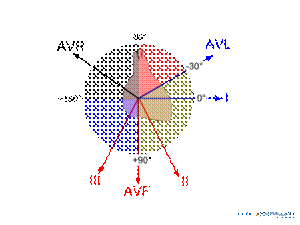
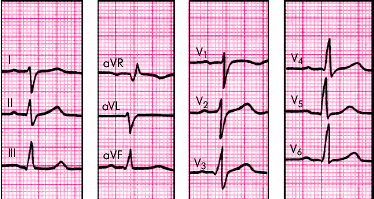
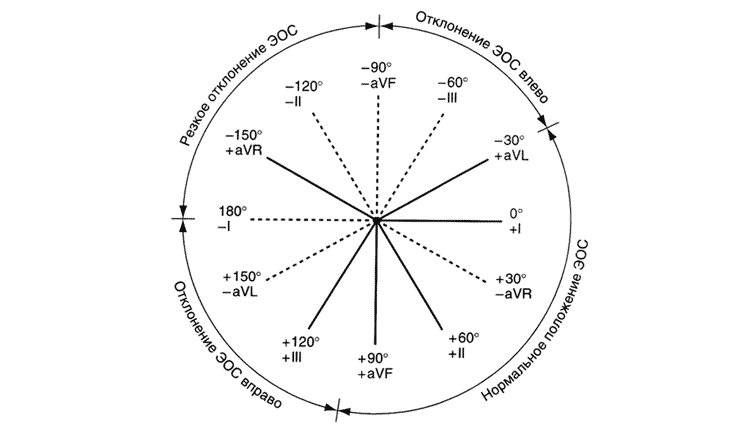
Мысленно поместим результирующий вектор возбуждения желудочков внутрь треугольника Эйнтховена. Угол, образованный направлением результирующего вектора и осью I стандартного отведения, и есть искомый угол альфа.
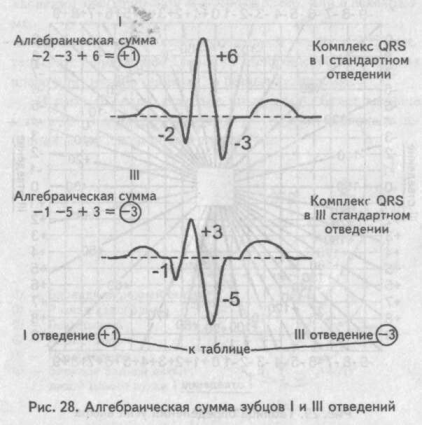
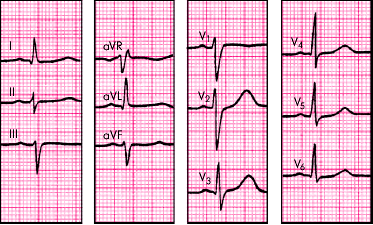
Величину угла альфа находят по специальным таблицам или схемам, предварительно определив на электрокардиограмме алгебраическую сумму зубцов желудочкового комплекса (Q + R + S) в I и III стандартных отведениях. Найти алгебраическую сумму зубцов желудочкового комплекса достаточно просто: измеряют в миллиметрах величину каждого зубца одного желудочкового комплекса QRS, учитывая при этом, что зубцы Q и S имеют знак минус (—), поскольку находятся ниже изоэлектрической линии, а зубец К — знак плюс (+). Если какой-либо зубец на электрокардиограмме отсутствует, то его значение приравнивается к нулю (0).
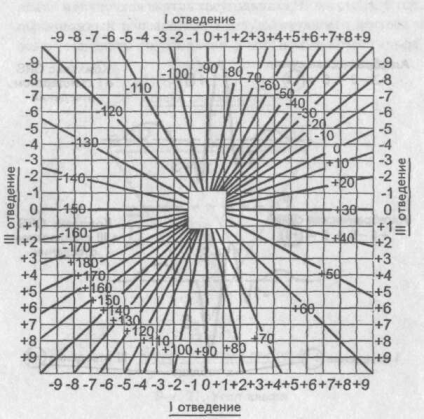
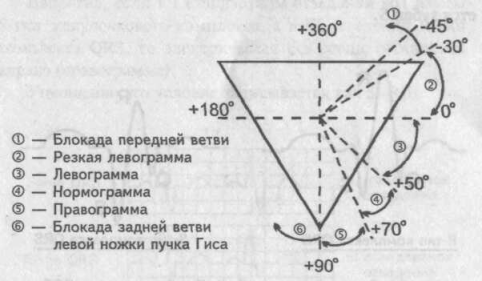
Далее, сопоставляя найденную алгебраическую сумму зубцов для I и III стандартных отведений, по таблице определяют значение угла альфа. В нашем случае он равен минус 70°. Таблица определения положения электрической оси сердца (по Дьеду)
Таблица определения угла альфа
Если угол альфа находится в пределах 50—70°, говорят о нормальном положении электрической оси сердца (электрическая ось сердца не отклонена), или нормограмме. При отклонении электрической оси сердца вправо угол альфа будет определяться в пределах 70—90°. В обиходе такое положение электрической оси сердца называют правограммой.
Если угол альфа будет больше 90° (например, 97°), считают, что на данной ЭКГ имеет место блокада задней ветви левой ножки пучка Гиса. Определяя угол альфа в пределах 50—0° говорят об отклонении электрической оси сердца влево, или о левограмме. Изменение угла альфа в пределах 0 — минус 30° свидетельствует о резком отклонении электрической оси сердца влево или, иными словами, о резкой левограмме. И наконец, если значение у г л а альфа будет меньше минус 30° (например, минус 45°) — говорят о блокаде передней ветви левой ножки пучка Гиса.
Пределы отклонения электрической оси сердца
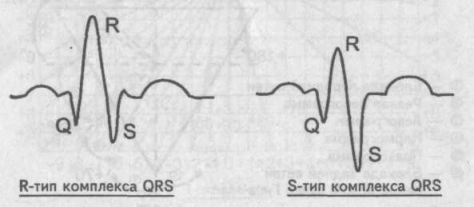
Определение отклонения электрической оси сердца по углу альфа с использованием таблиц и схем производят в основном врачи кабинетов функциональной диагностики, где соответствующие таблицы и схемы всегда под рукой. Однако определить отклонение электрической оси сердца можно и без необходимых таблиц. В этом случае отклонение электрической оси находят по анализу зубцов R и S в I и III стандартных отведениях. При этом понятие алгебраической суммы зубцов желудочкового комплекса комплекса QRS, заменяют визуально понятием «определяющий зубец» сопоставляя по абсолютной величине зубцы R и S . Говорят о «желудочковом комплексе R-типа», подразумевая, что в данном желудочковом комплексе более высоким является зубец К. Напротив, в «желудочковом комплексе S-типа» определяющим зубцом комплекса QRS является зубец S.
Сопоставление зубцов К и 3 комплекса QRS
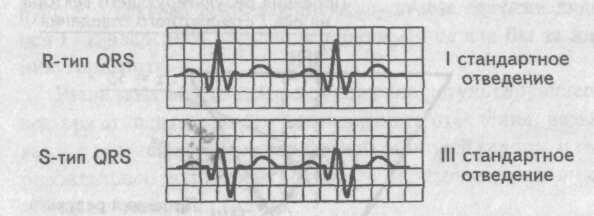
Если на электрокардиограмме в I стандартном отведении желудочковый комплекс представлен R-типом, а комплекс QRS в III стандартном отведении имеет форму S-типа, то в данном случае электрическая ось сердца отклонена влево (левограмма).
Схематично это условие записывается как RI-SIII.
Визуальное определение электрической оси сердца
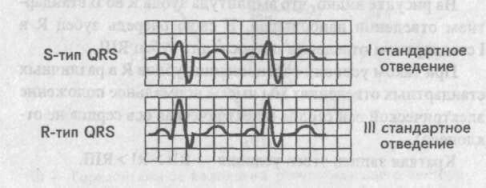
. Левограмма Напротив, если в I стандартном отведении мы имеем S-тип желудочкового комплекса, а в III отведении R-тип комплекса QRS, то электрическая ось сердца отклонена вправо (правограмма). Упрощенно это условие записывается как SI-RIII.
Визуальное определение электрической оси сердца
. Правограмма Результирующий вектор возбуждения желудочков расположен в норме во фронтальной плоскости так, что его направление совпадает с направлением оси II стандартного отведения.
Нормальное положение электрической оси сердца
(нормограмма) На рисунке видно, что амплитуда зубца R во II стандартном отведении наибольшая. В свою очередь зубец К в I стандартном отведении превосходит зубец RIII. При таком условии соотношения зубцов R в различных стандартных отведениях мы имеем нормальное положение электрической оси сердца (электрическая ось сердца не отклонена). Краткая запись этого условия — RII>RI>RIII.
Наиболее часто встречающиеся тригонометрические формулы:
(lacktriangleright) Основные тождества: [egin <|l|l|>hline sin^2 alpha+cos^2 alpha =1& mathrm, alpha cdot mathrm, alpha =1 &(sinalpha
e 0, cosalpha
e 0)[0.5ex] hline & mathrm, alpha=dfrac<sin alpha> <cos alpha>&mathrm, alpha =dfrac<cos alpha> <sin alpha>& 1+mathrm^2, alpha =dfrac1 <cos^2 alpha>& 1+mathrm^2, alpha=dfrac1<sin^2 alpha>& (cosalpha
e 0)& (sinalpha
e 0) hline end]
(lacktriangleright) Формулы сложения углов: [egin <|l|r|>hline & sin<(alphapm eta)>=sinalphacdot cosetapm sinetacdot cosalpha & cos<(alphapm eta)>=cosalphacdot coseta mp sinalphacdot sineta & hline & mathrm, (alphapm eta)=dfrac<mathrm, alphapm mathrm, eta><1 mp mathrm, alphacdot mathrm, eta> & mathrm, (alphapmeta)=-dfrac<1mp mathrm, alphacdot mathrm, eta><mathrm, alphapm mathrm, eta>& cosalphacoseta
e 0&sinalphasineta
e 0 hline end]
(lacktriangleright) Формулы двойного и тройного углов: [egin <|lc|cr|>hline sin <2alpha>=2sin alphacos alpha & qquad &qquad & cos<2alpha>=cos^2alpha -sin^2alpha sin alphacos alpha =dfrac12sin <2alpha>&& & cos<2alpha>=2cos^2alpha -1 & & & cos<2alpha>=1-2sin^2 alpha hline &&& mathrm, 2alpha = dfrac<2mathrm, alpha><1-mathrm^2, alpha> && & mathrm, 2alpha = dfrac<mathrm^2, alpha-1><2mathrm, alpha>&&& cosalpha
e 0, cos2alpha
e 0 &&& sinalpha
e 0, sin2alpha
e 0 hline &&& sin <3alpha>=3sin alpha -4sin^3alpha && & cos<3alpha>=4cos^3alpha -3cos alpha&&& hline end]
(lacktriangleright) Формулы понижения степени: [egin <|lc|cr|>hline &&& sin^2alpha=dfrac<1-cos<2alpha>>2 &&& cos^2alpha=dfrac<1+cos<2alpha>>2&&& hline end]
(lacktriangleright) Формулы произведения функций: [egin <|c|>hline sinalphasineta=dfrac12igg(cos<(alpha-eta)>-cos<(alpha+eta)>igg)\ cosalphacoseta=dfrac12igg(cos<(alpha-eta)>+cos<(alpha+eta)>igg)\ sinalphacoseta=dfrac12igg(sin<(alpha-eta)>+sin<(alpha+eta)>igg)\ hline end]
(lacktriangleright) Выражение синуса и косинуса через тангенс половинного угла: [egin <|l|r|>hline & sin<2alpha>=dfrac<2mathrm, alpha><1+mathrm^2, alpha> & cos<2alpha>=dfrac<1-mathrm^2, alpha><1+mathrm^2, alpha>& cosalpha
e 0 & sinalpha
e 0 hline end]
(lacktriangleright) Формула вспомогательного аргумента: [egin <|c|>hline ext<Частный случай> hline sinalphapm cosalpha=sqrt2cdot sin<left(alphapm dfrac<pi>4
ight)>\ sqrt3sinalphapm cosalpha=2sin<left(alphapm dfrac<pi>6
ight)>\ sinalphapm sqrt3cosalpha=2sin<left(xpm dfrac<pi>3
ight)>\ hline ext<Общий случай> hline asinalphapm bcosalpha=sqrtcdot sin<(alphapm phi)>, cosphi=dfrac a<sqrt>, sinphi=dfrac b<sqrt>\ hline end]
Зная идею вывода формул, вы можете запомнить лишь несколько из них. Тогда остальные формулы вы всегда сможете быстро вывести.
Вывод всех основных тождеств был рассказан в предыдущем разделе “Введение в тригонометрию”.
(lacktriangleright) Вывод формулы косинуса разности углов (cos<(alpha -eta)>=cosalphacoseta+sinalphasineta)
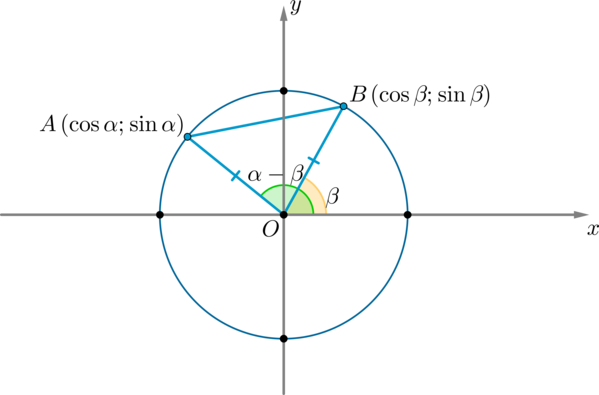
Рассмотрим тригонометрическую окружность и на ней углы (alpha) и (eta) . Пусть этим углам соответствуют точки (A) и (B) соответственно. Тогда координаты этих точек: (A(cosalpha;sinalpha), B(coseta;sineta)) .
Рассмотрим ( riangle AOB: angle AOB=alpha-eta) . По теореме косинусов:
(AB^2=AO^2+BO^2-2AOcdot BOcdot cos(alpha-eta)=1+1-2cos(alpha-eta) (1)) (т.к. (AO=BO=R) – радиус окружности)
По формуле расстояния между двумя точками на плоскости:
Таким образом, сравнивая равенства ((1)) и ((2)) :
Отсюда и получается наша формула.
(lacktriangleright) Вывод остальных формул суммы/разности углов:
Остальные формулы с легкостью выводятся с помощью предыдущей формулы, свойств четности/нечетности косинуса/синуса и формул приведения (sin x=cos(90^circ-x)) и (cos x=sin (90^circ-x)) :
разделим числитель и знаменатель дроби на (cosalphacoseta
e 0)
(при (cosalpha=0 Rightarrow mathrm,(alphapmeta)=mp mathrm,eta) , при (coseta=0 Rightarrow mathrm,(alphapmeta)=pm mathrm,alpha) ):
Таким образом, данная формула верна только при (cosalphacoseta
e 0) .
5) Аналогично, только делением на (sinalphasineta
e 0) , выводится формула котангенса суммы/разности двух углов.
(lacktriangleright) Вывод формул двойного и тройного углов:
Данные формулы выводятся с помощью предыдущих формул:
1) (sin 2alpha=sin(alpha+alpha)=sinalphacosalpha+sinalphacosalpha=2sinalphacosalpha)
Используя основное тригонометрическое тождество (sin^2alpha+cos^2alpha=1) , получим еще две формулы для косинуса двойного угла:
разделим числитель и знаменатель дроби на (cos^2alpha
e 0) (при (cosalpha=0 Rightarrow mathrm,2alpha=0) ):
Таким образом, эта формула верна только при (cosalpha
e 0) , а также при (cos2alpha
e 0) (чтобы существовал сам (mathrm,2alpha) ).
По тем же причинам при (sinalpha
e 0, sin2alpha
e 0) .
5) (sin3alpha=sin(alpha+2alpha)=sinalphacos2alpha+cosalphasin2alpha=sinalpha(1-2sin^2alpha)+cosalphacdot 2sinalphacosalpha=)
6) Аналогично выводится, что (cos3alpha=cos(alpha+2alpha)=4cos^3alpha-3cosalpha)
(lacktriangleright) Вывод формул понижения степени:
Данные формулы — просто по-другому записанные формулы двойного угла для косинуса:
1) (cos2alpha=2cos^2alpha-1 Rightarrow cos^2alpha=dfrac<1+cos2alpha>2)
2) (cos2alpha=1-2sin^2alpha Rightarrow sin^2alpha=dfrac<1-cos2alpha>2)
Заметим, что в данных формулах степень синуса/косинуса равна (2) в левой части, а в правой части степень косинуса равна (1) .
(lacktriangleright) Вывод формул произведения функций:
1) Сложим формулы косинуса суммы и косинуса разности двух углов:
Получим: (cos(alpha+eta)+cos(alpha-eta)=2cosalphacoseta Rightarrow cosalphacoseta=dfrac12Big(cos(alpha-eta)+cos(alpha+eta)Big))
2) Если вычесть из формулы косинуса суммы косинус разности, то получим:
3) Сложим формулы синуса суммы и синуса разности двух углов:
(lacktriangleright) Вывод формул суммы/разности функций:
Обозначим (alpha+eta=x, alpha-eta=y) . Тогда: (alpha=dfrac2, eta=dfrac2) . Подставим эти значения в предыдущие три формулы:
Получили формулу суммы косинусов.
Получили формулу разности косинусов.
Получили формулу суммы синусов.
4) Формулу разности синусов можно вывести из формулы суммы синусов:
Аналогично выводится формула суммы котангенсов.
(lacktriangleright) Вывод формул выражения синуса и косинуса через тангенс половинного угла:
(разделим числитель и знаменатель дроби на (cos^2alpha
e 0) (при (cosalpha=0) и (sin2alpha=0) ):)
2) Так же, только делением на (sin^2alpha) , выводится формула для косинуса.
(lacktriangleright) Вывод формул вспомогательного угла:
Данные формулы выводятся с помощью формул синуса/косинуса суммы/разности углов.
Рассмотрим выражение (asin x+bcos x) . Домножим и разделим это выражение на (sqrt,) :
(asin x+bcos x=sqrtleft(dfrac a<sqrt>sin x+ dfrac b<sqrt>cos x
ight)=sqrtig(a_1sin x+b_1cos xig))
Заметим, что таким образом мы добились того, что (a_1^2+b_1^2=1) , т.к. (left(dfrac a<sqrt>
ight)^2+left(dfrac b<sqrt>
ight)^2=dfrac=1)
Таким образом, можно утверждать, что существует такой угол (phi) , для которого, например, (cos phi=a_1, sin phi=b_1) . Тогда наше выражение примет вид:
(sqrt,ig(cos phi sin x+sin phicos xig)=sqrt,sin (x+phi)) (по формуле синуса суммы двух углов)
Значит, формула выглядит следующим образом: [<large,sin (x+phi),>> quad ext <где >cos phi=dfrac a<sqrt>] Заметим, что мы могли бы, например, принять за (cos phi=b_1, sin phi=a_1) и тогда формула выглядела бы как [asin x+bcos x=sqrt,cos (x-phi)]
(lacktriangleright) Рассмотрим некоторые частные случаи формул вспомогательного угла:
(a) sin xpmcos x=sqrt2,left(dfrac1<sqrt2>sin xpmdfrac1<sqrt2>cos x
ight)=sqrt2, sin left(xpmdfrac<pi>4
ight))
(b) sqrt3sin xpmcos x=2left(dfrac<sqrt3>2sin xpm dfrac12cos x
ight)=2, sin left(xpmdfrac<pi>6
ight))
(c) sin xpmsqrt3cos x=2left(dfrac12sin xpmdfrac<sqrt3>2cos x
ight)=2,sinleft(xpmdfrac<pi>3
ight))
Положения электрической оси
Положение оси определяется:
- Скоростными и качественными показателями прохождения импульса по проводящей системе миокарда.
- Способностью мышечного слоя к сокращению.
- Изменениями в организме, влияющими как на работу сердца в целом, так и его проводящей системы в частности.
У здорового человека, электрическая ось может занимать несколько положений.
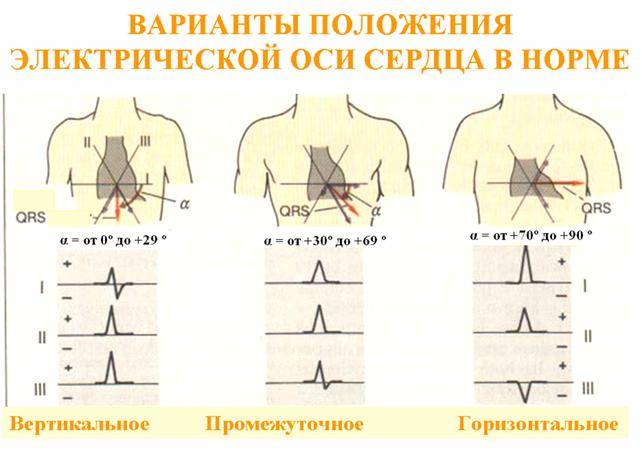
Итак, нормальным считается положение оси, находящееся в пределах от 0 до 90, при этом, она может быть направлена как вниз, так и в левую сторону. Направление электрической оси напрямую зависит от индивидуальных особенностей в анатомическом строении человека и бывает:
- Вертикальным. Характерно для худощавых людей высокого роста с небольшой грудной клеткой.
- Горизонтальным. Характерно для людей небольшого роста, с избыточным весом и широкой грудной клеткой. Положение оси, в таком случае, колеблется между 15 и -30
Отклонения оси
Как правило, анатомическое строение человека представляет собой смешанный тип, именно поэтому, электрическая ось может отклоняться от вертикали или горизонтали и иметь промежуточное положение. Смещение ЭОС – не диагноз, а следствие индивидуальных особенностей в строении или протекающих в организме болезней. Таким образом, ось сердца может быть отклонена:
Влево
Расположение электрической оси сердца от -30 дос-90 считается аномальным и может свидетельствовать об увеличении левого желудочка в размерах (гипертрофию). ГЛЖ так же не является диагнозом, но указывает на такие заболевания, как:
- Гипертензия – сопротивление сосудов кровотоку.
- Инфаркт левого желудочка.
- Врожденные или приобретенные пороки сердца.
- Кардиомиопатия – нарушение способности к сокращению мышцы.
- Миокардит.
- Переизбыток и отложение кальция в сердечной мышце.
Кроме вышеперечисленного, причиной отклонения оси в левую сторону может стать нарушение в функционировании клапана ЛЖ, его недостаточность, блокада сердечной мышцы или нарушение проводимости в ЛЖ. Таким заболеваниям подвержены люди, перенесшие ревматическую лихорадку, кроме того, в группу риска входят спортсмены.
Вправо
Расположение электрической оси сердца от +90 до +180 считается патологией и может указывать на увеличение правого желудочка. Так как именно из него кровь поступает в легкие, причиной возникновения ГПЖ может стать:
- Заболевания дыхательного аппарата, вызывающие гипертрофию.
- Инфаркт правого желудочка.
- Нарушение проводимости ПЖ.
- Деформация легочной артерии.
- Гипертония.
- Непроходимость кровотока в ЛА, в результате образования тромбов.
- Пороки сердца, приводящие к застою в легких.
- Эмфизема.
Причиной отклонения оси в правую сторону может стать ишемическая болезнь, сердечная недостаточность и кардиомиопатия.
Симптомы
Отклонение горизонтально электрической оси может не сопровождаться выраженной симптоматикой и не проявлять себя долгое время. Как правило, самочувствие пациента ухудшается при наступлении осложнений гипертрофии сердечной мышцы.
Признаками отклонения ЭОС от нормы могут стать головные боли, отдышка, удушье, отечность конечностей. Проявление любого, из вышеперечисленных признаков, является основанием для обращения к кардиологу и полному обследованию организма.
Лечение
Важно понимать, что вышеперечисленные заболевания не могут быть диагностированы исключительно по факту смещения горизонтальной электрической оси. Расположение ЭОС за пределами границ от 0 до +900 является показанием к консультации кардиолога и дальнейшим обследованиям
Наиболее распространенной причиной отклонения оси сердца является гипертрофия. Симптоматика, сопровождающая заболевание, позволит поставить предварительный диагноз, подтвердить или опровергнуть который впоследствии сможет ультразвуковое исследование. В том случае, когда ранее снятые ЭКГ не зафиксировали патологии, а отклонения проявились за достаточно короткий промежуток времени, причиной смещений ЭОС может являться блокада.
ВАЖНО! Само по себе смещение не требует лечения, назначаемая терапия направлена на устранение причин возникновения патологии. Видео:
Видео:
Причины отклонения оси сердца
Электрическая ось сердца отражает направление распространения импульса по органу, поэтому она может изменяться не только при отклонении органа от его нормального положения (0 – (+90) градусов), но и при следующих патологических изменениях:
- Гипертрофия желудочков – увеличение толщины миокарда приводит к изменению формы органа и нарушению его функций. Гипертрофия является синдромом, который может наблюдаться при большом количестве заболеваний, в том числе ишемической патологии сердца (ИБС), клапанных пороках, хронических болезнях легких и т.д. Горизонтальное положение электрической оси на ЭКГ в данном случае может быть признаком патологии.
- Выраженная гипертрофия предсердий – толщина миокарда желудочков в норме значительно больше передне-заднего размера стенки предсердий. Поэтому к отклонению ЭОС могут привести только выраженные изменения данных отделов сердца. К этому состоянию нередко приводят стенозы (сужение) атриовентрикулярных клапанов и легочные заболевания (чаще вызывает отклонение ЭОС вправо).
- Дилатация отделов сердца – увеличение размеров полостей желудочков и предсердий также сопровождается изменением формы органа и его смещением. Дилатация может являться следствием длительного повышения артериального давления, миокардиты и панкардиты (воспаление всех сердечных оболочек), ИБС.
- Аневризма сердца – это истончение и «растяжение» одного из участков сердечной стенки (нередко верхушки сердца). Наличие аневризмы приводит к увеличению вмещаемого объема крови в полости и нарушению нормального кровотока. Следует отметить, что возможным осложнением аневризмы является ее разрыв, который часто приводит к летальному исходу, поэтому данную патологию необходимо своевременно выявлять и проводить лечение.
- Кардиомиопатии – группа врожденных патологий, сопровождающихся нарушением нормальной структуры сердечной стенки. Может проявляться в следующих вариантах: гипертрофия, дилатация камер или уменьшение размеров органа (рестриктивное нарушение).
- Наличие дополнительных проводящих путей. Дополнительные нервные пучки, соединяющие генераторы импульса, могут становиться причиной нарушения нормального распространения импульса. Их наличие определяется с помощью стандартной методики электрокардиографии.
- Блокады проводящих путей и синдром слабости синусового узла – нарушения генерации и проведения электрических импульсов могут нарушать положения ЭОС, за счет изменения направления вектора.
-
Декстрокардия – аномальное (правостороннее) положение сердца является одной из редких состояний, при которых электрическая ось сердца выражено отклонена вправо, при этом другие патологические симптомы у пациента отсутствуют.
Нормальное расположение ЭОС и причины ее смещения
Электрическая ось сердца — понятие, которое отображает электрические процессы в этом органе. Направление ЭОС показывает все биоэлектрические изменения в сумме, происходящие при работе сердечной мышцы.
Во время снятия электрокардиограммы каждый электрод фиксирует биоэлектрическую реакцию в строго отведенной части миокарда. Затем врачи для расчета положения и угла ЭОС представляют грудную клетку в виде системы координат, чтобы в дальнейшем спроецировать на нее показатели электродов.
Возможно горизонтальное положение ЭОС, вертикальное и ряд других вариантов.
Электрическая ось сердца — понятие, которое отображает электрические процессы в этом органе.
Важность проводящей системы сердца для ЭОС
Проводящая система сердечной мышцы — это атипичные мышечные волокна, которые соединяют различные части органа и помогают ему сокращаться синхронно.
Началом ее считается синусовый узел, располагающийся между устьями полых вен, поэтому у здоровых людей сердечный ритм синусовый. Когда в синусовом узле возникает импульс, миокард сокращается.
Если происходит сбой работы проводящей системы, электрическая ось меняет свое положение, так как именно там происходят все изменения перед сокращением сердечной мышцы.
Направления оси и ее смещение
Так как вес левого желудочка сердечной мышцы у полностью здоровых взрослых больше, чем правого, там все электрические процессы происходят сильнее. Поэтому ось сердца обращена на него.
- Нормальное положение. Если спроецировать местонахождение сердца на предполагаемую систему координат, то нормальным будет считаться направление левого желудочка от +30 до +70 градусов. Но оно зависит от особенностей каждого человека, поэтому нормой этого показателя у разных людей считается диапазон от 0 до +90 градусов.
- Горизонтальное положение (от 0 до +30 градусов). Отображается на кардиограмме у низкорослых людей с широкой грудиной.
- Вертикальное положение. ЭОС находится в диапазоне от +70 до +90 градусов. Наблюдается у высокорослых людей с узкой грудной клеткой.
Варианты расположения ЭОС.
Существуют болезни, при которых происходит смещение оси:
- Отклонение влево. Если ось отклоняется влево, это может свидетельствовать об увеличении (гипертрофии) левого желудочка, которое указывает на его перегрузку. Такое состояние часто вызывается артериальной гипертензией, протекающей длительное время, когда кровь с трудом проходит по сосудам. В итоге левый желудочек усиленно работает. Отклонение влево возникает при различных блокадах, поражениях клапанного аппарата. При прогрессирующей сердечной недостаточности, когда орган не может выполнять полностью свои функции, электрокардиограмма также фиксирует смещение оси влево. Все эти заболевания заставляют левый желудочек работать на износ, поэтому его стенки становятся толще, импульс по миокарду проходит намного хуже, ось отклоняется влево.
- Смещение вправо. Отклонение электрической оси сердца вправо чаще всего происходит при увеличении правого желудочка, например, если у человека имеются сердечные заболевания. Это могут быть кардиомиопатия, ишемическая болезнь, аномалии строения сердечной мышцы. Правое отклонение вызывают и такие проблемы с дыхательной системой, как обструкция легких, бронхиальная астма.
Показатели нормы ЭОС
| Ребенок от рождения до года. | Вертикальная. | 60–150 ударов. |
| Дети от года до 6 лет. | Вертикальная нормальная, иногда горизонтальная. | 95–128 ударов. |
| Дети и подростки в возрасте от 7 до 15 лет. | Нормальная или вертикальная. | 65–90 ударов. |
| Взрослые. | Нормальная. | 60–90 ударов, ритм регулярный синусовый. |
Итак, у здоровых людей направление оси сердца может быть нормальным, горизонтальным, вертикальным, сердечный ритм — синусовый регулярный.
Если ритм не синусовый, то это свидетельствует о каком-либо заболевании. Ритм синусовый нерегулярный — это показатель заболевания, если он сохраняется и во время задержки дыхания. Смещение сердечной оси влево или вправо может указывать на проблемы с сердцем, органами дыхания. Диагноз ни в коем случае не должен ставиться только на основании смещения ЭОС.
Определить заболевание и назначить лечение может врач-кардиолог после ряда дополнительных исследований.
Поиск ближайшей клиники Найдите ближайшую к дому клинику в Вашем городе
Как клинически проявляется синдром удлиненного QT?
Симптоматика врожденной формы синдрома начинает проявляться еще в детском возрасте. Если ребенок родился глухонемым, врач уже имеет право заподозрить синдром Джервелла-Ланге-Нильсена. Если же ребенок хорошо слышит и способен издавать звуки (гуление, речь), но у него наблюдаются эпизоды потери сознания, необходимо подумать о синдроме Романа-Уорда. Потеря сознания может наблюдаться во время крика, плача, стресса или при физической нагрузке. Обычно обморок сопровождается частым пульсом (более 150-200 в минуту) и ощущением учащенного сердцебиения – сердце трепещет в груди. Эпизоды обмороков могут возникать как редко, так и до нескольких раз в день.
По мере взросления подобные симптомы без лечения сохраняются, и могут привести к внезапной сердечной смерти.
Клинические проявления приобретенной формы также характеризуются обмороками с тахикардией, а в межприступный период отмечается головокружение, общая слабость и утомляемость, обусловленные синусовой брадикардией (пульс менее 50 в минуту).
Методы диагностики
При ГПЖ патологические изменения фиксируются не только в миокарде. Со временем для них характерно распространение на легочные артерии и сосуды, что вызывает развитие других недугов:
- склероз аорты;
- гипертензия малого круга кровообращения;
- синдром Эйзенменгера (превышение давления в легочной артерии над аортальным).
Своевременная диагностика ГПЖ позволяет не только предотвратить развитие этих патологий, но и значительно облегчить борьбу с синдромом в целом. Подтвердить или опровергнуть наличие правожелудочной гипертрофии можно только благодаря аппаратым кардиологическим исследованиям:
- электрокардиография;
- эхокардиография (ультразвуковое исследование структуры сердечной мышцы).
Электрокардиограмма как метод диагностики ГПЖ менее показателен. Гипертрофия правого желудочка на ЭКГ выражается только в изменени зубцов кардиограммы, что может свидетельствовать только о факте изменения размеров желудочка, степень выраженности патологии таким образом определить нельзя.
Синдром ГПЖ на электрокардиографии «засвечивается» только при средней и острой формах течения.
Гораздо большую диагностическую ценность имеет эхокардиограмма.
Данный метод исследования позволяет определить не только наличие увеличения правожелудочной области, но и ее точные размеры, а также диагностировать дефекты структуры тканей сердца.
Эхокардиографию как метод диагностики ГПЖ часто сочетают с допплерографией, что позволяет дополнительно исследовать направление и скорость кровяных потоков.
Такой способ исследования дает возможность определить правожелудочную гипертрофию даже в умеренной форме течения, благодаря чему можно предотвратить прогрессирование роста кардиомицитов в сердечной мышце.
Постановка диагноза
Смещение ЭОС не является самостоятельным заболеванием. Такое отклонение провоцируется иными патологическими процессами. По этой причине, если на электрокардиограмме удалось определить отклонение электрической оси, по одному только ЭКГ поставить точный диагноз не получится. Пациенту рекомендуют пройти дополнительное диагностическое обследование.
Современные клиники имеют в распоряжении соответствующий инструментарий, используя который удаётся конкретизировать точные причины, провоцирующие сдвиг ЭОС. В качестве инструментальной диагностики применяются:
- велоэргометрия (состояние сердечной мышцы оценивается после дополнительной нагрузки, в качестве которой пациентам предлагают беговую дорожку или велотренажёр);
- УЗИ сердца (визуализируется структура органа, оценивается степень нарушений);
- кардиограмма;
- рентген грудной клетки;
- ангиография (оценивается состояние артерий);
- эхокардиоскопия (оценивается состояние желудочков сердца).
УЗИ сердца ка метод диагностики
Определение смещения электрической оси сердца и точные причины такого смещения позволят врачу разработать план лечения.
Лечение
Отклонение электрической оси сердца влево от нормального положения само по себе не является заболеванием. Это признак, определяемый при помощи инструментального исследования, который позволяет выявить нарушения в работе сердечной мышцы.
Ишемия, сердечная недостаточность и некоторые кардиопатии лечатся при помощи лекарственных препаратов. Дополнительное соблюдение диеты и здорового образа жизни приводит к нормализации состояния пациента.
В тяжелых случаях требуется оперативное вмешательство, например, при врожденных или приобретенных пороках сердца. При тяжелом нарушении проводящей системы может понадобиться трансплантация кардиостимулятора, который будет подавать сигналы непосредственно на миокард и вызывать его сокращение.
Чаще всего отклонение не является угрожающим симптомом. Но если ось меняет свое положение резко, достигает значений более 90, то это может свидетельствовать о блокаде ножек пучка Гисса и грозит остановкой сердца. Такой пациент требует срочной госпитализации в отделение интенсивной терапии. Резкое и выраженное отклонение электрической оси сердца влево выглядит так:
Обнаружение смещения электрической оси сердца не повод для беспокойства. Но при выявлении этого признака следует немедленного обратиться к врачу для дальнейшего обследования и выявления причины такого состояния. Ежегодные плановые проведения электрокардиографии позволяют своевременно обнаружить нарушения в работе сердца и незамедлительно начать терапию.
ЭОС, это сокращение от термина «Электрическая ось сердца», который применяют в функциональной диагностике и кардиологии. Он отражает электрические процессы, происходящие в сердце.
Направлением электрической оси сердца называют сумму биоэлектрических изменений, которые возникают при каждом сокращении сердечной мышцы.
Сердце является трёхмерным органом, из расчета направления электрической оси сердца, грудная клетка должна быть представлена в виде системы координат.
На электроды в процессе снятия электрокардиограммы передается биоэлектрический сигнал, который инициируется в каждом участке миокарда. Спроецировав сигналы с электродов на условную систему координат, вычисляют и угол электрической оси, расположение определяется расположением и мощностью электрических сигналов.
Проводящая система миокарда состоит из хорошо иннервированных атипичных мышечных волокон, обеспечивающих синхронное сокращение сердца.
Когда в синусовом узле возникает электрический импульс, который передается через предсердно-желудочковый узел к пучку Гиса и начинается сокращение сердца.
Проводящая система сердца представляет собой сильный источник электрических импульсов, и в ней раньше всего начинаются электрические изменения, которые предшествуют сердечному сокращению. Если в этой системе имеются нарушения, электрическая ось сердца заметно меняет свое положение, что может быть зафиксировано.
Норма положения электрической оси сердца
Поскольку сердечная мышца левого желудочка значительно больше, чем правого, то и электрические процессы, имеющие место в левом желудочке, будут сильнее, и электрическая ось сердца будет направляться на него.
Спроецировав на системе координат положение сердца здорового человека, обнаружим, что левый желудочек будет находиться в области от +30 до + 70 градусов, что и считается нормальным положением оси. При этом следует учитывать, что направление оси весьма зависимо от индивидуальных особенностей, в том числе анатомических, каждого человека и у здоровых людей может колебаться от 0 до +90 градусов:
В частности, вертикальное положение ЭОС, это диапазон (+ 70)–(+90) градусов, характерно для астеников худых и высоких людей.
Для гиперстеников, невысоких, коренастых людей с широкой грудной клеткой характерно горизонтальное положение электрической оси сердца в диапазоне 0 –(+ 30) градусов.
Естественно, чаще встречаются люди с промежуточными типами телосложения, соответственно и ЭОС занимает промежуточное значение.
У здоровых людей могут встречаться, вертикальное и полу вертикальное, горизонтальное и полу горизонтальное, а также нормальное положение ЭОС.
У совершенно здорового человека в заключении после ЭКГ могут написать, например, что ритм синусовый, ЭОС вертикальная, ЧСС – 78, и это является вариантом нормы.
Смещение сердца вокруг продольной оси дает возможность найти положение органа в пространстве и, нередко, бывает дополнительным фактором при диагностике различных патологий.
Электрическая ось сердца (ЭОС)
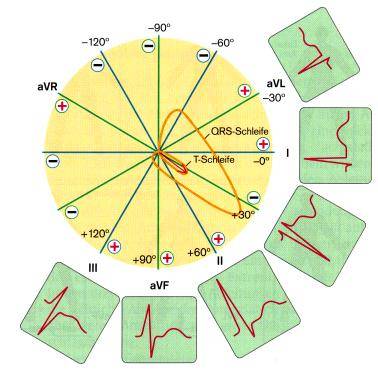
Если нарисовать круг и через его центр провести линии, соответствующие направлениям трех стандартных и трех усиленных отведений от конечностей, то получим 6-осевую систему координат. При записи ЭКГ в этих 6 отведениях записывают 6 проекций суммарной ЭДС сердца, по которым можно оценить расположение патологического очага и электрическую ось сердца.
Формирование 6-осевой системы координат. Отсутствующие отведения заменяются продолжением уже имеющихся.
Электрическая ось сердца — это проекция суммарного электрического вектора ЭКГ-комплекса QRS (он отражает возбуждение желудочков сердца) на фронтальную плоскость. Количественно электрическая ось сердца выражается углом α между самой осью и положительной (правой) половиной оси I стандартного отведения, расположенной горизонтально.
Наглядно видно, что одна и та же ЭДС сердца в проекциях на разные отведения дает различные формы кривых.
Правила определения положения ЭОС во фронтальной плоскости такие: электрическая ось сердца совпадает с тем из 6 первых отведений, в котором регистрируются самые высокие положительные зубцы, и перпендикулярна тому отведению, в котором величина положительных зубцов равна величине отрицательных зубцов. Два примера определения электрической оси сердца приведены в конце статьи.
Варианты положения электрической оси сердца:
- нормальное: 30° > α α α α α
Полная блокада передней ветви левой ножки пучка Гиса. ЭОС резко отклонена влево (α ≅− 30°), т.к. самые высокие положительные зубцы видны в aVL, а равенство зубцов отмечается во II отведении, которое перпендикулярно aVL.
Полная блокада задней ветви левой ножки пучка Гиса. ЭОС резко отклонена вправо (α ≅ +120°), т.к. самые высокие положительные зубцы видны в III отведении, а равенство зубцов отмечается в отведении aVR, которое перпендикулярно III.
Электрокардиограмма отражает только электрические процессы в миокарде: деполяризацию (возбуждение) и реполяризацию (восстановление) клеток миокарда.
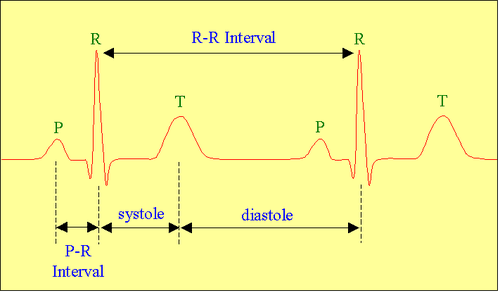
Соотношение интервалов ЭКГ с фазами сердечного цикла (систола и диастола желудочков).
В норме деполяризация приводит к сокращению мышечной клетки, а реполяризация — к расслаблению. Для упрощения дальше я буду вместо “деполяризации-реполяризации” иногда использовать “сокращение-расслабление”, хотя это не совсем точно: существует понятие “электромеханическая диссоциация“, при которой деполяризация и реполяризация миокарда не приводят к его видимому сокращению и расслаблению.
Элементы нормальной ЭКГ
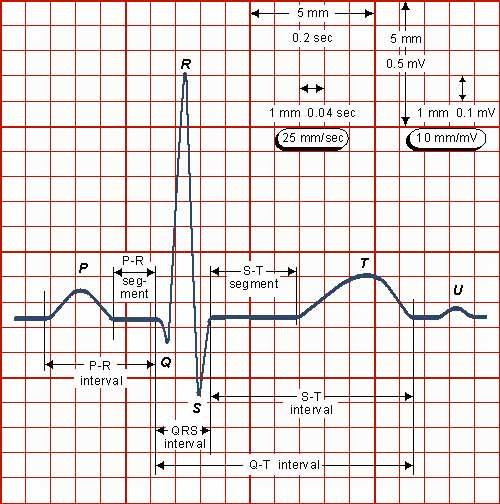
Прежде, чем перейти к расшифровке ЭКГ, нужно разобраться, из каких элементов она состоит.
Зубцы и интервалы на ЭКГ. Любопытно, что за рубежом интервал P-Q обычно называют P-R.
Любая ЭКГ состоит из зубцов, сегментов и интервалов.
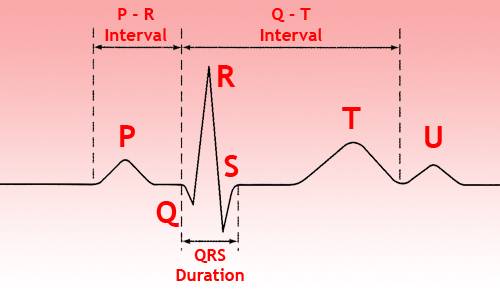
ЗУБЦЫ — это выпуклости и вогнутости на электрокардиограмме. На ЭКГ выделяют следующие зубцы:
- P (сокращение предсердий),
- Q, R, S (все 3 зубца характеризуют сокращение желудочков),
- T (расслабление желудочков),
- U (непостоянный зубец, регистрируется редко).
СЕГМЕНТЫ Сегментом на ЭКГ называют отрезок прямой линии (изолинии) между двумя соседними зубцами. Наибольшее значение имеют сегменты P-Q и S-T. Например, сегмент P-Q образуется по причине задержки проведения возбуждения в предсердно-желудочковом (AV-) узле.
ИНТЕРВАЛЫ Интервал состоит из зубца (комплекса зубцов) и сегмента. Таким образом, интервал = зубец + сегмент. Самыми важными являются интервалы P-Q и Q-T.
Зубцы, сегменты и интервалы на ЭКГ
Обратите внимание на большие и мелкие клеточки (о них ниже)
Дата добавления: 2015-10-12 ; просмотров: 13134 . Нарушение авторских прав
ПОРЯДОК ДЕЙСТВИЙ ПРИ ОПРЕДЕЛЕНИИ ЭЛЕКТРИЧЕСКОЙ ОСИ СЕРДЦА
1. Измеряем величину зубцов q (если есть) R и S в I отведении и проводим нехитрое вычисление: R — (q+S) = величина (длина) первого вектора (а)
2. Измеряем величину зубцов q (если есть) R и S в aVF отведении и проводим нехитрое вычисление: R — (q+S) = величина (длина) воторого вектора (b)
3. Находим на оси координат ось подписанную «I» и откладываем на ней величину первого вектора — a (красный цвет)
4. Находим на оси координат ось подписанную «aVF» и откладываем на ней величину второго вектора — b (синий цвет)
5. Опускаем перпендикуляры с осей, так чтобы получился прямоугольник (в данном случае) или параллелограмм.
6. Проводим результирующий вектор (зеленый цвет) от точки пересечения всех осей до пересечения перпендикуляров
7. Измеряем угол образованный между нулевой осью и результирующим (зеленым) вектором, это и будет угол альфа или электрическая ость сердца.
Если посмотреть на картинку то все становится понятным, гораздо сложнее все это описывать в тексте, но есть один момент которые важно соблюдать:
Если после вычисления длины вектора получилось отрицательное число, то откладывать вектор нужно соответственно на отрицательную часть оси (обозначена на оси координат пунктиром), то есть в другую сторону от места переселения всех осей!
Посмотрите на первый «круг», если при вычислении R(aVF)-S(aVF) вы получаете отрицательное число, к примеру (-6,5 мм), то откладывать это вектор нужно в другом направлении
Будьте также внимательны с осями aVL и aVR, обратите внимание где у них находится положительная и отрицательная часть
На втором «круге» представлен вариант когда вы хотите взять другие отведения для определения оси. Здесь после опущения перпендикуляров образуется параллелограмм, но суть от этого не меняется.
Теперь давайте разберемся какие варианты электрической оси бывают.
Ну что, теперь давайте рассмотрим 5 примеров ЭКГ с различными осями.
Нормальная электрическая ось сердца
Направление оси сердца вычисляется в градусах. Для этого используют такое понятие, как угол альфа. Его образует горизонтальная линия, которую проводят через электрический центр сердца. Чтобы его определить, ось первого отведения ЭКГ смещается к центру Эйнтховена. Это треугольник, вершинами его служат кисти разведенных в сторону рук и левая стопа.
У здорового человека электрическая ось колеблется в пределах 30 — 70 градусов. Это обусловлено тем, что левый желудочек сильнее развит, чем правый, следовательно, импульсов от него исходит больше. Такое положение сердца бывает при нормостеническом телосложении, а ЭКГ называется нормограммой.
А здесь подробнее том, когда у людей сердце справа.
Патологические отклонения оси: о чем они говорят и каковы последствия?
Непосредственно ситуация не может служить основанием для постановки конкретного диагноза, только указывая на наличие электрических нарушений. Ни один кардиолог не станет убеждать вас в наличии патологии только по ЭОС. Чтобы установить факт заболевания, необходимо подкрепить заключение обследования правильным клиническим опросом и дополнительными диагностическими мерами.
На положение ЭОС влияет ряд факторов:
- врожденные сердечные пороки;
- вторичные изменения в анатомических соотношениях между правыми и левыми отделами сердца;
- аномальное расположение органов в грудной полости (декстрокардия, викарная эмфизема после лобэктомии);
- деформация грудной клетки (кифоз, сколиоз, килевидное или воронкообразное искривление);
- сбои в проводящей системе органа (особенно в пучках Гисса), которые вызывают нарушения сердцебиения;
- кардиомиопатии различного генеза;
- длительный анамнез гипертонической и ишемической болезни сердца (ИБС);
- хроническая сердечная недостаточность;
- болезни органов дыхания с обструктивным компонентом (ХОБЛ, бронхиальная астма, эмфизема);
- декомпенсированная печеночная недостаточность (асцит, метеоризм).
При каких заболеваниях наблюдаются нарушения?
Отклонение электрической оси сердца влево (левограмма) (угол α от 0 до -30 0 ) имеет несколько причин:
- Гипертрофия левой половины сердца. Угол α прямо пропорционален степени роста массы ЛЖ. Патология развивается при идиопатической кардиомиопатии, артериальной гипертензии, чрезмерных нагрузках («спортивное сердце»), ИБС, кардиосклерозе.
- Инфаркт миокарда (с некрозом по задней стенке).
- Патология внутрисердечной проводимости. Чаще всего это блокада левой ножки или передне-верхней ветви пучка Гисса.
- Желудочковая тахикардия.
- Клапанные пороки сердца.
- Миокардит.
Выделяют также резкое отклонение ЭОС влево, когда угол α >-30 0 .
Отклонение электрической оси сердца вправо (правограмма) (угол α > +90 0 ) наблюдается при:
- Сбоях в проведении нервного импульса по волокнам пучка Гисса.
- Стенозе легочного ствола (когда повышается давление в правом желудочке).
- ИБС.
- Инфаркте миокарда правых отделов.
- Кардиореспираторных заболеваниях, сформировавших «легочное сердце» (при этом ЛЖ неполноценно функционирует и возникает перегрузка правого желудочка).
- Тромбоэмболии ветвей легочной артерии (из-за закупорки нарушается газообмен в легких, сужаются сосуды малого круга кровообращения и возникает перегрузка ПЖ).
- Стенозе митрального клапана (после ревматической лихорадки). Срастание между собой створок препятствует полноценному изгнанию крови с левого предсердия, что вызывает легочную гипертензию и перегружает ПЖ.
Резкое отклонение ЭОС вправо наблюдается при значении угла α = +120 0 .
Стоит помнить, что ни одно с вышеперечисленных заболеваний не может быть диагностировано на основании исключительно положения ЭОС. Этот параметр – только вспомогательный критерий при выявлении любого патологического процесса.
Отклонение оси зачастую – не признак острого состояния. Но если зарегистрировано резкое нарушение ЭОС с достижением значения более +90 0 , то это может свидетельствовать о внезапном расстройстве проводимости в миокарде и угрожать остановкой сердца. Такие пациенты требуют немедленной специализированной медицинской помощи с целью поиска причины столь резкого изменения направления тока.
Экг эос — когда проводиться процедура, расшифровка результатов
Мысленно поместим результирующий вектор возбуждения желудочков внутрь треугольника Эйнтховена. Угол, образованный направлением результирующего вектора иосью I стандартного отведения, и есть искомый угол альфа.
Угол альфа
Величину угла альфа находят по специальным таблицам или схемам, предварительно определив на электрокардиограмме алгебраическую сумму зубцов желудочкового комплекса (Q R S) в I и III стандартных отведениях.
Найти алгебраическую сумму зубцов желудочкового комплекса достаточно просто: измеряют в миллиметрах величину каждого зубца одного желудочкового комплекса QRS, учитывая при этом, что зубцы Q и S имеют знак минус (—), поскольку находятся ниже изоэлектрической линии, а зубец R — знак плюс ( ).
Алгебраическая сумма зубцов отведений I и III
Далее, сопоставляя найденную алгебраическую сумму зубцов для I и III стандартных отведений, по таблице определяют значение угла альфа. В нашем случае он равен ми-нус 70°.
Визуальное определение угла альфа
Есть еще один самый простой и любимый студентами метод определения положения ЭОС с помощью карандаша. Он бывает действенным не во всех случаях, но иногда упрощает определение сердечной оси, позволяет определить нормальная она или есть смещение.
Противоположную заостренную часть карандаша направляем на зубец R в то отведение, где он максимальный. Если не пишущая часть карандаша находится в правом верхнем углу, а заострённый кончик пишущей части в левом нижнем, то такое положение говорит о нормальном положении оси сердца.
Если карандаш располагается практически горизонтально, можно предположить смещение оси влево или её горизонтальное положение, а если карандаш принимает положение ближе к вертикальному, то ЭОС отклонена вправо.
Найти алгебраическую сумму зубцов желудочкового комплекса достаточно просто: измеряют в миллиметрах величину каждого зубца одного желудочкового комплекса QRS, учитывая при этом, что зубцы Q и S имеют знак минус (—), поскольку находятся ниже изоэлектрической линии, а зубец R — знак плюс ( ).
Предсердные экстрасистолы
1)зубец P расположен перед комплексом QRS;
2)форма зубца Р в пределах одного отведения отличается от синусового, (изменяется форма, амплитуда и полярность);
3)интервал PQ предсердной экстрасистолы в пределах нормы, или укорочен;
4)комплекс QRS не изменѐн;
5)компенсаторная пауза, как правило, неполная.
1)наличие перед каждым тахикардитическим комплексом QRS зубца P измененной формы или полярности (например, отрицательный P в отведениях II, III, aVF);
2)желудочковые комплексы QRS не изменены;
3)возможно удлинение интервала PQ более 0,20 сек.
Частота предсердной тахикардии относительно небольшая и редко превышает 130 в мин. Если зубцы P во время пароксизма последовательно меняют форму или даже полярность, можно думать о многофокусной
(политопной) предсердной тахикардии.
Таблица определения положения электрической оси сердца (по Дьеду)
Таблица определения угла альфа
Если угол альфа находится в пределах 50—70°, говорят о нормальном положении электрической оси сердца (электрическая ось сердца не отклонена), или нормограмме.
При отклонении электрической ось сердца вправо угол альфа будет определяться в пределах 70—90°. В обиходе такое положение электрической оси сердца называют правограммой.
Если угол альфа будет больше 90° (например, 97°), считают, что на данной ЭКГ имеет место блокада задней ветви левой ножки пучка Гиса.
Определяя угол альфа в пределах 50—0° говорят об отклонении электрической оси сердца влево, или о левограмме.
И наконец, если значение угла альфа будет меньше минус 30° (например, минус 45°) — говорят о блокаде передней ветви левой ножки пучка Гиса.
Пределы отклонения электрической оси сердца
Определение отклонения электрической оси сердца по углу альфа с использованием таблиц и схем производят в основном врачи кабинетов функциональной диагностики, где соответствующие таблицы и схемы всегда под рукой.
Однако определить отклонение электрической оси сердца можно и без необходимых таблиц.
В этом случае отклонение электрической оси находят по анализу зубцов R и S в I и III стандартных отведениях. При этом понятие алгебраической суммы зубцов желудочкового комплекса заменяют понятием «определяющий зубец» комплекса QRS, визуально сопоставляя по абсолютной величине зубцы R и S .
Говорят о «желудочковом комплексе R-типа», подразумевая, что в данном желудочковом комплексе более высоким является зубец R. Напротив, в «желудочковом комплексе S-типа» определяющим зубцом комплекса QRS является зубец S.Сопоставление зубцов R и S комплекса QRS
Однако когда сердце отклоняется от своего нормального анатомического положения в грудной клетке (астеническое и гиперстеническое телосложения, гипертрофия желудочков, заболевания легких и др.), передняя и задняя стенки могут быть представлены другими отделами сердца. Это необходимо учитывать для точной топической диагностики патологических процессов, происходящих в том или ином отделе сердца.
Помимо топической диагностики патологического процесса в различных отделах миокарда, электрокардиографические отведения позволяют проследить отклонение электрической оси сердца и определить его электрическую позицию. Об этих понятиях мы и поговорим ниже.
Глава III
Электрическая ось и электрическая позиция сердца
III.1. Результирующий вектор
Электрическая ось и электрическая позиция сердца неразрывно связаны с понятием результирующего вектора возбуждения желудочков во фронтальной плоскости.
Результирующий вектор возбуждения желудочков представляет собой сумму трех моментных векторов возбуждения: межжелудочковой перегородки, верхушки и основания сердца. Этот вектор имеет определенную направленность в пространстве, которое мы интерпретируем в трех плоскостях: фронтальной, горизонтальной и сагиттальной. В каждой из них результирующий вектор имеет свою проекцию.
Рис. 26. Проекция вектора в различных плоскостях
III.2. Электрическая ось сердца
Электрической осью сердца называется проекция результирующего вектора возбуждения желудочков во фронтальной плоскости.
Электрическая ось сердца может отклоняться от своего нормального положения либо влево, либо вправо.
Точное отклонение электрической оси сердца определяют по углу альфа (α).
III.3. Угол α
Мысленно поместим результирующий вектор возбуждения желудочков внутрь треугольника Эйнтховена. Угол, образованный направлением результирующего вектора и осью I стандартного отведения, и есть искомый угол альфа.
Рис. 27. Угол альфа.
Величину угла альфа находят по специальным таблицам или схемам, предварительно определив на электрокардиограмме алгебраическую сумму зубцов желудочкового комплекса (Q + R + S) в I и III стандартных отведениях.
Найти алгебраическую сумму зубцов желудочкового комплекса достаточно просто: измеряют в миллиметрах величину каждого зубца одного желудочкового комплекса QRS, учитывая при этом, что зубцы Q и S имеют знак минус (—), поскольку находятся ниже изоэлектрической линии, а зубец R — знак плюс (+). Если какой-либо зубец на электрокардиограмме отсутствует, то его значение приравнивается к нулю (0).
Рис. 28. Алгебраическая сумма зубцов I и III отведений
Далее, сопоставляя найденную алгебраическую сумму зубцов для I и III стандартных отведений, по таблице определяют значение угла альфа. В нашем случае он равен минус 70°.
Таблица определения положения электрической оси сердца (по Дьеду)
Рис. 29. Таблица определения угла альфа
Если угол альфа находится в пределах 50–70°, говорят о нормальном положении электрической оси сердца (электрическая ось сердца не отклонена), или нормограмме.
При отклонении электрической ось сердца вправо угол альфа будет определяться в пределах 70–90°. В обиходе такое положение электрической оси сердца называют правограммой.
Если угол альфа будет больше 90° (например, 97°), считают, что на данной ЭКГ имеет место блокада задней ветви левой ножки пучка Гиса.
Определяя угол альфа в пределах 50—0° говорят об отклонении электрической оси сердца влево, или о левограмме.
Изменение угла альфа в пределах 0 — минус 30° свидетельствует о резком отклонении электрической оси сердца влево или, иными словами, о резкой левограмме.
И наконец, если значение угла альфа будет меньше минус 30° (например, минус 45°) — говорят о блокаде передней ветви левой ножки пучка Гиса.
Рис. 30. Пределы отклонения электрической оси сердца