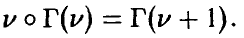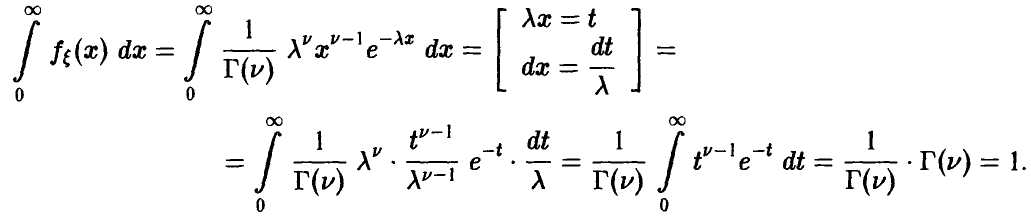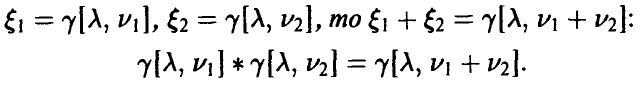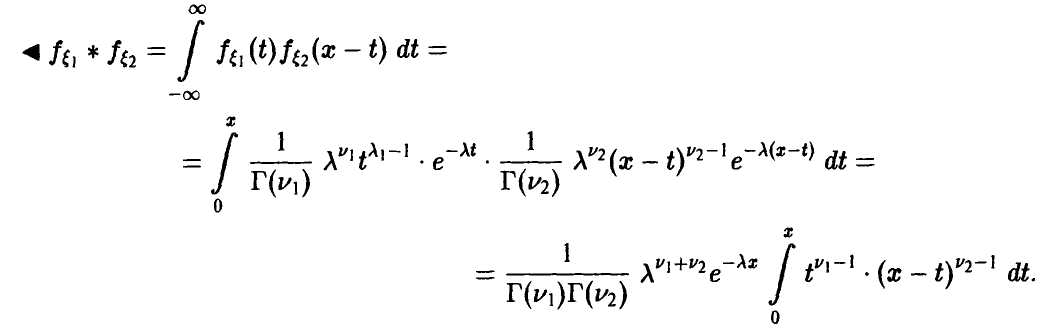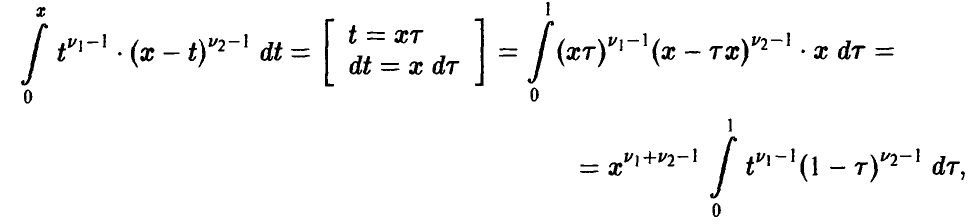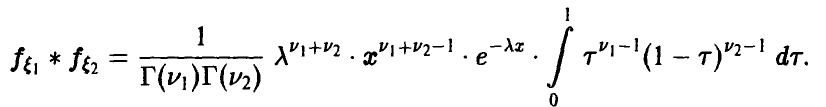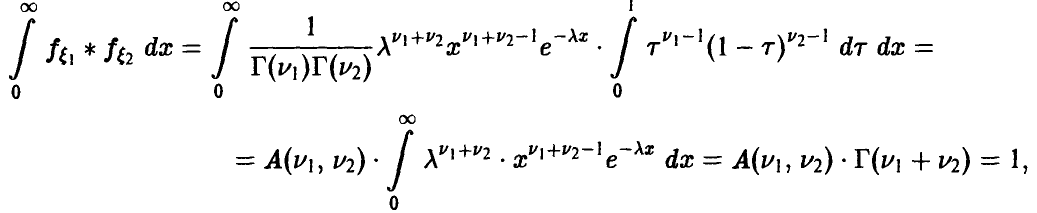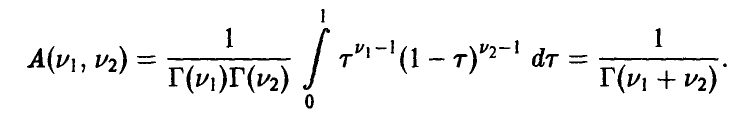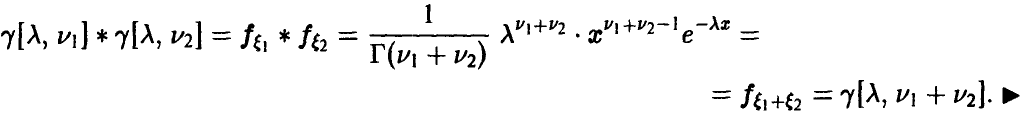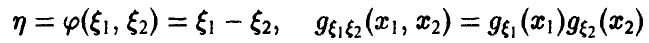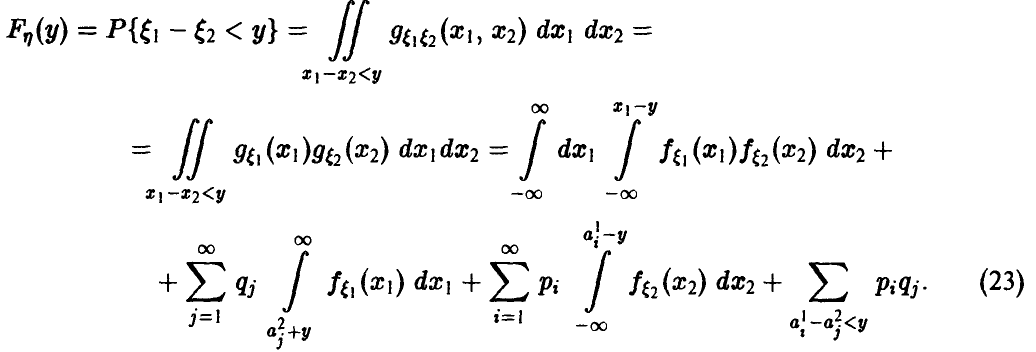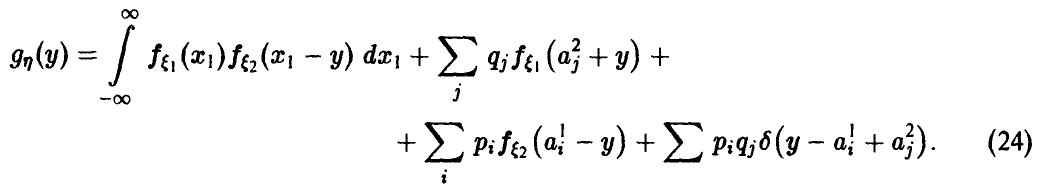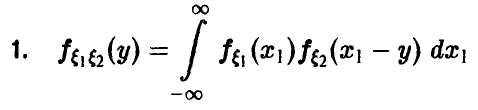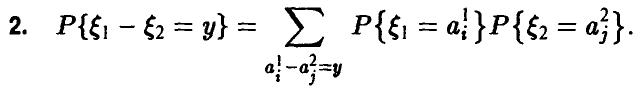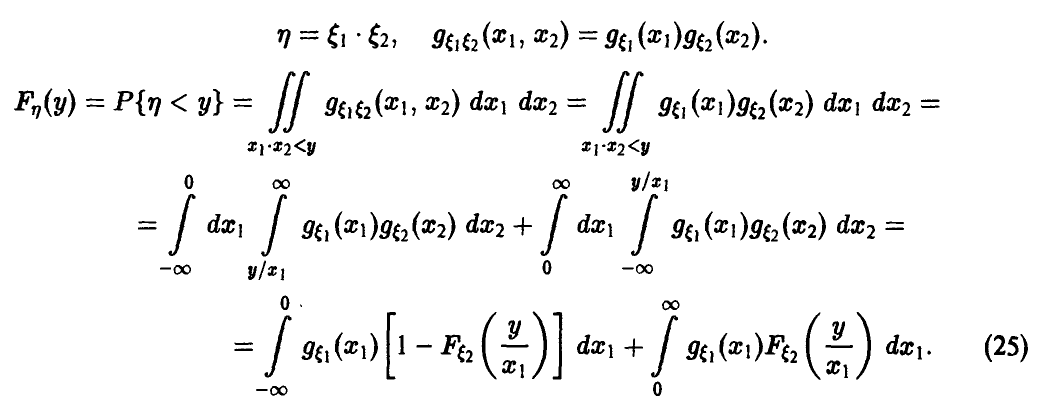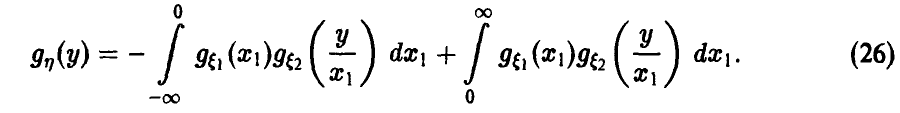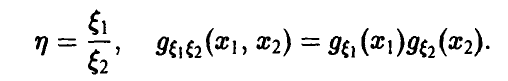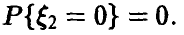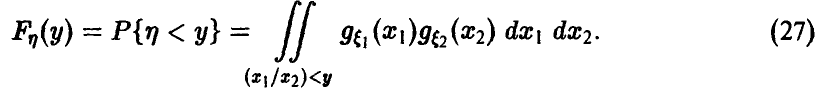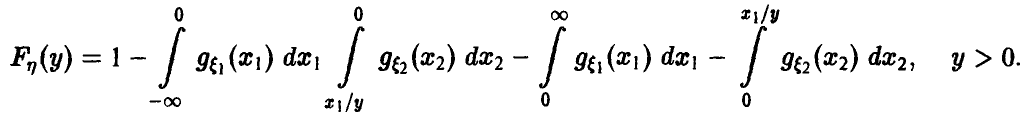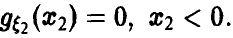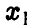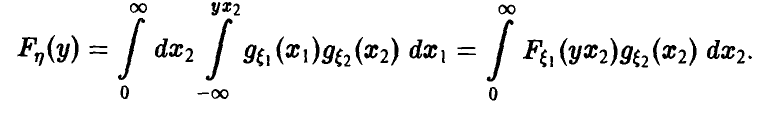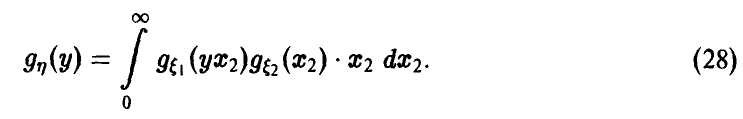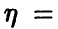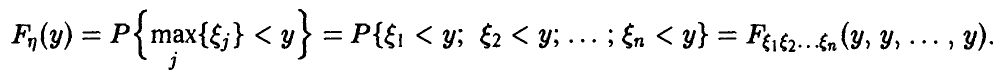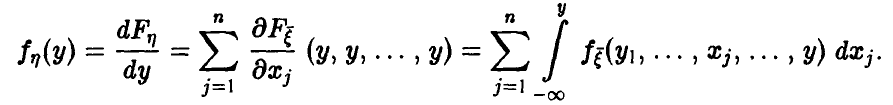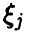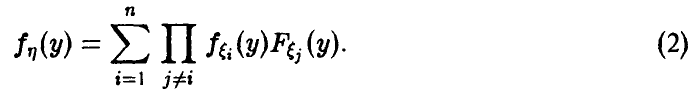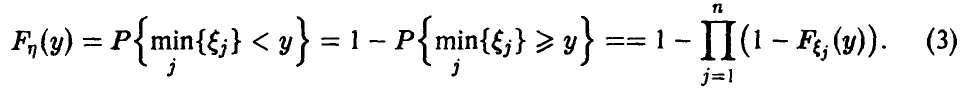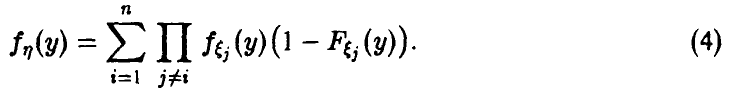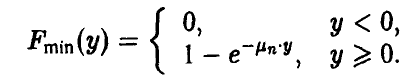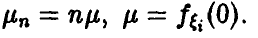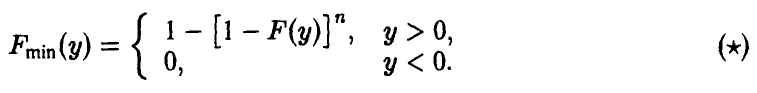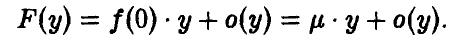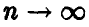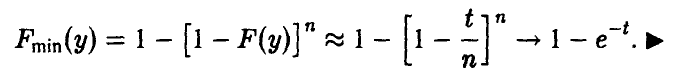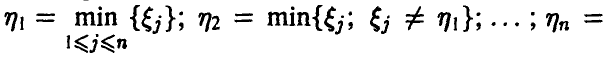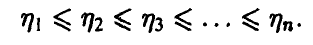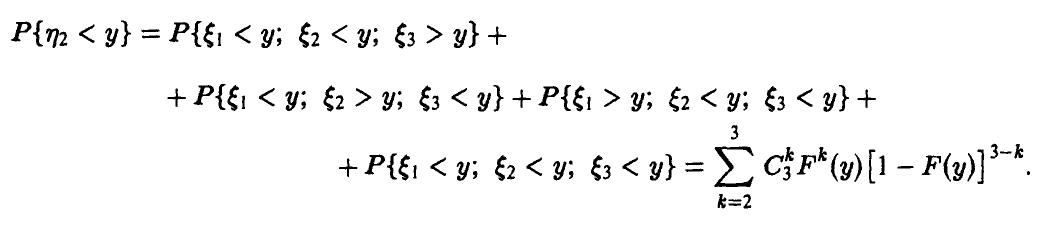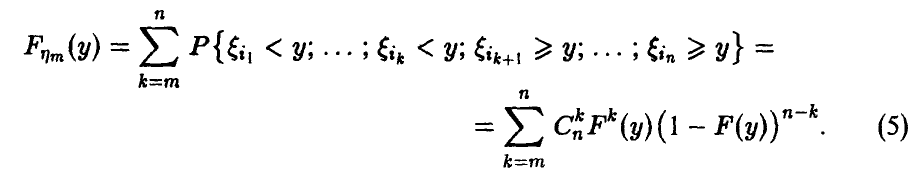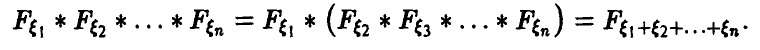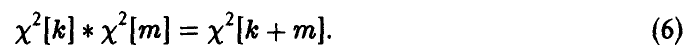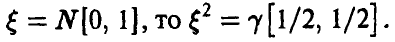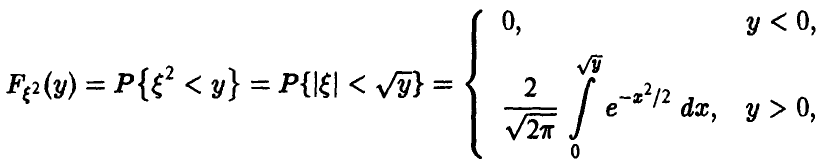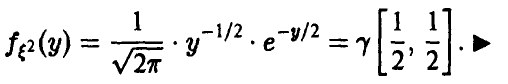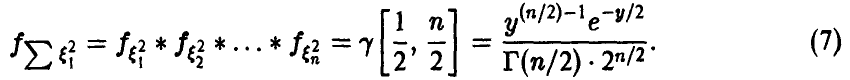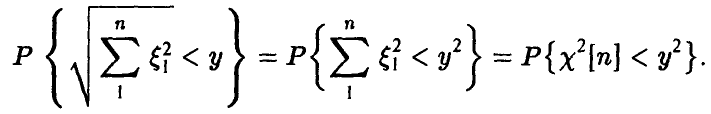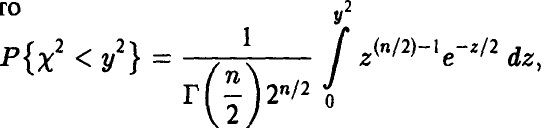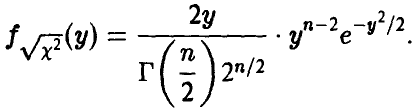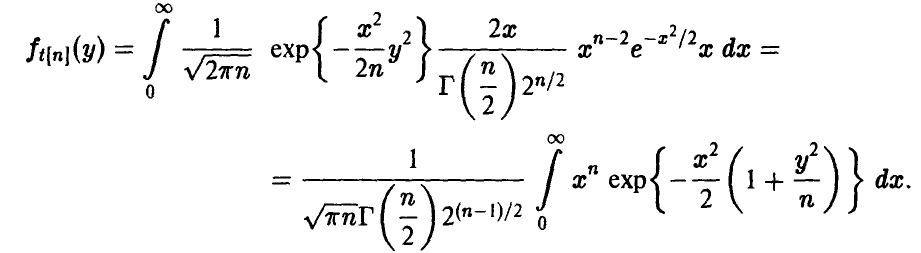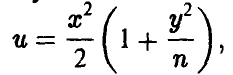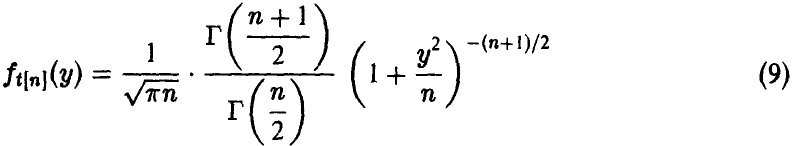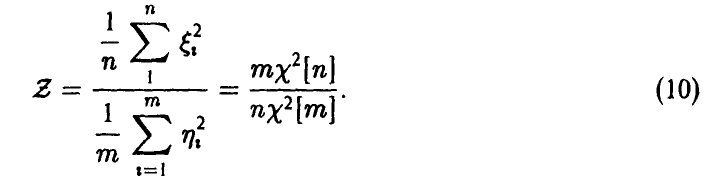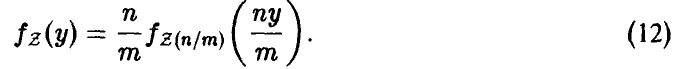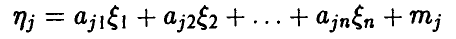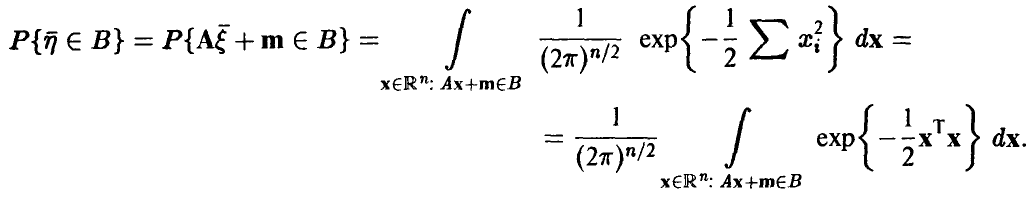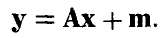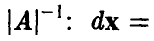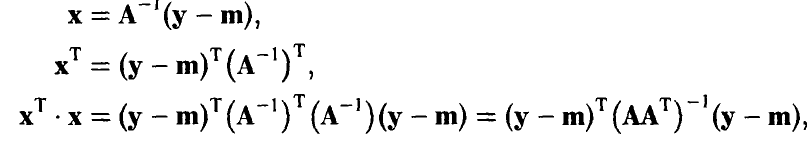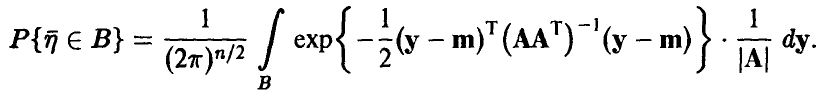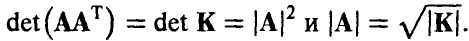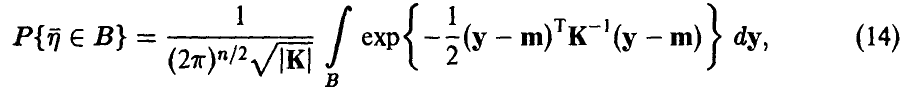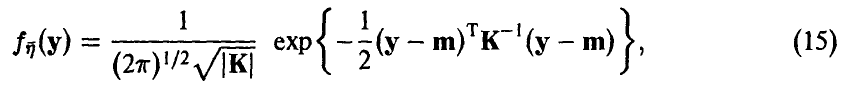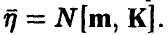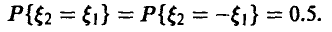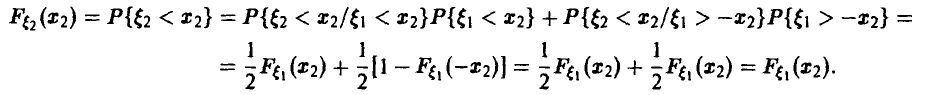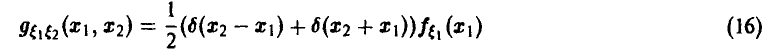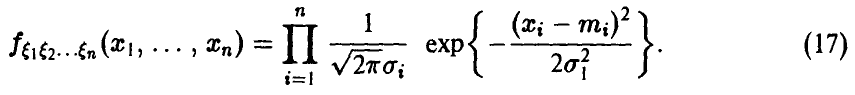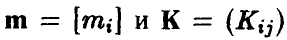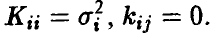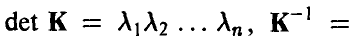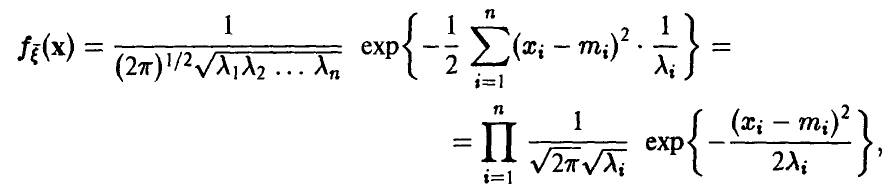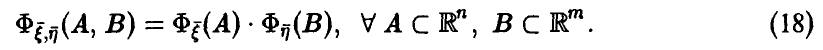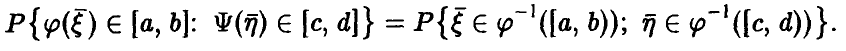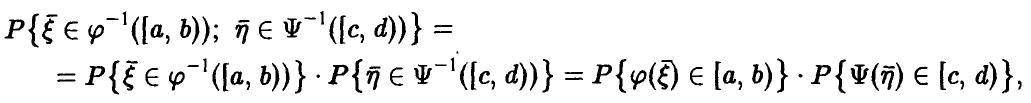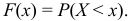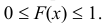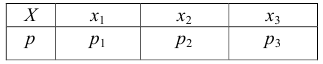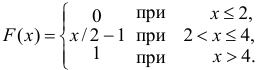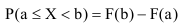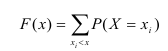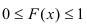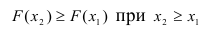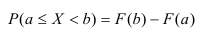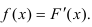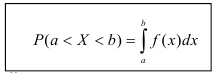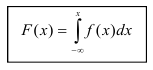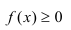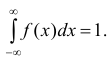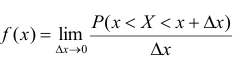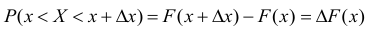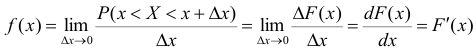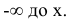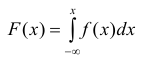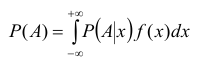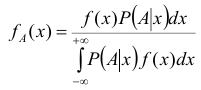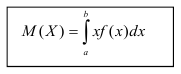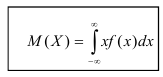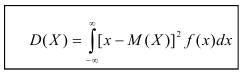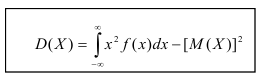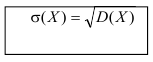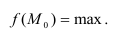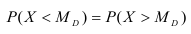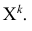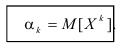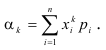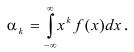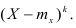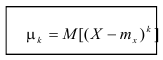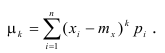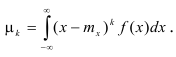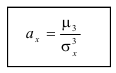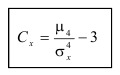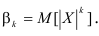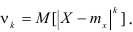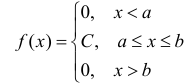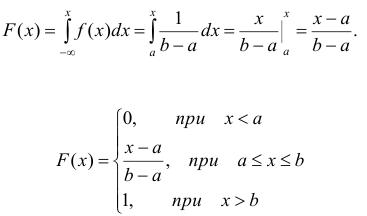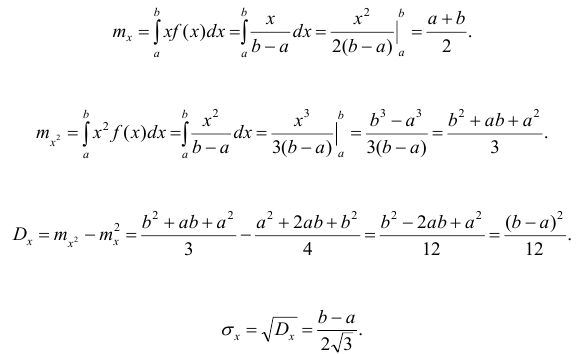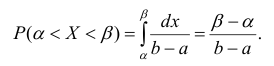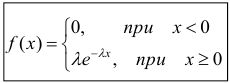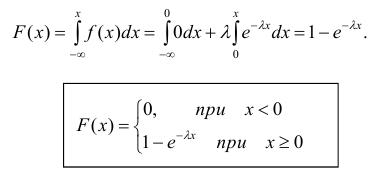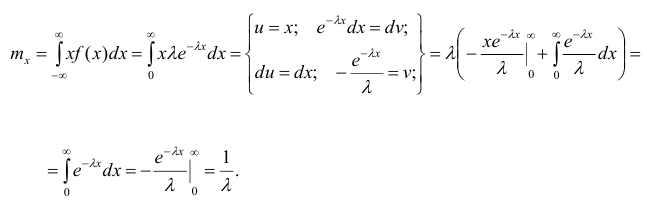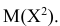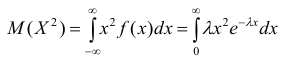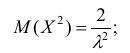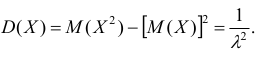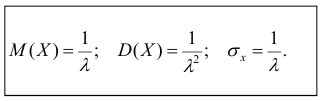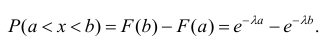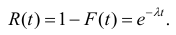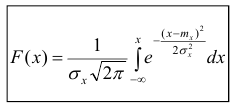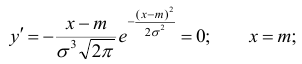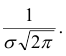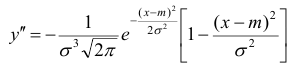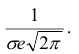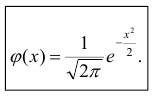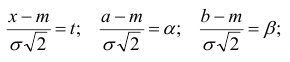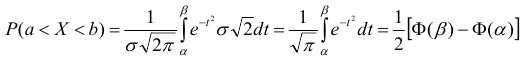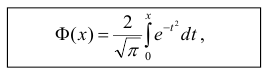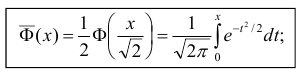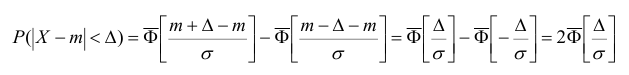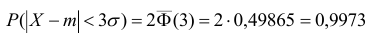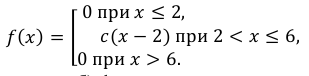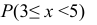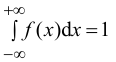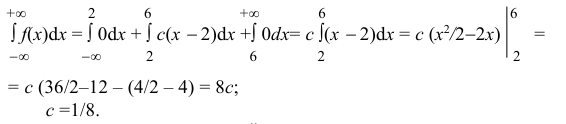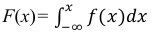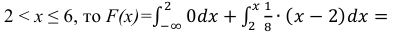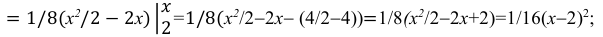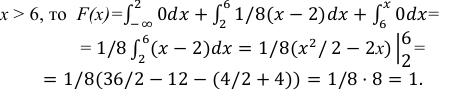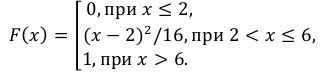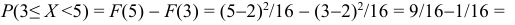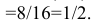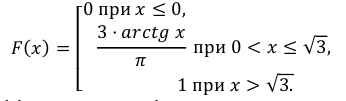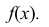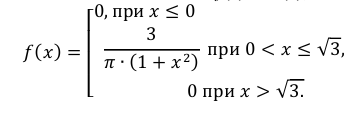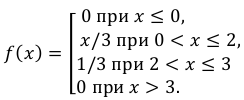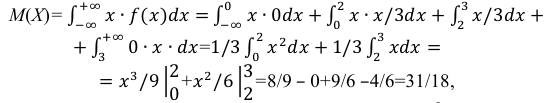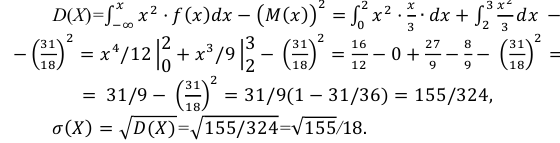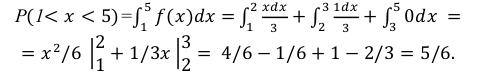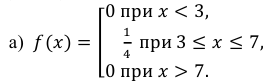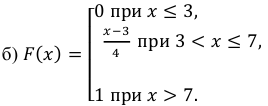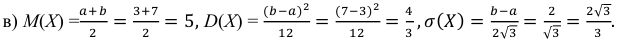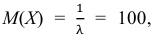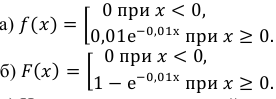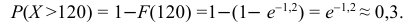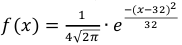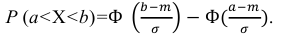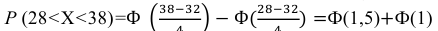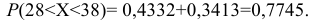Нормальное распределение
Нормальное
распределение
– это совокупность объектов, в которой
крайние значения некоторого признака
– наименьшее и наибольшее – появляются
редко; чем ближе значение признака к
математическому ожиданию, тем чаще оно
встречается.
Закон
распределения
вероятностей непрерывной случайной
величины Х
называется нормальным,
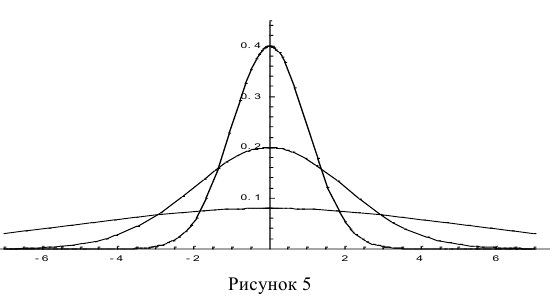
если ее дифференциальная функция f(x)
определяется формулой:
где а
совпадает с математическим ожиданием
величины
Х: а=М(Х),
параметр
совпадает со средним квадратическим
отклонением величины Х:
=
(Х).
Диаграмма
нормального распределения симметрична
относительно точки а
(математического ожидания). Медиана,
среднее арифметическое нормального
распределения равны тоже а.
При этом в точке а
функция f(x)
достигает своего максимума, который
равен
.
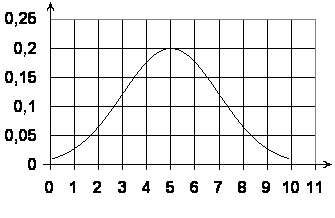
Пример
3:
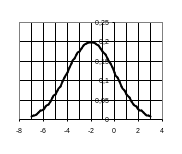
График плотности вероятности нормального
распределения непрерывной величины X
изображен на рисунке. Определите
математическое ожидание, среднее
квадратическое отклонение и максимальное
значение дифференциальной функции
распределения.
Решение.
П
о
графику можно найти максимальное
значение дифференциальной функции
распределения, оно составляет 0,2. Функция
достигает максимума в точке x=5,
следовательно, математическое ожидание
M(X)=5.
В точке максимума функция плотности
вероятности примет вид:
,
следовательно,
В
MS Excel для вычисления значений нормального
распределения используются функция
НОРМРАСП,
которая
вычисляет значения вероятности нормальной
функции распределения для указанного
среднего и стандартного отклонения.
Функция
имеет параметры:
НОРМРАСП
(х;
среднее;
стандартное_откл;
интегральная),
х
– значения выборки, для которых строится
распределение;
среднее
– среднее арифметическое выборки;
стандартное_откл
– стандартное отклонение распределения;
интегральная
– логическое значение, определяющее
форму функции. Если интегральная имеет
значение ИСТИНА(1), то функция НОРМРАСП
возвращает интегральную функцию
распределения; если это аргумент имеет
значение ЛОЖЬ (0), то вычисляется значение
функции плотности распределения.
Если
среднее = 0 и стандартное_откл = 1, то
функция НОРМРАСП
возвращает стандартное нормальное
распределение.
Пример
4:
Составить дифференциальную функцию
распределения непрерывной величины
X,
если известно, что величина распределена
по нормальному закону с параметрами:
математическое ожидание равно -2, а
среднее квадратическое отклонение 2.
Изобразить полученную функцию с помощью
MS Excel.
Решение.
Дифференциальная
функция распределения непрерывной
величины X,
распределенной по нормальному закону,
имеет вид:
где а
– математическое ожидание;
– среднее квадратическое отклонение.
По условию задачи математическое
ожидание
а=-2;
среднее квадратическое отклонение =2,
следовательно
.
Для
построения графика необходимо выбрать
начальное значение для переменной x.
Серединное значение совпадает с
математическим ожиданием а,
начальное значение отстоит от серединного
не менее чем на ,
поэтому примем начальное значение x=-5.
Запишем в ячейку A1 значение -5, в ячейку
А2 – формулу =А1+0,2 и «протянем» эту
формулу до ячейки А31, в которой получится
значение 1. В ячейку B1 внесем формулу:
=1/(2*КОРЕНЬ(2*ПИ()))*EXP(-((A1+2)^2)/8) и «протянем»
эту формулу до ячейки В31. Выделяем ячейки
в диапазоне А1:В31, выбираем Мастер
диаграмм
Точечная
диаграмма со значениями, соединенными
сглаживающими линиями без маркеров, в
результате получаем график плотности
вероятности нормального распределения.
Пример
5:
Построить график нормальной функции
распределения f(x)
при x,
меняющемся от 19,8 до 28,8 с шагом 0,5, a=24,3
и
=1,5.
Решение.
1.
В ячейку А1 вводим символ случайной
величины х,
а в ячейку B1 – символ функции плотности
вероятности – f(x).
2.
Вводим в диапазон А2:А21 значения х
от 19,8 до 28,8 с шагом 0,5. Для этого
воспользуемся маркером автозаполнения:
в ячейку А2 вводим левую границу диапазона
(19,8), в ячейку A3 левую границу плюс шаг
(20,3). Выделяем блок А2:А3. Затем за правый
нижний угол протягиваем мышью до ячейки
А21 (при нажатой левой кнопке мыши).
3.
Устанавливаем табличный курсор в
ячейку В2 и для получения значения
вероятности воспользуемся специальной
функцией — нажимаем на панели инструментов
кнопку Вставка
функции
fx.
В появившемся диалоговом окне Мастер
функций – шаг 1 из 2 слева в поле Категория
указаны виды функций. Выбираем
Статистическая.
Справа в поле Функция
выбираем функцию НОРМРАСП.
Нажимаем на кнопку ОК.
4.
Появляется диалоговое окно НОРМРАСП.
В рабочее поле X
вводим адрес ячейки А2 щелчком мыши на
этой ячейке. В рабочее поле Среднее
вводим с клавиатуры значение
математического ожидания (24,3). В
рабочее поле Стандартное_откл
вводим с клавиатуры значение
среднеквадратического отклонения
(1,5). В рабочее поле Интегральная
вводим с клавиатуры вид функции
распределения (0). Нажимаем на кнопку
ОК.
5.
В ячейке В2 появляется вероятность р
= 0,002955. Указателем мыши за правый нижний
угол табличного курсора протягиванием
(при нажатой левой кнопке мыши) из ячейки
В2 до В21 копируем функцию НОРМРАСП
в диапазон В3:В21.
6.
По полученным данным строим искомую
диаграмму нормальной функции
распределения. Щелчком указателя
мыши на кнопке на панели инструментов
вызываем Мастер
диаграмм.
В появившемся диалоговом окне выбираем
тип диаграммы График,
вид – развитие процесса по времени или
по категориям.
После
нажатия кнопки Далее
указываем диапазон данных – В1:В21 (с
помощью мыши). Проверяем, положение
переключателя Ряды в: столбцах. Выбираем
закладку Ряд
и с помощью мыши вводим диапазон подписей
оси X:
А2:А21. Нажав на кнопку Далее,
вводим названия осей Х,
f(x)
и нажимаем на кнопку Готово.
П
олучен
приближенный график нормальной функции
плотности распределения:
Задания
для самостоятельного выполнения
Задание
1.
Закон распределения случайной
величины Х задан таблицей:
|
Х |
0,2 |
0,4 |
0,6 |
0,8 |
1 |
|
Р |
0,1 |
0,2 |
0,4 |
р4 |
0,1 |
Найдите
p4?
Задание
2.
Закон
распределения случайной величины Х
задан таблицей:
|
Х |
3 |
4 |
5 |
6 |
7 |
|
Р |
р1 |
0,15 |
р3 |
0,25 |
0,35 |
Найдите
вероятности
р1
р3,
если известно, что р3
в 4 раза больше р1?
Задание
3.
Закон
распределения случайной величины
Х
задан таблицей:
|
Х |
2 |
3 |
5 |
|
р |
0,3 |
0,1 |
0,6 |
Найдите
М(Х)
, D(X)
и (Х).
Задание
4.
В
денежной лотерее выпущено 100 билетов.
Разыгрываются 1 выигрыш в 500 руб.
и 10 выигрышей по 100 руб. Найдите закон
распределения случайного выигрыша Х
для владельца одного лотерейного билета.
Определите минимальную стоимость
одного билета
-
При
некоторых условиях стрельбы вероятность
попадания в цель равна 0,8. Производится
10 выстрелов. Какова вероятность, что
число попаданий в цель будет не менее
двух? -
Два
равносильных противника играют в
шахматы. Что вероятнее:
а)
выиграть одну партию из двух или две
партии из четырех?
б)
выиграть не менее двух партий из четырех
или не менее трех партий из пяти?
Задание
7.
Известно,
что непрерывная случайная величина
распределена по нормальному закону,
математическое ожидание равно 4.
Определите значение среднего
квадратического отклонения, если
максимальное значение дифференциальной
функции распределения составляет 0,4.
Постройте график нормального распределения.
Задание
8.
Известно,
что непрерывная случайная величина
распределена по нормированному закону,
где х меняется от 10 до 20. Постройте график
распределения.
Задание
9.
Вероятность
попадания в цель при стрельбе из орудия
р = 0,6. Найдите математическое ожидание
общего числа попаданий, если будет
произведено 10 выстрелов.
Вопросы
для самоконтроля
-
Чему
равна сумма всех возможных вероятностей
в законе распределения дискретной
случайной величины?
-
Можно
ли применять формулу Бернулли для
зависимых испытаний?
-
Какими
должны быть испытания, чтобы можно было
применять формулу Бернулли? -
Чему
равно значение непрерывной случайной
величины при котором функция плотности
вероятности этой величины достигает
максимального значения?
-
Приведите
пример непрерывной случайной величины,
распределенной по нормальному закону? -
Как
найти вероятность того, что в n независимых
испытаниях событие A появится хотя бы
один раз?
Математическая
статистика
Основные
умения:
рассчитывать основные статистические
показатели для решения профессиональных
задач; осуществлять самостоятельную
деятельность по сбору, обработке,
группировке, анализу информации;
использовать методы математической
статистики в психолого-педагогических
исследованиях.
Основной
величиной в статистических измерениях
является единица
статистической совокупности (например,
любой из критериев оценки качества
педагога-исследователя). Единица
статистической совокупности характеризуется
набором признаков или параметров.
Значения каждого параметра или признака
могут быть различными и в целом
образовывать ряд случайных значений
x1,
х2,
…,
хn.
Переменная
(variable)
– это параметр измерения, который можно
контролировать или которым можно
манипулировать в исследовании. Так как
значения переменных не постоянны, нужно
научиться описывать их изменчивость.
Для
этого придуманы описательные или
дескриптивные статистики: минимум,
максимум, среднее, дисперсия, стандартное
отклонение, медиана, квартили, мода.
Относительное
значение параметра
– это отношение числа объектов, имеющих
этот показатель, к величине выборки.
Выражается относительным числом или в
процентах (процентное значение).
Пример
1:
Успеваемость в классе = числу положительных
итоговых отметок, деленному на число
всех учащихся класса. Умножение этого
значения на 100 дает успеваемость в
процентах. 25/100=25%
Удельное
значение
данного признака – это расчетная
величина, показывающая количество
объектов с данным показателем, которое
содержалось бы в условной выборке,
состоящей из 10, 100, 1000 и т. д. объектов.
Пример
2:
Для
сравнения уровня правонарушений в
разных регионах берется удельная
величина – количество
правонарушений на 1000 человек
(N).
Минимум
и максимум
– это минимальное и максимальное
значения переменной.
Размах
(R)
–
это
разность между максимальным и минимальным
значением переменной: R= max–min.
Среднее
арифметическое
может вычисляться как по необработанным
первичным данным, так и по результатам
группировки этих данных.
Для
несгруппированных данных:
(1)
где
n
– объем выборки; xi
– значения выборки.
Для
сгруппированных данных:
(2)
где
n
– объем выборки; k
– число интервалов группировки; ni
–
частоты интервалов; xi
– срединные значения интервалов.
Пример
3:
Наблюдение посещаемости четырех
внеклассных мероприятий в экспериментальном
(20 учащихся) и контрольном (30) классах
дали значения (соответственно): 18, 20, 20,
18 и 15, 23, 10, 28. Среднее значение посещаемости
в обоих классах получается одинаковое
– 19. Однако видно, что в контрольном
классе этот показатель подчинен
воздействию каких-то специфических
факторов.
Медианой
(Ме)
называется такое значение признака X,
когда одна половина значений
экспериментальных данных меньше ее, а
вторая половина – больше.
Для
вычисления медианы несгруппированных
данных выборку сортируют, находят ранг
R
(порядковый номер) медианы:
(3)
Медианой
будет значение признака, стоящее на RМе
месте в ранжированной выборке. Для
нахождения медианы в случае сгруппированных
данных:
(4)
где
хMeН
– нижняя граница медианного интервала;
h
– ширина интервалов группировки;
nxMe–1
– накопленная частота интервала,
предшествующего медианному; nMe
– частота медианного интервала.
Мода
(Мо)
представляет собой значение признака,
встречающегося в выборке наиболее
часто.
Если
распределение имеет несколько мод, то
говорят, что оно мультимодально
или многомодально
(имеет два или более «пика»). Для
несгруппированных данных мода – это
значение признака с наибольшей
частотой появления.
Для
сгруппированных данных:
(5)
где
xMoH
– нижняя граница модального интервала,
nMo
– частота интервала.
Пример
4:
Найти
среднее арифметическое, моду и медиану
распределения студентов по числу баллов,
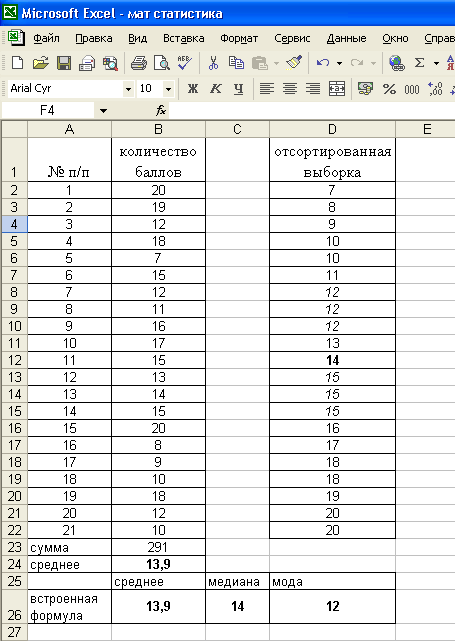
полученных ими на экзамене: 20 19 12 18 7
15 12 11 16 17 15 13 14 15 20 8 9 10 18 12 10.
Решение.
Решим
данную задачу, используя электронные
таблицы MS
Excel.
Внесите
данные задачи в столбец В листа электронных
таблиц, начиная со второй строки. В
столбец А внесите № п/п, проставив
которые получим последний №, соответствующий
объему выборки n=21.
Поставив
курсор в ячейку В23 введем формулу
нахождения среднего значения
=СРЗНАЧ(В2:В22). Можно ввести собственную
формулу: =СУММ(В2:В22)/21.
Для
вычисления медианы, расположим данные
в порядке возрастания: скопируем данные
в столбец D, выделим столбец и отсортируем.
Найдем ранг медианы по формуле (3):
На 11-м месте в ранжированной выборке
стоит значение 14. Ме=14. Используя
встроенную функцию: =МЕДИНА(В2:В22),
получаем то же значение 14.
Для
нахождения моды воспользуемся
ранжированной выборкой, в которой можно
заметить, что наиболее часто (3 раза)
встречаются значения 12 и 15 – значения
несмежные, поэтому выборка имеет 2 моды
и называется бимодальной. Используя
встроенную функцию: =МОДА (В2:В22). Получаем
значение 12 (Excel не рассматривает случаи
бимодальных распределений).
Пример
5:
Дано
распределение семей по числу детей.
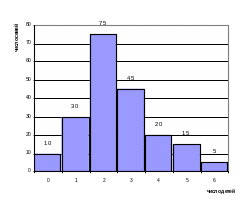
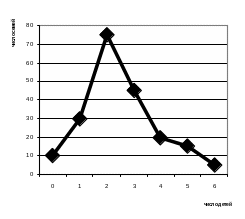
Найти моду, медиану и среднее арифметическое.
Построить гистограмму и полигон
распределения.
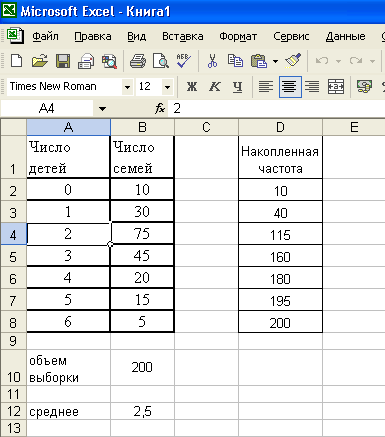
|
Число |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
Число |
10 |
30 |
75 |
45 |
20 |
15 |
5 |
Решение.
Значением
признака будет являться число детей, а
частотой – число семей, в которых
содержится такое количество детей.
Найдем среднее арифметическое количества
детей в семье.
Внесем
таблицу на лист электронных таблиц:
число детей – в столбец А; число семей
в столбец В. Данные в таблице являются
сгруппированными.
Н
айдем
общий объем выборки, суммируя данные
столбца числа семей, и занесем в ячейку
В10 формулу =СУММ(В2:В8), получим n=200.
Для нахождения значения среднего
арифметического сгруппированных данных
воспользоваться встроенной функции
невозможно, поэтому применяем формулу
(2) – сумма произведений значений
столбцов А и В =СУММПРОИЗВ(A2:A8;B2:B8)/B10 и
занесем формулу в ячейку В12, получим
.
Для
нахождения медианы необходимо определить
медианный интервал. Медианным
будет
тот интервал, в котором накопленная
частота впервые окажется больше n/2
(n/2=200/2=100).
В столбец D занесем значения накопленных
частот: в D2 – В2, в D3=D2+B3 и т.д. Замечаем,
что накопленная частота больше 100 равная
115 соответствует значению признака 2
ребенка в семье. Ме=2.
Мо=2,
т.к. это значение признака встречается
наиболее часто – 75 раз.
|
Построим |
Построим |
||||
|
|
|
||||
Для
оценки степени разброса (отклонения)
какого-то показателя от его среднего
значения, наряду с максимальным и
минимальным значениями, используются
понятия дисперсии и стандартного
отклонения.
Дисперсия
выборки или выборочная дисперсия
(от
английского variance)
– это
мера изменчивости
переменной.
Термин впервые введен Фишером в 1918
году.
Дисперсия
меняется от нуля до бесконечности.
Крайнее значение 0 означает отсутствие
изменчивости, когда значения переменной
постоянны.
Стандартное
отклонение, среднее квадратическое
отклонение (от
английского standard
deviation) вычисляется
как корень квадратный из дисперсии. Чем
выше дисперсия или стандартное отклонение,
тем сильнее разбросаны значения
переменной относительно среднего.
Пример
7: По данным примера 3,
где приводиится посещаемость четырех
внеклассных мероприятий в экспериментальном
(20 учащихся) и контрольном (30) классах,
рассчитаем дисперсию и стандартное
отклонение:
|
Классы |
|
D(x) |
|
|
Экспериментальный |
19 |
1 |
1 |
|
Контрольный |
19 |
48,5 |
8 |
Это
означает, что в одном классе посещаемость
высокая, стабильная, а в другом –
отличается непостоянством.
Задания
для самостоятельного выполнения
Задание
1. Найти
среднее арифметическое, моду и медиану
распределения абитуриентов по числу
баллов, полученных ими на экзамене: 80
69 72 44 51 38 62
Задание
2. Рассчитать
описательную статистику для следующего
распределения температуры тела больных
в изоляторе за день: 38 40 37 38 38 40 37 37
38 38 37 39 38 39 38 39 37. Построить дискретный
вариационный ряд и гистограмму, начертить
полигон частот.
Задание
3.
По результатам исследования на вопрос
анкеты: «укажите степень владения
иностранным языком», ответы распределились
следующим образом:
1
– владею свободно – 25
2
– владею в достаточной степени для
общения – 50
3
– владею, но испытываю трудности при
общении – 250
4
– понимаю с трудом – 170
5
– не владею – 10
Найти
среднее значение, медиану и моду выборки.
Постройте гистограмму и полигон частот
по имеющимся данным. Сделайте вывод.
Задание
4.
Педагог-исследователь
провел тестирование интеллекта по тесту
Векслера у 20 школьников и получил
следующие данные: 6, 9, 5, 7, 10, 8, 9, 10, 8, 11, 9,
12, 9, 8, 10, 11, 9, 10, 8, 10. Отсортируйте полученные
данные по убыванию, рассчитайте среднее
значение, моду, медиану, эксцесс и
ассиметрию выборки.
Вопросы
для самоконтроля
-
В
каких случаях применяется аппарат
математической статистики?
-
Для
чего предназначен раздел математической
статистики: описательная статистика?
-
Как
характеризует распределение выборки
стандартное отклонение, ассиметрия и
эксцесс?
-
В
каких случаях необходим аппарат
математической статистики в деятельности
педагога?
Задача установления закона распределения функции от случайных величин по заданному закону распределения аргументов является основной.
Общая схема рассуждений здесь следующая. Пусть 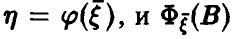
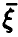
где 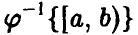
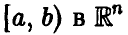
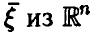
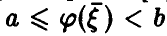
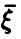
Аналогично, в принципе, может быть найден закон распределения и векторной функции случайных аргументов.
Сложность реализации схемы (*)-(**) зависит только от конкретного вида функции 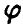
Настоящая глава посвящена реализации схемы (*)-(**) в конкретных, важных для приложений, ситуациях.
Функции одного переменного
Пусть 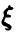
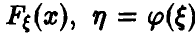
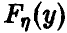
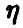
где через 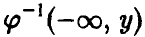
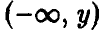
Монотонное преобразование случайной величины
Пусть 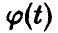
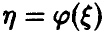
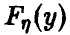
(здесь 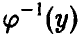
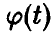
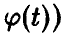
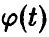
В частности, если 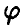
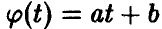
а при а < О
Линейные преобразования не меняют характера распределения, а сказываются лишь на его параметрах.
Линейное преобразование равномерной на [а, b] случайной величины
Пусть 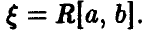
Линейное преобразование нормальной 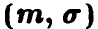
Пусть 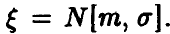
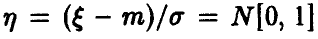
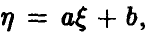
◄ Пусть, например, а > 0. Из (4) заключаем, что
Положим в последнем интеграле u = ах + b. Эта замена дает
Важное тождество, являющееся источником многих интересных приложений, может быть получено из соотношения (3) при
Лемма:
Если 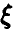
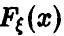
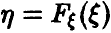

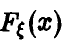
На промежутке же 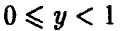
Одним из возможных путей использования доказанной леммы является, например, процедура моделирования случайной величины с произвольным законом распределения 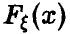
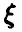
В заключение заметим, что если случайная величина 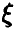
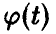
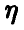
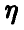
Если 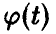
Распределение квадрата равномерной на [—1, 1] случайной величины
Пусть 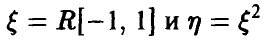
Отсюда для плотности 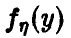
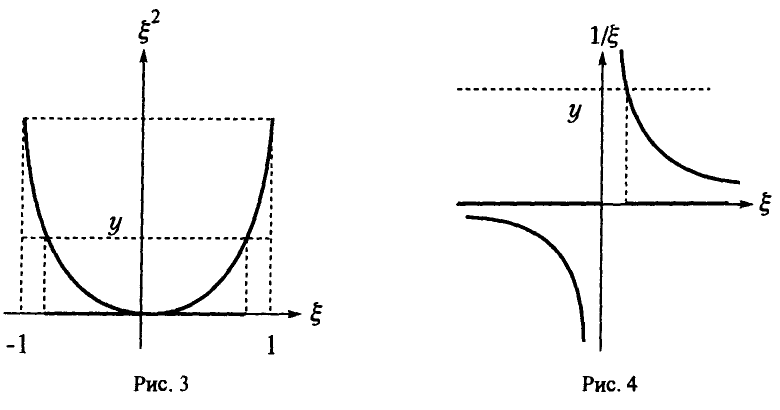
Распределение случайной величины, обратной к случайной величине с распределением Коши
Пусть 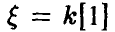
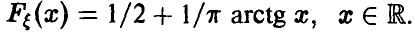
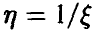
Таким образом, если
Функции двух переменных. Действия над случайными величинами
Пусть 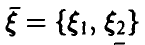
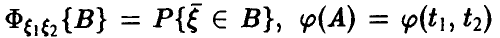
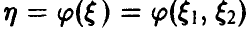
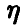
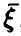
Распределение максимума двух случайных величин
Пусть 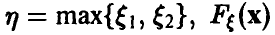
Если вектор 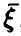
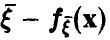
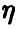
Если дополнительно компоненты 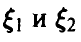
а в случае непрерывности
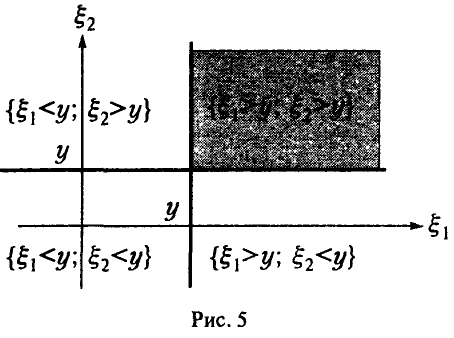
Распределение минимума двух случайных величин
Пусть 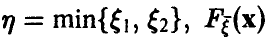
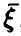
Для последней вероятности получаем (рис. 5).
Действительно, из
следует
а из последнего легко получается (5).
Окончательно имеем
В случае непрерывности 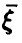
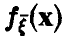
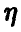
Если 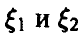
и для непрерывных
Отметим важную особенность экспоненциального распределения — если 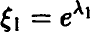
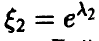
Действительно, (9) дает
Более того, как будет показано ниже, при достаточно широких предположениях относительно распределения независимых случайных величин 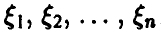
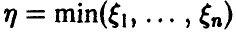
Сложение случайных величин. Свертка распределений
Пусть 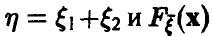
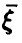
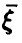
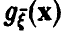
(здесь 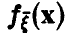
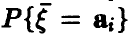
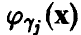
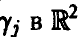
В частности, если вектор 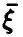
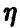
и плотность распределения ц дается соотношением
Если 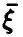
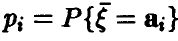
— ее ряд распределения.
Рассмотрим теперь процедуру сложения независимых случайных величин. В этом случае соотношения (10) и (12) приобретают более компактный и завершенный вид.
Пусть ) 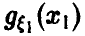
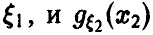
В случае независимости £i и £2 получаем
и соотношение (10) можно записать в виде
Обобщенная плотность суммы независимых случайных величин дается в этом случае соотношением
Отметим следующие, важные для приложений, частные случаи соотношений (15) и (16):
непрерывны и независимы, тогда сумма непрерывна и
2. 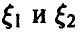
3. 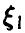
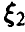
4. 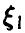
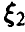
5. 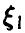
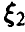
Закон распределения суммы независимых случайных величин называется сверткой законов распределения слагаемых.
Например, соотношение (17) дает формулу свертки плотностей, (18) — свертки рядов распределения, (20) — свертки плотности с рядом распределения. Обычно свертка обозначается знаком «*». Это обозначение дает возможность символически представить функцию распределения суммы независимых слагаемых в виде
плотность распределения в виде
и т. д.
Как правило, при сложении независимых случайных величин характер распределения меняется, даже если складываются одинаково распределенные случайные величины.
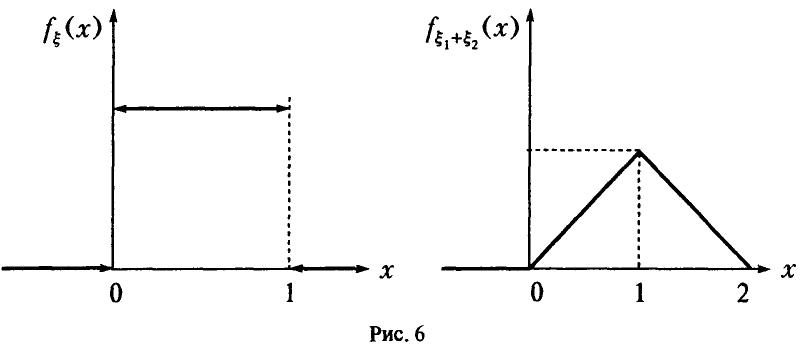
Пример:
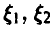
Таким образом, свертка двух равномерных на [0, 1] случайных величин есть «треугольная» случайная величина (рис. 6).
Пример:
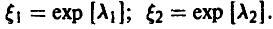
Свертка двух экспоненциальных не является экспоненциальной случайной величиной (рис. 7).
Она является представителем семейства гамма-законов распределения (см. ниже).
Устойчивые относительно свертки распределения играют важную роль в теории и приложениях. Не касаясь вопроса о том, каким условиям должны удовлетворять и как описываются распределения, инвариантные относительно свертки, отметим инвариантность следующих часто встречающихся в приложениях распределений: нормального, пуассонова, гамма-распределения, распределения Коши и распределения Бернулли.
Сформулируем и докажем соответствующие утверждения для нормального распределения, распределения Пуассона и для гамма-распределения.
Теорема:
Если
◄ По формуле (15) имеем
Элементарный (но несколько утомительный) подсчет дает
Поэтому
Отметим, что нормальное распределение в некотором смысле «устойчиво» относительно свертки, а именно, если сумма двух независимых случайных величин имеет нормальное распределение, то оказывается слагаемые обязательно нормальны!
Теорема:
Если
Гамма-плотности
Будем говорить, что случайная величина 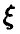
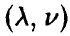
Обозначение:
Здесь 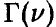
Отметим следующие, хорошо известные свойства гамма-функции:
— натуральное.
В справедливости этих свойств легко убедиться, интегрируя (22) по частям.
Определение плотности (22) корректно, так как для любых 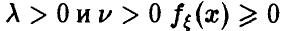
Имеет место теорема.
Теорема:
Если
В последнем интеграле положим 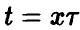
откуда
Поскольку 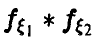
где
Отсюда окончательно заключаем, что
Другие действия над случайными величинами
Задача нахождения закона распределения результата других арифметических действий над случайными величинами решается аналогично. Отметим здесь основные соотношения для случая независимых операндов, следующие из (*)-(**).
Вычитание
(см. соотношения (13)—(14)).
Обобщенная плотность разности 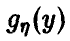
Частные случаи (24), соответственно, для непрерывных
и дискретных случайных величин
Аналоги соотношений (19), (20) и (21) очевидны.
Умножение
Выражение для обобщенной плотности произведения
Аналоги соотношений (17)-(21) очевидны.
Деление
Будем дополнительно предполагать, что
Аналогично для у > 0 имеем
Для дальнейшего нам понадобится выражение функции и плотности распределения частного в предположении, что знаменатель неотрицателен:
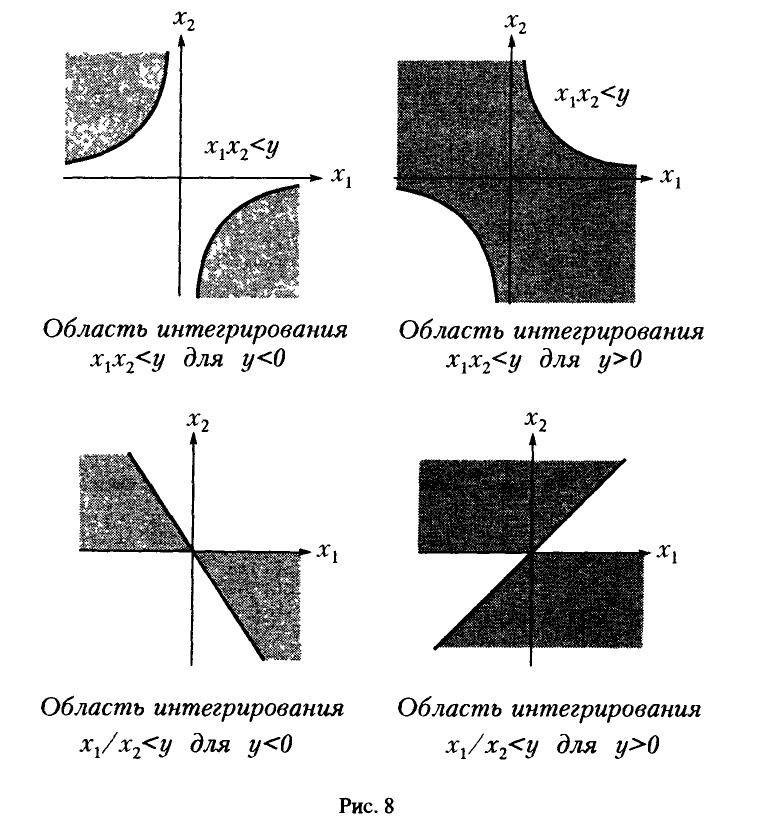
Учитывая вид области интегрирования (рис. 8, 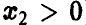
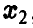
Обобщенная плотность при этом дается равенством
Функции нескольких переменных
В этом разделе мы остановимся на некоторых специфических функциях п переменных и их законах распределения, часто встречающихся в приложениях и играющих важную роль в статистике.
Экстремумы и порядковые статистики
Распределение максимума n случайных величин
Очевидное обобщение рассуждений предыдущего пункта (см. (1)) дает: если 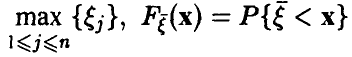
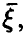
Если вектор 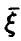
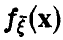
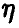
В случае независимости компонент вектора 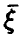
а в предположении непрерывности
Распределение минимума n случайных величин
Обобщая соотношение (8) дословным повторением выкладок, получаем для вектора 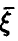
Для непрерывных 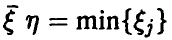
Заметим, что здесь, как и для случая двухкомпонентного вектора 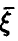
Если n достаточно велико, то оказывается, что этот результат — экспоненциальное минимума — слабо зависит от характера распределения компонент. Точнее, имеет место следующее утверждение.
Теорема:
Пусть случайные величины 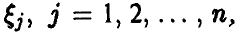
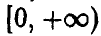

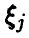
Здесь
◄ Соотношение (3) в условиях теоремы дает
В силу непрерывности 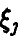
Из соотношения (*) ясно, что при 
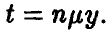
Указанное обстоятельство является теоретическим осмыслением т. н. «принципа слабого звена», широко используемого в теории надежности — надежность агрегата, функционирование которого необходимо зависит от надежности большого количества составляющих, определяется надежностью самого ненадежного из них и описывается экспоненциальным распределением.
Распределение порядковых статистик
Пусть 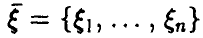
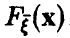
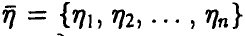
порядковыми статистиками, если 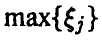
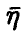
Найдем закон распределения m-й компоненты 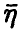
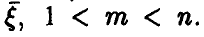
Для того, чтобы вторая порядковая статистика приняла значение, меньшее у, нужно чтобы не менее двух из трех компонент вектора 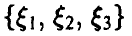
Аналогично для произвольных m и n
Кратные свертки. Некоторые специальные распределения
Столь же очевидно обобщается на случай произвольного конечного числа слагаемых понятие свертки случайных величин
Общие формулы при этом уже достаточно громоздки и необозримы, если только сворачиваемые распределения не являются устойчивыми относительно свертки — в последнем случае ситуация в техническом плане не сложнее, чем в случае двух переменных.
Особо отметим, что для нормальных, независимых в совокупности случайных величин из свойств линейного преобразования и теоремы 1 следует, что, если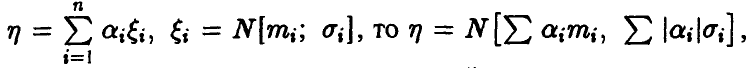
Распределение 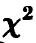
Пусть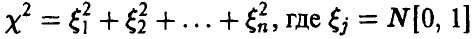
Распределение суммы квадратов п независимых нормальных с параметрами (0, 1) случайных величин называется 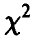
Читается — хи-квадрат. Обозначение: 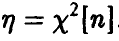
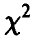
Для нахождения закона распределения случайной величины 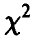
◄ Действительно,
откуда
В силу устойчивости гамма-распределения относительно свертки получаем
t-распределение Стьюдента
Пусть 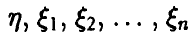
Распределение случайной величины t называется распределением Стьюдента с n степенями свободы.
Обозначение: t = t[n].
Найдем выражение для закона распределения t[n]. Отметим, что числитель рассматриваемого отношения нормален с параметрами 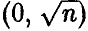
Из (7) заключаем, что
отсюда для плотности 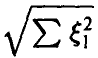
Поэтому для частного t[n], следуя (28), получаем
Делая в последнем интеграле замену
приходим к формуле
Заметим, что при 
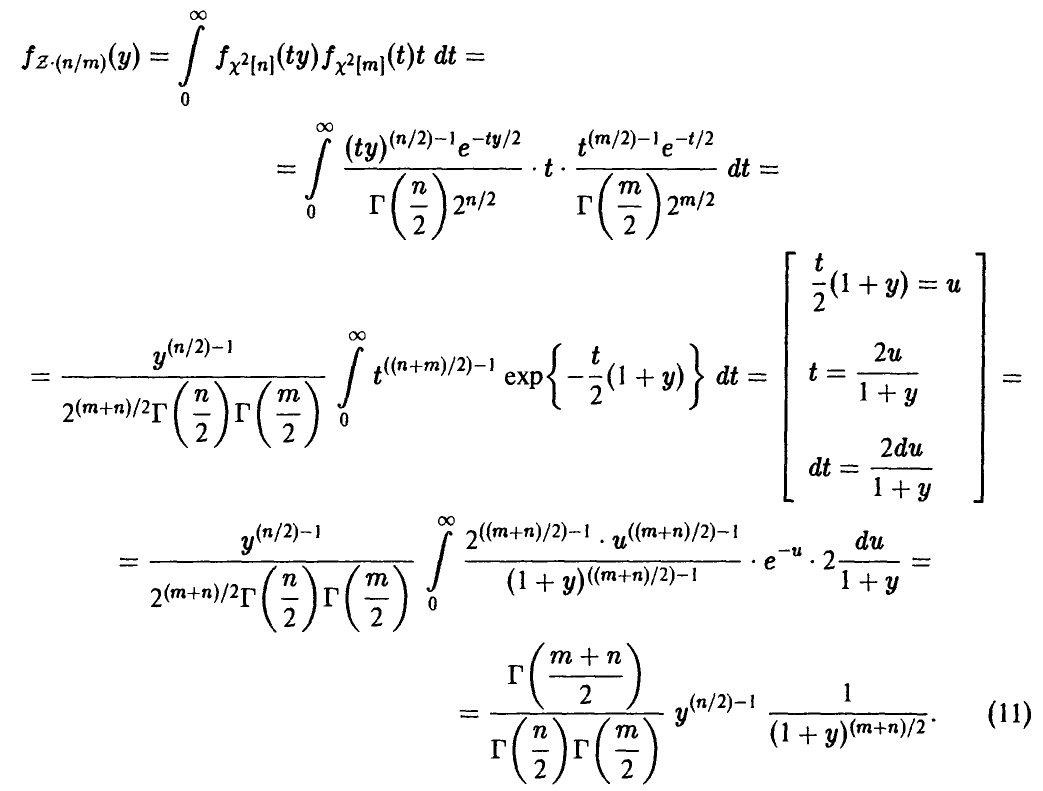
Z -распределение Фишера
Пусть 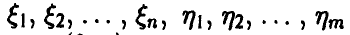
Величина Z называется случайной величиной Фишера-Снедекора. Обозначение Z = Z[n, m].
Закон распределения случайной величины Z найдем, используя (28) и (7). Имеем
Из соотношения (4) для линейного преобразования 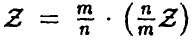
Многомерное нормальное распределение
Пусть 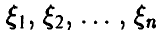
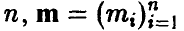
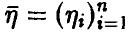
Отметим, что каждая компонента 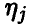
и, в силу сделанного выше замечания, является нормальной случайной величиной.
Найдем закон распределения вектора (13). Пусть 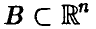
Сделаем в последнем интеграле замену переменных, положив
В силу невырожденности А эта замена невырождена и ее якобиан равен 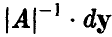
поэтому для любого борелевского 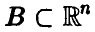
Положим 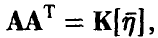
Для закона распределения вектора 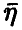
отсюда следует, что 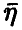
т. е. полностью определяется матрицей К и вектором m.
Распределение (14)-(15) называется невырожденным нормальным п-мерным распределением с параметрами (К, m). Обозначение
Отметим, что здесь К — симметричная, положительно определенная матрица, 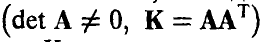
Компоненты нормального случайного вектора — нормальные случайные величины. Однако нормальности компонент недостаточно для того, чтобы вектор был нормальным в смысле определения, данного выше.
Пример:
Пусть 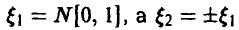
◄ Компонента 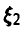
В то же время, совместное распределение 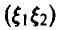
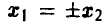
и не является плотностью совместного нормального распределения (15). ►
Отметим еще одно важное свойство компонент нормального вектора: они независимы тогда и только тогда, когда матрица К — диагонально.
◄ Действительно, если 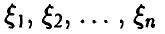
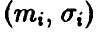
Легко убедиться в том, что плотность (17).имеет вид (15) с
Обратно, пусть 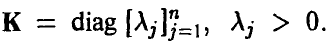
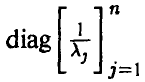
т. е. представима в виде произведения нормальных плотностей, каждая из которых является индивидуальной плотностью распределения г-й компоненты, что и означает независимость компонент 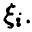
Пусть теперь 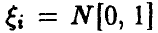
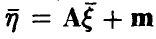
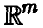
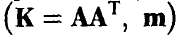
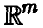
Независимость функций независимых аргументов
В заключение этой главы рассмотрим одно важное свойство функций случайных аргументов.
Пусть 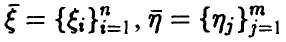
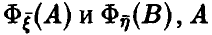
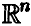
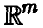
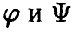
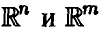
Теорема:
Если векторы 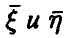
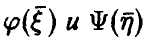
◄ Из независимости векторов 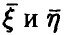
Рассмотрим
В силу соотношения (18) последняя вероятность представима в виде
откуда и следует искомое. ►
Функция распределения случайной величины
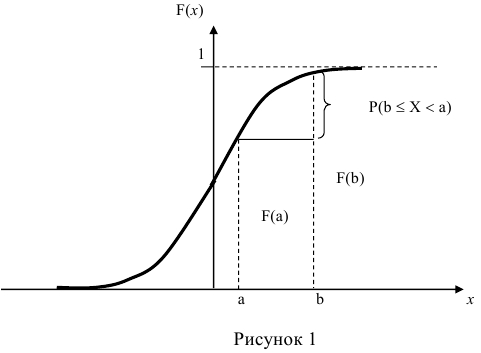
Функцией распределения случайной величины называют функцию 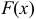
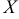
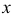
Геометрически 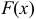
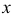
Иногда вместо термина «Функция распределения» используют термин «Интегральная функция».
Случайную величину называют непрерывной, если её функция распределения есть непрерывная, кусочно — дифференцируемая функция с непрерывной производной.
Свойства функции распределения
1) Значения функции распределения принадлежат отрезку [0, 1]:
2) 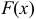
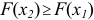
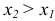
3) Вероятность того, что случайная величина 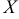
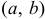
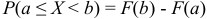
4) Вероятность того, что непрерывная, случайная величина 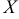
5) Если возможное значение случайной величины 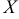
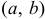
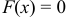
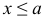
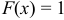
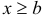
6) Если возможное значение непрерывной случайной величины расположены на всей оси, то 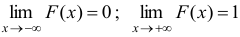
График функции распределения
График функции распределения непрерывной случайной величины, возможные значения которой принадлежат интервалу 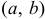
График функции распределения дискретной случайной величины имеет ступенчатый вид. На рис. 14 изображен график функции распределения дискретной случайной величины 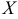
Пример:
Построить график функции
Найти вероятность того, что в результате испытания случайная величина 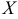
Решение:
График функции изображен на рис. 15. Вероятность того, что случайная величина 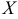
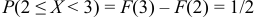
На этой странице размещён краткий курс лекций по теории вероятностей и математической статистике с теорией, формулами и примерами решения задач:
Теория вероятностей краткий курс для школьников и студентов
Возможно вам будут полезны эти страницы:
Решение заданий и задач по предметам:
- Теория вероятностей
- Математическая статистика
Дополнительные лекции по теории вероятностей:
- Случайные события и их вероятности
- Случайные величины
- Числовые характеристики случайных величин
- Законы больших чисел
- Статистические оценки
- Статистическая проверка гипотез
- Статистическое исследование зависимостей
- Теории игр
- Вероятность события
- Теорема умножения вероятностей
- Формула полной вероятности
- Теорема о повторении опытов
- Нормальный закон распределения
- Определение законов распределения случайных величин на основе опытных данных
- Системы случайных величин
- Нормальный закон распределения для системы случайных величин
- Вероятностное пространство
- Классическое определение вероятности
- Геометрическая вероятность
- Условная вероятность
- Схема Бернулли
- Многомерные случайные величины
- Предельные теоремы теории вероятностей
- Оценки неизвестных параметров
- Генеральная совокупность
Содержание:
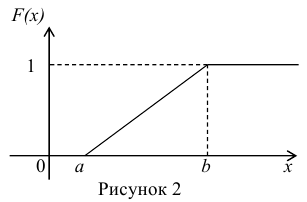
Непрерывные случайные величины: функция распределения случайной величины:
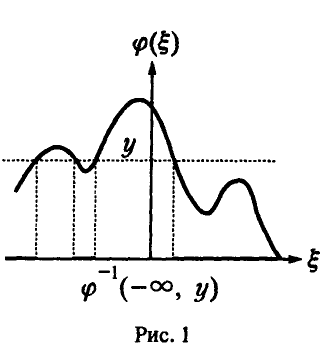
Если вычислить вероятность появления непрерывной случайной величины не составляет особого труда, то решение основной задачи теории вероятностей для непрерывной случайной величины несёт большие трудности. Поэтому в материалах сегодняшней лекции мы рассмотрим методы определения вероятности попадания непрерывной случайной величины на интервал с помощью функции распределения.
Функция распределения непрерывной случайной величины
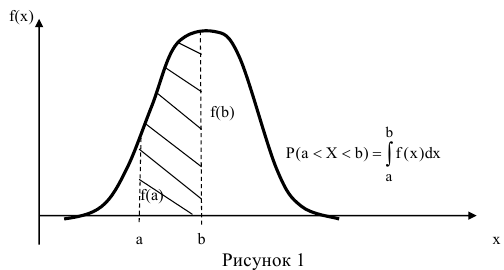
Зная функцию распределения непрерывной случайной величины, задача определения вероятности её попадания на интервал (а; b) может быть решена следующим образом.
По известной функции распределения вероятность попадания непрерывной случайной величины на интервал (а; b) равна приращению функции распределения на этом участке (рис. 1).
Во всех рассмотренных выше случаях случайная величина определялась путём задания значений самой величины и вероятностей этих значений.
Однако такой метод применим далеко не всегда. Например, в случае непрерывной случайной величины, её значения могут заполнять некоторый произвольный интервал. Очевидно, что в этом случае задать все значения случайной величины просто нереально.
Даже в случае, когда это сделать можно, зачастую задача решается чрезвычайно сложно. Рассмотренный только что пример даже при относительно простом условии (приборов только четыре) приводит к достаточно неудобным вычислениям, а если в задаче будет несколько сотен приборов?
Поэтому встает задача по возможности отказаться от индивидуального подхода к каждой задаче и найти по возможности наиболее общий способ задания любых типов случайных величин.
Пусть х — действительное число. Вероятность события, состоящего в том, что X примет значение, меньшее х, т.е. X
Определение. Функцией распределения называют функцию F(x), определяющую вероятность того, что случайная величина X в результате испытания примет значение, меньшее х.
F(x) = Р(Х < х)
Функцию распределения также называют интегральной функцией. Функция распределения существует как для непрерывных, так и для дискретных случайных величин. Она полностью характеризует случайную величину и является одной из форм закона распределения.
Для дискретной случайной величины функция распределения имеет
Знак неравенства под знаком суммы показывает, что суммирование распространяется на те возможные значения случайной величины, которые меньше аргумента х.
Функция распределения дискретной случайной величины X разрывна и возрастает скачками при переходе через каждое значение
Так для примера, который мы будем рассматривать на следующем
Свойства функции распределения
1) значения функции распределения принадлежат отрезку [0, 1].
2) F(x) — неубывающая функция.
3) Вероятность того, что случайная величина примет значение, заключенное в интервале (а, b) , равна приращению функции распределения на этом интервале.
4) На минус бесконечности функция распределения равна нулю, на плюс бесконечности функция распределения равна единице.
5) Вероятность того, что непрерывная случайная величина X примет одно определенное значение, равна нулю.
Таким образом, не имеет смысла говорить о каком — либо конкретном значении случайной величины. Интерес представляет только вероятность попадания случайной величины в какой — либо интервал, что соответствует большинству практических задач.
Заключение по лекции:
В лекции мы рассмотрели методы решения основной задачи теории вероятностей — определения вероятности попадания непрерывной случайной величины на интервал с помощью функции распределения.
Плотность вероятности. Числовые характеристики. Моменты случайных величин
Если вычислить вероятность появления непрерывной случайной величины не составляет особого труда, то решение основной задачи теории вероятностей для непрерывной случайной величины несёт большие трудности. Поэтому в материалах сегодняшней лекции мы рассмотрим методы определения вероятности попадания непрерывной случайной величины на интервал с помощью плотности
распределения.
Плотность распределения
Функция распределения полностью характеризует случайную величину, однако, имеет один недостаток. По функции распределения трудно судить о характере распределения случайной величины в небольшой окрестности той или иной точки числовой оси.
Определение. Плотностью распределения вероятностей непрерывной случайной величины X называется функция f(x) — первая производная от функции распределения F(x).
Плотность распределения также называют дифференциальной функцией. Для описания дискретной случайной величины плотность распределения неприемлема.
Смысл плотности распределения состоит в том, что она показывает как часто появляется случайная величина X в некоторой окрестности точки х при повторении опытов.
После введения функций распределения и плотности распределения можно дать следующее определение непрерывной случайной величины.
Определение. Случайная величина X называется непрерывной, если её функция распределения F(x) непрерывна на всей оси ОХ, а плотность распределения f(x) существует везде, за исключением (может быть, конечного числа точек).
Зная плотность распределения, можно вычислить вероятность того, что некоторая случайная величина X примет значение, принадлежащее заданному интервалу.
Теорема. Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (а, b), равна определенному интегралу от плотности распределения, взятому в пределах от а до b.
Доказательство этой теоремы основано на определении плотности распределения и третьем свойстве функции распределения (см. лекцию тема № 10).
Геометрически это означает, что вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (а, b), равна площади криволинейной трапеции, ограниченной осью ОХ, кривой распределения f(x) и прямыми х=а и х=b.
Геометрически вероятность Р(а < X < b) представляется в виде заштрихованной области, ограниченной кривой распределения и осью Ох на интервале(а; b) (рис 1).
Функция распределения может быть легко найдена, если известна плотность распределения, по формуле:
Свойства плотности распределения
1) Плотность распределения — неотрицательная функция.
2) Несобственный интеграл от плотности распределения в пределах от —
Плотность распределения
можно представить как:
тогда
Поэтому иногда функцию плотности распределения f(x) называют также дифференциальной функцией распределения или дифференциальным законом распределения величины X, а функцию распределения F(x) -интегральной функцией распределения или интегральным законом распределения.
Следует заметить, что интеграл 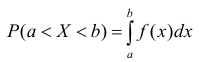
Р(х < X < х + dx) = dF(x) = f(x)dx
Величину f(x)dx называют элементом вероятности.
По своему содержанию элемент вероятности есть вероятность попадания случайной величины X на элементарный участок dx, прилежащий к точке X.
Функция распределения случайной величины X по известной плотности распределения может быть найдена, как интеграл от плотности распределения в интервале от
В схеме непрерывных случайных величин можно вывести аналогии формулы полной вероятности и формулы Бейеса, рассмотренные при изучении темы 4.
Обозначим Р(А /х) условную вероятность события А при условии Х= х. Заменяя в формуле полной вероятности вероятность гипотезы элементом вероятности f(x)dx, а сумму — интегралом, получим полную вероятность события А.
Данная формула называется интегральной формулой полной вероятности.
Соответствующий аналог в схеме непрерывных случайных величин имеет и формула Бейеса. Обозначив условную плотность распределения случайной величины X при условии, что в результате опыта появилось событие A через 
Данная формула называется интегральной формулой Бейеса.
Числовые характеристики непрерывных случайных величин
Пусть непрерывная случайная величина X задана функцией распределения f(x). Допустим, что все возможные значения случайной величины принадлежат отрезку [а,b].
Математическое ожидание
Определение. Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат отрезку [а,b], называется определенный интеграл
Если возможные значения случайной величины рассматриваются на всей числовой оси, то математическое ожидание находится по формуле:
При этом, конечно, предполагается, что несобственный интеграл сходится.
Дисперсия
Определение. Дисперсией непрерывной случайной величины называется математическое ожидание квадрата её отклонения.
По аналогии с дисперсией дискретной случайной величины, для практического вычисления дисперсии используется формула:
Среднеквадратичное отклонение
Определение. Средним квадратичным отклонением называется квадратный корень из дисперсии.
Мода
Определение. Модой 
Если многоугольник распределения для дискретной случайной величины или кривая распределения для непрерывной случайной величины имеет два или несколько максимумов, то такое распределение называется двухмодальным или многомодальным.
Если распределение имеет минимум, но не имеет максимума, то оно
называется антимодальным.
Медиана
Определение. Медианой 
Геометрически медиана — абсцисса точки, в которой площадь, ограниченная кривой распределения делится пополам.
Отметим, что если распределение одномодальное, то мода и медиана совпадают с математическим ожиданием.
Начальный момент
Определение. Начальным моментом порядка k случайной величины X называется математическое ожидание величины
Для дискретной случайной величины:
Для непрерывной случайной величины:
Начальный момент первого порядка равен математическому ожиданию.
Центральный момент
Определение. Центральным моментом порядка k случайной величины X называется математическое ожидание величины
Для дискретной случайной величины:
Для непрерывной случайной величины:
Центральный момент первого порядка всегда равен нулю, а центральный момент второго порядка равен дисперсии. Центральный момент третьего порядка характеризует асимметрию распределения.
Коэффициент асимметрии
Определение. Отношение центрального момента третьего порядка к среднеквадратическому отклонению в третьей степени называется коэффициентом асимметрии.
Эксцесс
Определение. Для характеристики островершинности и плосковершинности распределения используется величина, называемая эксцессом.
Кроме рассмотренных величин используются также так называемые абсолютные моменты:
Абсолютный начальный момент:
Абсолютный центральный момент:
Абсолютный центральный момент первого порядка называется средним арифметическим отклонением.
Заключение по лекции:
В лекции мы рассмотрели методы решения основной задачи теории вероятностей — определения вероятности попадания непрерывной случайной величины на интервал с помощью плотности распределения.
Законы распределения непрерывных величин: нормальное, равномерное, показательное
В материалах сегодняшней лекции мы рассмотрим законы распределения непрерывных величин.
Равномерное распределение
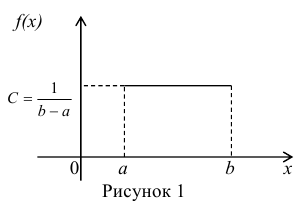
Определение. Непрерывная случайная величина имеет равномерное распределение на отрезке [а,b], если на этом отрезке плотность
распределения случайной величины постоянна, а вне его равна нулю.
Постоянная величина С может быть определена из условия равенства единице площади, ограниченной кривой распределения, представленной на рис. 1
Получаем 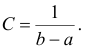
Найдём функцию распределения F(x) на отрезке [а,b] (рис. 2).
Для того, чтобы случайная величина подчинялась закону равномерного распределения необходимо, чтобы её значения лежали внутри некоторого определенного интервала, и внутри этого интервала значения этой случайной величины были бы равновероятны.
Определим математическое ожидание и дисперсию случайной величины, подчиненной равномерному закону распределения.
Вероятность попадания случайной величины в заданный интервал:
Показательное распределение
Определение. Показательным (экспоненциальным) называется распределение вероятностей непрерывной случайной величины X, которое описывается плотностью
где 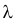
Найдём закон распределения.
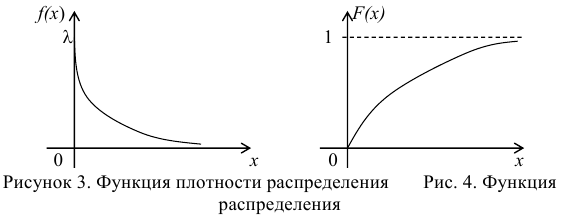
Графики функции распределения и плотности распределения представлены на рис. 3, 4.
Найдём математическое ожидание случайной величины, подчинённой показательному распределению.
Результат получен с использованием того факта, что
Для нахождения дисперсии найдём величину
Дважды интегрируя по частям, аналогично рассмотренному случаю, получим:
Тогда
Итого:
Видно, что в случае показательного распределения математическое ожидание и среднеквадратическое отклонение равны.
Также легко определить и вероятность попадания случайной величины, подчиненной показательному закону распределения, в заданный интервал.
Показательное распределение широко используется в теории надёжности.
Допустим, некоторое устройство начинает работать в момент времени to=0, а через какое- то время t происходит отказ устройства.
Обозначим Т непрерывную случайную величину — длительность безотказной работы устройства.
Таким образом, функция распределения F(t) = P(T
Вероятность противоположного события (безотказная работа в течение времени t) равна R(t) = P(T>t) — l — F(t).
Функция надежности
Определение. Функцией надёжности R(t) называют функцию, определяющую вероятность безотказной работы устройства в течение времени t.
Часто на практике длительность безотказной работы подчиняется показательному закону распределению.
Вообще говоря, если рассматривать новое устройство, то вероятность отказа в начале его функционирования будет больше, затем количество отказов снизится и будет некоторое время иметь практически одно и то же значение. Затем (когда устройство выработает свой ресурс) количество отказов будет возрастать.
Другими словами, можно сказать, что функционирование устройства на протяжении всего существования (в смысле количества отказов) можно описать комбинацией двух показательных законов (в начале и конце функционирования) и равномерного закона распределения.
Функция надёжности для какого- либо устройства при показательном законе распределения равна:
Данное соотношение называют показательным законом надежности.
Важным свойством, позволяющим значительно упростить решение задач теории надежности, является то, что вероятность безотказной работы устройства на интервале времени t не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности времени t.
Таким образом, безотказная работа устройства зависит только от интенсивности отказов 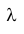
прошлом.
Так как подобным свойством обладает только показательный закон распределения, то этот факт позволяет определить, является ли закон распределения случайной величины показательным или нет.
Нормальный закон распределения
Определение. Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности
Нормальный закон распределения также называется законом Гаусса.
Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.
Можно легко показать, что параметры 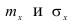
Найдём функцию распределения F(x).
График плотности нормального распределения называется нормальной кривой или кривой Гаусса.
Нормальная кривая обладает следующими свойствами:
1) Функция определена на всей числовой оси.
2) При всех х функция распределения принимает только положительные значения.
3) Ось ОХ является горизонтальной асимптотой графика плотности вероятности, т.к. при неограниченном возрастании по абсолютной величине аргумента л значение функции стремится к нулю.
4) Найдём экстремум функции.
Т.к. при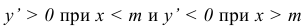
5) Функция является симметричной относительно прямой x = а, т.к. разность
(х — а) входит в функцию плотности распределения в квадрате.
6) Для нахождения точек перегиба графика найдем вторую производную функции плотности.
При 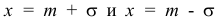
В этих точках значение функции равно
Построим график функции плотности распределения (рис. 5).
Построены графики при м =0 и трёх возможных значениях среднеквадратичного отклонения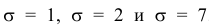
Если а > 0, то график сместится в положительном направлении, если а < 0 — в отрицательном.
При а = 0 и 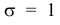
Функция Лапласа
Найдём вероятность попадания случайной величины, распределенной по нормальному закону, в заданный интервал.
Обозначим
Тогда
Т.к. интеграл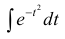
которая называется функцией Лапласа или интегралом вероятностей.
Значения этой функции при различных значениях х посчитаны и приводятся в специальных таблицах.
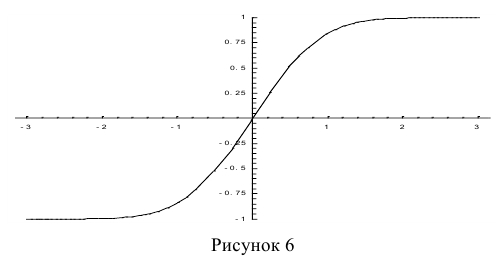
На рис. 6 показан график функции Лапласа.
Функция Лапласа обладает следующими свойствами:
- 1) Ф(0) = 0;
- 2) Ф(-х) = — Ф(х);
- 3)
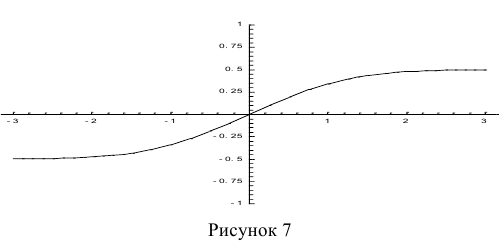
Функцию Лапласа также называют функцией ошибок и обозначают
erf х.
Ещё используется нормированная функция Лапласа, которая связана с функцией Лапласа соотношением:
На рис. 7 показан график нормированной функции Лапласа.
Правило трёх сигм
При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм.
Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины
Если принять 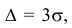
Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую, чем утроенное среднее квадратичное отклонение, практически равна нулю.
Это правило называется правилом трех сигм.
Не практике считается, что если для какой-либо случайной величины выполняется правило трёх сигм, то эта случайная величина имеет нормальное распределение.
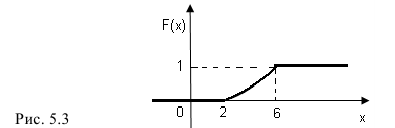
Пример:
Случайная величина Х задана плотностью распределения вероятностей:
Найти: а) значение с; б) функцию распределения F(х) и построить ее график; в)
Решение:
а) Значение с найдем из условия нормировки:
Следовательно,
б) Известно, что
Поэтому, если
если
если
Таким образом,
График функции F(х) изображен на рис. 5. 3.
в)
Пример:
Случайная величина Х задана функцией распределения:
Найти дифференциальную функцию распределения
Решение:
Так как 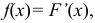
Пример:
Случайная величина Х задана дифференциальной функцией
Найти 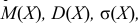
Решение:
Некоторые законы распределения непрерывной случайной величины
Пример:
Случайная величина Х равномерно распределена на отрезке [3;7]. Найти:
а) плотность распределения вероятностей 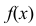
б) функцию распределения 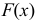
в)
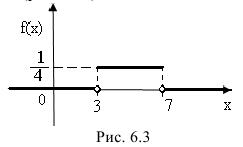
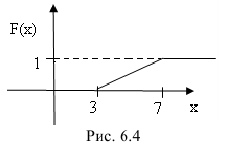
Решение: Воспользовавшись формулами, рассмотренными выше, при а = 3, b = 7, находим:
Построим ее график (рис. 6.3):
Построим ее график (рис. 6.4):
Пример:
Среднее время безотказной работы прибора равно 100 ч.
Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти:
а) плотность распределения вероятностей;
б) функцию распределения;
в) вероятность того, что время безотказной работы прибора превысит 120 ч.
Решение.
По условию математическое ожидание
откуда 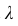
Следовательно,
в) Искомую вероятность найдем, используя функцию распределения:
Пример:
Случайная величина Х распределена нормально с математическим ожиданием 32 и дисперсией 16. Найти: а) плотность распределения вероятностей 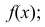
Решение:
По условию m = 32, σ2 = 16, следовательно, σ = 4, тогда
а)
б) Воспользуемся формулой:
Подставив a = 28, b = 38, m = 32, σ = 4, получим
По таблице значений функции Ф(х) находим Ф(1,5) = 0,4332, Ф(1) = 0,3413.
Итак, искомая вероятность:
Заключение по лекции:
В лекции мы рассмотрели законы распределения непрерывных величин.
- Закон больших чисел
- Генеральная и выборочная совокупности
- Интервальные оценки параметров распределения
- Алгебра событий — определение и вычисление
- Правило «трех сигм» в теории вероятности
- Производящие функции
- Теоремы теории вероятностей
- Основные законы распределения дискретных случайных величин
Функции случайных величин
Определение функции случайных величин. Функция дискретного случайного аргумента и ее числовые характеристики. Функция непрерывного случайного аргумента и ее числовые характеристики. Функции двух случайных аргументов. Определение функции распределения вероятностей и плотности для функции двух случайных аргументов.
Закон распределения вероятностей функции одной случайной величины
При решении задач, связанных с оценкой точности работы различных автоматических систем, точности производства отдельных элементов систем и др., часто приходится рассматривать функции одной или нескольких случайных величин. Такие функции также являются случайными величинами. Поэтому при решении задач необходимо знать законы распределения фигурирующих в задаче случайных величин. При этом обычно известны закон распределения системы случайных аргументов и функциональная зависимость.
Таким образом, возникает задача, которую можно сформулировать так.
Дана система случайных величин , закон распределения которой известен. Рассматривается некоторая случайная величина Y как функция данных случайных величин:
(6.1)
Требуется определить закон распределения случайной величины , зная вид функций (6.1) и закон совместного распределения ее аргументов.
Рассмотрим задачу о законе распределения функции одного случайного аргумента
Пусть — дискретная случайная величина, имеющая ряд распределения
Тогда также дискретная случайная величина с возможными значениями
. Если все значения
различны, то для каждого
события
и
тождественны. Следовательно,
и искомый ряд распределения имеет вид
Если же среди чисел есть одинаковые, то каждой группе одинаковых значений
нужно отвести в таблице один столбец и соответствующие вероятности сложить.
Для непрерывных случайных величин задача ставится так: зная плотность распределения случайной величины
, найти плотность распределения
случайной величины
. При решении поставленной задачи рассмотрим два случая.
Предположим сначала, что функция является монотонно возрастающей, непрерывной и дифференцируемой на интервале
, на котором лежат все возможные значения величины
. Тогда обратная функция
существует, при этом являясь также монотонно возрастающей, непрерывной и дифференцируемой. В этом случае получаем
(6.2)
Пример 1. Случайная величина распределена с плотностью
Найти закон распределения случайной величины , связанной с величиной
зависимостью
.
Решение. Так как функция монотонна на промежутке
, то можно применить формулу (6.2). Обратная функция по отношению к функции
есть
, ее производная
. Следовательно,
Рассмотрим случай немонотонной функции. Пусть функция такова, что обратная функция
неоднозначна, т. е. одному значению величины
соответствует несколько значений аргумента
, которые обозначим
, где
— число участков, на которых функция
изменяется монотонно. Тогда
(6.3)
Пример 2. В условиях примера 1 найти распределение случайной величины .
Решение. Обратная функция неоднозначна. Одному значению аргумента
соответствуют два значения функции
Применяя формулу (6.3), получаем:
Закон распределения функции двух случайных величин
Пусть случайная величина является функцией двух случайных величин, образующих систему
, т. е.
. Задача состоит в том, чтобы по известному распределению системы
найти распределение случайной величины
.
Пусть — плотность распределения системы случайных величин
. Введем в рассмотрение новую величину
, равную
, и рассмотрим систему уравнений
Будем полагать, что эта система однозначно разрешима относительно
и удовлетворяет условиям дифференцируемости.
Плотность распределения случайной величины
Заметим, что рассуждения не изменяются, если введенную новую величину положить равной
.
Математическое ожидание функции случайных величин
На практике часто встречаются случаи, когда нет особой надобности полностью определять закон распределения функции случайных величин, а достаточно только указать его числовые характеристики. Таким образом, возникает задача определения числовых характеристик функций случайных величин помимо законов распределения этих функций.
Пусть случайная величина является функцией случайного аргумента
с заданным законом распределения
Требуется, не находя закона распределения величины , определить ее математическое ожидание
Пусть — дискретная случайная величина, имеющая ряд распределения
Составим таблицу значений величины и вероятностей этих значений:
Эта таблица не является рядом распределения случайной величины , так как в общем случае некоторые из значений могут совпадать между собой и значения в верхней строке не обязательно идут в возрастающем порядке. Однако математическое ожидание случайной величины
можно определить по формуле
(6.4)
так как величина, определяемая формулой (6.4), не может измениться от того, что под знаком суммы некоторые члены будут заранее объединены, а порядок членов изменен.
Формула (6.4) не содержит в явном виде закон распределения самой функции , а содержит только закон распределения аргумента
. Таким образом, для определения математического ожидания функции
вовсе не требуется знать закон распределения функции
, а достаточно знать закон распределения аргумента
.
Для непрерывной случайной величины математическое ожидание вычисляется по формуле
где — плотность распределения вероятностей случайной величины
.
Рассмотрим случаи, когда для нахождения математического ожидания функции случайных аргументов не требуется знание даже законов распределения аргументов, а достаточно знать только некоторые их числовые характеристики. Сформулируем эти случаи в виде теорем.
Теорема 6.1. Математическое ожидание суммы как зависимых, так и независимых двух случайных величин равно сумме математических ожиданий этих величин:
Теорема 6.2. Математическое ожидание произведения двух случайных величин равно произведению их математических ожиданий плюс корреляционный момент:
Следствие 6.1. Математическое ожидание произведения двух некоррелированных случайных величин равно произведению их математических ожиданий.
Следствие 6.2. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.
Дисперсия функции случайных величин
По определению дисперсии имеем . Следовательно,
, где
.
Приведем расчетные формулы только для случая непрерывных случайных аргументов. Для функции одного случайного аргумента дисперсия выражается формулой
(6.5)
где — математическое ожидание функции
;
— плотность распределения величины
.
Формулу (6.5) можно заменить на следующую:
Рассмотрим теоремы о дисперсиях, которые играют важную роль в теории вероятностей и ее приложениях.
Теорема 6.3. Дисперсия суммы случайных величин равна сумме дисперсий этих величин плюс удвоенная сумма корреляционных моментов каждой из слагаемых величин со всеми последующими:
Следствие 6.3. Дисперсия суммы некоррелированных случайных величин равна сумме дисперсий слагаемых:
Теорема 6.4. Дисперсия произведения двух независимых случайных величин вычисляется по формуле
Корреляционный момент функций случайных величин
Согласно определению корреляционного момента двух случайных величин и
, имеем
Раскрывая скобки и применяя свойства математического ожидания, получаем
(6.6)
Рассмотрим две функции случайной величины
Согласно формуле (6.6)
отсюда
т.е. корреляционный момент двух функций случайных величин равен математическому ожиданию произведения этих функций минус произведение из математических ожиданий.
Рассмотрим основные свойства корреляционного момента и коэффициента корреляции.
Свойство 1. От прибавления к случайным величинам постоянных величин корреляционный момент и коэффициент корреляции не изменяются.
Свойство 2. Для любых случайных величин и
абсолютная величина корреляционного момента не превосходит среднего геометрического дисперсий данных величин:
где — средние квадратические отклонения величин
и
.
Следствие 6.5. Для любых случайных величин и
абсолютная величина коэффициента корреляции не превосходит единицы:
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
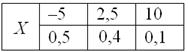
2.2.7. Функция распределения случайной величины
Стандартное обозначение:
И для дискретной, и для непрерывной случайной величины она определяется одинаково:
, где
– вероятность того, что случайная величина
примет значение,
МЕНЬШЕЕ, чем переменная , которая«пробегает» все действительные значения от «минус» до
«плюс» бесконечности.
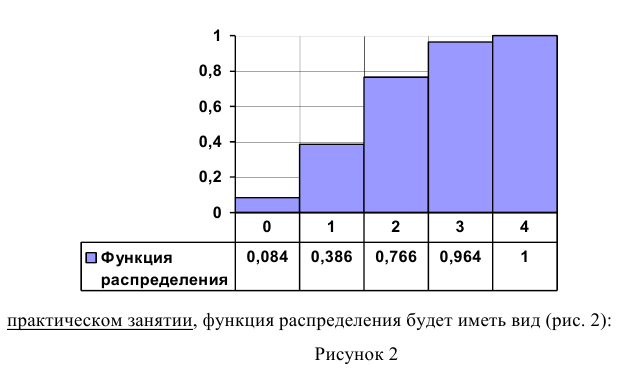
Построим функцию распределения для нашей подопытной игры:
Начинаем разбираться. Чему, например, равно значение ? Это вероятность того, что выигрыш будет меньше, чем –20. И это невозможное событие:
. Совершенно понятно, что
и для всех «икс» из интервала
, а также для
. Почему? По определению функции распределения:
– вы согласны? Функция
возвращает вероятность того,
что в точке выигрыш
будет СТРОГО МЕНЬШЕ «минус» пяти.
Таким образом: , если
.
На интервале функция
, поскольку левее
любой точки этого интервала есть только одно значение случайной величины, которое появляется с вероятностью 0,5. Кроме того,
сюда же следует отнести точку ,
так как:
– очень хорошо осознайте этот
момент!
Таким образом, если , то
Далее рассматриваем промежуток . СТРОГО ЛЕВЕЕ любой точки этого промежутка находятся два выигрыша
, поэтому:
И, наконец, если , то
, ибо все значения
случайной величины
лежат СТРОГО левее
любой точки интервала
Заметим, кстати, важную особенность: коль скоро функция характеризует вероятность, то
она может принимать значения лишь из промежутка – и никакие другие!
Итак, функция распределения вероятностей ДСВ является кусочной и, как многие знают, в таких случаях принято использовать
фигурные скобки:
График данной функции имеет разрывный «ступенчатый» вид:
Причём, функция или её
график однозначно определяют сам закон распределения: в точке высота «ступеньки» (разрыв) составляет
(следим по графику), в точке
«скачок» разрыва равен
и, наконец, в точке
он равен в точности
.
Таким образом, функция распределения вероятностей – это ещё один способ ЗАДАТЬ случайную величину. И этот способ
особо важен для непрерывной случайной величины – по той причине, что её невозможно описать таблицей (ввиду бесконечного и
несчётного количества принимаемых значений). Однако, всему своё время, и НСВ – тоже.
Освоим технические моменты решения типовой задачи:
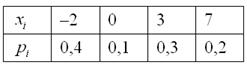
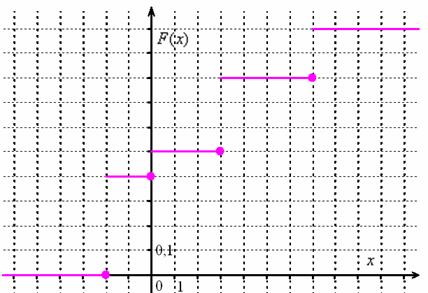
Задача 93
Построить функцию распределения случайной величины
Найти вероятности того, что случайная величина примет значение из следующих промежутков:
…, пожалуй, достаточно.
Решение: На практике удобно использовать формальный алгоритм построения функции распределения:
Сначала берём первое значение и составляем нестрогое неравенство
. На этом промежутке
.
На промежутке (между
и
):
На промежутке (между
и
):
На промежутке (между
и
):
И, наконец, если строго
больше самого последнего значения , то:
Легко заметить, что с увеличением «икс» идёт накопление (суммирование) вероятностей, и поэтому функцию иногда называют интегральной функцией распределения. В
практических задачах проведённые выше действия обычно выполняют устно, а результат сразу записывают под единую скобку:
Выполним чертёж:
и проконтролируем правильность решения с помощью «скачков» графика: в точке «скачок» равен
, в точке
составляет
, в точке
равен
, и, наконец, в точке
–
.
При выполнении чертежа от руки оптимален следующий масштаб:
горизонтальная ось: 1 ед. = 2 или 1 тетрадная клетка;
вертикальная ось: 0,1 = 1 тетрадная клетка.
На левых концах ступенек (кроме нижнего луча) можно ставить выколотые точки – дело вкуса. Левый нижний луч следует прочертить жирно
(чтобы он не сливался с координатной осью) и до конца оси! Правая верхняя линия не должна заканчиваться раньше
острия оси! Такие оплошности могут говорить о непонимании функции распределения, а это, как вы понимаете, скверно. То было ручное
построение. Ну а о том, как строить такие красивые графики в Экселе можно узнать в этом ролике на Ютубе, к слову, полигон (многоугольник) распределения строится ещё проще.
Переходим ко второй части задания, её коротко можно сформулировать так:


Полную и свежую версию этой книги в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин


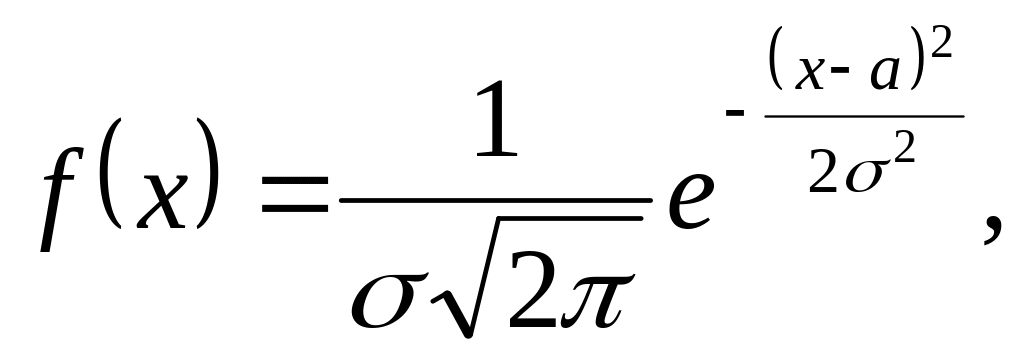
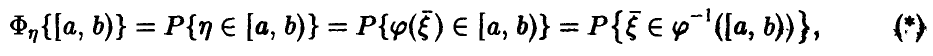
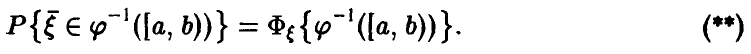

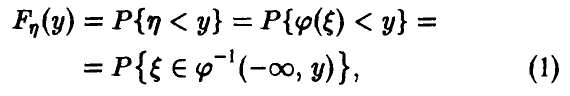
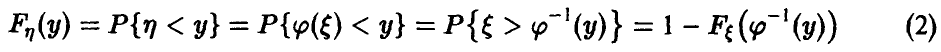

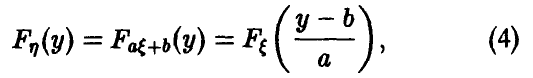
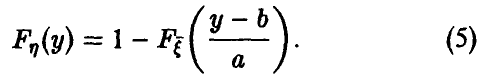
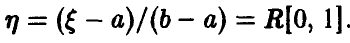
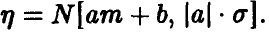
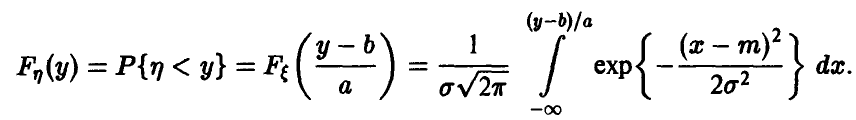
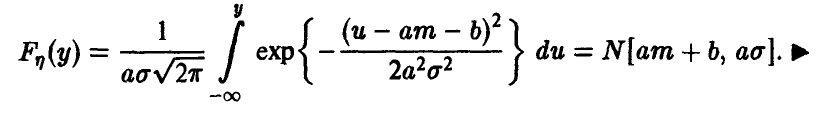
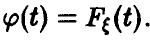
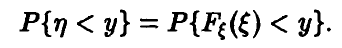
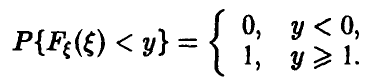
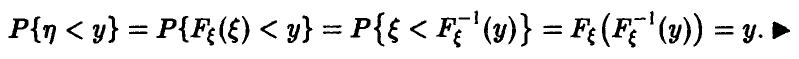
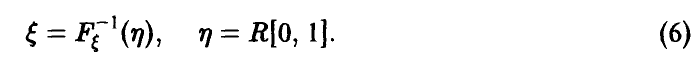
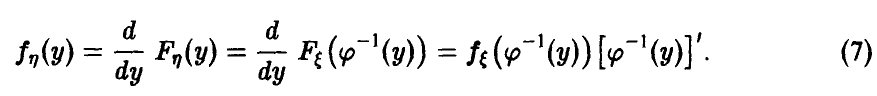
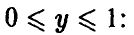
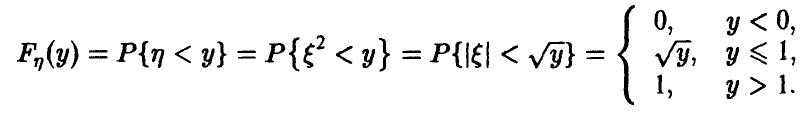
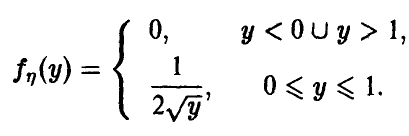
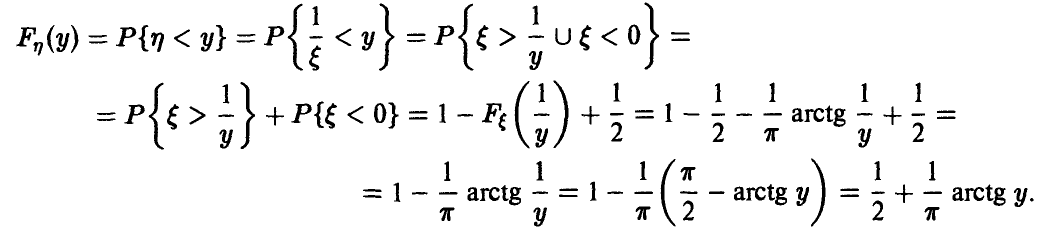
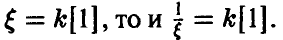
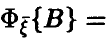
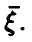
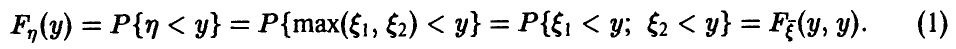
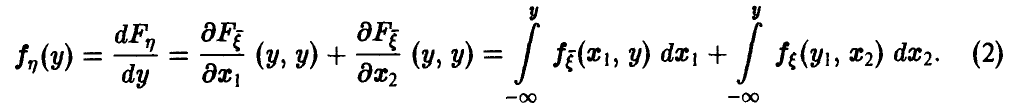

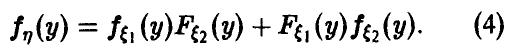
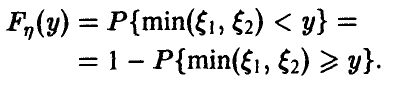
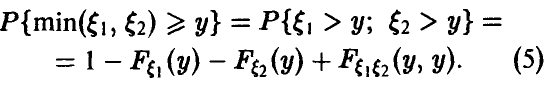
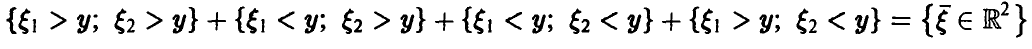
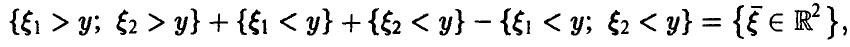
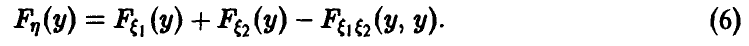
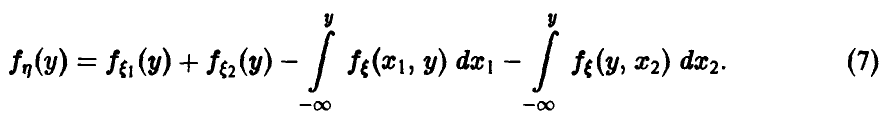
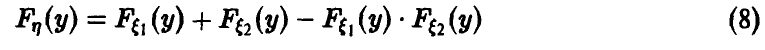
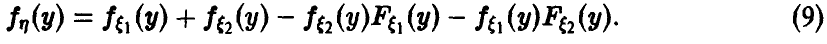
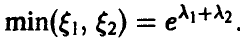
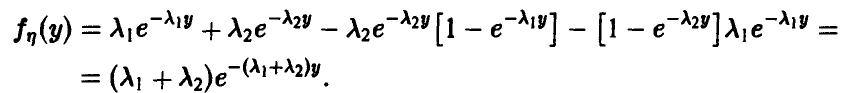
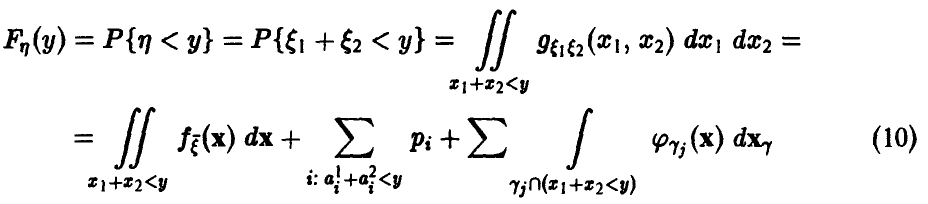
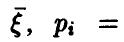
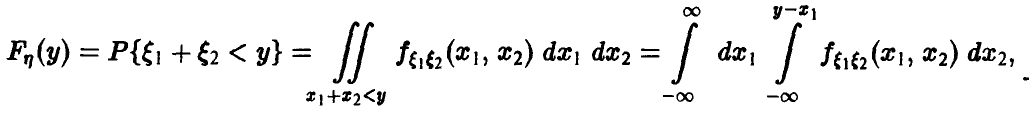
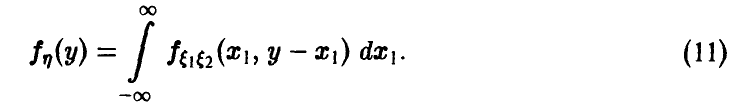
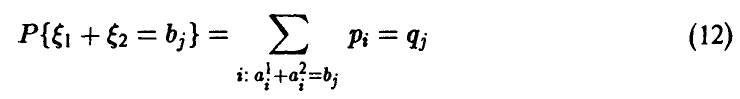
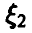
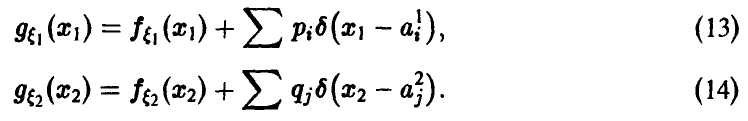
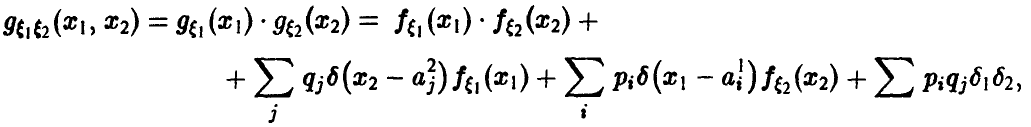
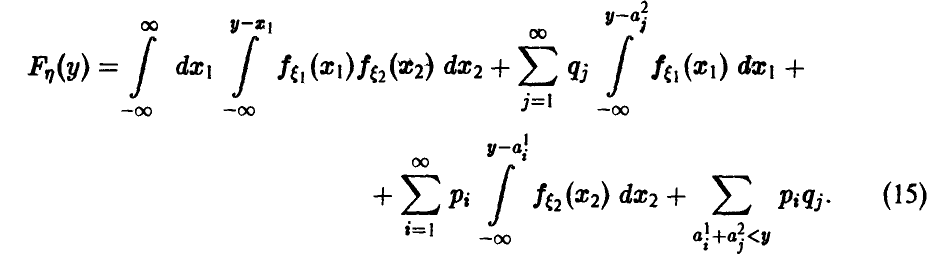
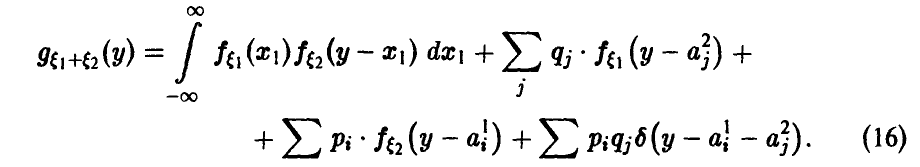
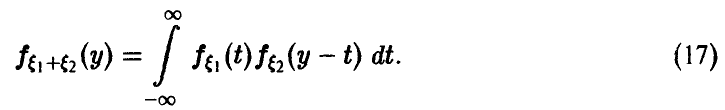
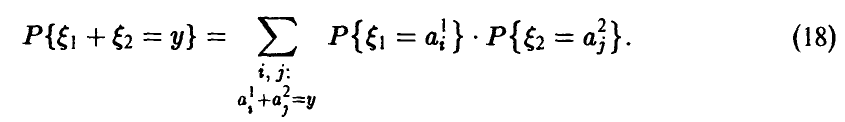
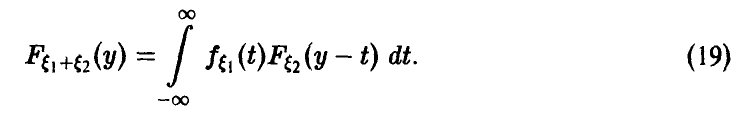
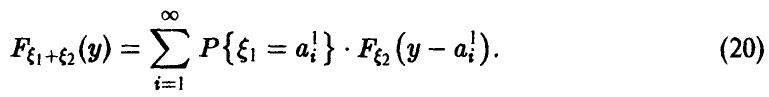
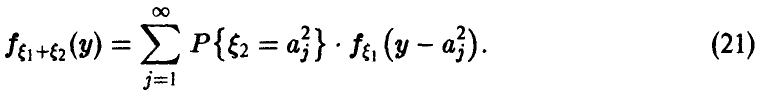
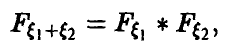
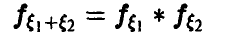
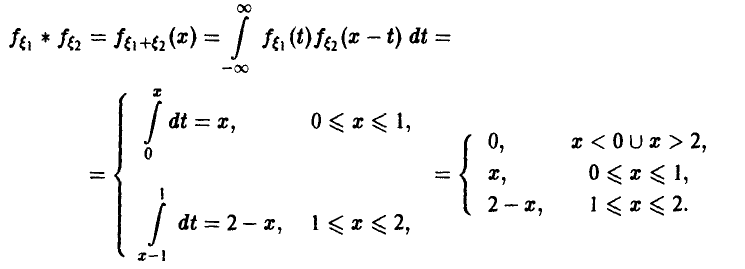
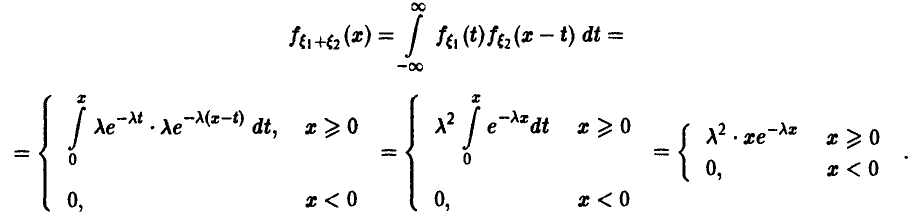
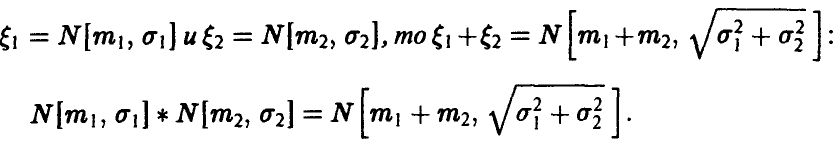
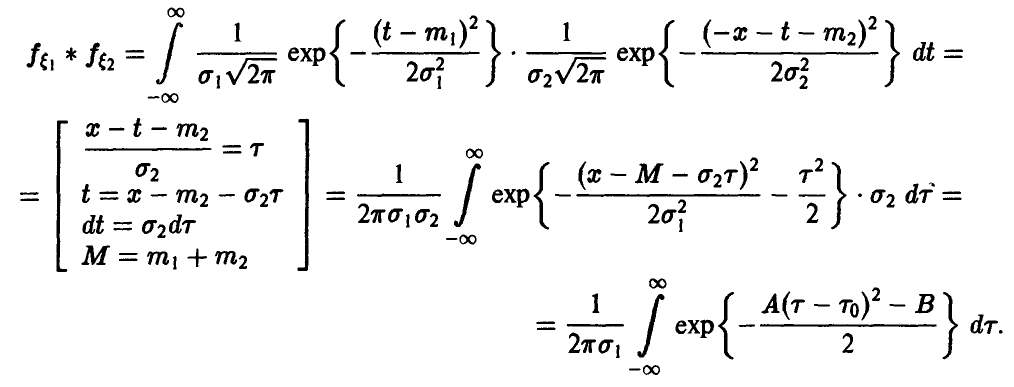
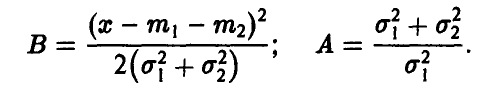
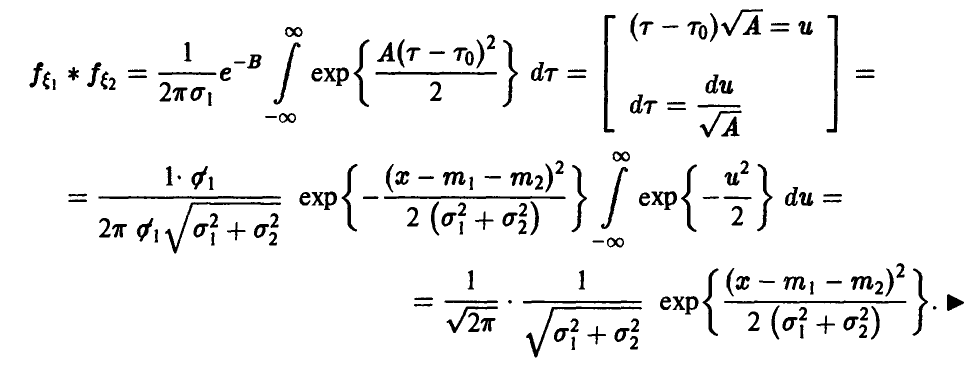
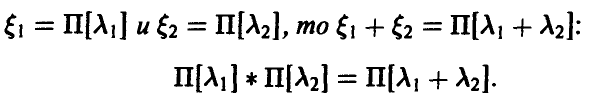
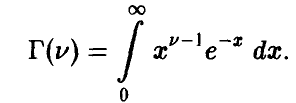
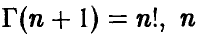 — натуральное.
— натуральное.