Как найти максимум функции в maple - Исправление недочетов и поиск решений вместе с Examum.ru

extrema

find relative extrema of an expression

Calling Sequence

Parameters

Description

Examples

	Calling Sequence
	extrema(expr, constraints) extrema(expr, constraints, vars) extrema(expr, constraints, vars, ‘s‘)

Parameters

expr	—	expression whose extrema are to be found
constraints	—	constraint or set of constraints
vars	—	variable or set of variables
s	—	unevaluated name

Description

•

The extrema function can be used to find extreme values of a multivariate expression with zero or more constraints. Candidates for extreme value points can also be returned. The extrema are returned as a set, and the candidates are returned as a set of sets of equations in the appropriate variables.

•

expr must be an algebraic expression. The constraints may be specified as either expressions or equations. When a constraint is given as an expression, it is understood that constraint = 0. If no constraints are to be given, then the empty set {} is used in the parameter list. If vars is not given then all name indeterminates in the expr and constraints are used. vars must be specified if the fourth parameter s is given. The candidates for the extreme value points are returned in s.

•	When the candidates cannot be expressed in closed form, s will contain the system of equations which when solved will produce these candidates.

•	This function employs the method of Lagrange multipliers.

Examples

>	extrema⁡a⁢x2+b⁢x+c,,x

−b24⁢a+c

(1)

>	extrema⁡a⁢x⁢y⁢z,x2+y2+z2=1,x,y,z

max⁡0,−3⁢a9,3⁢a9,min⁡0,−3⁢a9,3⁢a9

(2)

>	f ≔ x2+y212−z&semi;g1 ≔ x2+y2−16&semi;g2 ≔ x+y+z=10

f≔x2+y2−z

g1≔x2+y2−16

g2≔x+y+z=10

(3)

>	extrema⁡f,g1,g2,x,y,z,'s'

−6−4⁢2,−6+4⁢2

(4)

x=−2⁢2,y=−2⁢2,z=4⁢2+10,x=2⁢2,y=2⁢2,z=−4⁢2+10

(5)

46.Html. Нумерованные списки.

Списки
являются важным средством структурирования
текста и применяются во всех языках
разметки. В НТМL имеются следующие виды
списков:

-ненумерованный
список (неупорядоченный) (Unordered Lists <UL>);

-нумерованный
список (упорядоченный) (Ordered Lists <OL>);

-список
определений.

Теги
для ненумерованных и нумерованных
списков — это основа HTML.
Теги для ненумерованных и нумерованных
списков — это основа HTML.
HTML
3.2 добавляет несколько атрибутов к тегам
списков для выбора разных схем нумерации
в нумерованных.
Элемент
OL
используется с целью задания нумерованных
списков, имеет атрибуты type=1,
или A,
или aб
или I
или I
для задания вида нумерации и start
для указания с какого индекса принимается
нумерация списка. Элемент включает в
себя дополнит. элементнт <LI>,
который задаёт элементы списков.
Синтаксис: <OL,
type=1
start=1><LI>элементс
писка <LI>,элемент
списка <OL>

Нумерованные
списки

Нумерованные
списки
— тег <OL>

Нумерованные
списки. Тег <OL>
вместе с атрибутом ТYРЕ=
в HTML
3.2 позволяет создавать нумерованные
списки, используя в качестве номеров
не только обычные числа, но и строчные
и прописные буквы, а также строчные и
прописные римские цифры. При необходимости
можно даже смешивать эти типы нумерации
в одном списке:

<ОL ТYРЕ=1> Тег
создает список с нумерацией в формате
1., 2., 3., 4. и т.д.

<ОL ТYРЕ=А> Тег
создает список с нумерацией в формате
А., В., С., D. и т.д.

<OL ТYРЕ=а> Тег
создает список с нумерацией в формате
а., b., с., d. и т.д.

<ОL ТYРЕ=I> Тег
создает список с нумерацией в формате
I., II., III., IV. и т.д.

<ОL
ТYРЕ=i>
Тег создает список с нумерацией в формате
i.,
ii.,
iii.,
iv.
и т.д.

Атрибут
START=n
позволяет задать начальное значение
для нумерованного списка при использовании
арабских цифр.

<ОL
ТYРЕ=1 start=4>
Тег создает список с нумерацией в формате
1., 2., 3., 4. и т.д. начиная с цифры 4.

<UL>

<LI> первый
элемент </LI>

<LI> второй
элемент </LI>

<LI> третий
элемент </LI>

</UL>

Если вместо <UL>
(Unordered List, что означает ненумерованный
список) поставить <OL> (Ordered List,
нумерованный список), список получится
нумерованным.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Важным разделом математики является исследование аналитических функций. Оно обычно заключается в определении координат особых точек функции и ее значений в этих точках, а также в выяснении особенностей функции, таких как наличие точек разрыва, асимптот, точек перегибов, разрывов и т. д.

Maple 16, как и более ранние версии этого пакета, позволяют студенту полностью исследовать функции и строить их графики.

С помощью функции fsolve легко находятся значения независимой переменной x функций вида f(x), при которых f(x)=0 (корни этого уравнения). При этом данная функция позволяет (в отличие от функции solve) изолировать корни функции f(x) указанием примерного интервала их существования. Ряд функций служит для вычисления экстремумов, максимумов и минимумов функций, а также для определения их непрерывности.

Для исследования функций на непрерывность Maple 16 имеет функцию iscont, записываемую в ряде форм: iscont(expr, x=a..b), iscont(expr, x=a..b, ‘closed’) и iscont( expr, x=a.. b, ‘open’).

Функции, не имеющие непрерывности, доставляют много хлопот. В Maple 16 функция discont(f, х) позволяет определить точки, в которых нарушается непрерывность функции f(x). Она вычисляет все точки в пределах изменениях от $$-infty$$ до $$infty.$$ Результаты вычислений могут содержать особые экстра переменные с именами вида _Zn- и _NNn-. В частности, они позволяют оценить периодические нарушения непрерывности функций.

Многие операции, такие как интегрирование и дифференцирование, чувствительны к особенностям функций, в частности к их разрывам и особым точкам. Функция singular(ехрr, vars) позволяет найти особые (сингулярные) точки выражения ехрг, в которых она испытывает разрывы. Дополнительно в числе параметров может указываться необязательный список переменных.

Функция extrema позволяет найти экстремумы выражения ехрr (как максимумы, так и минимумы) при ограничениях constraints и переменных vars, по которым ищется экстремум: extrema(expr, constraints), extrema(expr, constraints, vars) и extrema(expr, constraints, vars, ‘s’).

Ограничения constraints и переменные vars могут задаваться одиночными объектами или списками ряда ограничений и переменных. Найденные координаты точки экстремума присваиваются переменной ‘s’. При отсутствии ограничений в виде равенств или неравенств вместо них записывается пустой список {}.

Функция extrema возвращает как значения экстремумов, так и значения аргументов, при которых экстремумы наблюдаются.

Часто нужно найти минимум или максимум заданной функции. Для поиска минимумов и максимумов выражений (функций) ехрr служат функции стандартной библиотеки: minimize(expr, opt1, opt2, …, optn) и maximize(expr, opt1, opt2, …, optn).

Эти функции могут разыскивать максимумы и минимумы для функций как одной, так и нескольких переменных. С помощью опций optl, opt2, … , optn можно указывать дополнительные данные для поиска.

Для вычисления пределов функции f в точке x=a используются следующие функции: limit(f, x=a, dir) и Limit(f, x=a, dir).

Здесь f – алгебраическое выражение, х – имя переменной, dir – параметр, указывающий на направление поиска предела (left — слева, right — справа, real — в области вещественных значений, complex — в области комплексных значений). Значением а может быть бесконечность (как положительная, так и отрицательная).

Для нахождения производной применяют дифференциальный оператор, который можно записывать в следующих формах: D(f) или D[i](f), где параметр f — выражение или имя функции, i — положительное целое число, выражение или последовательность. Этот оператор позволяет сократить запись, т.е. D(f)=unapply(diff(f(x), x), x) а в форме D(f)(x) = diff(f(x), x). Для нахождения n–й производной используют (D@@n)(f).

Для построения двумерных графиков служит функция plot. Она задается в виде: plot(f, h, v) и plot(f, h, v,…) ,где f — визуализируемая функция (или функции), h — переменная с указанием области ее изменения по горизонтали, v — необязательная переменная с указанием области изменения функции по вертикали, далее может следовать параметр или набор параметров, задающих стиль построения графика (толщину и цвет кривых, тип кривых, метки на них и т.д.). Обычно записывают plot(f(x), x=a..b). Диапазон изменения независимой переменной x задается как a..b, где a и b — минимальное и максимальное значение x, .. (две точки) — составной символ, указывающий на изменение независимой переменной. Разумеется, имя х здесь дано условно — независимая переменная может иметь любое допустимое имя.

Помимо построения самой кривой f(x) необходимо задать ряд других свойств графиков, например вывод координатных осей, тип и цвет линий графика и др. Это достигается применением параметров графика — специальных указаний для Maple. Графики обычно (хотя и не всегда) строятся сразу в достаточно приемлемом виде. Это достигается тем, что многие параметры задаются по умолчанию и пользователь, по крайней мере начинающий, может о них ничего не знать. Однако язык Maple 16 позволяет задавать управляющие параметры и в явном виде.

Пример

Исследовать функцию и построить график

$$y=frac{x^3}{x-1}$$

Исследуем функцию средствами Maple 16:

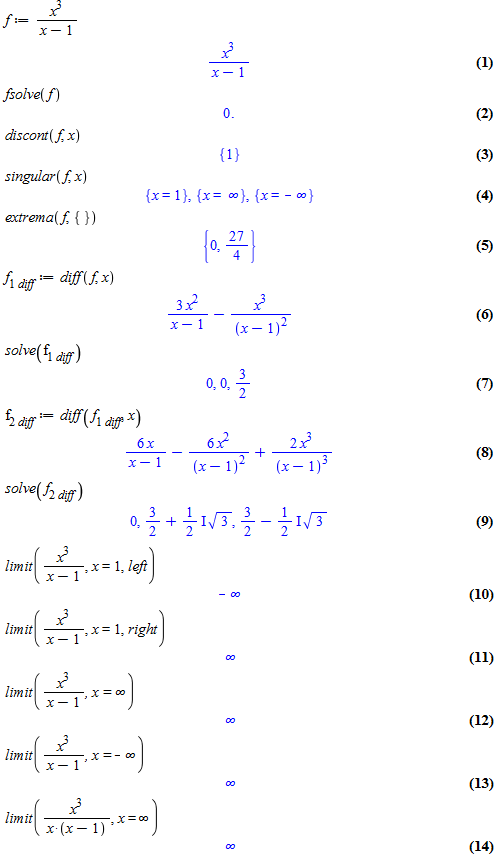
Построим график функции при помощи Maple 16:

Источник