Теорема: Пусть аналитична в
и
. Если
, в которой
, то
в
. Иными словами, модуль не постоянной функции не может достигать своей верхней границы внутри области аналитичности — только на ее границе.
Доказательство: Пусть и
. Рассмотрим множество
точек из
, в которых
. Известно, что
. Покажем, что
открыто. Пусть
. По теореме о среднем
достаточно малого
:


на
. Обозначим
на
. Тогда имеем:



. Мы показали, что если
, то
. Отсюда следует, что
открыто (любая точка лежит в нем вместе с окрестностью). Рассмотрим множество
. Покажем, что оно открыто.
— непрерывная вещественная функция
это неравенство выполняется в некоторой окрестности точки
— открыто. Следовательно, область
образуется двумя открытыми непересекающимися множествами, а значит
является двусвязным, как область, следовательно либо
, либо
. Но известно, что
. Следовательно
является константой на всей
.
Получили: . В силу аналитичности функции (а значит, и аналитичности модуля) имеем:
Заменив здесь по условиям Коши-Римана частные производные и решив относительно них систему алгебраических уравнений с ненулевыми коэффициентами, нетрудно получить, что . Следовательно
. Теорема доказана.
| < Предыдущая | Следующая > |
|---|
- ГЛАВНАЯ >
- ПРЕДМЕТЫ >
- ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО >
- ПРИНЦИП МАКСИМУМА МОДУЛЯ АНАЛИТИЧЕСКОЙ ФУНКЦИИ
Принцип максимума модуля аналитической функции
НАВИГАЦИЯ ПО СТРАНИЦЕ
Принцип максимума модуля
Доказательство
НАВИГАЦИЯ ПО СТРАНИЦЕ
Принцип максимума модуля
Доказательство
Нам важно твое мнение
Остался ли ты доволен контентом, который опубликован на этой странице?
Спасибо, принято!
Напиши, что не так с вопросом в форме обратной связи, мы постараемся разобраться в ближайшее время.
Принцип максимума модуля для аналитической функции:
Если аналитичная в и то достигает максимального значения на границе.
Доказательство.
Предположим обратное: что
всюду на окружности
Теперь на ZNZN можно делать свои конспекты
Легко создавать, делиться и просматривать с устройств
Доступно в ПК-версии сайта
Нам важно твое мнение
Остался ли ты доволен контентом, который опубликован на этой странице?
Спасибо, принято!
Напиши, что не так с вопросом в форме обратной связи, мы постараемся разобраться в ближайшее время.
Для любых последовательностей чисел 



Вот это да. Спасибо за указанный факт.
Используя его, последовательность 


![$f(z)=suplimits_{xin[0,x_0]}|g(x)|+f_1(z).$ $f(z)=suplimits_{xin[0,x_0]}|g(x)|+f_1(z).$](https://dxdy-01.korotkov.co.uk/f/4/c/e/4ce6a8e35d39fb12c2837cb29c764f0c82.png)


И не понадобилось никаких действительнозначных аналитических функций, аналитических продолжение…
Построение 
Построим целую функцию 

Тогда
где 
Обалденная конструкция, завораживает)
Странно, что в брошюре по целым функциям из которой я взял это задания, оно идёт в самом начале главы один, а факторизация целых функций рассматривается во второй главе, гм.
Лемма:
Знач-ие голоморф. в обл. G
ф-ии f
в любой т. z
равно среднему арифм. ее значений на
любой окр-ти Г с центром z,
принадл. вместе с внутренностью обл. G.
Теорема
1: Если ф. f
голоморф. в обл. G
с Сz
и модуль |f|
достигает локал. максимума в нек. т. z0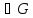
в G.
Док-во:
Положим |f(z0)|=M,
очевидно, 0≤M<
Выберем число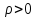
чтобы кругU(z0,
вместе с границей лежал вG
и чтобы |f(z)|≤M
в замыкании z
В случ. M=0
имеем f=0,и,
согласно принципу единств-и, f=0
в G.
Пусть M>0.
Рассужд. от прот-го, покаж., что |f|=M
в

Предпол., что в
где 0<r<
0≤t0≤
2
в кот. |f(z*)|<M,
тогда в виду непрер-ти
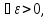
что наT1=[t0—

выполн. нер-во
Кроме того, ф , 0≤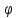
на дополн. T2=
[t0+


Используя теор. о среднем для голоморф.
ф-ции, имеемf(z0)=
Откуда
|f|=M
в U(z0,
Следствие1:
Максимум |f|,
голоморф. в обл. и непрер. в ее замыкании,
может достигаться только на границе
этой обл., при усл-иии, что f(z)≠const.
Следствие
2(Вейерштрасса): Пусть
дан ряд f1(z)+…+fn(z)+…
(1) все члены кот.- ф-ции, голоморф. в обл.
G
и непрер. в G,
тогда если ряд (1) сход. равном. на границе
обл. G
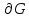
то он сход-ся также равномер. на замкн.
обл.
22.Нули
голоморф.ф-и. Порядок нуля. Изолированность
нулей голоморф.ф-и.
Опр.Если ф-яголоморфн. в обл-ти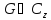
то кажд. т.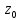
в кот.
наз. нулем ф-ии.
Утв.
в кот. ф-яfголоморф. и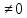
может содерж. лишь конечное число нулей
ф-иf.
Док-во.Д-но, предположение по
мн-ва нулей приводит к
вGхотя бы 1-й предел. т.
мн-ва ф-иfи, сл-но, к
рав-вуf=0.
Утв.Мн-во
нулей голоморф.вGф-ии

или счетно.
Док-во.Обл-тьGможно
представ. в виде объединения замкн. мн-в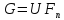

где

Т.к. в кажд.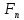
нулей ф.fконечно, то вGоно конечно или счетно.
Опр.Пустьfголоморф.вобл-тиG,

обл-тиG,
Числоmназ. порядком
(кратностью) нуля
если ее разложение в ряд Тейл. в окр. т.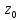
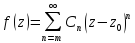
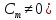

Очев, что т.
нулем пор-каmголоморф.ф.fтиттк
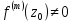
Пример.Т.
для ф-ииsinz-zнулем пор-ка 3, а т.
ф-ииsinzнулем пор-ка 1.Опр.Приm=1 нуль ф.fназ. простым.
Утв.Голоморф.ф., имеющая нули, либо тожд.
нулю, либо ее нули – изолир. т. (без
док-ва).
23.
Представление рядом Лорана ф-и,
голоморф.в кольце. Интегральные ф-лы
Коши для коэфф-в ряда Лорана.
Теор.
1.Пусть ф-яfголоморф.в
кольце


тогда вKф.fпредставима
в виде суммыf=S+T,
гдеS(z) –
сумма степ. ряда
сходящ. в круге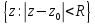
а
ф-ии ряда
сходящ. вне замыкания круга
Коэф. этих рядов выраж. ф-лой:

Док-во.Зафикс.
т.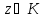
возьмем числа

Пусть
внутр. и внешн. граничн. окр-ти кольца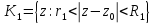
Пусть
леж. внутри
Т.к.
голоморф. ф. от
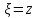
то по интегр. т. Коши для остального
контура имеем
откуда
где

Разложим подынтегр. ф. в 1-м из интегралов
по полож, а во 2-м – по отриц. степеням
разности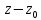
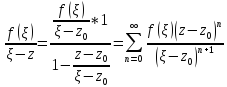

Получ. ряды сход.равном. соотв-но на

т.к.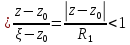





поэтому после почленного интегрир.
рядов получ. разлож.

коэф-ами:

Ряд с суммойS(z)
сход.в круге
а ряд с сум.T(z)
сход-ся вне замык. круга
Т.к. ф-я


то в силу интегр. т. Коши о составном
конт., интегрирование по

ф-лах


центр. в т.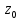
лежащей в кольце К. 1-й ряд в теор. 1S(z)
–обыкн. степ. ряд и изображ. ф-юf,
голоморф. в круге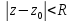
2-й рядT(z)
можно рассм. как обыкн. степ.ряд, если

В новых обозначениях ряд примет вид
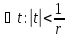
голоморф. при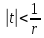
Возвращаясь к перем.z,
видим, что рядT(z)
изобр.T(z),
голом. вне замкн. круга
Преставл. голоморф.ф.
коэф.
-
можно
запис. короче
.
24.Ряд
Лорана, его правильная и главная части.
Единственность ряда Лорана.
[ P.S.Теор. 1.Пусть ф-яfголоморф.в
кольце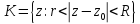


тогда вKф.fпредставима
в виде суммыf=S+T,
гдеS(z) –
сумма степ. ряда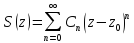
сходящ. в круге
а
ф-ии ряда
сходящ. вне замыкания круга
Коэф. этих рядов выраж. ф-лой:

]
Опр.Разлож.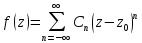
целым степеням
рядом Лорана ф.fв кольце
К. СуммаS(z)
с неотриц. степенями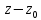
степенями –главной частью.
Теор.В
данном круговом кольце
образом разлагается в ряд Лорана.
Док-во.Пусть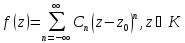

где
Ряд (5) сход.равном. Умножив (5) на
получ.
Здсеь ряд также сход.равномерно на
поэтому, интегрир. его почленно на
получ:
что совпад. с (1).
25.Прав.иизолиров.
особые т. голоморф. ф-и. Критерий прав.т.
Классификация особых изолир. т-к. Ряд
Лорана в окрестности особ.т.
Пусть ф-я
f(z) явл.
голоморф.внекот. окр-ти
Опр. 1.Если

получ. ф-юf(z),
голоморф.во всем круге
то т.
Если такого числа не
то т.
Теор.Для
того, чтобы ф.f(z),
голоморф.в

необх. и достат., чтобы

в кот.f(z)
огранич. по модулю.
Док-во.Необх.
очевидна. Достат. – много.
Следствие.
Чтобы т.
необх. и достат., чтобы в
был неогранич., т.е. чтобы выполн.
Опр. 2.Изолир.
особ.т.
для кот. выполн.
наз.полюсом голоморф. ф. f.Изолир.
особ.т., для кот.

Теор. 2.Чтобы т.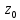
необх. и достат., чтобы эта т. была нулем
ф.
Док-во.Большое.
Опр. 3.Т.
если т.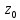
нулем порядкаmдля ф.
Приm=1 полюс наз. простым,
а приm>1 – кратным.
Теор. 3.Чтобы т.
ф.f, необх. и достат., чтобы
лорановск. разлож. ф.f(см.
22-23) имело вид: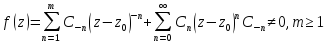
(3).
Док-во.Большое.
След.Изолир.
особ.т.
явл. для нее существенно особ. т.
титткларановск. разлож. ф.fв
окр. т.

членов с отриц. степенями
26.Теорема
Сохоцкого.
Теор. 1.Если
особ. т. голоморф. ф.f, то
для
сход. к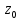

такая, что

Док-во.Большое. [Случай бескон. удал. т.Пустьf(z) голоморф.
в
тогда ф.
голоморф.в обл.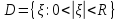

Опр. 1.

прав. т., полюсом порядкаmили
сущ. особ. т. ф.f(z),
голоморф. в К, (см. 25) в зав-ти от того,
будет ли т.
прав. т., полюсом порядкаmили сущ. особ. т. для ф-ии
В указ. случ. ф.
в окр-ти т.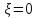

второе ур-ие не видно.
посл. случ. беск. мн-во коэф.

Опр. 2.Разлож.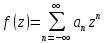
голоморф. в кольце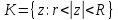
ф.fв ряд Лорана наз. рядом
Лорана в бесконечности. Главная часть
(см. 24) ряда Лорана в беск-ти наз.
совокупность членов с полож. степенями,
а прав.частью – все ост. члены.]
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
МАКСИМУМА МОДУЛЯ ПРИНЦИП
- МАКСИМУМА МОДУЛЯ ПРИНЦИП
-
теорема, выражающая одно из основных свойств модуля аналитич. функции. Пусть f(z) — регулярная аналитическая, или голоморфная, функция пкомплексных переменных
в области Dкомплексного числового пространства
отличная от константы,
М. м. п. в локальной форме утверждает, что ни в какой точке
не может достигаться локальный максимум модуля f(z), т. е. не существует окрестности, V(z0) точки z°, в к-рой выполняется неравенство ,
Если, кроме того,
то z0 не может быть и точкой локального минимума модуля f(z). Равносильная формулировка М. м. п. в глобальной форме состоит в том, что при тех же условиях модуль аналитич. функции f(z) не может ..достигать своей верхней грани
ни в какой точке
Следовательно, если f(z) непрерывна в конечной замкнутой области D, то наибольшее значение Мдостигается только в граничных точках области D. Приведенные формулировки М. м. п. сохраняют силу и в том случае, если f(z) — голоморфная функция на связном комплексном (аналитическом) многообразии, в частности на римановой поверхности или на римановой области D.
М. м. п. допускает обобщения в различных направлениях. Во-первых, вместо голоморфности f(z) достаточно предположить только, что f(z)=u(z)+iv(z) — (комплексная) гармоническая функция. Другое обобщение связано с тем, что для голоморфной функции f(z) модуль |f(z)| есть логарифмически субгармоническая функция. Если f(z) — ограниченная голоморфная функция в конечной области
и условие
выполняется для всех точек
кроме точек нек-рого множества
внешней емкости нуль (в пространстве
), то
всюду в D. См. также Двух констант теорема, Фрагмена — Линделёфа теорема.
М. м. п. обобщается и на голоморфные отображения. Пусть
— голоморфное отображение области
впространство
то, — голоморфные функции в
— евклидова норма. Тогда ни в какой точке
функция ||f(z)|| не может достигать локального максимума. М. м. п. справедлив всякий раз, когда выполняется сохранения области принцип.
Лит.:[1] Стоилов С., Теория функций комплексного переменного, пер. с рум., М., 1962; [2] В л а д и м и р о в В. С., Методы теории функций многих комплексных переменных, М., 1964; [3] Ш а б а т Б. В., Введение в комплексный анализ, 2 изд., ч. 1-2, М., 1976. Е. Д. Соломенцев.
Математическая энциклопедия. — М.: Советская энциклопедия.
.
1977—1985.
Полезное
Смотреть что такое «МАКСИМУМА МОДУЛЯ ПРИНЦИП» в других словарях:
-
МАКСИМУМА МОДУЛЯ ПРИНЦИП — утверждение, согласно к рому аналитическая функция одного или неск. комплексных неременных, отличная от постоянной, не может внутри области аналитичности достигать своего максимального по абс. величине значения. В частности, если аналитич. ф ция… … Физическая энциклопедия
-
Принцип максимума модуля (значения) — Принцип максимума модуля (в теории функций комплексных переменных) Принцип максимума для уравнения теплопроводности Принцип максимума Понтрягина (в теории оптимального управления) … Википедия
-
Принцип максимума модуля — У этого термина существуют и другие значения, см. Принцип максимума. В этой статье отсутствует вступление. Пожалуйста, допишите вводную секцию, кратко раскрывающую тему статьи. Формулировка Если … Википедия
-
Принцип Фрагмена — Линделёфа — Для аналитических функций справедлив так называемый принцип максимума модуля, который предписывает четкое расположение максимума модуля для аналитической в некоторой ограниченной области функции исключительно на границе этой области. В общем… … Википедия
-
Принцип максимума — модуля (в теории функций комплексных переменных) Принцип максимума для уравнения теплопроводности Принцип максимума Понтрягина (в теории оптимального управления) … Википедия
-
Принцип максимума (значения) — Принцип максимума модуля (в теории функций комплексных переменных) Принцип максимума для уравнения теплопроводности Принцип максимума Понтрягина (в теории оптимального управления) … Википедия
-
Принцип Фрагмена — Линделёфа — Для аналитических функций справедлив так называемый принцип максимума модуля, который предписывает четкое расположение максимума модуля для аналитической в некоторой ограниченной области функции исключительно на границе этой области. В общем… … Википедия
-
Принцип Фрагмена—Линделёфа — Для аналитических функций справедлив так называемый принцип максимума модуля, который предписывает четкое расположение максимума модуля для аналитической в некоторой ограниченной области функции исключительно на границе этой области. В общем… … Википедия
-
Принцип Фрагмена — Для аналитических функций справедлив так называемый принцип максимума модуля, который предписывает четкое расположение максимума модуля для аналитической в некоторой ограниченной области функции исключительно на границе этой области. В общем… … Википедия
-
АРГУМЕНТА ПРИНЦИП — геометрический принцип теории функций комплексного переменного, формулируемый следующим образом: пусть ограниченная область на комплексной плоскости , причем граница является непрерывной кривой, ориентация к рой согласована с ; если функция… … Математическая энциклопедия







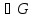



 .
. в области Dкомплексного числового пространства
в области Dкомплексного числового пространства  отличная от константы,
отличная от константы,  М. м. п. в локальной форме утверждает, что ни в какой точке
М. м. п. в локальной форме утверждает, что ни в какой точке  не может достигаться локальный максимум модуля f(z), т. е. не существует окрестности, V(z0) точки z°, в к-рой выполняется неравенство ,
не может достигаться локальный максимум модуля f(z), т. е. не существует окрестности, V(z0) точки z°, в к-рой выполняется неравенство , Если, кроме того,
Если, кроме того,  то z0 не может быть и точкой локального минимума модуля f(z). Равносильная формулировка М. м. п. в глобальной форме состоит в том, что при тех же условиях модуль аналитич. функции f(z) не может ..достигать своей верхней грани
то z0 не может быть и точкой локального минимума модуля f(z). Равносильная формулировка М. м. п. в глобальной форме состоит в том, что при тех же условиях модуль аналитич. функции f(z) не может ..достигать своей верхней грани 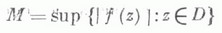
 Следовательно, если f(z) непрерывна в конечной замкнутой области D, то наибольшее значение Мдостигается только в граничных точках области D. Приведенные формулировки М. м. п. сохраняют силу и в том случае, если f(z) — голоморфная функция на связном комплексном (аналитическом) многообразии, в частности на римановой поверхности или на римановой области D.
Следовательно, если f(z) непрерывна в конечной замкнутой области D, то наибольшее значение Мдостигается только в граничных точках области D. Приведенные формулировки М. м. п. сохраняют силу и в том случае, если f(z) — голоморфная функция на связном комплексном (аналитическом) многообразии, в частности на римановой поверхности или на римановой области D.  и условие
и условие 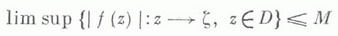
 кроме точек нек-рого множества
кроме точек нек-рого множества  внешней емкости нуль (в пространстве
внешней емкости нуль (в пространстве 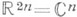 ), то
), то 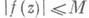 всюду в D. См. также Двух констант теорема, Фрагмена — Линделёфа теорема.
всюду в D. См. также Двух констант теорема, Фрагмена — Линделёфа теорема.  — голоморфное отображение области
— голоморфное отображение области 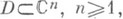 впространство
впространство 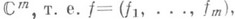
 то, — голоморфные функции в
то, — голоморфные функции в  — евклидова норма. Тогда ни в какой точке
— евклидова норма. Тогда ни в какой точке  функция ||f(z)|| не может достигать локального максимума. М. м. п. справедлив всякий раз, когда выполняется сохранения области принцип.
функция ||f(z)|| не может достигать локального максимума. М. м. п. справедлив всякий раз, когда выполняется сохранения области принцип.