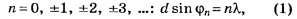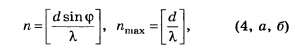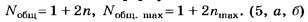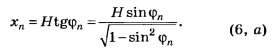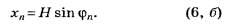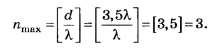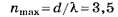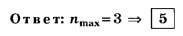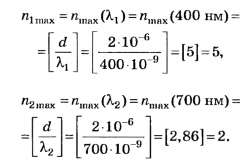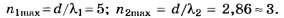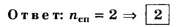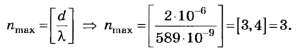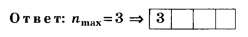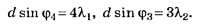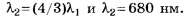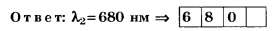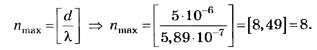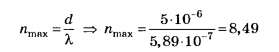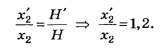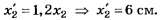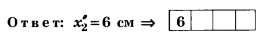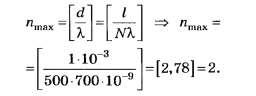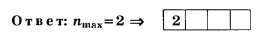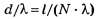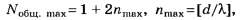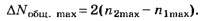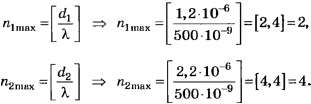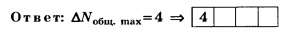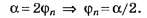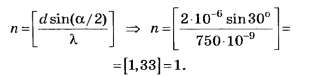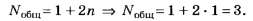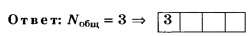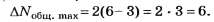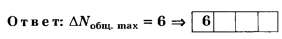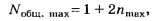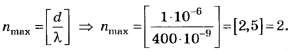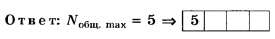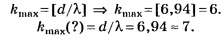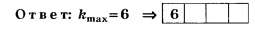Петрович Г. И. О порядке главных максимумов от дифракционной решётки в решениях задач централизованного тестирования // Фiзiка: праблемы выкладання. – 2009. – № 3. – С. 34-40.
При перпендикулярном (нормальном) падении параллельного пучка монохроматического света на дифракционную решётку на экране в фокальной плоскости собирающей линзы, расположенной параллельно дифракционной решётке, наблюдается неоднородная картина распределения освещённости разных участков экрана (дифракционная картина).
Главные максимумы этой дифракционной картины удовлетворяют следующим условиям:
где n — порядок главного дифракционного максимума, d — постоянная (период) дифракционной решётки, λ— длина волны монохроматического света, φn— угол между нормалью к дифракционной решётке и направлением на главный дифракционный максимум n-го порядка.
Постоянная (период) дифракционной решётки длиной l
где N — количество щелей (штрихов), приходящихся на участок дифракционной решётки длиной I.
Наряду с длиной волны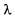
Для электромагнитных волн (света) в вакууме
где с = 3 *108 м/с — скорость распространения света в вакууме.
Выделим из формулы (1) наиболее трудно математически определяемые формулы для порядка главных дифракционных максимумов:
где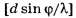
Недоопределённые аналоги формул (4, а,б) без символа […] в правых частях содержат в себе потенциальную опасность подмены физически обоснованной операции выделения целой части числа 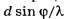
Подсознательная тенденция (ложный след) подмены операции выделения целой части числа d*sin(φ/λ) операцией округления
этого числа до целочисленного значения по математическим правилам ещё более усиливается, когда речь идёт о тестовых заданиях типа В на определение порядка главных дифракционных максимумов.
В любых тестовых заданиях типа В численные значения искомых физических величин по договорённости округляются до целочисленных значений. Однако в математической литературе нет единых(го) правил(а) округления чисел.
В справочной книге В. А. Гусева, А. Г. Мордковича по математике для учащихся [1] и белорусском учебном пособии Л. А. Латотина, В. Я. Чеботаревского по математике для IV класса [2] приводятся по существу одни и те же два правила округления чисел. В [1] они сформулированы так: «При округлении десятичной дроби до какого-нибудь разряда все следующие за этим разрядом цифры заменяются нулями, а если стоят после запятой, то их отбрасывают. Если первая следующая за этим разрядом цифра больше или равна пяти, то последнюю оставшуюся цифру увеличивают на 1. Если же первая следующая за этим разрядом цифра меньше 5, то последнюю оставшуюся цифру не изменяют».
В справочнике М. Я. Выгодского по элементарной математике [3], выдержавшем двадцать семь (!) изданий, написано (с. 74): «Правило 3. Если отбрасывается цифра 5, а за ней нет значащих цифр, то округление производится до ближайшего чётного числа, т.е. последняя сохраняемая цифра остаётся неизменной, если она чётная, и усиливается (увеличивается на 1), если она нечётная».
Ввиду существования различных правил округления чисел следовало бы правила округления десятичных чисел явно сформулировать в «Инструкции для учащихся», прилагаемой к заданиям централизованного тестирования по физике. Это предложение приобретает дополнительную актуальность, так как в белорусские вузы поступают и проходят обязательное тестирование не только граждане Беларуси и России, но и других стран, и заведомо неизвестно, какими правилами округления чисел они пользовались при обучении в своих странах.
Во всех случаях округление десятичных чисел будем производить по правилам, приведённым в [1], [2].
После вынужденного отступления, возвратимся к обсуждению рассматриваемых физических вопросов.
С учётом нулевого (n = 0) главного максимума и симметричного расположения остальных главных максимумов относительно него общее количество наблюдаемых главных максимумов от дифракционной решётки подсчитывается по формулам:
Если расстояние от дифракционной решётки до экрана, на котором наблюдается дифракционная картина, обозначить через Н, то координата главного дифракционного максимума n-го порядка при отсчёте от нулевого максимума равна
Если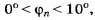
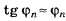
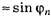
Задачи на рассматриваемую тему часто предлагают на тестированиях по физике.
Начнём обзор с рассмотрения российских тестов, использовавшихся белорусскими вузами на начальном этапе, когда тестирование в Беларуси было необязательным и проводилось отдельными учебными заведениями на свой страх и риск как альтернатива обычной индивидуальной письменно-устной форме проведения вступительных экзаменов.
Тест № 7 [4]
А32. Наибольший порядок спектра, который можно наблюдать при дифракции света с длиной волны λ на дифракционной решётке с периодом d=3,5λ равен
1) 4; 2) 7; 3) 2; 4) 8; 5) 3.
Решение
При освещении дифракционной решётки монохроматическим светом ни о каких спектрах не может быть и речи. В условии задачи речь должна идти о главном дифракционном максимуме наибольшего порядка при перпендикулярном падении монохроматического света на дифракционную решётку.
По формуле (4, б)
Из недоопределённого условия
на множестве целых чисел, после округления получаем nmах=4.
Только благодаря несовпадению целой части числа d/λ с его округлённым целочисленным значением правильное решение (nmах=3) отличается от неправильного (nmax=4) на тестовом уровне.
Изумительная миниатюра, несмотря на огрехи формулировки, с филигранно выверенным по всем трём версиям округления чисел ложным следом!
А18. Если постоянная дифракционной решётки d=2 мкм, то для нормально падающего на решётку белого света 400 нм <λ< 700 нм наибольший полностью наблюдаемый порядок спектра равен
1)1; 2)2; 3)3; 4)4; 5)5.
Решение
Очевидно, что nсп=min(n1max, n2max)
По формуле (4, б)
Округляя числа d/λ до целочисленных значений по правилам [1] — [3], получаем:
Благодаря тому, что целая часть числа d/λ2 отличается от его округлённого целочисленного значения, данное задание позволяет на тестовом уровне объективно отличить правильное решение (nсп=2) от неправильного (nсп=3). Прекрасная задача с одним ложным следом!
ЦТ 2002 г. Тест № 3 [5]
В5. Найдите наибольший порядок спектра для жёлтой линии Na (λ= 589 нм), если постоянная дифракционной решётки d = 2 мкм.
Решение
Задание сформулировано научно некорректно. Во-первых, при освещении дифракционной решётки монохроматическим светом, как уже отмечалось выше, не может быть и речи о спектре (спектрах). В условии задачи речь должна идти о наибольшем порядке главного дифракционного максимума.
Во-вторых, в условии задания должно быть указано, что свет падает нормально (перпендикулярно) на дифракционную решётку, ибо только этот частный случай рассматривается в курсе физики средних общеобразовательных учреждений. Считать это ограничение подразумевающимся по умолчанию нельзя: в тестах все ограничения должны быть указаны явно! Тестовые задания должны представлять собою самодостаточные, научно корректные задания.
С учётом вышеприведённых уточнений
Число 3,4, округлённое до целочисленного значения по правилам арифметики [1] — [3], также даёт 3. Именно поэтому данное задание следует признать простым и, по большому счёту, неудачным, так как на тестовом уровне оно не позволяет объективно различить правильное решение, определяемое по целой части числа 3,4, от неправильного решения, определяемого по округлённому целочисленному значению числа 3,4. Различие обнаруживается только при подробном описании хода решения, что и сделано в данной статье.
Дополнение 1. Решите вышеприведённую задачу, заменив в её условии d=2 мкм на d=1,6 мкм. Ответ: nmax = 2.
ЦТ 2002 г. Тест 4 [5]
В5. На дифракционную решётку направляется свет от газоразрядной лампы. На экране получаются дифракционные спектры излучения лампы. Линия с длиной волны λ1= 510 нм в спектре четвёртого порядка совпадает с линией длины волны λ2 в спектре третьего порядка. Чему равна λ2(в [нм])?
Решение
В данной задаче основной интерес представляет не решение задачи, а формулировка её условия.
При освещении дифракционной решётки немонохроматическим светом(λ1, λ2) вполне естественно говорить (писать) о дифракционных спектрах, которых в принципе нет при освещении дифракционной решётки монохроматическим светом.
В условии задания следовало бы указать, что свет от газоразрядной лампы падает нормально на дифракционную решётку.
Кроме того, следовало бы изменить филологический стиль третьего предложения в условии задания. Режет слух оборот «линия с длиной волны λ», его можно было бы заменить на «линия, соответствующая излучению длиной волны λ» или на более краткий — «линия, соответствующая длине волны λ».
Формулировки тестов должны быть научно корректными и литературно безупречными. Тесты формулируют совсем не так, как исследовательские и олимпиадные задачи! В тестах всё должно быть точно, конкретно, однозначно.
С учётом приведённого уточнения условия задания имеем:
Так как по условию задания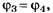
ЦТ 2002 г. Тест № 5 [5]
В5. Найдите наибольший порядок дифракционного максимума для жёлтой линии натрия с длиной волны 5,89·10-7 м, если период дифракционной решётки равен 5 мкм.
Решение
По сравнению с заданием В5 из теста № 3 ЦТ 2002 г. данное задание сформулировано точнее, тем не менее в условии задания речь следовало бы вести не о «дифракционном максимуме», а о «главном дифракционном максимуме«.
Наряду с главными дифракционными максимумами всегда имеются ещё и вторичные дифракционные максимумы [6, с. 617, 618]. Не объясняя этого нюанса в школьном курсе физики, тем более надо строго соблюдать сложившуюся научную терминологию и вести речь только о главных дифракционных максимумах.
Кроме того, следовало бы указать, что свет падает нормально на дифракционную решётку.
С учётом вышеприведённых уточнений
Из неопределённого условия
по правилам математического округления числа 8,49 до целочисленного значения опять же получаем 8. Поэтому данное задание, как и предыдущее, следует признать неудачным.
Дополнение 2. Решите вышеприведённое задание, заменив в его условии d=5 мкм на (1=А мкм. Ответ: nmax=6.)
Пособие РИКЗ 2003 г. Тест № 6 [7]
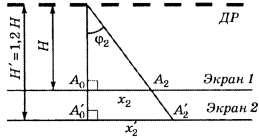
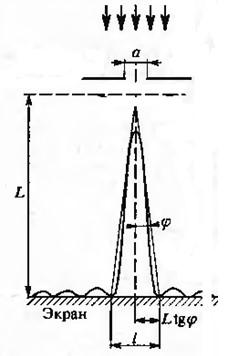
В5. Если второй дифракционный максимум находится на расстоянии 5 см от центра экрана, то при увеличении расстояния от дифракционной решётки до экрана на 20% этот дифракционный максимум будет находиться на расстоянии … см.
Решение
Условие задания сформулировано неудовлетворительно: вместо «дифракционный максимум» надо «главный дифракционный максимум», вместо «от центра экрана» — «от нулевого главного дифракционного максимума».
Как видно из приведённого рисунка,
Отсюда
Пособие РИКЗ 2003 г. Тест № 7 [7]
В5. Определите наибольший порядок спектра в дифракционной решётке, имеющей 500 штрихов на 1 мм, при освещении её светом с длиной волны 720 нм.
Решение
Условие задания сформулировано крайне неудачно в научном отношении (см. уточнения заданий № 3 и 5 из ЦТ 2002 г.).
Есть претензии и к филологическому стилю формулировки задания. Вместо словосочетания «в дифракционной решётке» надо было бы использовать словосочетание «от дифракционной решётки», а вместо «свет с длиной волны» — «светом, длина волны которого». Длина волны — не нагрузка к волне, а её основная характеристика.
С учётом уточнений
По всем трём вышеприведённым правилам округления чисел округление числа 2,78 до целочисленного значения даёт 3.
Последний факт даже при всех недостатках формулировки условия задания делает его интересным, так как позволяет на тестовом уровне различить правильное (nmax=2) и неправильное (nmax=3) решения.
Много заданий на рассматриваемую тему содержится в ЦТ 2005 г. [8].
В условиях всех этих заданий (В1) надо добавить ключевое слово «главный» перед словосочетанием «дифракционный максимум» (см. комментарии к заданию В5 ЦТ 2002 г. Тест № 5).
К сожалению, во всех вариантах тестов В1 ЦТ 2005 г. численные значения d (l,N) и λ подобраны неудачно и всегда дают в дробях
число «десятых» меньше 5, что не позволяет на тестовом уровне отличить операцию выделения целой части дроби (правильное решение) от операции округления дроби до целочисленного значения (ложный след). Это обстоятельство ставит под сомнение целесообразность использования этих заданий для объективной проверки знаний абитуриентов по рассматриваемой теме.
Похоже на то, что составители тестов увлеклись, образно говоря, приготовлением различных «гарниров к блюду», не думая об улучшении качества основной компоненты «блюда» — подборе численных значений d (l,N) и λ с целью увеличения числа «десятых» в дробях d/λ=l/(N*λ).
ЦТ 2005 г. Вариант 4 [8]
В1. На дифракционную решётку, период которой d1=1,2 мкм, падает нормально параллельный пучок монохроматического света с длиной волны λ=500 нм. Если её заменить на решётку, период которой d2=2,2 мкм, то число максимумов увеличится на … .
Решение
Вместо «свет с длиной волны λ» надо «свет длиной волны λ» . Стиль, стиль и ещё раз стиль!
Так как
то с учётом того, что X — const, a d2>di,
По формуле (4, б)
Следовательно, ΔNобщ. max=2(4-2)=4
При округлении чисел 2,4 и 4,4 до целочисленных значений тоже получаем соответственно 2 и 4. По этой причине данное задание следует признать простым и даже неудачным.
Дополнение 3. Решите вышеприведённую задачу, заменив в её условии λ=500 нм на λ=433 нм (синяя линия в спектре водорода).
Ответ: ΔNобщ. max=6
ЦТ 2005 г. Вариант 6
В1. На дифракционную решётку с периодом d= 2 мкм падает нормально параллельный пучок монохроматического света с длиной волны λ=750 нм. Количество максимумов, которые можно наблюдать в пределах угла а=60°, биссектриса которого перпендикулярна плоскости решётки, равно … .
Решение
Словосочетание «света с длиной волны λ» уже обсуждалось выше в ЦТ 2005 г., вариант 4.
Второе предложение в условии данного задания можно было бы упростить и записать так: «Количество наблюдаемых главных максимумов в пределах угла а = 60°» и далее по тексту исходного задания.
Очевидно, что
По формуле (4, а)
По формуле (5, а)
Это задание, как и предыдущее, не позволяет на тестовом уровне объективно определить уровень понимания обсуждаемой темы абитуриентами.
Дополнение 4. Выполните вышеприведённое задание, заменив в его условии λ=750 нм на λ= 589 нм (жёлтая линия в спектре натрия). Ответ: No6щ=3.
ЦТ 2005 г. Вариант 7
В1. На дифракционную решётку, имеющую N1— 400 штрихов на l=1 мм длины, падает параллельный пучок монохроматического света с длиной волны λ=400 нм. Если её заменить решёткой, имеющей N2=800 штрихов на l=1 мм длины, то количество дифракционных максимумов уменьшится на … .
Решение
Опустим обсуждение неточностей формулировки задания, так как они те же, что и в предыдущих заданиях.
Из формул (4, б), (5, б) следует, что
Следовательно,
Комментарии о качестве данного задания опустим, «рука… колоть устала»!
Дополнение 5. Решите вышеприведённую задачу, заменив в её условии λ=400 нм на λ=461 нм (голубая линия в спектре стронция). Ответ: ∆N=6.
ЦТ 2005 г. Вариант 8
В1. На дифракционную решётку с d=1 мкм падает нормально параллельный пучок монохроматического света. Если длина волны света λ=400 нм, то число максимумов, которые образует эта решётка, равно … .
Решение
Злополучное «с» уже перекочевало от «света с длиной волны» к «решётке с d=1 мкм». Появилось и новое жаргонное выражение — «число максимумов, которые образует эта решётка». Сама по себе «решётка» не образует дифракционной картины, поэтому следовало бы написать «количество главных максимумов, образованных освещённой решёткой, равно…».
По формулам (5, б), (4, б)
По версии округления чисел [1], [2] целочисленное значение числа 2,5 равно 3, а по версии М. Я. Выгодского [3] — 2.
В сравнении с российским заданием А32 из № 7 Тестов по физике [4], которое рассмотрено выше, данный белорусский тест является ущербным, но на фоне белорусских тестов ЦТ 2005 г. на рассматриваемую в данной статье тему он является лучшим, несмотря на неточности его формулировки.
Итак, Nобщ. max=1+2*2=5 а по версии округления чисел [1], [2] Nобщ. max= 1+2*3 =7 (ложный след).
Благодаря этому ложному следу, данное задание в рамках версии округления чисел [1], [2] позволяет на тестовом уровне отличить правильное решение (Nобщ. max=5) от неправильного (Nобщ. max=7).
ЦТ 2008 г. Вариант 1 [9]
В12. На дифракционную решётку нормально падает параллельный пучок монохроматического света длиной волны λ=720 нм. Если период решётки d = 5 мкм, то максимальный порядок kmax дифракционного спектра … .
Решение
Задание сформулировано научно некорректно (см. условия предыдущих заданий), но численные значения величин d и λ подобраны удачно и на тестовом уровне правильное решение, определяемое по целой части числа
Задания В12 из других вариантов тестов ЦТ 2008 г. предлагаю читателям рассмотреть самостоятельно.
Вывод
За многие годы проведения централизованных тестирований по физике так и не созданы качественные задания на определение порядка главных дифракционных максимумов при перпендикулярном освещении дифракционной решётки монохроматическим светом: то ли условия заданий были сформулированы некорректно, то ли численные значения величин d(l, N) и X были подобраны неудачно и не позволяли на тестовом уровне отличить правильное решение от неправильного.
Список использованной литературы
1. Математика: справочные материалы: кн. для учащихся / В. А. Гусев, А. Г. Мордкович. — Москва : Просвещение, 1988.
2. Математика: учеб. пособие для 4-го класса общеобр. школы с рус. яз. обуч. / Л. А. Лату-тин, В. Д. Чеботаревский; пер. с бел. яз. Т. В. Водневой. — 2-е изд. — Минск : Нар. асвета, 2002.
3. Справочник по элементарной математике. — 27-е изд., испр. / М. Я. Выгодский. — Москва : Наука, 1986.
4. Тесты по физике. 11 кл. / Центр тестирования Министерства образования России. — Москва : Просвещение, 2001.
5. Тесты. Физика. Русский язык: варианты и ответы централизованного тестирования: пособие для подготовки к тестированию / Респ. ин-т контроля знаний. — Минск : Асар, 2003.
6. Справочник по физике для инженеров и студентов вузов. — 6-е изд., испр. / Б. М. Яворский, А. А. Детлаф. — Москва : Наука, 1974.
7. Тесты: Физика. Материалы для подготовки к централизованному тестированию / Респ. ин-т контроля знаний. — Мозырь : Белый Ветер, 2003.
8. Централизованное тестирование. Физика: сб. тестов / Респ. ин-т контроля знаний Мин-ва образования Респ. Беларусь. — Минск : Юнипресс, 2005.
9. Централизованное тестирование. Физика: сб. тестов / Респ. ин-т контроля знаний Мин-ва образования Респ. Беларусь. — Минск : Аверсэв, 2008.
В рамках геометрической оптики, распространение луча в оптически однородной среде — прямолинейное, однако в природе существует ряд явлений, где можно наблюдать отклонение от этого условия.
Дифракция – явление огибания световыми волнами встреченных препятствий. В школьной физике изучаются две дифракционные системы (системы, при прохождении луча в которых наблюдается дифракция):
- дифракция на щели (прямоугольном отверстии)
- дифракция на решётке (набор равноотстоящих друг от друга щелей)
Дифракция на щели — дифракция на прямоугольном отверстии (рис. 1).
Рис. 1. Дифракция на щели
Пусть дана плоскость со щелью, шириной , на которую под прямым углом падает пучок света А. Большинство света проходит на экран, однако часть лучей дифрагирует на краях щели (т.е. отклоняется от своего первоначального направления). Далее эти лучи интерферируют друг с другом с образованием дифракционной картины на экране (чередование ярких и тёмных областей). Рассмотрение законов интерференции достаточно сложно, поэтому ограничимся основными выводами.
Полученная дифракционная картина на экране состоит из чередующихся областей с дифракционными максимумами (максимально светлыми областями) и дифракционными минимумами (максимально тёмными областями). Эта картина симметрична относительно центрального светового пучка. Положение максимумов и минимумов описывается углом относительно вертикали, под которым они видны, и зависит от размера щели и длины волны падающего излучения. Положение этих областей можно найти используя ряд соотношений:
- для дифракционных максимумов
(1)
- где
Нулевым максимумом дифракции называется центральная точка на экране под щелью (рис. 1).
- для дифракционных минимумов
(2)
- где
Вывод: по условиям задачи необходимо выяснить: максимум или минимум дифракции необходимо найти и использовать соответствующее соотношение (1) или (2).
Дифракция на дифракционной решётке.
Дифракционной решёткой называется система, состоящая из чередующихся щелей, равноотстоящих друг от друга (рис. 2).
Рис. 2. Дифракционная решётка (лучи)
Так же, как и для щели, на экране после дифракционной решётки будет наблюдаться дифракционная картина: чередование светлых и тёмных областей. Вся картина есть результат интерференции световых лучей друг с другом, однако на картину от одной щели будет воздействовать лучи от других щелей. Тогда дифракционная картина должна зависеть от количества щелей, их размеров и близкорасположенности.
Введём новое понятие — постоянная дифракционной решётки:
(3)
- где
Тогда положения максимумов и минимумов дифракции:
- для главных дифракционных максимумов (рис. 3)
(4)
- где
Рис. 3. Дифракционная решётка (максимумы)
- для дифракционных минимумов
(5)
- где
Отдельным вопросом задач на дифракцию является вопрос о наибольшем количестве максимумов, которые можно наблюдать в текущей системе. Наибольший угол, под которым можно наблюдать максимум — , тогда, исходя из (4):
(6)
Главное помнить, что число максимумов — число, т.е. от полученного ответа необходимо брать только целую часть.
Вывод: по условиям задачи необходимо выяснить: максимум или минимум дифракции необходимо найти и использовать соответствующее соотношение (4) или (5).
Общий вывод: задачи на дифракцию должны содержать в себе словосочетания, связанные с «дифракцией». Далее разбираемся с объектом: щель или дифракционная решётка и используем соответствующие соотношения для минимума или максимума.
В сегодняшней статье традиционно разбираем решение задач по физике. Тема: дифракция света.
Подпишитесь на наш телеграм, чтобы регулярно получать интересные новости. А если хотите поучаствовать в акции или оформить заказ со скидкой, обязательно загляните на наш второй канал для клиентов.
Дифракция: решение задач
Глупо начинать решать задачи на дифракцию, не зная, что это такое. Поэтому, сначала почитайте теорию, а уже потом приступайте к практике. Рекомендуем держать под рукой полезные формулы и руководствоваться универсальной памяткой по решению физических задач.
Кстати, дифракцию многие путают с дисперсией. Чтобы такого не случилось с вами, читайте отдельный материал в нашем блоге.
Задача на дифракцию №1
Условие
Найти расстояние между кристаллографическими плоскостями кристалла, дифракционный максимум первого порядка от которых в рентгеновских лучах с длиной волны λ = 1,5 нм наблюдается под углом 30°.
Решение
Дифракция в кристалле описывается формулой Брэгга-Вульфа:
2dsinθ=kλ
Отсюда находим искомое расстояние:
d=λ2sinθ
Вычислим:
d=1,5·10-92sin30=1,5·10-9 м
Ответ: 1.5 нм.
Задача на дифракцию №2
Условие
На узкую щель шириной a=2·10-4 cм падает по нормали плоская монохроматическая волна (λ=0,66 мкм). Определите ширину центрального дифракционного максимума на экране, если расстояние от щели до экрана равно L=1 м.
Решение
Ширина центрального максимума равна расстоянию между минимумами первого порядка. Эти минимумы наблюдаются под углами, которые находятся из соотношения:
asinφ=±λ
Расстояние между минимумами равно (для малых углов):
l=2Ltgφ≈2Lsinφ
Получим:
l=2Lλa
Найдем:
l=2·0,66·10-62·10-6=0,66 м
Ответ: 0.66 м.
Задача на дифракцию №3
Условие
На дифракционную решетку нормально падает пучок света от разрядной трубки. Чему должна быть равна постоянная дифракционной решетки, чтобы в направлении φ=41° совпадали максимумы двух линий: λ1 = 6563 А ̇ и λ2 = 4102 А ̇?
Решение
Направление главных максимумов дифракционной решётки:
csinφ=mλ, (m=1,2,3…)
Запишем это условие для заданных длин волн и приравняем правые части:
csinφ=m1λ1csinφ=m2λ2m1λ1=m2λ2 ⇒ m2=m1λ1λ2=m165634102=1,6m1
Так как m1 и m2 целые числа, то последнее равенство справедливо при m1=5 и m2=8. Подставив m1=5 в самую первую формулу, получим:
сsinφ=5λ1c=5λ1sinφ
Произведём вычисления:
c=5·6563sin41°=50018 A≈500 нм
Ответ: c=500 нм
Задача на дифракцию №4
Условие
На экран с отверстием диаметром 2 мм падает нормально плоская волна (0,5·10-6 м). Определить, на каком расстоянии от центра отверстия находится самый дальний дифракционный минимум.
Решение
Самый дальний минимум будет наблюдаться, когда будет открыто две зоны Френеля: k=2
Для параллельного пучка света имеем:
rk=kbλ
Так как rk=d2, то:
d24=kbλb=d24kλ
Получаем:
b=2·10-324·2·5·10-7=1 м
Ответ: b=1 м.
Задача на дифракцию №5
Условие
На дифракционную решётку падает нормально свет с длиной волны 590 нм. Найти угол, под которым наблюдается максимум 6-го порядка. Период решётки 37мкм. Ответ получить в градусах.
Решение
Направление на главный максимум m-го порядка определяется выражением:
dsinφ=mλ
Отсюда:
φ=arcsinmλd
Здесь m – порядок дифракции, λ – длина волны света, d – период решетки.
Получаем:
φ=arcsin6·590·10-937·10-6=5,49°
Ответ: φ=5,49°
Нужно больше задач? Не проблема! Вот вам задачи на интерференцию света с решениями.
Вопросы на тему «Дифракция света»
Вопрос 1. Что такое дифракция?
Ответ. Дифракцией называется огибание волнами препятствий, встречающихся на их пути, или в более широком смысле – любое отклонение распространения волн вблизи препятствий от законов геометрической оптики. Благодаря дифракции волны могут попадать в область геометрической тени, огибать препятствия, проникать через небольшие отверстия в экранах и т. д.
Вопрос 2. Приведите пример проявления дифракции из жизни.
Ответ. Звук за углом дома хорошо слышен, это потому что звуковая волна огибает дом. Это ни что иное, как проявление дифракции.
Вопрос 3. Какие есть типы дифракции?
Ответ. В зависимости от дифракционной картины различают дифракцию Фраунгофера и дифракцию Френеля.
- тип дифракции, при котором дифракционная картина образуется параллельными пучками, называется дифракцией Фраунгофера. Параллельные лучи проявятся, если экран и источник находятся в бесконечности. Практически применяются две линзы: в фокусе одной – источник света, а в фокусе другой – экран.
- Если преграда, на которой происходит дифракция, находится вблизи от экрана или от источника света, на котором проистекает наблюдение, то фронт дифрагированных или падающих волн имеет криволинейную поверхность (в частности, сферическую). Этот случай называется дифракцией Френеля.
Вопрос 4. Что такое дифракционная решетка?
Ответ. Дифракционная решётка представляет собой оптический прибор, действие которого основано на применении явления дифракции света. Это совокупность большого числа регулярно расположенных штрихов (выступов, щелей), нанесённых на некоторую поверхность.
При падении на решетку плоской монохроматической волны в фокальной плоскости линзы наблюдается дифракционная картина. Она является результатом двух процессов: дифракции света от каждой щели и интерференции пучков света, дифрагированных от всех щелей.
Вопрос 5. Каким проявлением природы света является дифракция?
Ответ. Дифракция – проявление волновой природы света.
Нужна помощь в решении задач и других студенческих заданий? Обращайтесь за ней в специальный студенческий сервис в любое время суток.
Применение поверхностей первого и второго порядков
в задачах на экстремум функций
Общая постановка задачи поиска экстремума функций приведена здесь. Рассмотрим задачу поиска безусловного экстремума функций двух переменных.
Аналитический метод поиска локального безусловного экстремума
Пусть задана дважды непрерывно дифференцируемая функция двух переменных.
Точка называется точкой локального минимума, если существует такая окрестность этой точки, для всех точек которой выполняется условие
Если знак неравенства заменить на знак
, то получится определение локального максимума. Точки локального минимума или максимума называются точками локального экстремума функции.
Требуется найти точки локального экстремума функции .
Порядок решения поставленной задачи содержит два этапа.
На первом этапе при помощи необходимых условий экстремума первого порядка:
(4.74)
находятся стационарные точки , «подозрительные» на наличие локального экстремума (частные производные первого порядка в точке
равны нулю).
На втором этапе проверяются достаточные условия экстремума, а если они не выполняются, то и необходимые условия второго порядка. Они следуют из формулы Тейлора для приращения функции в точке (учитывая члены до второго порядка включительно):
где
а члены с производными первого порядка отсутствуют, так как точка удовлетворяет (4.74).
Равенство
(4.75)
можно рассматривать как уравнение поверхности второго порядка относительно неизвестных
. Уравнение (4.75) можно записать в матричной форме
(4.76)
где — матрица квадратичной формы, называемая матрицей Гессе.
Она составлена из частных производных второго порядка, вычисленных в стационарной точке
Как показано в разд.4.4.1, при помощи поворота системы координат вокруг оси можно квадратичную форму в правой части (4.76) привести к каноническому виду
(4.77)
где — собственные значения матрицы Гессе
.
В зависимости от знаков собственных значений возможны следующие случаи:
1) если собственные значения одного знака, то поверхность (4.77) представляет собой эллиптический параболоид: выпуклый при
(рис.4.58,а), или вогнутый при
(рис.4.58,б);
2) если собственные значения имеют разные знаки, то поверхность (4.77) представляет собой гиперболический параболоид (рис.4.58,в при
);
3) если одно из собственных значений равно нулю (например, при ), то поверхность (4.77) представляет собой параболический цилиндр: выпуклый при
(рис.4.58,2) или вогнутый при
(рис.4.58,д).
В случае эллиптического параболоида стационарная точка является либо точкой локального минимума функции при
, либо точкой локального максимума функции при
. В случае гиперболического параболоида (
и
имеют разные знаки) в стационарной точке
нет экстремума. В случае выпуклого параболического цилиндра можно сказать, что точка
не может быть точкой максимума, но может быть точкой минимума, в случае вогнутого параболического цилиндра точка
не может быть точкой минимума, но может быть точкой максимума. Таким образом, если хотя бы одно собственное значение равно нулю, судить о наличии экстремума в точке
нельзя, так как нужны дополнительные исследования, учитывающие в формуле Тейлора члены выше второго порядка.
Алгоритм исследования функции на локальный экстремум
1. Составить и решить систему (4.74) — найти стационарные точки . Если система не имеет решения, то точек локального экстремума нет.
2. Составить матрицу Гессе и найти ее собственные значения
и
, решая характеристическое уравнение
3. Проверить выполнение следующих условий.
а) Если
, то
— точка локального минимума.
б) Если
, то
— точка локального максимума.
в) Если
, то
может быть точкой локального минимума (требуется дополнительное исследование).
г) Если
, то
может быть точкой локального максимума (требуется дополнительное исследование).
д) Если и
разных знаков
, то
не является точкой локального экстремума.
Пример 4.25. Найти экстремумы функции .
Решение.. Решая систему уравнений
находим стационарные точки и
.
Составляем матрицу Гессе .
В стационарной точке матрица Гессе
. Найдем собственные значения матрицы Гессе. Характеристическое уравнение
имеет корни разных знаков. Следовательно, точка
не является точкой экстремума (см. п.3,»д» алгоритма).
В стационарной точке матрица Гессе
. Характеристическое уравнение
имеет два положительных корня . Следовательно, точка
является точкой минимума (см. п.3,»а» алгоритма).
Применение графических методов поиска экстремума функции
Рассмотрим постановку задачи поиска условного экстремума функции трех переменных. Пусть заданы:
а) функция трех переменных
;
б) множество допустимых решений .
Требуется найти такую точку из множества допустимых решений, которой соответствует минимальное значение функции
на этом множестве:
Алгоритм графического метода поиска условного (или безусловного экстремума) функции аналогичен алгоритму, рассмотренному ранее для функции двух переменных. Однако его применение на практике ограничивается возможностями изображения пространственных фигур. Как правило, используется плоское изображение пространственных фигур, т.е. проекции этих фигур на плоскость, что не дает полного представления о взаимном их расположении.
Ниже рассматриваются задачи, в которых минимизируемая функция и функции, задающие ограничения, являются многочленами трех переменных первой или второй степени. Построение множества допустимых решений и поверхностей уровня функции сводится к построению алгебраических поверхностей первого или второго порядков. В этих задачах применение графического метода упрощается.
Напомним, что поверхностью уровня функции называется геометрическое место точек пространства, в которых функция принимает постоянное значение, т.е.
.
Если функция является многочленом первой степени, то ее поверхности уровня
при разных значениях постоянной
представляют собой семейство параллельных плоскостей (несобственный пучок плоскостей).
Если функция является многочленом второй степени, то ее поверхности уровня
при разных значениях постоянной
представляют собой поверхности второго порядка. Поскольку уравнения разных поверхностей уровня отличаются только свободными членами, то собственные векторы, собственные значения
, а также инварианты
остаются постоянными для всех поверхностей уровня
. Следовательно, тип поверхности и канонический базис остаются постоянными для всех поверхностей уровня квадратичной функции.
Пример 4.26. Графическим методом найти экстремумы:
Решение.
1) 1. Множество допустимых решений строить не нужно, так как оно совпадает со всем пространством:
.
2. Поверхность уровня при
представляет собой эллипсоид (рис.4.59,а), при
— мнимый конус с единственной вещественной точкой
, при
— мнимый эллипсоид. При увеличении постоянной
полуоси эллипсоида пропорционально увеличиваются. На рис.4.59,а изображены эллипсоиды
и
Стрелками указаны направления наискорейшего возрастания функции.
3. Из пункта 2 следует, что допустимые значения функции определяются не равенством .
4. В точке достигается безусловный минимум функции, так как в этой точке функция принимает наименьшее значение по сравнению со значениями в других точках пространства, а наибольшего значения функция не достигает.
2) Решается задача поиска условного экстремума с ограничениями типа равенств и неравенств.
1. Строим множество допустимых решений — часть плоскости
в первом октанте, т.е. плоский треугольник с вершинами
(рис.4.59,б).
2. Поверхности уровня функции
представляют собой семейство параллельных плоскостей, каждая из которых перпендикулярна оси аппликат. На рис.4.59,б изображены три плоскости уровня
. При
или
плоскость
не имеет общих точек с треугольником
; при
плоскость
имеет общие точки с треугольником
, в частности, при
плоскости
принадлежит сторона
треугольника, при
плоскости
принадлежит вершина
треугольника.
3. Из пункта 2 следует, что допустимые значения функции определяются неравенством .
4. Наименьшее значение на множестве , равное нулю, функция достигает в любой точке отрезка
; наибольшее значение на множестве
, равное единице, функция достигает в точке
.
3) Решается задача поиска условного экстремума с ограничением типа равенств.
1. Строим множество допустимых решений — сфера
единичного радиуса с центром в начале координат (рис.4.60).
2. Поверхности уровня представляют собой либо однополостный гиперболоид вращения при
(например, однополостный гиперболоид
(рис.4.60,а)), либо круговой конус
при
(рис.4.60,б), либо двуполостный гиперболоид вращения при
(например, двуполостный гиперболоид
(рис.4.60,в)). При
поперечные полуоси однополостного гиперболоида
больше единицы, и он не имеет общих точек со сферой единичного радиуса. При
продольная полуось двуполостного гиперболоида
больше единицы, и он не имеет общих точек со сферой
. При
поверхность уровня
имеет общие точки с заданной сферой.
3. Из п.2 следует, что допустимые значения функции определяются неравенством .
4. Наименьшее значение на множестве , равное –1, функция достигает в точках
— вершинах двуполостного гиперболоида
(рис.4.60,в); наибольшее значение на множестве
, равное единице, функция достигает в точках окружности
т.е. в точках горлового эллипса (в данном случае окружности) однополостного гиперболоида вращения
(рис.4.60,а).
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Дифракция света.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: дифракция света, дифракционная решётка.
Если на пути волны возникает препятствие, то происходит дифракция — отклонение волны от прямолинейного распространения. Это отклонение не сводится к отражению или преломлению, а также искривлению хода лучей вследствие изменения показателя преломления среды.Дифракция состоит в том, что волна огибает край препятствия и заходит в область геометрической тени.
Пусть, например, плоская волна падает на экран с достаточно узкой щелью (рис. 1). На выходе из щели возникает расходящаяся волна, и эта расходимость усиливается с уменьшением ширины щели.
 |
| Рис. 1. Дифракция на щели |
Вообще, дифракционные явления выражены тем отчётливей, чем мельче препятствие. Наиболее существенна дифракция в тех случаях, когда размер препятствия меньше или порядка длины волны. Именно такому условию должна удовлетворять ширина щели на рис. 1.
Дифракция, как и интерференция, свойственна всем видам волн — механическим и электромагнитным. Видимый свет есть частный случай электромагнитных волн; неудивительно поэтому, что можно наблюдать
дифракцию света.
Так, на рис. 2 изображена дифракционная картина, полученная в результате прохождения лазерного луча сквозь небольшое отверстие диаметром 0,2мм.
 |
| Рис. 2. Дифракция лазерного луча на отверстии |
Мы видим, как и полагается, центральное яркое пятно; совсем далеко от пятна расположена тёмная область — геометрическая тень. Но вокруг центрального пятна — вместо чёткой границы света и тени! — идут чередующиеся светлые и тёмные кольца. Чем дальше от центра, тем менее яркими становятся светлые кольца; они постепенно исчезают в области тени.
Напоминает интерференцию, не правда ли? Это она и есть; данные кольца являются интерференционными максимумами и минимумами. Какие же волны тут интерферируют? Скоро мы разберёмся с этим вопросом, а заодно и выясним, почему вообще наблюдается дифракция.
Но прежде нельзя не упомянуть самый первый классический эксперимент по интерференции света — опыт Юнга, в котором существенно использовалось явление дифракции.
Опыт Юнга.
Всякий эксперимент с интерференцией света содержит некоторый способ получения двух когерентных световых волн. В опыте с зеркалами Френеля, как вы помните, когерентными источниками являлись два изображения одного и того же источника, полученные в обоих зеркалах.
Самая простая идея, которая возникла прежде всего, состояла в следующем. Давайте проколем в куске картона два отверстия и подставим под солнечные лучи. Эти отверстия будут когерентными вторичными источниками света, поскольку первичный источник один — Солнце. Следовательно, на экране в области перекрытия пучков, расходящихся от отверстий, мы должны увидеть интерференционную картину.
Такой опыт был поставлен задолго до Юнга итальянским учёным Франческо Гримальди (который открыл дифракцию света). Интерференции, однако, не наблюдалось. Почему же? Вопрос это не очень простой, и причина заключается в том, что Солнце — не точечный, а протяжённый источник света (угловой размер Солнца равен 30 угловым минутам). Солнечный диск состоит из множества точечных источников, каждый из которых даёт на экране свою интерференционную картину. Накладываясь, эти отдельные картины «смазывают» друг друга, и в результате на экране получается равномерная освещённость области перекрытия пучков.
Но если Солнце является чрезмерно «большим», то нужно искусственно создать точечный первичный источник. С этой целью в опыте Юнга использовано маленькое предварительное отверстие (рис. 3).
 |
| Рис. 3. Схема опыта Юнга |
Плоская волна падает на первое отверстие, и за отверстием возникает световой конус, расширяющийся вследствие дифракции. Он достигает следующих двух отверстий, которые становятся источниками двух когерентных световых конусов. Вот теперь — благодаря точечности первичного источника — в области перекрытия конусов будет наблюдаться интерференционная картина!
Томас Юнг осуществил этот эксперимент, измерил ширину интерференционных полос, вывел формулу
и с помощью этой формулы впервые вычислил длины волн видимого света. Вот почему этот опыт вошёл в число самых знаменитых в истории физики.
Принцип Гюйгенса–Френеля.
Напомним формулировку принципа Гюйгенса: каждая точка, вовлечённая в волновой процесс, является источником вторичных сферических волн; эти волны распространяются от данной точки, как из центра, во все стороны и накладываются друг на друга.
Но возникает естественный вопрос: а что значит «накладываются»?
Гюйгенс свёл свой принцип к чисто геометрическому способу построения новой волновой поверхности как огибающей семейства сфер, расширяющихся от каждой точки исходной волновой поверхности. Вторичные волны Гюйгенса — это математические сферы, а не реальные волны; их суммарное действие проявляется только на огибающей, т. е. на новом положении волновой поверхности.
В таком виде принцип Гюйгенса не давал ответа на вопрос, почему в процессе распространения волны не возникает волна, идущая в обратном направлении. Не объяснёнными оставались и дифракционные явления.
Модификация принципа Гюйгенса состоялась лишь спустя 137 лет. Огюстен Френель заменил вспомогательные геометрические сферы Гюйгенса на реальные волны и предположил, что эти волны интерферируют друг с другом.
Принцип Гюйгенса–Френеля. Каждая точка волновой поверхности служит источником вторичных сферических волн. Все эти вторичные волны являются когерентными ввиду общности их происхождения от первичного источника (и, стало быть, могут интерферировать друг с другом); волновой процесс в окружающем пространстве есть результат интерференции вторичных волн.
Идея Френеля наполнила принцип Гюйгенса физическим смыслом. Вторичные волны, интерферируя, усиливают друг друга на огибающей своих волновых поверхностей в направлении «вперёд», обеспечивая дальнейшее распространение волны. А в направлении «назад» происходит их интерференция с исходной волной, наблюдается взаимное гашение, и обратная волна не возникает.
В частности, свет распространяется там, где вторичные волны взаимно усиливаются. А в местах ослабления вторичных волн мы будем видеть тёмные участки пространства.
Принцип Гюйгенса–Френеля выражает важную физическую идею: волна, удалившись от своего источника, в дальнейшем «живёт своей жизнью» и уже никак от этого источника не зависит. Захватывая новые участки пространства, волна распространяется всё дальше и дальше вследствие интерференции вторичных волн, возбуждённых в различных точках пространства по мере прохождения волны.
Как принцип Гюйгенса–Френеля объясняет явление дифракции? Почему, например, происходит дифракция на отверстии? Дело в том, что из бесконечной плоской волновой поверхности падающей волны экранное отверстие вырезает лишь маленький светящийся диск, и последующее световое поле получается в результате интерференции волн вторичных источников, расположенных уже не на всей плоскости, а лишь на этом диске. Естественно, новые волновые поверхности теперь не будут плоскими; ход лучей искривляется, и волна начинает распространяться в разных направлениях, не совпадающих с первоначальным. Волна огибает края отверстия и проникает в область геометрической тени.
Вторичные волны, испущенные различными точками вырезанного светлого диска, интерферируют друг с другом. Результат интерференции определяется разностью фаз вторичных волн и зависит от угла отклонения лучей. В результате возникает чередование интерференционных максимумов и минимумов — что мы и видели на рис. 2.
Френель не только дополнил принцип Гюйгенса важной идеей когерентности и интерференции вторичных волн, но и придумал свой знаменитый метод решения дифракционных задач, основанный на построении так называемых зон Френеля. Изучение зон Френеля не входит в школьную программу — о них вы узнаете уже в вузовском курсе физики. Здесь мы упомянем лишь, что Френелю в рамках своей теории удалось дать объяснение нашего самого первого закона геометрической оптики — закона прямолинейного распространения света.
Дифракционная решётка.
Дифракционная решётка — это оптический прибор, позволяющий получать разложение света на спектральные составляющие и измерять длины волн. Дифракционные решётки бывают прозрачными и отражательными.
Мы рассмотрим прозрачную дифракционную решётку. Она состоит из большого числа щелей ширины , разделённых промежутками ширины
(рис. 4). Свет проходит только сквозь щели; промежутки свет не пропускают. Величина
называется периодом решётки.
 |
| Рис. 4. Дифракционная решётка |
Дифракционная решётка изготавливается с помощью так называемой делительной машины, которая наносит штрихи на поверхность стекла или прозрачной плёнки. При этом штрихи оказываются непрозрачными промежутками, а нетронутые места служат щелями. Если, например, дифракционная решётка содержит 100 штрихов на миллиметр, то период такой решётки будет равен: d= 0,01 мм= 10 мкм.
Сперва мы посмотрим, как проходит сквозь решётку монохроматический свет, т. е. свет со строго определённой длиной волны. Отличным примером монохроматического света служит луч лазерной указки длина волны около 0,65 мкм).
На рис. 5 мы видим такой луч, падающий на одну из дифракционных решёток стандартного набора. Щели решётки расположены вертикально, и на экране за решёткой наблюдаются периодически расположенные вертикальные полосы.
 |
| Рис. 5. Дифракция лазерного луча на решётке |
Как вы уже поняли, это интерференционная картина. Дифракционная решётка расщепляет падающую волну на множество когерентных пучков, которые распространяются по всем направлениям и интерферируют друг с другом. Поэтому на экране мы видим чередование максимумов и минимумов интерференции — светлых и тёмных полос.
Теория дифракционной решётки весьма сложна и во всей своей полноте оказывается далеко за рамками школьной программы. Вам следует знать лишь самые элементарные вещи, связанные с одной-единственной формулой; эта формула описывает положения максимумов освещённости экрана за дифракционной решёткой.
Итак, пусть на дифракционную решётку с периодом падает плоская монохроматическая волна (рис. 6). Длина волны равна
.
 |
| Рис. 6. Дифракция на решётке |
Для большей чёткости интерференционной картины можно поставить линзу между решёткой и экраном, а экран поместить в фокальной плоскости линзы. Тогда вторичные волны, идущие параллельно от различных щелей, соберутся в одной точке экрана (побочном фокусе линзы). Если же экран расположен достаточно далеко, то особой необходимости в линзе нет — лучи, приходящие в данную точку экрана от различных щелей, будут и так почти параллельны друг другу.
Рассмотрим вторичные волны, отклоняющиеся на угол .Разность хода между двумя волнами, идущими от соседних щелей, равна маленькому катету прямоугольного треугольника с гипотенузой
; или, что то же самое, эта разность хода равна катету
треугольника
. Но угол
равен углу
, поскольку это острые углы со взаимно перпендикулярными сторонами. Следовательно, наша разность хода равна
.
Интерференционные максимумы наблюдаются в тех случаях, когда разность хода равна целому числу длин волн:
(1)
При выполнении этого условия все волны, приходящие в точку от различных щелей, будут складываться в фазе и усиливать друг друга. Линза при этом не вносит дополнительной разности хода — несмотря на то, что разные лучи проходят через линзу разными путями. Почему так получается? Мы не будем вдаваться в этот вопрос, поскольку его обсуждение выходит за рамки ЕГЭ по физике.
Формула (1) позволяет найти углы, задающие направления на максимумы:
. (2)
При получаем
Это центральный максимум, или максимум нулевого порядка.Разность хода всех вторичных волн, идущих без отклонения, равна нулю, и в центральном максимуме они складываются с нулевым сдвигом фаз. Центральный максимум — это центр дифракционной картины, самый яркий из максимумов. Дифракционная картина на экране симметрична относительно центрального максимума.
При получаем угол:
.
Этот угол задаёт направления на максимумы первого порядка. Их два, и расположены они симметрично относительно центрального максимума. Яркость в максимумах первого порядка несколько меньше, чем в центральном максимуме.
Аналогично, при имеем угол:
.
Он задаёт направления на максимумы второго порядка. Их тоже два, и они также расположены симметрично относительно центрального максимума. Яркость в максимумах второго порядка несколько меньше, чем в максимумах первого порядка.
Примерная картина направлений на максимумы первых двух порядков показана на рис. 7.
 |
| Рис. 7. Максимумы первых двух порядков |
Вообще, два симметричных максимума k-го порядка определяются углом:
. (3)
При небольших соответствующие углы обычно невелики. Например, при
мкм и
мкм максимумы первого порядка расположены под углом
.Яркость максимумов k-го порядка постепенно убывает с ростом k. Сколько всего максимумов можно увидеть? На этот вопрос легко ответить с помощью формулы (2). Ведь синус не может быть больше единицы, поэтому:
.
Используя те же числовые данные, что и выше, получим: . Следовательно, наибольший возможный порядок максимума для данной решётки равен 15.
Посмотрите ещё раз на рис. 5. На экране мы видны 11 максимумов. Это центральный максимум, а также по два максимума первого, второго, третьего, четвёртого и пятого порядков.
С помощью дифракционной решётки можно измерить неизвестную длину волны. Направляем пучок света на решётку (период которой мы знаем), измеряем угол на максимум первого
порядка, пользуемся формулой (1) и получаем:
.
Дифракционная решётка как спектральный прибор.
Выше мы рассматривали дифракцию монохроматического света, каковым является лазерный луч. Часто приходится иметь дело с немонохроматическим излучением. Оно является смесью различных монохроматических волн, которые составляют спектр данного излучения. Например, белый свет — это смесь волн всего видимого диапазона, от красного до фиолетового.
Оптический прибор называется спектральным, если он позволяет раскладывать свет на монохроматические компоненты и тем самым исследовать спектральный состав излучения. Простейший спектральный прибор вам хорошо известен — это стеклянная призма. К числу спектральных приборов относится также и дифракционная решётка.
Предположим, что на дифракционную решётку падает белый свет. Давайте вернёмся к формуле (2) и подумаем, какие выводы из неё можно сделать.
Положение центрального максимума () не зависит от длины волны. В центре дифракционной картины сойдутся с нулевой разностью хода все монохроматические составляющие белого света. Поэтому в центральном максимуме мы увидим яркую белую полосу.
А вот положения максимумов порядка определяются длиной волны. Чем меньше
, тем меньше угол
для данного
. Поэтому в максимуме k-го порядка монохроматические волны разделяются в пространстве: самой близкой к к центральному максимуму окажется фиолетовая полоса, самой далёкой — красная.
Следовательно, в каждом порядке белый свет раскладывается решёткой в спектр.
Максимумы первого порядка всех монохроматических компонент образуют спектр первого порядка; затем идут спектры второго, третьего и так далее порядков. Спектр каждого порядка имеет вид цветной полосы, в которой присутствуют все цвета радуги — от фиолетового до красного.
Дифракция белого света показана на рис. 8. Мы видим белую полосу в центральном максимуме, а по бокам — два спектра первого порядка. По мере возрастания угла отклонения цвет полос меняется от фиолетового к красному.
 |
| Рис. 8. Дифракция белого света на решётке |
Но дифракционная решётка не только позволяет наблюдать спектры, т. е. проводить качественный анализ спектрального состава излучения. Важнейшим достоинством дифракционной решётки является возможность количественного анализа — как уже говорилось выше, мы с её помощью можем измерять длины волн. При этом измерительная процедура весьма проста: фактически она сводится к измерению угла направления на максимум.
Естественными примерами дифракционных решёток, встречающихся в природе, являются перья птиц, крылья бабочек, перламутровая поверхность морской раковины. Если, прищурившись, посмотреть на солнечный свет, то можно увидеть радужную окраску вокруг ресниц.Наши ресницы действуют в данном случае как прозрачная дифракционная решётка на рис. 6, а в качестве линзы выступает оптическая система роговицы и хрусталика.
Спектральное разложение белого света, даваемое дифракционной решёткой, проще всего наблюдать, глядя на обычный компакт-диск (рис. 9). Оказывается, дорожки на поверхности диска образуют отражательную дифракционную решётку!
 |
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Дифракция света.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
07.05.2023