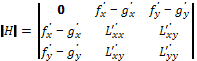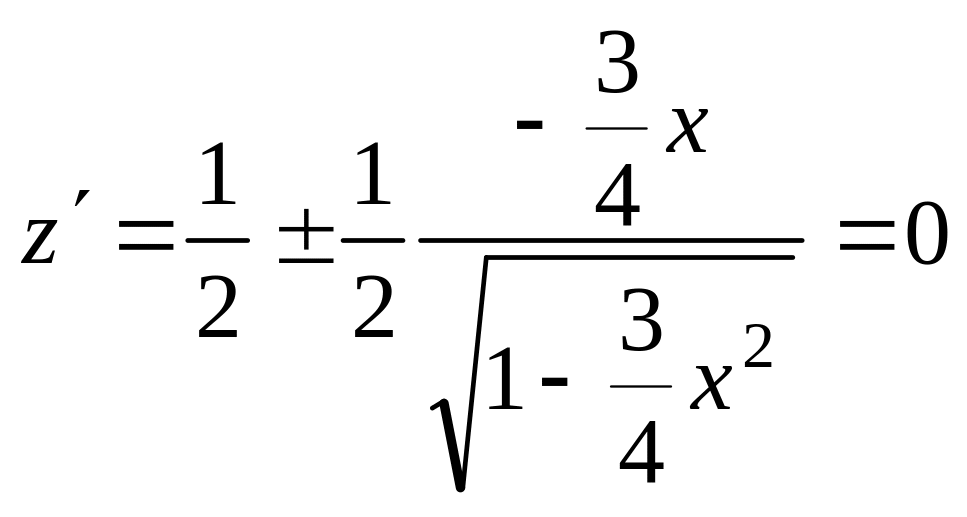Как найти максимум системы

Экстремумы функции двух переменных

Экстремум функции двух переменных: определения, необходимые и достаточные условия, локальный характер

Понятие экстремумов функции двух переменных вводится подобно тому, как это было сделано для функции одной переменной.

Определение. Точками экстремума функции двух переменных называются точки минимума и максимума этой функции. Значения самой функции в точках экстремума называются экстремумами функции двух переменных.

Определение. Точка P(x 0 , y 0 ) называется точкой максимума функции двух переменных z = z(x, y) , если значение функции в этой точке больше, чем в точках её окрестности. Значение функции в точке максимума называется максимумом функции двух переменных.

Определение. Точка P(x 0 , y 0 ) называется точкой максимума функции двух переменных z = z(x, y) , если значение функции в этой точке больше, чем в точках её окрестности. Значение функции в точке максимума называется максимумом функции двух переменных.

Теорема (необходимый признак экстремума функции двух переменных). Если точка P(x 0 , y 0 ) — точка экстремума функции двух переменных z = z(x, y) , то первые частные производные функции (по «иксу» и по «игреку») в этой точке равны нулю или не существуют:

.

Определение. Точки, в которой первые частные производные функции двух переменных равны нулю, называются стационарными точками.

Определение. Точки, в которой первые частные производные функции двух переменных равны нулю или не существуют, называются критическими точками.

Как и в случае с функцией одной переменной, необходимое условие существования экстремума функции двух переменных не является достаточным. Встречаются немало функций, в случаях которых первая частная производная функции равна нулю или не существует, но экстремумов в соответствующих точках нет. Каждая точка экстремума является критической точкой, но не каждая критическая точка является экстремумом.

Достаточный признак существования экстремума функции двух переменных. В точке P существует экстремум функции двух переменных, если в окрестности этой точки полное приращение функции не меняет знак. Так как в критической точке первый полный дифференциал равен нулю, то приращение функции определяет второй полный дифференциал

.

Наилучшее понимание применения полного дифференциала придёт при изучении и практическом применении шагов 3 и 4 алгоритма нахождения экстремумов функции двух переменных, который следует вторым пунктом этого урока.

Локальный характер экстремумов функции двух переменных. Максимум функции двух переменных на каком-либо участке области определения функции не обязательно является максимумом во всей области определения, так же как и минимум на каком-либо участке не является минимумом во всей области определения. Пусть мы рассматриваем высоту волн на участке прибрежной области моря (участок меньше области). Тогда на этом участке мы можем зафиксировать (по-крайней мере, зрительно) наибольшую высоту волны. Но на другом участке, на котором ветер вызывает бОльшую высоту волн, мы фиксируем минимальную высоту волны. Это к тому, что максимум высоты волны на первом участке может оказаться меньше, чем минимум высоты волны на втором участке. Поэтому, как и в случае экстремума функции одной переменной, необходимо уточнить это понятие и говорить об экстремумах как о локальных экстремумах функции двух переменных.

Алгоритм нахождения экстремумов функции двух переменных и примеры решений

Наибольший интерес представляет алгоритм нахождения экстремумов функции двух переменных, так как он, во-первых, отличается от алгоритма нахождения экстремумов функции одной переменных, а во-вторых, по аналогии с ним можно составить алгоритм нахождения функции трёх переменных. В частности, потребуется вычислять определители.

Итак, алгоритм нахождения экстремумов функции двух переменных.

Дана функция двух переменных .

Шаг 1. Находим частные производные и .

Шаг 2. Составляем систему уравнений из равенств этих производных нулю (их равенство нулю и есть необходимый признак существования экстремума):

Решения этой системы уравнений являются точками возможного экстремума — критическими точками.

Шаг 3. Пусть является критической точкой, найденной на шаге 2. Чтобы убедиться, что в ней существует экстремум функции двух переменных, находим частные производные второго порядка

как частные производные от частных производных первого порядка, найденных на шаге 1.

Шаг 4. Присваиваем частным производным второго порядка, найденным на шаге 3, буквенные обозначения:

Находим определитель и проверяем достаточный признак существования экстремума.

Если , то экстремума в найденной критической точке нет,

если , то экстремум в найденной критической точке есть,

если , то требуются дополнительные исследования.

Если экстремум в найденной точке есть и если , то в этой точке существует минимум функции двух переменных, если , то максимум.

Шаг 5. Подставляем значения критической точки, в которой найден экстремум, в исходную функцию двух переменных и получаем значение экстремума функции двух переменных (минимума или максимума).

Примеры начнём с более сложного, в котором составленная система уравнений имеет несколько решений, а, значит, найдено несколько критических точек.

Пример 1. Найти экстремумы функции двух переменных .

Решение. Следуем изложенному выше алгоритму.

Шаг 1. Находим частные производные:

.

Шаг 2. Составляем систему уравнений из равенств этих производных нулю:

Делим первое уравнение системы на 3, а второе на 6 и получаем

Из второго уравнения выражаем , подставляем в первое уравнение и получаем

Умножаем это уравнение на и получаем

.

Производим замену переменной: и получаем

.

Решаем полученное квадратное уравнение: .

Так как и , то

Таким образом, получили четыре критических точки — точки возможного экстремума.

Шаг 4. Находим определитель :

, т. е. экстремума в найденной критической точке нет,

, т. е. экстремума в найденной критической точке нет,

и , т. е. в найденной критической точке есть минимум функции двух переменных,

и , т. е. в найденной критической точке есть максимум функции двух переменных.

Шаг 5. Подставляем значения критической точки, в которой найден экстремум, в исходную функцию двух переменных и получаем значения экстремума функции двух переменных:

,

В следующем примере — только одна критическая точка.

Пример 2. Найти экстремумы функции двух переменных .

Шаг 1. Находим частные производные:

.

Шаг 2. Составляем систему уравнений из равенств этих производных нулю:

Решаем систему уравнений:

Таким образом, получили критическую точку — точку возможного экстремума.

Шаг 3. Находим частные производные второго порядка

Шаг 4. Находим определитель , т. е. в найденной критической точке есть экстремум, причём так как , то это минимум.

Шаг 5. Подставляем значения критической точки, в которой найден экстремум, в исходную функцию двух переменных и получаем значение экстремума функции двух переменных:

.

Найти экстремумы функции двух переменных самостоятельно, а затем посмотреть решение

Пример 3. Найти экстремумы функции двух переменных

.

Пример 4. Найти экстремумы функции двух переменных

.

Экстремум функции двух переменных. Примеры исследования функций на экстремум.

Пусть функция $z=f(x,y)$ определена в некоторой окрестности точки $(x_0,y_0)$. Говорят, что $(x_0,y_0)$ – точка (локального) максимума, если для всех точек $(x,y)$ некоторой окрестности точки $(x_0,y_0)$ выполнено неравенство $f(x,y) f(x_0,y_0)$, то точку $(x_0,y_0)$ называют точкой (локального) минимума.

Точки максимума и минимума часто называют общим термином – точки экстремума.

Если $(x_0,y_0)$ – точка максимума, то значение функции $f(x_0,y_0)$ в этой точке называют максимумом функции $z=f(x,y)$. Соответственно, значение функции в точке минимума именуют минимумом функции $z=f(x,y)$. Минимумы и максимумы функции объединяют общим термином – экстремумы функции.

Алгоритм исследования функции $z=f(x,y)$ на экстремум

1. Найти частные производные $frac<partial z><partial x>$ и $frac<partial z><partial y>$. Составить и решить систему уравнений $ left < begin& frac<partial z><partial x>=0;\ & frac<partial z><partial y>=0. end right.$. Точки, координаты которых удовлетворяют указанной системе, называют стационарными.
2. Найти $frac<partial^2z><partial x^2>$, $frac<partial^2z><partial xpartial y>$, $frac<partial^2z><partial y^2>$ и вычислить значение $Delta=frac<partial^2z><partial x^2>cdot frac<partial^2z><partial y^2>-left(frac<partial^2z><partial xpartial y>right)^2$ в каждой стационарной точке. После этого использовать следующую схему:
   1. Если $Delta > 0$ и $frac<partial^2z><partial x^2>> 0$ (или $frac<partial^2z><partial y^2>> 0$), то в исследуемая точка есть точкой минимума.
   2. Если $Delta > 0$ и $frac<partial^2z><partial x^2>0$, то $frac<partial^2z><partial x^2>cdot frac<partial^2z><partial y^2>-left(frac<partial^2z><partial xpartial y>right)^2 > 0$. А отсюда следует, что $frac<partial^2z><partial x^2>cdot frac<partial^2z><partial y^2>> left(frac<partial^2z><partial xpartial y>right)^2 ≥ 0$. Т.е. $frac<partial^2z><partial x^2>cdot frac<partial^2z><partial y^2>> 0$. Если произведение неких величин больше нуля, то эти величины одного знака. Т.е., например, если $frac<partial^2z><partial x^2>> 0$, то и $frac<partial^2z><partial y^2>> 0$. Короче говоря, если $Delta > 0$ то знаки $frac<partial^2z><partial x^2>$ и $frac<partial^2z><partial y^2>$ совпадают.

   Исследовать на экстремум функцию $z=4x^2-6xy-34x+5y^2+42y+7$.

   Будем следовать указанному выше алгоритму. Для начала найдём частные производные первого порядка:

   Сократим каждое уравнение этой системы на $2$ и перенесём числа в правые части уравнений:

   Мы получили систему линейных алгебраических уравнений. Мне в этой ситуации кажется наиболее удобным применение метода Крамера для решения полученной системы.

   Значения $x=2$, $y=-3$ – это координаты стационарной точки $(2;-3)$. Теперь приступим ко второму шагу алгоритма. Найдём частные производные второго порядка:

   Вычислим значение $Delta$:

   Так как $Delta > 0$ и $frac<partial^2 z> <partial x^2>> 0$, то согласно алгоритму точка $(2;-3)$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $(2;-3)$:

   $$ z_<min>=z(2;-3)=4cdot 2^2-6cdot 2 cdot (-3)-34cdot 2+5cdot (-3)^2+42cdot (-3)+7=-90. $$

   Ответ: $(2;-3)$ – точка минимума; $z_<min>=-90$.

   Исследовать на экстремум функцию $z=x^3+3xy^2-15x-12y+1$.

   Будем следовать указанному выше алгоритму. Для начала найдём частные производные первого порядка:

   Сократим первое уравнение на 3, а второе – на 6.

   Если $x=0$, то второе уравнение приведёт нас к противоречию: $0cdot y-2=0$, $-2=0$. Отсюда вывод: $xneq 0$. Тогда из второго уравнения имеем: $xy=2$, $y=frac<2>$. Подставляя $y=frac<2>$ в первое уравнение, будем иметь:

   Получили биквадратное уравнение. Делаем замену $t=x^2$ (при этом имеем в виду, что $t > 0$):

   Если $t=1$, то $x^2=1$. Отсюда имеем два значения $x$: $x_1=1$, $x_2=-1$. Если $t=4$, то $x^2=4$, т.е. $x_3=2$, $x_4=-2$. Вспоминая, что $y=frac<2>$, получим:

   Итак, у нас есть четыре стационарные точки: $M_1(1;2)$, $M_2(-1;-2)$, $M_3(2;1)$, $M_4(-2;-1)$. На этом первый шаг алгоритма закончен.

   Теперь приступим ко второму шагу алгоритма. Найдём частные производные второго порядка:

   Теперь будем вычислять значение $Delta$ в каждой из найденных ранее стационарных точек. Начнём с точки $M_1(1;2)$. В этой точке имеем:

   Так как $Delta(M_1) 0$ и $left.frac<partial^2 z><partial x^2>right|_ > 0$, то согласно алгоритму $M_3(2;1)$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_3$:

   $$ z_<min>=z(2;1)=2^3+3cdot 2cdot 1^2-15cdot 2-12cdot 1+1=-27. $$

   Осталось исследовать точку $M_4(-2;-1)$. В этой точке получим:

   Так как $Delta(M_4) > 0$ и $left.frac<partial^2 z><partial x^2>right|_ 0$ (так как оба сомножителя $36$ и $(2^2-1^2)$ положительны) и можно не находить конкретное значение $Delta$. Правда, для типовых расчётов это замечание бесполезно, – там требуют довести вычисления до числа 🙂

   Исследовать на экстремум функцию $z=x^4+y^4-2x^2+4xy-2y^2+3$.

   Будем следовать алгоритму. Для начала найдём частные производные первого порядка:

   Сократим оба уравнения на $4$:

   Добавим к второму уравнению первое и выразим $y$ через $x$:

   Подставляя $y=-x$ в первое уравнение системы, будем иметь:

   Из полученного уравнения имеем: $x=0$ или $x^2-2=0$. Из уравнения $x^2-2=0$ следует, что $x=-sqrt<2>$ или $x=sqrt<2>$. Итак, найдены три значения $x$, а именно: $x_1=0$, $x_2=-sqrt<2>$, $x_3=sqrt<2>$. Так как $y=-x$, то $y_1=-x_1=0$, $y_2=-x_2=sqrt<2>$, $y_3=-x_3=-sqrt<2>$.

   Первый шаг решения окончен. Мы получили три стационарные точки: $M_1(0;0)$, $M_2(-sqrt<2>,sqrt<2>)$, $M_3(sqrt<2>,-sqrt<2>)$.

   Теперь приступим ко второму шагу алгоритма. Найдём частные производные второго порядка:

   Теперь будем вычислять значение $Delta$ в каждой из найденных ранее стационарных точек. Начнём с точки $M_1(0;0)$. В этой точке имеем:

   $$Delta(M_1)=16cdot((3cdot 0^2-1)(3cdot 0^2-1)-1)=16cdot 0=0.$$

   Так как $Delta(M_1) = 0$, то согласно алгоритму требуется дополнительное исследование, ибо ничего определённого про наличие экстремума в рассматриваемой точке сказать нельзя. Оставим покамест эту точку в покое и перейдём в иным точкам.

   Исследуем точку $M_2(-sqrt<2>,sqrt<2>)$. В этой точке получим:

   Так как $Delta(M_2) > 0$ и $left.frac<partial^2 z><partial x^2>right|_ > 0$, то согласно алгоритму $M_2(-sqrt<2>,sqrt<2>)$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_2$:

   Аналогично предыдущему пункту исследуем точку $M_3(sqrt<2>,-sqrt<2>)$. В этой точке получим:

   Так как $Delta(M_3) > 0$ и $left.frac<partial^2 z><partial x^2>right|_ > 0$, то согласно алгоритму $M_3(sqrt<2>,-sqrt<2>)$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_3$:

   Настал черёд вернуться к точке $M_1(0;0)$, в которой $Delta(M_1) = 0$. Согласно алгоритму требуется дополнительное исследование. Под этой уклончивой фразой подразумевается «делайте, что хотите» :). Общего способа разрешения таких ситуаций нет, – и это понятно. Если бы такой способ был, то он давно бы вошёл во все учебники. А покамест приходится искать особый подход к каждой точке, в которой $Delta = 0$. Ну что же, поисследуем поведение функции в окрестности точки $M_1(0;0)$. Сразу отметим, что $z(M_1)=z(0;0)=3$. Предположим, что $M_1(0;0)$ – точка минимума. Тогда для любой точки $M$ из некоторой окрестности точки $M_1(0;0)$ получим $z(M) > z(M_1) $, т.е. $z(M) > 3$. А вдруг любая окрестность содержит точки, в которых $z(M) 3$? Тогда в точке $M_1$ точно не будет максимума.

   Рассмотрим точки, у которых $y=x$, т.е. точки вида $(x,x)$. В этих точках функция $z$ будет принимать такие значения:

   $$ z(x,x)=x^4+x^4-2x^2+4xcdot x-2cdot x^2+3=2x^4+3. $$

   Так как в любой окрестности точки $M_1(0;0)$ имеем $2x^4 > 0$, то $2x^4+3 > 3$. Вывод: любая окрестность точки $M_1(0;0)$ содержит точки, в которых $z > 3$, посему точка $M_1(0;0)$ не может быть точкой максимума.

   Точка $M_1(0;0)$ не является ни точкой максимума, ни точкой минимума. Вывод: $M_1$ вообще не является точкой экстремума.

   Ответ: $(-sqrt<2>,sqrt<2>)$, $(sqrt<2>,-sqrt<2>)$ – точки минимума функции $z$. В обеих точках $z_<min>=-5$.

   Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).

   5.8. Экстремум функции многих переменных

   Рассмотрим вопрос анализа «в статике» с использованием положений линейной алгебры и дифференциального исчисления, а также условий, которые позволяют идентифицировать точки оптимума. Такие условия используются для проверки выбранных точек и дают возможность выяснить, являются ли точки точками минимума, максимума или седловыми точками.

   Определение. Экстремумом функции двух переменных называется её максимальное или минимальное значение на заданном множестве изменения переменных.

   Экстремумы и методы их нахождения имеют широкое применение в экономических исследованиях, при выборе наилучших вариантов инвестиций, производственных программ, вложения денег в покупки и т. п.

   Определение. Значение функции F(M) в точке М0 называется Максимумом (минимумом), если оно является набольшим (наименьшим) по сравнению с ее значениями во всех достаточно близких точках:

   .

   

   Пример 53. На рис. 37 представлен график функции двух переменных, точка М0(5, , в которой достигается максимум функции, окрестность точки М0(5, , максимальное значение функции F(X, Y), равное F(5, ; на рис. 38 – график функции точка М0(4, 9), в которой достигается минимум функции, окрестность точки М0(4, 9), минимальное значение функции F(4, 9).

   Из определения экстремума функции видно, что понятие экстремума является локальным. Другими словами, можно сказать, что приведенное определение экстремума является определением локального экстремума, функция может иметь несколько локальных максимумов или минимумов. Ясно, что при нахождении лучшего решения следует ориентироваться на наибольший из локальных максимумов, если ищется наибольшее значение функции, и на наименьший из локальных минимумов, если ищется наименьшее значение функции.

   Определение. Наибольшая величина из локальных максимумов называется Глобальным максимумом, наименьший из локальных минимумов – Глобальным минимумом.

   Задача нахождения локальных экстремумов, а тем более глобальных, для функции нескольких переменных является достаточно трудной, в общем случае для произвольного числа переменных практически неразрешимой. Для выпуклых функций разработаны специальные методы нахождения экстремумов.

   Замечание. Любой локальный экстремум выпуклой функции является глобальным.

   Определение. Функция многих переменных может иметь максимум или минимум (экстремум) только в точках, лежащих внутри области определения функции, в которых все ее частные производные первого порядка равны нулю или не существуют. Такие точки называются Критическими.

   Замечание. Это необходимые условия экстремума, но недостаточные, они могут выполняться и в точках, где нет экстремума.

   Это определение дает схему нахождения экстремальных точек. Составляется система уравнений относительно переменных Х и У:

   Решение системы представляет собой пары (х0, у0), (х1, у1) и т. д., которые называются точками «подозрительными» на экстремум, т. е., если функция имеет экстремумы, то они могут достигаться только в этих точках. Для определения, достигается ли в каждой из найденных точек максимальное (минимальное) значение или в рассматриваемой точке нет экстремума, требуется проведение дополнительных исследований.

   Найдя частные производные и приравняв их к нулю, получаем систему уравнений:

   

   Решение этой системы очевидно: Х = 0, у = 1. Поскольку Z  0 при всех Х, у, то ясно, что найденная точка (0, 1) есть точка минимума.

   Решение. Найдем частные производные и приравняем их к нулю:

   

   Точка (0, 0) является «подозрительной». Однако экстремума функция в этой точке не имеет, так как в любой окрестности этой точки она принимает значения разных знаков, а в самой точке (0, 0) значение функции равно нулю.

   Рассмотрим Достаточные условия экстремума для функции двух переменных.

   Пусть функция z = f(x, y) непрерывна со своими частными производными первого и второго порядка в некоторой окрестности точки М(х0, у0). Пусть в этой точке выполнены необходимые условия экстремума:

   

   В этой точке пусть вычислены частные производные второго порядка.

   

   Тогда Достаточные условия максимума и минимума имеют вид:

   2) если D 0, при этом А = 6 > 0 и, следовательно, в точке М1 – минимум.

   Пример 57. Исследовать на экстремум функцию

   Решение. Ищем критические точки:

   

   Находим М0(1, 0) и М1(-1, 0). Эти точки принадлежат области определения исследуемой функции: - 1, то> 0. Здесь оказалось, что вблизи точки М разность Не сохраняет знака, вследствие чего в точке М нет экстремума.

   Замечание. Для функций с числом переменных больше двух достаточные условия экстремума имеют сложный вид и требуют глубоких знаний по математическому анализу

   Пример 59. Исследовать на экстремум функцию

   Решение. Ищем критические точки:

   

   Эти частные производные не обращаются в нуль ни при каких значениях X, Y, Z; они не существуют (обращаются в бесконечность) в точке М(0, 0, 0). Эта точка лежит внутри области определения функции W, которая представляет совокупность всех точек (X, Y, Z) пространства. Поэтому М(0, 0, 0) критическая точка.

   Исследуя знак разности Вблизи точки М, убеждаемся, что при любых отличных от нуля значениях Х, Y, Z она сохраняет положительный знак. Поэтому М есть точка минимума,

   1. Дайте определение функции многих переменных.

   2. Приведите примеры функций многих переменных, используемых в экономике.

   3. Что называется графиком функции двух переменных? Приведите примеры.

   4. Сформулируйте определение множества (линии) уровня функции двух переменных. Может ли множество уровня функции двух переменных не быть линией?

   5. Опишите взаимосвязь между градиентом функции двух переменных и ее линией уровня.

   6. Перечислите основные свойства градиента функции.

   7. Дайте определение возрастающей (убывающей) функции многих переменных.

   8. В каком случае функция является вогнутой?

   9. Всегда ли локальный экстремум выпуклой функции является глобальным?

   10. Дайте определение экстремума функции двух переменных.

   11. Сформулируйте достаточные условия максимума и минимума функции двух переменных.

   источники:

   http://math1.ru/education/funct_sev_var/extr2.html

   http://matica.org.ua/metodichki-i-knigi-po-matematike/metody-optimizatcii-nekrasova-m-g/5-8-ekstremum-funktcii-mnogikh-peremennykh

Изучение
экстремумов математических объектов,
задаваемых несколькими функциями,
является более сложной задачей. В общем
случае задачу можно сформулировать
так: найти экстремум функции

,
заданной системой функций

(13)

К

такой системе сводится задача на условный
максимум производственной функции

при бюджетном ограничении
,
в котором денежные средства
,
отпущенные на закупку ресурсов, уже не
являются постоянной величиной
,
а зависят от величины выпуска

и «подпитываются» долей дохода:
.
Чем лучше работает предприятие, тем
большие средства оно может отпустить
на закупку сырья, энергообеспечение,
аренду и т.д. Задача на условный экстремум
с переменным бюджетным ограничением
формулируется так

Н
а
рис.7.18 изображен график функции
Кобба-Дугласа. Рассмотрены три варианта
уравнения связи. При

условный экстремум находится в точке

.
Если
,
условный максимум перемещается в точку

.
Наконец, при

условный максимум оказывается в точке

.

Если величина

возникает положи­тельная обратная
связь, если
—
отрицательная. Простым преобразованием
второго уравнения задача с обратной
связью сводится к исследованию на
экстремум в системе функций

Поиск решения начнем с нахождения
множества таких точек на координатной
плоскости Oxy, в которых
значения функций системы равны

.

Решение этого уравнения

подставим в одну из функций

и исследуем на экстремум функцию

.
Критическая точка

для функции

задает стационарную точку

на плоскости Oxy, в
которой возможен экстремум

.

Поскольку

и

,
найдем производную по

,
которая в критической точке

будет равна нулю:

и

Отсюда при условии

и

получим

(14)

_{Найденное выражение представляет
необходимые условия в задаче на условный
экстремум с обратной связью.}

Метод Лагранжа
при исследовании на условный экстремум
в системах функций

Поскольку каждое уравнение системы при
исследовании на экстремум можно привести
к виду

и
,
то в критической точке должен быть
равен нулю дифференциал каждой функции

Умножим первое и второе равенства на

и

соответственно, причем
,

не равны нулю одновременно

Слева в равенстве стоит дифференциал
функции, которую назовем функцией
Лагранжа и обозначим через

Сама функция имеет вид

Исследуя функцию

на локальный экстремум, подберем один
из множителей
,

так, чтобы в некоторой точке
было
выполнено равенство

Поскольку дифференциал функции

равен нулю, то

также, причем
.

Таким образом, система

выражает необходимые условия локального
экстремума функции
.
Система содержит две переменные величины

и два параметра

и
.
Для нахождения 4-х неизвестных добавим
уравнение связи

и одно из равенств

или
.

Итак, условия первого порядка при
нахождении локального экстремума
функции Лагранжа и условного экстремума
с обратной связью функции

сформулированы:

Последнее условие можно заменить на
равенство
+

,
поскольку

Из первых двух уравнений системы найдем

,
считая

и

,

что совпадает с равенством (14).

Перейдем к достаточным условиям условного
экстремума с обратной связью. Возьмем
дифференциал от обеих частей в уравнении
связи

,

откуда, считая, что
,
найдем

Подставим выражение во второй дифференциал
функции Лагранжа

.

Преобразуя, получим

.

Второй сомножитель в скобках переписываем
как окаймленный гессиан

.

Его знак к критической точке указывает
на локальный минимум или максимум
функции
,
а, следовательно, на условный минимум
или максимум функции
:

если

то

если

то

ПРИМЕР 1. Найти
экстремум в системе функций

Решение. Функция
Лагранжа задачи на условный экстремум
с обратной связью имеет вид

.

Найдем необходимые
условия

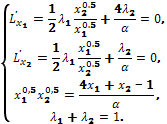
Разделив 1-е
уравнение на 2-е, получим

Подставим в 3-е уравнение, будем иметь

.
Для функции Кобба-Дугласа в стационарной
точке существует максимум. Его величина

На рис. 7.18 представлены условные максимумы
для трех значений
.
При при отсутствии обратной связи

получим стандартный условный экстремум

,
точка

В случае положительной обратной связи
с коэффициентом

имеем
,
точка

При отрицательной обратной связи с
коэффициентом

максимум

соответствует точке

Если исследуемая
функция не является дифференцируемой,
метод Лагранжа не применим.

ПРИМЕР 2. Исследовать
на экстремум функцию

,
заданную системой уравнений

Решение. Область
значений функции

.
Найдем корни уравнения

,

для чего возведем
его в квадрат

.

П
осле
сокращения уравнение примет вид

.
Следовательно,

или

.
При

получим

.
Очевидно, минималь­ное значение

равно

при

и

.
Другой случай

приводит к тому же результату. Отметим,
что

пред­ставляет глобаль­ный минимум
функции

.
На рис. 7.17 изображены графики функций

и

,
Пересе­каю­щиеся по плоскостям

и

.
Линии пересечения поверхностей указаны
красным цветом.

Некоторые из функций системы могут
быть заданы в неявном или параметрическом
виде.

П
РИМЕР
3. Исследовать на
экстремум функцию

,
заданную системой уравнений

Решение. Подставим

в первое уравнение:

.

Представим уравнение
как квадратное относительно

:

.

Его решение

подставим во второе
уравнение системы. Получим

.

Исследуем функцию

на экстремум с помощью производной.

.

Уравнение

при

имеет решение

.
При

решение

.
Исследование знаков производной
показывает, что в точке

достигается максимум

,
в точке

— минимум

.

Окончательно,
получаем
,

.

Графики обеих
функций представлены на рис. 7.20. Стрелками
указаны минимум и максимум функции

,
причем минимум наблюдается, а максимум
скрыт под поверхностью сферы. Для
улучшения обзора из сферы удалена часть
поверхности.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Экстремум функции двух переменных. Примеры исследования функций на экстремум.

Пусть функция $z=f(x,y)$ определена в некоторой окрестности точки $(x_0,y_0)$. Говорят, что $(x_0,y_0)$ – точка (локального) максимума, если для всех точек $(x,y)$ некоторой окрестности точки $(x_0,y_0)$ выполнено неравенство $f(x,y)< f(x_0,y_0)$. Если же для всех точек этой окрестности выполнено условие $f(x,y)> f(x_0,y_0)$, то точку $(x_0,y_0)$ называют точкой (локального) минимума.

Точки максимума и минимума часто называют общим термином – точки экстремума.

Если $(x_0,y_0)$ – точка максимума, то значение функции $f(x_0,y_0)$ в этой точке называют максимумом функции $z=f(x,y)$. Соответственно, значение функции в точке минимума именуют минимумом функции $z=f(x,y)$. Минимумы и максимумы функции объединяют общим термином – экстремумы функции.

Алгоритм исследования функции $z=f(x,y)$ на экстремум

1. Найти частные производные $frac{partial z}{partial x}$ и $frac{partial z}{partial y}$. Составить и решить систему уравнений $
   left { begin{aligned}
   & frac{partial z}{partial x}=0;\
   & frac{partial z}{partial y}=0.
   end{aligned} right.$. Точки, координаты которых удовлетворяют указанной системе, называют стационарными.
2. Найти $frac{partial^2z}{partial x^2}$, $frac{partial^2z}{partial xpartial y}$, $frac{partial^2z}{partial y^2}$ и вычислить значение $Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2$ в каждой стационарной точке. После этого использовать следующую схему:
   1. Если $Delta > 0$ и $frac{partial^2z}{partial x^2} > 0$ (или $frac{partial^2z}{partial y^2} > 0$), то в исследуемая точка есть точкой минимума.
   2. Если $Delta > 0$ и $frac{partial^2z}{partial x^2} < 0$ (или $frac{partial^2z}{partial y^2} < 0$), то в исследуемая точка есть точкой максимума.
   3. Если $Delta < 0$, то в расматриваемой стационарной точке экстремума нет.
   4. Если $Delta = 0$, то ничего определённого про наличие экстремума сказать нельзя; требуется дополнительное исследование.

Примечание (желательное для более полного понимания текста): показатьскрыть

Пример №1

Исследовать на экстремум функцию $z=4x^2-6xy-34x+5y^2+42y+7$.

Решение

Будем следовать указанному выше алгоритму. Для начала найдём частные производные первого порядка:

$$
frac{partial z}{partial x}=8x-6y-34; frac{partial z}{partial y}=-6x+10y+42.
$$

Составим систему уравнений $ left { begin{aligned}
& frac{partial z}{partial x}=0;\
& frac{partial z}{partial y}=0.
end{aligned} right.$:

$$
left { begin{aligned}
& 8x-6y-34=0;\
& -6x+10y+42=0.
end{aligned} right.
$$

Сократим каждое уравнение этой системы на $2$ и перенесём числа в правые части уравнений:

$$
left { begin{aligned}
& 4x-3y=17;\
& -3x+5y=-21.
end{aligned} right.
$$

Мы получили систему линейных алгебраических уравнений. Мне в этой ситуации кажется наиболее удобным применение метода Крамера для решения полученной системы.

$$ begin{aligned}
& Delta=left| begin{array} {cc} 4 & -3\ -3 & 5 end{array}right|=4cdot 5-(-3)cdot (-3)=20-9=11;\
& Delta_x=left| begin{array} {cc} 17 & -3\ -21 & 5 end{array}right|=17cdot 5-(-3)cdot (-21)=85-63=22;\
& Delta_y=left| begin{array} {cc} 4 & 17\ -3 & -21 end{array}right|=4cdot (-21)-17cdot (-3)=-84+51=-33.end{aligned} \
x=frac{Delta_{x}}{Delta}=frac{22}{11}=2; ; y=frac{Delta_{y}}{Delta}=frac{-33}{11}=-3.
$$

Значения $x=2$, $y=-3$ – это координаты стационарной точки $(2;-3)$. Теперь приступим ко второму шагу алгоритма. Найдём частные производные второго порядка:

$$
frac{partial^2 z}{partial x^2}=8; frac{partial^2 z}{partial y^2}=10; frac{partial^2 z}{partial x partial y}=-6.
$$

Вычислим значение $Delta$:

$$
Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2=
8cdot 10-(-6)^2=80-36=44.
$$

Так как $Delta > 0$ и $frac{partial^2 z}{partial x^2} > 0$, то согласно алгоритму точка $(2;-3)$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $(2;-3)$:

$$
z_{min}=z(2;-3)=4cdot 2^2-6cdot 2 cdot (-3)-34cdot 2+5cdot (-3)^2+42cdot (-3)+7=-90.
$$

Ответ: $(2;-3)$ – точка минимума; $z_{min}=-90$.

Пример №2

Исследовать на экстремум функцию $z=x^3+3xy^2-15x-12y+1$.

Решение

Будем следовать указанному выше алгоритму. Для начала найдём частные производные первого порядка:

$$
frac{partial z}{partial x}=3x^2+3y^2-15; frac{partial z}{partial y}=6xy-12.
$$

Составим систему уравнений $ left { begin{aligned}
& frac{partial z}{partial x}=0;\
& frac{partial z}{partial y}=0.
end{aligned} right.$:

$$
left { begin{aligned}
& 3x^2+3y^2-15=0;\
& 6xy-12=0.
end{aligned} right.
$$

Сократим первое уравнение на 3, а второе – на 6.

$$
left { begin{aligned}
& x^2+y^2-5=0;\
& xy-2=0.
end{aligned} right.
$$

Если $x=0$, то второе уравнение приведёт нас к противоречию: $0cdot y-2=0$, $-2=0$. Отсюда вывод: $xneq 0$. Тогда из второго уравнения имеем: $xy=2$, $y=frac{2}{x}$. Подставляя $y=frac{2}{x}$ в первое уравнение, будем иметь:

$$
x^2+left(frac{2}{x} right)^2-5=0;\
x^2+frac{4}{x^2}-5=0;\
x^4-5x^2+4=0.
$$

Получили биквадратное уравнение. Делаем замену $t=x^2$ (при этом имеем в виду, что $t > 0$):

$$
t^2-5t+4=0;\
begin{aligned}
& D=(-5)^2-4cdot 1 cdot 4=9;\
& t_1=frac{-(-5)-sqrt{9}}{2}=frac{5-3}{2}=1;\
& t_2=frac{-(-5)+sqrt{9}}{2}=frac{5+3}{2}=4.end{aligned}
$$

Если $t=1$, то $x^2=1$. Отсюда имеем два значения $x$: $x_1=1$, $x_2=-1$. Если $t=4$, то $x^2=4$, т.е. $x_3=2$, $x_4=-2$. Вспоминая, что $y=frac{2}{x}$, получим:

begin{aligned}
& y_1=frac{2}{x_1}=frac{2}{1}=2;\
& y_2=frac{2}{x_2}=frac{2}{-1}=-2;\
& y_3=frac{2}{x_3}=frac{2}{2}=1;\
& y_4=frac{2}{x_4}=frac{2}{-2}=-1.
end{aligned}

Итак, у нас есть четыре стационарные точки: $M_1(1;2)$, $M_2(-1;-2)$, $M_3(2;1)$, $M_4(-2;-1)$. На этом первый шаг алгоритма закончен.

Теперь приступим ко второму шагу алгоритма. Найдём частные производные второго порядка:

$$
frac{partial^2 z}{partial x^2}=6x; frac{partial^2 z}{partial y^2}=6x; frac{partial^2 z}{partial x partial y}=6y.
$$

Найдём $Delta$:

$$
Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2=
6xcdot 6x-(6y)^2=36x^2-36y^2=36(x^2-y^2).
$$

Теперь будем вычислять значение $Delta$ в каждой из найденных ранее стационарных точек. Начнём с точки $M_1(1;2)$. В этой точке имеем:

$$Delta(M_1)=36(1^2-2^2)=-108.$$

Так как $Delta(M_1) < 0$, то согласно алгоритму в точке $M_1$ экстремума нет.

Исследуем точку $M_2(-1;-2)$. В этой точке имеем:

$$Delta(M_2)=36((-1)^2-(-2)^2)=-108.$$

Так как $Delta(M_2) < 0$, то согласно алгоритму в точке $M_2$ экстремума нет.

Исследуем точку $M_3(2;1)$. В этой точке получим:

$$
Delta(M_3)=36(2^2-1^2)=108;;; left.frac{partial^2 z}{partial x^2}right|_{M_3}=6cdot 2=12.
$$

Так как $Delta(M_3) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_3} > 0$, то согласно алгоритму $M_3(2;1)$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_3$:

$$
z_{min}=z(2;1)=2^3+3cdot 2cdot 1^2-15cdot 2-12cdot 1+1=-27.
$$

Осталось исследовать точку $M_4(-2;-1)$. В этой точке получим:

$$
Delta(M_4)=36((-2)^2-(-1)^2)=108;;; left.frac{partial^2 z}{partial x^2}right|_{M_4}=6cdot (-2)=-12.
$$

Так как $Delta(M_4) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_4} < 0$, то согласно алгоритму $M_4(-2;-1)$ есть точкой максимума функции $z$. Максимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_4$:

$$
z_{max}=z(-2;-1)=(-2)^3+3cdot (-2)cdot (-1)^2-15cdot (-2)-12cdot (-1)+1=29.
$$

Исследование на экстремум завершено. Осталось лишь записать ответ.

Ответ:

• $(2;1)$ – точка минимума, $z_{min}=-27$;
• $(-2;-1)$ – точка максимума, $z_{max}=29$.

Примечание

Вычислять значение $Delta$ в общем случае нет необходимости, потому что нас интересует лишь знак, а не конкретное значение данного параметра. Например, для рассмотренного выше примера №2 в точке $M_3(2;1)$ имеем $Delta=36cdot(2^2-1^2)$. Здесь очевидно, что $Delta > 0$ (так как оба сомножителя $36$ и $(2^2-1^2)$ положительны) и можно не находить конкретное значение $Delta$. Правда, для типовых расчётов это замечание бесполезно, – там требуют довести вычисления до числа

Пример №3

Исследовать на экстремум функцию $z=x^4+y^4-2x^2+4xy-2y^2+3$.

Решение

Будем следовать алгоритму. Для начала найдём частные производные первого порядка:

$$
frac{partial z}{partial x}=4x^3-4x+4y; frac{partial z}{partial y}=4y^3+4x-4y.
$$

Составим систему уравнений $ left { begin{aligned}
& frac{partial z}{partial x}=0;\
& frac{partial z}{partial y}=0.
end{aligned} right.$:

$$
left { begin{aligned}
& 4x^3-4x+4y=0;\
& 4y^3+4x-4y=0.
end{aligned} right.
$$

Сократим оба уравнения на $4$:

$$
left { begin{aligned}
& x^3-x+y=0;\
& y^3+x-y=0.
end{aligned} right.
$$

Добавим к второму уравнению первое и выразим $y$ через $x$:

$$
y^3+x-y+(x^3-x+y)=0;\
y^3+x^3=0; y^3=-x^3; y=-x.
$$

Подставляя $y=-x$ в первое уравнение системы, будем иметь:

$$
x^3-x-x=0;\
x^3-2x=0;\
x(x^2-2)=0.
$$

Из полученного уравнения имеем: $x=0$ или $x^2-2=0$. Из уравнения $x^2-2=0$ следует, что $x=-sqrt{2}$ или $x=sqrt{2}$. Итак, найдены три значения $x$, а именно: $x_1=0$, $x_2=-sqrt{2}$, $x_3=sqrt{2}$. Так как $y=-x$, то $y_1=-x_1=0$, $y_2=-x_2=sqrt{2}$, $y_3=-x_3=-sqrt{2}$.

Первый шаг решения окончен. Мы получили три стационарные точки: $M_1(0;0)$, $M_2(-sqrt{2},sqrt{2})$, $M_3(sqrt{2},-sqrt{2})$.

Теперь приступим ко второму шагу алгоритма. Найдём частные производные второго порядка:

$$
frac{partial^2 z}{partial x^2}=12x^2-4; frac{partial^2 z}{partial y^2}=12y^2-4; frac{partial^2 z}{partial x partial y}=4.
$$

Найдём $Delta$:

$$
Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2=
(12x^2-4)(12y^2-4)-4^2=\
=4(3x^2-1)cdot 4(3y^2-1)-16=16(3x^2-1)(3y^2-1)-16=16cdot((3x^2-1)(3y^2-1)-1).
$$

Теперь будем вычислять значение $Delta$ в каждой из найденных ранее стационарных точек. Начнём с точки $M_1(0;0)$. В этой точке имеем:

$$Delta(M_1)=16cdot((3cdot 0^2-1)(3cdot 0^2-1)-1)=16cdot 0=0.$$

Так как $Delta(M_1) = 0$, то согласно алгоритму требуется дополнительное исследование, ибо ничего определённого про наличие экстремума в рассматриваемой точке сказать нельзя. Оставим покамест эту точку в покое и перейдём в иным точкам.

Исследуем точку $M_2(-sqrt{2},sqrt{2})$. В этой точке получим:

begin{aligned}
& Delta(M_2)=16cdot((3cdot (-sqrt{2})^2-1)(3cdot (sqrt{2})^2-1)-1)=16cdot 24=384;\
& left.frac{partial^2 z}{partial x^2}right|_{M_2}=12cdot (-sqrt{2})^2-4=24-4=20.
end{aligned}

Так как $Delta(M_2) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_2} > 0$, то согласно алгоритму $M_2(-sqrt{2},sqrt{2})$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_2$:

$$
z_{min}=z(-sqrt{2},sqrt{2})=(-sqrt{2})^4+(sqrt{2})^4-2(-sqrt{2})^2+4cdot (-sqrt{2})sqrt{2}-2(sqrt{2})^2+3=-5.
$$

Аналогично предыдущему пункту исследуем точку $M_3(sqrt{2},-sqrt{2})$. В этой точке получим:

begin{aligned}
& Delta(M_3)=16cdot((3cdot (sqrt{2})^2-1)(3cdot (-sqrt{2})^2-1)-1)=16cdot 24=384;\
& left.frac{partial^2 z}{partial x^2}right|_{M_3}=12cdot (sqrt{2})^2-4=24-4=20.
end{aligned}

Так как $Delta(M_3) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_3} > 0$, то согласно алгоритму $M_3(sqrt{2},-sqrt{2})$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_3$:

$$
z_{min}=z(sqrt{2},-sqrt{2})=(sqrt{2})^4+(-sqrt{2})^4-2(sqrt{2})^2+4cdot sqrt{2}(-sqrt{2})-2(-sqrt{2})^2+3=-5.
$$

Настал черёд вернуться к точке $M_1(0;0)$, в которой $Delta(M_1) = 0$. Согласно алгоритму требуется дополнительное исследование. Под этой уклончивой фразой подразумевается «делайте, что хотите» :). Общего способа разрешения таких ситуаций нет, – и это понятно. Если бы такой способ был, то он давно бы вошёл во все учебники. А покамест приходится искать особый подход к каждой точке, в которой $Delta = 0$. Ну что же, поисследуем поведение функции в окрестности точки $M_1(0;0)$. Сразу отметим, что $z(M_1)=z(0;0)=3$. Предположим, что $M_1(0;0)$ – точка минимума. Тогда для любой точки $M$ из некоторой окрестности точки $M_1(0;0)$ получим $z(M) > z(M_1) $, т.е. $z(M) > 3$. А вдруг любая окрестность содержит точки, в которых $z(M) < 3$? Тогда в точке $M_1$ уж точно не будет минимума.

Рассмотрим точки, у которых $y=0$, т.е. точки вида $(x,0)$. В этих точках функция $z$ будет принимать такие значения:

$$
z(x,0)=x^4+0^4-2x^2+4xcdot 0-2cdot 0^2+3=x^4-2x^2+3=x^2(x^2-2)+3.
$$

В всех достаточно малых окрестностях $M_1(0;0)$ имеем $x^2-2 < 0$, посему $x^2(x^2-2) < 0$, откуда следует $x^2(x^2-2)+3 < 3$. Вывод: любая окрестность точки $M_1(0;0)$ содержит точки, в которых $z < 3$, посему точка $M_1(0;0)$ не может быть точкой минимума.

Но, может быть, точка $M_1(0;0)$ – точка максимума? Если это так, то для любой точки $M$ из некоторой окрестности точки $M_1(0;0)$ получим $z(M) < z(M_1) $, т.е. $z(M) < 3$. А вдруг любая окрестность содержит точки, в которых $z(M) > 3$? Тогда в точке $M_1$ точно не будет максимума.

Рассмотрим точки, у которых $y=x$, т.е. точки вида $(x,x)$. В этих точках функция $z$ будет принимать такие значения:

$$
z(x,x)=x^4+x^4-2x^2+4xcdot x-2cdot x^2+3=2x^4+3.
$$

Так как в любой окрестности точки $M_1(0;0)$ имеем $2x^4 > 0$, то $2x^4+3 > 3$. Вывод: любая окрестность точки $M_1(0;0)$ содержит точки, в которых $z > 3$, посему точка $M_1(0;0)$ не может быть точкой максимума.

Точка $M_1(0;0)$ не является ни точкой максимума, ни точкой минимума. Вывод: $M_1$ вообще не является точкой экстремума.

Ответ: $(-sqrt{2},sqrt{2})$, $(sqrt{2},-sqrt{2})$ – точки минимума функции $z$. В обеих точках $z_{min}=-5$.

Найти $frac<partial^2z><partial x^2>$, $frac<partial^2z><partial xpartial y>$, $frac<partial^2z><partial y^2>$ и вычислить значение $Delta=frac<partial^2z><partial x^2>cdot frac<partial^2z><partial y^2>-left(frac<partial^2z><partial xpartial y>right)^2$ в каждой стационарной точке. После этого использовать следующую схему:

1. Если $Delta > 0$ и $frac<partial^2z><partial x^2>> 0$ (или $frac<partial^2z><partial y^2>> 0$), то в исследуемая точка есть точкой минимума.
2. Если $Delta > 0$ и $frac<partial^2z><partial x^2>0$, то $frac<partial^2z><partial x^2>cdot frac<partial^2z><partial y^2>-left(frac<partial^2z><partial xpartial y>right)^2 > 0$. А отсюда следует, что $frac<partial^2z><partial x^2>cdot frac<partial^2z><partial y^2>> left(frac<partial^2z><partial xpartial y>right)^2 ≥ 0$. Т.е. $frac<partial^2z><partial x^2>cdot frac<partial^2z><partial y^2>> 0$. Если произведение неких величин больше нуля, то эти величины одного знака. Т.е., например, если $frac<partial^2z><partial x^2>> 0$, то и $frac<partial^2z><partial y^2>> 0$. Короче говоря, если $Delta > 0$ то знаки $frac<partial^2z><partial x^2>$ и $frac<partial^2z><partial y^2>$ совпадают.

Исследовать на экстремум функцию $z=4x^2-6xy-34x+5y^2+42y+7$.

Будем следовать указанному выше алгоритму. Для начала найдём частные производные первого порядка:

Сократим каждое уравнение этой системы на $2$ и перенесём числа в правые части уравнений:

Мы получили систему линейных алгебраических уравнений. Мне в этой ситуации кажется наиболее удобным применение метода Крамера для решения полученной системы.

Значения $x=2$, $y=-3$ – это координаты стационарной точки $(2;-3)$. Теперь приступим ко второму шагу алгоритма. Найдём частные производные второго порядка:

Вычислим значение $Delta$:

Так как $Delta > 0$ и $frac<partial^2 z> <partial x^2>> 0$, то согласно алгоритму точка $(2;-3)$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $(2;-3)$:

$$ z_<min>=z(2;-3)=4cdot 2^2-6cdot 2 cdot (-3)-34cdot 2+5cdot (-3)^2+42cdot (-3)+7=-90. $$

Ответ: $(2;-3)$ – точка минимума; $z_<min>=-90$.

Исследовать на экстремум функцию $z=x^3+3xy^2-15x-12y+1$.

Будем следовать указанному выше алгоритму. Для начала найдём частные производные первого порядка:

Сократим первое уравнение на 3, а второе – на 6.

Если $x=0$, то второе уравнение приведёт нас к противоречию: $0cdot y-2=0$, $-2=0$. Отсюда вывод: $xneq 0$. Тогда из второго уравнения имеем: $xy=2$, $y=frac<2>$. Подставляя $y=frac<2>$ в первое уравнение, будем иметь:

Получили биквадратное уравнение. Делаем замену $t=x^2$ (при этом имеем в виду, что $t > 0$):

Если $t=1$, то $x^2=1$. Отсюда имеем два значения $x$: $x_1=1$, $x_2=-1$. Если $t=4$, то $x^2=4$, т.е. $x_3=2$, $x_4=-2$. Вспоминая, что $y=frac<2>$, получим:

Итак, у нас есть четыре стационарные точки: $M_1(1;2)$, $M_2(-1;-2)$, $M_3(2;1)$, $M_4(-2;-1)$. На этом первый шаг алгоритма закончен.

Теперь приступим ко второму шагу алгоритма. Найдём частные производные второго порядка:

Теперь будем вычислять значение $Delta$ в каждой из найденных ранее стационарных точек. Начнём с точки $M_1(1;2)$. В этой точке имеем:

Так как $Delta(M_1) 0$ и $left.frac<partial^2 z><partial x^2>right|_ > 0$, то согласно алгоритму $M_3(2;1)$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_3$:

$$ z_<min>=z(2;1)=2^3+3cdot 2cdot 1^2-15cdot 2-12cdot 1+1=-27. $$

Осталось исследовать точку $M_4(-2;-1)$. В этой точке получим:

Так как $Delta(M_4) > 0$ и $left.frac<partial^2 z><partial x^2>right|_ 0$ (так как оба сомножителя $36$ и $(2^2-1^2)$ положительны) и можно не находить конкретное значение $Delta$. Правда, для типовых расчётов это замечание бесполезно, – там требуют довести вычисления до числа

Исследовать на экстремум функцию $z=x^4+y^4-2x^2+4xy-2y^2+3$.

Будем следовать алгоритму. Для начала найдём частные производные первого порядка:

Сократим оба уравнения на $4$:

Добавим к второму уравнению первое и выразим $y$ через $x$:

Подставляя $y=-x$ в первое уравнение системы, будем иметь:

Из полученного уравнения имеем: $x=0$ или $x^2-2=0$. Из уравнения $x^2-2=0$ следует, что $x=-sqrt<2>$ или $x=sqrt<2>$. Итак, найдены три значения $x$, а именно: $x_1=0$, $x_2=-sqrt<2>$, $x_3=sqrt<2>$. Так как $y=-x$, то $y_1=-x_1=0$, $y_2=-x_2=sqrt<2>$, $y_3=-x_3=-sqrt<2>$.

Первый шаг решения окончен. Мы получили три стационарные точки: $M_1(0;0)$, $M_2(-sqrt<2>,sqrt<2>)$, $M_3(sqrt<2>,-sqrt<2>)$.

Теперь приступим ко второму шагу алгоритма. Найдём частные производные второго порядка:

Теперь будем вычислять значение $Delta$ в каждой из найденных ранее стационарных точек. Начнём с точки $M_1(0;0)$. В этой точке имеем:

$$Delta(M_1)=16cdot((3cdot 0^2-1)(3cdot 0^2-1)-1)=16cdot 0=0.$$

Так как $Delta(M_1) = 0$, то согласно алгоритму требуется дополнительное исследование, ибо ничего определённого про наличие экстремума в рассматриваемой точке сказать нельзя. Оставим покамест эту точку в покое и перейдём в иным точкам.

Исследуем точку $M_2(-sqrt<2>,sqrt<2>)$. В этой точке получим:

Так как $Delta(M_2) > 0$ и $left.frac<partial^2 z><partial x^2>right|_ > 0$, то согласно алгоритму $M_2(-sqrt<2>,sqrt<2>)$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_2$:

Аналогично предыдущему пункту исследуем точку $M_3(sqrt<2>,-sqrt<2>)$. В этой точке получим:

Так как $Delta(M_3) > 0$ и $left.frac<partial^2 z><partial x^2>right|_ > 0$, то согласно алгоритму $M_3(sqrt<2>,-sqrt<2>)$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_3$:

Настал черёд вернуться к точке $M_1(0;0)$, в которой $Delta(M_1) = 0$. Согласно алгоритму требуется дополнительное исследование. Под этой уклончивой фразой подразумевается «делайте, что хотите» :). Общего способа разрешения таких ситуаций нет, – и это понятно. Если бы такой способ был, то он давно бы вошёл во все учебники. А покамест приходится искать особый подход к каждой точке, в которой $Delta = 0$. Ну что же, поисследуем поведение функции в окрестности точки $M_1(0;0)$. Сразу отметим, что $z(M_1)=z(0;0)=3$. Предположим, что $M_1(0;0)$ – точка минимума. Тогда для любой точки $M$ из некоторой окрестности точки $M_1(0;0)$ получим $z(M) > z(M_1) $, т.е. $z(M) > 3$. А вдруг любая окрестность содержит точки, в которых $z(M) 3$? Тогда в точке $M_1$ точно не будет максимума.

Рассмотрим точки, у которых $y=x$, т.е. точки вида $(x,x)$. В этих точках функция $z$ будет принимать такие значения:

$$ z(x,x)=x^4+x^4-2x^2+4xcdot x-2cdot x^2+3=2x^4+3. $$

Так как в любой окрестности точки $M_1(0;0)$ имеем $2x^4 > 0$, то $2x^4+3 > 3$. Вывод: любая окрестность точки $M_1(0;0)$ содержит точки, в которых $z > 3$, посему точка $M_1(0;0)$ не может быть точкой максимума.

Точка $M_1(0;0)$ не является ни точкой максимума, ни точкой минимума. Вывод: $M_1$ вообще не является точкой экстремума.

Ответ: $(-sqrt<2>,sqrt<2>)$, $(sqrt<2>,-sqrt<2>)$ – точки минимума функции $z$. В обеих точках $z_<min>=-5$.

Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).

Условные экстремумы и функция Лагранжа

В задачах оптимизации возникает необходимость найти экстремумы функции двух и более переменных при условии, что существует связь между переменными этой связи, заданная уравнением . В этом случае говорят, что требуется найти условный экстремум.

Для того чтобы найти условный экстремум требуется находить частные производные и решать системы уравнений Существует алгоритм нахождения условного экстремума из трёх шагов, который сейчас и разберём на примере, и геометрический смысл условного экстремума, который должен дойти до каждого при разборе этого самого примера.

Итак, алгоритм, который разберём на примере самой распространённой задачи — нахождение условного экстремума функции двух переменных..

Шаг 1. Вводится функция Лагранжа

,

где первое слагаемое — сама исходная функция, а второе слагаемое со знаком минус — левая часть уравнения условия связи, умноженная на (лямбда) — множитель Лагранжа.

Пример 1. Найти условные экстремумы функции двух переменных , выражающей площадь прямоугольника через его стороны x и y при условии , означающем, что существует верёвка, которой можно ограничить этот прямоугольник, и длина этой верёвки равна 100.

Шаг 1. Решение. Приведём уравнение условия связи к требуемому виду с нулём в правой части:

.

Составим функцию Лагранжа:

.

Шаг 2. Составляем систему уравнений из равенств частных производных нулю и уравения условия связи (необходимый признак существования условного экстремума):

Решения этой системы уравнений являются точками возможного условного экстремума — стационарными точками или, как ещё говорят, критическими точками.

Решение. Найдём частные производные функции Лагранжа и составим из их равенств нулю и уравнения условия связи систему уравнений:

Из первого и второго уравнений выразим соответственно x и y :

Подставим эти выражения в третье уравнение и найдём значение множителя Лагранжа:

Подставим теперь значение множителя Лагранжа в выражения для x и y и найдём значения переменных исходной функции:

Получили и . Эти значения являются также координатами стационарной точки. Таким образом, получили стационарную точку .

Шаг 3. Пусть является стационарной точкой, найденной на шаге 2. Чтобы определить, является ли условный экстремум минимумом или максимумом, нужно найти второй дифференциал функции Лагранжа

и в полученном выражении подставить вместо «лямбды» её значения (значения множителя Лагранжа), найденные на шаге 2.

Если значение второго дифференциала функции Лагранжа меньше нуля (), то стационарная точка является точкой максимума, если больше нуля (), то стационарная точка является точкой минимума. Если значение второго дифференциала функции Лагранжа равно нулю, то требуются дополнительные исследования, но такие случаи практически не попадаются в задачах, задаваемых студентам.

Координаты стационарных точек подставляются в исходную точку и, таким образом, мы окончательно находим условные экстремумы (или минимум и максимум или что-то одно из этих экстремумом).

Решение. Найдём второй дифференциал функции Лагранжа:

В нашем случае, так как первое и третье составляющие равны нулю, нам не придётся подставлять в них значения множителя Лагранжа. Зато нужно найти отношения между дифференциалами dx и dy :

Так как полученные значения — противоположные по знаку, то получаем, что в любом случае .

Теперь можем найти значение условного экстремума исходной функции, являющееся максимумом:

.

Это заданная исходной функцией максимальная площадь прямоугольника, который можно ограничить верёвкой, длина которой равна 100.

Пример 2. Найти условные экстремумы функции двух переменных при условии .

Шаг 1. Составим функцию Лагранжа:

.

Шаг 2. Найдём частные производные функции Лагранжа и составим из их равенств нулю и уравнения условия связи систему уравнений:

Из первого и второго уравнений выразим соответственно x и y :

Подставим эти выражения в третье уравнение и найдём значения множителя Лагранжа:

Подставим теперь значение множителя Лагранжа в выражения для x и y и найдём значения переменных исходной функции при двух значениях множителя Лагранжа:

Эти значения икса и игрека являются координатами двух стационарных точек. Таким образом, получили стационарные точки .

Шаг 3. Найдём частные производные второго порядка функции Лагранжа:

:

Найдём второй дифференциал функции Лагранжа по формуле

:

.

Установим знак второго дифференциала функции Лагранжа при значении множителя Лагранжа :

Получили значение, меньшее нуля, следовательно, точка — точка условного максимума:

.

Установим знак второго дифференциала функции Лагранжа при значении множителя Лагранжа :

Получили значение, большее нуля, следовательно, точка — точка условного минимума:

.

Таким образом, условные экстремумы заданной функции найдены.

Пример 3. Найти условные экстремумы функции двух переменных при условии .

Шаг 1. Составим функцию Лагранжа:

.

Шаг 2. Найдём частные производные функции Лагранжа и составим из их равенств нулю и уравнения условия связи систему уравнений:

Из первого и второго уравнений выразим соответственно x и y :

Получаем, что , однако подстановка этих значений переменных в третье уравнение системы не даёт верного равенства. Поэтому считаем, что на самом деле второй сомножитель равенства равен нулю: . Отсюда получаем

Ищем координаты стационарных точек при значении множителя Лагранжа . Тогда из выражений для икса и игрека из системы уравнений следует, что . Из третьего уравнения системы получаем:

Получили две стационарные точки:

Ищем координаты стационарных точек при значении множителя Лагранжа . Тогда из выражений для икса и игрека из системы уравнений следует, что .

На основании вычислений двух первых стационарных точек получилаем ещё две стационарные точки:

Шаг 3. Найдём частные производные второго порядка функции Лагранжа:

:

Найдём второй дифференциал функции Лагранжа по формуле

:

.

Установим знак второго дифференциала функции Лагранжа при значении множителя Лагранжа :

Получили значение, меньшее нуля, следовательно, точки — точки условного максимума:

.

Установим знак второго дифференциала функции Лагранжа при значении множителя Лагранжа :

Получили значение, большее нуля, следовательно, точки — точки условного минимума:

.

Таким образом, условные экстремумы заданной функции найдены.

Аналогичным образом можно находить условные экстремумы функций трёх и более переменных.

Как найти стационарные точки системы уравнений

Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!

Контакты

Администратор, решение задач
Роман

Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym

Решение задач
Андрей

facebook:
dniprovets25

Заказать задачи по любым предметам можно здесь от 10 минут

Экстремум функции двух переменных

Как найти?

Постановка задачи

Найти экстремум функции двух переменных $ z = z(x,y) $

План решения

Экстремумы функции двух переменных возможны в стационарных точках функции. Стационарными точками называются точки $ M(x_1,y_1), M(x_2,y_2)… $, в которых первые частные производные функции равны нулю: $ z(x,y) = 0 $

Для нахождения стационарных точек (подозрительных на экстремум) составляем систему:

$$ begin{cases} z’_x = 0 \ z’_y = 0 end{cases} $$

Решая систему получаем точки $ M(x_1,y_1), M(x_2,y_2)… $, каждую из которых нужно проверить на экстремум.

Проверку осуществляется с помощью подстановки точек в выражение, называемое достаточным условием существования экстремума:

$$ A = z»_{xx} cdot z»_{yy} — (z»_{xy})^2 $$

Если в точке $ M(x_1,y_1) $:

1. $ A>0 $ и $ z»_{xx} > 0 $, то $ M(x_1,y_1) $ точка минимума
2. $ A >0 $ и $ z»_{xx} < 0 $, то $ M(x_1,y_1) $ точка максимума
3. $ A < 0 $, то $ M(x_1,y_1) $ не является точкой экстремума
4. $ A = 0 $, то требуется дополнительное исследование (по определению)

Итак, необходимо выполнить действия:

1. Найти частные производные первого порядка. Приравнять их к нулю и решить систему уравнений. Получить точки $ M(x_1,y_1), M(x_2,y_2),… $
2. Найти частные производные второго порядка в точках $ M(x_1,y_1), M(x_2,y_2),… $
3. Используя достаточное условие существования экстремума делаем вывод о наличии экстремума в точках $ M(x_1,y_1), M(x_2,y_2),… $

Примеры решений

Пример 1

Найти экстремумы функции двух переменных $ z = x^2 -xy +y^2 $

Решение

Находим частные производные первого порядка: $$ z’_x = 2x — y $$ $$ z’_y = -x + 2y $$ Приравниваем полученные выражения к нулю и решаем систему двух уравнений: $$ begin{cases} 2x-y = 0 \ -x + 2y = 0 end{cases} $$ Решив систему получаем стационарную точку (подозрительные на экстремум): $$ M (0,0) $$ Далее вычисляем значения частных производных второго порядка в точке $ M $: $$ z»_{xx} Big |_M = 2 $$ $$ z»_{yy} Big |_M= 2 $$ $$ z»_{xy} Big |_M = -1 $$ Подставляя найденные значения в достаточное условие экстремума функции, проводим исследование знаков: $$ A = Big |_M = z»_{xx} Big |_M cdot z»_{yy} Big |_M — (z»_{xy} Big |_M)^2 = 2 cdot 2 — (-1)^2 = 3 $$ Так как получили $ A > 0 $ и $ z»_{xx} > 0 $, то получается $ M(0,0) $ точка минимума. Наименьшее значение находится в минимуме и равно: $$ z_{min} (0,0) = 0^2 — 0 cdot 0 + 0^2 = 0 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

В точке $ M(0,0) $ находится минимум функции; $ z_{min} = 0 $

Пример 2

Найти экстремумы функции двух переменных $ z = x^3 + y^3 — 15xy $

Решение

Составляем систему уравнений из частных производных первого порядка: $$ begin{cases} z’_x = 3x^2 — 15y = 0 \ z’_y = 3y^2 — 15x =0 end{cases} $$ Получаем стационарные точки $ M_1(0,0) $ и $ M_2(5,5) $, которые необходимо проверить через достаточное условие экстремума. Вычисляем значение частных прозводных второго порядка в точке $ M_1 $: $$ z»_{xx} Big |_{M_1} = 6x Big |_{M_1} = 0 $$ $$ z»_{yy} Big |_{M_1} = 6y Big |_{M_2} = 6y Big |_{M_2} = 0 $$ $$ z»_{xy} Big |_{M_1} = -15 $$ Подставляем данные значения в формулу достаточного условия экстремума: $$ A Big |_{M_1} = 0 cdot 0 — (-15)^2 = -225 $$ Так как $ A < 0 $, то в точке $ M_1(0,0) $ экстремума нет. Получаем значения частных производных 2 порядка в $ M_2 $: $$ z»_{xx} Big |_{M_2} = 6x Big |_{M_2} = 6 cdot 5 = 30 $$ $$ z»_{yy} Big |_{M_2} = 6y Big |_{M_2} = 6 cdot 5 = 30 $$ $$ z»_{xy} Big |_{M_2} = -15 $$ Вычисляем значение выражения достаточного условия экстремума: $$ A = 30 cdot 30 — (-15)^2 = 900 — 225 = 675 $$ Получили $ A > 0 $ и $ z»_{xx} > 0 $, то значит, $ M_2(5,5) $ точка минимума. Наименьшее значение функции $ z = x^3 + y^3 — 15xy $ равно: $$ z_{min} |_{M_2} = 5^3 + 5^3 — 15 cdot 5 cdot 5 = 125 + 125 — 375 = -125 $$

Ответ

В $ M_1 (0,0) $ экстремума нет, в $ M_2(5,5) $ минимум функции $ z_{min}=-125 $