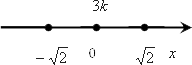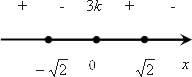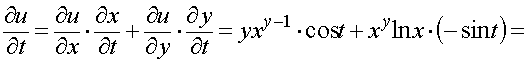12. Исследование функций с помощью производной
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Поиск точек экстремума у сложных функций
(blacktriangleright) Сложная функция (композиция двух функций) — это функция (f=f(x)), представимая в виде (f=f(t(x))), где (t=t(x)) – функция, являющаяся “новой переменной” для функции (f).
То есть в такой функции можно ввести новую переменную (t) так, что функция полностью будет зависеть от этой новой переменной.
(blacktriangleright) Производная такой функции ищется по правилу: [{Large{f'(x)=f'(t)cdot t'(x)}}]
Примеры:
(1)) Функция (f(x)=cos {(x^2+1)}). Если сделать замену (t(x)=x^2+1), то функция примет вид (f(t)=cos t).
Найдем (f'(t)=(cos t)’=-sin t=(text{переход к переменной
}x)=-sin
{(x^2+1)})
Найдем (t'(x)=(x^2+1)’=2x)
Значит, (f'(x)=-2xcdot sin{(x^2+1)})
(2)) Функция (f(x)=x^3 +x^2). Для этой функции не существует никакой замены, кроме тождественной ((t(x)=x)). Значит она – не сложная.
Ее производную можно найти обычным способом, т.к. она элементарная:
(f'(x)=3x^2+2x)
(3)) Функция (f(x)=sin x^2 + x). Для этой функции не существует никакой замены, кроме тождественной ((t(x)=x)).
Но обычными способами вычислить ее производную не удастся. Заметим, что эта функция представлена в виде суммы двух, причем одна из них сложная ((g(x)=sin x^2)), а другая – элементарная ((h(x)=x)).
Т.к. мы знаем, что (f’=g’+h’), то найдем в отдельности производные функций (g) и (h).
Тогда (f'(x)=2xcdot cos x^2 + 1)
(blacktriangleright) Для того, чтобы найти точки экстремума, необходимо схематично изобразить график функции.
В задачах из данной подтемы это можно сделать с помощью производной: найти промежутки возрастания ((f’>0)) и убывания ((f'<0)) функции, критические точки (где (f’=0) или (f’) не существует).
[begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{1} & c & 0\&&\
textbf{2} & x^a & acdot x^{a-1}\&&\
textbf{3} & ln x & dfrac1x\&&\
textbf{4} & log_ax & dfrac1{xcdot ln a}\&&\
textbf{5} & e^x & e^x\&&\
textbf{6} & a^x & a^xcdot ln a\&&\
textbf{7} & sin x & cos x\&&\
textbf{8} & cos x & -sin x\[1ex]
hline
end{array} quad quad quad quad
begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{9} & mathrm{tg}, x & dfrac1{cos^2 x}\&&\
textbf{10} & mathrm{ctg}, x & -,dfrac1{sin^2 x}\&&\
textbf{11} & arcsin x & dfrac1{sqrt{1-x^2}}\&&\
textbf{12} & arccos x & -,dfrac1{sqrt{1-x^2}}\&&\
textbf{13} & mathrm{arctg}, x & dfrac1{1+x^2}\&&\
textbf{14} & mathrm{arcctg}, x & -,dfrac1{1+x^2}\[0.5ex]
hline
end{array}]
Задание
1
#2363
Уровень задания: Равен ЕГЭ
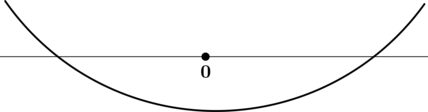
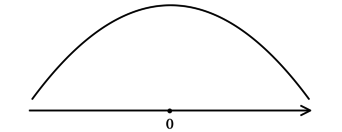
Найдите точку минимума функции (y = e^{x^2 + 1}).
ОДЗ: (x) – произвольный.
1) [y’ = e^{x^2 + 1}cdot 2x = 2xe^{x^2 + 1}]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [2xe^{x^2 + 1} = 0qquadLeftrightarrowqquad x = 0,.] Производная существует при любом (x).
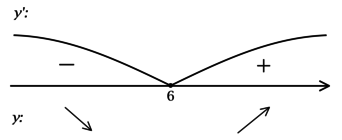
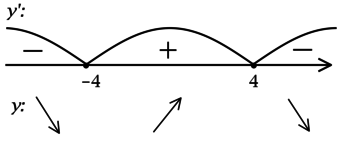
2) Найдём промежутки знакопостоянства (y’):
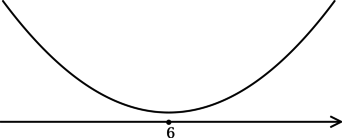
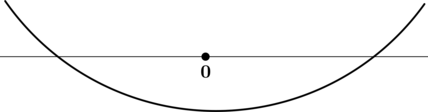
3) Эскиз графика:
Таким образом, (x = 0) – точка минимума функции (y).
Ответ: 0
Задание
2
#2364
Уровень задания: Равен ЕГЭ
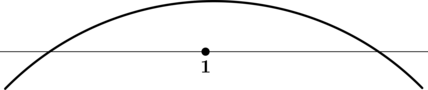
Найдите точку максимума функции (y = e^{-x^2 + 2x}).
ОДЗ: (x) – произвольный.
1) [y’ = e^{-x^2 + 2x}cdot (-2x + 2) = -2(x — 1)e^{-x^2 + 2x}]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [-2(x — 1)e^{-x^2 + 2x} = 0qquadLeftrightarrowqquad x = 1,.] Производная существует при любом (x).
2) Найдём промежутки знакопостоянства (y’):
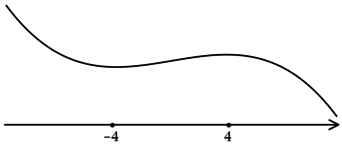
3) Эскиз графика:
Таким образом, (x = 1) – точка максимума функции (y).
Ответ: 1
Задание
3
#887
Уровень задания: Равен ЕГЭ
Найдите точку минимума функции
(y = e^{x^2 — 2016x + 2017}).
1) [y’ = e^{x^2 — 2016x + 2017}cdot(2x — 2016).]
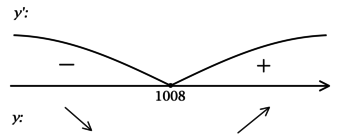
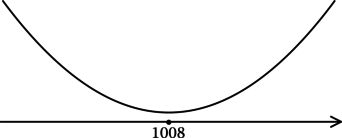
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [e^{x^2 — 2016x + 2017}cdot(2x — 2016) = 0qquadLeftrightarrowqquad x — 2016 = 0] (так как (e^t > 0) при любом (t)), откуда находим (x = 1008). Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.
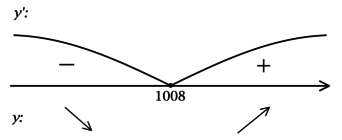
2) Найдём промежутки знакопостоянства (y’):
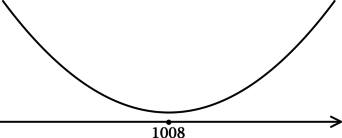
3) Эскиз графика (y):
Таким образом, (x = 1008) – точка минимума функции (y).
Ответ: 1008
Задание
4
#885
Уровень задания: Равен ЕГЭ
Найдите точку минимума функции
(y = log_{7}(x^2 + 16x + 100)).
ОДЗ: (x^2 + 16x + 100 > 0). Решим на ОДЗ:
1) [y’ = dfrac{1}{ln 7}cdotdfrac{2x + 16}{x^2 + 16x + 100}.]
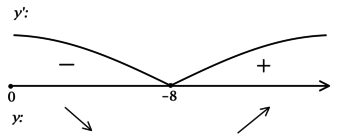
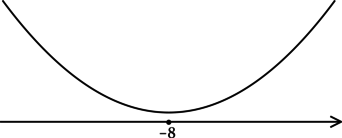
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [dfrac{1}{ln 7}cdotdfrac{2x + 16}{x^2 + 16x + 100} = 0qquadLeftrightarrowqquad 2x + 16 = 0] – на ОДЗ, откуда находим (x = -8). Так как (x^2 + 16x + 100 = x^2 + 16x + 64 + 36 = (x+8)^2 + 36 > 0), то производная определена для любого (x). Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.
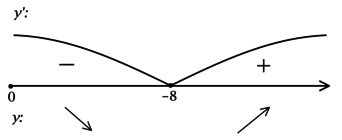
2) Найдём промежутки знакопостоянства (y’):
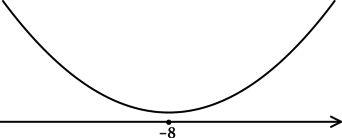
3) Эскиз графика (y):
Таким образом, (x = -8) – точка минимума функции (y).
Ответ: -8
Задание
5
#886
Уровень задания: Равен ЕГЭ
Найдите точку минимума функции
(y = log_{2016}(x^2 — 10x + 201)).
ОДЗ: (x^2 — 10x + 201 > 0). Решим на ОДЗ:
1) [y’ = dfrac{1}{ln 2016}cdotdfrac{2x — 10}{x^2 — 10x + 201}.]
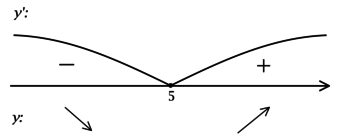
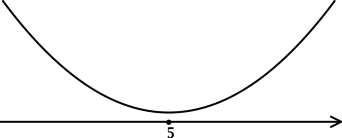
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [dfrac{1}{ln 2016}cdotdfrac{2x — 10}{x^2 — 10x + 201} = 0qquadLeftrightarrowqquad 2x — 10 = 0] – на ОДЗ, откуда находим (x = 5). Так как (x^2 — 10x + 201 = x^2 — 10x + 25 + 176 = (x-5)^2 + 176 > 0), то производная определена для любого (x). Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.
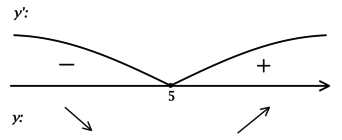
2) Найдём промежутки знакопостоянства (y’):
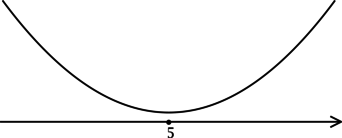
3) Эскиз графика (y):
Таким образом, (x = 5) – точка минимума функции (y).
Ответ: 5
Задание
6
#888
Уровень задания: Равен ЕГЭ
Найдите точку минимума функции
(y = sqrt{x^2 — 12x + 40}).
ОДЗ: (x^2 — 12x + 40 geq 0). Решим на ОДЗ:
1) [y’ = dfrac{2x — 12}{2sqrt{x^2 — 12x + 40}} = dfrac{x — 6}{sqrt{x^2 — 12x + 40}}.]
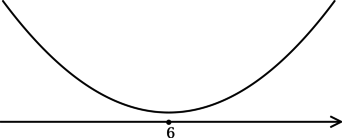
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [dfrac{x — 6}{sqrt{x^2 — 12x + 40}} = 0qquadLeftrightarrowqquad x — 6 = 0] – на ОДЗ, откуда находим (x = 6). Так как (x^2 — 12x + 40 = x^2 — 12x + 36 + 4 = (x-6)^2 + 4 > 0), то производная функции (y) определена при любом (x). Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.
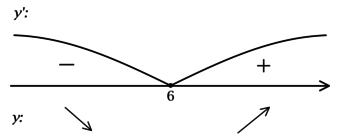
2) Найдём промежутки знакопостоянства (y’):
3) Эскиз графика (y):
Таким образом, (x = 6) – точка минимума функции (y).
Ответ: 6
Задание
7
#889
Уровень задания: Равен ЕГЭ
Найдите точку максимума функции
(y = sqrt{-x^2 + 2 — 6x}).
ОДЗ: (-x^2 + 2 — 6x geq 0), что равносильно (x^2 + 6x — 2leq 0), откуда находим (-3-sqrt{11} leq x leq -3 + sqrt{11}). Решим на ОДЗ:
1) [y’ = dfrac{-2x — 6}{2sqrt{-x^2 + 2 — 6x}} = -dfrac{x + 3}{sqrt{-x^2 + 2 — 6x}}.]
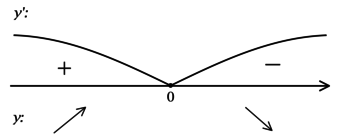
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [y’ = 0qquadLeftrightarrowqquad -dfrac{x + 3}{sqrt{-x^2 + 2 — 6x}} = 0qquadLeftrightarrowqquad x + 3 = 0] – на ОДЗ, откуда находим (x = -3). Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.
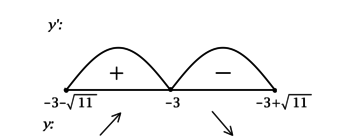
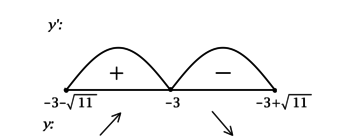
2) Найдём промежутки знакопостоянства (y’) на ОДЗ:
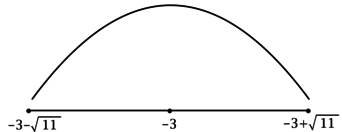
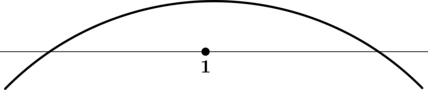
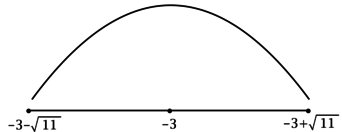
3) Эскиз графика (y):
Таким образом, (x = -3) – точка максимума функции (y).
Ответ: -3

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
1 марта 2014
Сегодня мы изучим еще более сложную задачу на поиск точек экстремума из ЕГЭ по математике. Взгляните:
Найдите произведение всех точек максимума функции:
[y={{x}^{4}}{{e}^{-{{x}^{2}}}}]
Общая схема нахождения точки максимума и минимума
Сразу хочу обратить ваше внимание: в степени стоит именно $-{{x}^{2}}$, не линейная функция, а именно квадратичная. И, следовательно, для решения этой задачи нам придется привлекать производную сложной функции. Но прежде чем мы начнем решать эту задачу, хотелось бы вспомнить общий алгоритм. Напомню, что для нахождения экстремума нам потребуется выполнить четыре последовательных шага:
- Первый шаг самый простой и самый очевидный: найти[{y}’].
- Вторым делом мы приравниваем ${y}’$ к нулю и находим корни уравнения. При этом на практике крайне редко встречается, когда ответов будет больше двух, максимум трех —[{y}’=0;{{x}_{1}},{{x}_{2}}…]
- Третий шаг — мы чертим координатную ось $x$ и отмечаем на не все наши полученные значения. Обратите внимание: эти корни отмечаются закрашенными точками. Кроме того, нужно отметить такие значения, в которых ${y}’$ не существует. Они отмечаются выколотыми, и в дальнейшем решении задачи не участвуют, но влияют на знак. После того как мы отметим все нули производной и значения, в которой она не существует, необходимо отметить знаки производной на каждом из получившемся интервалов. Разумеется, особо большого выбора здесь не дано: будет либо «плюс», либо «минус», т. е. ${y}’$ между своими нулями либо положительная, либо отрицательная:
- Четвертый шаг: на основании полученной картинки мы выписываем точки максимума и минимума. Напомню, что если в каком-то корне ${y}’$ меняет свой знак с плюса на минус, то это означает, что это значение является точкой максимума. А если в заданной точке минус переходит в плюс, то данное значение является точкой минимума. При этом помните, что считывание знаков всегда идет слева направо, т. е. в направлении, совпадающим с положительным направлением оси х.
Решение задачи B15 — вычисление точек максимума
Хватит теории, давайте решим нашу задачу. В первую очередь заметим, что перед нами произведение двух функций, следовательно, для решения задачи потребуется вспомнить формулу производной произведения, а именно:
[{{left( fcdot g right)}^{prime }}={f}’cdot g+fcdot {g}’]
Шаг 1: Вычисление производной сложной функции
Давайте воспользуемся этой формулой для нахождения производной сложной функции:
[{y}’={{left( {{x}^{4}}cdot {{e}^{-{{x}^{2}}}} right)}^{prime }}={{left( {{x}^{4}} right)}^{prime }}cdot {{e}^{-{{x}^{2}}}}+{{x}^{4}}…]
При вычислении у нас может возникнуть заминка, поэтому давайте выпишем сложную функцию отдельно. Перед нами производная сложной функции, следовательно, чтобы найти ее, необходимо ввести новую переменную:
[-{{x}^{2}}=t]
Получим:
[{{left( {{e}^{-{{x}^{2}}}} right)}^{prime }}={{left( {{e}^{t}} right)}^{prime }}cdot {t}’]
Это и есть формула производной сложной функции. Другими словами, если мы вводим новую переменную, то в дальнейшем мы обязаны умножить на производную этой переменной, чтобы получить производную исходной функции. Давайтепосчитаем:
[{{left( {{e}^{-{{x}^{2}}}} right)}^{prime }}={{left( {{e}^{t}} right)}^{prime }}cdot {t}’={{e}^{-{{x}^{2}}}}cdot {{left( -{{x}^{2}} right)}^{prime }}={{e}^{-{{x}^{2}}}}cdot text{ }left( -2x right)]
Производная сложной функции найдена. Возвращаемся к нашей исходной функции и дописываем:
[{y}’={{left( {{x}^{4}}cdot {{e}^{-{{x}^{2}}}} right)}^{prime }}={{left( {{x}^{4}} right)}^{prime }}cdot {{e}^{-{{x}^{2}}}}+{{x}^{4}}cdot {{e}^{-{{x}^{2}}}}cdot left( -2x right)=]
[={{x}^{3}}cdot {{e}^{-{{x}^{2}}}}left( 4cdot 1cdot 1+xcdot 1cdot left( -2x right) right)={{x}^{3}}cdot {{e}^{-{{x}^{2}}}}left( 4-2{{x}^{2}} right)=]
[=2{{x}^{3}}cdot {{e}^{-{{x}^{2}}}}left( 2-{{x}^{2}} right)]
Шаг 2: Приравниваем производную к нулю
Переходим ко второму шагу и приравниваем ее к нулю. Решаем полученное уравнение:
[2{{x}^{3}}cdot {{e}^{-{{x}^{2}}}}left( 2-{{x}^{2}} right)=0]
Произведение равно 0, когда хотя бы один из множителей равен 0. Очевидно, что 2 никогда не равна 0, поэтому остаются следующие варианты:
[left[ begin{align}& {{x}^{3}}=0, \& {{e}^{-{{x}^{2}}}}=0, \& 2-{{x}^{2}}=0. \end{align} right.=>left[ begin{align}& x=0, \& varnothing , \& {{x}^{2}}=2. \end{align} right.=>left[ begin{align}& x=0, \& x=sqrt{2}, \& x=-sqrt{2}. \end{align} right.]
Шаг 3: Отмечаем корни и находим знаки производной
Итого у нас три корня, причем первый из них имеет третью кратность.
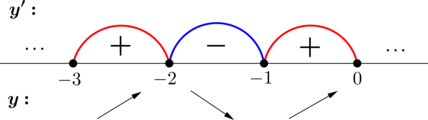
Переходим к третьему шагу и отмечаем все три значения на координатной оси:
Осталось разобраться со знаками. Давайте возьмем какое-нибудь большое число, например, 1000, и подставим наше число в ${y}’$:
[2{{x}^{3}}cdot {{e}^{-{{x}^{2}}}}left( 2-{{x}^{2}} right)]
итоге первое число будет отрицательным, т. е. будет стоять «минус». Затем,[sqrt{2}]является корнем первой кратности, следовательно, при переходе через него знак поменяется. Знак также поменяется при переходе через 0, потому что 0 является корнем третьей кратности, а 3 — это число нечетное. Напоминаю, что при переходе через корень нечетной кратности знак меняется, а при переходе через корень четной кратности — 2, 8 и т. д. знак остается прежним. В нашем случае все меняется. И при переходе через корень[-sqrt{2}]знак также меняется:
Шаг 4: Нахождение точек максимума функции
Прекрасно, мы отметили все корни, переходим с условию задачи: от нас требуется найти произведение всех точек максимума, т. е. такие значения, которые согласно нашему четвертому шагу стоят на границе между «плюсом» и «минусом». Таких у нас будет две:[sqrt{2}]и[-sqrt{2}].
А теперь возвращаемся к условию задачи и смотрим: от нас требуется найти их произведение. Запишем:
[-sqrt{2}text{ }!!cdot!!text{ }sqrt{text{2}}=-2]
Ответ к задаче будет -2.
Замечание о производной сложной функции
Основная проблема, с которой столкнется большинство учеников — это производная сложной функции. К сожалению, в школе недостаточно уделяют внимание как производным вообще, так и сложным производным в частности. В результате многие ученики не то, что производную сложной функции не могут вспомнить, они даже не подозревают о существовании формулы производной произведения. Очень часто я наблюдаю такую ситуацию: человек хочет сосчитать производную произведения, и считает ее следующим образом:
[{{left( {{x}^{4}} right)}^{prime }}cdot {{left( {{e}^{-{{x}^{2}}}} right)}^{prime }}]
Другими словами, многие ученики искренне считают, что производная произведения равна произведению производных. Это неправильно, ни в коем случае нельзя так считать, а правильно считать нужно с помощью специальной формулы:
[{{left( fcdot g right)}^{prime }}={f}’cdot g+fcdot {g}’]
Надеюсь, этот урок поможет тем, кто готовится к ЕГЭ по математике. Смотрите другие видеоуроки, решайте задачи — и никакие экзамены вам будут не страшны!
Смотрите также:
- Задача B15: что делать с квадратичной функцией
- Специфика работы с логарифмами в задаче B15
- Десятичные дроби
- Тест: простейшие показательные уравнения (1 вариант)
- Как решать задачи про летающие камни?
- B4: счетчики на электричество
Теорема. Пусть u
= f (х, у) задана
в области D и пусть х = х(t
) и у = у(t
) определены
в области , причём,
когда , то
х и у принадлежат области D . Пусть
функция u дифференцируема в точке
M0 (x0, y0, z0),
а функции х(t
) и
у(t
) дифференцируемы
в соответствующей точке t0,
то сложная функция u =
f [x(t), y(t)]=F (t) дифференцируема
в точке t0 и
имеет место равенство:

Доказательство. Так
как u дифференцируема по условию в точке
(x0, y0),
то её полное приращение представляется
в виде

Разделив
это соотношение на ,
получим:

Перейдём
к пределу при и
получим формулу

Замечание
1. Если u = u(x, y)
и x = x, y = y(x),
то полная производная функции u по
переменной х
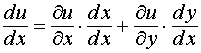

Последнее
равенство можно использовать для
доказательства правила дифференцирования
функции одной переменной, заданной
неявно в виде F(x, y) = 0,
где y = y(x)
(см. тему № 3 и пример
14).
Имеем: 
Отсюда 
(6.1)
Вернёмся
к примеру
14 темы
№ 3:




Как
видим, ответы совпали.
Замечание
2. Пусть u = f (х, у),
где х = х(t , v), у = у(t , v).
Тогда u есть в конечном счёте сложная
функция двух переменных t и v .
Если теперь функция u дифференцируема
в точке M0 (x0, y0),
а функции х и у дифференцируемы
в соответствующей точке (t0, v0),
то можно говорить о частных производных
по t и v от
сложной функции в точке (t0, v0).
Но если мы говорим о частной производной
по t в указанной точке, то вторая
переменная v считается постоянной и
равной v0.
Следовательно, речь идёт о производной
только от сложной функции по t и,
следовательно, мы можем воспользоваться
выведенной формулой. Таким образом,
получим:
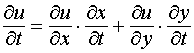

Пример 13. Найти
полную производную функции u = x y, где x
= sin t, y
= cos t .
.
41. Экстремумы функции нескольких переменных.
Экстремум
функции нескольких переменных. Необходимые
и достаточные условия существования
экстремума
Определение
7. Точка называется точкой минимума
(максимума) функции , если существует
такая окрестность точки , что для всех
точек из этой окрестности выполняется
неравенство , ().
Точки
минимума и максимума функции называются
точками экстремума, а значения функции
в этих точках — экстремумами функции
(минимумом и максимумом соответственно).
Заметим,
что минимум и максимум функции имеют
локальный характер, так как значение
функции в точке сравнивается с ее
значениями в точках, достаточно близких
к .
Теорема
1 (необходимые условия экстремума). Если
— точка экстремума дифференцируемой
функции , то ее частные производные и в
этой точке равны нулю: .
Точки,
в которых частные производные первого
порядка равны нулю, называются критическими
или стационарными. В критических точках
функция может иметь экстремум, а может
и не иметь.
Теорема
2 (достаточное условие экстремума). Пусть
функция : а) определена в некоторой
окрестности критической точки , в которой
и ; б) имеет непрерывные частные производные
второго порядка . Тогда, если , то функция
в точке имеет экстремум: максимум, если
А<0; минимум, если А>0; если , то функция
в точке экстремума не имеет. В случае
вопрос о наличии экстремума остается
открытым.
При
исследовании функции двух переменных
на экстремум рекомендуется использовать
следующую схему:
1.
Найти частные производные первого
порядка: и .
2.
Решить систему уравнений и найти
критические точки функции.
3.
Найти частные производные второго
порядка: , , .
4.
Вычислить значения частных производных
второго порядка в каждой критической
точке и, используя достаточные условия,
сделать вывод о наличии экстремума.
5.
Найти экстремумы функции.
Пример
6. Найти экстремумы функции .
Решение.
1. Находим частные производные и :
2.
Для определения критических точек
решаем систему уравнений
или
Из
первого уравнения системы находим: .
Подставляя найденное значение y во
второе уравнение, получим
откуда
Находим
значения y, соответствующие значениям
. Подставляя значения в уравнение ,
получим: .
Таким
образом, имеем две критические точки:
и .
3.
Находим частные производные второго
порядка:
4.
Вычисляем значения частных производных
второго порядка в каждой критической
точке. Для точки имеем:
,
, .
Так
как
,
то
в точке экстремума нет.
В
точке :
,
,
и,
следовательно,
.
Значит,
в силу достаточного условия экстремума,
в точке функция имеет минимум, так как
в этой точке и .
5.
Находим значение функции в точке :
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Тема 11.
Исследование функций с помощью производной
11
.
02
Поиск точек экстремума у сложных функций
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
исследование функций с помощью производной
Решаем задачи
Найдите точку минимума функции .
Показать ответ и решение
ОДЗ: – произвольный.
1)
Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна или не существует):
Производная существует при любом .
2) Найдём промежутки знакопостоянства :
3) Эскиз графика:
Таким образом, – точка минимума функции
.
Найдите точку максимума функции .
Показать ответ и решение
ОДЗ: – произвольный.
1)
Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна или не существует):
Производная существует при любом .
2) Найдём промежутки знакопостоянства :
3) Эскиз графика:
Таким образом, – точка максимума функции
.
Найдите точку максимума функции
Показать ответ и решение
1 способ.
Заметим, что
Следовательно, . Так как
, то
.
Заметим, что при функция
является возрастающей, так как при увеличении
значение
также растет. А при
функция является убывающей. Следовательно,
– точка
максимума.
2 способ.
Найдем производную функции.
Найдем нули производной:
Заметим, что подходит по ОДЗ (
). Найдем знаки производной справа и
слева от точки :
Таким образом, по определению точка является точкой максимума.
Найдите точку максимума функции
Показать ответ и решение
Найдем ОДЗ: что равносильно
откуда находим
1) Найдем производную:
Найдём критические точки, то есть внутренние точки области определения функции, в которых её производная равна 0 или не
существует:
— на ОДЗ, откуда находим Для того, чтобы найти точки локального максимума/минимума функции, нужно понять,
как схематично выглядит её график.
2) Найдём промежутки знакопостоянства на ОДЗ:
3) Эскиз графика
Таким образом, — точка максимума функции
Найдите точку минимума функции
Показать ответ и решение
Выпишем ОДЗ:
1) Найдем производную:
Найдём критические точки, то есть внутренние точки области определения функции, в которых её производная равна 0 или не
существует:
— на ОДЗ, откуда находим Так как
то производная функции
определена при любом Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично
выглядит её график.
2) Найдём промежутки знакопостоянства
3) Эскиз графика
Таким образом, — точка минимума функции
Найдите точку минимума функции
Найдите точку минимума функции
Показать ответ и решение
Найдем производную заданной функции:
Легко видеть, что первый множитель определен и не равен нулю при любом
Второй множитель зануляется при
Применим метод интервалов для определения знаков производной.
Критическая точка встречается ровно один раз, следовательно, в ней знак будет
меняться.
Теперь можем нарисовать эскиз графика. На промежутке
производная функции отрицательна, то есть исходная функция будет
убывать. На промежутке производная положительна, то есть исходная
функция будет возрастать.
По эскизу видно, что точка является точкой минимума, так
как в ней производная меняет знак с «» на «
» при проходе слева
направо.
Найдите точку минимума функции
Показать ответ и решение
Выпишем ОДЗ:
1) Найдем производную:
Найдём критические точки, то есть внутренние точки области определения функции, в которых её производная равна 0 или не
существует:
— на ОДЗ, откуда находим Так как
то производная
определена для любого Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично
выглядит её график.
2) Найдём промежутки знакопостоянства
3) Эскиз графика
Таким образом, — точка минимума функции
Найдите точку минимума функции
.
Показать ответ и решение
1)
Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна или не существует):
(так как при любом
), откуда находим
. Для того, чтобы найти точки
локального максимума/минимума функции, нужно понять, как схематично выглядит её
график.
2) Найдём промежутки знакопостоянства :
3) Эскиз графика :
Таким образом, – точка минимума функции
.
Найдите точку минимума функции
Показать ответ и решение
Выпишем ОДЗ:
1) Найдем производную:
Найдём критические точки, то есть внутренние точки области определения функции, в которых её производная равна 0 или не
существует:
— на ОДЗ, откуда находим Так как
то производная определена
для любого Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит
её график.
2) Найдём промежутки знакопостоянства
3) Эскиз графика
Таким образом, — точка минимума функции
Найдите точку максимума функции
.
Показать ответ и решение
1)
Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна или не существует):
(так
как при любом
), откуда находим
. Для того, чтобы найти точки локального
максимума/минимума функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства на ОДЗ:
3) Эскиз графика :
Таким образом, – точка максимума функции
.
Найдите точку локального максимума функции
.
Показать ответ и решение
1)
Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна или не существует):
(так как при любом
), откуда находим
. Для того, чтобы найти точки
локального максимума/минимума функции, нужно понять, как схематично выглядит её
график.
2) Найдём промежутки знакопостоянства :
3) Эскиз графика :
Таким образом, – точка локального максимума функции
.
Найдите точку локального максимума функции , лежащую на отрезке
.
Показать ответ и решение
ОДЗ: – произвольный.
1)
Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна или не существует):
Второе уравнение последней совокупности не имеет решений ни при каких , следовательно,
производная равна только при
. Производная существует при любом
.
2) Найдём промежутки знакопостоянства (здесь бесконечно много промежутков, знаки
производной в которых чередуются):
3) Найдём промежутки знакопостоянства на
:
Таким образом, – точка локального максимума функции
на отрезке
.
Найдите точку локального максимума функции .
Показать ответ и решение
ОДЗ: .
1)
– на
ОДЗ.
Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна или не существует):
Производная не существует при , но эти точки не являются внутренними для
области определения.
2) Найдём промежутки знакопостоянства :
3) Эскиз графика :
Таким образом, – точка локального максимума функции
.
Экстремум функции двух переменных. Примеры исследования функций на экстремум.
Пусть функция $z=f(x,y)$ определена в некоторой окрестности точки $(x_0,y_0)$. Говорят, что $(x_0,y_0)$ – точка (локального) максимума, если для всех точек $(x,y)$ некоторой окрестности точки $(x_0,y_0)$ выполнено неравенство $f(x,y)< f(x_0,y_0)$. Если же для всех точек этой окрестности выполнено условие $f(x,y)> f(x_0,y_0)$, то точку $(x_0,y_0)$ называют точкой (локального) минимума.
Точки максимума и минимума часто называют общим термином – точки экстремума.
Если $(x_0,y_0)$ – точка максимума, то значение функции $f(x_0,y_0)$ в этой точке называют максимумом функции $z=f(x,y)$. Соответственно, значение функции в точке минимума именуют минимумом функции $z=f(x,y)$. Минимумы и максимумы функции объединяют общим термином – экстремумы функции.
Алгоритм исследования функции $z=f(x,y)$ на экстремум
- Найти частные производные $frac{partial z}{partial x}$ и $frac{partial z}{partial y}$. Составить и решить систему уравнений $
left { begin{aligned}
& frac{partial z}{partial x}=0;\
& frac{partial z}{partial y}=0.
end{aligned} right.$. Точки, координаты которых удовлетворяют указанной системе, называют стационарными. - Найти $frac{partial^2z}{partial x^2}$, $frac{partial^2z}{partial xpartial y}$, $frac{partial^2z}{partial y^2}$ и вычислить значение $Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2$ в каждой стационарной точке. После этого использовать следующую схему:
- Если $Delta > 0$ и $frac{partial^2z}{partial x^2} > 0$ (или $frac{partial^2z}{partial y^2} > 0$), то в исследуемая точка есть точкой минимума.
- Если $Delta > 0$ и $frac{partial^2z}{partial x^2} < 0$ (или $frac{partial^2z}{partial y^2} < 0$), то в исследуемая точка есть точкой максимума.
- Если $Delta < 0$, то в расматриваемой стационарной точке экстремума нет.
- Если $Delta = 0$, то ничего определённого про наличие экстремума сказать нельзя; требуется дополнительное исследование.
Примечание (желательное для более полного понимания текста): показатьскрыть
Пример №1
Исследовать на экстремум функцию $z=4x^2-6xy-34x+5y^2+42y+7$.
Решение
Будем следовать указанному выше алгоритму. Для начала найдём частные производные первого порядка:
$$
frac{partial z}{partial x}=8x-6y-34; frac{partial z}{partial y}=-6x+10y+42.
$$
Составим систему уравнений $ left { begin{aligned}
& frac{partial z}{partial x}=0;\
& frac{partial z}{partial y}=0.
end{aligned} right.$:
$$
left { begin{aligned}
& 8x-6y-34=0;\
& -6x+10y+42=0.
end{aligned} right.
$$
Сократим каждое уравнение этой системы на $2$ и перенесём числа в правые части уравнений:
$$
left { begin{aligned}
& 4x-3y=17;\
& -3x+5y=-21.
end{aligned} right.
$$
Мы получили систему линейных алгебраических уравнений. Мне в этой ситуации кажется наиболее удобным применение метода Крамера для решения полученной системы.
$$ begin{aligned}
& Delta=left| begin{array} {cc} 4 & -3\ -3 & 5 end{array}right|=4cdot 5-(-3)cdot (-3)=20-9=11;\
& Delta_x=left| begin{array} {cc} 17 & -3\ -21 & 5 end{array}right|=17cdot 5-(-3)cdot (-21)=85-63=22;\
& Delta_y=left| begin{array} {cc} 4 & 17\ -3 & -21 end{array}right|=4cdot (-21)-17cdot (-3)=-84+51=-33.end{aligned} \
x=frac{Delta_{x}}{Delta}=frac{22}{11}=2; ; y=frac{Delta_{y}}{Delta}=frac{-33}{11}=-3.
$$
Значения $x=2$, $y=-3$ – это координаты стационарной точки $(2;-3)$. Теперь приступим ко второму шагу алгоритма. Найдём частные производные второго порядка:
$$
frac{partial^2 z}{partial x^2}=8; frac{partial^2 z}{partial y^2}=10; frac{partial^2 z}{partial x partial y}=-6.
$$
Вычислим значение $Delta$:
$$
Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2=
8cdot 10-(-6)^2=80-36=44.
$$
Так как $Delta > 0$ и $frac{partial^2 z}{partial x^2} > 0$, то согласно алгоритму точка $(2;-3)$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $(2;-3)$:
$$
z_{min}=z(2;-3)=4cdot 2^2-6cdot 2 cdot (-3)-34cdot 2+5cdot (-3)^2+42cdot (-3)+7=-90.
$$
Ответ: $(2;-3)$ – точка минимума; $z_{min}=-90$.
Пример №2
Исследовать на экстремум функцию $z=x^3+3xy^2-15x-12y+1$.
Решение
Будем следовать указанному выше алгоритму. Для начала найдём частные производные первого порядка:
$$
frac{partial z}{partial x}=3x^2+3y^2-15; frac{partial z}{partial y}=6xy-12.
$$
Составим систему уравнений $ left { begin{aligned}
& frac{partial z}{partial x}=0;\
& frac{partial z}{partial y}=0.
end{aligned} right.$:
$$
left { begin{aligned}
& 3x^2+3y^2-15=0;\
& 6xy-12=0.
end{aligned} right.
$$
Сократим первое уравнение на 3, а второе – на 6.
$$
left { begin{aligned}
& x^2+y^2-5=0;\
& xy-2=0.
end{aligned} right.
$$
Если $x=0$, то второе уравнение приведёт нас к противоречию: $0cdot y-2=0$, $-2=0$. Отсюда вывод: $xneq 0$. Тогда из второго уравнения имеем: $xy=2$, $y=frac{2}{x}$. Подставляя $y=frac{2}{x}$ в первое уравнение, будем иметь:
$$
x^2+left(frac{2}{x} right)^2-5=0;\
x^2+frac{4}{x^2}-5=0;\
x^4-5x^2+4=0.
$$
Получили биквадратное уравнение. Делаем замену $t=x^2$ (при этом имеем в виду, что $t > 0$):
$$
t^2-5t+4=0;\
begin{aligned}
& D=(-5)^2-4cdot 1 cdot 4=9;\
& t_1=frac{-(-5)-sqrt{9}}{2}=frac{5-3}{2}=1;\
& t_2=frac{-(-5)+sqrt{9}}{2}=frac{5+3}{2}=4.end{aligned}
$$
Если $t=1$, то $x^2=1$. Отсюда имеем два значения $x$: $x_1=1$, $x_2=-1$. Если $t=4$, то $x^2=4$, т.е. $x_3=2$, $x_4=-2$. Вспоминая, что $y=frac{2}{x}$, получим:
begin{aligned}
& y_1=frac{2}{x_1}=frac{2}{1}=2;\
& y_2=frac{2}{x_2}=frac{2}{-1}=-2;\
& y_3=frac{2}{x_3}=frac{2}{2}=1;\
& y_4=frac{2}{x_4}=frac{2}{-2}=-1.
end{aligned}
Итак, у нас есть четыре стационарные точки: $M_1(1;2)$, $M_2(-1;-2)$, $M_3(2;1)$, $M_4(-2;-1)$. На этом первый шаг алгоритма закончен.
Теперь приступим ко второму шагу алгоритма. Найдём частные производные второго порядка:
$$
frac{partial^2 z}{partial x^2}=6x; frac{partial^2 z}{partial y^2}=6x; frac{partial^2 z}{partial x partial y}=6y.
$$
Найдём $Delta$:
$$
Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2=
6xcdot 6x-(6y)^2=36x^2-36y^2=36(x^2-y^2).
$$
Теперь будем вычислять значение $Delta$ в каждой из найденных ранее стационарных точек. Начнём с точки $M_1(1;2)$. В этой точке имеем:
$$Delta(M_1)=36(1^2-2^2)=-108.$$
Так как $Delta(M_1) < 0$, то согласно алгоритму в точке $M_1$ экстремума нет.
Исследуем точку $M_2(-1;-2)$. В этой точке имеем:
$$Delta(M_2)=36((-1)^2-(-2)^2)=-108.$$
Так как $Delta(M_2) < 0$, то согласно алгоритму в точке $M_2$ экстремума нет.
Исследуем точку $M_3(2;1)$. В этой точке получим:
$$
Delta(M_3)=36(2^2-1^2)=108;;; left.frac{partial^2 z}{partial x^2}right|_{M_3}=6cdot 2=12.
$$
Так как $Delta(M_3) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_3} > 0$, то согласно алгоритму $M_3(2;1)$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_3$:
$$
z_{min}=z(2;1)=2^3+3cdot 2cdot 1^2-15cdot 2-12cdot 1+1=-27.
$$
Осталось исследовать точку $M_4(-2;-1)$. В этой точке получим:
$$
Delta(M_4)=36((-2)^2-(-1)^2)=108;;; left.frac{partial^2 z}{partial x^2}right|_{M_4}=6cdot (-2)=-12.
$$
Так как $Delta(M_4) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_4} < 0$, то согласно алгоритму $M_4(-2;-1)$ есть точкой максимума функции $z$. Максимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_4$:
$$
z_{max}=z(-2;-1)=(-2)^3+3cdot (-2)cdot (-1)^2-15cdot (-2)-12cdot (-1)+1=29.
$$
Исследование на экстремум завершено. Осталось лишь записать ответ.
Ответ:
- $(2;1)$ – точка минимума, $z_{min}=-27$;
- $(-2;-1)$ – точка максимума, $z_{max}=29$.
Примечание
Вычислять значение $Delta$ в общем случае нет необходимости, потому что нас интересует лишь знак, а не конкретное значение данного параметра. Например, для рассмотренного выше примера №2 в точке $M_3(2;1)$ имеем $Delta=36cdot(2^2-1^2)$. Здесь очевидно, что $Delta > 0$ (так как оба сомножителя $36$ и $(2^2-1^2)$ положительны) и можно не находить конкретное значение $Delta$. Правда, для типовых расчётов это замечание бесполезно, – там требуют довести вычисления до числа 
Пример №3
Исследовать на экстремум функцию $z=x^4+y^4-2x^2+4xy-2y^2+3$.
Решение
Будем следовать алгоритму. Для начала найдём частные производные первого порядка:
$$
frac{partial z}{partial x}=4x^3-4x+4y; frac{partial z}{partial y}=4y^3+4x-4y.
$$
Составим систему уравнений $ left { begin{aligned}
& frac{partial z}{partial x}=0;\
& frac{partial z}{partial y}=0.
end{aligned} right.$:
$$
left { begin{aligned}
& 4x^3-4x+4y=0;\
& 4y^3+4x-4y=0.
end{aligned} right.
$$
Сократим оба уравнения на $4$:
$$
left { begin{aligned}
& x^3-x+y=0;\
& y^3+x-y=0.
end{aligned} right.
$$
Добавим к второму уравнению первое и выразим $y$ через $x$:
$$
y^3+x-y+(x^3-x+y)=0;\
y^3+x^3=0; y^3=-x^3; y=-x.
$$
Подставляя $y=-x$ в первое уравнение системы, будем иметь:
$$
x^3-x-x=0;\
x^3-2x=0;\
x(x^2-2)=0.
$$
Из полученного уравнения имеем: $x=0$ или $x^2-2=0$. Из уравнения $x^2-2=0$ следует, что $x=-sqrt{2}$ или $x=sqrt{2}$. Итак, найдены три значения $x$, а именно: $x_1=0$, $x_2=-sqrt{2}$, $x_3=sqrt{2}$. Так как $y=-x$, то $y_1=-x_1=0$, $y_2=-x_2=sqrt{2}$, $y_3=-x_3=-sqrt{2}$.
Первый шаг решения окончен. Мы получили три стационарные точки: $M_1(0;0)$, $M_2(-sqrt{2},sqrt{2})$, $M_3(sqrt{2},-sqrt{2})$.
Теперь приступим ко второму шагу алгоритма. Найдём частные производные второго порядка:
$$
frac{partial^2 z}{partial x^2}=12x^2-4; frac{partial^2 z}{partial y^2}=12y^2-4; frac{partial^2 z}{partial x partial y}=4.
$$
Найдём $Delta$:
$$
Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2=
(12x^2-4)(12y^2-4)-4^2=\
=4(3x^2-1)cdot 4(3y^2-1)-16=16(3x^2-1)(3y^2-1)-16=16cdot((3x^2-1)(3y^2-1)-1).
$$
Теперь будем вычислять значение $Delta$ в каждой из найденных ранее стационарных точек. Начнём с точки $M_1(0;0)$. В этой точке имеем:
$$Delta(M_1)=16cdot((3cdot 0^2-1)(3cdot 0^2-1)-1)=16cdot 0=0.$$
Так как $Delta(M_1) = 0$, то согласно алгоритму требуется дополнительное исследование, ибо ничего определённого про наличие экстремума в рассматриваемой точке сказать нельзя. Оставим покамест эту точку в покое и перейдём в иным точкам.
Исследуем точку $M_2(-sqrt{2},sqrt{2})$. В этой точке получим:
begin{aligned}
& Delta(M_2)=16cdot((3cdot (-sqrt{2})^2-1)(3cdot (sqrt{2})^2-1)-1)=16cdot 24=384;\
& left.frac{partial^2 z}{partial x^2}right|_{M_2}=12cdot (-sqrt{2})^2-4=24-4=20.
end{aligned}
Так как $Delta(M_2) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_2} > 0$, то согласно алгоритму $M_2(-sqrt{2},sqrt{2})$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_2$:
$$
z_{min}=z(-sqrt{2},sqrt{2})=(-sqrt{2})^4+(sqrt{2})^4-2(-sqrt{2})^2+4cdot (-sqrt{2})sqrt{2}-2(sqrt{2})^2+3=-5.
$$
Аналогично предыдущему пункту исследуем точку $M_3(sqrt{2},-sqrt{2})$. В этой точке получим:
begin{aligned}
& Delta(M_3)=16cdot((3cdot (sqrt{2})^2-1)(3cdot (-sqrt{2})^2-1)-1)=16cdot 24=384;\
& left.frac{partial^2 z}{partial x^2}right|_{M_3}=12cdot (sqrt{2})^2-4=24-4=20.
end{aligned}
Так как $Delta(M_3) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_3} > 0$, то согласно алгоритму $M_3(sqrt{2},-sqrt{2})$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_3$:
$$
z_{min}=z(sqrt{2},-sqrt{2})=(sqrt{2})^4+(-sqrt{2})^4-2(sqrt{2})^2+4cdot sqrt{2}(-sqrt{2})-2(-sqrt{2})^2+3=-5.
$$
Настал черёд вернуться к точке $M_1(0;0)$, в которой $Delta(M_1) = 0$. Согласно алгоритму требуется дополнительное исследование. Под этой уклончивой фразой подразумевается «делайте, что хотите» :). Общего способа разрешения таких ситуаций нет, – и это понятно. Если бы такой способ был, то он давно бы вошёл во все учебники. А покамест приходится искать особый подход к каждой точке, в которой $Delta = 0$. Ну что же, поисследуем поведение функции в окрестности точки $M_1(0;0)$. Сразу отметим, что $z(M_1)=z(0;0)=3$. Предположим, что $M_1(0;0)$ – точка минимума. Тогда для любой точки $M$ из некоторой окрестности точки $M_1(0;0)$ получим $z(M) > z(M_1) $, т.е. $z(M) > 3$. А вдруг любая окрестность содержит точки, в которых $z(M) < 3$? Тогда в точке $M_1$ уж точно не будет минимума.
Рассмотрим точки, у которых $y=0$, т.е. точки вида $(x,0)$. В этих точках функция $z$ будет принимать такие значения:
$$
z(x,0)=x^4+0^4-2x^2+4xcdot 0-2cdot 0^2+3=x^4-2x^2+3=x^2(x^2-2)+3.
$$
В всех достаточно малых окрестностях $M_1(0;0)$ имеем $x^2-2 < 0$, посему $x^2(x^2-2) < 0$, откуда следует $x^2(x^2-2)+3 < 3$. Вывод: любая окрестность точки $M_1(0;0)$ содержит точки, в которых $z < 3$, посему точка $M_1(0;0)$ не может быть точкой минимума.
Но, может быть, точка $M_1(0;0)$ – точка максимума? Если это так, то для любой точки $M$ из некоторой окрестности точки $M_1(0;0)$ получим $z(M) < z(M_1) $, т.е. $z(M) < 3$. А вдруг любая окрестность содержит точки, в которых $z(M) > 3$? Тогда в точке $M_1$ точно не будет максимума.
Рассмотрим точки, у которых $y=x$, т.е. точки вида $(x,x)$. В этих точках функция $z$ будет принимать такие значения:
$$
z(x,x)=x^4+x^4-2x^2+4xcdot x-2cdot x^2+3=2x^4+3.
$$
Так как в любой окрестности точки $M_1(0;0)$ имеем $2x^4 > 0$, то $2x^4+3 > 3$. Вывод: любая окрестность точки $M_1(0;0)$ содержит точки, в которых $z > 3$, посему точка $M_1(0;0)$ не может быть точкой максимума.
Точка $M_1(0;0)$ не является ни точкой максимума, ни точкой минимума. Вывод: $M_1$ вообще не является точкой экстремума.
Ответ: $(-sqrt{2},sqrt{2})$, $(sqrt{2},-sqrt{2})$ – точки минимума функции $z$. В обеих точках $z_{min}=-5$.