Самый простой способ
Разумеется, проще всего получить минимальный и максимальный элементы массива с помощью функций min() и max():
$arr = [8, 4, 12, 9];
$max = max($arr); // 12
$min = min($arr); // 4Однако на форумах часто просят написать скрипт, не использующий эти функции. Чаще всего этого требуют преподаватели учебных учреждений.
Условия задачи
1. Найти наибольший наименьший элементы в одномерном числовом массиве.
2. Определить номер минимального и максимального элементов заданного одномерного массива.
3. Найти минимальное и максимальное значение в ассоциативном массиве.
Общий принцип поиска элементов
Во всех решениях мы будем использовать одну и ту же логику.
Согласно условию, нам необходимо объявить числовой массив произвольной длины. Также объявим 4 переменные, в которые будем помещать найденные значения и их ключи:
<?php
$arr = [12, 4, 182, 1, 2.587];
$min = null;
$min_key = null;
$max = null;
$max_key = null;Далее перебираем массив в цикле и на каждой итерации проверяем, больше ли текущее значение, чем самое большое, что мы находили до этого.
И если больше — будем записывать в $max новое максимальное значение, а в $max_key его ключ. Абсолютно также поступим и с минимальными ключом и значением.
Пример с циклом foreach:
foreach($arr as $k => $v)
{
if($v > $max)
{
$max = $v;
$max_key = $k;
}
if($v < $min)
{
$min = $v;
$min_key = $k;
}
}На данном этапе наш код уже будет работать, но это ещё не всё. Попробуем изменить исходный массив и посмотрим на результат:
<?php
$arr = [0, -12];
$max = null;
foreach($arr as $v)
{
if($v > $max)
$max = $v;
}
var_dump($max); // -12Максимальным должно быть число 0, но скрипт вывел -12. Дело в том, что PHP не считает истинным выражение 0 > null, поэтому ноль на первой итерации цикла не записался в переменную $max.
Для решения этой проблемы просто добавим условие, что если $max === null, т.е. если это первая итерация, то в любом случае записываем текущее значение в $min и $max:
<?php
$arr = [0, -12];
$max = null;
foreach($arr as $v)
{
if($v > $max or $max === null)
$max = $v;
}
var_dump($max); // -12Минимальный и максимальный элементы с циклом FOREACH
Решение:
<?php
$arr = [12, 4, 182, 1, 2.587];
$min = null;
$min_key = null;
$max = null;
$max_key = null;
foreach($arr as $k => $v)
{
if($v > $max or $max === null)
{
$max = $v;
$max_key = $k;
}
if($v < $min or $min === null)
{
$min = $v;
$min_key = $k;
}
}
echo "Min value: $min <br> Min key: $min_key <br>";
echo "Max value: $max <br> Max key: $max_key";Минимальный и максимальный элементы с циклом WHILE
Решение 1: счётчик + count()
Цикл будет выполняться до тех пор, пока значение счётчика $i не превысит количество элементов массива.
<?php
$arr = [12, 4, 182, 1, 2.587];
$min = null;
$min_key = null;
$max = null;
$max_key = null;
$i = 0;
while($i < count($arr))
{
if($arr[$i] > $max or $max === null)
{
$max = $arr[$i];
$max_key = $i;
}
if($arr[$i] < $min or $min === null)
{
$min = $arr[$i];
$min_key = $i;
}
$i++;
}
echo "Min value: $min <br> Min key: $min_key <br>";
echo "Max value: $max <br> Max key: $max_key";Решение 2: счётчик + isset()
Запускаем вечный цикл while и в каждой итерации цикла проверяем существование следующего элемента с помощью isset(). Если его нет — выходим из цикла оператором break:
<?php
$arr = [12, 4, 182, 1, 2.587];
$min = null;
$min_key = null;
$max = null;
$max_key = null;
$i = 0;
while(true)
{
if(isset($arr[$i]))
{
if($arr[$i] > $max or $max === null)
{
$max = $arr[$i];
$max_key = $i;
}
if($arr[$i] < $min or $min === null)
{
$min = $arr[$i];
$min_key = $i;
}
}
else
break;
$i++;
}
echo "Min value: $min <br> Min key: $min_key <br>";
echo "Max value: $max <br> Max key: $max_key";Решение 3: list() + each()
Функция each() возвращает ключ и значение текущего элемента массива и смещает его внутренний указатель на единицу. Функция list() используется просто для удобства — с её помощью мы превращаем массив, который возвращает функция each, в две разные переменные:
<?php
$arr = [12, 4, 182, 1, 2.587];
$min = null;
$min_key = null;
$max = null;
$max_key = null;
$i = 0;
while(list($k, $v) = each($arr))
{
if($v > $max or $max === null)
{
$max = $v;
$max_key = $k;
}
if($v < $min or $min === null)
{
$min = $v;
$min_key = $k;
}
}
echo "Min value: $min <br> Min key: $min_key <br>";
echo "Max value: $max <br> Max key: $max_key";Получился практически аналог foreach. Единственный минус в том, что начиная с PHP 7.2 функция each() объявлена устаревшей.
Решение 4: current() + next()
Это решение похоже на предыдущее с each(). Получаем текущий элемента массива функцией current() и смещаем внутренний указатель массива функцией next(). Получить текущий ключ массива можно с помощью функции key().
<?php
$arr = [12, 4, 182, 1, 2.587];
$min = null;
$min_key = null;
$max = null;
$max_key = null;
$i = 0;
while($v = current($arr))
{
if($v > $max or $max === null)
{
$max = $v;
$max_key = key($arr);
}
if($v < $min or $min === null)
{
$min = $v;
$min_key = key($arr);
}
next($arr);
}
echo "Min value: $min <br> Min key: $min_key <br>";
echo "Max value: $max <br> Max key: $max_key";Наибольший и наименьший элементы с циклом FOR
Решение 1: счётчик + count()
Вводим счётчик $i и увеличиваем его после каждой итерации. Цикл прекратится как только значение счётчика превысит количество элементов массива.
<?php
$arr = [12, 4, 182, 1, 2.587];
$min = null;
$min_key = null;
$max = null;
$max_key = null;
for($i = 0; $i < count($arr); $i++)
{
if($arr[$i] > $max or $max === null)
{
$max = $arr[$i];
$max_key = $i;
}
if($arr[$i] < $min or $min === null)
{
$min = $arr[$i];
$min_key = $i;
}
}
echo "Min value: $min <br> Min key: $min_key <br>";
echo "Max value: $max <br> Max key: $max_key";Решение 2: счётчик + isset()
В отличие от предыдущего варианта, мы не смотрим на количество элементов массива, а запускаем вечный цикл и в каждой итерации проверяем существование следующего элемента, и если его нет — прерываем цикл командой break:
<?php
$arr = [12, 4, 182, 1, 2.587];
$min = null;
$min_key = null;
$max = null;
$max_key = null;
for($i = 0; true; $i++)
{
if(!isset($arr[$i]))
break;
if($arr[$i] > $max or $max === null)
{
$max = $arr[$i];
$max_key = $i;
}
if($arr[$i] < $min or $min === null)
{
$min = $arr[$i];
$min_key = $i;
}
}
echo "Min value: $min <br> Min key: $min_key <br>";
echo "Max value: $max <br> Max key: $max_key";Решение 3: each() + list()
Функция each() возвращает массив с ключом и значением текущего элемента массива, а list() превращает этот массив в 2 разные переменные. После последнего элемента функция each() вернёт false и цикл прекратит работу.
<?php
$arr = [12, 4, 182, 1, 2.587];
$min = null;
$min_key = null;
$max = null;
$max_key = null;
$i = 0;
for(; list($k, $v) = each($arr);)
{
if($v > $max or $max === null)
{
$max = $v;
$max_key = $k;
}
if($v < $min or $min === null)
{
$min = $v;
$min_key = $k;
}
}
echo "Min value: $min <br> Min key: $min_key <br>";
echo "Max value: $max <br> Max key: $max_key";Решение 4: current() + next()
С помощью функции next() смещаем внутренний указатель массива, а функции current() и key() возвращают текущие ключ и значение. Первое и последнее выражение цикла оставляем пустыми.
<?php
$arr = [12, 4, 182, 1, 2.587];
$min = null;
$min_key = null;
$max = null;
$max_key = null;
$i = 0;
for(; $v = current($arr);)
{
if($v > $max or $max === null)
{
$max = $v;
$max_key = key($arr);
}
if($v < $min or $min === null)
{
$min = $v;
$min_key = key($arr);
}
next($arr);
}
echo "Min value: $min <br> Min key: $min_key <br>";
echo "Max value: $max <br> Max key: $max_key";Максимальное значение в ассоциативном массиве
В ассоциативных массивах отсутствует порядок или системность в названиях ключей, поэтому циклы со счётчиками здесь недоступны.
Но мы всё ещё можем использовать цикл foreach и те решения для while и for, где используются функции each() и next(), поскольку они используют не ключи, а внутренний указатель массива.
a_list = [
[9, 2, 3],
[4, 5, 6],
[7, 8, 1]
]
b_list = [1, 2, 3, 4, 5, 6, 78, 0]
индекс наибольшего элемента списка b_list:
index_b_max = b.index(max(b))
индекс наименьшего элемента списка списков a_list:
a_min = a_list[0][0]
index_a_min = 0, 0
for i, sublist in enumerate(a_list):
for j, el in enumerate(sublist):
if el < a_min:
a_min = el
index_a_min = i, j
поменять местами:
a_list[index_a_min[0]][index_a_min[1]], b_list[index_b_max] = b_list[index_b_max], a_list[index_a_min[0]][index_a_min[1]]
результат:
>>> a_list
[[9, 2, 3], [4, 5, 6], [7, 8, 78]]
>>> b_list
[1, 2, 3, 4, 5, 6, 1, 0]
UPD сам не знаю, откуда я взял «поменять местами» в условии?..
Просто значение максимального элемента b_list записать на место минимального в a_list:
a_list[index_a_min[0]][index_a_min[1]] = max(b_list)
Какой алгоритм для поиска максимума в случайном массиве использовать? В статье собрано 5 эффективных must-have алгоритмов.
Если хочешь подтянуть свои знания, загляни на наш курс «Алгоритмы и структуры данных», на котором ты:
- углубишься в решение практических задач;
- узнаешь все про сложные алгоритмы, сортировки, сжатие данных и многое другое.
Ты также будешь на связи с преподавателем и другими студентами.
В итоге будешь браться за сложные проекты и повысишь чек за свою работу 🙂
Интересно, хочу попробовать
Самый быстрый и простейший алгоритм
Следует пояснить, что под «быстротой» алгоритма будет подразумеваться его асимптотическая сложность, а не физическое время выполнения.
В действительности, единственный способ точно найти самое большое число в случайном массиве будет перебор каждого числа в поисках максимума. Поэтому сложность такого алгоритма – O(N). Они называются линейными.
Простейшая реализация алгоритма на С:
#include <stdio.h>
int main()
{
int array[100];
int maximum, size, index = 0;
printf("Введите длину массива (не больше 100)n");
scanf("%d", &size);
printf("Введите %d целых чисел массиваn", size);
for (int i = 0; i < size; i++)
scanf("%d", &array[i]);
maximum = array[0]; // За изначальный максимум берем первый элемент массива
for (int i = 1; i < size; i++)
{
if (array[i] > maximum)
{
maximum = array[i];
index = i;
}
}
printf("Максимум находится в позиции %d и его значение %d.n", index, maximum);
return 0;
}
А как насчет распараллеливания?
После прочтения абзаца выше многие могут предложить поиск максимума с помощью параллельных вычислений, потому что он будет быстрее. И это так, если мы говорим о физическом времени. Но несмотря на то, сколько у вас есть процессов, вам всё равно придется просмотреть каждый элемент массива. Сложность алгоритма остается такой же, O(N).
Рассмотрим ситуацию на примере. Есть 200 карточек, на каждой из которых случайное число. Ваша задача найти карточку с самым большим числом. Допустим, друг согласился помочь, забрав половину карточек. Теперь каждый из вас ищет максимум из 100 карточек, вместо 200. Как только вы оба закончите, останется сравнить максимумы обеих половин. Время сократилось вдвое, но просмотреть пришлось все 200 карточек.
Сама по себе задача является так называемой чрезвычайно параллельной задачей, что ещё раз подтверждает возможность её решения именно распараллеливанием, без ущерба для конечного результата.
Задача о разборчивой невесте
Есть ещё один вариант нахождения максимума в случайном массиве.
Идем по первой половине всех значений в массиве. Запоминаем самое большое. Назовём его Х. Далее проходим по второй половине. Когда (и если) находим значение, которое больше Х, останавливаемся. Обозначим его Y. Какова вероятность того, что Y – максимум в массиве?
Чтобы это утверждение было истинным, Y должно находиться во второй половине массива. А так как значения в массиве случайны, шанс такого = 50%. Тогда если второй максимум присутствует в первой половине, это гарантирует, что найден правильный максимум.
Вероятность, что второй максимум в первой половине также = 50%. Посему вероятность, что и второй максимум в первой половине, и первый максимум во второй половине, равна 25%.
В итоге, такой алгоритм гарантирует точность 25% в нахождении максимума в массиве случайных чисел. Можно улучшить алгоритм, если искать второй максимум не в первой половине (1/2), а в 1/e (основание натурального логарифма) части массива. Этот способ впервые был предложен для решения задачи о разборчивой невесте или задачи секретаря (The Secretary Problem).
Аналоговый алгоритм
Спагетти-сортировка — прекрасный аналоговый алгоритм для решения задачи нахождения максимума в массиве.
Представим, что в массиве только N целых чисел. Возьмите N не приготовленных палочек спагетти, длина каждой сопоставляется с единственным значением в массиве.
Соберите спагетти в руку. Аккуратно, чтобы не сломать, поставьте горсть на ровную поверхность. В результате выше всех будет видна самая длинная (максимум) соломинка.
Асимптотическая сложность такого алгоритма – O(1). Но в цифровом мире он не применим.
Квантовый алгоритм
Алгоритм Гровера (или схема Гровера) используется в квантовых вычислениях для решения задач перебора. С его помощью сложность поиска максимума уменьшается до O(sqrt(N)) (большая О от корня N).
Данный способ решения может быть применен только на квантовом компьютере, что сильно умаляет его полезность в современном мире, но его нельзя не упомянуть.
Источник
Хотите дополнить? Ждём ваши предложения в комментариях 
13.1. Поиск максимального (минимального) элемента в массиве
|
Очень часто для решения задачи требуется находить не заданный элемент массива, а максимальный (наибольший) или минимальный (наименьший) элемент. Рассмотрим задачу нахождения максимального элемента. Если в массиве один-единственный элемент, то он и есть максимальный. Если элементов больше одного, то максимальным в массиве из i элементов является максимум из a[i] и максимального среди первых i — 1 элементов. Находить максимум будем последовательно, сравнивая текущий элемент с максимумом, найденным на предыдущем шаге. Если текущий элемент больше, то значение максимума, найденное на предыдущем шаге, нужно обновить (пример 13.1). Данный алгоритм находит значение максимального элемента, но не позволяет определить, на каком месте в массиве расположен этот максимальный элемент. Будем использовать переменную n_max для хранения индекса максимального элемента. Значение переменной n_max будет изменятся тогда, когда изменяется значение максимального элемента (пример 13.2). Если в массиве несколько элементов имеют максимальное значение, то значением переменной n_max будет индекс первого из них. Если использовать условие a[i] >= max, то переменная n_max будет хранить индекс последнего из максимальных элементов. Если известен индекс i элемента массива, то значение этого элемента можно получить, обратившись к элементу по индексу: a[i]. Поэтому при поиске максимального элемента достаточно хранить только его индекс n_max. Значение максимального элемента — a[n_max] (пример 13.3). Поиск минимального элемента осуществляется аналогично. В программе достаточно заменить знак > в условии оператора ветвления на знак < (пример 13.4). Имя переменной для хранения номера минимального элемента — n_min. |
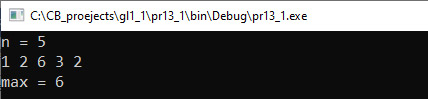
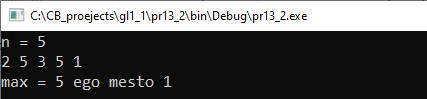
Пример 13.1. V. Программа: #include <iostream> #include <vector> using namespace std; int main() { int n; cout << «n = «; cin >> n; vector <int> a(n); for (int i = 0; i < n; i++) cin >> a[i]; //поиск максимального элемента int Max = a[0]; for (int i = 1; i < n; i++) if (a[i] > Max) Max = a[i]; cout << «max = « << Max; cout << endl; return 0; } VI. Тестирование. Пример 13.2. V. Программа: #include <iostream> #include <vector> using namespace std; int main() { int n; cout << «n = «; cin >> n; vector <int> a(n); for (int i = 0; i < n; i++) cin >> a[i]; //поиск максимального элемента int Max = a[0], n_max = 0; for (int i = 1; i < n; i++) if (a[i] > Max){ Max = a[i]; n_max = i; } cout << «max = « << Max; cout << » ego mesto « << n_max; cout << endl; return 0; } VI. Тестирование. Пример 13.3. Фрагмент программы: int n_max = 0; for (int i = 1; i < n; i++) if (a[i] > a[n_max]) n_max = i; cout << «max = « << a[n_max]; cout << » ego mesto « << n_max; Пример 13.4. Фрагмент программы: int n_min = 0; for (int i = 1; i < n; i++) if (a[i] < a[n_min]) n_min = i; |
13.2. Решение задач с использованием алгоритма поиска максимального (минимального) элементов
|
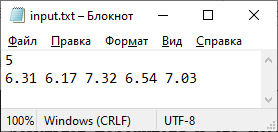
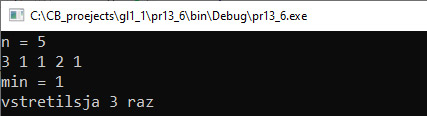
Пример 13.5. В массиве хранится информация о результатах спортсменов, участвовавших в лыжной гонке. Определить результат победителя и его номер. Данные прочитать из текстового файла. Этапы выполнения задания I. Исходные данные: массив a — числа, являющиеся временем прохождения трассы, количество спортсменов — n. II. Результат: a[n_min] — минимальное время, n_min — номер победителя. III. Алгоритм решения задачи. 1. Ввод исходных данных. IV. Описание переменных: n, n_min – int, а – vector <double>. Пример 13.6. Определить, сколько раз в линейном массиве встречается элемент, равный минимальному. Этапы выполнения задания I. Исходные данные: массив а, количество чисел n. II. Результат: a[n_min] — минимальный элемент, k — количество минимальных. III. Алгоритм решения задачи. 1. Ввод исходных данных. IV. Описание переменных: n, n_min, k — int, а – vector <int>. Пример 13.7. Задан массив из слов. Найти в нем самое длинное и самое короткое слово. Этапы выполнения задания I. Исходные данные: массив а, количество cлов n. II. Результат: a[n_min] — короткое слово, a[n_max] — длинное слово. III. Алгоритм решения задачи. 1. Ввод исходных данных. IV. Описание переменных: n, n_min, n_max – int, а – vector <string>. [1] Сравнение строк осуществляется лексикографически: s1 < s2, если для первого несовпадающего символа с номером i верно, что s1[i] < s2[i], или все символы строк совпадают, но s1 короче s2. |
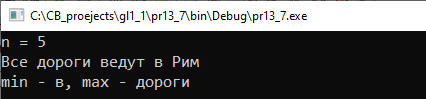
Пример 13.5. V. Программа: #include <iostream> #include <fstream> #include <vector> using namespace std; int main() { setlocale(0,«»); ifstream fin(«input.txt»); int n; fin >> n; vector <double> a(n); for (int i = 0; i < n; i++) fin >> a[i]; //поиск минимального элемента int n_min = 0; for (int i = 1; i < n; i++) if (a[i] < a[n_min]) n_min = i; cout << «победитель — лыжник №»; cout << n_min + 1 << endl; cout << «его время — «<< a[n_min]; cout << endl; return 0; } IV. Тестирование. Пример 13.6. V. Программа: #include <iostream> #include <vector> using namespace std; int main() { int n; cout << «n = «; cin >> n; vector <int> a(n); for (int i = 0; i < n; i++) cin >> a[i]; //поиск минимального элемента int n_min = 0; for (int i = 1; i < n; i++) if (a[i] < a[n_min]) n_min = i; //подсчет количества int k = 0; for (int i = 0; i < n; i++) if (a[i] == a[n_min]) k++; cout << «min = «<< a[n_min]; cout << endl << «vstretilsja «; cout << k << » raz» << endl; return 0; } VI. Тестирование. Пример 13.7. V. Программа: #include <iostream> #include <vector> #include <string> using namespace std; using namespace std::__cxx11; int main() { int n; cout << «n = «; cin >> n; vector <string> a(n); for (int i = 0; i < n; i++) cin >> a[i]; //поиск минимального слова int n_min = 0; for (int i = 1; i < n; i++) if (a[i].length() < a[n_min].length()) n_min = i; //поиск максимального слова int n_max = 0; for (int i = 1; i < n; i++) if (a[i].length() > a[n_max].length()) n_max = i; cout << «min — «<< a[n_min]; cout << «, max — «<< a[n_max]; cout << endl; return 0; } VI. Тестирование. |
Вопросы к параграфу
 |
1. Какой элемент массива является максимальным? Какой минимальным? 2. Как найти максимальный элемент в массиве? 3. Как найти минимальный элемент? 4. Каким образом определить номер первого элемента, равного максимальному? 5. Как определить номер последнего элемента, равного минимальному? |
Упражнения


1. Измените программы из примеров 13.1 и 13.2 так, чтобы находился минимальный элемент в массиве.
2. Для примера 13.5 выполните перечисленные задания.
1. Найдите номер спортсмена, пришедшего на финиш последним.
2. Определите, был ли победитель единственным или есть еще лыжник, прошедший трассу с таким же результатом (см. пример 13.6).
3. Добавьте еще один массив и введите в него фамилии спортсменов. Реализуйте пункты 1 и 2 так, чтобы выводилась фамилия, а не номер (см. пример 12.9).
3. Напишите программу, которая заменит в массиве нулями все элементы, равные минимальному.
4. Напишите программу, которая заменит в массиве нулями все элементы, стоящие перед максимальным. Предполагается, что в массиве единственный максимальный элемент.
5. Напишите программу, которая заменит нулями все элементы в массиве, стоящие после минимального. Если минимальных элементов несколько, то заменять нужно элементы, стоящие после последнего минимального.
6. Напишите программу, которая определит, какой из элементов — минимальный или максимальный — встречается в массиве раньше (имеет меньший индекс).
7. Напишите программу, которая определит, какой из элементов — минимальный или максимальный — встречается в массиве чаще.
8. Напишите программу, которая запишет в новый массив те элементы из исходного, которые расположены между минимальным или максимальным (по индексам).
9. В массиве хранится информация о стоимости автомобилей. Определите стоимость самого дорогого автомобиля и его номер в массиве. Если есть несколько таких автомобилей, то выведите все номера.
10. В массиве хранится информация о среднесуточной температуре декабря. Определите, сколько в декабре было дней с самой низкой и с самой высокой температурой.
11. Размеры n прямоугольников хранятся в двух массивах (длина и ширина). Найдите прямоугольник с минимальным периметром. (Вывести номер прямоугольника и значение периметра.)
12. Известны данные о массе (в кг) и объеме (в см3) n предметов, изготовленных из различных материалов. Найдите предметы с минимальной и максимальной плотностями. Вывести номер предмета и значение плотности.
13. Задан массив из слов. Найдите в нем самое длинное слово, заканчивающееся буквой «а».
14. Задан массив из слов. Найдите в нем самое короткое слово, начинающееся с заглавной буквы.
15. Задан массив из слов. Найдите в нем слово, в котором максимальное количество гласных букв. Если таких слов несколько, выведите все.
16. Задан массив из слов. Найдите в нем слово, в котором минимальное количество согласных букв. Если таких слов несколько, то выведите самое длинное из них.
Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
Given an array, write functions to find the minimum and maximum elements in it.
The most simplest way to find min and max value of an element is to use inbuilt function sort() in java. So, that value at 0th position will min and value at nth position will be max.
C++
#include <iostream>
#include <algorithm>
using namespace std;
int main() {
int a[] = { 1, 423, 6, 46, 34, 23, 13, 53, 4 };
int n = sizeof(a) / sizeof(a[0]);
sort(a, a + n);
cout << "min-" << a[0] << " max-" << a[n - 1] << endl;
return 0;
}
Java
import java.util.*;
class Array {
public static void main(String[] args) {
int a[]={1,423,6,46,34,23,13,53,4};
Arrays.sort(a);
System.out.println("min-"+a[0]+" max-"+a[a.length-1]);
}
}
Python3
import sys
a = [1, 423, 6, 46, 34, 23, 13, 53, 4]
a_sorted = sorted(a)
min_value = a_sorted[0]
max_value = a_sorted[-1]
print(f"min-{min_value} max-{max_value}")
C#
using System;
class GFG {
static void Main()
{
int[] arr = { 1, 423, 6, 46, 34, 23, 13, 53, 4 };
int n = arr.Length;
Array.Sort(arr);
Console.WriteLine("min-" + arr[0] + " max-"
+ arr[n - 1]);
}
}
Javascript
function findMinMax(arr) {
let min = arr[0];
let max = arr[0];
for (let i = 1; i < arr.length; i++) {
if (arr[i] < min) {
min = arr[i];
} else if (arr[i] > max) {
max = arr[i];
}
}
return { min, max };
}
const arr = [1, 423, 6, 46, 34, 23, 13, 53, 4];
const { min, max } = findMinMax(arr);
console.log(min-${min} max-${max});
Time complexity : O(n log(n))
Auxiliary Space : O(n)
C++
#include <bits/stdc++.h>
using namespace std;
int getMin(int arr[], int n)
{
int res = arr[0];
for (int i = 1; i < n; i++)
res = min(res, arr[i]);
return res;
}
int getMax(int arr[], int n)
{
int res = arr[0];
for (int i = 1; i < n; i++)
res = max(res, arr[i]);
return res;
}
int main()
{
int arr[] = { 12, 1234, 45, 67, 1 };
int n = sizeof(arr) / sizeof(arr[0]);
cout << "Minimum element of array: " << getMin(arr, n)
<< "n";
cout << "Maximum element of array: " << getMax(arr, n);
return 0;
}
C
#include <stdio.h>
int max(int num1, int num2)
{
return (num1 > num2) ? num1 : num2;
}
int min(int num1, int num2)
{
return (num1 > num2) ? num2 : num1;
}
int getMin(int arr[], int n)
{
int res = arr[0];
for (int i = 1; i < n; i++)
res = min(res, arr[i]);
return res;
}
int getMax(int arr[], int n)
{
int res = arr[0];
for (int i = 1; i < n; i++)
res = max(res, arr[i]);
return res;
}
int main()
{
int arr[] = { 12, 1234, 45, 67, 1 };
int n = sizeof(arr) / sizeof(arr[0]);
printf("Minimum element of array: %d n",
getMin(arr, n));
printf("Maximum element of array: %d n",
getMax(arr, n));
return 0;
}
Java
import java.io.*;
class GFG {
static int getMin(int arr[], int n)
{
int res = arr[0];
for (int i = 1; i < n; i++)
res = Math.min(res, arr[i]);
return res;
}
static int getMax(int arr[], int n)
{
int res = arr[0];
for (int i = 1; i < n; i++)
res = Math.max(res, arr[i]);
return res;
}
public static void main(String[] args)
{
int arr[] = { 12, 1234, 45, 67, 1 };
int n = arr.length;
System.out.println("Minimum element of array: " + getMin(arr, n));
System.out.println("Maximum element of array: " + getMax(arr, n));
}
}
Python3
def getMin(arr, n):
res = arr[0]
for i in range(1,n):
res = min(res, arr[i])
return res
def getMax(arr, n):
res = arr[0]
for i in range(1,n):
res = max(res, arr[i])
return res
arr = [12, 1234, 45, 67, 1]
n = len(arr)
print ("Minimum element of array:", getMin(arr, n))
print ("Maximum element of array:", getMax(arr, n))
C#
using System;
class GFG
{
static int getMin(int []arr,
int n)
{
int res = arr[0];
for (int i = 1; i < n; i++)
res = Math.Min(res, arr[i]);
return res;
}
static int getMax(int []arr,
int n)
{
int res = arr[0];
for (int i = 1; i < n; i++)
res = Math.Max(res, arr[i]);
return res;
}
public static void Main ()
{
int []arr = {12, 1234, 45, 67, 1};
int n = arr.Length;
Console.Write("Minimum element" +
" of array: " +
getMin(arr, n) + "n" );
Console.Write("Maximum element" +
" of array: " +
getMax(arr, n));
}
}
PHP
<?php
function getMin($arr, $n)
{
$res = $arr[0];
for ($i = 1; $i < $n; $i++)
$res = min($res, $arr[$i]);
return $res;
}
function getMax($arr, $n)
{
$res = $arr[0];
for ($i = 1; $i < $n; $i++)
$res = max($res, $arr[$i]);
return $res;
}
$arr = array(12, 1234, 45, 67, 1);
$n = sizeof($arr);
echo "Minimum element of array: "
, getMin($arr, $n), "n";
echo "Maximum element of array: "
,getMax($arr, $n);
?>
Javascript
<script>
function getMin(arr, n)
{
let res = arr[0];
for(let i = 1; i < n; i++)
res = Math.min(res, arr[i]);
return res;
}
function getMax(arr, n)
{
let res = arr[0];
for(let i = 1; i < n; i++)
res = Math.max(res, arr[i]);
return res;
}
let arr = [ 12, 1234, 45, 67, 1 ];
let n = arr.length;
document.write("Minimum element" +
" of array: " +
getMin(arr, n) + "<br/>");
document.write("Maximum element" +
" of array: " +
getMax(arr, n));
</script>
Output
Minimum element of array: 1 Maximum element of array: 1234
Time Complexity: O(n)
Auxiliary Space: O(1), as no extra space is used
Recursive Solution
C++
#include <bits/stdc++.h>
using namespace std;
int getMin(int arr[], int n)
{
return (n == 1) ? arr[0] : min(arr[0],
getMin(arr + 1, n - 1));
}
int getMax(int arr[], int n)
{
return (n == 1) ? arr[0] : max(arr[0],
getMax(arr + 1, n - 1));
}
int main()
{
int arr[] = { 12, 1234, 45, 67, 1 };
int n = sizeof(arr) / sizeof(arr[0]);
cout << "Minimum element of array: " <<
getMin(arr, n) << "n";
cout << "Maximum element of array: " <<
getMax(arr, n);
return 0;
}
Java
import java.io.*;
public class GFG
{
static int getMin(int arr[], int i, int n)
{
return (n == 1) ? arr[i] : Math.min(arr[i],
getMin(arr,i + 1 , n - 1));
}
static int getMax(int arr[], int i, int n)
{
return (n == 1) ? arr[i] : Math.max(arr[i],
getMax(arr ,i + 1, n - 1));
}
public static void main(String[] args)
{
int arr[] = { 12, 1234, 45, 67, 1 };
int n = arr.length;
System.out.print("Minimum element of array: " +
getMin(arr, 0, n) + "n");
System.out.println("Maximum element of array: " +
getMax(arr, 0, n));
}
}
Python3
def getMin(arr, n):
if(n==1):
return arr[0]
else:
return min(getMin(arr[1:], n-1), arr[0])
def getMax(arr, n):
if(n==1):
return arr[0]
else:
return max(getMax(arr[1:], n-1), arr[0])
arr = [12, 1234, 45, 67, 1]
n = len(arr)
print("Minimum element of array: ",
getMin(arr, n));
print("Maximum element of array: ",
getMax(arr, n));
C#
using System;
class GFG
{
static int getMin(int []arr, int i, int n)
{
return (n == 1) ? arr[i] : Math.Min(arr[i],
getMin(arr,i + 1 , n - 1));
}
static int getMax(int []arr, int i, int n)
{
return (n == 1) ? arr[i] : Math.Max(arr[i],
getMax(arr ,i + 1, n - 1));
}
public static void Main(String[] args)
{
int []arr = { 12, 1234, 45, 67, 1 };
int n = arr.Length;
Console.WriteLine("Minimum element of array: " +
getMin(arr, 0, n));
Console.WriteLine("Maximum element of array: " +
getMax(arr, 0, n));
}
}
Javascript
<script>
function getMin(arr , i , n) {
return (n == 1) ? arr[i] : Math.min(arr[i], getMin(arr, i + 1, n - 1));
}
function getMax(arr , i , n) {
return (n == 1) ? arr[i] : Math.max(arr[i], getMax(arr, i + 1, n - 1));
}
var arr = [ 12, 1234, 45, 67, 1 ];
var n = arr.length;
document.write("Minimum element of array: " + getMin(arr, 0, n) + "<br/>");
document.write("Maximum element of array: " + getMax(arr, 0, n));
</script>
Output
Minimum element of array: 1 Maximum element of array: 1234
Time Complexity: O(n)
Auxiliary Space: O(n), as implicit stack is used due to recursion
Using Library functions:
We can use min_element() and max_element() to find minimum and maximum of array.
C++
#include <bits/stdc++.h>
using namespace std;
int getMin(int arr[], int n)
{
return *min_element(arr, arr + n);
}
int getMax(int arr[], int n)
{
return *max_element(arr, arr + n);
}
int main()
{
int arr[] = { 12, 1234, 45, 67, 1 };
int n = sizeof(arr) / sizeof(arr[0]);
cout << "Minimum element of array: " << getMin(arr, n) << "n";
cout << "Maximum element of array: " << getMax(arr, n);
return 0;
}
Java
import java.util.Arrays;
class GFG {
static int getMin(int arr[], int n) {
return Arrays.stream(arr).min().getAsInt();
}
static int getMax(int arr[], int n) {
return Arrays.stream(arr).max().getAsInt();
}
public static void main(String[] args) {
int arr[] = {12, 1234, 45, 67, 1};
int n = arr.length;
System.out.println("Minimum element of array: " + getMin(arr, n));
System.out.println("Maximum element of array: " + getMax(arr, n));
}
}
Python3
def getMin(arr,n):
return min(arr)
def getMax(arr,n):
return max(arr)
if __name__=='__main__':
arr = [12,1234,45,67,1]
n = len(arr)
print("Minimum element of array: "
,getMin(arr, n))
print("Maximum element of array: "
,getMax(arr, n))
C#
using System;
using System.Linq;
class GFG
{
static int getMin(int []arr, int n)
{
return arr.Min();
}
static int getMax(int []arr, int n)
{
return arr.Max();
}
public static void Main(String[] args)
{
int []arr = {12, 1234, 45, 67, 1};
int n = arr.Length;
Console.WriteLine("Minimum element of array: " +
getMin(arr, n));
Console.WriteLine("Maximum element of array: " +
getMax(arr, n));
}
}
PHP
<?php
function getMin(&$arr, $n)
{
return min($arr);
}
function getMax(&$arr, $n)
{
return max($arr);
}
$arr = array(12, 1234, 45, 67, 1 );
$n = sizeof($arr);
echo "Minimum element of array: " .
getMin($arr, $n) . "n";
echo "Maximum element of array: " .
getMax($arr, $n);
?>
Javascript
<script>
function getMin(arr , n)
{
return Math.min.apply(Math,arr);
}
function getMax(arr , n) {
return Math.max.apply(Math,arr);
}
var arr = [ 12, 1234, 45, 67, 1 ];
var n = arr.length;
document.write("Minimum element of array: " +
getMin(arr, n)+"<br/>");
document.write("Maximum element of array: "
+ getMax(arr, n));
</script>
Output
Minimum element of array: 1 Maximum element of array: 1234
Time Complexity: O(n)
Auxiliary Space: O(1), as no extra space is used
This article is contributed by Aarti_Rathi. Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.
Last Updated :
31 Mar, 2023
Like Article
Save Article