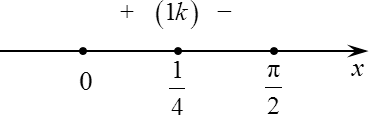Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.
Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.
Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.
Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.
В точках экстремумов (т.е. максимумов и минимумов) производная
равна нулю.
Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.
Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).
Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?
Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).
Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).


Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:
— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.
С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).
Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с (-13): до (-13) производная положительна т.е. функция растет, после — производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.
(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.
(- 9): функция возрастает, а потом убывает – максимум.
(-7): минимум.
(3): максимум.
Все вышесказанное можно обобщить следующими выводами:
— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
— Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.
Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:
- Найдите производную функции (f'(x)).
- Найдите корни уравнения (f'(x)=0).
- Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
- Определите знак производной в каждом промежутке (методом интервалов).
- Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
- Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
— если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
— если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
— если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.
Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:
(15x^4-60x^2=0) (|:15)
(x^4-4x^2=0)
(x^2 (x^2-4)=0)
(x=0) (x^2-4=0)
(x=±2)
3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:
Теперь очевидно, что точкой максимума является (-2).
Ответ. (-2).
Смотрите также:
Связь функции и её производной | 7 задача ЕГЭ
Разбор задач на поиск экстремумов, минимумов и максимумов
Скачать статью
Содержание:
- Глобальный и локальный максимум
- Исследование
- Область допустимых аргументов
- Асимптоты
- Производная и экстремумы
- Концы интервала и сравнение результатов
- Видео
Глобальный и локальный максимум
Максимум бывает локальным или глобальным. Точка локального максимума — это аргумент, который при подстановке в f(x) даёт значение не меньше, чем в других точках из области около этого аргумента. Для глобального максимума эта область расширяется до всей области допустимых аргументов. Для минимума всё наоборот. Экстремум — это локальное экстремальное — минимальное или максимальное — значение.
Как правило, если математиков интересует глобально самое большое значение f(x), то в интервале, не на всей оси аргументов. Подобные задачи обычно сформулированы фразой «найдите точку максимума функции на отрезке». Здесь подразумевается, что надо выявить аргумент, при котором она не меньше, чем на всём остальном указанном отрезке. Поиск локального экстремума является одним из шагов решения такой задачи.
Дано y = f(x). Требуется определить пик функции на указанном отрезке. f(x) может достигать его в точке:
- экстремума, если она попадает в указанный отрезок,
- разрыва,
- ограничивающей заданный отрезок.
Исследование
Пик f(x) на отрезке или в интервале находится путём исследования данной функции. План исследования для нахождения максимума на отрезке (или интервале):
Найти область допустимых аргументов и пересечения этой области с областью исследования.
- Выявить асимптоты. Они равны пределу при стремлении аргумента к точкам разрыва.
- Определить первую производную и вычислить экстремальные точки и выяснить поведение функции в окрестности этих точек.
- Рассчитать значение f(x) в точках, ограничивающих область исследования.
- Сравнить экстремум со значением функции в точках разрыва и на концах интервала. Определить среди них наибольшее.
Теперь подробно разберем каждый шаг и рассмотрим некоторые примеры.
Область допустимых аргументов
Область допустимых аргументов — это те x, при подстановке которых в f(x) она не престаёт существовать.Область допустимых аргументов ещё называют областью определения. Например, y = x^2 определена на всей оси аргументов. А y = 1/x определена для всех аргументов, кроме x = 0.
Найти пересечение области допустимых аргументов и исследуемого отрезка (интервала) требуется для того, чтобы исключить из рассмотрения ту часть интервала, где функция не определена. Например, требуется найти минимум y = 1/x на отрезке от -2 до 2. На самом деле требуется исследовать два полуинтервала от -2 до 0 и от 0 до 2, так как уравнение у = 1/0 не имеет решения.
Асимптоты

Если на исследуемом отрезке имеется вертикальная асимптота, около которой функция стремится в бесконечность с плюсом, то пик f(x) на здесь не определяется. А если бы определялся, то аргумент, при котором достигается максимум, совпал бы с точкой пересечения асимптоты и оси аргументов.
Производная и экстремумы
Значение производной в определенной показывает под каким углом проходит касательная к функции в выбранной точке. Отрицательное значение говорит о том, что функция здесь убывает. Аналогично положительная производная говорит о возрастании f(x). Отсюда появляются два условия.
1) Производная в точке экстремума либо нулевая, либо неопределенная. Это условие необходимое, но недостаточно. Продифференцируем y = x^3, получим уравнение производной: y = 3*x^2. Подставим в последнее уравнение аргумент «0», и производная обратится в нуль. Однако, это не экстремум для y = x^3. У неё не может быть экстремумов, она убывает на всей оси аргументов.
2) Достаточно, чтобы при пересечении точки экстремума у производной менялся знак. То есть, до максимума f(x) растёт, а после максимума она убывает — производная была положительной, а стала отрицательной.
После того как аргументы для локального максимума были найдены их надо подставить в исходное уравнение и получить максимальное значение f(x).
Концы интервала и сравнение результатов
При поиске максимума на отрезке необходимо проверить значение на концах отрезка. Например, для y = 1/x на отрезке [1; 7] максимум будет в точке x = 1. Даже если внутри отрезка есть локальный максимум, нет никакой гарантии, что значение на одном из концов отрезка не будет больше этого максимума.
Теперь необходимо сравнить значения в точках разрыва (если f(x) здесь не стремится в бесконечность), на концах исследуемого интервала и экстремум функции. Наибольшее из этих значений и будет максимумом функции на заданном участке прямой.
Для задачи с формулировкой «Найдите точку минимума функции» необходимо выбрать наименьшее из локальных минимумов и значений на концах интервала и в точках разрыва.
Видео
10 апреля 2014
Сегодня мы продолжаем рассматривать задачи на экстремумы из ЕГЭ по математике. Итак, задача:
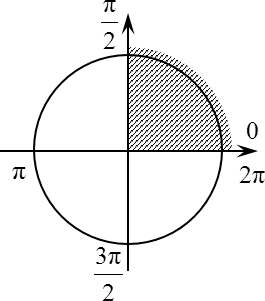
Задача B15. Найдите точку максимума на отрезке (0; π/2):
y = (3 − 12x) sin x − 12 cos x + 16
Сразу сделаю небольшое лирическое отступление. Дело в том, что это предпоследний урок из серии уроков, посвященным производным в ЕГЭ по математике. И сразу скажу, что оба эти урока будут посвящены тригонометрии, а точнее, нестандартным задачам на тригонометрию.
Вот и сейчас перед нами довольно-таки нестандартная задача. Хотя, как мы убедимся через пару минут, решается она довольно просто.
Решение задач на точки максимума и минимума
Давайте в первую очередь посмотрим, что от нас требуется. А требуется найти точку максимума. Заметьте: не наибольшее или наименьшее значение, а именно точку максимума. Из этого сразу следует, что наши любимые приемы, чтобы как-то подобрать х, как-то выделить красиво значение функции — в данной задаче эти приемы не работают просто потому, что значение функции нас не интересует.
Давайте работать по старинке. Прежде всего, я запишу общий алгоритм решения подобных задач.
- В первую очередь нас интересует производная: y‘ = ?
- Второй шаг — производную мы приравниваем к нулю и решаем полученное уравнение, находим корни. Их редко получается больше, чем две штуки: y‘ = 0; x1, x2, …;
- Третьим шагом мы берем эти корни и оставляем только те из них, которые лежат на интервале, указанном в условии задачи — в нашем случае речь идет об интервале (0; π/2). Итак, интересуют только те корни, которые лежат на обозначенном интервале или отрезке: x1, x2 ∈ (0; π/2);
- Наконец, мы чертим прямую, отмечаем на ней концы отрезка, а также все корни, которые лежат внутри этого отрезка. Затем смотрим знаки. Там, где «плюс» переходит в «минус», будет точка максимума. И наоборот: там, где «минус» переходит в «плюс», будет точка минимума.
Вот и все, что нам нужно знать для решения сегодняшней задачи.
Замечание по поводу тригонометрических функций
Однако некоторые ученики скажут: «На третьем этапе мы отбираем корни только в тех задачах, где требуется найти значение функции, а не точку максимума или минимума. Зачем выполнять отбор корней?»
Согласен, в большинстве задач на поиск точки экстремума отбирать точки не нужно, однако в нашем случае речь идет о тригонометрических функциях, и, как следствие, уравнение y‘ = 0 будет иметь бесконечное множество корней. Вы что будете отмечать множество корней?
А еще нужно искать между ними знаки, смотреть, где «плюс» переходить в «минус». Это бред! Поэтому, когда вы видите, что в задаче требуется найти производную тригонометрической функции, просто запомните для себя: мы в любом случае отбираем корни на интервале, независимо от того, требуется ли от нас найти значение функции или просто точку минимума или максимума.
При вычислении точек максимума/минимума тригонометрической функции отбор корней на отрезке не просто желателен — такой отбор становится необходимостью!
Это замечание существенно упрощает задачу, потому что лучше отметить один или два корня и посмотреть знаки вокруг них, чем бегать по всей числовой прямой и выяснять, где стоят плюсы, а где — минусы.
Решение задачи B15 на тригонометрию
Все, с разъяснениями мы закончили, переходим к решению конкретной задачи.
Производная тригонометрической функции
Итак, первый шаг: нужно найти производную функции:
y‘ = ((3 − 12x) sin x − 12 cos x + 16)’ = ((3 − 12x) · sin x)’ − (12 cos x)’
Первое слагаемое у нас представляет собой произведение двух функций, в каждой из которых присутствует элемент х, следовательно, нам нужно посчитать производную произведения. Напомню формулу производной произведения:
(f · g)’ = f ‘ · g + f · g‘
Запомните, что производная произведения не равна произведению производных. Считаем:
((3 − 12x) · sin x)’ = (3 − 12x)’ · sin x + (3 − 12x) · (sin x)’ = −12 · sin x + (3 − 12x) · cos x
Все, мы посчитали первое слагаемое. Переходим ко второму:
(12 cos x)’ = −12 sin x
Теперь подставляем два значения в нашу исходную формулу. Получим:
y‘ = −12 · sin x + (3 − 12x) · cos x − (− 12 sin x) = (3 − 12x) cos x
Находим точки экстремума
Мы нашли производную и выполнили первый шаг нашего алгоритма. Переходим ко второму шагу:
(3 − 12x) cos x = 0
Произведение равно 0, когда хотя бы один из множителей равен 0. Получаем:
3 − 12x = 0
cos x = 0
Из первого уравнения легко находится х:
x = 3/12 = 1/4
А второе равнение — это обычное тригонометрическое равнение. Мы можем сразу записать ответ:
x = π/2 + πn, n ∈ Z
Прекрасно, второй шаг нашего алгоритма выполнен!
Отбор корней тригонометрического уравнения на отрезке
Итак, мы нашли вес корни. Теперь отбираем те корни, которые лежат на интервале (0; π/2).
Пока отложим корти, которые получились из тригонометрического уравнения, потому что это более сложная конструкция, и таких корней бесконечное множество.
Решать будем с помощью тригонометрического круга. Давайте отметим все точки в пределах (0; π/2):
Нижняя точка нас не устраивает, как и не устраивает верхняя точка, потому что они лежат на концах интервала. А сами концы нас не устраивает просто потому, что в исходном условии задачи концы интервала обозначены выколотыми точками, т. е. круглыми скобками. Следовательно, точка π/2 нас тоже не интересует, и поэтому нужно вычеркнуть весь набор корней.
Остается лишь один корень — 1/4. Возникает вопрос: принадлежит ли он интервалу (0; π/2)? Проверяется это очень просто: приравниваем 1/4 с 0 и π/2:
0 ∨ 1/4 ∨ π/2
То, что 1/4 больше, чем 0, а вот с π/2 придется немного повозиться.
1/4 ∨ π/2 > 2 · 3 = 6
0 < 1/4 < π/2
Следовательно, корень 1/4 принадлежит к интересующему нас интервалу (0; π/2). На этом можно было бы закончить решение, потому что мы нашли единственный корень, который нас интересует и который лежит на рассматриваемом интервале и, следовательно, только он может являться ответом.
Можно записать ответ: 1/4 или 0,25.
Проверка корней тригонометрического уравнения
Однако давайте убедимся, что это действительно точка максимума. Для этого начертим прямую, т. е. перейдем к 4-ому шагу, отметим точку 1/4, а также концы интервала 0 и π/2.
Здесь же отметим знаки. Для этого подставляем любое число в пределах от 0 до 1/4 в изначальную производную. Например, какую-нибудь одну тысячную:
y‘ (0,001) = (3 − 0, 012) ∙ cos 0,001 > 0
Очевидно, что это число будет больше 0. Кроме того, cos x в пределах промежутка (0; π/2) везде положительный.
Произведение двух положительных чисел является положительным числом. Следовательно, в пределах от 0 до 1/4 знак будет «плюс». А число 1/4 является корнем первой кратности, так как у нас нет никаких квадратов, т. е. при переходе через него знак поменяется:
Мы получаем, что в точке x = 1/4 знак производной меняется с «плюса» на «минус». Следовательно, точка x = 1/4 является точкой максимума. Теперь задача точно решена, и мы еще раз убедились, что ответом будет число 0,25.
Особенности решения задач B15 с тригонометрией
Итого, несмотря на довольно угрожающий вид функции, все решается просто и быстро. Главное — не забывайте, по какой формуле считается производная произведения, иначе ответ точно получится неправильный.
Кроме того, настоятельно рекомендую вам потренироваться в отборе корней на интервале, иначе вы замучаетесь отмечать бесконечный набор корней на числовой прямой.
В остальном же это стандартная задача B15 на экстремумы, которая решается классическими приемами из математического анализа и вполне доступна среднестатистическому ученику.
Надеюсь, этот урок поможет тем, кто готовится к ЕГЭ по математике. А у меня на сегодня все. С вами был Павел Бердов. До новых встреч!
Смотрите также:
- Иррациональные функции в задаче B15: показательная функция и линейная замена
- Задача B15: Линейные выражения под знаком тригонометрической функции
- Тест к уроку «Сложение и вычитание дробей» (легкий)
- Тест: простейшие показательные уравнения (1 вариант)
- Задача B5: вычисление площади методом обводки
- Обход точек в стереометрии — 2
Наталья Игоревна Восковская
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Экстремумы функции
Для того чтобы ввести понятие наибольшего и наименьшего значения функций, вначале познакомимся с таким понятием, как экстремумы функций. Это понятие нам будет необходимо не для самого определения значений таких функций, а для построения схемы нахождения таких промежутков для конкретно заданных функций.
Определение 1
Точка $x’$ входящая в область определения функции называется точкой экстремума, если она либо будет точкой максимума, либо будет точкой минимума для функции $f(x)$.
Определение 2
Точка $x’$ будет называться точкой максимума для введенной функции $f(x)$, если у она имеет такую окрестность, что для всех точек $x$, которые входят в эту окрестность, будет верно $f(x)le f(x'{rm })$.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Определение 3
Точка $x_0$ будет называться точкой минимума для введенной функции $f(x)$, если она имеет такую окрестность, что для всех точек $x$, которые входят в эту окрестность, будет верно $f(x)ge f(x'{rm })$.
Чтобы полностью разобраться в данном понятии, далее введем понятие критической точки функции.
Определение 4
Точка $x’$ будет называться критической точкой для данной функции $f(x)$, если выполняются два следующих условия:
- Точка $x’$ является внутренней точкой для области определения данной функции;
- $f’left(x'{rm }right)=0$ или не существует.
Сформулируем без доказательства теоремы о необходимом (теорема 1) и достаточном (теорема 2) условии для существования точки экстремума.
Если $y=f(x)$ имеет экстремум в точке $x_0$, то либо её производная в ней равняется нулю, либо производная в ней не существует.
«Точки экстремума, наибольшее и наименьшее значение на промежутке» 👇
Теорема 2
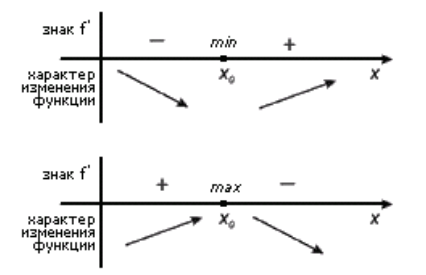
Пусть точка $x’$ будет критической для $y=f(x)$ и принадлежит интервалу $(a,b)$, причем на каждом интервале $left(a,x'{rm }right) и (x'{rm },b)$ производная $f'(x)$ существует и сохраняет один и тот же знак. В этом случае:
- Если в $(a,x'{rm })$ $f’left(xright) >0$, а в $(x'{rm },b)$ $f’left(xright)
- Если в $(a,x'{rm })$ $f’left(xright)0$, то $x’$ —будет точкой минимума для этой функции.
- Если и в $(a,x'{rm })$, и в $(x'{rm },b)$ производная $имеет один и тот же постоянный знак$, то $x’$ не будет точкой экстремума для этой функции.
На рисунке 1 мы можем наглядно увидеть смысл теоремы 2.
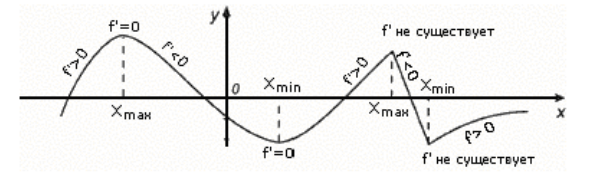
Рисунок 1.
Примеры точек экстремумов вы можете видеть на рисунке 2.
Рисунок 2.
Правило исследования на экстремум
- Найти $D(f)$;
- Найти $f'(x)$;
- Найти точки, где $f’left(xright)=0$;
- Найти точки, где $f'(x)$ не будет существовать;
- Отметить на координатной прямой $D(f)$ и все найденные в 3 и 4 пункте точки;
- Определить знак $f'(x)$ на полученных промежутках;
- Используя теорему 2, сделать заключение по поводу всех найденных точек.
Понятие наибольшего и наименьшего значений
Определение 5
Функция $y=f(x)$, которая имеет областью определения множество $X$, имеет наибольшее значение в точке $x’in X$, если выполняется
[fleft(xright)le f(x’)]
Определение 6
Функция $y=f(x)$, которая имеет областью определения множество $X$, имеет наименьшее значение в точке $x’in X$, если выполняется
[fleft(xright)ge f(x’)]
Чтобы найти наименьшее и наибольшее значение заданной функции на каком либо отрезке необходимо произвести следующие действия:
- Найти $f'(x)$;
- Найти точки, в которых $f’left(xright)=0$;
- Найти точки, в которых $f'(x)$ не будет существовать;
- Выкинуть из точек, найденных в пунктах 2 и 3 те, которые не лежат в отрезке $[a,b]$;
- Вычислить значения в оставшихся точках и на концах $[a,b]$;
- Выбрать из этих значений наибольшее и наименьшее.
Примеры задач
Пример 1
Найти наибольшее и наименьшее значения на [0,6]: $fleft(xright)=x^3-3x^2-45x+225$
Решение.
- $f’left(xright)=3x^2-6x-45$;
- $f’left(xright)=0$;
- [3x^2-6x-45=0]
- [x^2-2x-15=0]
- [x=5, x=-3]
- $f'(x)$ существует на всей $D(f)$;
- $5in left[0,6right]$;
-
Значения:
[fleft(0right)=225] [fleft(5right)=50] [fleft(6right)=63]
-
Наибольшее значение равняется $225$, наименьшее равняется $50.$
Ответ: $max=225, min=50$.
Пример 2
Найти наибольшее и наименьшее значения на [-1,1]:$fleft(xright)=frac{x^2-4x+4}{x-2}$
Решение.
[fleft(xright)=frac{x^2-4x+4}{x-2}=frac{{(x-2)}^2}{x-2}=x-2, xne 2]
-
$f’left(xright)=(x-2)’=1$;
Точек экстремума нет.
-
Значения:
[fleft(-1right)=-3] [fleft(1right)=-1]
Ответ: $max=-1, min=-3$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Максимумы, минимумы и экстремумы функций
Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.
Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.
Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.
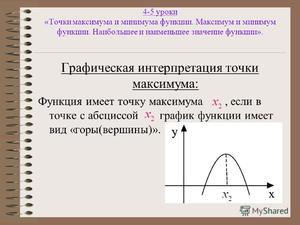
Минимумы и максимумы вместе именуют экстремумами функции.
Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.
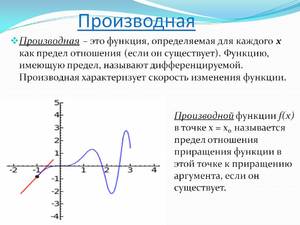
В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.
Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.
Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).
Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?
Давайте вместе найдем количество точек экстремума функции по графику производной на примере:
У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).
Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).
Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:
— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.
С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.
Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).
Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.
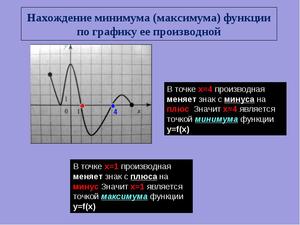
Начнем с (-13): до (-13) производная положительна т.е. функция растет, после — производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.
(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.
(- 9): функция возрастает, а потом убывает – максимум.
Все вышесказанное можно обобщить следующими выводами:
— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
— Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.
Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:
- Найдите производную функции (f'(x)).
- Найдите корни уравнения (f'(x)=0).
- Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
- Определите знак производной в каждом промежутке (методом интервалов).
- Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
- Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
— если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
— если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
— если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.
Всё! Точки максимумов и минимумов найдены.
Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.
Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:
3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:
Теперь очевидно, что точкой максимума является (-2).
Задание 11 Профильного ЕГЭ по математике
Задание 11 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.
Вот какие типы задач могут встретиться в этом задании:
Нахождение точек максимума и минимума функций
Исследование сложных функций
Нахождение наибольших и наименьших значений функций на отрезке
Нахождение точек максимума и минимума функций
1. Найдите точку максимума функции
Найдем производную функции.
Приравняем производную к нулю. Получим:
Исследуем знаки производной.
В точке производная меняет знак с «плюса» на «минус». Значит, — точка максимума функции
2. Найдите точку минимума функции
Найдем производную функции.
Приравняем производную к нулю.
Определим знаки производной.
В точке производная меняет знак с «минуса» на «плюс». Значит, — точка минимума функции
Исследование сложных функций
3. Найдите точку максимума функции
Перед нами сложная функция Возможно, вы знаете формулы производной сложной функции. Но вообще-то их изучают на первом курсе вуза, поэтому мы решим задачу более простым способом.
Так как функция монотонно возрастает, точка максимума функции .будет при том же , что и точка максимума функции А ее найти легко.
при . В точке производная меняет знак с «плюса» на «минус». Значит, — точка максимума функции .
Заметим, что точку максимума функции можно найти и без производной.
Графиком функции является парабола ветвями вниз, и наибольшее значение достигается в вершине параболы, то есть при
4. Найдите абсциссу точки максимума функции
Напомним, что абсцисса — это координата по
Снова сложная функция. Применяем тот же прием, что и в предыдущей задаче.
Так как функция монотонно возрастает, точка максимума функции является и точкой максимума функции
Это вершина квадратичной параболы
Нахождение наибольших и наименьших значений функций на отрезке
5. Найдите наибольшее значение функции на отрезке
Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке.
Будем искать точку максимума функции с помощью производной. Найдем производную и приравняем ее к нулю.
Найдем знаки производной.
В точке производная равна нулю и меняет знак с «+» на «-«. Значит, x = — 2 — точка максимума функции . Поскольку при функция убывает, В этой задаче значение функции на концах отрезка искать не нужно.
6. Найдите наименьшее значение функции на отрезке
Найдем производную функции и приравняем ее к нулю.
Найдем знаки производной.
Точка — точка минимума функции . Точка не лежит на отрезке Поэтому


7. Найдите наименьшее значение функции на отрезке
Иногда перед тем, как взять производную, формулу функции полезно упростить.
Мы применили формулу для логарифма произведения. при
Если 


Значит, — точка минимума функции . В этой точке и достигается наименьшее значение функции на отрезке
8. Найдите наибольшее значение функции на отрезке
Найдем производную функции
Приравняем производную к нулю:
Найдем знаки производной на отрезке
При знак производной меняется с «плюса» на «минус». Значит, — точка максимума функции
Мы нашли точку максимума, но это еще не все. Сравним значения функции в точке максимума и на конце отрезка, то есть при и
Заметим, что если вам попадется такая задача в первой части ЕГЭ по математике, то находить значение функции при не обязательно. Как мы видим, это значение — число иррациональное. А в первой части ЕГЭ по математике ответом может быть только целое число или конечная десятичная дробь.
9. Найдите наименьшее значение функции на отрезке [0;2].
Снова сложная функция. Запишем полезные формулы:
Найдем производную функции

10. Найдите наибольшее значение функции на отрезке
Как всегда, возьмем производную функции и приравняем ее к нулю.
По условию, . На этом отрезке условие выполняется только для Найдем знаки производной слева и справа от точки
В точке производная функции меняет знак с «плюса» на «минус». Значит, точка — точка максимума функции . Других точек экстремума на отрезке функция не имеет, и наибольшее значение функции на отрезке достигается при
11.Найдите наименьшее значение функции на отрезке
Найдем производную функции и приравняем ее к нулю. 
Что это значит? Производная функции не равна нулю ни в какой точке. Это значит, что знак производной в любой точке одинаков, а функция не имеет экстремумов и является монотонной.
Поскольку , получим, что 
Значит, наименьшее свое значение функция принимает в левом конце отрезка , то есть при
Как найти точку максимума функции?

Глобальный и локальный максимум
Максимум бывает локальным или глобальным. Точка локального максимума — это аргумент, который при подстановке в f(x) даёт значение не меньше, чем в других точках из области около этого аргумента. Для глобального максимума эта область расширяется до всей области допустимых аргументов. Для минимума всё наоборот. Экстремум — это локальное экстремальное — минимальное или максимальное — значение.
Как правило, если математиков интересует глобально самое большое значение f(x), то в интервале, не на всей оси аргументов. Подобные задачи обычно сформулированы фразой «найдите точку максимума функции на отрезке». Здесь подразумевается, что надо выявить аргумент, при котором она не меньше, чем на всём остальном указанном отрезке. Поиск локального экстремума является одним из шагов решения такой задачи.
Дано y = f(x). Требуется определить пик функции на указанном отрезке. f(x) может достигать его в точке:
- экстремума, если она попадает в указанный отрезок,
- разрыва,
- ограничивающей заданный отрезок.
Исследование
Пик f(x) на отрезке или в интервале находится путём исследования данной функции. План исследования для нахождения максимума на отрезке (или интервале):
Найти область допустимых аргументов и пересечения этой области с областью исследования.
- Выявить асимптоты. Они равны пределу при стремлении аргумента к точкам разрыва.
- Определить первую производную и вычислить экстремальные точки и выяснить поведение функции в окрестности этих точек.
- Рассчитать значение f(x) в точках, ограничивающих область исследования.
- Сравнить экстремум со значением функции в точках разрыва и на концах интервала. Определить среди них наибольшее.
Теперь подробно разберем каждый шаг и рассмотрим некоторые примеры.
Область допустимых аргументов
Область допустимых аргументов — это те x, при подстановке которых в f(x) она не престаёт существовать.Область допустимых аргументов ещё называют областью определения. Например, y = x^2 определена на всей оси аргументов. А y = 1/x определена для всех аргументов, кроме x = 0.
Найти пересечение области допустимых аргументов и исследуемого отрезка (интервала) требуется для того, чтобы исключить из рассмотрения ту часть интервала, где функция не определена. Например, требуется найти минимум y = 1/x на отрезке от -2 до 2. На самом деле требуется исследовать два полуинтервала от -2 до 0 и от 0 до 2, так как уравнение у = 1/0 не имеет решения.
Асимптоты

Если на исследуемом отрезке имеется вертикальная асимптота, около которой функция стремится в бесконечность с плюсом, то пик f(x) на здесь не определяется. А если бы определялся, то аргумент, при котором достигается максимум, совпал бы с точкой пересечения асимптоты и оси аргументов.
Производная и экстремумы

Значение производной в определенной показывает под каким углом проходит касательная к функции в выбранной точке. Отрицательное значение говорит о том, что функция здесь убывает. Аналогично положительная производная говорит о возрастании f(x). Отсюда появляются два условия.
1) Производная в точке экстремума либо нулевая, либо неопределенная. Это условие необходимое, но недостаточно. Продифференцируем y = x^3, получим уравнение производной: y = 3*x^2. Подставим в последнее уравнение аргумент «0», и производная обратится в нуль. Однако, это не экстремум для y = x^3. У неё не может быть экстремумов, она убывает на всей оси аргументов.
2) Достаточно, чтобы при пересечении точки экстремума у производной менялся знак. То есть, до максимума f(x) растёт, а после максимума она убывает — производная была положительной, а стала отрицательной.
После того как аргументы для локального максимума были найдены их надо подставить в исходное уравнение и получить максимальное значение f(x).
Концы интервала и сравнение результатов
При поиске максимума на отрезке необходимо проверить значение на концах отрезка. Например, для y = 1/x на отрезке [1; 7] максимум будет в точке x = 1. Даже если внутри отрезка есть локальный максимум, нет никакой гарантии, что значение на одном из концов отрезка не будет больше этого максимума.
Теперь необходимо сравнить значения в точках разрыва (если f(x) здесь не стремится в бесконечность), на концах исследуемого интервала и экстремум функции. Наибольшее из этих значений и будет максимумом функции на заданном участке прямой.
Для задачи с формулировкой «Найдите точку минимума функции» необходимо выбрать наименьшее из локальных минимумов и значений на концах интервала и в точках разрыва.
Видео
http://ege-study.ru/zadanie-12-profilnogo-EGE-po-matematike
http://liveposts.ru/articles/other-at/kak-najti-tochku-maksimuma-funktsii

 Найти область допустимых аргументов и пересечения этой области с областью исследования.
Найти область допустимых аргументов и пересечения этой области с областью исследования.