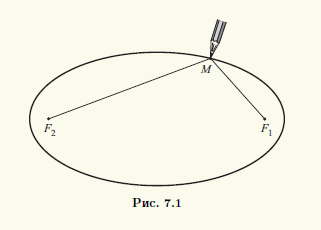
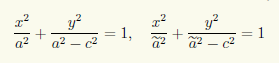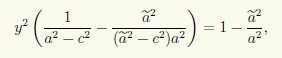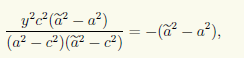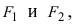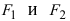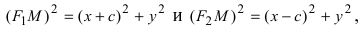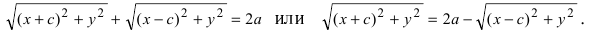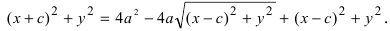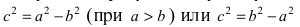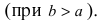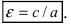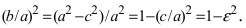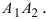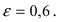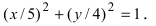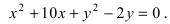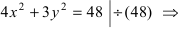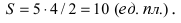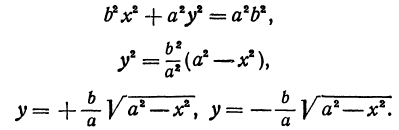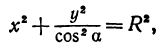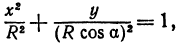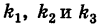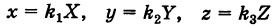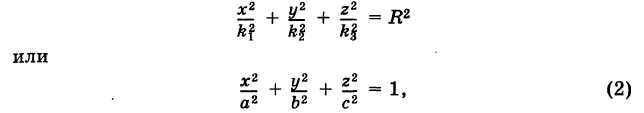Определение 7.1. Множество всех точек на плоскости, для которых сумма расстояний до двух фиксированных точек F1 и F2 есть заданная постоянная величина, называют эллипсом.
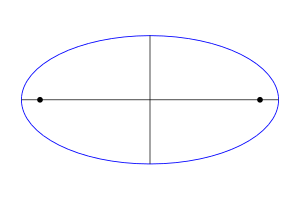
Определение эллипса дает следующий способ его геометрического построения. Фиксируем на плоскости две точки F1 и F2, а неотрицательную постоянную величину обозначим через 2а. Пусть расстояние между точками F1 и F2 равно 2c. Представим себе, что нерастяжимая нить длиной 2а закреплена в точках F1 и F2, например, при помощи двух иголок. Ясно, что это возможно лишь при а ≥ с. Натянув нить карандашом, начертим линию, которая и будет эллипсом (рис. 7.1).
Итак, описываемое множество не пусто, если а ≥ с. При а = с эллипс представляет собой отрезок с концами F1 и F2, а при с = 0, т.е. если указанные в определении эллипса фиксированные точки совпадают, он является окружностью радиуса а. Отбрасывая эти вырожденные случаи, будем далее предполать, как правило, что а > с > 0.
Фиксированные точки F1 и F2 в определении 7.1 эллипса (см. рис. 7.1) называют фокусами эллипса, расстояние между ними, обозначенное через 2c, — фокальным расстоянием, а отрезки F1M и F2M, соединяющие произвольную точку M на эллипсе с его фокусами, — фокальными радиусами.
Вид эллипса полностью определяется фокальным расстоянием |F1F2| = 2с и параметром a, а его положение на плоскости — парой точек F1 и F2.
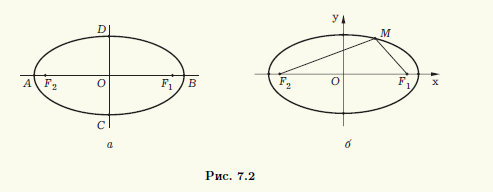
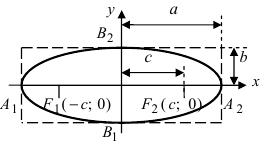
Из определения эллипса следует, что он симметричен относительно прямой, проходящей через фокусы F1 и F2, а также относительно прямой, которая делит отрезок F1F2 пополам и перпендикулярна ему (рис. 7.2, а). Эти прямые называют осями эллипса. Точка O их пересечения является центром симметрии эллипса, и ее называют центром эллипса, а точки пересечения эллипса с осями симметрии (точки A, B, C и D на рис. 7.2, а) — вершинами эллипса.
Число a называют большой полуосью эллипса, а b = √(a2 — c2) — его малой полуосью. Нетрудно заметить, что при c > 0 большая полуось a равна расстоянию от центра эллипса до тех его вершин, которые находятся на одной оси с фокусами эллипса (вершины A и B на рис. 7.2, а), а малая полуось b равна расстоянию от центра эллипса до двух других его вершин (вершины C и D на рис. 7.2, а).
Уравнение эллипса. Рассмотрим на плоскости некоторый эллипс с фокусами в точках F1 и F2, большой осью 2a. Пусть 2c — фокальное расстояние, 2c = |F1F2| < 2a. Согласно определению 7.1 эллипса, его образуют те точки M, для которых |F1M| + |F2M| = 2a.
Выберем прямоугольную систему координат Oxy на плоскости так, чтобы ее начало совпало с центром эллипса, а фокусы находились на оси абсцисс (рис. 7.2, б). Такую систему координат называют канонической для рассматриваемого эллипса, а соответствующие переменные — каноническими.
В выбранной системе координат фокусы имеют координаты F1(c;0), F2(—c;0). Используя формулу расстояния между точками, запишем условие |F1M| + |F2M| = 2a в координатах:
√((x — c)2 + y2) + √((x + c)2 + y2) = 2a. (7.2)
Это уравнение неудобно, так как в нем присутствуют два квадратных радикала. Поэтому преобразуем его. Перенесем в уравнении (7.2) второй радикал в правую часть и возведем в квадрат:
(x — c)2 + y2 = 4a2 — 4a√((x + c)2 + y2) + (x + c)2 + y2.
После раскрытия скобок и приведения подобных слагаемых получаем
√((x + c)2 + y2) = a + εx
где ε = c/a. Повторяем операцию возведения в квадрат, чтобы убрать и второй радикал: (x + c)2 + y2 = a2 + 2εax + ε2x2, или, учитывая значение введенного параметра ε, (a2 — c2) x2/a2 + y2 = a2 — c2. Так как a2 — c2 = b2 > 0, то
x2/a2 + y2/b2 = 1, a > b > 0. (7.4)
Уравнению (7.4) удовлетворяют координаты всех точек, лежащих на эллипсе. Но при выводе этого уравнения использовались неэквивалентные преобразования исходного уравнения (7.2) — два возведения в квадрат, убирающие квадратные радикалы. Возведение уравнения в квадрат является эквивалентным преобразованием, если в обеих его частях стоят величины с одинаковым знаком, но мы этого в своих преобразованиях не проверяли.
Мы можем не проверять эквивалентность преобразований, если учтем следующее. Пара точек F1 и F2, |F1F2| = 2c, на плоскости определяет семейство эллипсов с фокусами в этих точках. Каждая точка плоскости, кроме точек отрезка F1F2, принадлежит какому-нибудь эллипсу указанного семейства. При этом никакие два эллипса не пересекаются, так как сумма фокальных радиусов однозначно определяет конкретный эллипс. Итак, описанное семейство эллипсов без пересечений покрывает всю плоскость, кроме точек отрезка F1F2. Рассмотрим множество точек, координаты которых удовлетворяют уравнению (7.4) с данным значением параметра a. Может ли это множество распределяться между несколькими эллипсами? Часть точек множества принадлежит эллипсу с большой полуосью a. Пусть в этом множестве есть точка, лежащая на эллипсе с большой полуосью а. Тогда координаты этой точки подчиняются уравнению
т.е. уравнения (7.4) и (7.5) имеют общие решения. Однако легко убедиться, что система
при ã ≠ a решений не имеет. Для этого достаточно исключить, например, x из первого уравнения:
что после преобразований приводит к уравнению
не имеющему решений при ã ≠ a, поскольку 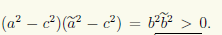
Вид эллипса. Рассмотренный выше геометрический способ построения эллипса дает достаточное представление о внешнем виде эллипса. Но вид эллипса можно исследовать и с помощью его канонического уравнения (7.4). Например, можно, считая у ≥ 0, выразить у через x: y = b√( 1 — x2/a2), и, исследовав эту функцию, построить ее график. Есть еще один способ построения эллипса. Окружность радиуса a с центром в начале канонической системы координат эллипса (7.4) описывается уравнением x2 + y2 = а2. Если ее сжать с коэффициентом a/b > 1 вдоль оси ординат, то получится кривая, которая описывается уравнением x2 + (ya/b)2 = a2, т. е. эллипс.
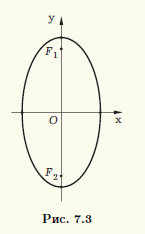
Замечание 7.1. Если ту же окружность сжать с коэффициентом a/b < 1 вдоль оси ординат, т. е. фактически растянуть в этом направлении, то получится кривая, которая описывается уравнением (7.4), в котором a < b. Это тоже эллипс, но в системе координат Oxy (рис. 7.3) его фокусы расположены на вертикальной оси симметрии. Каноническую систему координат для этого эллипса можно получить в результате поворота системы Oxy на 90°, что соответствует замене переменных x’ = y, y’ = — x.
Эксцентриситет эллипса. Отношение фокального расстояния эллипса к его большой оси называют эксцентриситетом эллипса и обозначают через ε. Для эллипса, заданного
каноническим уравнением (7.4), ε = 2c/2a = с/a. Если же в (7.4) параметры a и b связаны неравенством a < b, то фокусы расположены на вертикальной оси симметрии эллипса, с = √(b2 — a2), ε = 2c/2b = c/b.
При с =0, когда эллипс превращается в окружность, и ε = 0. В остальных случаях 0 < ε < 1. Если зафиксировать фокусы эллипса и менять его форму, устремляя эксцентриситет к единице, то в пределе получим отрезок, соединяющий фокусы, который можно назвать вырожденным эллипсом с a = с и b = 0. Если же, наоборот, зафиксировать параметр a и устремить ε к нулю, то в пределе мы получим окружность радиуса a. Эта предельная ситуация соответствует равенству параметров a и b уравнения (7.4).
Уравнение (7.3) эквивалентно уравнению (7.4), поскольку эквивалентны уравнения (7.4) и (7.2) . Поэтому уравнением эллипса является и (7.3). Кроме того, соотношение (7.3) интересно тем, что дает простую, не содержащую радикалов, формулу для длины |F2M| одного из фокальных радиусов точки M(x; у) эллипса: |F2M| = a + εx.
Аналогичная формула для второго фокального радиуса может быть получена из соображений симметрии либо повторением выкладок, в которых перед возведением в квадрат уравнения (7.2) в правую часть переносится первый радикал, а не второй. Итак, для любой точки M(x; у) на эллипсе (см. рис. 7.2)
|F1M | = a — εx, |F2M| = a + εx, (7.6)
и каждое из этих уравнений является уравнением эллипса.
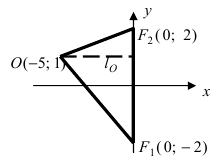
Пример 7.1. Найдем каноническое уравнение эллипса с большой полуосью 5 и эксцентриситетом 0,8 и построим его.
Зная большую полуось эллипса a = 5 и эксцентриситет ε = 0,8, найдем его малую полуось
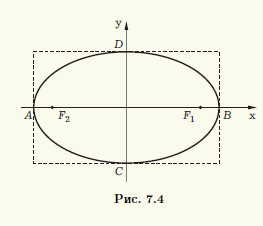
b. Поскольку b = √(a2 — с2), а с = εa = 4, то b = √(52 — 42) = 3. Значит каноническое уравнение имеет вид x2/52 + y2/32 = 1. Для построения эллипса удобно изобразить прямоугольник с центром в начале канонической системы координат, стороны которого параллельны осям симметрии эллипса и равны его соответствующим осям (рис. 7.4). Этот прямоугольник пересекается с
осями эллипса в его вершинах A(—5; 0), B(5; 0), C(0; -3), D(0; 3), причем сам эллипс вписан в него. На рис. 7.4 указаны также фокусы F1,2(±4; 0) эллипса.
Геометрические свойства эллипса. Перепишем первое уравнение в (7.6) в виде |F1M| = (а/ε — x)ε. Отметим, что величина а/ε — x при а > с положительна, так как фокус F1 не принадлежит эллипсу. Эта величина представляет собой расстояние до вертикальной прямой d: x = а/ε от точки M(x; у), лежащей левее этой прямой. Уравнение эллипса можно записать в виде
|F1M|/(а/ε — x) = ε
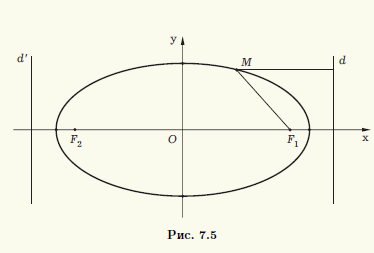
Оно означает, что этот эллипс состоит из тех точек M(x; у) плоскости, для которых отношение длины фокального радиуса F1M к расстоянию до прямой d есть величина постоянная, равная ε (рис. 7.5).
У прямой d есть » двойник » — вертикальная прямая d’, симметричная d относительно центра эллипса, которая задается уравнением x = —а/ε. Относительно d’ эллипс описывается так же, как и относительно d. Обе прямые d и d’ называют директрисами эллипса. Директрисы эллипса перпендикулярны той оси симметрии эллипса, на которой расположены его фокусы, и отстоят от центра эллипса на расстояние а/ε = а2/с (см. рис. 7.5).
Расстояние p от директрисы до ближайшего к ней фокуса называют фокальным параметром эллипса. Этот параметр равен
p = a/ε — c = (a2 — c2)/c = b2/c
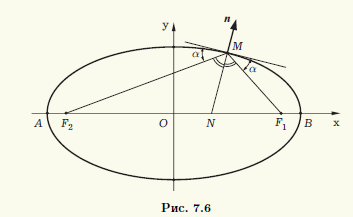
Эллипс обладает еще одним важным геометрическим свойством: фокальные радиусы F1M и F2M составляют с касательной к эллипсу в точке M равные углы (рис. 7.6).
Это свойство имеет наглядный физический смысл. Если в фокусе F1 расположить источник света, то луч, выходящий из этого фокуса, после отражения от эллипса пойдет по второму фокальному радиусу, так как после отражения он будет находиться под тем же углом к кривой, что и до отражения. Таким образом, все лучи, выходящие из фокуса F1, сконцентрируются во втором фокусе F2, и наоборот. Исходя из данной интерпретации указанное свойство называют оптическим свойством эллипса.
Определение эллипсa
Определение.
Эллипс — это замкнутая плоская кривая, сумма расстояний от каждой точки которой до двух точек F1 и F2 равна постоянной величине. Точки F1 и F2 называют фокусами эллипса.
F1M1 + F2M1 = F1M2 + F2M2 = A1A2 = const
Элементы эллипсa
F1 и F2 — фокусы эллипсa
Оси эллипсa.
А1А2 = 2a — большая ось эллипса (проходит через фокусы эллипса)
B1B2 = 2b — малая ось эллипса (перпендикулярна большей оси эллипса и проходит через ее центр)
a — большая полуось эллипса
b — малая полуось эллипса
O — центр эллипса (точка пересечения большей и малой осей эллипса)
Вершины эллипсa A1, A2, B1, B2 — точки пересечения эллипсa с малой и большой осями эллипсa
Диаметр эллипсa — отрезок, соединяющий две точки эллипса и проходящий через его центр.
Фокальное расстояние c — половина длины отрезка, соединяющего фокусы эллипсa.
Эксцентриситет эллипсa e характеризует его растяженность и определяется отношением фокального расстояния c к большой полуоси a. Для эллипсa эксцентриситет всегда будет 0 < e < 1, для круга e = 0, для параболы e = 1, для гиперболы e > 1.
Фокальные радиусы эллипсa r1, r2 — расстояния от точки на эллипсе до фокусов.
Радиус эллипсa R — отрезок, соединяющий центр эллипсa О с точкой на эллипсе.
| R = | ab | = | b |
| √a2sin2φ + b2cos2φ | √1 — e2cos2φ |
где e — эксцентриситет эллипсa, φ — угол между радиусом и большой осью A1A2.
Фокальный параметр эллипсa p — отрезок который выходит из фокуса эллипсa и перпендикулярный большой полуоси:
Коэффициент сжатия эллипсa (эллиптичность) k — отношение длины малой полуоси к большой полуоси. Так как малая полуось эллипсa всегда меньше большей, то k < 1, для круга k = 1:
k = √1 — e2
где e — эксцентриситет.
Сжатие эллипсa (1 — k ) — величина, которая равная разности между единицей и эллиптичностью:
Директрисы эллипсa — две прямые перпендикулярные фокальной оси эллипса, и пересекающие ее на расстоянии
ae
от центра эллипса. Расстояние от фокуса до директрисы равно
pe
.
Основные свойства эллипсa
1. Угол между касательной к эллипсу и фокальным радиусом r1 равен углу между касательной и фокальным радиусом r2 (Рис. 2, точка М3).
2. Уравнение касательной к эллипсу в точке М с координатами (xM, yM):
3. Если эллипс пересекается двумя параллельными прямыми, то отрезок, соединяющий середины отрезков образовавшихся при пересечении прямых и эллипса, всегда будет проходить через центр эллипсa. (Это свойство дает возможность построением с помощью циркуля и линейки получить центр эллипса.)
4. Эволютой эллипсa есть астероида, что растянута вдоль короткой оси.
5. Если вписать эллипс с фокусами F1 и F2 у треугольник ∆ ABC, то будет выполнятся следующее соотношение:
| 1 = | F1A ∙ F2A | + | F1B ∙ F2B | + | F1C ∙ F2C |
| CA ∙ AB | AB ∙ BC | BC ∙ CA |
Уравнение эллипсa
Каноническое уравнение эллипсa:
Уравнение описывает эллипс в декартовой системе координат. Если центр эллипсa О в начале системы координат, а большая ось лежит на абсциссе, то эллипсa описывается уравнением:
Если центр эллипсa О смещен в точку с координатами (xo, yo), то уравнение:
| 1 = | (x — xo)2 | + | (y — yo)2 |
| a2 | b2 |
Параметрическое уравнение эллипсa:
| { | x = a cos α | де 0 ≤ α < 2π |
| y = b sin α |
Радиус круга вписанного в эллипс
Круг, вписан в эллипс касается только двух вершин эллипсa B1 и B2. Соответственно, радиус вписанного круга r будет равен длине малой полуоси эллипсa OB1:
r = b
Радиус круга описанного вокруг эллипсa
Круг, описан вокруг эллипсa касается только двух вершин эллипсa A1 и A2. Соответственно, радиус описанного круга R будет равен длине большой полуоси эллипсa OA1:
R = a
Площадь эллипсa
Формула определение площади эллипсa:
S = πab
Площадь сегмента эллипсa
Формула площади сегмента, что находится по левую сторону от хорды с координатами (x, y) и (x, -y):
| S = | πab | — | b | ( | x | √ | a2 — x2 + a2 ∙ arcsin | x | ) |
| 2 | a | a |
Периметр эллипсa
Найти точную формулу периметра эллипсa L очень тяжело. Ниже приведена формула приблизительной длины периметра. Максимальная погрешность этой формулы ~0,63 %:
| L ≈ 4 | πab + (a — b)2 |
| a + b |
Длина дуги эллипсa
Формулы определения длины дуги эллипсa:
1. Параметрическая формула определения длины дуги эллипсa через большую a и малую b полуоси:
| t2 | ||
| l = | ∫ | √a2sin2t + b2cos2t dt |
| t1 |
2. Параметрическая формула определения длины дуги эллипсa через большую полуось a и эксцентриситет e:
| t2 | ||
| l = | ∫ | √1 — e2cos2t dt, e < 1 |
| t1 |
(схема 21)
Эллипсом называется
геометрическое место точек плоскости, сумма расстояний от каждой из которых до
двух данных точек этой плоскости, называемых
фокусами, есть величина постоянная, равная 2a.
Обозначим фокусы через F1 и F2,
расстояние между ними через 2c, а сумму расстояний от произвольной точки эллипса до
фокусов – через 2a. По определению 2a>2c, то есть a>c .
Выберем систему координат
так, чтобы
фокусы F1 и F2
лежали на оси 0x, а начало координат совпадало с серединой отрезка F1F2. Тогда фокусы имют координаты: F1(–c;0) и F2(c;0). Пусть M(x;y) –
произвольная точка эллипса (текущая точка). Тогда по определению эллипса можно записать
По сути, мы получили уравнение эллипса. Упростим его с помощью ряда несложных математических преобразований:
Так как, a>c, то a2–c2>0, то можно обозначить a2–c2=b2. Тогда
последнее уравнение имеет вид:

Это
уравнение равносильно первоначальному. Оно называется каноническим уравнением
эллипса – кривой
второго порядка.
Установим форму эллипса, пользуясь его каноническим
уравнением.
1. Уравнение (2.17) содержит x и y
только в четных степенях, поэтому
если точка (x;y)
принадлежит эллипсу, то
ему также принадлежат
точки (–x;y), (x;–y), (–x;–y). Отсюда: эллипс симметричен относительно осей 0x и 0y, а также
относительно точки O(0;0), которую называют центром эллипса.
2. Найдем точки пересечения эллипса с осями координат.
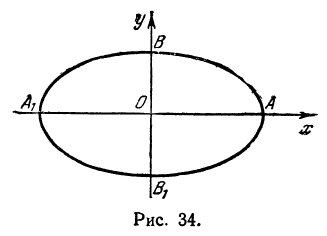
Положив y=0, найдем точки A1(a;0) и A2(–a;0), в которых ось 0x пересекает эллипс. Положив в уравнении
(2.17) x=0, находим точки пересечения эллипса с осью 0y: B1(0;b) и B2(0;–b). Точки A1, A2, B1, B2 называются вершинами эллипса. Отрезки А1А2,
В1В2, а также
их длины 2a и 2b – соответственно большая и малая оси эллипса (рис. 2.4).
3. Из уравнения (2.17) следует, что каждое слагаемое в
левой части не превосходит единицы,
т.е.:

Следовательно, все точки эллипса лежат внутри
прямоугольника, ограниченного прямыми x= ± a
и y= ± b.
4. В уравнении (2.17) левая часть – сумма
неотрицательных слагаемых, т.е. при возрастании одного слагаемого другое будет
уменьшаться, если |x| возрастает, |y|
уменьшается и наоборот.
Из сказанного следует, что эллипс имеет форму
овальной замкнутой кривой. Форма эллипса зависит от отношения
(2.17) принимает вид: x2+y2=a2. Отношение 

0<ε<1, так как 0<c<a.
Отсюда видно, что чем меньше эксцентриситет эллипса,
тем будет менее эллипс сплющенным; при ε=0 эллипс
превращается в окружность.
Пусть M(x;y) – произвольная точка эллипса с фокусами F1 и F2. Длины
отрезков |MF1|=r1 и |MF2|=r2 – фокальные
радиусы точки M, r1+r2=2a. Имеют место формулы: r1=a+εx и r2=a – εx.
Прямые 
эллипса.
Если r – расстояние от произвольной точки до какого–нибудь фокуса,
d –
расстояние от этой же точки до соответствующей этому фокусу директрисы (рис. 2.5), то отношение
постоянная, равная эксцентриситету эллипса: 
Из равенства a2–c2=b2
следует, что a>b. Если же
наоборот, то уравнение (2.17) определяет эллипс, большая ось которого 2b лежит на
оси 0y, а малая ось 2a – на оси 0x. Фокусы такого
эллипса находятся в точках F1(0;c) и F2(0;–c), где 
Пример 2.5. Составить уравнение линии, для каждой точки
которой отношение расстояний от нее до
точки A(3;0) и до прямой x=12, равно числу ε=0,5. Полученное
уравнение привести к простейшему виду.
Решение. Пусть M(x;y) – текущая (произвольная) точка искомого
геометрического множества точек. Опустим перпендикуляр MB на прямую
. Тогда точка B(12;y). По условию задачи

По формуле расстояния
двумя точками получаем:
Отсюда
Полученное уравнение представляет собой эллипс вида 
Определим фокусы эллипса F1(–c;0) и F2(c;0). Для эллипса справедливо равенство b2=a2–c2,
откуда c2=a2–b2 =9 и c=3. То есть,
F1(–3;0) и F1(3;0)–
фокусы эллипса (точки F2 и A совпадают).
Эксцентриситет эллипса
Примечание. Если эллипс (окружность) вращать вокруг одной из его
осей, то описываемая им поверхность будет эллипсоидом вращения (сферой)
Пример 2.6. В геодезии используется система географических координат,
основанная на понятии геоида. Геоид – поверхность Земли,
ограниченная уровенной поверхностью, продолженной под континенты. Поверхность
геоида отличается от физической поверхности Земли, на которой резко выражены
горы и океанические впадины.
Тело, поверхность которого более всего соответствует
поверхности геоида, имеет определенные размеры и ориентирована соответственно в
теле Земли, называется референц–эллипсоидом. В нашей стране с 1946 года для всех
геодезических работ принят референц–эллипсоид Красовского с
параметрами a=6 378 245 м, b=6 356 863 м, α=1: 298,3.
Линия, проходящая вертикально через центр эллипсоида
является полярной осью. Линия, проходящая через центр эллипсоида,
перпендикулярно к полярной оси, – экваториальной осью. При пересечении
поверхности эллипсоида плоскостью, проходящей через его центр, перпендикулярно
к полярной оси, образуется окружность, называемая экватором. Окружность,
полученная от пересечения поверхности эллипсоида плоскостью, параллельной
плоскости экватора, называется параллелью. Линия пересечения
поверхности эллипсоида с плоскостью, проходящей через заданную точку и полярную
ось, называется меридианом данной точки. Положение точки на земной поверхности
определяется пересечением параллели и меридиана, проходящих через нее. Угол φ между плоскостью экватора и отвесной
линией называется географической широтой. Для определения долгот
точек один из меридианов (Гринвичский) принимают за начальный или нулевой. Угол
λ, составленный плоскостью меридиана,
проходящего через данную точку, и плоскостью начального меридиана, называется
географической долготой
Гипербола – геометрическое место точек плоскости, модуль разности расстояний от
каждой из которых до двух данных точек этой плоскости – фокусов, есть величина
постоянная, равная 2a.
Обозначим фокусы через
F1 и F2, расстояние между ними через 2c, а модуль
разности расстояний от каждой точки
гиперболы до фокусов через 2a. По определению 2a<2c, то есть a<c.
Выберем систему координат x0y так, чтобы фокусы F1 и F2 лежали на оси 0x, а начало координат совпало с серединой отрезка F1F2. Тогда фокусы будут иметь координаты F1(c;0) и F2(–c;0). На этой основе выведем уравнение гиперболы. Пусть M(x;y) – ее произвольная точка. Тогда по определению |MF1–MF2|=2a, то есть

где
b2=a2–c2.
Гипербола – линия 2–го порядка.
Установим форму гиперболы, исходя из ее канонического
уравнения.
1. Уравнение (2.18) содержит x и y только в
четных степенях. Следовательно, гипербола симметрична относительно осей координат
0x и 0y, и относительно точки O(0;0) – центра гиперболы.
2. Найдем точки пересечения гиперболы с осями координат. Положив в
уравнении (2.18) y=0, находим две точки пересечения гиперболы с осью 0x: A1(a;0) и A2(–a;0).
Положив в (2.18) x=0, получаем y2= – b2,
чего быть не может. Т.е. гипербола ось 0y не пересекает.
Точки A1(a;0) и A2(–a;0) – вершины гиперболы, а отрезок |A1A2|=2a – действительная ось. Отрезок |B1B2|=2b,
соединяющий точки B1(0;b) и B2(0;–b) – мнимая ось (рис. 2.6). Прямоугольник
со сторонами 2a и 2b – основной
прямоугольник гиперболы.
3. Из уравнения (2.18) следует, что уменьшаемое 
от прямой x=a (правая
ветвь гиперболы) и слева от прямой x=–a (левая
ветвь) (рис. 2.6).
4. Из уравнения (2.18) гиперболы видно, что
когда |x| возрастает, то |y| также
возрастает. Это
следует из того, что разность 
сохраняет значение, равноe единице. Следовательно, гипербола имеет форму,
состоящую из двух неограниченных ветвей.
Прямая L называется асимптотой некоторой неограниченной кривой, если расстояние d от точки M этой кривой до прямой L стремится к нулю при неограниченном
удалении точки M вдоль кривой
от начала координат.
Покажем, что гипербола 

данные прямые и гипербола (2.18) симметричны относительно координатных
осей, то достаточно рассмотреть только точки, расположенные в первой четверти.
Возьмем на прямой 
ту же абсциссу, что и точка M(x;y) на гиперболе 
Очевидно: так как числитель есть величина постоянная, а знаменатель дроби увеличивается с возравстанием переменной х, то длина отрезка |MN| стремится
к нулю. Так как |MN| больше
расстояния d от точки M до прямой L, то d стремится к нулю тем более (и подавно). Следовательно, прямые

асимптоты гиперболы (рис. 2.7).
Построение гиперболы начинают с нанесения ее основного прямоугольника на координатную плоскость. Далее проводят диагонали этого прямоугольника, которые являются асимптотами гиперболы, затем отмечают ее вершины, фокусы и строят ветви гиперболы.
Эксцентриситет гиперболы –
отношение расстояния между фокусами к величине её действительной оси,
обозначается ε: 
как у гиперболы c>a, то
эксцентриситет ее больше единицы. Эксцентриситет характеризует форму гиперболы. Так как 
эксцентриситет гиперболы, тем меньше отношение 
значит, тем более вытянут ее основной прямоугольник.
Эксцентриситет
равносторонней гиперболы равен 

,
для точек
правой ветви гиперболы имеют вид: r1=εx+a, r2=εx–a; для точек
левой ветви: r1=–(εx+a), r2=–(εx–a).
Прямые
гиперболы. Тот факт, что для гиперболы ε>1, то 
левая – между центром и левой вершиной. Директрисы
гиперболы имеют тоже свойство 
Уравнение 
на рисунке 2.7 пунктиром).
Значит, гиперболы

имеют общие
асимптоты. Такие гиперболы называются сопряженными.
Примечание. Если у кривой 2–го порядка смещен центр в некоторую
точку O’(x0;y0), то она
называется нецентральной кривой. Уравнение такой кривой имеет вид:
Примечание. При вращении гиперболы вокруг ее действительной оси
образуется двуполостный гиперболоид, вокруг ее мнимой оси – однополостный гиперболоид
Подробно данные уравнения рассмотрены в теме:
«Исследование общего уравнения 2–ой степени» (смотри схему 10), частными
случаями которого являются данные формулы.
Вопросы
для самопроверки
Эллипс:
Определение: Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек
Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы
Рис. 29. Вывод уравнения эллипса.
Расстояние между фокусами (фокусное расстояние) равно 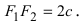
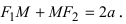
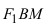
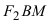
соответственно. Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим 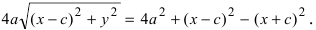
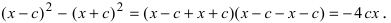
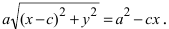
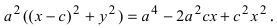
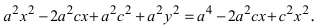
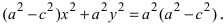
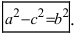
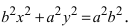
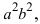
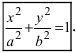
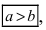
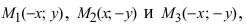
Определение: Найденные точки называются вершинами эллипса.
Рис. 30. Вершины, фокусы и параметры эллипса
Определение: Если 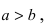
Определение: Эксцентриситетом эллипса называется отношение фокусного рас- стояния к большой полуоси эллипса
Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству 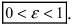
Если 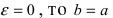
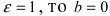
Пример:
Составить уравнение эллипса, если его большая полуось а = 5, а его эксцентриситет
Решение:
Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр 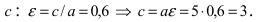
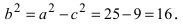
Пример:
Найти площадь треугольника, две вершины которого находятся в фокусах эллипса 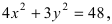
Решение:
Для определения координат фокусов эллипса и центра окружности преобразуем их уравнения к каноническому виду. Эллипс:
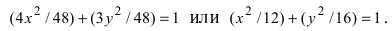
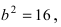
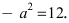
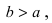
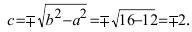
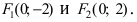
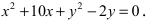
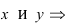
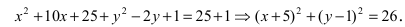
Построим в декартовой системе координат треугольник 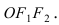
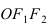
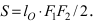
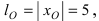
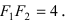
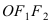
Эллипс в высшей математике
Рассмотрим уравнение
где 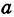
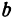
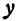
Отсюда видно, что уравнение (2) определяет две функции. Пока независимое переменное 
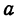

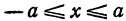
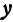
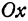
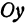
При 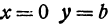
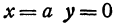
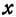

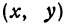
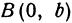
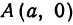
Полученная линия называется эллипсом. Число 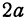
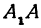
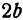
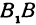
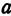
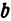
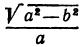
Пример:
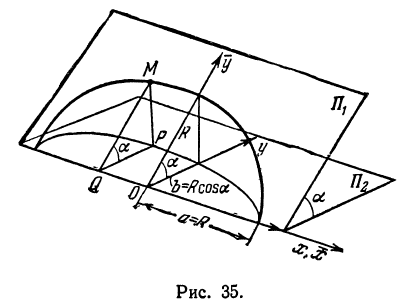
Найти проекцию окружности на плоскость, не совпадающую с плоскостью окружности.
Решение:
Возьмем две плоскости, пересекающиеся под углом 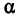
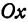
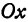
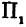
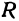
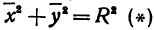
Пусть точка 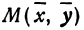
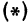
Обозначим проекцию точки 
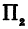
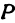
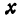
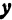


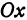
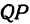
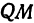
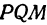
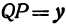
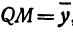
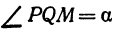
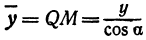


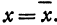
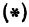
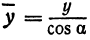
или
а это есть уравнение эллипса с полуосями 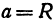
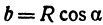
Таким образом, эллипс является проекцией окружности на плоскость, расположенную под углом к плоскости окружности.
Замечание. Окружность можно рассматривать как эллипс с равными полуосями.
Уравнение эллипсоида
Определение: Трехосным эллипсоидом называется поверхность, полученная в результате равномерной деформации (растяжения или сжатия) сферы по трем взаимно перпендикулярным направлениям.
Рассмотрим сферу радиуса R с центром в начале координат:
где Х, У, Z — текущие координаты точки сферы.
Пусть данная сфера подвергнута равномерной деформации в направлении координатных осей 
В результате сфера превратится в эллипсоид, а точка сферы М (X, У, Z) с текущими координатами Х, У, Z перейдет в точку эллипсоидам 
(рис. 206). Отсюда
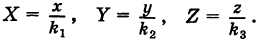
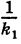
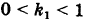
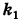
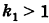
Подставляя эти формулы в уравнение (1), будем иметь
где 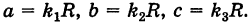
Величины 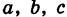
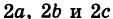
Если две полуоси эллипсоида равны между собой, то эллипсоид называется эллипсоидом вращения, так как может быть получен в результате вращения эллипса вокруг одной из его осей. Например, в геодезии считают поверхность земного шара эллипсоидом вращения с полуосями
а = b = 6377 км и с = 6356 км.
Если а = b = с, то эллипсоид превращается в сферу.
- Гипербола
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность
Эллипс, его фокусы и главные оси
Эллипс как коническое сечение, его фокусы и директрисы, получаемые геометрически с помощью шаров Данделена.
Э́ллипс (др.-греч. ἔλλειψις «опущение; нехватка, недостаток (эксцентриситета до 1)») — замкнутая кривая на плоскости, которая может быть получена как пересечение плоскости и кругового цилиндра или как ортогональная проекция окружности на плоскость.
Окружность является частным случаем эллипса. Наряду с гиперболой и параболой, эллипс является коническим сечением и квадрикой.
Определение
Эллипс — геометрическое место точек M евклидовой плоскости, для которых сумма расстояний до двух данных точек [math]displaystyle{ F_1 }[/math] и [math]displaystyle{ F_2 }[/math] (называемых фокусами) постоянна и больше расстояния между фокусами, то есть
- [math]displaystyle{ |F_1M|+|F_2M|=2cdot a }[/math], причём [math]displaystyle{ |F_1F_2|lt 2cdot a. }[/math]
Другие определения
Эллипс также можно определить как:
- фигуру, которую можно получить из окружности, применяя аффинное преобразование
- ортогональную проекцию окружности на плоскость
- пересечение плоскости и кругового цилиндра.
Связанные определения
- Проходящий через фокусы эллипса отрезок AB, концы которого лежат на эллипсе, называется большой осью данного эллипса. Длина большой оси равна 2a в вышеприведённом уравнении.
- Отрезок CD, перпендикулярный большой оси эллипса, проходящий через центральную точку большой оси, концы которого лежат на эллипсе, называется малой осью эллипса.
- Точка пересечения большой и малой осей эллипса называется его центром.
- Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях называются, соответственно, большой полуосью и малой полуосью эллипса, и обозначаются a и b.
- Расстояния [math]displaystyle{ r_1 }[/math] и [math]displaystyle{ r_2 }[/math] от каждого из фокусов до данной точки на эллипсе называются фокальными радиусами в этой точке.
- Расстояние [math]displaystyle{ c=frac{|F_1 F_2|}{2} }[/math] называется фокальным расстоянием.
- Величина [math]displaystyle{ e = frac{c}{a} = sqrt{1 — frac{b^2}{a^2}} }[/math] называется эксцентриситетом.
- Диаметром эллипса называют произвольную хорду, проходящую через его центр. Сопряжёнными диаметрами эллипса называют пару его диаметров, обладающих следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре.
- Радиус эллипса в данной точке это отрезок, соединяющий центр эллипса с точкой, а также его длина, которая вычисляется по формуле [math]displaystyle{ r=frac{ab}{sqrt{b^2 cos^2varphi + a^2 sin^2varphi}} = frac{b}{sqrt{1 — e^2 cos^2varphi}} }[/math], где [math]displaystyle{ varphi }[/math] — угол между радиусом и большой полуосью.
- Фокальным параметром [math]displaystyle{ p=frac{b^2}{a} }[/math] называется половина длины хорды, проходящей через фокус и перпендикулярной большой оси эллипса.
- Отношение длин малой и большой полуосей называется коэффициентом сжатия эллипса или эллиптичностью: [math]displaystyle{ k = frac{b}{a} }[/math]. Величина, равная [math]displaystyle{ (1-k) = frac{a-b}{a}, }[/math] называется сжатием эллипса. Для окружности коэффициент сжатия равен единице, сжатие — нулю. Коэффициент сжатия и эксцентриситет эллипса связаны соотношением [math]displaystyle{ k^2=1-e^2. }[/math]
- Для каждого из фокусов существует прямая, называемая директрисой, такая, что отношение расстояния от произвольной точки эллипса до его фокуса к расстоянию от этой точки до данной прямой равно эксцентриситету эллипса. Весь эллипс лежит по ту же сторону от такой прямой, что и фокус. Уравнения директрис эллипса в каноническом виде записываются как [math]displaystyle{ x = pmfrac{p}{eleft(1-e^2right)} }[/math] для фокусов [math]displaystyle{ left(pmfrac{pe}{1-e^2},,0right) }[/math] соответственно. Расстояние между фокусом и директрисой равно [math]displaystyle{ frac{p}{e} }[/math].
Соотношения между элементами эллипса
Части эллипса (описание см. в разделе «Связанные определения»)
- [math]displaystyle{ boldsymbol a }[/math] — большая полуось;
- [math]displaystyle{ boldsymbol b }[/math] — малая полуось;
- [math]displaystyle{ boldsymbol c }[/math] — фокальное расстояние (полурасстояние между фокусами);
- [math]displaystyle{ boldsymbol p }[/math] — фокальный параметр;
- [math]displaystyle{ boldsymbol r_p }[/math] — перифокусное расстояние (минимальное расстояние от фокуса до точки на эллипсе);
- [math]displaystyle{ boldsymbol r_a }[/math] — апофокусное расстояние (максимальное расстояние от фокуса до точки на эллипсе);
[math]displaystyle{ a^2 = b^2 + c^2; }[/math]
[math]displaystyle{ e = frac{c}{a} = sqrt{1 — frac{b^2}{a^2}};;;(0 leqslant e lt 1); }[/math]
[math]displaystyle{ p = frac{b^2}{a}. }[/math]
| [math]displaystyle{ boldsymbol a }[/math] | [math]displaystyle{ boldsymbol b }[/math] | [math]displaystyle{ boldsymbol c }[/math] | [math]displaystyle{ boldsymbol p }[/math] | [math]displaystyle{ boldsymbol {r_p} }[/math] | [math]displaystyle{ boldsymbol {r_a} }[/math] | |
|---|---|---|---|---|---|---|
| [math]displaystyle{ boldsymbol a }[/math] — большая полуось | [math]displaystyle{ boldsymbol a }[/math] | [math]displaystyle{ a = frac{b}{sqrt{1-e^2}} }[/math] | [math]displaystyle{ a = frac{c}{e} }[/math] | [math]displaystyle{ a = frac{p}{1-e^2} }[/math] | [math]displaystyle{ a = frac{r_p}{1-e} }[/math] | [math]displaystyle{ a = frac{r_a}{1+e} }[/math] |
| [math]displaystyle{ boldsymbol b }[/math] — малая полуось | [math]displaystyle{ b = a sqrt{1-e^2} }[/math] | [math]displaystyle{ boldsymbol b }[/math] | [math]displaystyle{ b = frac{c~sqrt{1-e^2}}{e} }[/math] | [math]displaystyle{ b = frac{p}{sqrt{1-e^2}} }[/math] | [math]displaystyle{ b = r_psqrt{frac{1+e}{1-e}} }[/math] | [math]displaystyle{ b = r_asqrt{frac{1-e}{1+e}} }[/math] |
| [math]displaystyle{ boldsymbol c }[/math] — фокальное расстояние | [math]displaystyle{ c = ae }[/math] | [math]displaystyle{ c = frac{be}{sqrt{1-e^2}} }[/math] | [math]displaystyle{ boldsymbol c }[/math] | [math]displaystyle{ c = frac{pe}{1-e^2} }[/math] | [math]displaystyle{ c = frac{r_pe}{1-e} }[/math] | [math]displaystyle{ c = frac{r_ae}{1+e} }[/math] |
| [math]displaystyle{ boldsymbol p }[/math] — фокальный параметр | [math]displaystyle{ p = a(1-e^2) }[/math] | [math]displaystyle{ p = b~sqrt{1-e^2} }[/math] | [math]displaystyle{ p = c~frac{1-e^2}{e} }[/math] | [math]displaystyle{ boldsymbol p }[/math] | [math]displaystyle{ p = r_p (1+e) }[/math] | [math]displaystyle{ p = r_a (1-e) }[/math] |
| [math]displaystyle{ boldsymbol r_p }[/math] — перифокусное расстояние | [math]displaystyle{ r_p = a(1-e) }[/math] | [math]displaystyle{ r_p = b~sqrt{frac{1-e}{1+e}} }[/math] | [math]displaystyle{ r_p = c~frac{1-e}{e} }[/math] | [math]displaystyle{ r_p = frac{p}{1+e} }[/math] | [math]displaystyle{ boldsymbol r_p }[/math] | [math]displaystyle{ r_p = r_afrac{1-e}{1+e} }[/math] |
| [math]displaystyle{ boldsymbol r_a }[/math] — апофокусное расстояние | [math]displaystyle{ r_a = a(1+e) }[/math] | [math]displaystyle{ r_a = b~sqrt{frac{1+e}{1-e}} }[/math] | [math]displaystyle{ r_a = c~frac{1+e}{e} }[/math] | [math]displaystyle{ r_a = frac{p}{1-e} }[/math] | [math]displaystyle{ r_a = r_p~frac{1+e}{1-e} }[/math] | [math]displaystyle{ boldsymbol r_a }[/math] |
Координатное представление
Эллипс как кривая второго порядка
Эллипс является центральной невырожденной кривой второго порядка и удовлетворяет общему уравнению вида
- [math]displaystyle{ a_{11}x^2 + a_{22}y^2+2a_{12}xy+2a_{13}x+2a_{23}y+a_{33}=0 }[/math]
при инвариантах [math]displaystyle{ D gt 0 }[/math] и [math]displaystyle{ Delta I lt 0 }[/math], где:
- [math]displaystyle{ Delta=begin{vmatrix} a_{11} & a_{12} & a_{13} \ a_{12} & a_{22} & a_{23} \ a_{13} & a_{23} & a_{33} end{vmatrix}, }[/math]
- [math]displaystyle{ D=begin{vmatrix} a_{11} & a_{12} \ a_{12} & a_{22}end{vmatrix}=a_{11}a_{22} — a_{12}^2, }[/math]
- [math]displaystyle{ I=operatorname{tr}begin{pmatrix} a_{11} & a_{12} \ a_{12} & a_{22}end{pmatrix}=a_{11}+a_{22}. }[/math]
Соотношения между инвариантами кривой второго порядка и полуосями эллипса (верно только при условии, что центр эллипса совпадает с началом координат и [math]displaystyle{ a_{33}=-1 }[/math]):
- [math]displaystyle{ Delta = -frac{1}{a^2}frac{1}{b^2}, }[/math]
- [math]displaystyle{ D = frac{1}{a^2}frac{1}{b^2}, }[/math]
- [math]displaystyle{ I = frac{1}{a^2}+frac{1}{b^2}. }[/math]
Соотношения
Если переписать общее уравнение в виде
- [math]displaystyle{ A X^2 + B X Y + C Y^2 + D X + E Y + F = 0, }[/math]
то координаты центра эллипса:
- [math]displaystyle{ h = frac{B E — 2 C D}{4 A C — B^2}, k = frac{B D — 2 A E}{4 A C — B^2}, }[/math]
угол вращения определяется из выражения
- [math]displaystyle{ tg(2 Theta) = frac{B}{A — C}. }[/math]
Направления векторов осей:
- [math]displaystyle{ begin{pmatrix}
B & (C-A+sqrt{(C-A)^2+B^2})
end{pmatrix}, begin{pmatrix}
B & (C-A-sqrt{(C-A)^2+B^2})
end{pmatrix}, }[/math]
отсюда
- [math]displaystyle{ operatorname{tg}Theta = frac{C-A pm sqrt{(C-A)^2+B^2}}{B}. }[/math]
Длины полуосей определяются выражениями
- [math]displaystyle{ a=sqrt{frac{2 F’ (sqrt{(A-C)^2+B^2}+A+C)}{4 A C-B^2}}, }[/math]
- [math]displaystyle{ b=sqrt{frac{2 F’}{sqrt{(A-C)^2+B^2}+A+C}.} }[/math]
Обратное соотношение — коэффициенты общего уравнения из параметров эллипса — можно получить, подставив в каноническое уравнение (см. раздел ниже) выражение для поворота системы координат на угол Θ и переноса в точку [math]displaystyle{ (x_c,, y_c) }[/math]:
- [math]displaystyle{ frac{x’^2}{a^2}+frac{y’^2}{b^2}=1, }[/math]
- [math]displaystyle{ x’=(x-x_c) cosTheta + (y-y_c) sinTheta, }[/math]
- [math]displaystyle{ y’=-(x-x_c) sinTheta + (y-y_c) cosTheta. }[/math]
Выполнив подстановку и раскрыв скобки, получим следующие выражения для коэффициентов общего уравнения:
- [math]displaystyle{ A=a^2 sin^2Theta + b^2 cos^2Theta, }[/math]
- [math]displaystyle{ B=2(b^2-a^2) sinTheta cosTheta, }[/math]
- [math]displaystyle{ C=a^2 cos^2Theta + b^2 sin^2Theta, }[/math]
- [math]displaystyle{ D=-2 A x_c-B y_c, }[/math]
- [math]displaystyle{ E=-B x_c-2 C y_c, }[/math]
- [math]displaystyle{ F=A x_c^2+C y_c^2+ B x_c y_c-a^2 b^2. }[/math]
Если ввести только угол, а центр эллипса оставить в начале координат, то
- [math]displaystyle{ D=0, }[/math]
- [math]displaystyle{ E=0, }[/math]
- [math]displaystyle{ F=-a^2 b^2. }[/math]
Следует заметить, что в уравнении общего вида эллипса, заданного в декартовой системе координат, коэффициенты [math]displaystyle{ A, B, C, D, E, F }[/math] (или, что то же самое, [math]displaystyle{ a_{11}, 2a_{12}, a_{22}, 2a_{13}, 2a_{23}, a_{33} }[/math]) являются определёнными с точностью до произвольного постоянного множителя, то есть приведённая выше запись и
- [math]displaystyle{ A k X^2 + B k X Y + C k Y^2 + D k X + E k Y + F k = 0, }[/math]
где [math]displaystyle{ k ne 0, }[/math] являются эквивалентными. Нельзя ожидать, что выражение
- [math]displaystyle{ 1/a^2 + 1/b^2 = A k+C k }[/math]
будет выполняться при любом [math]displaystyle{ k }[/math].
Соотношение между инвариантой [math]displaystyle{ I }[/math] и полуосями в общем виде выглядит следующим образом:
- [math]displaystyle{ frac{1}{a^2}+frac{1}{b^2} = frac{A+C}{F cdot (A cdot h^2+B cdot h cdot k+C cdot k^2 — 1)} = frac{I}{F’}, }[/math]
где [math]displaystyle{ F’ = F cdot (A cdot h^2+B cdot h cdot k+C cdot k^2 — 1) }[/math] — коэффициент [math]displaystyle{ F }[/math] при переносе начала координат в центр эллипса, когда уравнение приводится к виду
- [math]displaystyle{ A X^2 + B X Y + C Y^2 + F’ = 0. }[/math]
Другие инварианты находятся в следующих соотношениях:
- [math]displaystyle{ -frac{Delta}{F’^3} = frac{D}{F’^2} = frac{1}{a^2}frac{1}{b^2}. }[/math]
Каноническое уравнение
Для любого эллипса можно найти декартову систему координат такую, что эллипс будет описываться уравнением:
- [math]displaystyle{ frac{x^2}{a^2}+frac{y^2}{b^2}=1. }[/math]
Это уравнение называется каноническим уравнением эллипса. Оно описывает эллипс с центром в начале координат, оси которого совпадают с осями координат[Комм. 1].
Соотношения
Для определённости положим, что [math]displaystyle{ 0 lt b leqslant a. }[/math]
В этом случае величины [math]displaystyle{ a }[/math] и [math]displaystyle{ b }[/math] — соответственно, большая и малая полуоси эллипса.
Зная полуоси эллипса, можно вычислить:
- его фокальное расстояние и эксцентриситет [math]displaystyle{ left|F_1F_2right|=2sqrt{a^2-b^2},;;;e=frac{sqrt{a^2-b^2}}{a}lt 1, }[/math]
- координаты фокусов эллипса [math]displaystyle{ left(ae,,0right), left(-ae,,0right). }[/math]
Эллипс имеет две директрисы, уравнения которых можно записать как
- [math]displaystyle{ x=frac{a}{e},;;;x=-frac{a}{e}. }[/math]
Фокальный параметр (то есть половина длины хорды, проходящей через фокус и перпендикулярной оси эллипса) равен
- [math]displaystyle{ p=frac{b^2}{a}. }[/math]
Фокальные радиусы, то есть расстояния от фокусов до произвольной точки кривой [math]displaystyle{ left(x,,yright) }[/math]:
- [math]displaystyle{ r_1 = a + ex,;;;r_2 = a — ex. }[/math]
Уравнение диаметра, сопряжённого хордам с угловым коэффициентом [math]displaystyle{ k }[/math]:
- [math]displaystyle{ y=-frac{b^2}{a^2k}x. }[/math]
Уравнение касательной к эллипсу в точке [math]displaystyle{ (x_0,y_0) }[/math] имеет вид:
- [math]displaystyle{ frac{xx_0}{a^2} + frac{yy_0}{b^2} =1. }[/math]
Условие касания прямой [math]displaystyle{ y=mx+k }[/math] и эллипса [math]displaystyle{ frac{x^2}{a^2}+frac{y^2}{b^2}=1 }[/math] записывается в виде соотношения [math]displaystyle{ k^2=m^2a^2 + b^2. }[/math]
Уравнение касательных, проходящих через точку [math]displaystyle{ left(x_1, y_1right) }[/math]:
- [math]displaystyle{ frac{y-y_1}{x-x_1}=frac{-x_1y_1 pm sqrt{b^2x_1^2 + a^2y_1^2 — a^2b^2}}{a^2 — x_1^2}. }[/math]
Уравнение касательных, имеющих данный угловой коэффициент [math]displaystyle{ k }[/math]:
- [math]displaystyle{ y=kx pm sqrt{k^2a^2 + b^2}, }[/math]
точки касания такой прямой эллипса (или что то же самое, точки эллипса, где касательная имеет угол с тангенсом, равным [math]displaystyle{ k }[/math]):
- [math]displaystyle{ x=mpfrac{ka^2}{sqrt{k^2a^2 + b^2}}, y=pmfrac {b^2}{sqrt{k^2a^2 + b^2}}. }[/math]
Уравнение нормали в точке [math]displaystyle{ left(x_1, y_1right): }[/math]
- [math]displaystyle{ frac{y-y_1}{x-x_1}=frac{a^2y_1}{b^2x_1}. }[/math]
Уравнения в параметрической форме
Геометрическая иллюстрация параметризации эллипса (анимация)
Каноническое уравнение эллипса может быть параметризовано:
- [math]displaystyle{ begin{cases} x = a,cos t \ y = b,sin t end{cases};;; 0 leqslant t leqslant 2pi, }[/math]
где [math]displaystyle{ t }[/math] — параметр.
Только в случае окружности (то есть при [math]displaystyle{ a=b }[/math]) параметр [math]displaystyle{ t }[/math] является углом между положительным направлением оси абсцисс и радиус-вектором данной точки.
В полярных координатах
Если принять фокус эллипса за полюс, а большую ось — за полярную ось, то его уравнение в полярных координатах [math]displaystyle{ left(rho, varphiright) }[/math] будет иметь вид
- [math]displaystyle{ rho = frac{p}{1 pm e cos varphi}, }[/math]
где e — эксцентриситет, а p — фокальный параметр.
Знак минус соответствует помещению полюса полярных координат в левый фокус, а знак плюс — в правый.
Вывод уравнения
Пусть r1 и r2 — расстояния до данной точки эллипса от первого и второго фокусов.
Пусть также полюс системы координат находится в первом фокусе, а угол [math]displaystyle{ varphi }[/math] отсчитывается от направления на второй фокус.
Тогда из определения эллипса следует, что
- [math]displaystyle{ r_1 + r_2 = 2a }[/math].
Отсюда [math]displaystyle{ r_2^2=left( 2a — r_1 right)^2 = 4a^2 — 4ar_1 + r_1^2 }[/math].
С другой стороны, из теоремы косинусов
- [math]displaystyle{ r_2^2 = r_1^2 + 4c^2 — 4r_1c cos varphi. }[/math]
Исключая [math]displaystyle{ r_2 }[/math] из последних двух уравнений, получаем
- [math]displaystyle{ r_1 = frac{a^2-c^2}{a-c cos varphi}=frac{a(1-c^2/a^2) }{1-c/acosvarphi}. }[/math]
Учитывая, что [math]displaystyle{ p = a(1-e^2) }[/math] и [math]displaystyle{ e=frac{c}{a} }[/math], получаем искомое уравнение.
Если принять центр эллипса за полюс, а большую ось — за полярную ось, то его уравнение в полярных координатах [math]displaystyle{ left(rho, varphiright) }[/math] будет иметь вид
- [math]displaystyle{ rho = frac{b}{sqrt{1-e^2 cos^2 varphi}} = frac{ab}{sqrt{a^2 sin^2 varphi + b^2 cos^2 varphi}}. }[/math]
Длина дуги эллипса (
s) в зависимости от его параметра (
θ)
Длина дуги эллипса
Длина дуги плоской линии определяется по формуле:
- [math]displaystyle{ l = int limits_{t_1}^{t_2} sqrt{left(frac{dx}{dt}right) ^2+left(frac{dy}{dt}right)^2} ,dt. }[/math]
Воспользовавшись параметрическим представлением эллипса, получаем следующее выражение:
- [math]displaystyle{ l = int limits_{t_1}^{t_2} sqrt{a^2 sin^2 t + b^2 cos^2 t},dt. }[/math]
После замены [math]displaystyle{ b^2 = a^2 left(1 — e^2 right) }[/math] выражение для длины дуги принимает окончательный вид:
- [math]displaystyle{ l = a int limits_{t_1}^{t_2} sqrt{1 — e^2 cos^2 t},dt,;;; e lt 1. }[/math]
Получившийся интеграл принадлежит семейству эллиптических интегралов, которые в элементарных функциях не выражаются, и сводится к эллиптическому интегралу второго рода [math]displaystyle{ E left(t,e right) }[/math]. В частности, периметр эллипса равен:
- [math]displaystyle{ l = 4a int limits_{0}^{pi/2} sqrt{1 — e^2 cos^2 t},dt = 4aE(e), }[/math]
где [math]displaystyle{ E left(e right) }[/math] — полный эллиптический интеграл второго рода.
Приближённые формулы для периметра
[math]displaystyle{ L approx 4frac{pi ab + (a-b)^2}{a+b}. }[/math]
Максимальная погрешность этой формулы [math]displaystyle{ approx 0{,}63 % }[/math] при эксцентриситете эллипса [math]displaystyle{ approx 0{,}988 }[/math] (соотношение осей [math]displaystyle{ approx1/6{,}5 }[/math]).
Погрешность всегда положительна.
Приблизительно в два раза меньшие погрешности в широком диапазоне эксцентриситетов дает формула:
[math]displaystyle{ L approx 4 cdot left(a^x+b^xright)^left(1/xright) }[/math], где [math]displaystyle{ x=frac{ln 2}{lnfrac{pi}{2}}. }[/math]
Максимальная погрешность этой формулы [math]displaystyle{ approx 0{,}36 % }[/math] при эксцентриситете эллипса [math]displaystyle{ approx0{,}980 }[/math] (соотношение осей [math]displaystyle{ approx1/5 }[/math])
Погрешность также всегда положительна.
Существенно лучшую точность при [math]displaystyle{ 0{,}05lt a/blt 20 }[/math] обеспечивает формула Рамануджана:
[math]displaystyle{ L approx pileft[ 3(a+b)-sqrt{(3a+b)(a+3b)} right]. }[/math]
При эксцентриситете эллипса [math]displaystyle{ approx0{,}980 }[/math] (соотношение осей [math]displaystyle{ approx1/5 }[/math]) погрешность составляет [math]displaystyle{ approx 0{,}02 % }[/math].
Погрешность всегда отрицательна.
Ещё точней оказалась вторая формула Рамануджана:
[math]displaystyle{ L approx pi (a+b)left [1+frac{3 left (frac{a-b}{a+b} right )^2}{10+sqrt{4-3 left (frac{a-b}{a+b} right )^2}} right ]. }[/math]
Точные формулы для периметра
Джеймс Айвори[1] и Фридрих Бессель[2] независимо друг от друга получили формулу для периметра эллипса:
- [math]displaystyle{ L = pi (a+b) left [1+sum limits_{n=1}^{infty} left [ frac{(2n-1)!!}{(2n-1)cdot 2^n cdot n!}left ( frac {a-b}{a+b}right )^n right ]^2right ]. }[/math]
Альтернативная формула
- [math]displaystyle{ L = frac{2 pi a N(1-e^2)}{M(sqrt{1-e^2})}, }[/math]
где [math]displaystyle{ M(x) }[/math] — арифметико-геометрическое среднее 1 и [math]displaystyle{ x }[/math],
а [math]displaystyle{ N(x) }[/math] — модифицированное арифметико-геометрическое среднее 1 и [math]displaystyle{ x }[/math], которое было введено С. Ф. Адлаем в статье 2012 года[3].
Площадь эллипса и его сегмента
Площадь эллипса вычисляется по формуле
- [math]displaystyle{ S = pi a b. }[/math]
Площадь сегмента между дугой[en], выпуклой влево, и вертикальной хордой, проходящей через точки [math]displaystyle{ left(x,,yright) }[/math] и [math]displaystyle{ left(x,,-yright), }[/math] можно определить по формуле[4]:
- [math]displaystyle{ S = frac{pi a b}{2} — frac{b}{a} left(x,sqrt{a^2 — x^2} + a^2 arcsin frac{x}{a} right). }[/math]
Если эллипс задан уравнением
[math]displaystyle{ A x^2+ B x y + C y^2 = 1 }[/math], то площадь можно определить по формуле
- [math]displaystyle{ S = frac{2pi}{sqrt{ 4 A C — B^2 }}. }[/math]
Другие свойства
- Оптические
- Свет от источника, находящегося в одном из фокусов, отражается эллипсом так, что отраженные лучи пересекутся во втором фокусе.
- Свет от источника, находящегося вне любого из фокусов, отражается эллипсом так, что отраженные лучи ни в каком фокусе не пересекутся.
- Если [math]displaystyle{ F_1 }[/math] и [math]displaystyle{ F_2 }[/math] — фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой [math]displaystyle{ (F_1X) }[/math] равен углу между этой касательной и прямой [math]displaystyle{ (F_2X) }[/math].
- Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.
- Эквивалентная формулировка: через середины двух любых параллельных хорд эллипса проходит какой-либо диаметр эллипса. В свою очередь, любой диаметр эллипса всегда проходит через центр эллипса.
- Эволютой эллипса является астроида, вытянутая вдоль вертикальной оси.
- Точки пересечения эллипса с осями являются его вершинами.
- Эксцентриситет эллипса, то есть отношение [math]displaystyle{ e = frac{c}{a} = sqrt{1 — frac{b^2}{a^2}};;;(0 leqslant e lt 1), }[/math] характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.
- Если эксцентриситет эллипса равен нулю (что то же самое, что фокальное расстояние равно нулю: [math]displaystyle{ F_1 F_2=0 }[/math]), то эллипс вырождается в окружность.
- Экстремальные свойства[5]
- Если [math]displaystyle{ F }[/math] — выпуклая фигура и [math]displaystyle{ T_n }[/math] — вписанный в [math]displaystyle{ F }[/math] [math]displaystyle{ n }[/math]-угольник максимальной площади, то
- [math]displaystyle{ S(T_n)ge S(F)cdotfrac{n}{2cdotpi}{sin(2cdotpi/n)}, }[/math]
- Если [math]displaystyle{ F }[/math] — выпуклая фигура и [math]displaystyle{ T_n }[/math] — вписанный в [math]displaystyle{ F }[/math] [math]displaystyle{ n }[/math]-угольник максимальной площади, то
-
- где [math]displaystyle{ S(F) }[/math] обозначает площадь фигуры [math]displaystyle{ F }[/math].
- Более того, равенство достигается в том и только в том случае, если [math]displaystyle{ F }[/math] ограничено эллипсом.
- Среди всех выпуклых замкнутых кривых, ограничивающих данную площадь, эллипсы и только они имеет максимальную аффинную длину.
- где [math]displaystyle{ S(F) }[/math] обозначает площадь фигуры [math]displaystyle{ F }[/math].
- Если произвольный эллипс вписан в треугольник ABC и имеет фокусы P и Q, тогда для него справедливо соотношение[6]
-
- [math]displaystyle{ frac{overline{PA} cdot overline{QA}}{overline{CA} cdot overline{AB}} + frac{overline{PB} cdot overline{QB}}{overline{AB} cdot overline{BC}} + frac{overline{PC} cdot overline{QC}}{overline{BC} cdot overline{CA}} = 1. }[/math]
- Если лестницу (бесконечно тонкий отрезок прямой) прислонить к вертикальной стенке с горизонтальным полом, и один конец лестницы будет скользить по стенке (всё время касаясь её) а второй конец лестницы будет скользить по полу (всё время касаясь его), тогда любая фиксированная точка лестницы (не на её концах), будет двигаться по дуге некоторого эллипса. Это свойство остаётся верным, если мы возьмём точку не внутри лестницы-отрезка, а на её мыслимом продолжении. Последнее свойство используется в описанном выше[⇦] эллипсографе.
- Касательная, проходящая через точку [math]displaystyle{ (x_0,y_0) }[/math], принадлежащую эллипсу, имеет следующее уравнение:
- [math]displaystyle{ frac{x x_0}{a^2}+frac{y y_0}{b^2}=1. }[/math]
Построение эллипса
|
|
Построение эллипса с помощью иголок, нитки и карандаша |
Инструментами для рисования эллипса являются:
- эллипсограф
- две иголки, воткнутые в фокусы эллипса и соединённые ниткой длиной 2a, которую оттягивают карандашом. Способ был придуман Джеймсом Максвеллом в возрасте 14 лет и при запросе его отца в Эдинбургское королевское общество оказался ранее неизвестным[7].
При помощи циркуля или циркуля и линейки можно построить любое количество точек, принадлежащих эллипсу, но не весь эллипс целиком.
Эллипсы, связанные с треугольником
- Эллипс Брокара — эллипс с фокусами в точках Брокара
- Эллипс Мандарта
- Эллипс Штейнера
См. также
- Кривая второго порядка
- Парабола
- Каустика
- Эллипсоид
- Эллипсограф
- Гипербола
- Окружность Аполлония
- Овал Кассини
Комментарии
- ↑ Если же в правой части стоит единица со знаком минус, то получившееся уравнение
- [math]displaystyle{ frac{x^2}{a^2}+frac{y^2}{b^2}=-1 }[/math]
описывает мнимый эллипс, он не имеет точек на вещественной плоскости.
Примечания
- ↑ Ivory J. A new series for the rectification of the ellipsis (англ.) // Transactions of the Royal Society of Edinburgh. — 1798. — Vol. 4. — P. 177—190. — doi:10.1017/s0080456800030817.
- ↑ Bessel F. W. Über die Berechnung der geographischen Längen und Breiten aus geodätischen Vermesssungen (нем.) // Astron. Nachr.. — 1825. — Bd. 4. — S. 241—254. — doi:10.1002/asna.18260041601. — Bibcode: 1825AN……4..241B. В англ. переводе: Bessel F. W. The calculation of longitude and latitude from geodesic measurements (1825) (англ.) // Astron. Nachr.. — 2010. — Vol. 331. — P. 852—861. — doi:10.1002/asna.201011352. — arXiv:0908.1824.
- ↑ Adlaj S. An eloquent formula for the perimeter of an ellipse (англ.) // Notices of the AMS. — 2012. — Vol. 76, iss. 8. — P. 1094—1099. — doi:10.1090/noti879.
- ↑ Корн, 1978, с. 68.
- ↑ Фейеш Тот Л. Глава II, §§ 4, 6 // Расположения на плоскости, на сфере и в пространстве. — М.: Физматгиз, 1958. — 364 с.
- ↑ Allaire P. R., Zhou J., Yao H. Proving a nineteenth century ellipse identity (англ.) // Mathematical Gazette. — 2012. — Vol. 96, no. 535. — P. 161—165.
- ↑ Карцев В. П. Максвелл. — М.: Молодая гвардия, 1974. (Серия «Жизнь замечательных людей»). С. 26—28.
Литература
- Корн Г., Корн Т. Свойства окружностей, эллипсов, гипербол и парабол // Справочник по математике. — 4-е издание. — М.: Наука, 1978. — С. 70—73.
- Селиванов Д. Ф. Эллипс // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- А. В. Акопян, А. А. Заславский. Геометрические свойства кривых второго порядка, — М.: МЦНМО, 2007. — 136 с.
- И. Бронштейн. Эллипс // Квант, № 9, 1970.
- А. И. Маркушевич. Замечательные кривые // «Популярные лекции по математике», выпуск 4.
Ссылки
- S.Sykora, Approximations of Ellipse Perimeters and of the Complete Elliptic Integral E(x). Review of known formulae (англ.)
- Grard P. Michon. Perimeter of an Ellipse (Final Answers) (англ.), 2000—2005. — 20 c.
- Видео: Как нарисовать эллипс