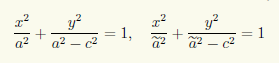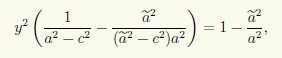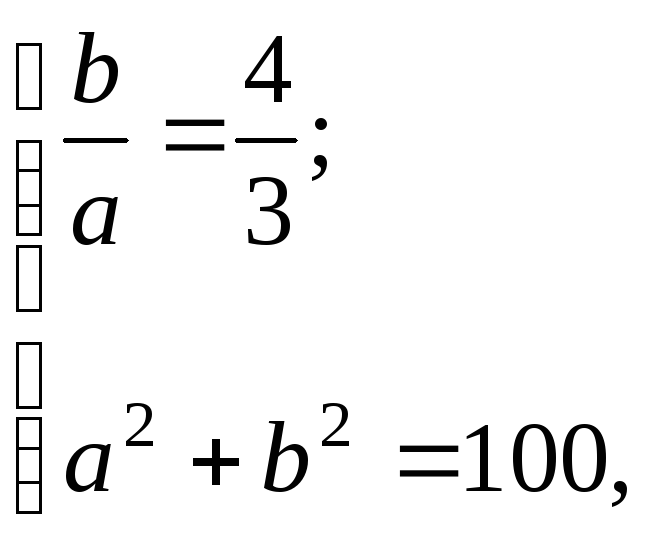Окружностью называется замкнутая плоская кривая, все точки которой равноудалены от заданной точки (центра окружности). Расстояние от любой точки окружности (Pleft( right)) до ее центра называется радиусом . Центр окружности и сама окружность лежат в одной и той же плоскости. Уравнение окружности радиуса (R) с центром в начале координат ( каноническое уравнение окружности ) имеет вид
( + = ).
Уравнение окружности радиуса (R) с центром в произвольной точке (Aleft( right)) записывается как
( <left( right)^2> + <left( right)^2> = ).
Уравнение окружности, проходящей через три точки , записывается в виде: (left| <begin<*<20>> <+ > & x & y & 1\ & <> & <> & 1\ & <> & <> & 1\ & <> & <> & 1 end> right| = 0.\)
Здесь (Aleft( <,> right)), (Bleft( <,> right)), (Cleft( <,> right)) − три точки, лежащие на окружности.
Уравнение окружности в параметрической форме
( left < beginx &= R cos t \ y &= Rsin t end right., ;;0 le t le 2pi),
где (x), (y) − координаты точек окружности, (R) − радиус окружности, (t) − параметр.
Общее уравнение окружности
(A + A + Dx + Ey + F = 0)
при условии (A ne 0), (D^2 + E^2 > 4AF).
Центр окружности расположен в точке с координатами (left( right)), где
(a = — largefrac<<2A>>normalsize,;;b = — largefrac<<2A>>normalsize.)
Радиус окружности равен
(R = sqrt <largefrac<<+ — 4AF>><<2left| A right|>>normalsize> )
Эллипсом называется плоская кривая, для каждой точки которой сумма расстояний до двух заданных точек ( фокусов эллипса ) постоянна. Расстояние между фокусами называется фокусным расстоянием и обозначается через (2c). Середина отрезка, соединяющего фокусы, называется центром эллипса . У эллипса есть две оси симметрии: первая или фокальная ось, проходящая через фокусы, и перпендикулярная ей вторая ось. Точки пересечения этих осей с эллипсом называются вершинами . Отрезок, соединяющий центр эллипса с вершиной, называется полуосью эллипса . Большая полуось обозначается через (a), малая полуось − через (b). Эллипс, центр которого находится в начале координат, а полуоси лежат на координатных прямых, описывается следующим каноническим уравнением :
(largefrac<<>><<>>normalsize + largefrac<<>><<>>normalsize = 1.)
Сумма расстояний от любой точки эллипса до его фокусов постоянна:
( + = 2a),
где (), () − расстояния от произвольной точки (Pleft( right)) до фокусов () и (), (a) − большая полуось эллипса.
Соотношение между полуосями эллипса и фокусным расстоянием
( = + ),
где (a) − большая полуось эллипса, (b) − малая полуось, (c) − половина фокусного расстояния.
Уравнение эллипса в параметрической форме
( left < beginx &= acos t \ y &= bsin t end right., ;;0 le t le 2pi),
где (a), (b) − полуоси эллипса, (t) − параметр.
Общее уравнение эллипса
(A + Bxy + C + Dx + Ey + F = 0),
где ( — 4AC Общее уравнение эллипса, полуоси которого параллельны осям координат
(A + C + Dx + Ey + F = 0),
где (AC > 0).
Периметр эллипса
(L = 4aEleft( e right)),
где (a) − большая полуось эллипса, (e) − эксцентриситет, (E) − полный эллиптический интеграл второго рода.
Площадь эллипса
(S = pi ab)
Эллипс — определение и вычисление с примерами решения
Эллипс:
Определение: Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек
Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы
Рис. 29. Вывод уравнения эллипса.
Расстояние между фокусами (фокусное расстояние) равно Согласно определению эллипса имеем Из треугольников и по теореме Пифагора найдем
соответственно. Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим Раскроем разность квадратов Подставим найденное выражение в уравнение и сократим обе части равенства на 4, тогда оно перейдет в уравнение Вновь возведем обе части равенства в квадрат Раскрывая все скобки в правой части уравнения, получим Соберем не- известные в левой части, а все известные величины перенесем в правую часть уравнения, получим Введем обозначение для разности, стоящей в скобках Уравнение принимает вид Разделив все члены уравнения на получаем каноническое уравнение эллипса: Если то эллипс вытянут вдоль оси Ох, для противоположного неравенства — вдоль оси Оу (при этом фокусы тоже расположены на этой оси). Проанализируем полученное уравнение. Если точка М(х; у) принадлежит эллипсу, то ему принадлежат и точки следовательно, эллипс симметричен относительно координатных осей, которые в данном случае будут называться осями симметрии эллипса. Найдем координаты точек пересечения эллипса с декартовыми осями:
- т.е. точками пересечения эллипса с осью абсцисс будут точки
- т.е. точками пересечения эллипса с осью ординат будут точки (Рис. 30).
Определение: Найденные точки называются вершинами эллипса.
Рис. 30. Вершины, фокусы и параметры эллипса
Определение: Если то параметр а называется большой, а параметр b — малой полуосями эллипса.
Определение: Эксцентриситетом эллипса называется отношение фокусного рас- стояния к большой полуоси эллипса
Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству Кроме того, эта характеристика описывает форму эллипса. Для демонстрации этого факта рассмотрим квадрат отношения малой полуоси эллипса к большой полуоси
Если и эллипс вырождается в окружность. Если и эллипс вырождается в отрезок
Пример:
Составить уравнение эллипса, если его большая полуось а = 5, а его эксцентриситет
Решение:
Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр Зная параметр с, можно вычислить малую полуось эллипса Следовательно, каноническое уравнение заданного эллипса имеет вид:
Пример:
Найти площадь треугольника, две вершины которого находятся в фокусах эллипса а третья вершина — в центре окружности
Решение:
Для определения координат фокусов эллипса и центра окружности преобразуем их уравнения к каноническому виду. Эллипс:
Следовательно, большая полуось эллипса а малая полуось Так как то эллипс вытянут вдоль оси ординат Оу. Определим расположение фокусов данного эллипса Итак, Окружность: Выделим полные квадраты по переменным Следовательно, центр окружности находится в точке О(-5; 1).
Построим в декартовой системе координат треугольник Согласно школьной формуле площадь треугольника равна Высота а основание Следовательно, площадь треугольника равна:
Эллипс в высшей математике
где и —заданные положительные числа. Решая его относительно , получим:
Отсюда видно, что уравнение (2) определяет две функции. Пока независимое переменное по абсолютной величине меньше , подкоренное выражение положительно, корень имеет два значения. Каждому значению , удовлетворяющему неравенству соответствуют два значения , равных по абсолютной величине. Значит, геометрическое место точек, определяемое уравнением (2), симметрично относительно оси . Так же можно убедиться в том, что оно симметрично и относительно оси . Поэтому ограничимся рассмотрением только первой четверти.
При , при . Кроме того, заметим, что если увеличивается, то разность уменьшается; стало быть, точка будет перемещаться от точки вправо вниз и попадет в точку . Из соображений симметрии изучаемое геометрическое место точек будет иметь вид, изображенный на рис. 34.
Полученная линия называется эллипсом. Число является длиной отрезка , число —длиной отрезка . Числа и называются полуосями эллипса. Число эксцентриситетом.
Пример:
Найти проекцию окружности на плоскость, не совпадающую с плоскостью окружности.
Решение:
Возьмем две плоскости, пересекающиеся под углом (рис. 35). В каждой из этих плоскостей возьмем систему координат, причем за ось примем прямую пересечения плоскостей, стало быть, ось будет общей для обеих систем. Оси ординат различны, начало координат общее для обеих систем. В плоскости возьмем окружность радиуса с центром в начале координат, ее уравнение .
Пусть точка лежит на этой окружности, тогда ее координаты удовлетворяют уравнению .
Обозначим проекцию точки на плоскость буквой , а координаты ее—через и . Опустим перпендикуляры из и на ось , это будут отрезки и . Треугольник прямоугольный, в нем , ,, следовательно, . Абсциссы точек и равны, т. е. . Подставим в уравнение значение , тогда cos
а это есть уравнение эллипса с полуосями и .
Таким образом, эллипс является проекцией окружности на плоскость, расположенную под углом к плоскости окружности.
Замечание. Окружность можно рассматривать как эллипс с равными полуосями.
Уравнение эллипсоида
Определение: Трехосным эллипсоидом называется поверхность, полученная в результате равномерной деформации (растяжения или сжатия) сферы по трем взаимно перпендикулярным направлениям.
Рассмотрим сферу радиуса R с центром в начале координат:
где Х, У, Z — текущие координаты точки сферы.
Пусть данная сфера подвергнута равномерной деформации в направлении координатных осей с коэффициентами деформации, равными
В результате сфера превратится в эллипсоид, а точка сферы М (X, У, Z) с текущими координатами Х, У, Z перейдет в точку эллипсоидам (х, у, z) с текущими координатами х, у, г, причем
Иными словами, линейные размеры сферы в направлении оси Ох уменьшаются в раз, если , и увеличиваются в раз, если и т. д.
Подставляя эти формулы в уравнение (1), будем иметь
где Уравнение (2) связывает текущие координаты точки М’ эллипсоида и, следовательно, является уравнением трехосного эллипсоида.
Величины называются полуосями эллипсоида; удвоенные величины называются осями эллипсоида и, очевидно, представляют линейные размеры его в направлениях деформации (в данном случае в направлениях осей координат).
Если две полуоси эллипсоида равны между собой, то эллипсоид называется эллипсоидом вращения, так как может быть получен в результате вращения эллипса вокруг одной из его осей. Например, в геодезии считают поверхность земного шара эллипсоидом вращения с полуосями
а = b = 6377 км и с = 6356 км.
Если а = b = с, то эллипсоид превращается в сферу.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Гипербола
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
окружность
Определение: Окружность — это линия второго порядка, которая представляет собой геометрическое место точек плоскости, равноудаленных от одной заданной точки, называемой центром.
Если центр находится в начале координат, то окружность задается каноническим уравнением второй степени вида: х2+у2=R2 , где R — радиус окружности; х,у — текущие координаты точек, лежащих на окружности.
Для вывода данного уравнения возьмем на окружности произвольную точку М(х;у). Отрезок ОМ=R является гипотенузой в прямоугольном треугольнике ОМР, а катеты определяются координатами х и у точки М. Уравнение окружности получается по теореме Пифагора: х2+у2=R2, которое называется каноническим уравнением окружности с несмещенным центром.
Если центр окружности находится в точке С(х0;у0), то уравнение окружности со смещенным центром будет иметь
Построение окружности выполняется с помощью циркуля.
эллипс
Определение: Эллипс — это линия второго порядка, которая представляет собой геометрическое место точек плоскости, сумма расстояний от которых до двух заданных точек, называемых фокусами, есть величина постоянная и равная большой оси эллипса.
Эллипс с несмещенным центром задается каноническим уравнением второй степени вида:
где а и в — полуоси, х,у — текущие координаты точек, лежащих на эллипсе. Центр симметрии находится в начале координат. Осями симметрии служат координатные оси.
При рассмотрении эллипса возможны два случая:
- 1. Если ав, то а называется большая полуось, лежащая на координатной оси Ох, а в — малая полуось, лежащая на координатной оси Оу;
- 2. Если ав, то а называется малая полуось, лежащая на координатной оси Ох, а в-большая полуось, лежащая на координатной оси Оу.
Фокусы F1 и F2 всегда лежат на большой оси эллипса, причем симметрично относительно центра симметрии на расстоянии:
где величина «с» определяет фокусное расстояние.
Для характеристики формы эллипса вводится эксцентриситет.
Определение: Эксцентриситетом эллипса называется отношение фокусного расстояния к длине его большой полуоси:
=, если ав и =, если ва.
Значение эксцентриситета меняется в пределах 0??1. При этом форма эллипса изменяется от окружности (е=0, при а=в=R) и, вытягиваясь, вырождается в прямую (е=1, при а>>в).
Уравнение эллипса выводится из его основного свойства, представленного в определении. Возьмём на эллипсе произвольную точку М(х;у). Расстояния r1 и r2 от фокусов F1 и F2 до точки М(х;у) называются фокальными радиусами.
В соответствии с определением сумма фокальных радиусов есть величина постоянная, равная большой оси эллипса: r1 + r2 = 2а (при ав) — основное свойство эллипса. Для вывода уравнения эллипса необходимо выразить фокальные радиусы r1 и r2 через координаты точки М(х;у) и фокусов F1(с;0) и F2(-с;0)и подставить в это равенство.
Если центр симметрии смещен и находится в точке С(х0;у0), то уравнение эллипса со смещенным центром имеет вид:
Построение эллипса рассмотрим ниже на примерах.
Пример. Определить вид, параметры и построить линию, заданную уравнением:
Решение: 1. Это эллипс с несмещенным центром вида:
2. Найдем параметры: — большая полуось на оси Ох;
— малая полуось на оси Оу;
Фокусы F1(4.6;0) и F2(-4.6;0) лежат на большой оси, совпадающей с осью Ох, симметрично, на расстоянии с=4.6 относительно начала координат.
- 3. Построение эллипса (см. рисунок выше) выполним по этапам:
- 1) строим систему координат Оху;
- 2) на координатных осях симметрично относительно начала координат откладываем большую и малую полуоси (а=5, в=2) и показываем вершины эллипса А1,А2,В1,В2;
- 3) через вершины эллипса параллельно координатным осям строим осевой прямоугольник;
- 4) вписываем эллипс в осевой прямоугольник;
- 5) на большой оси, совпадающей с осью Ох, симметрично относительно начала координат показываем фокусы F1(4.6;0) и F2(-4.6;0).
Определение 7.1. Множество всех точек на плоскости, для которых сумма расстояний до двух фиксированных точек F1 и F2 есть заданная постоянная величина, называют эллипсом.
Определение эллипса дает следующий способ его геометрического построения. Фиксируем на плоскости две точки F1 и F2, а неотрицательную постоянную величину обозначим через 2а. Пусть расстояние между точками F1 и F2 равно 2c. Представим себе, что нерастяжимая нить длиной 2а закреплена в точках F1 и F2, например, при помощи двух иголок. Ясно, что это возможно лишь при а ≥ с. Натянув нить карандашом, начертим линию, которая и будет эллипсом (рис. 7.1).
Итак, описываемое множество не пусто, если а ≥ с. При а = с эллипс представляет собой отрезок с концами F1 и F2, а при с = 0, т.е. если указанные в определении эллипса фиксированные точки совпадают, он является окружностью радиуса а. Отбрасывая эти вырожденные случаи, будем далее предполать, как правило, что а > с > 0.
Фиксированные точки F1 и F2 в определении 7.1 эллипса (см. рис. 7.1) называют фокусами эллипса, расстояние между ними, обозначенное через 2c, — фокальным расстоянием, а отрезки F1M и F2M, соединяющие произвольную точку M на эллипсе с его фокусами, — фокальными радиусами.
Вид эллипса полностью определяется фокальным расстоянием |F1F2| = 2с и параметром a, а его положение на плоскости — парой точек F1 и F2.
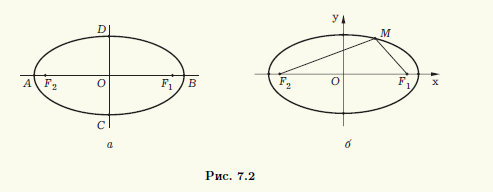
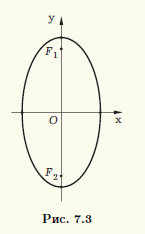
Из определения эллипса следует, что он симметричен относительно прямой, проходящей через фокусы F1 и F2, а также относительно прямой, которая делит отрезок F1F2 пополам и перпендикулярна ему (рис. 7.2, а). Эти прямые называют осями эллипса. Точка O их пересечения является центром симметрии эллипса, и ее называют центром эллипса, а точки пересечения эллипса с осями симметрии (точки A, B, C и D на рис. 7.2, а) — вершинами эллипса.
Число a называют большой полуосью эллипса, а b = √(a2 — c2) — его малой полуосью. Нетрудно заметить, что при c > 0 большая полуось a равна расстоянию от центра эллипса до тех его вершин, которые находятся на одной оси с фокусами эллипса (вершины A и B на рис. 7.2, а), а малая полуось b равна расстоянию от центра эллипса до двух других его вершин (вершины C и D на рис. 7.2, а).
Уравнение эллипса. Рассмотрим на плоскости некоторый эллипс с фокусами в точках F1 и F2, большой осью 2a. Пусть 2c — фокальное расстояние, 2c = |F1F2| < 2a. Согласно определению 7.1 эллипса, его образуют те точки M, для которых |F1M| + |F2M| = 2a.
Выберем прямоугольную систему координат Oxy на плоскости так, чтобы ее начало совпало с центром эллипса, а фокусы находились на оси абсцисс (рис. 7.2, б). Такую систему координат называют канонической для рассматриваемого эллипса, а соответствующие переменные — каноническими.
В выбранной системе координат фокусы имеют координаты F1(c;0), F2(—c;0). Используя формулу расстояния между точками, запишем условие |F1M| + |F2M| = 2a в координатах:
√((x — c)2 + y2) + √((x + c)2 + y2) = 2a. (7.2)
Это уравнение неудобно, так как в нем присутствуют два квадратных радикала. Поэтому преобразуем его. Перенесем в уравнении (7.2) второй радикал в правую часть и возведем в квадрат:
(x — c)2 + y2 = 4a2 — 4a√((x + c)2 + y2) + (x + c)2 + y2.
После раскрытия скобок и приведения подобных слагаемых получаем
√((x + c)2 + y2) = a + εx
где ε = c/a. Повторяем операцию возведения в квадрат, чтобы убрать и второй радикал: (x + c)2 + y2 = a2 + 2εax + ε2x2, или, учитывая значение введенного параметра ε, (a2 — c2) x2/a2 + y2 = a2 — c2. Так как a2 — c2 = b2 > 0, то
x2/a2 + y2/b2 = 1, a > b > 0. (7.4)
Уравнению (7.4) удовлетворяют координаты всех точек, лежащих на эллипсе. Но при выводе этого уравнения использовались неэквивалентные преобразования исходного уравнения (7.2) — два возведения в квадрат, убирающие квадратные радикалы. Возведение уравнения в квадрат является эквивалентным преобразованием, если в обеих его частях стоят величины с одинаковым знаком, но мы этого в своих преобразованиях не проверяли.
Мы можем не проверять эквивалентность преобразований, если учтем следующее. Пара точек F1 и F2, |F1F2| = 2c, на плоскости определяет семейство эллипсов с фокусами в этих точках. Каждая точка плоскости, кроме точек отрезка F1F2, принадлежит какому-нибудь эллипсу указанного семейства. При этом никакие два эллипса не пересекаются, так как сумма фокальных радиусов однозначно определяет конкретный эллипс. Итак, описанное семейство эллипсов без пересечений покрывает всю плоскость, кроме точек отрезка F1F2. Рассмотрим множество точек, координаты которых удовлетворяют уравнению (7.4) с данным значением параметра a. Может ли это множество распределяться между несколькими эллипсами? Часть точек множества принадлежит эллипсу с большой полуосью a. Пусть в этом множестве есть точка, лежащая на эллипсе с большой полуосью а. Тогда координаты этой точки подчиняются уравнению
т.е. уравнения (7.4) и (7.5) имеют общие решения. Однако легко убедиться, что система
при ã ≠ a решений не имеет. Для этого достаточно исключить, например, x из первого уравнения:
что после преобразований приводит к уравнению
не имеющему решений при ã ≠ a, поскольку 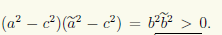
Вид эллипса. Рассмотренный выше геометрический способ построения эллипса дает достаточное представление о внешнем виде эллипса. Но вид эллипса можно исследовать и с помощью его канонического уравнения (7.4). Например, можно, считая у ≥ 0, выразить у через x: y = b√( 1 — x2/a2), и, исследовав эту функцию, построить ее график. Есть еще один способ построения эллипса. Окружность радиуса a с центром в начале канонической системы координат эллипса (7.4) описывается уравнением x2 + y2 = а2. Если ее сжать с коэффициентом a/b > 1 вдоль оси ординат, то получится кривая, которая описывается уравнением x2 + (ya/b)2 = a2, т. е. эллипс.
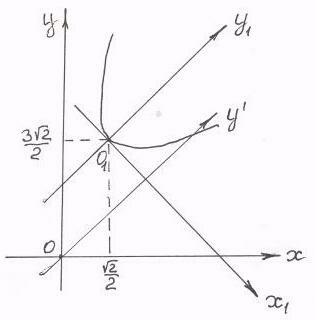
Замечание 7.1. Если ту же окружность сжать с коэффициентом a/b < 1 вдоль оси ординат, т. е. фактически растянуть в этом направлении, то получится кривая, которая описывается уравнением (7.4), в котором a < b. Это тоже эллипс, но в системе координат Oxy (рис. 7.3) его фокусы расположены на вертикальной оси симметрии. Каноническую систему координат для этого эллипса можно получить в результате поворота системы Oxy на 90°, что соответствует замене переменных x’ = y, y’ = — x.
Эксцентриситет эллипса. Отношение фокального расстояния эллипса к его большой оси называют эксцентриситетом эллипса и обозначают через ε. Для эллипса, заданного
каноническим уравнением (7.4), ε = 2c/2a = с/a. Если же в (7.4) параметры a и b связаны неравенством a < b, то фокусы расположены на вертикальной оси симметрии эллипса, с = √(b2 — a2), ε = 2c/2b = c/b.
При с =0, когда эллипс превращается в окружность, и ε = 0. В остальных случаях 0 < ε < 1. Если зафиксировать фокусы эллипса и менять его форму, устремляя эксцентриситет к единице, то в пределе получим отрезок, соединяющий фокусы, который можно назвать вырожденным эллипсом с a = с и b = 0. Если же, наоборот, зафиксировать параметр a и устремить ε к нулю, то в пределе мы получим окружность радиуса a. Эта предельная ситуация соответствует равенству параметров a и b уравнения (7.4).
Уравнение (7.3) эквивалентно уравнению (7.4), поскольку эквивалентны уравнения (7.4) и (7.2) . Поэтому уравнением эллипса является и (7.3). Кроме того, соотношение (7.3) интересно тем, что дает простую, не содержащую радикалов, формулу для длины |F2M| одного из фокальных радиусов точки M(x; у) эллипса: |F2M| = a + εx.
Аналогичная формула для второго фокального радиуса может быть получена из соображений симметрии либо повторением выкладок, в которых перед возведением в квадрат уравнения (7.2) в правую часть переносится первый радикал, а не второй. Итак, для любой точки M(x; у) на эллипсе (см. рис. 7.2)
|F1M | = a — εx, |F2M| = a + εx, (7.6)
и каждое из этих уравнений является уравнением эллипса.
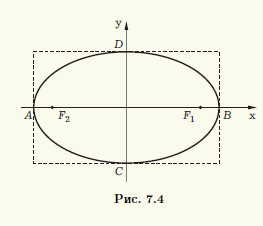
Пример 7.1. Найдем каноническое уравнение эллипса с большой полуосью 5 и эксцентриситетом 0,8 и построим его.
Зная большую полуось эллипса a = 5 и эксцентриситет ε = 0,8, найдем его малую полуось
b. Поскольку b = √(a2 — с2), а с = εa = 4, то b = √(52 — 42) = 3. Значит каноническое уравнение имеет вид x2/52 + y2/32 = 1. Для построения эллипса удобно изобразить прямоугольник с центром в начале канонической системы координат, стороны которого параллельны осям симметрии эллипса и равны его соответствующим осям (рис. 7.4). Этот прямоугольник пересекается с
осями эллипса в его вершинах A(—5; 0), B(5; 0), C(0; -3), D(0; 3), причем сам эллипс вписан в него. На рис. 7.4 указаны также фокусы F1,2(±4; 0) эллипса.
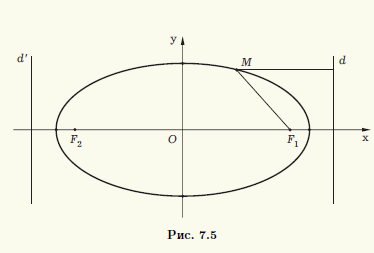
Геометрические свойства эллипса. Перепишем первое уравнение в (7.6) в виде |F1M| = (а/ε — x)ε. Отметим, что величина а/ε — x при а > с положительна, так как фокус F1 не принадлежит эллипсу. Эта величина представляет собой расстояние до вертикальной прямой d: x = а/ε от точки M(x; у), лежащей левее этой прямой. Уравнение эллипса можно записать в виде
|F1M|/(а/ε — x) = ε
Оно означает, что этот эллипс состоит из тех точек M(x; у) плоскости, для которых отношение длины фокального радиуса F1M к расстоянию до прямой d есть величина постоянная, равная ε (рис. 7.5).
У прямой d есть » двойник » — вертикальная прямая d’, симметричная d относительно центра эллипса, которая задается уравнением x = —а/ε. Относительно d’ эллипс описывается так же, как и относительно d. Обе прямые d и d’ называют директрисами эллипса. Директрисы эллипса перпендикулярны той оси симметрии эллипса, на которой расположены его фокусы, и отстоят от центра эллипса на расстояние а/ε = а2/с (см. рис. 7.5).
Расстояние p от директрисы до ближайшего к ней фокуса называют фокальным параметром эллипса. Этот параметр равен
p = a/ε — c = (a2 — c2)/c = b2/c
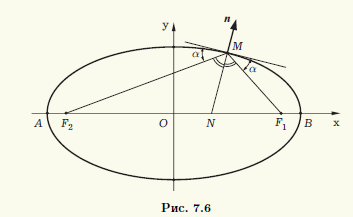
Эллипс обладает еще одним важным геометрическим свойством: фокальные радиусы F1M и F2M составляют с касательной к эллипсу в точке M равные углы (рис. 7.6).
Это свойство имеет наглядный физический смысл. Если в фокусе F1 расположить источник света, то луч, выходящий из этого фокуса, после отражения от эллипса пойдет по второму фокальному радиусу, так как после отражения он будет находиться под тем же углом к кривой, что и до отражения. Таким образом, все лучи, выходящие из фокуса F1, сконцентрируются во втором фокусе F2, и наоборот. Исходя из данной интерпретации указанное свойство называют оптическим свойством эллипса.
Примеры решения задач
Задача 6.1.
Найти полуоси, координаты фокусов и
эксцентриситет эллипса
Решение.
Разделив данное уравнение эллипса на
,
приведем его к виду.
Отсюда следует, что большая полуось
эллипса,
а малая полуось.
Известно, что,
поэтому
.
Следовательно,
координаты фокусов
и
,
а его эксцентриситет.
Ответ.
Задача 6.2.
Эллипс касается оси ординат в начале
координат, а центр симметрии его находится
в точке
.
Составить уравнение эллипса, если его
эксцентриситет равен.
Решение.
Выполним чертеж (рис. 2.35).
|
Каноническое В |
Рис. 2.35 |
Известно, что
.
Следовательно, для нахождениянадо знать
.
Найдемиз формулы эксцентриситета:
,
,
откуда.
Значит,,
Итак, уравнение
искомого эллипса
Ответ.
Задача 6.3.
Определитель траекторию точки
,
которая при своем движении остается
втрое ближе к точке,
чем к прямой
|
Решение.
Расстояние между
Следовательно, |
Рис. |
После преобразований
получаем искомое уравнение:
.
Таким образом,
точка
движется по эллипсу. При этом большая
ось эллипса и его фокусы расположены
на оси
Ответ.
.
Задача 6.4.
Действительная
полуось гиперболы
,
эксцентриситетСоставить каноническое уравнение
гиперболы и начертить ее.
Решение.
Эксцентриситет гиперболы
Следовательно,
,
,
откуда фокусы
гиперболы
,
,
а мнимая полуось.
Искомым уравнением гиперболы будет
.
|
Рис. 2.37 |
Вершины гиперболы: |
Ответ.
.
Задача 6.5. Дана
равносторонняя гипербола
.
Найти уравнение эллипса, фокусы которого
находятся в фокусах гиперболы, если
известно, что эллипс проходит через
точку.
Решение.
Для данной гиперболы
.
Следовательно, из соотношенияполучаем
,
откуда.
Значит, фокусы гиперболыи
.
В этих же точках находятся фокусы
эллипса.
Обозначим через
и
соответственно большую и малую полуоси
эллипса. Тогда при условии, что,
будем иметьДля определения
и
используем еще одно условие: что точка
лежит на эллипсе, т.е. ее координаты
должны удовлетворять уравнению эллипса
(6.8)
Это значит, что
Таким образом, для определения
и
имеем систему уравнений
решив которую,
получим
,
Подставив эти значения в уравнение
(6.8), найдем
Ответ.
Задача 6.6.
Асимптоты гиперболы имеют уравнения
.
Фокусы лежат на осии расстояние между ними равно
.
Написать каноническое уравнение
гиперболы и начертить ее.
Решение.
Так как фокусы гиперболы лежат на оси
,
то ее каноническое уравнение имеет вид
Разрешив уравнение
асимптот относительно
,
получим,
откуда.
Кроме того,,
т.е.Так как для гиперболы
,
то для нахожденияи
получим систему уравнений
|
Рис. |
решив |
Ответ.
Задача 6.7.
Составить уравнение параболы и ее
директрисы, если парабола проходит
через точки пересечения прямой
и окружности
и симметрична относительно оси
.
Решение.
Найдем точки пересечения заданных
линий, решив совместно их уравнения:
В результате
получим два решения
и
.
Точки пересеченияи
.
Так как парабола проходит через точкуи симметрична относительно оси
,
то в этой точке будет находиться вершина
параболы. Поэтому уравнение параболы
имеет вид.
Так как парабола проходит через точку,
то координаты этой точки удовлетворяют
уравнению параболы:,
,
Итак, уравнением
параболы будет
,
уравнение директрисыили
,
откуда
Ответ.
;
Задача 6.8.
Мостовая арка имеет форму параболы.
Определить параметр
этой параболы, зная, что пролет арки
равен,
а высота
Решение. выберем
прямоугольную систему координат так,
чтобы вершина параболы (мостовой арки)
находилась в начале координат, а ось
симметрии совпадала с отрицательным
направлением оси
.
В таком случае каноническое уравнение
параболы имеет вид,
а концы хорды аркии
.
Подставив координаты одного из концов
хорды (например,)
в уравнение параболы и решив полученное
уравнение относительно,
получим
Ответ.
Задача 6.9.
Привести уравнение кривой
к каноническому виду и построить эту
кривую.
Решение.
В уравнении
,
,
,
,
,
Вычислим дискриминант старших членов:
.
Так как
,
данная линия является кривой эллиптического
типа.
Найдем центр кривой
из системы
Решив ее, получим
,
.
С помощью
параллельного переноса осей координат
в центр
уравнение кривой в новой системе
приводится к виду:
,
подставив в исходное
уравнение кривой, получим
(6.9)
Для дальнейшего
упрощения уравнения (6.9) применим правило
приведения квадратичной формы к
каноническому виду. Составим
характеристическое уравнение
или
.
Отсюда
.
Повернув теперь
оси координат так, чтобы направления
осей
и
совпадали с главными направлениями
квадратичной формы, уравнение (6.5)
приведем к каноническому виду
или

Из уравнения видно,
что это эллипс с полуосями
,
.
Чтобы построить этот эллипс найдем
главное направление, соответствующее
характеристическому числу(его мы приняли за ось
в каноническом уравнении). Подставив
коэффициенты нашего уравнения в систему
получим
Полагая
,
находим, что.
Единичный вектор
оси
имеет в системе
координаты
и
.
Следовательно,,
а.
|
Повернув систему Задача и |
Рис. 3.39 |
Решение.
В исходном уравнении
,
,
,
,
,
Дискриминант старших членов
Следовательно,
уравнение определяет нецентральную
линию второго порядка, т.е. линию
параболического типа.
Составим
характеристическое уравнение квадратичной
формы старших членов:
или
Отсюда
,
Найдем главное
направление, соответствующее
характеристическому числу
.
Для этого подставим в систему
коэффициенты
нашего уравнения. Получим
Полагая
,
имеем.
Следовательно, главное направление,
соответствующее характеристическому
числу,
определяется вектором.
Нормируя его, находим единичный вектор:.
Это значит, что,
а,
т.е. поворачиваем системуна угол
.
Используя теперь
равенства (6.10), имеем:
Следовательно,
уравнение (10.17) в системе координат
принимает вид
(6.11)
Уравнение (6.11)
определяет параболу. Для приведения
его к каноническому виду найдем координаты
нового начала. Сгруппируем члены с
одинаковыми переменными и выделим
полный квадрат:
|
Рис. |
После параллельного |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
-
Полуось эллипса
Свойства
a, b — полуоси
c, d — оси
P — окружность
S — площадьПолуоси эллипса представляют собой его радиусы, расположенные относительно друг друга под углом 90 градусов. Чтобы значения полуосей были актуальными для расчета площади и длины окружности, отрезки должны лежать на осях симметрии эллипса. Значения полуосей эллипса можно взять из уравнения, задающего его в плоскости. Чтобы найти полуоси эллипса, необходимо извлечь квадратный корень из соответствующих знаменателей.
x^2/a^2 +y^2/b^2 =1Тогда, зная полуоси эллипса, можно найти его площадь и периметр по следующим формулам.
S=πab
P=4 (πab+(a-b))/(a+b)
Каноническое уравнение эллипса имеет вид
где a – большая полуось; b – малая полуось. Точки F1(c,0) и F2(-c,0) − c называются
a, b — полуоси эллипса.
Нахождение фокусов, эксцентриситета, директрис эллипса, если известно его каноническое уравнение.
Определение гиперболы. Фокусы гиперболы.
Определение. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная, меньшая расстояния между фокусами.
По определению |r1 – r2|= 2a. F1, F2 – фокусы гиперболы. F1F2 = 2c.
Каноническое уравнение гиперболы. Полуоси гиперболы. Построение гиперболы, если известно ее каноническое уравнение.
Каноническое уравнение:
Большая полуось гиперболы составляет половину минимального расстояния между двумя ветвями гиперболы, на положительной и отрицательной сторонах оси (слева и справа относительно начала координат). Для ветви расположенной на положительной стороне, полуось будет равна:
Если выразить её через коническое сечение и эксцентриситет, тогда выражение примет вид:
Нахождение фокусов, эксцентриситета, директрис гиперболы, если известно ее каноническое уравнение.
Эксцентриситет гиперболы
Определение. Отношение называется эксцентриситетом гиперболы, где с –
половина расстояния между фокусами, а – действительная полуось.
С учетом того, что с2 – а2 = b2:
Если а = b, e = , то гипербола называется равнобочной (равносторонней).
Директрисы гиперболы
Определение. Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a/e от него, называются директрисами гиперболы. Их уравнения: .
Теорема. Если r – расстояние от произвольной точки М гиперболы до какого- либо фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r/d – величина постоянная, равная эксцентриситету.
Определение параболы. Фокус и директриса параболы.
Парабола. Параболой называется геометрическое место точек, каждая из которых одинаково удалена от заданной фиксированной точки и от заданной фиксированной прямой. Точка, о которой идет речь в определении, называется фокусом параболы, а прямая — ее директрисой.
Каноническое уравнение параболы. Параметр параболы. Построение параболы.
Каноническое уравнение параболы в прямоугольной системе координат: (или , если поменять местами оси).
Построение параболы при заданной величине параметра p выполняется в следующей последовательности:
Проводят ось симметрии параболы и откладывают на ней отрезок KF=p;
Через точку K перпендикулярно оси симметрии проводят директрису DD1;
Отрезок KF делят пополам получают вершину 0 параболы;
От вершины отмеряют ряд произвольных точек 1, 2, 3, 5, 6 с постепенно увеличивающемся расстоянием между ними;
Через эти точки проводят вспомогательные прямые перпендикулярные оси параболы;
На вспомогательных прямых делают засечки радиусом равным расстоянию от прямой до директрисы;
Полученные точки соединяют плавной кривой.
Точки F
1 (–c
, 0) и F
2 (c
, 0), где называются фокусами эллипса
, при этом величина 2c
определяет междуфокусное расстояние
.
Точки А
1 (–а
, 0), А
2 (а
, 0), В
1 (0, –b
), B
2 (0, b
) называются вершинами эллипса
(рис. 9.2), при этом А
1 А
2 = 2а
образует большую ось эллипса, а В
1 В
2 – малую, – центр эллипса.
Основные параметры эллипса, характеризующие его форму:
ε
= с
/a
– эксцентриситет эллипса
;
– фокальные радиусы эллипса
(точка М
принадлежит эллипсу), причем r
1 = a
+ εx
, r
2 = a
– εx
;
– директрисы эллипса
.
Для эллипса справедливо: директрисы не пересекают границу и внутреннюю область эллипса, а также обладают свойством
Эксцентриситет эллипса выражает его меру «сжатости».
Если b
> a
> 0, то эллипс задается уравнением (9.7), для которого вместо условия (9.8) выполняется условие
Тогда 2а
– малая ось, 2b
– большая ось, – фокусы (рис. 9.3). При этом r
1 + r
2 = 2b
,
ε
= c
/b
, директрисы определяются уравнениями:
При условии имеем (в виде частного случая эллипса) окружность радиуса R
= a
. При этом с
= 0, а значит, ε
= 0.
Точки эллипса обладают характеристическим свойством
: сумма расстояний от каждой из них до фокусов есть величина постоянная, равная 2а
(рис. 9.2).
Для параметрического задания эллипса
(формула (9.7)) в случаях выполнения условий (9.8) и (9.9) в качестве параметра t
может быть взята величина угла между радиус-вектором точки, лежащей на эллипсе, и положительным направлением оси Ox
:
Если центр эллипса с полуосями находится в точке то его уравнение имеет вид:
Пример 1.
Привести уравнение эллипса x
2 + 4y
2 = 16 к каноническому виду и определить его параметры. Изобразить эллипс.
Решение
.
Разделим уравнение x
2 + 4y
2 = 16 на 16, после чего получим:
По виду полученного уравнения заключаем, что это каноническое уравнение эллипса (формула (9.7)), где а
= 4 – большая полуось, b
= 2 – малая полуось. Значит, вершинами эллипса являются точки A
1 (–4, 0), A
2 (4, 0), B
1 (0, –2), B
2 (0, 2). Так как – половина междуфокусного расстояния, то точки являются фокусами эллипса. Вычислим эксцентриситет:
Директрисы D
1 , D
2 описываются уравнениями:
Изображаем эллипс (рис. 9.4).
Пример 2.
Определить параметры эллипса
Решение.
Сравним данное уравнение с каноническим уравнением эллипса со смещенным центром. Находим центр эллипса С
: Большая полуось малая полуось прямые – главные оси. Половина междуфокусного расстояния а значит, фокусы Эксцентриситет Директрисы D
1 и D
2 могут быть описаны с помощью уравнений: (рис. 9.5).
Пример 3.
Определить, какая кривая задается уравнением, изобразить ее:
1) x
2 + y
2 + 4x
– 2y
+ 4 = 0; 2) x
2 + y
2 + 4x
– 2y
+ 6 = 0;
3) x
2 + 4y
2 – 2x
+ 16y
+ 1 = 0; 4) x
2 + 4y
2 – 2x
+ 16y
+ 17 = 0;
Решение.
1) Приведем уравнение к каноническому виду методом выделения полного квадрата двучлена:
x
2 + y
2 + 4x
– 2y
+ 4 = 0;
(x
2 + 4x
) + (y
2 – 2y
) + 4 = 0;
(x
2 + 4x
+ 4) – 4 + (y
2 – 2y
+ 1) – 1 + 4 = 0;
(x
+ 2) 2 + (y
– 1) 2 = 1.
Таким образом, уравнение может быть приведено к виду
(x
+ 2) 2 + (y
– 1) 2 = 1.
Это уравнение окружности с центром в точке (–2, 1) и радиусом R
= 1 (рис. 9.6).
2) Выделяем полные квадраты двучленов в левой части уравнения и получаем:
(x
+ 2) 2 + (y
– 1) 2 = –1.
Это уравнение не имеет смысла на множестве действительных чисел, так как левая часть неотрицательна при любых действительных значениях переменных x
и y
, а правая – отрицательна. Поэтому говорят, что это уравнение «мнимой окружности» или оно задает пустое множество точек плоскости.
3) Выделяем полные квадраты:
x
2 + 4y
2 – 2x
+ 16y
+ 1 = 0;
(x
2 – 2x
+ 1) – 1 + 4(y
2 + 4y
+ 4) – 16 + 1 = 0;
(x
– 1) 2 + 4(y
+ 2) 2 – 16 = 0;
(x
– 1) 2 + 4(y
+ 2) 2 = 16.
Значит, уравнение имеет вид:
Полученное уравнение, а следовательно, и исходное задают эллипс. Центр эллипса находится в точке О
1 (1, –2), главные оси задаются уравнениями y
= –2, x
= 1, причем большая полуось а
= 4, малая полуось b
= 2 (рис. 9.7).
4) После выделения полных квадратов имеем:
(x
– 1) 2 + 4(y
+ 2) 2 – 17 + 17 = 0 или (x
– 1) 2 + 4(y
+ 2) 2 = 0.
Полученное уравнение задает единственную точку плоскости с координатами (1, –2).
5) Приведем уравнение к каноническому виду:
Очевидно, оно задает эллипс, центр которого находится в точке главные оси задаются уравнениями причем большая полуось малая полуось (рис. 9.8).
Пример 4.
Записать уравнение касательной к окружности радиуса 2 с центром в правом фокусе эллипса x
2 + 4y
2 = 4 в точке пересечения с осью ординат.
Решение.
Уравнение эллипса приведем к каноническому виду (9.7):
Значит, и правый фокус – Поэтому, искомое уравнение окружности радиуса 2 имеет вид (рис. 9.9):
Окружность пересекает ось ординат в точках, координаты которых определяются из системы уравнений:
Получаем:
Пусть это точки N
(0; –1) и М
(0; 1). Значит, можно построить две касательные, обозначим их Т
1 и Т
2 . По известному свойству касательная перпендикулярна радиусу, проведенному в точку касания.
Пусть Тогда уравнение касательной Т
1 примет вид:
Значит, или Т
1: Оно равносильно уравнению
Определение 7.1.
Множество всех точек на плоскости, для которых сумма расстояний до двух фиксированных точек F 1 и F 2 есть заданная постоянная величина, называют эллипсом.
Определение эллипса дает следующий способ его геометрического построения. Фиксируем на плоскости две точки F 1 и F 2 , а неотрицательную постоянную величину обозначим через 2а. Пусть расстояние между точками F 1 и F 2 равно 2c. Представим себе, что нерастяжимая нить длиной 2а закреплена в точках F 1 и F 2 , например, при помощи двух иголок. Ясно, что это возможно лишь при а ≥ с. Натянув нить карандашом, начертим линию, которая и будет эллипсом (рис. 7.1).
Итак, описываемое множество не пусто, если а ≥ с. При а = с эллипс представляет собой отрезок с концами F 1 и F 2 , а при с = 0, т.е. если указанные в определении эллипса фиксированные точки совпадают, он является окружностью радиуса а. Отбрасывая эти вырожденные случаи, будем далее предполать, как правило, что а > с > 0.
Фиксированные точки F 1 и F 2 в определении 7.1 эллипса (см. рис. 7.1) называют фокусами эллипса
, расстояние между ними, обозначенное через 2c, — фокальным расстоянием
, а отрезки F 1 M и F 2 M, соединяющие произвольную точку M на эллипсе с его фокусами, — фокальными радиусами
.
Вид эллипса полностью определяется фокальным расстоянием |F 1 F 2 | = 2с и параметром a, а его положение на плоскости — парой точек F 1 и F 2 .
Из определения эллипса следует, что он симметричен относительно прямой, проходящей через фокусы F 1 и F 2 , а также относительно прямой, которая делит отрезок F 1 F 2 пополам и перпендикулярна ему (рис. 7.2, а). Эти прямые называют осями эллипса
. Точка O их пересечения является центром симметрии эллипса, и ее называют центром эллипса
, а точки пересечения эллипса с осями симметрии (точки A, B, C и D на рис. 7.2, а) — вершинами эллипса
.
Число a называют большой полуосью эллипса
, а b = √(a 2 — c 2) — его малой полуосью
. Нетрудно заметить, что при c > 0 большая полуось a равна расстоянию от центра эллипса до тех его вершин, которые находятся на одной оси с фокусами эллипса (вершины A и B на рис. 7.2, а), а малая полуось b равна расстоянию от центра эллипса до двух других его вершин (вершины C и D на рис. 7.2, а).
Уравнение эллипса.
Рассмотрим на плоскости некоторый эллипс с фокусами в точках F 1 и F 2 , большой осью 2a. Пусть 2c — фокальное расстояние, 2c = |F 1 F 2 |
Выберем прямоугольную систему координат Oxy на плоскости так, чтобы ее начало совпало с центром эллипса, а фокусы находились на оси абсцисс
(рис. 7.2, б). Такую систему координат называют канонической
для рассматриваемого эллипса, а соответствующие переменные — каноническими
.
В выбранной системе координат фокусы имеют координаты F 1 (c;0), F 2 (-c;0). Используя формулу расстояния между точками, запишем условие |F 1 M| + |F 2 M| = 2a в координатах:
√((x — c) 2 + y 2) + √((x + c) 2 + y 2) = 2a. (7.2)
Это уравнение неудобно, так как в нем присутствуют два квадратных радикала. Поэтому преобразуем его. Перенесем в уравнении (7.2) второй радикал в правую часть и возведем в квадрат:
(x — c) 2 + y 2 = 4a 2 — 4a√((x + c) 2 + y 2) + (x + c) 2 + y 2 .
После раскрытия скобок и приведения подобных слагаемых получаем
√((x + c) 2 + y 2) = a + εx
где ε = c/a. Повторяем операцию возведения в квадрат, чтобы убрать и второй радикал: (x + c) 2 + y 2 = a 2 + 2εax + ε 2 x 2 , или, учитывая значение введенного параметра ε, (a 2 — c 2) x 2 /a 2 + y 2 = a 2 — c 2 . Так как a 2 — c 2 = b 2 > 0, то
x 2 /a 2 + y 2 /b 2 = 1, a > b > 0. (7.4)
Уравнению (7.4) удовлетворяют координаты всех точек, лежащих на эллипсе. Но при выводе этого уравнения использовались неэквивалентные преобразования исходного уравнения (7.2) — два возведения в квадрат, убирающие квадратные радикалы. Возведение уравнения в квадрат является эквивалентным преобразованием, если в обеих его частях стоят величины с одинаковым знаком, но мы этого в своих преобразованиях не проверяли.
Мы можем не проверять эквивалентность преобразований, если учтем следующее. Пара точек F 1 и F 2 , |F 1 F 2 | = 2c, на плоскости определяет семейство эллипсов с фокусами в этих точках. Каждая точка плоскости, кроме точек отрезка F 1 F 2 , принадлежит какому-нибудь эллипсу указанного семейства. При этом никакие два эллипса не пересекаются, так как сумма фокальных радиусов однозначно определяет конкретный эллипс. Итак, описанное семейство эллипсов без пересечений покрывает всю плоскость, кроме точек отрезка F 1 F 2 . Рассмотрим множество точек, координаты которых удовлетворяют уравнению (7.4) с данным значением параметра a. Может ли это множество распределяться между несколькими эллипсами? Часть точек множества принадлежит эллипсу с большой полуосью a. Пусть в этом множестве есть точка, лежащая на эллипсе с большой полуосью а. Тогда координаты этой точки подчиняются уравнению
т.е. уравнения (7.4) и (7.5) имеют общие решения. Однако легко убедиться, что система
при ã ≠ a решений не имеет. Для этого достаточно исключить, например, x из первого уравнения:
что после преобразований приводит к уравнению
не имеющему решений при ã ≠ a, поскольку . Итак, (7.4) есть уравнение эллипса с большой полуосью a > 0 и малой полуосью b =√(a 2 — c 2) > 0. Его называют каноническим уравнением эллипса
.
Вид эллипса.
Рассмотренный выше геометрический способ построения эллипса дает достаточное представление о внешнем виде эллипса. Но вид эллипса можно исследовать и с помощью его канонического уравнения (7.4). Например, можно, считая у ≥ 0, выразить у через x: y = b√(1 — x 2 /a 2), и, исследовав эту функцию, построить ее график. Есть еще один способ построения эллипса. Окружность радиуса a с центром в начале канонической системы координат эллипса (7.4) описывается уравнением x 2 + y 2 = а 2 . Если ее сжать с коэффициентом a/b > 1 вдоль оси ординат
, то получится кривая, которая описывается уравнением x 2 + (ya/b) 2 = a 2 , т. е. эллипс.
Замечание 7.1.
Если ту же окружность сжать с коэффициентом a/b
Эксцентриситет эллипса
. Отношение фокального расстояния эллипса к его большой оси называют эксцентриситетом эллипса
и обозначают через ε. Для эллипса, заданного
каноническим уравнением (7.4), ε = 2c/2a = с/a. Если же в (7.4) параметры a и b связаны неравенством a
При с =0, когда эллипс превращается в окружность, и ε = 0. В остальных случаях 0
Уравнение (7.3) эквивалентно уравнению (7.4), поскольку эквивалентны уравнения (7.4) и (7.2) . Поэтому уравнением эллипса является и (7.3). Кроме того, соотношение (7.3) интересно тем, что дает простую, не содержащую радикалов, формулу для длины |F 2 M| одного из фокальных радиусов точки M(x; у) эллипса: |F 2 M| = a + εx.
Аналогичная формула для второго фокального радиуса может быть получена из соображений симметрии либо повторением выкладок, в которых перед возведением в квадрат уравнения (7.2) в правую часть переносится первый радикал, а не второй. Итак, для любой точки M(x; у) на эллипсе (см. рис. 7.2)
|F 1 M | = a — εx, |F 2 M| = a + εx, (7.6)
и каждое из этих уравнений является уравнением эллипса.
Пример 7.1.
Найдем каноническое уравнение эллипса с большой полуосью 5 и эксцентриситетом 0,8 и построим его.
Зная большую полуось эллипса a = 5 и эксцентриситет ε = 0,8, найдем его малую полуось
b. Поскольку b = √(a 2 — с 2), а с = εa = 4, то b = √(5 2 — 4 2) = 3. Значит каноническое уравнение имеет вид x 2 /5 2 + y 2 /3 2 = 1. Для построения эллипса удобно изобразить прямоугольник с центром в начале канонической системы координат, стороны которого параллельны осям симметрии эллипса и равны его соответствующим осям (рис. 7.4). Этот прямоугольник пересекается с
осями эллипса в его вершинах A(-5; 0), B(5; 0), C(0; -3), D(0; 3), причем сам эллипс вписан в него. На рис. 7.4 указаны также фокусы F 1,2 (±4; 0) эллипса.
Геометрические свойства эллипса.
Перепишем первое уравнение в (7.6) в виде |F 1 M| = (а/ε — x)ε. Отметим, что величина а/ε — x при а > с положительна, так как фокус F 1 не принадлежит эллипсу. Эта величина представляет собой расстояние до вертикальной прямой d: x = а/ε от точки M(x; у), лежащей левее этой прямой. Уравнение эллипса можно записать в виде
|F 1 M|/(а/ε — x) = ε
Оно означает, что этот эллипс состоит из тех точек M(x; у) плоскости, для которых отношение длины фокального радиуса F 1 M к расстоянию до прямой d есть величина постоянная, равная ε (рис. 7.5).
У прямой d есть » двойник » — вертикальная прямая d», симметричная d относительно центра эллипса, которая задается уравнением x = -а/ε. Относительно d» эллипс описывается так же, как и относительно d. Обе прямые d и d» называют директрисами эллипса
. Директрисы эллипса перпендикулярны той оси симметрии эллипса, на которой расположены его фокусы, и отстоят от центра эллипса на расстояние а/ε = а 2 /с (см. рис. 7.5).
Расстояние p от директрисы до ближайшего к ней фокуса называют фокальным параметром эллипса
. Этот параметр равен
p = a/ε — c = (a 2 — c 2)/c = b 2 /c
Эллипс обладает еще одним важным геометрическим свойством: фокальные радиусы F 1 M и F 2 M составляют с касательной к эллипсу в точке M равные углы (рис. 7.6).
Это свойство имеет наглядный физический смысл. Если в фокусе F 1 расположить источник света, то луч, выходящий из этого фокуса, после отражения от эллипса пойдет по второму фокальному радиусу, так как после отражения он будет находиться под тем же углом к кривой, что и до отражения. Таким образом, все лучи, выходящие из фокуса F 1 , сконцентрируются во втором фокусе F 2 , и наоборот. Исходя из данной интерпретации указанное свойство называют оптическим свойством эллипса
.
Эллипс
Эллипс. Фокусы. Уравнение эллипса.
Фокусное расстояние.
Большая и малая оси эллипса. Эксцентриситет.
Уравнение
касательной к эллипсу. Условие касания прямой
и эллипса.
Эллипсом
(рис.1
)
называется геометрическое место точек, сумма расстояний от которых до двух
заданных точек
F
1
и
F
2
,
называемых
фокусами
эллипса, есть величина постоянная.
Уравнение эллипса
(рис
.1
) :
Здесь
начало координат
является центром симметрии эллипса,
а
оси координат – его осями симметрии. При
a
>
b
фокусы эллипса лежат на оси ОХ
(рис.1) , при
a
<
b
фокусы эллипса лежат на оси О
Y
, а при
a
=
b
эллипс становится окружностью
(фокусы эллипса в этом случае совпадают с
центром окружности
). Таким образом,
окружность есть частный случай
эллипса
.
Отрезок
F
1 F
2
= 2
с
, где
,
называется фокусным расстоянием
. Отрезок
AB
= 2
a
называется большой осью эллипса
, а отрезок
CD
= 2
b
– малой осью
эллипса
. Число
e
=
c
/
a
,
e
< 1 называется эксцентриситетом
эллипса
.
Пусть
Р
(х
1 ,
у
1
) – точка эллипса, тогда
уравнение касательной к эллипсу
в