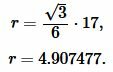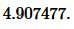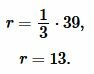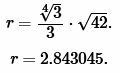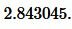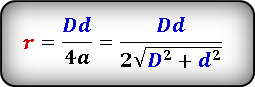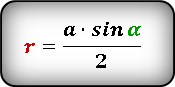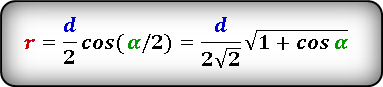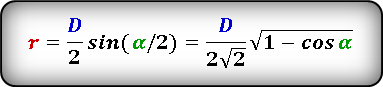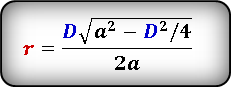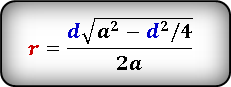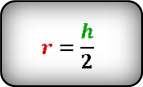Как найти малый радиус правильного треугольника

Радиус окружности правильного треугольника

Радиус окружности правильного треугольника — это
радиус вписанной и описанной около правильного
треугольника окружностей.

Если радиус окружности правильного треугольника неизвестен,
то его можно найти с помощью других величин в правильном
треугольнике. Под величинами я подразумеваю длину стороны,
площадь, периметр, высоту и так далее.

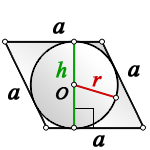
В правильном треугольнике радиус описанной окружности равен
двум радиусам вписанной окружности, и наоборот два радиуса
вписанной окружности равны радиусу описанной окружности.

Формулы радиуса окружности
правильного треугольника

Формулы радиуса окружности правильного треугольника — это
формулы, с помощью которых можно найти радиус вписанной
или описанной окружностей в правильном треугольнике,
зная другие величины в нем.

1. Формула радиуса вписанной окружности, выраженная через радиус описанной окружности.

Формула радиуса описанной окружности, выраженная через радиус вписанной окружности.

Формула радиуса вписанной окружности, выраженная через сторону.

Формула радиуса описанной окружности, выраженная через сторону.

Формула радиуса вписанной окружности, выраженная через периметр.

Формула радиуса описанной окружности, выраженная через периметр.

Формула радиуса вписанной окружности, выраженная через площадь.

Формула радиуса описанной окружности, выраженная через площадь.

Радиус вписанной окружности в равносторонний треугольник онлайн

С помощю этого онлайн калькулятора можно найти радиус вписанной в любой треугольник окружности, в том числе радиус вписанной в равносторонний треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности выберите тип треугольника, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Открыть онлайн калькулятор

1. Радиус вписанной в равносторонний треугольник окружности, если известна сторона треугольника

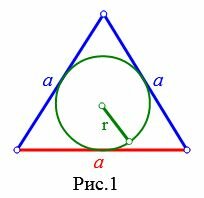
Пусть известна сторона a равностороннего треугольника (Рис.1). Выведем формулу вычисления радиуса вписанной в треугольник окружности.

Радиус вписанной в равнобедренный треугольник окружности через основание a и боковую сторону b вычисляется из следующей формулы:

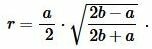(1)

Учитывая, что у равностороннего треугольника все стороны равны (( small a=b )), имеем:

( small r=frac<large a> <large 2>cdot sqrt<frac<large 2a-a><large 2a+a>> ) ( small =frac<large a> <large 2>cdot sqrt<frac<large a><large 3a>> ) ( small =frac<large a><large 2 cdot sqrt<3>> )

( small r=frac<large a><large 2 cdot sqrt<3>> )

(2)

или, умножив числитель и знаменатель на ( small sqrt <3>):

( small r=frac<large sqrt<3>> <large 6 >cdot a )

(3)

Пример 1. Известна сторона a=17 равностороннего треугольника. Найти радиус окружности вписанной в треугольник.

Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся одним из формул (2) и (3). Подставим значения ( small a=17 ) в (3):

Ответ:

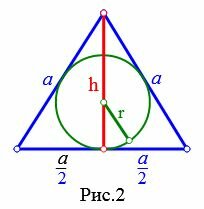
2. Радиус вписанной в равносторонний треугольник окружности, если известна высота треугольника

Пусть известна высота h равностороннего треугольника (Рис.2). Выведем формулу радиуса вписанной в треугольник окружности.

Выведем формулу стороны равностороннего треугольника через высоту. Из Теоремы Пифагора имеем:

( small h^2+left( frac<large a> <large 2>right) ^2=a^2.)

( small h^2+ frac<large a^2> <large 4>=a^2; ; ) ( small frac<large 3><large 4>a^2 =h^2; ; ) ( small a^2=frac<large4h^2><large 3>.)

( small a= frac<large 2h><large sqrt<3>> .)

(4)

Формула радиуса вписанной в равнобедренный треугольник окружности по основанию и высоте вычисляется из формулы

( small r= large frac> )

(5)

Подставляя (4) в (5), получим:

( small r= large frac<frac<large 2h^2><large sqrt<3>>><frac<large 2h><large sqrt<3>>+sqrt<frac<large 4h^2><large 3>+4h^2>> ) ( small = large frac<frac<large 2h^2><large sqrt<3>>><frac<large 2h><large sqrt<3>>+sqrt<frac<large 16h^2><large 3>>> ) ( small = large frac<frac<large 2h^2><large sqrt<3>>><frac<large 2h><large sqrt<3>>+frac<large 4h><large sqrt<3>>> ) ( small = large frac< 2h^2>< 6h>small =large frac<1> <3>small cdot h )

То есть, радиус вписанной в равносторонний треугольник окружности по высоте вычисляется из формулы:

( small r = large frac<1> <3>small cdot h )

(6)

Пример 2. Известна высота ( small h=39 ) равностороннего треугольника. Найти радиус окружности вписанной в треугольник.

Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (6). Подставим значение ( small h=39 ) в (6):

Ответ:

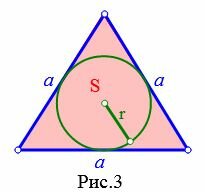
3. Радиус вписанной в равносторонний треугольник окружности, если известна площадь треугольника

Пусть известна площадь S равностороннего треугольника (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.

Площадь равностороннего треугольника по радиусу вписанной окружности вычисляется из следующей формулы:

( small S= 3cdot sqrt<3>r^2.)

( small r= large frac <sqrt[4]<3>> <3>small cdot sqrt )

(7)

Пример 3. Известна площадь равностороннего треугольника: ( small S=42 . ) Найти радиус окружности вписанной в треугольник.

Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (7). Подставим значение ( small S=42 ) в (7):

Ответ:

Правильный треугольник. Площадь правильного треугольника

Правильный треугольник — треугольник, у которого все стороны равны. Каждый угол правильного треугольника равен градусов.
Правильный треугольник называют еще равносторонним.

Каждая из высот правильного треугольника является также его медианой и биссектрисой.
Центры вписанной и описанной окружностей правильного треугольника совпадают.

Пусть сторона правильного треугольника равна .

Высота правильного треугольника:
Радиус окружности, вписанной в правильный треугольник: .
Радиус описанной окружности в два раза больше: .
Площадь правильного треугольника: .

Все эти формулы легко доказать. Если вы нацелены на решение задач части — докажите их самостоятельно.

. Сторона правильного треугольника равна . Найдите радиус окружности, вписанной в этот треугольник.

Задача решается в одну строчку. Радиус вписанной окружности .

. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна .

Сравним формулы для высоты правильного треугольника и радиуса вписанной окружности. Очевидно, радиус вписанной окружности равен высоты.

. Сторона правильного треугольника равна . Найдите радиус окружности, описанной около этого треугольника.

Радиус окружности, описанной вокруг правильного треугольника, равен .

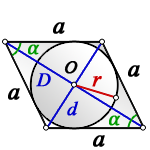
1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол

a — сторона ромба

D — большая диагональ

d — меньшая диагональ

α — острый угол

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в ромб через диагонали ( r ) :

Формула радиуса вписанной окружности в ромб через сторону и угол ( r ) :

Формула радиуса вписанной окружности в ромб через диагональ и угол ( r ) :

Формула радиуса вписанной окружности в ромб через диагональ и сторону ( r ) :

2. Радиус вписанной окружности ромба, равен половине его высоты

a — сторона ромба

h — высота

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в ромб ( r ) :

Правильный треугольник. Площадь правильного треугольника

Правильный треугольник — треугольник, у которого все стороны равны. Каждый угол правильного треугольника равен  градусов.
Правильный треугольник называют еще равносторонним.

Каждая из высот правильного треугольника является также его медианой и биссектрисой.
Центры вписанной и описанной окружностей правильного треугольника совпадают.

Пусть сторона правильного треугольника равна .

Высота правильного треугольника:
Радиус окружности, вписанной в правильный треугольник:
Радиус описанной окружности в два раза больше:
Площадь правильного треугольника:

Все эти формулы легко доказать. Если вы нацелены на решение задач части  — докажите их самостоятельно.

. Сторона правильного треугольника равна . Найдите радиус окружности, вписанной в этот треугольник.

Задача решается в одну строчку. Радиус вписанной окружности .

. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна .

Сравним формулы для высоты правильного треугольника и радиуса вписанной окружности. Очевидно, радиус вписанной окружности равен высоты.

Ответ: .

. Сторона правильного треугольника равна . Найдите радиус окружности, описанной около этого треугольника.

Радиус окружности, описанной вокруг правильного треугольника, равен .

Ответ: .

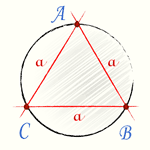
Окружность, описанная около правильного треугольника, обладает всеми свойствами описанной около произвольного треугольника окружности и, кроме того, имеет свои собственные свойства.

1) Центр описанной около треугольника окружности — точка пересечения серединных перпендикуляров к его сторонам.

Поскольку в равностороннем треугольнике медианы, высоты и биссектрисы совпадают, центр описанной около правильного треугольника окружности лежит в точке пересечения его медиан, высот и биссектрис.

Например, в правильном треугольнике ABC AB=BC=AC=a

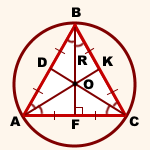
точка O — центр описанной окружности.

AK, BF и CD — медианы, высоты и биссектрисы треугольника ABC.

   

   

2) Расстояние от центра описанной окружности до вершин треугольника равно радиусу. Так как центр описанной около равностороннего треугольника окружности лежит на пересечении его медиан, а медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины, то радиус описанной окружности составляет две трети от длины медианы:

   

   

Таким образом, формула радиуса описанной около правильного треугольника окружности —

   

И обратно, сторона равностороннего треугольника через радиус описанной окружности —

   

3) Формула для нахождения площади правильного треугольника по его стороне —

   

Отсюда можем найти площадь через радиус описанной окружности:

   

Таким образом, формула площади площади правильного треугольника через радиус описанной окружности —

   

4) Центр описанной около правильного треугольника окружности совпадает с центром вписанной в него окружности.

5) Радиус описанной около равностороннего треугольника окружности в два раза больше радиуса вписанной окружности:

   

Радиус описанной окружности правильного треугольника, формула

Радиус описанной окружности правильного треугольника вычисляется по классической формуле

[
R = frac{a^3}{4sqrt{p(p-a)(p-a)(p-a)}}
]

где

[
p=frac{1}{2}(a+a+a)
]

(a — сторона правильного треугольника; R — радиус описанной окружности правильного треугольника)
После подстановок, преобразований и упрощений получается следующая формула:

[
R = frac{a}{sqrt{3}}
]

Вычислить, найти радиус описанной окружности правильного треугольника по формуле (3)

Радиус описанной окружности правильного треугольника	стр. 245