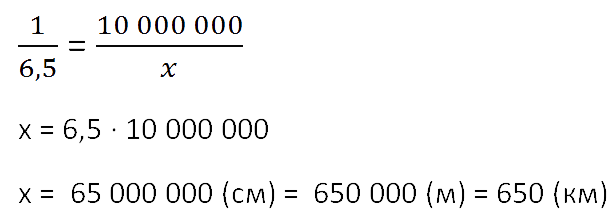План урока:
Отношение двух чисел
Определение пропорции
Масштаб
Отношение двух чисел
На уроке математики ребята выполняли самостоятельную работу. На решение самостоятельных заданий Наталья Ивановна выделила 15 минут, после чего попросила сдать тетради на проверку. Подумайте, какую часть урока заняла самостоятельная работа?
Чтобы дать ответ на данное задание, давайте вспомним, какую продолжительность имеет обычный урок? Всем известно, что стандартный урок длится 45 минут. Получается, из 45 минут только 15 дети решали самостоятельную работу. Следовательно, нужно выяснить, какая часть целого урока потрачена на самостоятельную работу. В арифметике для вычисления части от числа или определения во сколько раз одно число больше другого существует специальное понятие «Отношение чисел»:
Исходя из рассмотренного определения, необходимо составить отношение длительности самостоятельной работы к длительности целого урока. Таким образом, ответим на главный вопрос задачи. Запишем отношение (частное) двух чисел:
15/45 – данную дробь можно сократить, разделив числитель и знаменатель на 15.
15/45 = 1/3.
Выходит, что на самостоятельную работу класс потратил 1/3 всего урока.
Важно помнить, что числовое значение отношения чисел останется прежним, если каждый компонент отношения умножить или разделить на одно и то же число.
Например:
Давайте, составляющие отношения 6/7 умножим на 2, то есть на дробь 2/2.
6/7 × 2/2 (числитель умножаем на числитель, знаменатель на знаменатель);
Получаем:
6×2/7×2 = 12/14 – при сокращении на 2, получим исходную дробь.
Следовательно, числовое значение дроби не изменилось – 6/7 = 12/14.
При составлении отношений с использованием различных чисел и величин, важно помнить, что отношение будет верным, если все компоненты отношения выражены в одинаковых единицах измерения.
Разберем на примере.
В вазочке находился один килограмм конфет. Бабушка отсыпала 300 граммов сладостей в пакет. Определите, какую часть всех конфет отсыпала бабушка?
Чтобы ответить на главный вопрос задачи нужно составить отношение массы отсыпанных конфет к общей массе сладостей: 300 граммов/1 килограмм. Сразу определить числовое значение отношения не можем, составляющие имеют разные единицы измерения массы – грамм и килограмм. Выразим один килограмм в граммах:
1кг = 1000 грамм
Теперь определим, какую часть составили отсыпанные сладости:
Бабушка отсыпала 3/10 всех сладостей в пакет.
Запомни!
Если a и b числовые значения или значения, выраженные в одной и той же величине, тогда:
- отношение a/b, будет равно частному a и b;
- при условии, что a>b, отношение a/b говорит, во сколько раз a больше, чем b;
- при условии, что a<b, отношение a/b говорит, какую часть a составляет от b.
Определение пропорции
Руководитель детского хореографического кружка, для пошива костюмов своим воспитанникам, приобрел в магазине тканей 10 метров шелка, на сумму 420 рублей. Но купленной ткани не хватило. Какую сумму нужно потратить, чтобы купить еще 5 метров такого же материала?
Данную задачу можно решить двумя способами. Рассмотрим каждый из них подробно.
1 способ.
По условию нам известно, что 10 метров материала, стоит 420 рублей. Отсюда можно узнать цену одного метра. Для этого, общую сумму(420) необходимо разделить на количество приобретенной ткани(10):
420 : 10 = 42 рубля стоит один метр ткани.
Зная цену одного метра ткани, можно узнать стоимость пяти метров. Для этого стоимость одного метра (42), умножаем на количество таких метров (5):
42 × 5 = 210 рублей необходимо, для покупки 5 метров материала.
Этот способ известен еще из начальной школы. Но далеко не все задачи такого вида можно решить первым способом.
В этом случае используют второй способ решения задач такого вида.
2 способ.
Вначале, запишем краткое условие.
10м. – 420 р.
5м. – ? р.
Теперь нужно подумать. В нашем случае, количество материала уменьшается, следовательно,уменьшается стоимость покупки. Обозначим цену пяти метров материала – х.
Имеем,
10 – 420.
5 – х.
Для решения задач такого вида в математике существует специальное определение – «Пропорция»
Используя рассмотренное определение, подумаем, как составить пропорцию из чисел? Формировать пропорцию будем, опираясь на краткую запись условия задачи – десять относится к пяти как четыреста двадцать к иксу:
10/5 = 420/х.
Пропорция составлена и возникает вопрос, как вычислить неизвестный компонент?
Для вычисления неизвестной составляющей пропорции существует правило, которое называется «Основное свойство пропорции»:
Определим крайние и средние члены в составленном равенстве:
Крайними членами пропорции будут числа 10, х.
Средними членами пропорции будут числа 5, 420.
Запишем равенство произведений крайних и средних членов в составленной пропорции:
10/5 = 420/х;
10х = 5 × 420 – высчитываем произведение;
10х = 2100 – решаем как обычное уравнение;
х = 2100 : 10;
х = 210.
Выходит, 210 рублей необходимо для приобретения пяти метров материала.
Вот так на примере решения задачи мы разобрали новое определение. Запомните, пожалуйста, все правила и поиск неизвестного компонента в любых отношениях и пропорциях будет для вас только развлечением!
Продолжаем дальше знакомиться с пропорцией.
Прямая и обратная пропорциональная зависимость.
Рассмотрим ситуацию, в которой оказывается каждый, попадая в магазин.
Витя пришел в магазин за покупками. В кошельке ребенка лежало 300 рублей. Витя купил хлеб, молоко, масло, заплатил за товар. Денег у мальчика стало меньше. После посещения кондитерского отдела, где он купил карамель, пирожные, рулет денег стало совсем мало. Делаем вывод: чем больше покупок делает мальчик, тем меньше денег у него остается.
Значит, количество денег в нашем кошельке и количество покупок имеют обратно пропорциональную зависимость и являются обратно пропорциональными величинами.
А если взять ситуацию с оплатой за пользование водой и электроэнергией
Чем больше воды/электроэнергии мы используем, тем больше должны заплатить. В таком случае величины кубы воды/киловатты электроэнергии и денежные единицы называются прямо пропорциональными и имеют прямую пропорциональную зависимость.
Масштаб
Мама с Арсением решили нарисовать путь, который проходит мальчик, идя из дома в школу. Ребенок заволновался: «Как можно на листке бумаги нарисовать 450 метров пути?». Мама успокоила сына и рассказала, что именно для таких случаев и используется определение масштаба карты.
Рассмотрим решение задачи с использованием масштаба.
Расстояние на карте от Москвы до Киева составляет пять сантиметров. Вычислите, сколько километров от Москвы до Киева, если масштаб карты 1:15 000 000.
В первую очередь, нужно понимать, что масштаб 1:15 000 000 показывает, что 1 см карты содержит 15 000 000 сантиметров или 150 километров на местности.
Чтобы ответить на главный вопрос задачи,составим пропорцию. Для этого, расстояние на местности от Москвы до Киева примем за х:
1 : 150 = 5 : х.
Помним, произведение крайних членов пропорции равно произведению средних. Имеем:
х= 150 × 5;
х = 750.
Выходит, 750 километров – расстояние от Москвы до Киева.
Расчеты оказались верными. Вся справочная литература говорит о том, что расстояние Москва – Киев составляет примерно 755 км!
Теперь вы совершенно самостоятельно можете рассчитать абсолютно любое расстояние, имея под рукой линейку и карту!
Интересно!
С пропорциями мы сталкиваемся, ежедневно, ежеминутно. Все в нашем мире пропорционально. Любая вещь, предмет, техника, животные, растения – все имеет свои пропорции! Мы можем любоваться красивой архитектурой – благодаря пропорциям, наслаждаться цветками роз или ромашек – тоже не без участия пропорций. Природа создает все в строгой пропорциональности. В случае, когда пропорции отсутствуют, вещь или предмет нам кажутся неправильными. Ведь даже в нашем теле все имеет свои пропорции:
- длина ладони равна длине четырех пальцев, длина четырех ладошек(без учета пальцев) равна длине стопы, шесть ладоней – длина локтя, а четыре локтя в точности укажут на рост хозяина;
- длина человеческой ладони с пальцами составляет 1/10 роста человека;
- длина расставленных в стороны рук совпадает с длиной человеческого тела;
- стопа составляет 1/7 часть роста;
- длина от корней волос до кончика подбородка равна 1/10 роста.
Определение расстояний и превышений по бумажной карте.
Определение расстояния.
Для определения горизонтального расстояния по обычной карте, следует измерить длину линии и пересчитать пропорционально масштабу. Прямую линию можно измерить линейкой или циркулем-измерителем, извилистую (например, при измерении длины дороги или реки) — курвиметром (прибором, который можно катать по карте, а «колесико» отчитывает сантиметры).
Пересчет измеренной длины ведется пропорционально масштабу:
например, измеренное расстояние 2,5 см, а масштаб карты 1:50000 (т.е. в 1 см — 500 метров), тогда
1 см = 500 м
2,5 см = x м
x = (2,5 см * 500 м) / 1 см = 1250 м (по свойству пропорции).
При определении расстояний по мелкомасштабной карте также можно опираться на следующие сведения:
длина дуги 1° экватора
≈ 111,3 км (длина экватора 40 075 км/ 360°);
длина дуги 1° параллели 15° ≈ 108 км, 30° ≈ 96 км, 45° ≈ 79 км, 60° ≈ 56 км, 75° ≈ 29 км
(длина дуги 1° экватора (111,3 км) * cos (угла широты параллели));
длина дуги 1° меридиана ≈ 111,1 км ≈ 111 км (длина меридиана 20 004 км/ 180°).
Определение превышений.
Превышения на топографической карте показывают горизонтали. Горизонтали — это изолинии, которые соединяют одинаковые уровни высот. Под масштабом указано через сколько метров проведены сплошные горизонтали (например, через каждые 10 метров, т.е. на уровнях 10м, 20м, 30 м и т.д.), пунктиром могут быть проведены полугоризонтали между основными (где необходимо подчеркнуть характер рельефа), каждая пятая горизонталь для улучшения восприятия утолщена, пики высот подписаны дополнительно. Подписи горизонталей принято размещать верхом текста в сторону повышения высот, а в сторону понижения склона размещаются черточки, прикреплённые перпендикулярно горизонталям — бергштрихи, указывающие куда со склона потечет вода.

На примере пунктирной линии превышение между ее концами примерно 73 метра. Правый край чуть выше 210 м (≈212 м), левый чуть ниже 140 м (≈139 м).
При построении профиля следует учесть, что чем ближе (чаще) расположены горизонтали друг к другу, тем круче спуск.
На мелкомасштабных физических картах вместо горизонталей используют цветовую высотную шкалу — зелеными тонами низины, коричневыми — горы.
Определение длины линии в трехмерном пространстве.
Если расстояние по горизонтали между точками 400 метров, а разница высот между этими точками 300 метров, то длина линии в трехмерном пространстве между точками будет составлять 500 метров (подсчёт аналогичен вычислению гипотенузы по теореме Пифагора).
Вести пересчёт имеет смысл только при построении маршрута в горном рельефе с резкими перепадами высот. При достаточно плоском равнинном рельефе или при измерениях по мелкомасштабным картам длина линии в трехмерном пространстве практически не будет отличаться от горизонтального расстояния, учитывать перепад высот в таких случаях не имеет смысла.
На заданиях ОГЭ/ЕГЭ и в школьных задачах под определением расстояния по прямой подразумевается расстояние по горизонтали, учитывать, что точки могут находиться на разных высотах и пересчитывать длину линии с учетом этого не нужно!Определение расстояний и превышений по электронной карте.
Большинство электронных карт имеют инструменты для измерения расстояний по прямой или по дорогам специальным функционалом, например, построением маршрута. При построении маршрута большинство электронных карт (например, Яндекс-карты) учитывают все изгибы дороги, но не пересчитывают расстояния с учетом перепада высот (к примеру, перейти через ущелье по подвесному мосту, или по кратчайшей прямой траектории, но без моста, спустившись вниз и затем поднявшись на другой берег — это разные расстояния). Некоторые приложения навигации (например Maps.me при переходе в режим пешеходной или велонавигации) просчитывают расстояния с учётом перепада высот и отображают превышения.
Понятие масштаб тесно связано с отношением чисел и пропорциями.
Поэтому, если вы не уверены в своих знаниях по этим темам, настоятельно рекомендуем
изучить их еще раз.
Вы можете сделать это и на нашем ресурсе в темах
отношение чисел
и
пропорции.
Масштаб — важное понятие. Если вы научитесь его правильно понимать, он поможет
вам не только в математике, но и в географии, черчении, а порой и в физике.
Запомните!
Масштабом называют отношение длины отрезка на карте к длине соответствующего отрезка на местности (в реальности).
Масштаб записывают в виде отношения двух чисел. Первый член отношения обычно равен 1,
а второй член — число, показывающее во сколько раз длина единицы расстояния (см, м или км) на карте меньше
соответствующий единицы расстояния в реальности.
Разберёмся на примере:
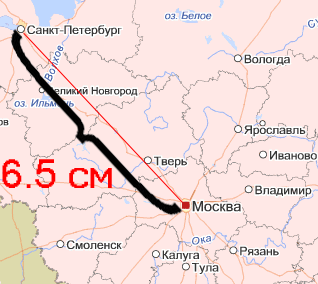
Ниже представлена часть карты с масштабом 1 : 10 000 000 (см). Такой масштаб означает, что
в 1 см на карте помещается 10 000 000 (см) реального расстояния,
или 100 000 (м), или 100 (км).
Говорят, что карта сделана в масштабе однадесятимиллионная (по названию десятичной дроби, в
которую может превратиться отношение
1 : 10 000 000 = 0,000 000 1.
Санкт-Петербург и Москва на карте соединены отрезком длиной в 6,5 (см).
Определим, сколько в реальности (км) между Москвой и Санкт-Петербургом.
Для решения этой задачи составим таблицу и занесём в неё нужные данные. Неизвестную величину обозначим за
«x».
| На карте | В реальности | |
|---|---|---|
| Масштаб | 1 (см) | 10 000 000 (см) |
| Расстояние между Москвой и Петербургом |
6,5 (см) | x (см) |
Составим и решим пропорцию:
Ответ: 650 км — приблизительное расстояние между Москвой и Санкт-Петербургом.
Теперь, зная, что такое масштаб, вы легко с помощью линейки можете измерить расстояние на карте или на чертеже и
рассчитать нужное расстояние в реальности.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
14 февраля 2016 в 19:27
Марина Трескина
Профиль
Благодарили: 0
Сообщений: 1
Марина Трескина
Профиль
Благодарили: 0
Сообщений: 1
помогите пожайлуста я немогу найти маштаб карты, точнее я не могу понять как его находить
Например
расстояние между пунктами М и К на карте = 3.4 см, а на местности 680км. Найди маштаб карты
0
Спасибо
Ответить
20 февраля 2016 в 16:15
Ответ для Марина Трескина
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Масштаб 1: 20 000 000
Подробно описано здесь.
А ещё, «масштаб» пишется с буквой «С».
0
Спасибо
Ответить
30 сентября 2016 в 14:49
Ответ для Марина Трескина
Ольга Чикалова-Елисеева
Профиль
Благодарили: 0
Сообщений: 2
Ольга Чикалова-Елисеева
Профиль
Благодарили: 0
Сообщений: 2
Доброго времени суток. Помогите пожалуйста, я в тупике.
Суть вопроса: плоскости примыкают друг другу под углом 45 градусов. Сами плоскости имеют наклон 5 градусов от внутреннего угла к внешнему. При таком условии градус примыкания должен измениться. Как рассчитать точный градус примыкания?
0
Спасибо
Ответить
30 сентября 2016 в 23:43
Ответ для Марина Трескина
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Попробуйте продублировать вопрос не в какой то теме, а отдельно. К сожалению, я не понимаю задачу. Может кто-нибудь на форуме сможет ответить. Удачи!
0
Спасибо
Ответить
8 февраля 2016 в 15:26
Лиана Мусилева
Профиль
Благодарили: 0
Сообщений: 1
Лиана Мусилева
Профиль
Благодарили: 0
Сообщений: 1
Какую длину имеет на карте отрезок, изображающий растояние 85км, если масштаб карты 1:1000000.
Как решить подробно с помощью таблицы?
0
Спасибо
Ответить
19 сентября 2016 в 11:55
Ответ для Лиана Мусилева
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
В данной теме очень подробно расписано с примерами. Рекомендую ознакомиться.
1
Спасибо
Ответить
13 октября 2015 в 20:41
Маргарита Помешкина
Профиль
Благодарили: 0
Сообщений: 3
Маргарита Помешкина
Профиль
Благодарили: 0
Сообщений: 3
расстояние на местности 7целых 3 десятых изоброжено на карте отрезком в 1 см.опредилите масштаб карты.
0
Спасибо
Ответить
13 октября 2015 в 20:45
Ответ для Маргарита Помешкина
Маргарита Помешкина
Профиль
Благодарили: 0
Сообщений: 3
Маргарита Помешкина
Профиль
Благодарили: 0
Сообщений: 3
решение
0
Спасибо
Ответить
15 сентября 2016 в 9:07
Ответ для Маргарита Помешкина
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Про масштаб и его вычисление можно прочитать здесь. Ответ: 1:730 000
0
Спасибо
Ответить
28 августа 2015 в 12:10
Амина Умирова
Профиль
Благодарили: 0
Сообщений: 1
Амина Умирова
Профиль
Благодарили: 0
Сообщений: 1
На карте чей масштаб 1:25000000 расстояние между двумя городами 12 см. Найдите истенное расстояние между двумя городами
0
Спасибо
Ответить
31 августа 2015 в 15:19
Ответ для Амина Умирова
Кристина Терёшкина
Профиль
Благодарили: 0
Сообщений: 1
Кристина Терёшкина
Профиль
Благодарили: 0
Сообщений: 1
Задача решается пропорцией.
1/12=25000000/x
Значит, 12 умножаем на 25000000.
Получается 300000000 Мы превращаем см в км.
Поэтому, 300000000(см)=3000000(м)=3000(км)
Ответ: расстояние между городами 3000 км
0
Спасибо
Ответить
Понятие масштаба
Чтобы понять, что такое масштаб в математике нужно вспомнить тему отношений чисел и пропорций.
Масштаб — это дробь, где в числителе единица, а в знаменателе то число, которое показывает во сколько раз уменьшено расстояние на плане местности, чем на самой местности.
Другими словами, масштабом называют отношение длины отрезка на карте к длине соответствующего отрезка на местности.
- Например, одна тысячная (1:1000) означает, что все расстояния на местности уменьшены в тысячу раз. Чем больше число в знаменателе дроби, тем больше уменьшение и тем больше охват территории.
Масштаб бывает трех видов:
- численный, выражается в числах 1:1000;
- именованный, выражается словами, то есть см переводим в м: в 1см 10м, 10м — это величина масштаба;
- линейный, зная величину масштаба, можно определить расстояния.
Определение масштаба на карте
На математике в 6 классе обязательно будут задания, как найти масштаб карты. Разберемся в этом вопросе.
Нужно потратить очень много сил, чтобы изобразить дом в натуральную величину, поэтому и придумали такой инструмент, как масштаб. Ведь намного проще описать большой объект в рисунке, чертеже или макете.
Масштаб — это отношение размера изображения к размеру изображаемого объекта.
Масштаб карты — это отношение длины отрезка на карте к его действительной длине на местности.
На карте Российской Федерации указан масштаб (1 : 500 000). Читается это так: карта сделана в масштабе одна пятисот тысячная. Такой масштаб значит, что в 1 см на карте помещается 500 000 см реального расстояния. То есть отрезок на изображении в 1 см соответствует отрезку на местности в 5 км. А если взять отрезок в 3 см, то на местности этот отрезок составит 15 км.
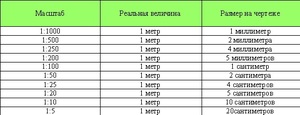
Численные масштабы карт и соответствующие им масштабы на местности:
Масштаб 1 : 100 000
- 1 мм на карте — 100 м (0,1 км) на местности
- 1 см на карте — 1000 м (1 км) на местности
- 10 см на карте — 10000 м (10 км) на местности
Масштаб 1 : 10000
- 1 мм на карте — 10 м (0,01 км) на местности
- 1 см на карте — 100 м (0,1 км) на местности
- 10 см на карте — 1000 м (1 км) на местности
Масштаб 1 : 5000
- 1 мм на карте — 5 м (0,005 км) на местности
- 1 см на карте — 50 м (0,05 км) на местности
- 10 см на карте — 500 м (0,5 км) на местности
Масштаб 1 : 2000
- 1 мм на карте — 2 м (0,002 км) на местности
- 1 см на карте — 20 м (0,02 км) на местности
- 10 см на карте — 200 м (0,2 км) на местности
Масштаб 1 : 1000
- 1 мм на карте — 100 см (1 м) на местности
- 1 см на карте — 1000 см (10 м) на местности
- 10 см на карте — 100 м на местности
Масштаб 1 : 500
- 1 мм на карте — 50 см (0,5 метра) на местности
- 1 см на карте — 5 м на местности
- 10 см на карте — 50 м на местности
Масштаб 1 : 200
- 1 мм на карте — 0,2 м (20 см) на местности
- 1 см на карте — 2 м (200 см) на местности
- 10 см на карте — 20 м (0,2 км) на местности
Масштаб 1 : 100
- 1 мм на карте — 0,1 м (10 см) на местности
- 1 см на карте — 1 м (100 см) на местности
- 10 см на карте — 10м (0,01 км) на местности
Определение масштаба и пропорций рисунка и расчет модельных элементов конструкции (4ч)
Цель работы: освоение методов масштабирования и пропорционирования при работе с эскизом модели.
Содержание работы:
1. Изучение принципов масштабирования и пропорционирования при работе с эскизом модели.
2. Выбор модели для анализа.
3. Оформление технического рисунка модели с использованием приемов масштабирования и расчет модельных элементов.
4. Оформление технического рисунка модели с использованием приемов пропорционирования и расчет модельных элементов.
5. Анализ результатов работы и формулировка выводов.
Пособия и инструменты: каталоги, журналы мод, эскизы и фотографии моделей одежды различных видов, чертежные принадлежности, калькулятор.
Методические указания
Работа выполняется студентами индивидуально. Каждый студент в соответствии с заданием выполняет все этапы содержания лабораторной работы. В отчете должны быть представлены художественный и технический рисунки выбранной для анализа модели, заполненные таблицы, художественно-конструктивное описание модели.
1. Изучение принципов масштабирования и пропорционирования при работе с эскизом модели студенты проводят самостоятельно по лекционному материалу и рекомендуемой литературе. Такая работа может быть выполнена в порядке домашней подготовки к лабораторной работе.
2. Модель для анализа студенты выбирают по согласованию с преподавателем на основе каталогов, журналов мод, эскизов и фотографий модных образцов одежды различных видов. Представляется художественный рисунок модели с обязательным изображением видов спереди и сзади (рис.1).
3. Анализ модели удобно проводить по ее техническому рисунку. Технический рисунок позволяет правильно выбрать прибавки и является основным источником информации при техническом моделировании.
Художественный эскиз модели
Рис. 1
Фигура в техническом рисунке (рис. 2) изображается в соответствии с пропорциями для высоких фигур, при этом используется модуль, равный высоте головы (без прически и головного убора).
Рост фигуры приблизительно включает 8 модулей, при этом на рисунке расстояние от макушки до линий груди — 2 модуля, до линии талии — 3 модуля, до линии бедер — 4 модуля.
Изображение человека дается в статике с нанесением конструктивных уровней плеч, груди, талии, бедер, коленей и низа (см. рис. 2). Также через все изображения следует провести центральные вертикальные линии, позволяющие судить о симметричности деталей и членений в модели. Ориентиром для проведения центральной вертикальной линии спереди является яремная впадина, пуговицы центральной застежки. При фронтальном расположении фигуры можно воспользоваться серединой расстоянии между элементами (линиями проймы, рельефами и др.)
Помимо вида спереди и сзади целесообразно представлять вид сбоку, особенно если есть фасонные или конструктивные элементы, видимые сбоку.
Метод масштабирования основан на определении масштаба рисунка, с помощью которого рассчитываются параметры модельных элементов и их месторасположение на чертеже конструкции.
Определяются два масштаба: вертикальный и горизонтальный.
Для установления вертикального
масштаба чаще всего используется рост фигуры:
Мв = Рв.нат / Рв.рис, (1)
где Рв.нат — размер в натуральную величину по вертикали, т.е. рост фигуры, на который проектируется одежда;
Рв.рис. — размер на рисунке по вертикали, т.е. рост фигуры на рисунке.
Горизонтальный
масштаб удобно определять через стандартные размеры деталей, например, ширину плеча:
Мг = Рг.нат / Рг.рис, (2)
где Рг.нат — размер в натуральную величину по горизонтали, т.е. ширина плечевого ската Шп в конструкции;
Рг.рис — соответствующий размер на рисунке по горизонтали —к.
Размеры любых деталей в натуральную величину в вертикальном и горизонтальном направлении рассчитываются с использованием соответствующих коэффициентов:
Размер детали по вертикали:
Рв.нат = Мв*Рв.рис. , (3)
Размер детали по горизонтали:
Рв.нат = Мв*Рв.рис. , (4)
Студенты обозначают на техническом рисунке участки, требуемые для определения масштабов, а также параметры модельных элементов, размеры которых требуется рассчитать с использованием масштабов.
Технический рисунок модели
Рис. 2
Результаты расчетов помещают в табл. 1, 2.
В табл. 1 данные графы 6 рассчитываются путем деления данных графы 2 на данные графы 4. В табл. 2 данные графы 6 рассчитываются путем произведения данных графы 2 и графы 5.
Таблица 1
Определение масштаба рисунка
| Участок в натуральную величину | Участок на рисунке | Условное обозначение масштаба | Величина масштаба |
| наименование | величина, см. | наименование | величина, см. |
Таблица 2
Размеры участков и элементов модельной конструкции
| Наименование участка, элемента | Величина на рисунке, см | Масштаб | Размеры искомого участка на чертеже, см |
| условное обозначение | величина |
4. Метод пропорционирования основан на определении пропорциональных соотношений между размерами деталей, других элементов конструкции и размерами всего изделия или его части.
Например, длину разреза на юбке в вертикальном направлении е— можно определить по отношению к длине всей юбки д (см. рис.2). Для этого составляется пропорция, устанавливающая, что соотношение размеров деталей на рисунке сохраняется для чертежа конструкции изделия в натуральную величину:
е / д = (Дразреза / Дюбки)черт., (5)
Тогда искомый размер детали (например, длина разреза в натуральную величину, т.е. на чертеже) можно найти по формуле:
е = (Дразреза / Дюбки)рис.* д, (6)
Если левую сторону равенства (5) обозначить коэффициентом пропорционирования Ki, то выше обозначенные формулы примут вид:
Ki = Р i рис / Р рис, (7)
где Ki — коэффициент пропорционирования, определяется по рисунку,
Pi — размер i-той детали по рисунку, размер которой требуется определить,
Р рис. — размер всей детали на рисунке, на которой находится i-й элемент и относительно которой производится поиск пропорций.
Тогда размер детали в натуральную величину, для чертежа, будет рассчитываться:
Р i черт = Ki* Р черт, (8)
где Р i черт — искомый размер i-той детали на чертеже,
Ki — коэффициент пропорционирования, определенный по рисунку,
Р черт — размер всей детали.
В примере с разрезом юбки Pi — длина разреза по вертикали, Р -длина юбки.
Аналогично можно определить глубину горловины переда а относительно длины жакета б (см. рис. 2), величину укорочения юбки с левой стороны и относительно длины юбки д, а также ширину выреза горловины в самом узком месте в и ширину отделочной строчки г – относительно ширины плеча к (или ширины переда жакета).
Рекомендуется также определить угол наклона рельефной линии с отделочной строчкой a.
По сравнению с методом масштабирования метод пропорционирования имеет большую точность, однако трудоемок, так как для каждого i-того элемента конструкции требуется рассчитать отдельный коэффициент Ki.
Студенты обозначают на техническом рисунке участки и параметры модельных элементов, размеры которых требуется рассчитать с использованием метода пропорционирования. Рекомендуется использовать те же участки, которые уже рассчитывались с помощью масштабов. Это позволит в дальнейшем провести сравнительный анализ обоих методов с точки зрения их точности и трудоемкости. Результаты расчетов помещают в табл. 3.
В табл. З данные графы 7 рассчитываются путем произведения данных графы 5 и графы 6.
Таблица 3
Определение пропорций рисунка и размеров деталей
| Наименование искомого участка | Вели-чина на рисун-ке, см | Наименова-ние всей детали | Величина всей детали, см | Коэффици- ент пропор-циониро- вания | Размеры искомого участка в натур. величину, см |
| на рисунке | в натур. величину | ||||
| Длина разреза юбки | 2,3 | длина юбки | 5,9 | 0,390 | 23,4 |
5. При анализе результатов лабораторной работы требуется сравнить рассматриваемые методы переноса модельных элементов с рисунка на чертеж с точки зрения их точности и трудоемкости. Выводы должны быть сформулированы конкретно по полученным результатам.
Контрольные вопросы:
1. В чем сущность метода масштабирования?
2. Каковы основные требования для нанесения на технический рисунок модели участков, размеры которых могут быть определены с помощью метода масштабирования?
3. Как рассчитать параметры модельного элемента при использовании масштаба рисунка?
4. В чем сущность метода пропорционирования?
5. Как рассчитать коэффициент пропорционирования?
6. Как правильно составить пропорцию для определения параметров модельной конструкции?
Литература:
1. Коблякова Е.Б., Г.С.Ивлева и др. Конструирование одежды с элементами САПР: Учебное пособие для вузов, М.: Легпромбытиздат, 1988.
2. Мартынова А.И., Андреева Е.Г. Конструктивное моделирование одежды: Учебное пособие для вузов, М.: МГАЛП, 1999.- 216с.
3. Матузова Е.М., Соколова Р.И., Гончарук Н.С. Разработка конструкций изделий по моделям. М.: Легкая и пищевая промышленность, 1983.
Лабораторная работа №2
Чаще всего среднестатистический житель нашей планеты сталкивается со словом «масштаб», изучая географию. Надпись в нижнем углу географической карты выглядит приблизительно таким образом: «Масштаб 1:100».
Это понятие означает отношение размера объекта на карте или плане к его фактической величине.
Содержание:
- Виды масштаба и способы его выражения
- Как определить масштаб объекта
- Инструкция для измерений и вычислений
- Особенности расчетов
- Онлайн-калькулятор
Виды масштаба и способы его выражения
На планах, картах и рисунках отношение между реальными и изображенными объектами может быть зафиксировано не только с помощью чисел, но и с помощью графика. Численное — записывается дробью. Зачастую числитель этой дроби приравнивается к единице, в то время как знаменатель указывает степень уменьшения. Например, надпись 1:100 говорит о том, что 1 см на плане отвечает 100 см на местности. Чем крупнее масштаб, тем меньше знаменатель: 1:10000 более крупный, чем 1:50 000.
Графические масштабы имеют линейный и поперечный подвиды. Линейный — это подвид, представленный наподобие маленькой линеечки, разделенной на эквивалентные отрезки. Поперечный — это специальный график, который еще называется «номограмма».
В архитектуре и проектировании используются типовые варианты масштабирования, их нельзя выбирать произвольно. Зачастую это масштабы уменьшения, например, 1:2, 1:10, 1:100 и так далее. Для изготовления таких изделий, как болт или гайка, используют масштабы увеличения 50:1;100:1.
Необходимо помнить, что все без исключения величины должны оставаться соразмерными. Если не учитывать первоначальные пропорции, то исследовать расстояния и габариты объектов будет невозможно.
Как определить масштаб объекта
Допустим, вы определяете масштаб впервые. Значит, начать вам нужно с простейшего измерения объектов, пропорции которых необходимо выяснить. Для этого возьмите план какого-нибудь строения, например, дома или квартиры. Идеально подойдет план участка с несколькими постройками. Обязательное условие — это должен быть реальный объект, так как нужно сопоставить размеры реального здания и его размеры на плане.
Инструкция для измерений и вычислений
Тщательно исследуйте план и определите здание, которым будете заниматься.
- Сделайте замеры строения на плане и зафиксируйте результат.
- Измерьте объект в реальности. Для этого понадобится рулетка или сантиметровая лента. Чтобы измерения получились достоверными лучше взять с собой помощника. Если такой возможности нет используйте деревянные колышки. Расставьте колышки в землю так, чтобы исходная отметка на рулетке или измерительной ленте совпадала с начальной точкой измерений.
- Произведите расчет: удобнее всего это сделать с помощью простейших математических вычислений.
К примеру, стена хозяйственной постройки реальной протяженностью 4 метра занимает на плане 2 см. Переводим эту величину в сантиметры и получаем, что 2 см на рисунке отвечает 400 см в реальности. При этом используем простое деление:
400:2= 200
Значит, 1 см изображенный на карте — это 2 м на территории.
Особенности расчетов
Итак, вам нужно представить какой-то рисунок, план или деталь. Как сделать это с наименьшими затратами времени и наиболее точно? Для этого необходимо: проект дома, изображение построек на карте или плане, чертеж деталей, калькулятор, принадлежности для черчения.
Удобнее всего чертить объекты, объемные детали или предметы, используя отношение 1:1. Это означает, что метр реальной местности пропорционален сантиметру на рисунке. Но чаще всего возникает необходимость применить масштабы другого порядка, такие как 1:2,1:10 и так далее. Это происходит в том случае, если территория большая, а изобразить ее надо компактно. Если объект совсем крошечный, но при производстве важны даже самые мелкие детали, его изображают используя масштаб 10:1 или даже больше.
Онлайн-калькулятор
Делаете планы и чертежи в большом количестве и спешите? Совсем нет времени даже на самые элементарные расчеты? Тут вам поможет калькулятор масштабирования онлайн. Это небольшая онлайн-программа, которая без труда позволяет быстро и точно сделать нужные вычисления.
Сервис предлагает заполнить минимальное количество информации:
- ввести необходимые величины — указать замеры местности или чертеж;
- выбрать желаемое соотношение;
- нажать кнопку «рассчитать».
Программа выдает результат примерно в таком виде:
Масштаб n:1 указывает, что X м на чертеже отвечает Y см на экземпляре.
Сервис поможет осуществить перевод данных в другой масштаб не только для чертежей и проектов, но и для применения в других областях и науках. Например, в фотографии, математике, а также в сфере программирования.
В какой бы сфере ни употреблялось масштабирование, данная программа-калькулятор значительно сэкономит время, потраченное на расчеты и вычисления. К тому же разработчики предлагают не только онлайн-версию для ПК, но и мобильную, для платформы Android.
Это во много раз упрощает работу с сервисом, ведь вы можете воспользоваться приложением в любой точке земного шара.