Прямые
относительно картинной и предметной
плоскостей могут быть расположены
произвольно. Масштаб, построенный на
произвольно направленной прямой,
называется масштабом в произвольном
направлении.
Известны четыре случая
произвольного расположения прямой в
предметном пространстве: горизонтальное,
фронтальное, особого иобщего
положения.
Рассмотрим построение
перспективного масштаба на каждой из
этих прямых.
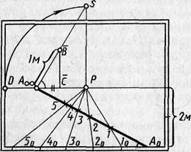
Перспективный масштаб
на произвольно направленной горизонтальной
прямой. Обоснование способа построения
этого масштаба и процесс его получения
рассмотрим на проецирующем аппарате
(рис. 105, а). Для упрощения доказательства
рассмотрим пример, когда прямая АоА’^
лежит в предметной плоскости и произвольно
направлена к основанию картины. Требуется
построить на ней перспективный масштаб.
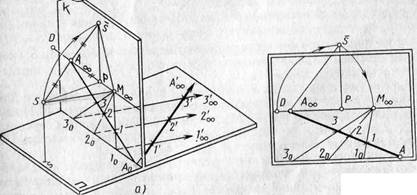
Рис
105
Сначала на основании картины,
начиная от точки Ао, откладывают отрезки
Ао-1о, 1о-2о, 2о-3о натурального масштаба.
Затем переносят циркулем отрезки с
основания картины на заданную прямую
AоAоо и соединяют отмеченные деления
прямыми 1о-1′, 2о-2′, 3о-3′. Эти прямые
параллельные, поскольку между ними
лежат по построению попарно равные
отрезки. Отсюда следует, что треугольники
1оАо1′, 2оАо2′, 3оАо3′ с общим углом при
вершине Ао будут равнобедренными и
подобными.
Далее строят перспективное
изображение прямой АоА’оо и пучка
параллельных прямых, заданных в предметном
пространстве. Для этого из точки зрения
проводят луч SMoo параллельно заданной
прямой и луч SMoo параллельно пучку прямых.
В пересечении этих лучей с картиной на
линии горизонта находят предельную
точку Аоо прямой АоА’оо и точку схода
Моо линий переноса. После этого строят
на картине перспективу прямой АоА оо и
пучка параллельных прямых 1оМоо, 2оМоо,
3оМоо- Данные линии переноса в пересечении
с прямой АоАос отметят точки делений
1, 2, 3 перспективного масштаба.
Заметим,
что треугольник SAоMoо, образовавшийся
в плоскости горизонта, подобен треугольнику
1оАо1′ (вследствие параллельности
сходственных сторон) и поэтому является
равнобедренным
Произведем
преобразования, повернув треугольник
AооSMoo вокруг линии горизонта и совместив
его с плоскостью картины. Точка зрения
S при совмещении с картиной будет
находиться на перпендикуляре, проведенном
из главной точки Р к линии горизонта, и
на расстоянии SP = SP. В совмещенном
равнобедренном треугольнике сторона
АооМоо -SMоо . Это позволяет найти на
картине точку схода Мое линий
переноса.
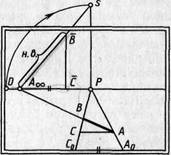
Выполним изложенные выше
построения на картине без проецирующего
аппарата (рис. 105, б). Для этого задают
картину с ее элементами. В предметной
плоскости картины изображают произвольно
направленную прямую АоАоо. Построение
перспективного масштаба на этой прямой
выполняют в такой последовательности.
Сначала откладывают на основании картины
от точки Ао заданные отрезки натурального
масштаба Ао-1о 1о-2о, 2о-3о. Затем на
перпендикуляре, проведенном из главной
точки картины к линии горизонта, отмечают
совмещенную точку зрения S, отложив PS =
PD. Далее на линии горизонта откладывают
отрезок АооМоо -AооS (как равные стороны
равнобедренного треугольника SAxMoo) и
определяют масштабную точку Моо.
Масштабная
точка — это точка схода линий переноса
для построения масштаба на произвольно
направленной прямой. Пользуясь масштабной
точкой Моо, при помощи линий переноса1оМоо,
2оМоо. 3оМоо переносят заданный натуральный
масштаб с основания картины на прямую
АОА ос-
Для построения на картине
перспективного масштаба на произвольно
направленной горизонтальной прямой
находят масштабную точку и с помощью
линий переноса (параллельных прямых в
натуре) переносят отрезки натурального
масштаба на заданную прямую.
80
Следовательно, для построения
перспективного масштаба на произвольно
направленной горизонтальной прямой
находят масштабную точку, положение
которой на линии горизонта для каждой
прямой различное.
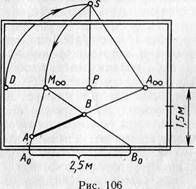
На картине (рис.
106) задан отрезок АВ. Требуется определить
его натуральную величину в масштабе
данной картины.
Сначала продолжают
отрезок до пересечения с линией горизонта
и находят предельную точку Аос этой
прямой. Затем определяют масштабную
точку для данной прямой. Для этого строят
совмещенную_ точку зрения S. Отложив PD
= PS, переносят расстояние AооS на линию
горизонта . Через масштабную точку М оо
и концы отрезка АВ проводят линии
переноса до пересечения с основанием
кар-гины. АОВО — натуральная величина
отрезка АВ, заданного в масштабе данной
картины. Если известен масштаб картины,
то величину отрезка определяют в
соответствующих единицах измерения. В
данном примере отрезок АВ равен 2,5 м.
Для
определения натуральной величины
произвольно направленного горизонтального
отрезка строят для него масштабную
точку и с помощью линий переноса выносят
этот отрезок на основание картины.
Используя масштаб картины, определяют
его натуральную величину.
Перспективный
масштаб на произвольно направленной
горизонтальной прямой можно определить
по-другому, применив способ построения
прямоугольного треугольника. На картине
(рис. 107) задана произвольно направленная
прямая А0Аоо, лежащая в предметной
плоскости. Требуется от точки Ао отложить
5 м в масштабе данной картины, если высота
точки зрения Ss = 2 м. Следовательно,
расстояние от основания картины до
линии горизонта определяет масштаб
данной картины и соответствует величине
2 м. Тогда половина этого расстояния
равна 1 м.
Сначала строят совмещенное
положение данной прямой, соединив
предельную точку Аоо с точкой S. Углы
при точках Аоо н Ао равны и соответствуют
величине углов в натуре. Далее от точки
Аоо на совмещенном положении прямой
откладывают 1 м — натуральную единицу
масштаба картины, через конец которой
проводят вертикальную прямую_ ВС.
После
этого полученный прямоугольный
треугольник АооВС строят в перспективе.
Направление гипотенузы — это и есть
положение прямой АоАоо в перспективе.
От точки Ао на основании картины
откладывают горизонтальный катет Ао1о
= -АооС. Второй катет ВС будет иметь
направление глубинной прямой, предельная
точка которой Р. Полученный треугольник
Ао1о1 является перспективным изображением
треугольника АооВС, а отрезок Ао1 равен
1 м в масштабе данной картины. Если на
основании картины отложены пять таких
же отрезков, то с помощью глубинных
прямых отмечают эти деления на заданной
прямой, соответствующие 5 м. Этим способом
можно решить обратную задачу. На картине
(рис. 108) в предметной плоскости задан
произвольно направленный отрезок АВ.
Требуется определить его натуральную
величину. Сначала строят в перспективе
прямоугольный треугольник ABC с гипотенузой
АВ. Для этого через концы отрезка проводят
глубинные прямые РСо и РА0 и горизонтальный
катет СА, натуральная величина которого
определяется_отрезком СоАо. Затем строят
совмещенное положение прямой AооS и
откладывают от точки А» на линии
горизонта натуральную величину катета
СоАо=АооС. Тогда вертикальный катет
определит конец В гипотенузы АооВ,
являющейся натуральной величиной
отрезка АВ.
Рис.
107
Рис.
108
Перспективный масштаб на
произвольно направленной фронтальной
прямой. Построение этого масштаба
частично рассмотрено в § 19 (рис. 101), где
натуральная величина фронтального
отрезка определена с помощью масштабов
широт и высот. Данный масштаб можно
построить и непосредственно на фронтальной
прямой. Чтобы показать это, обратимся
к построениям на картине (рис. 109) без
проецирующего аппарата.
Для этого
зададим фронтальную прямую АВ, заключим
ее в плоскость общего положения Q и
построим следы этой плоскости. У
фронтальной прямой точка А является
одновременно ее предметным следом А».
Следовательно, предметный след плоскости
Q пройдет через точку Ап в любом направлении
. (Из геометрии известно, что через прямую
можно провести бесчисленное множество
плоскостей.) При пересечении предметного
следа плоскости Q с основанием картины
отмечают точку Qo, через которую проводят
картинный след плоскости параллельно
данной прямой. (Две параллельные плоскости
— фронтальная и картинная — пересекаются
третьей Q, поэтому линии их пересечения
параллельны.)
Далее откладывают от
точки Qo на картинном следе отрезки
натурального масштаба Qo-1к, 1К-2К, 2К-Зк и
с помощью горизонтальных линий переноса,
параллельных предметному следу плоскости,
и точки схода Q^ переносят их на фронтальную
прямую. Полученные отрезки А-1, 1-2, 2-3
являются перспективным изображением
заданных отрезков.
Для построения
перспективного масштаба на произвольно
направленной фронтальной прямой ее
заключают в плоскость общего положения
и откладывают отрезки натурального
масштаба на ее картинном следе. Затем
переносят их на заданную прямую
горизонтальными линиями переноса,
точкой схода которых является предельная
точка предметного следа плоскости.
На
картине (рис. ПО) дан фронтальный отрезок
АВ. Требуется определить его натуральную
величину в масштабе данной картины.
Сначала
заключают отрезок в плоскость общего
положения Q. Для этого находят предметный
след прямой (Л») в пересечении отрезка
с его проекцией. Затем через точку А»
в произвольном направлении проводят
предметный след QоQоо плоскости и через
точку Qo параллельно отрезку АВ — ее
картинный след.
Далее через предельную
точку Qоо КОНЦЫ отрезка А и В проводят
линии переноса, которые на картинном
следе плоскости определят натуральную
величину АКВК отрезка АВ.
Определить
натуральную величину фронтального
отрезка можно и способом построения
прямоугольного треугольника, вынесенного
в плоскость картины. Рассмотрим этот
пример. На картине (рис. 111) задан
фронтальный отрезок АВ. Требуется
определить его натуральную величину.
Для этого через отрезок АВ и его проекцию
ab проводят фронтальную плоскость,
которая изобразится в виде прямоугольного
треугольника АВЬ. Отрезок АВ является
его гипотенузой. Прямоугольный треугольник
выносят в плоскость картины. Натуральную
величину горизонтального катета А0Ь0
определяют с помощью масштаба широт.
Вертикальный катет ВkBо определяют с
помощью масштаба высот. Тогда гипотенуза
АоВk будет натуральной величиной
заданного в перспективе фронтального
отрезка АВ.
Заметим, что для линий
переноса может быть взята любая точка
схода на линии горизонта. В данном
примере точкой схода является главная
точка картины Р.
Перспективный
масштаб на прямой особого положения.
Для построения натурального масштаба
на восходящей или нисходящей прямой
особого положения обратимся к обоснованию
его на картине (рис. 112) без проецирующего
аппарата.
На картине задана восходящая
прямая особого положения А»РВ с ее
проекцией А»Р. Требуется построить
на ней натуральный масштаб. Для этого
заключают ее в глубинную плоскость , у
которой предельной прямой является
линия главного вертикала. Предметный
след Q0Qoo глубинной плоскости пройдет
через главную точку Р и предметный след
А» прямой, а картинный след Q0QK — через
точку Qo перпендикулярно основанию
картины .
Обратимся к рисунку 105, б.
Заметим, что на нем произвольно
направленная прямая А0А»> лежит в
предметной плоскости, у которой основание
картины является ее картинным следом,
а линия горизонта — предельной прямой.
В этом случае перспективный масштаб
переносят на заданную прямую с помощью
масштабной точки М^.
Аналогичные
построения выполняют относительно
глубинной плоскости (см. рис. 112), в которой
находится восходящая прямая АпРа особого
положения. В этом примере совмещенную
точку зрения S заменяют дистанционной
(PS = PD). Тогда масштабную точку Мв для
восходящей прямой определяют, отложив
отрезок AooD=Aa0MB на предельной прямой
(линии главного вертикала) этой
плоскости.
Для переноса заданного
масштаба на восходящую прямую особого
положения через точку Ап проводят линию
переноса МВАП до пересечения с картинным
следом плоскости и определяют начальную
точку отсчета 0к. Затем откладывают от
нее отрезки натурального масштаба 0K-U,
1К-2К, 2К-<?к, которые переносят на заданную
прямую АПАХ при помощи линий переноса
с их точкой схода Мв-
Для построения
на картине перспективного масштаба на
прямой ..особого положения ее заключают
в глубинную плоскость и отклады-
вают
отрезки натурального масштаба на
картинном следе. Затем переносят их
линиями переноса с масштабной точкой
схода, расположенной на линии главного
вертикала.
Перспективный масштаб на
восходящую или нисходящую прямую особого
положения можно перенести по-другому
— способом построения прямоугольного
треугольника, вынесенного в плоскость
картины (см. рис. 111).
На картине (рис.
113) задан отрезок АВ нисходящей прямой
особого положения. Требуется определить
его натуральную величину. Заметим, что
отрезок АВ и его проекция ab находятся
в глубинной плоскости, которая на картине
изображена в виде прямоугольного
треугольника АаВ. Выносим его в картинную
плоскость. Для определения натуральной
величины горизонтального катета аВ
применяют масштаб глубин, а для
вертикального катета Аа- масштаб высот,
при этом с общей точкой схода D для линий
переноса. Тогда гипотенуза АКВО будет
натуральной величиной заданного отрезка
АВ нисходящей прямой особого
положения.
Рис. 113
Перспективный
масштаб на прямой общего положения.
Прямая, на которой необходимо построить
перспективный масштаб, расположена
произвольно в предметном пространстве
и может быть восходящей или нисходящей.
Рассмотрим этот случай только на картине
без обоснования построений на проецирующем
аппарате, поскольку он аналогичен
предыдущим примерам.
Зададим картину
с ее элементами и произвольно направленную
восходящую прямую ААао (рис. 114). Для
переноса на нее натурального масштаба
выполняют построения в следующей
последовательности.
Сначала проводят
через заданную прямую вспомогательную
проецирующую плоскость Q, перпендикулярную
картине. Тогда предметный след QoQoo этой
плоскости пройдет через точку Л=Л»
(предметный след прямой) и главную точку
картины Р как предельную точку глубинной
прямой. Затем отмечают точку Qo пересечения
предметного следа вспомогательной
плоскости с основанием картины.
Для
построения картинного следа Q0QK плоскости
Q проводят ее предельную прямую РАоо-
Затем через точку Qo параллельно предельной
прямой РАоо проводят картинный след
Q0QK вспомогательной плоскости Q.
84
85
Рис.
114
1
Рис. 115
Заметим, что
линии переноса должны лежать в плоскости
Q, а следовательно, масштабная точка М^
должна находиться на предельной прямой
РА «о этой плоскости. Для определения
положения масштабной точки Мао строят
на картине совмещенную точку зрения S
путем вращения точки зрения S вокруг
предельной прямой РАо^. Аналогично
предыдущим примерам совмещенная точка
зрения S будет находиться на перпендикуляре,
проведенном из главной точки_ Р к
предельной прямой РА^ данной плоскости
на расстоянии PS = PD. Тогда масштабную
точку М ^ определяют на предельной прямой
РАХ как конец отрезка А^М^ =AOOS.
Далее
через конец А и масштабную точку Моо
проводят линию переноса, которая в
пересечении с картинным следом Q0QK
вспомогательной плоскости определит
точку отсчета 0к. Отложив от точки 0к
отрезки натурального масштаба на
картинном следе плоскости (0к-1к, 1К-2К,
2К-Зк, 3К-4К), переносят их на заданную
прямую линиями переноса с масштабной
точкой схода Мао- Полученные отрезки
А-/, /-2, 2-3, 3-4 на восходящей прямой общего
положения являются перспективным
изображением натуральных отрезков,
заданных в масштабе картины.
Для
построения перспективного масштаба на
прямой общего положения ее заключают
в проецирующую плоскость, перпендикулярную
картине. Затем откладывают отрезки
натурального масштаба на картинном
следе плоскости и переносят их на
заданную прямую линиями переноса с
масштабной точкой схода, расположенной
на предельной прямой этой
плоскости.
Перспективный масштаб на
восходящей или нисходящей прямой общего
положения можно построить способом
прямоугольного треугольника, вынесенного
в плоскость картины с помощью масштабной
точки схода. Рассмотрим этот способ на
некоторых примерах.
На картине (рис.
115) задан отрезок АВ восходящей прямой
общего положения. Требуется определит^
его натуральную величину, применив
способ построения прямоугольного
треугольника.
Сначала через отрезок
АВ и его проекцию ab проводят
горизонтально-проецирующую плоскость.
Для этого продолжают проекцию
86
отрезка
ab, определяют ее предельную точку а»
и строят для масштабную точку М^. Затем
находят натуральную величину катетов
прямоугольного треугольника aobo и Ака0,
пользуясь линиями переноса с масштабной
точкой схода М х. Гипотенуза АКВО,
вынесенная в плоскость картины, будет
натуральной величиной заданного отрезка
АВ.
На картине (рис. 116) задан отрезок
АВ нисходящей прямой общего положения.
Требуется определить его натуральную
величину способом выноса его в плоскость
картины без построения прямоугольного
треугольника.
Для этого находят
предельную а^ и масштабную Мао точки
для проекции данной прямой. Затем с
помощью масштабной точки Моо и линий
переноса определяют натуральную величину
проекции отрезка aobo, а также размеры
высот Ака0 и ВКЬО точек Л и б от предметной
плоскости. Полученный в плоскости
картины отрезок АКВК является натуральной
величиной заданного.
Рис. 116
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
ОБЩИЕ ПОНЯТИЯ О ПЕРСПЕКТИВНЫХ МАСШТАБАХ
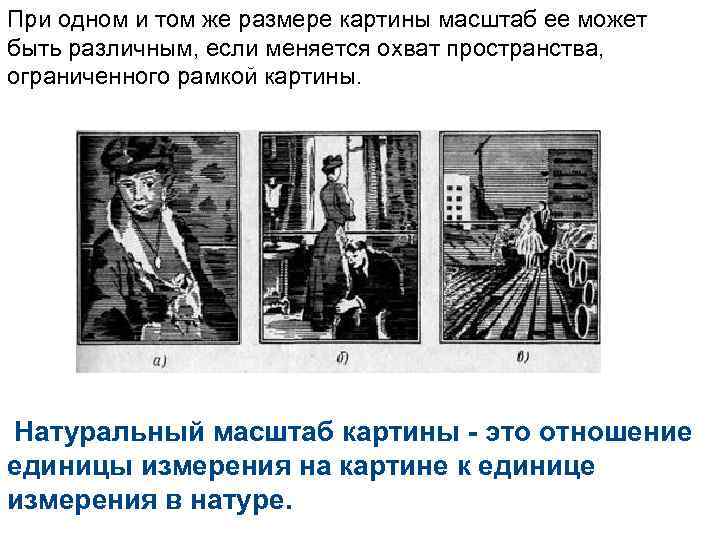
При одном и том же охвате пространства масштаб картины различен, если меняется величина ее рамки
При одном и том же размере картины масштаб ее может быть различным, если меняется охват пространства, ограниченного рамкой картины. Натуральный масштаб картины — это отношение единицы измерения на картине к единице измерения в натуре.
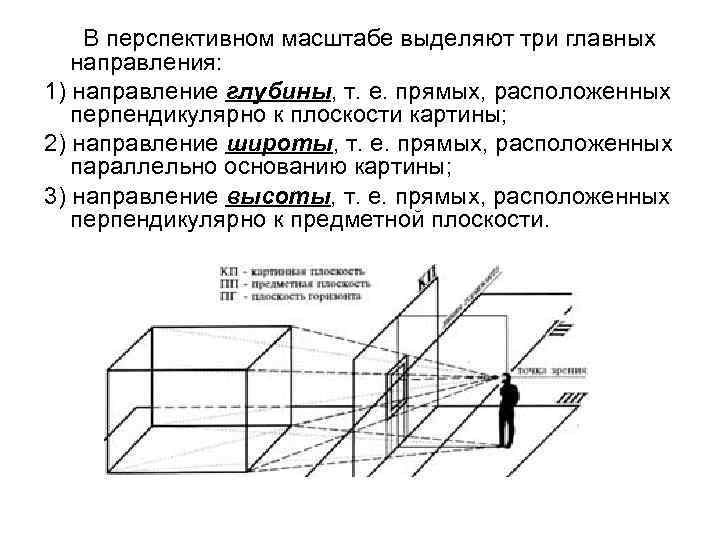
В перспективном масштабе выделяют три главных направления: 1) направление глубины, т. е. прямых, расположенных перпендикулярно к плоскости картины; 2) направление широты, т. е. прямых, расположенных параллельно основанию картины; 3) направление высоты, т. е. прямых, расположенных перпендикулярно к предметной плоскости.
МАСШТАБ ГЛУБИН — масштаб, построенный на прямой, перпендикулярной к плоскости картины D Р В A A 0 1 см В 0 Для построения перспективного масштаба глубин натуральные отрезки с основания картины переносят на глубинную прямую с помощью линии переноса, точкой схода которых является дистанционная точка.
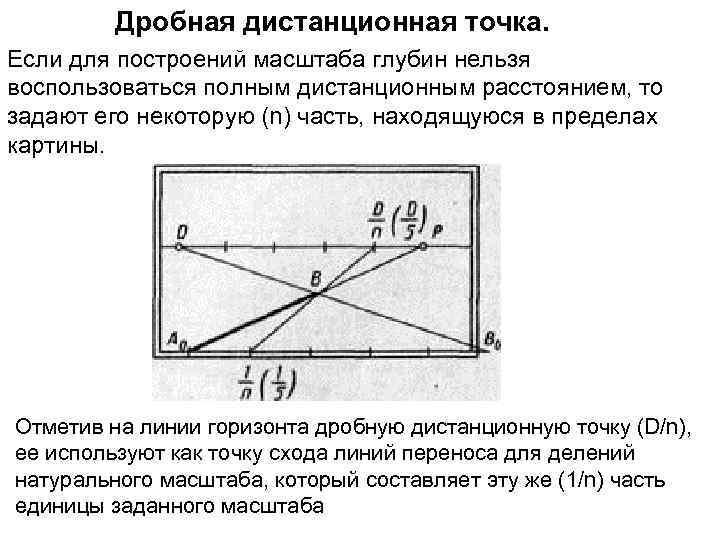
Дробная дистанционная точка. Если для построений масштаба глубин нельзя воспользоваться полным дистанционным расстоянием, то задают его некоторую (n) часть, находящуюся в пределах картины. Отметив на линии горизонта дробную дистанционную точку (D/n), ее используют как точку схода линий переноса для делений натурального масштаба, который составляет эту же (1/n) часть единицы заданного масштаба
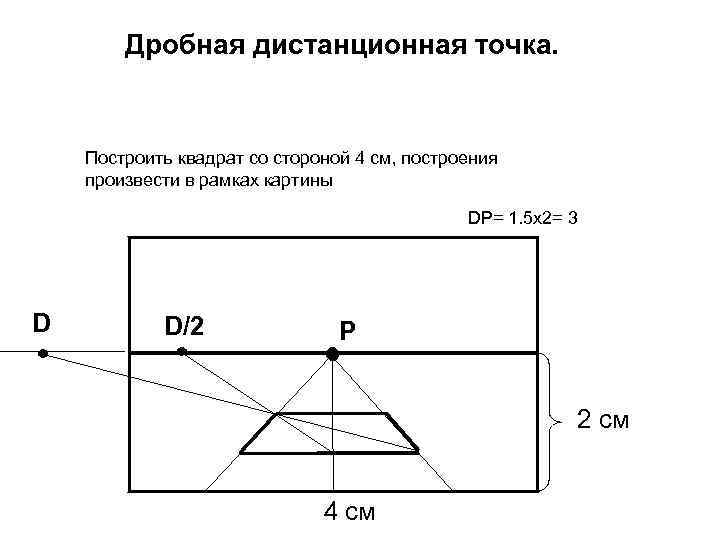
Дробная дистанционная точка. Построить квадрат со стороной 4 см, построения произвести в рамках картины DP= 1. 5 x 2= 3 D D/2 Р 2 см 4 см
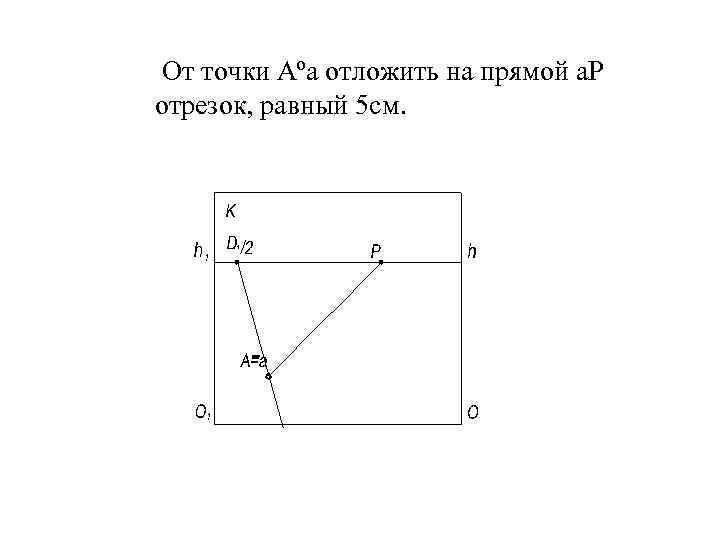
От точки Аºа отложить на прямой а. Р отрезок, равный 5 см.
МАСШТАБ ШИРОТ — масштаб, построенный на прямой, паралельной основанию картины Для построения перспективного масштаба широт натуральные отрезки с основания картины переносят на заданную прямую с помощью линий переноса, точкой схода которых на горизонте может быть любая точка, в том числе и главная.
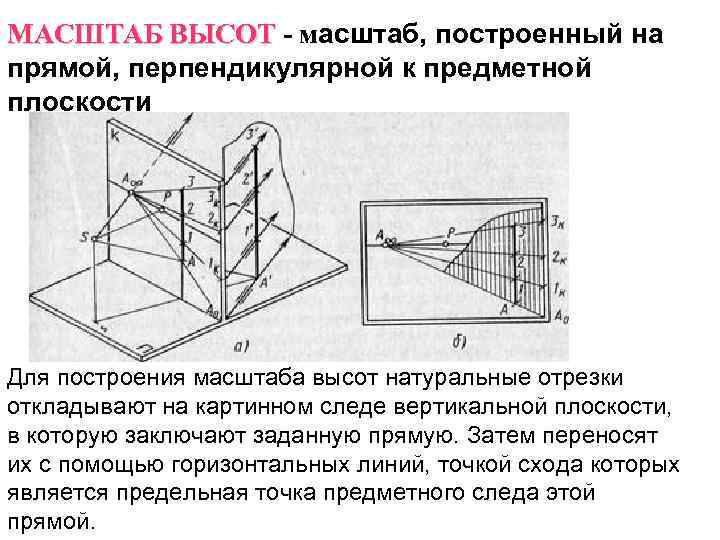
МАСШТАБ ВЫСОТ — масштаб, построенный на прямой, перпендикулярной к предметной плоскости Для построения масштаба высот натуральные отрезки откладывают на картинном следе вертикальной плоскости, в которую заключают заданную прямую. Затем переносят их с помощью горизонтальных линий, точкой схода которых является предельная точка предметного следа этой прямой.
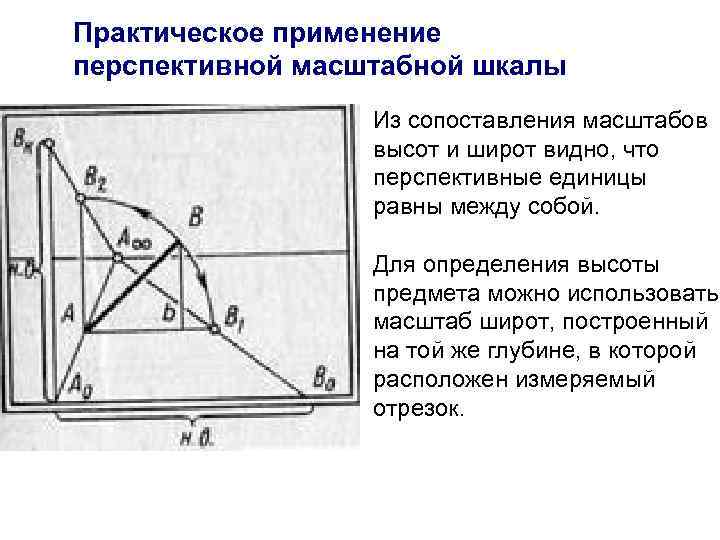
Практическое применение перспективной масштабной шкалы Из сопоставления масштабов высот и широт видно, что перспективные единицы равны между собой. Для определения высоты предмета можно использовать масштаб широт, построенный на той же глубине, в которой расположен измеряемый отрезок.
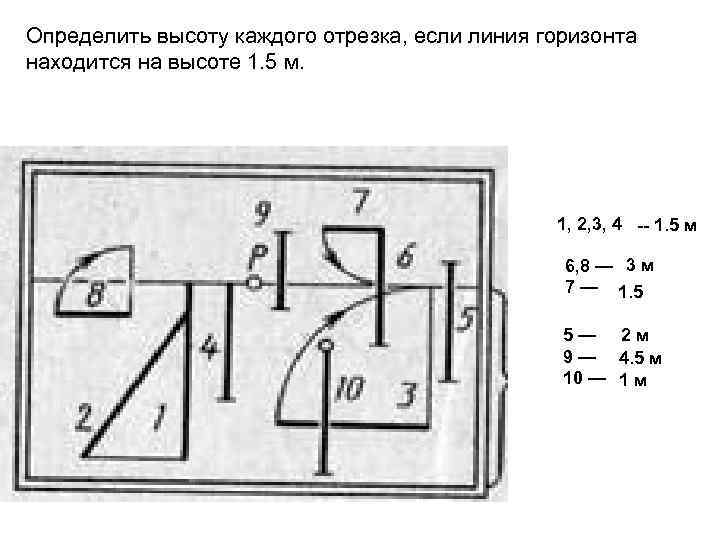
Определить высоту каждого отрезка, если линия горизонта находится на высоте 1. 5 м. 1, 2, 3, 4 — 1. 5 м 6, 8 — 3 м 7 — 1. 5 5— 2 м 9 — 4. 5 м 10 — 1 м
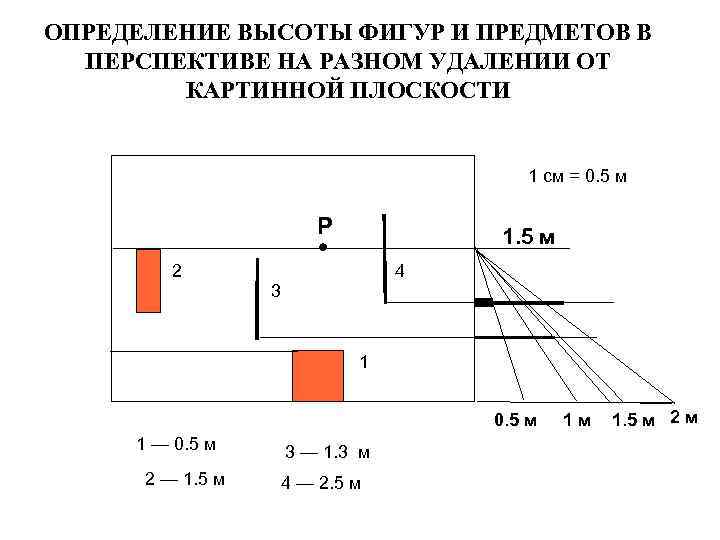
ОПРЕДЕЛЕНИЕ ВЫСОТЫ ФИГУР И ПРЕДМЕТОВ В ПЕРСПЕКТИВЕ НА РАЗНОМ УДАЛЕНИИ ОТ КАРТИННОЙ ПЛОСКОСТИ 1 см = 0. 5 м Р 2 1. 5 м 4 3 1 0. 5 м 1 — 0. 5 м 2 — 1. 5 м 3 — 1. 3 м 4 — 2. 5 м 1 м 1. 5 м 2 м
В некоторых случаях сюжетом картины предусматривается несколько горизонтальных плоскостей, а в связи с этим происходит изменение высоты точки зрения. А. Лактионов. Письмо с фронта. 1947 Государственная Третьяковская галерея, Москва
Рафаэль Санти Афинская школа («Философия»)1509 -1511 Фреска Станца делла Сеньятура, кабинет Папы римского (Ватикан).
Александр Иванов Явление Христа народу, 1837— 1857 Третьяковская галерея, Москва
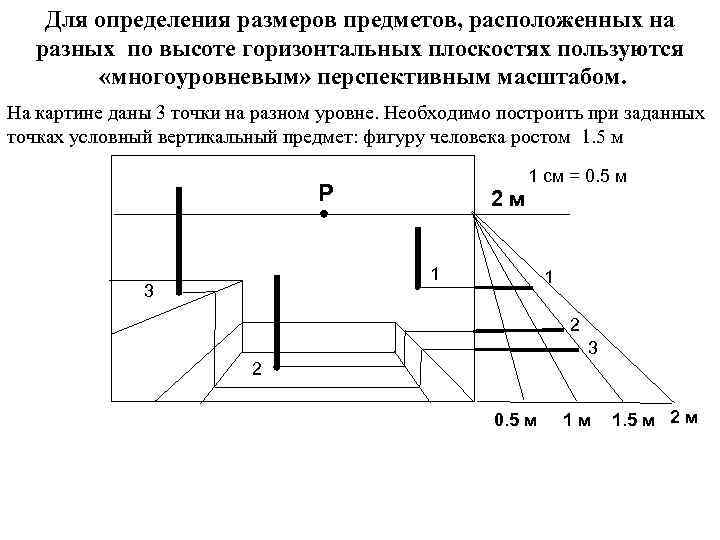
Для определения размеров предметов, расположенных на разных по высоте горизонтальных плоскостях пользуются «многоуровневым» перспективным масштабом. На картине даны 3 точки на разном уровне. Необходимо построить при заданных точках условный вертикальный предмет: фигуру человека ростом 1. 5 м 1 см = 0. 5 м Р 2 м 1 3 1 2 3 2 0. 5 м 1 м 1. 5 м 2 м
ПЕРСПЕКТИВНЫЙ МАСШТАБ НА ПРОИЗВОЛЬНО НАПРАВЛЕННОЙ ГОРИЗОНТАЛЬНОЙ ПРЯМОЙ Чтобы построить на картине перспективный масштаб на произвольно направленной горизонтальной прямой определяют на горизонте масштабную точку (Mᴔ) и с помощью линий переноса отрезки натурального масштаба переносят на заданную прямую. Масштабная точка — это точка схода линий переноса для построения масштаба на произвольно направленной прямой.
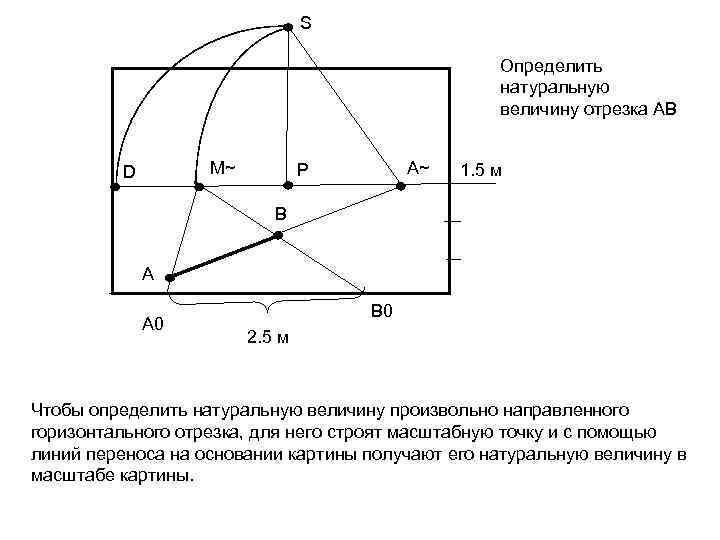
S Определить натуральную величину отрезка АВ М~ D А~ Р 1. 5 м В А А 0 В 0 2. 5 м Чтобы определить натуральную величину произвольно направленного горизонтального отрезка, для него строят масштабную точку и с помощью линий переноса на основании картины получают его натуральную величину в масштабе картины.
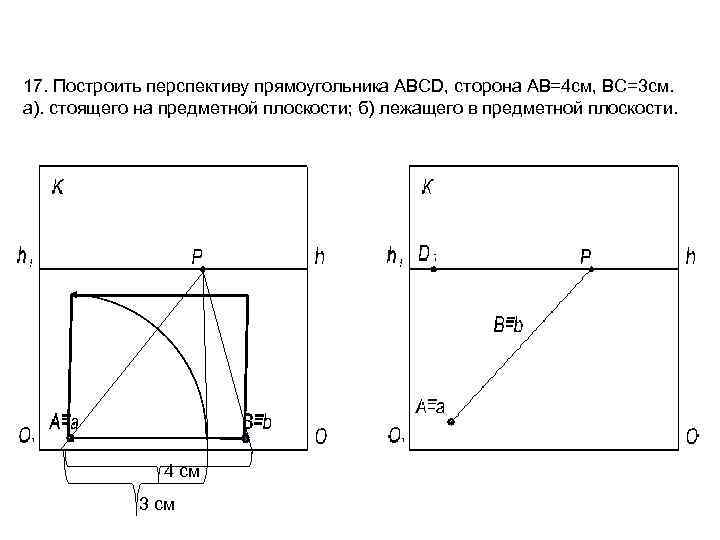
17. Построить перспективу прямоугольника ABCD, сторона АВ=4 см, BC=3 см. а). стоящего на предметной плоскости; б) лежащего в предметной плоскости. 4 см 3 см
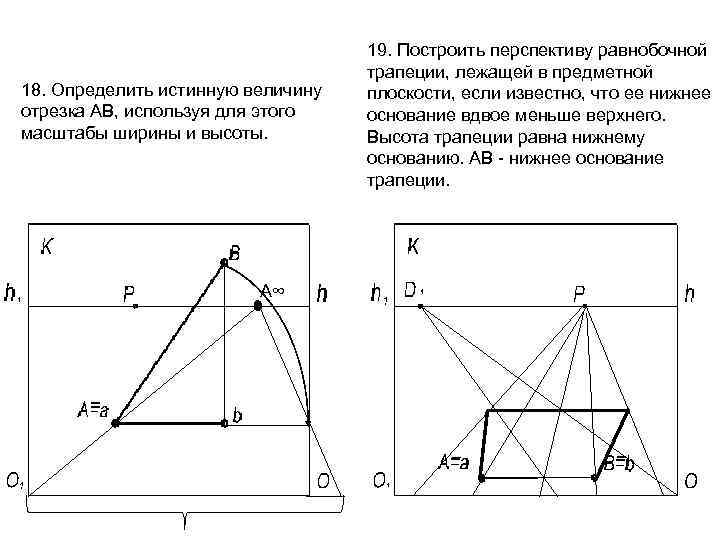
18. Определить истинную величину отрезка АВ, используя для этого масштабы ширины и высоты. A∞ 19. Построить перспективу равнобочной трапеции, лежащей в предметной плоскости, если известно, что ее нижнее основание вдвое меньше верхнего. Высота трапеции равна нижнему основанию. АВ — нижнее основание трапеции.
Перспективный масштаб
Перспективный масштаб необходим для правильного построения изображения предметов, отрезков прямых и плоских фигур, потому
что по мере их удаления от наблюдателя они уменьшаются, а по мере их приближения — увеличиваются и имеют свою истиную величину, когда находятся
в картинной плоскости.
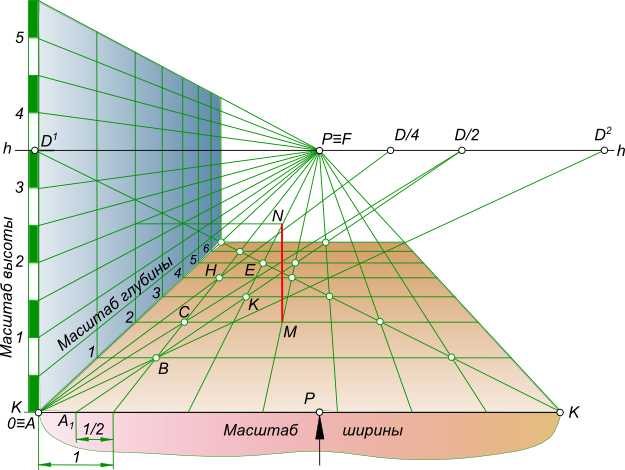
Перспективный масштаб включает в себя:
— Масштаб широты;
— Масштаб высоты;
— Масштаб глубины.
Перспективный масштаб широты представляет собой отрезок прямой на основании картины, равный единице измерения, взятой в масштабе. Если концы этого
отрезка соединить с точкой схода P≡F, то получим перспективное изображение двух горизонтальных прямых в натуре перпендикулярных к картине и взаимно параллельных.
Расстояние между этими прямыми будет на всем их протяжении равно 1 м.
Перспективный масштаб
Перспективный масштаб высоты представляет собой отрезок прямой на одной из вертикальных сторон картины, отложенный от основания картины, равный
единице измерения, взятой в масштабе. Соединив концы этого отрезка с точкой схода P≡F, получим перспективное изображение двух горизонтальных прямых в натуре
перпендикулярных к картине и взаимно параллельных. Также получаем возможность установить ту же величину прилюбом удалении в глубину картины.
Перспективный масштаб глубины представляет собой отрезок прямой, отложенный от одного из углов картины, равный
единице измерения, взятый в масштабе. Соединив концы этого отрезка с точкой отдаления D2, тогда на прямой, соединяющей угол картины с точкой схода F, получим в
перспективе изображения отрезков в натуре, перпендикулярных к картине и равных между собой. Также получаем возможность установить ту же величину при любом удалении
в глубину картины.
Перспективный масштаб позволяет построить перспективу сетки из квадратов определенных размеров. Данная сетка дает точное представление о размерах
пространства, изображенного на картине. Также он дает возможность определить высоту фигуры, на каком расстоянии находится фигура от картинной плоскости и от левой
или правой стены.
+