Приложения криволинейных интегралов
Краткая теория
Длина дуги
Длину дуги
плоской или пространственной линии
определяют по формуле:
Масса дуги
Если
– линейная плотность вещества в точках дуги,
то массу
дуги
определяют по формуле:
Статистические моменты
Статистические
моменты
и
плоской дуги
относительно координатных осей
и
определяют по формулам:
Моменты инерции
Моменты
инерции
,
плоской дуги
относительно координатных осей
и
определяют по формулам:
Полярный момент инерции
Полярный
момент инерции
плоской дуги
относительно начала координат определяют по
формуле:
Площадь фигуры
Площадь
фигуры, расположенной в плоскости
и ограниченной замкнутой линией
, вычисляют по формуле:
Работа, приложенная к точке, при перемещении по дуге
Работу, совершаемую силой
приложенной в точке
при перемещении ее по дуге
, вычисляют по формуле:
Примеры решения задач
Задача 1
Найти
момент инерции относительно оси
четверти однородной окружности
, расположенной в первом
квадранте.
Решение
Окружность
однородна, следовательно
, следовательно искомый
момент инерции:
Для
удобства вычислений перейдем к параметрическим уравнениям окружности
Тогда:
Ответ:
Задача 2
Найти
массу дуги кривой
от точки
до
, если плотность в каждой точке
ее равна абсциссе точки;
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Плотность
дуги:
Искомая масса будет выражаться
криволинейным интегралом 1-го рода:
Производная:
Искомая масса:
Ответ:
.
Задача 3
Найти
массу дуги окружности
, лежащей в первой
четверти, если плотность в каждой ее точке равна абсциссе точки.
Решение
Плотность:
Искомая масса будет
выражаться криволинейным интегралом 1-го рода:
Параметрическое
уравнение окружности:
Окружность лежит в
первой четверти, поэтому
Ответ:
.
Задача 4
Вычислить
работу силы
при обходе точки ее приложения по границе
области
в положительном направлении, начиная от точки
.
Решение
Искомая
работа будет равна криволинейному интегралу 2-го рода:
Для
вычисления интеграла воспользуемся формулой Грина:
Ответ:
.
Задача 5
Вычислить
работу силового поля
при перемещении материальной точки вдоль пути
.
Решение
Искомая работа будет
выражаться криволинейным интегралом 2-го рода:
Параметр
:
Перейдем к
определенному интегралу:
Искомая работа:
Ответ:
Задача 6
Вычислить
работу силы
при перемещении материальной точки вдоль линии
от точки
до точки
.
Решение
Искомая работа будет
выражаться криволинейным интегралом 2-го рода:
Криволинейный
интеграл 2-го рода можно свести к определенному интегралу по следующей формуле:
Получаем:
Ответ:
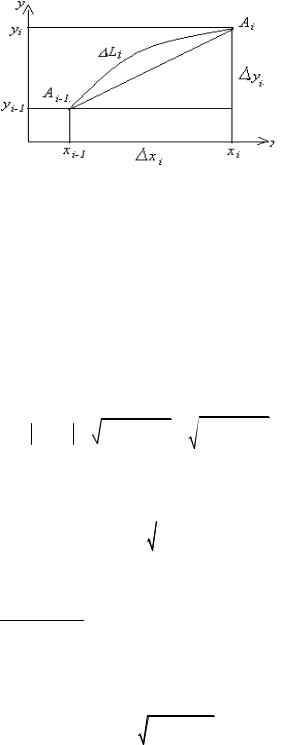
этого участка, умноженному на
получим формулу для вычисления длины дуги AB .
Рис. 54.3
Если отрезки, на которые делится кривая, достаточно малые, то длина li
отрезка кривой Ai−1Ai приблизительно равна длине хорды Ai−1Ai . По теореме Лагранжа приращение yi функции y = y(x) на участке (xi−1, xi ) равно значению производной в некоторой точке ξi
приращение xi , т.е. yi = y′(ξ i) xi . Таким образом, для плоского случая (рис.54.3) будем иметь
Li ≈ Ai−1Ai = 

и, следовательно,
.
|
L= ∫ dl = lim |
n |
′ 2 |
||||
|
∑ |
(ξi ) xi . |
|||||
|
1+ y |
||||||
|
AB |
n→∞ |
i=1 |
||||
|
Li→0 |
Нетрудно видеть, что под знаком предела стоит интегральная сумма для функции 1 на отрезке (a,b), и потому последний пре-
дел равен определенному интегралу от этой функции на этом отрезке. Таким образом,
b
L= ∫ dl = ∫ 1+ y′ 2(x)dx
AB a
102
Пусть теперь f (x, y)– произвольная непрерывная функция, определенная в точках близких к кривой AB . Так как, согласно определению, точка Pi
на отрезке кривой Ai−1Ai может выбираться произвольным образом, то вы-
|
берем ее так, чтобы она имела координаты (ξ |
, y'(ξ )) , где ξ |
есть то значение |
|||||||||||
|
i |
i |
i |
|||||||||||
|
аргумента x на отрезке (xi−1,xi ), при котором |
yi = y'(ξ ) |
xi . Отсюда |
|||||||||||
|
i |
|||||||||||||
|
n |
|||||||||||||
|
∫ |
f (x, y)dl = lim |
′ 2 |
(ξi ) |
xi . |
|||||||||
|
∑ f (ξi , y(ξi )) 1+ y |
|||||||||||||
|
AB |
n→∞ |
i=1 |
|||||||||||
|
Li→0 |
|||||||||||||
|
Приглядевшись к выражению под знаком предела, мы видим, что оно |
|||||||||||||
|
представляет |
интегральную |
сумму |
для |
функции |
|||||||||
|
g(x)= f (x,y(x)) 1+y’2(x) на отрезке (a,b)и потому предел равен |
опреде- |
ленному интегралу от этой функции на данном отрезке. В результате мы приходим к формуле
b
|
∫ |
f (x,y)dl = ∫ f (x,y(x)) |
′ 2 |
(x)dx. |
(54.5) |
||
|
1+ y |
||||||
|
AB |
a |
|||||
|
Если кривая AB на плоскости определена уравнением |
||||||
|
, , |
||||||
|
то |
||||||
|
d |
||||||
|
∫ |
f (x, y)dl = ∫ f (x(y), y) |
1+ x′2(y)dy . |
(54.6) |
|||
|
AB |
c |
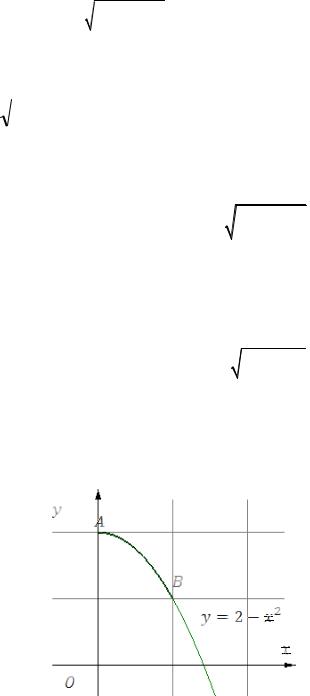
Пример. Найти массу части кривой y=2-x2соединяющей точки A(0,2) и B(1,1), если плотность распределения массы вдоль
кривой задана функцией ρ(x,y)=2x(рис.53.4).
Рис. 54.4
103

|
Решение. Так как y′ = −2x, то |
по формуле (54.3) искомая масса бу- |
|||||||||||||||
|
дет равна |
||||||||||||||||
|
1 |
1 |
1 |
||||||||||||||
|
M = ∫ ρ(x,y)d l = ∫2x 1+ |
4x2 dx = |
∫ 1+4x2 d(1+4x2) = |
||||||||||||||
|
AB |
0 |
4 |
0 |
|||||||||||||
|
1 |
1 |
|||||||||||||||
|
((1+4x2)3/ 2 |
||||||||||||||||
|
= |
1 |
= |
(5 5 −1) ≈1,7. |
|||||||||||||
|
6 |
0 |
6 |
||||||||||||||
Плоский случай. Параметрическое задание кривой. Пусть кривая AB
определена параметрическими уравнениями
x= x(t); y= y(t); α≤t ≤β,
где x(t)и y(t)дифференцируемые функции, производные которых непре-
|
рывны, причем значению t = α соответствует точка A, а значению t = β |
|||||||
|
соответствует точка B. В этом случае криволинейный интеграл |
|||||||
|
1-го рода вычисляется по формуле: |
|||||||
|
∫ |
β |
||||||
|
′ 2 |
′2 |
(t)dt. |
(54.7) |
||||
|
f (x, y)dl = ∫ f (x(t), y(t)) x |
(t) + y |
||||||
|
AB |
α |
Для её вывода достаточно в формуле (54.7) осуществить замену перемен-
|
ных x=x(t); a=x(α); b=x(β),dx = x′dt и вспомнить, что |
y′ |
= y′ / x′ . |
|
t |
x |
t tt |
|
Плоский случай. Уравнение кривой определено в полярных координа- |
тах. Попробуем вывести формулу для вычисления криволинейного инте-
|
грала 1-го рода в случае, когда кривая |
AB на плоскости задана уравнени- |
||
|
ем в полярных координатах: |
|||
|
r =r(ϕ) |
ϕ |
≤ϕ≤ϕ |
(54.8) |
|
1 |
2 |
Вспомним, что связь между декартовыми и полярными координатами определяется формулами x=rcosϕ, y=rsinϕ. Если в них вместо r под-
ставить его выражение из уравнения (54.8), то получится параметрическое уравнение кривой AB :
|
x=r(ϕ)cosϕ, |
y=r(ϕ)sinϕ. |
(54.9) |
в котором в качестве параметра выступает полярный угол ϕ, изменяющийся в пределах от ϕ1до ϕ2 . При этом
x′2 (ϕ)+ y′2 (ϕ) = (r′(ϕ)cosϕ − r(ϕ)sinϕ)2 + (r′ (ϕ)sinϕ + r(ϕ)cosϕ)2
= r2(ϕ)+ r′2(ϕ).
104
Подставляя это выражение в соотношение (54.7), получим формулу для вычисления криволинейных интегралов 1-го рода в случае, когда кривая АВ на плоскости задана в полярных координатах:
|
∫ |
ϕ2 |
|||
|
f (x, y)dl = ∫ f (rcosϕ,rsinϕ) r2 (ϕ)+ r′2 (ϕ)dϕ. |
(54.10) |
|||
|
AB |
ϕ1 |
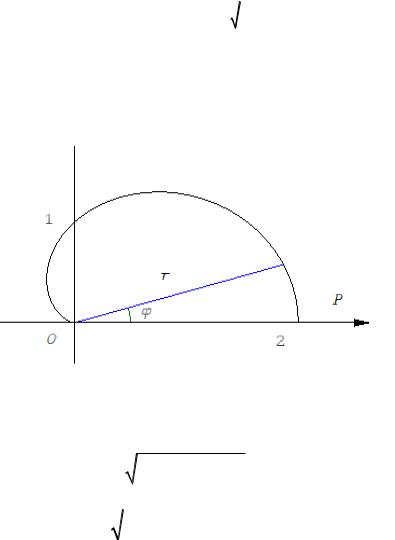
Пример. Найти массу половины кардиоиды r = (1+cosϕ), 0≤ ϕ≤ π,
если плотность ρ = r в каждой её точке.
Рис. 54.5
Пользуемся формулами (54.3) и (54.10):
π
M = ∫ ρdl = ∫r
|
AB |
0 |
||||||||||||
|
π |
|||||||||||||
|
(1+ cosϕ)2 |
+ (-sinϕ)2 dϕ = |
||||||||||||
|
= ∫(1+ cosϕ) |
|||||||||||||
|
0 |
|||||||||||||
|
π |
ϕ |
π |
πsin ϕ − |
sin |
3 ϕ |
||||||||
|
= ∫2cos2 |
2cos ϕ dϕ = 8∫(1− sin2 ϕ) d(sin ϕ) = 8 |
2 |
= |
16 |
|||||||||
|
2 |
3 |
3 |
|||||||||||
|
0 |
2 |
0 |
2 |
2 |
0 |
2 |
|||||||
Общий пространственный случай. Если кривая AB расположена в пространстве, то, как правило, она задается параметрическими уравнениями
x = x(t); y = y(t); z = z(t) α≤t ≤β,
причем параметру t =α соответствует точка A, а параметру t =β соответ-
|
ствует точка B . Предполагая, что производные x′(t), y′(t), z′(t) |
непрерыв- |
|
ны при α ≤ t ≤ β,а функция f(x,y,z) непрерывна в некоторой |
области D, |
|
105 |

окружающей кривую AB, и, проводя рассуждения, подобные приведенным для плоского случая, придем к следующей формуле:
|
β |
|||||||
|
′ 2 |
′ 2 |
′ 2 |
(t)dx. |
(54.11) |
|||
|
∫ f (x,y,z)dl =∫f (x(t),y(t),z(t)) x |
(t)+ y |
(t)+ z |
|||||
|
AB |
α |
54.3. Некоторые приложения криволинейного интеграла 1-ого рода. Определение пло щади цилиндрической поверхности. На рис.54.6 изображено ограждение переменной высоты некоторой гор изонтально расположенной территори и, ограниченной кривойL. Вопрос о расходе краски, необходимой для окр аски этого ограждения, сведется к нахождению его площади. Если ввести систему координат так, чтобы территория находилась в плоскости XOY, то можно считать, что данное огра ждение представляет собой часть цил индрической поверхности с направл яющей L и образующей, параллельной оси OZ, причем высота ограждения задается функцией z = f (x, y), определенной в каждой точке кривой L(рис.54.6). Если
рассмотреть часть п оверхности на небольшом участке кривой Ai−1Ai , то можно считать, что высота этой части постоянна и равна значению
|
функции z = f (x, y)в |
некоторой точке Pi (xi , yi ). |
В тако м случае площадь |
||
|
этого участка поверхн ости приблизительно равна |
Si ≈ z(xi, yi ) Li . |
|||
Рис. 54.6
Суммируя по всем уч асткам и переходя к пределу в поллучающейся интегральной сумме, мы придем к тому, что площадь всей б оковой поверхно-
сти ограждения будет определяться по формуле S = ∫ z(x, y)dl.
L
106
Вычисление массы, координат центра тяжести и моментов инерции материальной кривой. Часто математическую идеализацию пространственного материального объекта можно представить в виде пространственной кривойAB, вдоль которой распределена масса с линейной плотностью ρ(x, y,z) (рис.54.1). (Канаты, на которых подвешен мост через пролив Босфор, соединяющий Черное и Средиземные моря, можно рассматривать в качестве примера такого объекта. В качестве математической модели канатов можно рассматривать их осевые линии с постоянной линейной плотностью, равной массе тонкого слоя поперечного сечения). В таком случае основные механические характеристики подобных объектов могут быть вычислены с помощью криволинейного интеграла 1-ого рода.
а)Масса материальной кривой. Как мы уже знаем, масса М такой кривой может быть вычислена по формуле (54.3).
б) Моменты инерции Ix, I y, Izотносительно осей OX ,OY ,OZ . Перечисленные моменты вычисляются по следующим формулам
|
Ix = ∫(y2 +z2)ρ(x,y,z)dl, |
Iy = ∫(x2 +z2)ρ(x,y,z)dl, |
Iz = ∫(x2 +y2)ρ(x,y,z)dl. (54.12) |
|
AB |
AB |
AB |
|
Для их вывода, как обычно в таких ситуациях, |
разделяем кривую на мел- |
кие участки и считаем, что вся масса отрезка кривой (приблизительно рав-
|
ная ρ(ξi,ηi,νi) |
Li ) сосредоточена |
в некоторой ее точке P(ξi ,ηi ,νi ). Момент |
|||
|
инерции этой материальной точки относительно, например, оси OX, будет |
|||||
|
равен |
ее |
массе, умноженной |
на квадрат расстояния от |
оси, т.е. |
|
|
ρ(ξ ,η,ν ) L(η2 |
+ν 2 ). Суммируя по всем отрезкам кривой и переходя к пре- |
||||
|
i i i |
i |
i |
i |
||
|
делу, получаем искомые выражения. |
|||||
|
в) |
Kоординаты центра |
тяжести. Координаты центра |
тяжести |
C(xc, yc,zc ) материальной пространственной кривой могут быть высчитаны по формулам:
|
1 |
1 |
1 |
(54.13) |
||||||||
|
xc =M |
∫xρ(x,y,z)dl, yc =M |
∫yρ(x,y,z)dl, zc =M |
∫ |
(zρ(x,y,z)dl, |
|||||||
|
AB |
AB |
AB |
где M– масса кривой.
Пример. Найдем механические характеристики верхней полуок- ружности радиуса Rс центром в начале координат, вдоль которой равномерно распределена масса с плотностьюρ .В данном примере мы имеем дело с плоской кривой и потому в соответствующих формулах мы должны опустить переменную z. Очевидно, что масса M равна длине полуокружности, умноженной на ρ , т.е. M = πρR .
107
Рис.54.7
Для нахождения моментов инерции Ix и Iyсначала запишем уравнение полуокружности в пара метрическом виде
|
x = Rcost, |
y = Rsint, |
0 ≤ t ≤ π, |
а затем воспользуемсся формулой (54.11) (для плоского случая) и (54.8). Будем иметь
|
π |
||||||||||||||||
|
Ix = ∫ y2ρdl =∫ρy2(t) x′2(t)+ y′2(t)dt = |
||||||||||||||||
|
AB |
0 |
|||||||||||||||
|
π |
||||||||||||||||
|
= |
+ R2 cos2 tdt = |
|||||||||||||||
|
ρ∫ R2 sin2 t R2 sin2 t |
||||||||||||||||
|
0 |
||||||||||||||||
|
π |
π |
1 |
1 |
ρπR3 |
||||||||||||
|
=ρR3 ∫sin2 tdt = |
( |
t − |
sin2t) = |
. |
||||||||||||
|
0 |
2 |
4 |
2 |
|||||||||||||
|
0 |
||||||||||||||||
|
Нетрудно понять, что Iy |
имеет такое же значение. |
Что касается координат центра тяжести C(xc, yc ), то в силу симметрии xc = 0, а для вычисления yc опять используем параметрическое уравнение полуокружности:
|
1 |
1 |
π |
||||||||||
|
yc = |
∫ yρdl = |
∫ρy(t) x′ 2(t) + y′ 2(t)dt = |
||||||||||
|
M |
M |
|||||||||||
|
AB |
0 |
|||||||||||
|
1 |
π |
2R |
||||||||||
|
= |
∫ρRsint |
R2 sin2 t + R2 cos2 tdt = |
. |
|||||||||
|
πρR |
||||||||||||
|
0 |
π |
|||||||||||
108
Лекция 55. Криволинейные интегралы 2-г о рода (по координатам)
В данной лекци и мы рассмотрим еще одну интегральную конструкцию, которая, как и все рассмотренные ранее, изначально возникла при стремлении решить н екоторую прикладную задачу (именно в физике), а потом оказалась при менимой при решении других теоретических и прикладных задач. Речь идет о криволинейных интегралах 2 -го рода.
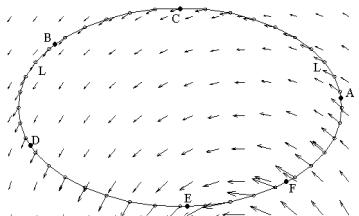
55.1. Определение и обозначения. Физическая зад ача, в которой подобная конструкция возникает, формулируется следующ им образом. Пусть в некоторой области D пространства определено силовое поле, т.е. на материальную точку ед иничной массы, помещенную в область D, действует зависящая от ее местонахождения вектор-сила F. И пусть в этой области материальная точка перемещается по кривой L из положения A в положение B. Требуется о пределить работу W сил данного поля при таком перемещении.
Рис. 55.1
На рисунке 55. 1 изображено плоское поле сил. Ясно, что при перемещении точки по кр ивой L по участку кривой ACB силы поля оказывают положительное воздействие, т.е. совершают положительную работу, а при движении по участку кривой DEF они оказывают отрицательное воздействие, т.е. совершают отрицательную работу. Точно также при спуске с горы мы ощущаем положительное воздействие силы тяжести, а при подъеме в гору нам приходится преодолевать отрицательное воздействие этой силы.
Если в пространстве введена декартова система к оординат, то сила,
действующая в точке M(x,y,z) может задаваться посредс твом ее разложе-
ния по единичным ве кторам i, j,k
109
|
F(x,y,z)=P(x,y,z)i |
+Q(x,y,z)j |
+R(x,y,z)k , |
где функции P(x,y, z),Q(x,y,z), R(x,y,z)являются проекциями силы на оси
|
OX,OY,OZ соответственно. |
В |
случае |
плоского |
поля |
сила задается |
||||||||
|
посредством разложения по единичным векторам i, j F(x,y)=P(x,y)i |
+Q(x,y)j |
||||||||||||
|
.В частности для поля, изображенного на рис. 55.1 |
|||||||||||||
|
P(x, y) = |
− y |
, |
Q(x, y) = |
x |
. |
||||||||
|
x2 + y2 |
x2 + y2 |
||||||||||||
|
Вспомним, что, если при перемещении вдоль отрезка прямой от точки A до |
|||||||||||||
|
точки Bсила F постооянна |
и составляет угол |
ϕ с напра влением |
вектора |
||||||||||
|
AB (рис.55.2а), то работа Wтакой силы |
вычисляется |
по формуле |
|||||||||||
|
, |
|||||||||||||
|
правую часть которой можно рассматривать |
как скалярное произведение |
||||||||||||
|
вектора-силы F и вектора перемещения AB |
и потому можно переписать |
||||||||||||
|
в виде |
|||||||||||||
|
= |
|||||||||||||
|
W |
( F , A B ) . |
(55.1) |
|||||||||||
Рис. 55.2
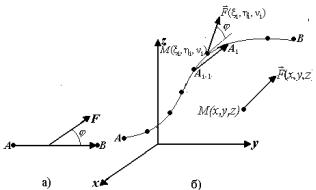
Ясно, что в случае к риволинейной траектории перемещ ения и непостоянной по величине и направлению силы, данная формула для подсчета работы неприменима. На помощь, как часто в подобных случаях, приходит интегральная методология. В согласии с ней, для решения поставленной задачи разобьем кривую Lна n отрезков (см. рис.55.2,б). Работа W сил
110
поля по кривой AB очевидно будет равна сумме работWi (i = 1,…, n) по этим отрезкам кривой. Если считать, что: а) сила поля на отрезке кривой
|
A A постоянна и равна силе F(ξi ,ηi ,νi ) |
действующей в некотором положе- |
||
|
i−1 i |
|||
|
нии M(ξi ,ηi ,νi ) на этом отрезке; б) перемещение происходит по отрезку |
|||
|
прямой, соединяющему точки Ai−1 и Ai ,то согласно формуле (55.1) |
|||
|
W=(F(ξη,ν),A A) |
. |
||
|
i |
i i i |
i−1 i |
|
Но скалярное произведение векторовF(ξi |
ηi,νi ) и Ai−1 Ai может быть вычисле- |
но как сумма произведений соответствующих координат этих векторов.
|
Координатами вектора F(ξi |
ηi,νi ) являются числа |
P(ξi ηi,νi), Q(ξi η,νi i), |
R(ξi ηi,νi), а координатами вектора Ai−1 Ai будут приращения координат при переходе от точки Ai−1к точке Ai т.е. числа xi, yi , zi . Следовательно,
W i ≈ P(ξi ηi ,νi ) xi + Q(ξi ηi ,νi ) yi + R(ξi ηi ,νi ) zi ) .
В таком случае вся работа сил поля будет приблизительно равна
n
W ≈ ∑(P(ξi ,ηi ,νi ) xi + Q(ξi ,ηi ,νi ) yi + R(ξi ,ηi ,νi ) zi ).
i=1
В качестве точного значения работы W естественно принять предел этой суммы при n→∞ и измельчении отрезков, на которые делится кривая L, т.е.
|
n |
|
|
W = lim |
∑(P(ξi ,ηi ,νi ) xi + Q(ξi ,ηi ,νi ) yi + R(ξi ,ηi ,νi ) zi )).. (55.2) |
|
n→∞ |
i=1 |
Отвлечемся теперь от физического содержания задачи и будем считать, что в некоторой области D пространства в окрестности пространственной кривойL, соединяющей точки A иB,определена некоторая функция
|
f(x,y,z).Если кривую AB разбить на n |
отрезков точками |
A0 = A ,A1,A2,A3,…,An = B,внутри каждого отрезка выбрать некоторую точку
Mi (ξi ,ηi ,νi )и сформировать интегральную сумму
|
n |
|
|
Sn =∑f(ξi ,ηi ,νi ) xi , |
(55.3) |
i=1
то предел этой суммы при n→∞ и li →0 (если он существует и не зави-
сит от способа деления кривой AB и от выбора точек M(ξη,ν )) обознача-
i i i i
ется, как
111
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
08.04.2015195.07 Кб88.doc
-
Теоретический минимум
Криволинейные и поверхностные интегралы часто встречаются в физике. Они бывают двух видов, первый из которых рассматривается здесь. Этот
тип интегралов строится согласно общей схеме, по которой вводятся определённые, двойные и тройные интегралы. Коротко напомним эту схему.
Имеется некоторый объект, по которому проводится интегрирование (одномерный, двумерный или трёхмерный). Этот объект разбивается на малые части,
в каждой из частей выбирается точка. В каждой из этих точек вычисляется значение подынтегральной функции и умножается на меру той части, которой
принадлежит данная точка (длину отрезка, площадь или объём частичной области). Затем все такие произведения суммируются, и выполняется предельный
переход к разбиению объекта на бесконечно малые части. Получающийся предел и называется интегралом.1. Определение криволинейного интеграла первого рода
Рассмотрим функцию
, определённую на кривой
. Кривая предполагается спрямляемой. Напомним, что это означает, грубо говоря,
что в кривую можно вписать ломаную со сколь угодно малыми звеньями, причём в пределе бесконечно большого числа звеньев длина ломаной должна оставаться
конечной. Кривая разбивается на частичные дуги длинойи на каждой из дуг выбирается точка
. Составляется произведение
,
проводится суммирование по всем частичным дугам. Затем осуществляется предельный переход с устремлением длины наибольшей
из частичных дуг к нулю. Предел является криволинейным интегралом первого рода
.
Важной особенностью этого интеграла, прямо следующей из его определения, является независимость от направления интегрирования, т.е.
.
2. Определение поверхностного интеграла первого рода
Рассмотрим функцию
, определённую на гладкой или кусочно-гладкой поверхности
. Поверхность разбивается на частичные области
с площадями, в каждой такой области выбирается точка
. Составляется произведение
, проводится суммирование
по всем частичным областям. Затем осуществляется предельный переход с устремлением диаметра наибольшей из всех частичных
областей к нулю. Предел является поверхностным интегралом первого рода
.
3. Вычисление криволинейного интеграла первого рода
Методика вычисления криволинейного интеграла первого рода просматривается уже из формальной его записи, а фактически следует непосредственно из
определения. Интеграл сводится к определённому, только нужно записать дифференциал дугикривой, вдоль которой проводится интегрирование.
Начнём с простого случая интегрирования вдоль плоской кривой, заданной явным уравнением. В этом случае дифференциал дуги
.
Затем в подынтегральной функции выполняется замена переменной, и интеграл принимает вид
,
где отрезокотвечает изменению переменной
вдоль той части кривой, по которой проводится интегрирование.
Очень часто кривая задаётся параметрически, т.е. уравнениями вида
. Тогда дифференциал дуги
.
Формула эта очень просто обосновывается. По сути, это теорема Пифагора. Дифференциал дуги — фактически длина бесконечно малой части кривой.
Если кривая гладкая, то её бесконечно малую часть можно считать прямолинейной. Для прямой имеет место соотношение
.
Чтобы оно выполнялось для малой дуги кривой, следует от конечных приращений перейти к дифференциалам:
.
Если кривая задана параметрически, то дифференциалы просто вычисляются:
и т.д.
Соответственно, после замены переменных в подынтегральной функции криволинейный интеграл вычисляется следующим образом:
,
где части кривой, по которой проводится интегрирование соответствует отрезок изменения параметра.
Несколько сложнее обстоит дело в случае, когда кривая задаётся в криволинейных координатах. Этот вопрос обычно обсуждается в рамках дифференциальной
геометрии. Приведём формулу для вычисления интеграла вдоль кривой, заданной в полярных координатах уравнением:
.
Приведём обоснование и для дифференциала дуги в полярных координатах. Подробное обсуждение построения координатной сетки полярной системы координат
см. здесь. Выделим малую дугу кривой, расположенную по отношению к координатным линиям так, как показано на рис. 1. В силу малости всех фигурирующих
дуг снова можно применить теорему Пифагора и записать:
.
Отсюда и следует искомое выражение для дифференциала дуги.
С чисто теоретической точки зрения достаточно просто понять, что криволинейный интеграл первого рода должен сводиться к своему частному случаю —
определённому интегралу. Действительно, выполняя замену, которая диктуется параметризацией кривой, вдоль которой вычисляется интеграл, мы устанавливаем
взаимно-однозначное отображение между частью данной кривой и отрезком изменения параметра. А это и есть сведение к интегралу
вдоль прямой, совпадающей с координатной осью — определённому интегралу.4. Вычисление поверхностного интеграла первого рода
После предыдущего пункта должно быть ясно, что одна из основных частей вычисления поверхностного интеграла первого рода — запись элемента поверхности
,
по которой выполняется интегрирование. Опять-таки начнём с простого случая поверхности, заданной явным уравнением. Тогда
.
Выполняется замена в подынтегральной функции, и поверхностный интеграл сводится к двойному:
,
где— область плоскости
, в которую проектируется часть поверхности, по которой проводится интегрирование.
Однако часто задать поверхность явным уравнением невозможно, и тогда она задаётся параметрически, т.е. уравнениями вида
.
Элемент поверхности в этом случае записывается уже сложнее:
.
Соответствующим образом записывается и поверхностный интеграл:
,
где— область изменения параметров, соответствующая части поверхности
, по которой проводится интегрирование.
5. Физический смысл криволинейного и поверхностного интегралов первого рода
Обсуждаемые интегралы обладают очень простым и наглядным физическим смыслом. Пусть имеется некоторая кривая, линейная плотность которой не является
константой, а представляет собой функцию точки. Найдём массу этой кривой. Разобьём кривую на множество малых элементов,
в пределах которых её плотность можно приближённо считать константой. Если длина маленького кусочка кривой равна, то его масса
, где
— любая точка выбранного кусочка кривой (любая, так как плотность в пределах
этого кусочка приближённо предполагается постоянной). Соответственно, масса всей кривой получится суммированием масс отдельных её частей:
.
Чтобы равенство стало точным, следует перейти к пределу разбиения кривой на бесконечно малые части, но это и есть криволинейный интеграл первого рода.
Аналогично разрешается вопрос о полном заряде кривой, если известна линейная плотность заряда.
Эти рассуждения легко переносятся на случай неравномерно заряженной поверхности с поверхностной плотностью заряда
. Тогда
заряд поверхности есть поверхностный интеграл первого рода
.
Замечание. Громоздкая формула для элемента поверхности, заданной параметрически, неудобна для запоминания. Другое выражение получается в дифференциальной геометрии,
оно использует т.н. первую квадратичную форму поверхности.Примеры вычисления криволинейных интегралов первого рода
Пример 1. Интеграл вдоль прямой.
Вычислить интеграл
вдоль отрезка прямой, проходящей через точкии
.
Сначала запишем уравнение прямой, вдоль которой проводится интегрирование:
. Найдём выражение для
:
.
Вычисляем интеграл:
Пример 2. Интеграл вдоль кривой на плоскости.
Вычислить интеграл
по дуге параболыот точки
до точки
.
Заданные точки
и
позволяют выразить переменную
из уравнения параболы:
.
Вычисляем интеграл:
.
Однако можно было проводить вычисления и иначе, пользуясь тем, что кривая задана уравнением, разрешённым относительно переменной
.
Если принять переменнуюза параметр, то это приведёт к небольшому изменению выражения для дифференциала дуги:
.
Соответственно, интеграл несколько изменится:
.
Этот интеграл легко вычисляется подведением переменной под дифференциал. Получится такой же интеграл, как и в первом способе вычисления.Пример 3. Интеграл вдоль кривой на плоскости (использование параметризации).
Вычислить интеграл
вдоль верхней половины окружности.
Можно, конечно, выразить из уравнения окружности одну из переменных, а затем провести остальные вычисления стандартно. Но можно использовать и
параметрическое задание кривой. Как известно, окружность можно задать уравнениями. Верхней полуокружности
отвечает изменение параметра в пределах. Вычислим дифференциал дуги:
.
Таким образом,
Пример 4. Интеграл вдоль кривой на плоскости, заданной в полярных координатах.
Вычислить интеграл
вдоль правого лепестка лемнискаты.
На чертеже выше изображена лемниската. Вдоль её правого лепестка нужно проводить интегрирование. Найдём дифференциал дуги для кривой:
.
Следующий шаг — определение пределов интегрирования по полярному углу. Ясно, что должно выполняться неравенство, а потому
.
Вычисляем интеграл:
Пример 5. Интеграл вдоль кривой в пространстве.
Вычислить интеграл
вдоль витка винтовой линии, соответствующего пределам изменения параметра
.
Вычисляем дифференциал дуги:
.
Подставляем в интеграл:
.
Примеры вычисления поверхностных интегралов первого рода
Пример 6. Интеграл по поверхности, заданной явно.
Вычислить интеграл
по поверхности тела.
Поверхность интегрирования состоит из двух частей: части плоскости
, которую обозначим
и поверхности
, заданной
уравнением. Эта поверхность представляет собой верхнюю половину конуса второго порядка. Проекция той её части,
по которой проводится интегрирование, на плоскостьпредставляет собой круг, ограниченный окружностью
.
Запишем элемент поверхности:
.
Таким образом, поверхностный интеграл сводится к следующему двойному:
где— круг
. Такой интеграл проще всего вычислять в полярных координатах:
.
Теперь интегрируем по плоскости
. Это совсем простое интегрирование, так как поверхностный интеграл сразу превращается
в двойной без каких-либо дополнительных вычислений. Он будет отличаться только множителемот только что вычисленного.
Окончательный ответ получается суммированием двух вычисленных интегралов:
.
Пример 7. Интеграл по сфере.
Вычислить интеграл
по верхней полусфере.
Можно выразить явно, например, аппликату из уравнения сферы и проводить вычисления дальше, но при интегрировании по сфере удобно использовать
сферические координаты. Тем более элемент поверхности сферы в этом случае хорошо известен:
.
Осталось только выполнить замену в подынтегральной функции:
.
Пример 7. Интеграл по параметрически заданной поверхности.
Вычислить интеграл
по части поверхности геликоида, отвечающей границам изменения параметров
.
Поверхность интегрирования задана параметрически, поэтому для написания элемента поверхности нужно предварительно вычислить три якобиана:
.
Таким образом, элемент поверхности
.
Следовательно, поверхностный интеграл сводится к следующему двойному:
.
Детали вычисления определённого интеграла здесь опущены: они не имеют отношения к теме. Тем более, сам интеграл достаточно простой.
Поделиться этой страницей

Рабчук Александр Викторович1, Самигуллина Ракия Гареевна2
1Уфимский государственный авиационный технический университет, к.т.н.. доцент кафедры математики
2Уфимский государственный авиационный технический университет, старший преподаватель каф. математики
Аннотация
Традиционно, такие разделы высшей математики как криволинейные и поверхностные интегралы, особенно их применение, вызывают затруднения у студентов при изучении. Поэтому в данной статье кратко дана теория и приведено много разобранных примеров взятых из различных источников, в частности из [1,2,3].
Rabchuk Aleksandr Viktorovich1, Samigullina Rakiya Gareevna2
1Ufa State Aviation Technical University, PhD in Technical Science, Assistant Professor of the Mathematic Department
2Ufa State Aviation Technical University, Senior teacher of the Mathematic Department
Abstract
By tradition, devides higher mathematics by contour and surface integrals ,particularly application, is difficult by students.Therefor in this article give theori and many look into examples from [1,2,3].
Библиографическая ссылка на статью:
Рабчук А.В., Самигуллина Р.Г. Приложения криволинейных интегралов. Часть 1 // Современная педагогика. 2014. № 10 [Электронный ресурс]. URL: https://pedagogika.snauka.ru/2014/10/2675 (дата обращения: 24.02.2023).
Приложения криволинейного интеграла первого рода
1. Если подынтегральная функция равна единиц, то криволинейный интеграл
равен длине S кривой L, т.е.
2. Пусть в плоскости Оху задана гладкая кривая L, на которой определена и непрерывна функция двух переменных z=f(x,y)≥0. Тогда можно построить цилиндрическую поверхность с направляющей L и образующей, параллельной оси Оz и заключенной между L и поверхностью z=f(x,y). Площадь этой цилиндрической поверхности можно вычислить по формуле
3. Если L=AB – материальная кривая с плотностью, равной ρ=ρ(х,у), то масса этой кривой вычисляется по формуле
(физический смысл криволинейного интеграла первого рода).
4. Статистические моменты материальной кривой L относительно координатных осей Ох и Оу соответственно равны
где ρ(х,у) – плотность распределения кривой L а
— координаты центра тяжести (центра масс) кривой L.
5. Интегралы
выражают моменты инерции кривой L с линейной плотностью ρ(х,у) относительно осей Ох, Оу и начала координат соответственно.
ПРИМЕРЫ:1. Вычислить криволинейный интеграл
где L – дуга параболы у2 = 2х, заключенная между точками (2, 2) и (8, 4).
Найдем дифференциал дуги dl для кривой
. Имеем
Следовательно, данный интеграл равен
Ответ:
2. Вычислить криволинейный интеграл
где L – контур треугольника АВО с вершинами А(1,0), В(0,1), О(0,0)
Поскольку
то остается вычислить криволинейный интеграл по каждому из отрезков АВ, ВО и ОА :
1) (АВ): так как уравнение прямой АВ имеет вид у=1 – х, то . Отсюда, учитывая, что х меняется от 0 до 1, получим
2) (ВО): рассуждая аналогично, находим х=0, 0 ≤ у ≤ 1, откуда
3) (ОА):
.
4) Окончательно
Ответ:
3. Вычислить криволинейный интеграл
где L – окружность
Введем полярные координаты
Тогда, поскольку
уравнение окружности примет вид
т.е.
а дифференциал дуги
При этом Следовательно,
Ответ:
4. Вычислить криволинейный интеграл первого рода от функции с тремя переменными
где L – дуга кривой, заданной параметрически
Перейдем в подынтегральном выражении к переменной t. Имеем для подынтегральной функции:
Теперь выразим через t дифференциал dl:
Таким образом,
Ответ:
5. Вычислить площадь части боковой поверхности кругового цилиндра , ограниченной снизу плоскостью Оху, а сверху поверхностью
Искомая площадь вычисляется по формуле
где L – окружность x2+y2=R2. Поверхность цилиндра и поверхность симметричны относительно координатных плоскостей Оxz и Oyz, поэтому можно ограничиться вычислением интеграла при условиях у≥0, х≥0, т.е. вычислить четверть искомой площади и результат умножить на 4. Имеем
Следовательно,
Получили определенный интеграл, который берем подстановкой
откуда
Ответ:
6. Найти массу четверти эллипса
расположенной в первой четверти, если линейная плотность в каждой точке пропорциональна ординате этой точки с коэффициентом k.
Поскольку р(х, у)=ky, имеем
L – четверть эллипса
Переходим к параметрическим координатам эллипса Напомним, что
— фокусное расстояние эллипса, а
— эксцентриситет эллипса. Находим
Переходим к вычислению массы
Воспользуемся формулой
где Получаем
Учитывая, что 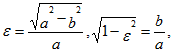
Ответ: .gif)
7. Найти координаты центра тяжести дуги окружности x2+y2=R2(0≤ x ≤R, 0≤ y ≤R).
Так как по условию задана четверть дуги окружности, то ее длина
В силу того, что биссектриса I координатного угла является осью симметрии, имеем
. Теперь находим
Ответ:
Приложения криволинейного интеграла второго рода
Интеграл
можно представить в виде скалярного произведения векторов F=Pi+Qi и ds=idx+jdy:
В таком случае
Выражает работу переменной силы F=Pi+Qj при перемещении материальной точки М=М(х,у) вдоль кривой L=AB от точки А до точки В.
При А=В кривая L замкнута, а соответствующий криволинейный интеграл по замкнутой кривой обозначается так:
В этом случае направление обхода контура иногда поясняется стрелкой на кружке, расположенном на знаке интеграла.
Предположим, что в плоскости Оху имеется односвязная область D (это значит, что в ней нет «дыр»), ограниченная кривой , (
— обозначение границы области D), а в области D и на ее границе
функции Р(х,у) и Q(х,у) непрерывны вместе со своими частными производными.
Теорема: Пусть А и В – произвольные точки области D, AmB и AnB – два произвольных пути (гладкие кривые), соединяющие эти точки (рис. 2).
Тогда следующие условия равносильны:
1. (условие Грина).
2. (криволинейный интеграл не зависит от пути интегрирования).
3. (интеграл по любому замкнутому пути равен нулю).
4. (выражение
представляет собой полный дифференциал некоторой функции
).
В случае выполнения любого из равносильных условий предыдущей теоремы криволинейный интеграл по любой кривой, соединяющей точки (хо, уо) и (х1, у1) из области D, можно вычислить при помощи формулы Ньютона-Лейбница
где U(x, y) – некоторая первообразная для P dx + Q dy.
С другой стороны, первообразная U(x, y) выражения P dx + Q dy может быть найдена при помощи криволинейного интеграла
В этих же условиях на функции Р(х,у) и Q(х,у), а также на область D, имеет место формула Грина, позволяющая свести криволинейный интеграл по замкнутому контуру к двойному интегралу
Здесь предполагается, что обход границы области D в криволинейном интеграле
совершается в положительном направлении, т.е. при таком обходе границы область D остается слева; для односвязной области это направление совпадает с направлением против часовой стрелки.
Заметим, что площадь S=S(D) области D может быть вычислена при помощи криволинейного интеграла второговрода:
(эта формула получается из формулы Грина с ).
ПРИМЕРЫ:1. Даны функции Р(х ,у) = 8х+4у+2, Q(х ,у) = 8у+2 и точки А(3, 6), В(3,0), С(0,6). Вычислить криволинейный интеграл
где:
1) L – отрезок ОА;
2) L – ломаная ОВА;
3) L – ломаная ОСА;
4) L – парабола, симметричная относительно оси Оу и проходящая через точки О и А;
5) проверить выполнимость условия Грина.
1) Отрезок ОА может быть записан в виде: у=2х, . Тогда dy=2dx и
2) Используем свойство аддитивности, вычисляя отдельно интеграл по отрезкам ОВ и ВА. Тогда:
а) ОВ: здесь у=0, 0≤х≤3, т.е. dy=0, откуда
б) ВА: х=3, 0≤у≤6, т.е. dx=0, и
Таким образом,
3) Этот интеграл вычислим аналогично предыдущему.
а) ОС: х=0, (т.е. dx=0), 0≤y≤6, откуда
б) СА: 0≤х≤3 , у=6, dy=0, следовательно,
Окончательно
4) Подставив координаты точки А(3;6) в равенство у=ах2 найдем уравнение данной параболы . При этом 0≤х≤3 и
откуда (путь ОА по параболе обозначим
)
5) Имеем
т.е. условие Грина не выполняется. Этот факт, а также вычисления в пунктах 1) – 4) этой задачи показывают, что данный криволинейный интеграл второго рода зависит от пути интегрирования.
2. Вычислить интеграл
где L – верхняя половина эллипса .gif)
Воспользуемся параметрическими уравнениями эллипса: х=a cost, y=b sin t,
т.е. dx = – a sin t dt, dy = b cos t dt. Подставляя в интеграл и учитывая направление обхода (откуда следует, что t меняется от π до 0), получаем
.gif)
3. Вычислить криволинейный интеграл
где L – отрезок, соединяющий точку С(2, 3, -1) с точкой D(3, -2, 0).
Составим параметрические уравнения отрезка СD, используя уравнения прямой, проходящей через две точки:
Отсюда . Далее, находим
подставляем все нужные выражения в данный интеграл, обозначенный через J, и вычисляем определенный интеграл:
Ответ:
4. Вычислить где К – отрезок прямой от А(0 ;0) до В (4; 3).
Уравнение прямой АВ имеет вид у=(3; 4)х. Находим у/= ¾ и, следовательно,
Ответ:
5. Вычислить если
Найдем
Тогда
Ответ:
6. Найти массу М дуги кривой x=t, y=t2/2, z=t3/3 (0≤ t ≤1), линейная плотность которой меняется по закону
Ответ:
7. Вычислить криволинейный интеграл от точки А(1, 0) до точки В(0, 2) (рис. 3):
1) по прямой 2х+у=2;
2) по дуге параболы 4х+у2=4;
3) по дуге эллипса x=cost, y=2sint.
1) Пользуясь данным уравнением линии интегрирования, преобразуем криволинейный интеграл в обыкновенный определенный интеграл с переменной х, затем вычисляем его:
у=2-2х, dy=-2dx,
2) Здесь удобно преобразовать криволинейный интеграл в обыкновенный интеграл с переменной у:
3) Преобразуем данный интеграл в обыкновенный с переменной t, затем вычисляем его: x=cost, dx=-sintdt; y=2sint; dy=2costdt:
Ответ: I1=1, I2=-1/5, I3=4/3.
8. Вычислить криволинейный интеграл между точками Е
(-1, 0) и Н (0, 1):
1) по прямой ЕН;
2) по дуге астроиды х=cos3t, y=sin3t.
1) Вначале составляем уравнение линии интегрирования – прямой ЕН, как уравнение прямой, проходящей через две известные точки: у-х=1.
Пользуясь этим уравнением и известной формулой для дифференциала дуги плоской кривой преобразуем данный криволинейный интеграл в обыкновенный интеграл с переменной х и вычисляем его:
2) Преобразуем данный интеграл в обыкновенный с переменной t, затем вычисляем:
ибо π/2≤ t ≤π;
Ответ:
9. Даны точки А(3, -6, 0) и В(-2, 4, 5). Вычислить криволинейный интеграл
1) по прямолинейному отрезку ОВ;
2) по дуге АВ окружности, заданной уравнениями x2+y2+z2=45, 2x+y=0.
1) Вначале составляем уравнения линии интегрирования – прямой ОВ.
Пользуясь общими уравнениями прямой, проходящей через две точки .gif)
Приравнивая эти равные отношения параметру t, преобразуем полученные канонические уравнения прямой ОВ к параметрическому виду: x=-2t, y=4t, z=5t.
Далее, пользуясь этими уравнениями, преобразуем данный криволинейный интеграл в обыкновенный интеграл с переменной t, затем вычисляем его
2) Преобразуем данные уравнения окружности к параметрическому виду. Полагая х=t, получим у=-2t (из второго данного уравнения), (из первого уравнения). Отсюда
.gif)
Ответ:
10. Вычислить криволинейные интегралы:
1)
2) вдоль периметра треугольника с
вершинами А(-1,0), В (0,2) и С (2,0)
Составив уравнение прямой АВ, у-2х=2, и исходя из этого уравнения, преобразуем криволинейный интеграл на отрезке АВ в обыкновенный интеграл с переменной х:
у=2х+2, dy=2dx,
Аналогичным путем вычисляя криволинейный интеграл на отрезках ВС и СА, получим
х=2-у, dx=-dy,
Следовательно,
2) Здесь подынтегральное выражение есть полный дифференциал функции двух переменных, ибо (уcosx)’y =(sinx)’x =cosx. Вследствии этого данный криволинейный интеграл, взятый по периметру данного треугольника равен нулю. Он будет равен нулю и по любому другому замкнутому контуру.
Ответ:
11. Найти длину кардиоиды x=2acost-acos2t, y=2asint-asin2t.
Применяем формулу
, исходя из данных параметрических уравнений кардиоиды и формулы для дифференциала дуги плоской кривой, преобразуем криволинейный интеграл формулы в обыкновенный интеграл с переменной t.
Ответ: L=16a.
12. Найти площадь, ограниченную замкнутой кривой:
1) эллипсом x=a cost, y=b sint;
2) петлей декартова листа х3+у3-3аху=0.
1) Применяем формулу
, исходя из данных параметрических уравнений эллипса, преобразуем криволинейный интеграл в обыкновенный интеграл с переменной t и вычисляем его:
2) Вначале преобразуем данное уравнение к параметрическому виду. Полагая у=хt, получим
Геометрический параметр t=y/x есть угловой коэффициент полярного радиуса ОМ (рис. 6), точка М(х, у) опишет всю петлю кривой при изменении t от 0 до +∞.
Преобразуя криволинейный интеграл формулы в обыкновенный интеграл с переменной t , получим
Ответ: S=3a2/2.
13. Найти массу дуги АВ кривой у=lnx, если в каждой ее точке линейная плотность пропорциональна квадрату абсциссы точки: хА=1, хВ=3.
Применяем формулу
, исходя из данного уравнения кривой, преобразуем криволинейный интеграл в обыкновенный с переменной х
Ответ:
14. Найти координаты центра тяжести дуги АВ винтовой линии х=аcost, y=asint, z=bt, если в каждой ее точке линейная плотность пропорциональна аппликате этой точки: tA=0, tB=π.
Применяя формулы
.gif)
Следовательно,
Ответ:
15. Вычислить работу, совершаемую силой тяжести при перемещении точки массы m по дуге АВ некоторой кривой.
Если выбрать прямоугольную систему координат так, чтобы направление оси Оz совпало с направлением силы тяжести, то действующая на точку сила
а ее проекции на оси координат Fx=P=O, Fy=Q=0, Fz=R=mg.
Искомая работа согласно формуле
Она зависит только от разности аппликат начала и конца пути, но не зависит от формы пути.
16. Найти работу силового поля, в каждой точке (х,у) которого напряжение (сила, действующая на единицу массы) , когда точка массы m описывает окружность x=accost, y=asint, двигаясь по ходу часовой стрелки.
Подставляя в формулу
проекции силы
действующей на точку: Fx=m(x+y), Fy= – mx, и преобразуя криволинейный интеграл в обыкновенный с переменной t, получим
Ответ: Е=2πma2.
Библиографический список
- Лунгу К.Н. Сборник задач по высшей математике. 1 курс – 7-е изд., – М.: Айрис-пресс, 2008.
- Лунгу К.Н. Сборник задач по высшей математике. 2 курс – 5-е изд., – М.: Айрис-пресс, 2007.
- Письменный Д.Т. Конспект лекций по высшей математике: полный курс – 7-е изд. – М.: Айрис-пресс, 2008.
Все статьи автора «Рабчук Александр Викторович»
Соберем в одном месте все формулы.
Масса [math]m[/math] гладкой кривой[math]L[/math], линейная плотность которой вдоль кривой [math]L[/math] равна [math]gamma(x,y,z)[/math], выражается криволинейным интегралом первого рода:
[math]m=int_{L}gamma(x,y,z);dl[/math]
Криволинейный интеграл равен обычному и совсем не опасному интегралу функции одной переменной 
* Если кривая задана параметрическими уравнениями [math]x=x(t), y=y(t), z=z(t),hspace{2mm}tin[alpha,beta][/math], то
[math]m=int_{alpha}^{beta}gamma(x(t),y(t),z(t))sqrt{x'(t)^2+y'(t)^2+z'(t)^2)};dthspace{10mm}(1)[/math]
* Если кривая лежит в плоскости [math]Oxy[/math], то [math]z(t)=0[/math] и получаем
[math]m=int_{alpha}^{beta}gamma(x(t),y(t))sqrt{x'(t)^2+y'(t)^2};dthspace{37mm}(2)[/math]
В частности, для плоской кривой, заданной уравнением [math]y=f(x), xin[a,b][/math] имеем
[math]m=int_{a}^{b}gamma(x,f(x))sqrt{1+f'(x)^2};dxhspace{47mm}(3)[/math]
* Если плоская кривая задана уравнением [math]rho=rho(phi}), hspace{3mm}phiin[alpha,beta][/math] в полярных координатах, то
[math]m=int_{alpha}^{beta}gamma(rhocosphi,rhosinphi)sqrt{rho^2+rho ‘^2};dphihspace{45mm}(4)[/math]
————————————————————————
В данной задаче надо применить формулу (3):
[math]gamma(x,y)=frac{2sqrt x-y}{sqrt{1+frac{1}{x}}},hspace{3mm}y=f(x)=2sqrt x-1, hspace{3mm}xin [0,4][/math]
[math]gamma(x,f(x))=frac{2sqrt x -(2sqrt x-1)}{sqrt{1+frac{1}{x}}}=frac{1}{{sqrt{1+frac{1}{x}}}[/math]
Так как
[math]f'(x)=frac{1}{sqrt x}[/math]
то
[math]sqrt{1+f'(x)^2}=sqrt{1+frac{1}{x}}[/math]
И получаем миленький интегральчик.



![[IMG]](http://corum.mephist.ru/tex/images/d708fe9bd92455e2a57581b34c85ef2e.gif) , определённую на кривой
, определённую на кривой ![[IMG]](http://corum.mephist.ru/tex/images/934cf4f6e8d65e941a602d24451533b6.gif) . Кривая предполагается спрямляемой. Напомним, что это означает, грубо говоря,
. Кривая предполагается спрямляемой. Напомним, что это означает, грубо говоря, ![[IMG]](http://corum.mephist.ru/tex/images/9cdbb5c9434771f4a28950a14b15d110.gif) и на каждой из дуг выбирается точка
и на каждой из дуг выбирается точка ![[IMG]](http://corum.mephist.ru/tex/images/cc8571bfde88bee994c211ef0fab3ef1.gif) . Составляется произведение
. Составляется произведение ![[IMG]](http://corum.mephist.ru/tex/images/1bdcc2035d794ee99803a476e06aaf71.gif) ,
,![[IMG]](http://corum.mephist.ru/tex/images/02b616a78fa57125e2fc9cffd3dde6e4.gif) . Затем осуществляется предельный переход с устремлением длины наибольшей
. Затем осуществляется предельный переход с устремлением длины наибольшей ![[IMG]](http://corum.mephist.ru/tex/images/cfc6b5947d3ee0288c456ad5fc5b0f63.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/f5fe53c3cd870f5deb8d4663485bd888.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/20c08b85a1d0a48a17a99f4d187a66a6.gif) . Поверхность разбивается на частичные области
. Поверхность разбивается на частичные области![[IMG]](http://corum.mephist.ru/tex/images/361b4dfbf3dfd90086cd1a49bb5509f1.gif) , в каждой такой области выбирается точка
, в каждой такой области выбирается точка ![[IMG]](http://corum.mephist.ru/tex/images/17eca1b92215dd8d05c9e946e1d21093.gif) , проводится суммирование
, проводится суммирование ![[IMG]](http://corum.mephist.ru/tex/images/b2408929574afd7e0d4512b907d16a64.gif) . Затем осуществляется предельный переход с устремлением диаметра наибольшей из всех частичных
. Затем осуществляется предельный переход с устремлением диаметра наибольшей из всех частичных ![[IMG]](http://corum.mephist.ru/tex/images/48c6e1ea0998d82f056f69aea759f333.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/910feb00094b33b5c70f55732b64f7ea.gif) кривой, вдоль которой проводится интегрирование.
кривой, вдоль которой проводится интегрирование.![[IMG]](http://corum.mephist.ru/tex/images/65f2257743b186eba8f198eccaf17074.gif) . В этом случае дифференциал дуги
. В этом случае дифференциал дуги![[IMG]](http://corum.mephist.ru/tex/images/3ccfd9f2940b212c66d70a711ba307d2.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/36a4dc9ccf2bdc09d800556724231fc6.gif) , и интеграл принимает вид
, и интеграл принимает вид![[IMG]](http://corum.mephist.ru/tex/images/97748655662d9563cb091e0ac7c7e8ab.gif) ,
,![[IMG]](http://corum.mephist.ru/tex/images/051f64bba458bf213f344c609f8ad9d8.gif) отвечает изменению переменной
отвечает изменению переменной ![[IMG]](http://corum.mephist.ru/tex/images/8725029ea89712eed8670bae64d30e47.gif) вдоль той части кривой, по которой проводится интегрирование.
вдоль той части кривой, по которой проводится интегрирование.![[IMG]](http://corum.mephist.ru/tex/images/0cf0014ae2c86e53fe2fd425ca0927bb.gif) . Тогда дифференциал дуги
. Тогда дифференциал дуги![[IMG]](http://corum.mephist.ru/tex/images/202e96d729d206de85ed83fa653e235d.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/7a92e446f396c0e1490861e42d2d5f77.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/3583b4ba497a8d2d21cffd9121814915.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/81f4e038cd323d83fe5af63a43709bea.gif) и т.д.
и т.д.![[IMG]](http://corum.mephist.ru/tex/images/841f924066c2337faa5ffe327a813e3b.gif) ,
,![[IMG]](http://corum.mephist.ru/tex/images/ded0bd74d590c3c19e6a319bf4e3342d.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/7bb6e7c7c9dfb62cdb3fd3b6fc28ef4a.gif) :
:![[IMG]](http://corum.mephist.ru/tex/images/ef99a684c9ed2755a762be3174ad674f.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/4bdb814cebea42f863a8d4aa76f719cf.gif) .
.![[IMG]](http://corum.mephist.ru/uploads/1369078311/gallery_20527_327_1233.png)
![[IMG]](http://corum.mephist.ru/tex/images/00eb9bd68968c6307f3bae47be1a311c.gif) ,
,![[IMG]](http://corum.mephist.ru/tex/images/c4965dbfa81791d0b69401c909817a07.gif) . Тогда
. Тогда![[IMG]](http://corum.mephist.ru/tex/images/a2081d0e16d7b7f2e5d88e080c2d78f3.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/4905e0dbcfb6f4f457b3603a9dc6b8d5.gif) ,
,![[IMG]](http://corum.mephist.ru/tex/images/3e41496c50f64ea502eb85888ab10489.gif) — область плоскости
— область плоскости ![[IMG]](http://corum.mephist.ru/tex/images/e2b5ec14765636839baff231db9fc100.gif) , в которую проектируется часть поверхности, по которой проводится интегрирование.
, в которую проектируется часть поверхности, по которой проводится интегрирование.![[IMG]](http://corum.mephist.ru/tex/images/a5d42e7598b26856eb7ca23f37465124.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/245f2a8e04a4a6b43f54e66236a382fe.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/4d9a7b1043df8caf038b4bd5c9882e46.gif) ,
,![[IMG]](http://corum.mephist.ru/tex/images/70007ddb70e7b9cd05fdb7cf0b5d85c7.gif) — область изменения параметров, соответствующая части поверхности
— область изменения параметров, соответствующая части поверхности ![[IMG]](http://corum.mephist.ru/tex/images/3ef4b80e145a013a7a8307f3a586a513.gif) . Найдём массу этой кривой. Разобьём кривую на множество малых элементов,
. Найдём массу этой кривой. Разобьём кривую на множество малых элементов, ![[IMG]](http://corum.mephist.ru/tex/images/25899cf2f842038f09e4103d1283bf47.gif) , где
, где ![[IMG]](http://corum.mephist.ru/tex/images/2c8472de48a92ef8fe91e28f619ad8e0.gif) — любая точка выбранного кусочка кривой (любая, так как плотность в пределах
— любая точка выбранного кусочка кривой (любая, так как плотность в пределах![[IMG]](http://corum.mephist.ru/tex/images/03e32161262d228c5ceaccbd5e8cb3a6.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/0d575cdfce74650dbf3f174ae3994905.gif)
![[IMG]](http://corum.mephist.ru/tex/images/c796c3151b0789d7960db74831ed807e.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/66b1863cd30a3346e1f4ba4066aa5eec.gif) . Тогда
. Тогда![[IMG]](http://corum.mephist.ru/tex/images/170ac80d3f6ba8244a0dc2c086647f76.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/7203c4d5ce12b37efc7e9652802ce068.gif)
![[IMG]](http://corum.mephist.ru/tex/images/1ea9a9a3bccbab245dd7c5c951c994ae.gif) и
и ![[IMG]](http://corum.mephist.ru/tex/images/3c3eb7fc9c4ed916bffac9ac6edf39cd.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/8c11a59d8a2d4149d2034094064f87c7.gif) . Найдём выражение для
. Найдём выражение для ![[IMG]](http://corum.mephist.ru/tex/images/bfe99f1804f139448849b7118e66eba2.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/1a1481d9a4450c5023a641460c952a0c.gif)
![[IMG]](http://corum.mephist.ru/tex/images/89db8118e3cdaed40ae4672fb859e3e7.gif)
![[IMG]](http://corum.mephist.ru/tex/images/0082013e719186581a80aa72b2215e8d.gif) от точки
от точки ![[IMG]](http://corum.mephist.ru/tex/images/845acbba436b6d52d8ddb3984a78bfc3.gif) до точки
до точки ![[IMG]](http://corum.mephist.ru/tex/images/26e89827b1ed339307508e650d5ea2ed.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/b8921ca1d75b852da96e95cda4aafeb8.gif) и
и ![[IMG]](http://corum.mephist.ru/tex/images/de80133e771f3ffb043b3ca894db2ccb.gif) позволяют выразить переменную
позволяют выразить переменную ![[IMG]](http://corum.mephist.ru/tex/images/f1f0350d0a6cc83ecff692a18ddc9b14.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/a51bbc88b7ff1ae67b9d881789b69faf.gif)
![[IMG]](http://corum.mephist.ru/tex/images/33bfe407f38888c96967eb75cae2e4aa.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/c09d2f2bd4891f0741c463814d9ceed6.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/a81ac755b9ea37ece78ca2bc23162c66.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/cdf3ba2b23d0d5b958ba92d04a96cf85.gif)
![[IMG]](http://corum.mephist.ru/tex/images/a4539aae9d269d63817a647a3f7bde25.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/d3173ffecd84ec102a21fbcb42a11add.gif) . Верхней полуокружности
. Верхней полуокружности![[IMG]](http://corum.mephist.ru/tex/images/453a6940f7ae43dc2796bc35abce28d4.gif) . Вычислим дифференциал дуги:
. Вычислим дифференциал дуги:![[IMG]](http://corum.mephist.ru/tex/images/adc00549cc0e2d7b28ceda257f6471df.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/2d87778d4d5f6f966dbb28fd7d8d1141.gif)
![[IMG]](http://corum.mephist.ru/tex/images/afbe2fc09cde2459069b6bfe282eea20.gif)
![[IMG]](http://corum.mephist.ru/tex/images/ab388d390aa714fdd57c6e2edacc3ebc.gif) .
.![[IMG]](http://corum.mephist.ru/uploads/1369078311/gallery_20527_327_1495.png)
![[IMG]](http://corum.mephist.ru/tex/images/51389c1a35d74bdb054e4b911442cbff.gif) :
:![[IMG]](http://corum.mephist.ru/tex/images/76f5c3b0b14937891f25348ad519d1e7.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/38094d18c1e0b2e071de9918232f091f.gif) , а потому
, а потому![[IMG]](http://corum.mephist.ru/tex/images/392e23837a24046fa43dd47eb39dd805.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/24d02fd2ccfac3575f83d34c0634c483.gif)
![[IMG]](http://corum.mephist.ru/tex/images/1bb75210192c79feabec7def5a25dfd6.gif)
![[IMG]](http://corum.mephist.ru/tex/images/fdf06af6bec6527e2d02a2d5966f11ee.gif) , соответствующего пределам изменения параметра
, соответствующего пределам изменения параметра ![[IMG]](http://corum.mephist.ru/tex/images/0fdad617b5f6227e089bf336792a4827.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/bc27693fc73856df297868756b5cf36f.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/1fd8f2cc814768c19f5466bc0de2e4c3.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/5160407bb73f1d47311efc536f4abf29.gif)
![[IMG]](http://corum.mephist.ru/tex/images/2b45161854c9e8e29e591d9cb53fb175.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/1509fe9b0302d871413424ae4a96c70a.gif) , которую обозначим
, которую обозначим ![[IMG]](http://corum.mephist.ru/tex/images/8e1755de529d9befeb1dc8eec5249f6e.gif) и поверхности
и поверхности ![[IMG]](http://corum.mephist.ru/tex/images/c326e4cfb793e1c2ef009be5bc6b1e6d.gif) , заданной
, заданной ![[IMG]](http://corum.mephist.ru/tex/images/34a4fd0bd897d2b1ce3d563a24638b7b.gif) . Эта поверхность представляет собой верхнюю половину конуса второго порядка. Проекция той её части,
. Эта поверхность представляет собой верхнюю половину конуса второго порядка. Проекция той её части, ![[IMG]](http://corum.mephist.ru/tex/images/4f73b6537fad5f21a34d0a01b977125c.gif) .
. ![[IMG]](http://corum.mephist.ru/tex/images/b99516ab3bb3393d0259775c876b3bb0.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/0a91cdfea6b44d3f5eea1815b2873d00.gif)
![[IMG]](http://corum.mephist.ru/tex/images/a34f765aa6c921ca3910b08c285e6367.gif) . Такой интеграл проще всего вычислять в полярных координатах:
. Такой интеграл проще всего вычислять в полярных координатах:![[IMG]](http://corum.mephist.ru/tex/images/e6776b8c7b7b9ed10bee90e6a8e7702e.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/60fc0ee50857029f56d99b512a03b28a.gif) от только что вычисленного.
от только что вычисленного.![[IMG]](http://corum.mephist.ru/tex/images/a2d28c197c2ad7f94cb2ca5a03708eb9.gif)
![[IMG]](http://corum.mephist.ru/tex/images/1009549fbffc334f9297d5403bd79132.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/faef6e7d0fe6e2ce24d3936204bc9ddd.gif)
![[IMG]](http://corum.mephist.ru/tex/images/e6a0be5acf8d5f624bef274834d579bd.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/fe876091faf081e8fee988a2c97a3d1f.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/51e8254fbff728e4c906f185e49f17bf.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/8a4f27dcfcb433394ae5d81e1230b7fd.gif)
![[IMG]](http://corum.mephist.ru/tex/images/dfe53a0d1c6e486a852b44a7c129ab64.gif) , отвечающей границам изменения параметров
, отвечающей границам изменения параметров ![[IMG]](http://corum.mephist.ru/tex/images/01aaa8def43795ba016ef6a78a9a0006.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/cc858a4926989625b6c145e358863250.gif)
![[IMG]](http://corum.mephist.ru/tex/images/175b33533f03600e1e88bad91395c38a.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/b2bb57267bd10ddb8d87df2ffb784d7a.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/7e94b21bc364c49c9c650450f1850fa6.gif) .
..gif)
.gif)
.gif)
.gif)
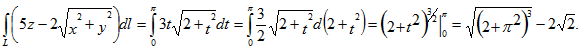
.gif)
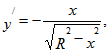
.gif)
.gif)
.gif)
.gif)
.gif)
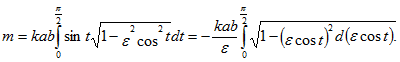
.gif)
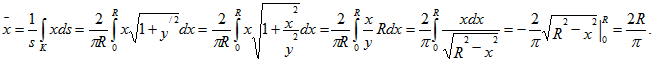
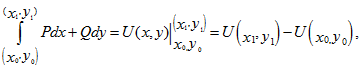
.gif)
.gif)
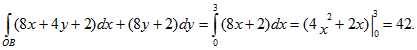
.gif)

.gif)
.gif)
.gif)
.gif)
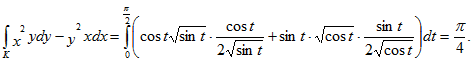
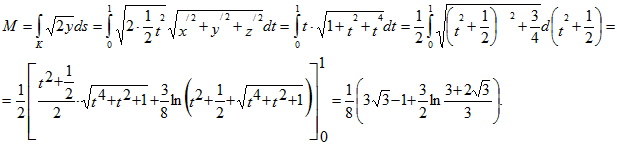
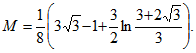
.gif)
.gif)

.gif)
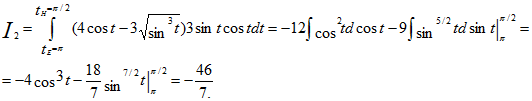
.gif)

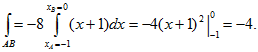
.gif)
.gif)
.gif)
.gif)

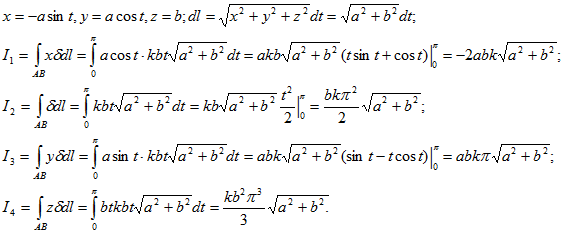
.gif)
